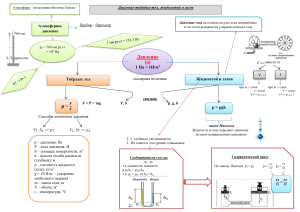
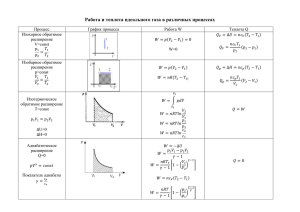
Автомат перекоса Рулевые устройства Состав атмосферы Изменение температуры с высотой Изменение скорости звука Ускорение хоккейной шайбы под действием силы Второй закон Ньютона Третий закон Ньютона Вязкость воздуха Сила трения о воздух Сжимаемость Трубка тока Трубка тока Уравнение Бернулли Уравнение Бернулли Способ измерения воздушной скорости Обтекание профиля Распределение давления по профилю Обтекание профиля Результирующая аэродинамическая сила Изменение R для симметричного и несимметричного профилей Основные координатные оси и составляющие результирующей аэродинамической силы Аэродинамическая сила 2 ρV /2 R = CR S 2 X = Cх S ρV /2 2 Y = Cy S ρV /2 Типовой профиль лопасти Элемент лопасти Распределение давления на профиле Обратный ток воздуха Образование вихрей Образование вихрей Волновое сопротивление Х=Хд+Хтр+Хинд+Хв Сопротивление Поляра профиля R D Fом R2 r r r R Угол установки лопасти Геометрическая крутка Изменение геометрической крутки лопасти по ее радиусу Коэффициент заполнения F Fлi ом Угол атаки несущего винта Угол азимутального положения лопасти Угол азимутального положения лопасти Характеристика режима работы НВ Vн cos н . н R Осевое обтекание Схематизация физической картины работы винта на режиме висения Т=mVот где m – секундная масса отбрасываемого воздуха, определяемая с помощью соотношения m= Vот Fстр= Vi Fом= ViR2. Здесь Fстр площадь поперечного сечения струи. Секундная мощность движущейся струи mVот TVот N . 2 2 Мощность затрачиваемая винтом на проталкивание воздуха Ni=TVi N=Ni или TVi = TVот и тогда 2 Vот=2Vi 2 2 2 Подставляя значения m и Vот получим T=R ViVот=2R Vi T 2 R 2 (Vi V y )Vi . Косое обтекание Схематизация физической картины работы винта на режиме косого обтекания Vн V1 Vi Элемент лопасти на висении Элемент лопасти в наборе Н Элемент лопасти на снижении Осевое обтекание V=0 υ P=атм + υ 2 Эпюра индуктивных скоростей Эпюра давления Идеальный и реальный НВ Эффективная площадь Влияние скорости и угла атаки н=15 Vi н=0 н=-15 0 Vн Составляющие сил в полусвязанной и скоростной системах координат Составляющие сил в полусвязанной и скоростной системах координат • Н - продольная сила; • Т - сила тяги; • S - поперечная сила. • Тх – пропульсивная сила; • Ту – подъемная сила; • Тz – боковая сила. Зависимость нормальной составляющей скорости от радиуса лопасти и ее азимутального положения Изменение подъемной силы сечения лопасти в зависимости от ее радиуса и азимутального положения при жестком креплении лопастей К образованию изгибающего и опрокидывающего моментов на несущем винте Возникновение кориолисовых сил Схема сил при движении лопасти в плоскости вращения Завал конуса несущего винта при маховом движении лопастей л a0 a1cos л b1sin л . Устранение изгибающего и опрокидывающего моментов Vвзм . Vн cos нsin л н r Распределение углов атаки по диску несущего винта Компенсатор взмаха a = л k л . b Образование зоны обратного обтекания на лопасти НВ вертолета Изменение зон срыва в зависимости от скорости полета вертолета (VH2 > VH1) Руление Уравнение сил при прямолинейном движении без юза ∑Fx = Tx - Xв - Fтр1 - Fтр2 = m*dV/dt ∑ Fy = Ty - G + Nр1 + Nр2 = 0 ∑ Fz = Tz - Tрв ± Fтр = 0 Руление. Условие отсутствия крена на рулении Tрвhрв = Tzb Руление. Юз и опрокидывающий момент. Руление. Опрокидывающий момент. Рулевой винт. Висение. ∑Fx0 = Tx - Xв = 0 (условие Vx=const=0); ∑ Fy0 = Ty - G - Yв = 0 (условие Vy=const=0) ∑ Fz0 = Tz - Tрв = 0 (условие Vz=const=0) Висение. ∑ Mx1 = TнвaT + Mxгш - Трвhрв = 0 (условие γ =const); ∑ Мy1 = Mрнв - Трвlрв = 0 (условие Ψ =const) ∑ Mz1 = -ТнвхT + Mzгш+ Mррв= 0 (условие υ =const) Висение. С левым боковым ветром. Висение. С левым боковым ветром. Висение. С правым боковым ветром. Висение. С правым боковым ветром. Висение. С попутным ветром. Висение. С попутным ветром. Набор высоты. Условия продольной балансировки ∑Fx = Tx - Xв - GsinΘ = 0 (Vx=const); ∑Fy = Ty - GcosΘ - Yст = 0 (Θ=const) ∑Mz1 = -ТнвхT + Mzгш+ Mррв= 0 (υ=const) Набор высоты. Условия боковой балансировки ∑Fz = Tz - Tрв = 0 (Vz=0) ∑Mx1 = TнвaT + Mxгш - Трвhрв = 0 (γ =const); ∑Мy1 = Mрнв - Трвlрв = 0 (МК=const) Указательница набора высоты. Снижение. Условия продольной балансировки ∑Fx = Tx + Xв - GsinΘ = 0 (Vx=const); ∑Fy = Ty - GcosΘ - Yст = 0 (Θ=const) ∑Mz1 = -ТнвхT + Mzгш+ Mррв= 0 (υ=const) Условия боковой балансировки ∑Fz = Tz - Tрв = 0 (Vz=0) ∑Mx1 = TнвaT + Mxгш - Трвhрв = 0 (γ =const); ∑Мy1 = Mрнв - Трвlрв = 0 (МК=const) Мощности в наборе и на снижении ГП Условия продольной балансировки ∑Fx = Tx - Xв - GsinΘ = 0 (Vx=const); ∑Fy = Ty - GcosΘ - Yст = 0 (Θ=const) ∑Mz1 = -ТнвхT + Mzгш+ Mррв= 0 (υ=const) Условия боковой балансировки ∑Fz = Tz - Tрв = 0 (Vz=0) ∑Mx1 = TнвaT + Mxгш - Трвhрв = 0 (γ =const); ∑Мy1 = Mрнв - Трвlрв = 0 (МК=const) Индуктивная мощность Профильная мощность Мощность движения Суммарная мощность Располагаемая мощность Коэфициент использования мощности Тяга и мощность ГП Кривые Н.Е.Жуковского Влияние высоты полета на располагаемую и потребную мощности Влияние температуры наружного воздуха на располагаемую и потребную мощности Влияние полетной массы на располагаемую и потребную мощности Диапазон высот и скоростей полета Эксплуатационные ограничения и их физическая сущность •1. Ограничения по скорости. V макс доп.- на H>1000 – 1500м ограничена по причине срыва потока на лопастях несущего винта и как следствие, ухудшения управляемости, непреднамеренного выхода за ограничения. V макс доп. – на H<1000-1500м ограничена по причине появления значительных напряжений в забустерной части системы управления от действия шарнирных моментов на лопастях несущего винта. Эксплуатационные ограничения и их физическая сущность •2. Ограничения по перегрузкам. n max. доп. = 1.5 – ограничена прочностью конструкции вертолёта. n min. доп. = 0.6 – ограничена условиями работы гидросистемы. n x – ограничена при разгоне только величиной располагаемой мощности, а при торможении возможностью увеличения оборотов несущего винта более допустимых. n z =(0,15 – 0,2) n y – ограничена прочностью конструкции хвостовой части вертолёта. Эксплуатационные ограничения и их физическая сущность 3. Ограничения по крену max. доп. = 450 – ограничен максимально допустимой эксплуатационной перегрузкой. Эксплуатационные ограничения и их физическая сущность Максимально допустимые углы крена в зависимости от высоты полёта, градус При массе вертолёта При массе вертолёта Высота, м 11100кг и менее Более 11100 50 - 3000 300 200 Более 3000 150 150 Эксплуатационные ограничения и их физическая сущность •3. Ограничения по крену. Примечание: 1. Форсированные виражи и развороты на высотах 50 – 1000м при нормальной взлётной массе и менее на скоростях полёта 120 – 250км/ч разрешается выполнять с кренами до 450 . 2. На высотах до 50м над рельефом местности допускается угол крена, по величине равный высоте полёта, но не больше значения, указанного в таблице. Эксплуатационные ограничения и их физическая сущность •4. Ограничения по тангажу. Максимально допустимый угол тангажа равный + 200 ограничен на восходящих фигурах возможностью выхода за ограничения по минимально допустимой скорости, а на нисходящих фигурах возможностью выхода за ограничения по максимально допустимой скорости. Эксплуатационные ограничения и их физическая сущность 5. Ограничения по угловой скорости разворота. На висении угловая скорость разворота ограничена величиной 12 0/С в виду малого запаса путевого управления, с целью исключения возможности попадания в самопроизвольный разворот. Вираж Схема сил, действующих на вертолет при выполнении виража Вираж – это полет вертолета в горизонтальной плоскости по замкнутой окружности с постоянным креном и поступательной скоростью без скольжения. Вираж Ввод в вираж выполняется координированным отклонением РУ и педалей. При вводе в левый вираж вертолет имеет тенденцию к изменению угла тангажа на пикирование, а при вводе в правый – на кабрирование. За 15-200 до намеченного ориентира или заданного направления координированным отклонением РУ и педали в сторону, обратную вращению, начать вывод вертолета из разворота с таким расчетом, чтобы к моменту выхода вертолета на заданный ориентир крен был убран полностью. Форсированные виражи и развороты с креном до 450 разрешается выполнять как при постоянном значении ОШ НВ, так и с изменением его положения в процессе разворота. При скоростях ввода менее 200км/ч форсированный разворот выполнять при постоянном значении ОШ, а на скоростях ввода 200-250км/ч - как при постоянном значении ОШ, так и с уменьшением его на 2-50 по УШВ. По достижении скорости 100км/ч плавным отклонением РУ от себя прекратить дальнейшее уменьшение скорости. Вираж Характеристики правильного виража вертолета Спираль Схема выполнения спирали Спираль – маневр, сочетающий вираж с набором высоты или снижением, при выполнении которого вертолет движется по спиральной траектории. Основное назначение спирали – набор высоты или снижение в ограниченном пространстве. Установившаяся правильная спираль выполняется с постоянными значениями угла крена, поступательной и вертикальной скорости, без скольжения. При прочих равных условиях разворот в спирали осуществляется с меньшим радиусом и за меньшее время, чем в вираже, благодаря искривлению траектории маневра не только в горизонтальной, но и в вертикальной плоскостях. Спираль Зависимость вертикальной скорости от угла крена и скорости полета при выполнении спирали Схема сил на РСНВ Элемент лопасти на РСНВ Виды самовращения Демпфирование Демпфирование Боковая устойчивость вертолета Боковая устойчивость вертолета