уравнение прямой


Y
M(x,y)
y


O
Определение 1. Две взаимно перпендикулярные
пересекающиеся прямые – оси, с общим началом,
на каждой из которых выбрано положительное
направление и задан единичный отрезок образуют
декартовую систему координат Oxy. Эти оси
называют осями координат, точку пересечения О –
началом координат. Одну из осей называют осью
абцисс – ось OX, другую – осью ординат – ось OY.
x
X

Определение 2. Координатами точки М в системе
координат Oxy называются проекции этой точки на
оси координат, которые обозначаются x –
абсцисса и y – ордината. Координаты точки
записывают так M(x,y
Метод координат позволяет решать
геометрические задачи алгебраическими
методами. Геометрия, использующая при решении
задач такие методы, называется аналитической.

Рассмотрим две основные задачи на
метод координат (на плоскости).


Пусть даны две точки

Найти длину отрезка |AB|

Решение.

Рассмотрим ΔABC-прямоугольный.
|AС|=|x2

Y
Задача 1. Длина отрезка
 x1 | ; |BC|=| y2  y1 |
Тогда по теореме Пифагора длина
B
y2
A
y1
C
x1
x2
X
гипотенузы:
или расстояние d между двумя точками
определится по формуле:
(1)



Пример 1.
Даны точки А(4;3), В(16;-6). Найти
расстояние между ними.
Решение.
(1)
Применяя (1), находим длину отрезка АВ:
Ответ: d=15.


Задача 2-деление отрезка в данном
отношении 
1) Пусть теперь на отрезке AB
зафиксирована точка М ,
AM
Y

таким образом, что

Найдем координаты этой точки: M ( xM ; yM )
MB
2) По теореме Рамса:  



AM
MB

A1M 1
yM
M 1B1
y1
Поскольку проекции отрезка делятся
точками Хм и Ум в том же отношении, в
котором точка М делит отрезок AB , то
можно записать:
y M  y1
x M  x1


y2  yM
x2  xM
3) Из полученных соотношении
найдем Хм и Ум:
x  x
xM 
1
1 
2
B
y2
M
A
A1
x1
M1
xM
y1  y2
yM 
1 
B1
X
x2
(2)

Замечание 1. Если точка М – середина отрезка, то
  1 получим:
x1  x2
y1  y 2
xM 
уM 
2
2
из формул (2)

(3)
Замечание 2.
В формуле (2) важен порядок
точек, за координаты берут точку, с которой
начинается отношения, так за первую точку A x1 ; y1 
при AM  
MB
Замечание 3. Если точки заданы в пространстве,
то формулы (1), (2) примут вид:
d
x2  x1    y2  y1 
2
2
 ( z 2  z1 ) 2
zM 
z1  z 2
1 
ПРИМЕР 1. Даны точки А(-2; 4), В(2; -2).
Найти:
1) длину отрезка АВ; координаты точки, которая
делит отрезок в отношении;
2) середину АВ;
3) координаты точки, которая делит отрезок в
отношении AM  1
MB
2
4) Сделать чертеж.
Y
M
r

О
p
Х
1
Рисунок 3
Y
M
r
p
О
Определяя величину
1
X

следует установить (по знакам x и y) четверть. В которой лежит искомый
угол, и учитывать, что
    
5
Рисунок 4
(Рис.4)

ПРИМЕР 2. Построить точки в полярной
системе координат, найти координаты
точек в декартовой системе:
M 1 ( 2 ), M ( 3; 5 ), М (5;  )
2
3
3
3

В аналитической геометрий всякую линию
рассматривают как геометрическое место точек,
обладающих одним общим свойством.
Определение 1. Уравнением линии на плоскости
называется уравнение, которому удовлетворяют
координаты и любой точки данной линии и не
удовлетворяют координаты любой точки, не лежащей
на этой линии.
В общем виде уравнение линий записывается:
В неявном виде: F(x,y)=0,
например ;
x2  y2  9  0
В явном виде (переменная у выражается через х):
у=f(x), например
y  х2  9






Пример. Дано уравнение линий х-у-2=0
Лежат ли на этой линий точки: С(-1;1), М(1;-1),
В(2;2)
Решение. Подставим координаты точек в
уравнение линий:
Точка С(-1;1):  1  1  2  0  С  линий;
Точка М(1;-1): 1  1  2  0  М  линий;
Аналогично, получим точка В(2;2) не
принадлежит линий.
Замечание. Не всегда уравнение F(x,y)=0 может
определять какую- нибудь линию, например:
1) уравнение
x 2  y 2  1  0 не определяет
никакой линий;
2
2
2) уравнение x  y  0 определяет только одну
точку О(0;0).
1) Задача. Дана линия как геометрическое место точек.
Составить уравнение этой линий
Уравнение линий составляют по следующему плану
(четыре шага):
1) Возьмем любую текущую точку на линий
М(х; у);
2) Запишем общее свойство всех точек линий;
3) Входящие в это равенство отрезки, углы
выразить через текущие координаты точки
М(х; у) и данные задачи.
4) Упростим уравнение.
Пример 2. Составить уравнение окружности с
центром в точке С(а;в) с радиусом R
Решение
1.Возьмем на окружности произвольную точку М(х; у);
2.Выразим общее свойство точек окружности
СМ  R;
3.Выразим СМ через текущие координаты точки
М(х; у) и данные координаты точки С(а;в): по
формуле длины отрезка
, 2
2
d
x2  x1 
  y 2  y1 
получим: СМ  ( х  a) 2  ( y  b) 2  R
4.Упростим, возведем обе части в квадрат, получим:
( x  a ) 2  ( y  b) 2  R 2
(4)
Замечание: Если центром окружности является начало
координат О(0;0), то уравнение окружности примет
вид
2
2
2
x y R





Пример. Составить уравнение биссектрисы первого
координатного угла
Решение.
y P
М
1) Возьмем на биссектрисе
произвольную точку М(х; у);
N
2) Выразим общее свойство
X
x
точек биссектрисы
MP  MN (*)
(точки равноудалены от осей координат):
3) Входящие в это равенство отрезки выразим через
координаты точек М(х; у),N(x:0),P(0;y)
MP  х; MN  у
4) Подставим в равенство (*), получим: х = у

2) Задача Построение линий по ее уравнению
Дано уравнение F(x,y)=0 , построить
соответствующую линию

Пример. Построить линию, определяемую
уравнением х 2
2

y0
Решение Выразим
из этого уравнения одну из
2
координат у  х , будем давать х
2
произвольные значения и находить
соответствующее значения у.



_______________________________________________
________________________________
ПРИМЕР 3. Написать уравнение траектории
точки М(x;y), которая при своем движении
остается втрое дальше от точки А (0;9), чем от
точки В(0;1).

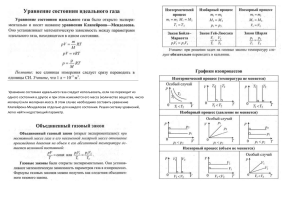
Определение 1 .Тангенс угла наклона прямой к
положительному направлению оси Ох будем
называть угловым коэффициентом этой прямой:
tgа  k
Уравнение прямой с угловым
коэффициентом, где k– угловой
коэффициент прямой,
b – начальная ордината отрезок, отсекаемый прямой на
оси Oy.
y  kxb
(1)
Y
y  kxb
а
b
Рисунок 1
X




1. Пуcть b=const :
а) если α острый угол с осью ОХ , то k = tgα > 0;
б) если α тупой угол с осью ОХ ,то k = tgα < 0 (рис. 2);
в) если α =0 => k = tg0 = 0 => уравнение имеет вид y
= b, проходит через точку B(0;b) параллельно оси ОХ
(рис.3).
k<0
В(0;b)
k>0

b
y=b




2. Пусть k=const:
а) если b=0, то прямая y = kx проходит через начало координат;
б) если b>0, то прямая отсекает отрезок от оси OYвыше оси OX;
в) если b<0, то прямая отсекает отрезок от оси OYниже оси OX
b>0
y = kx (b=0)
b<0








3. Если α = => k = tg = ∞ => прямая не имеет
2
2
углового коэффициента. Уравнение имеет вид х = а, т.е.
прямая проходит через точку А(а;0) параллельно оси ОУ
4. а) если α = 0 и b = 0
=> x = 0 – уравнение оси ОУ;
б) если α = 0 и b = 0
=> y = 0 – уравнение оси ОХ.
x=a
a






Пример . Каким образом, располагаются
прямые, в зависимости от значений k и b,
найти их угловые коэффициенты
1) у=3х - 2;
2) у=-1/2х+5;
3) 2у=5;
4) у=7х;
5) 3х+6=0.

• Пусть даны прямые l1 : y  k1  x  b1 , l2 : y  k2  x  b2 .
 1) Угол между прямыми:
Определение 3. Углом между двумя прямыми
называется острый угол , на который нужно повернуть I
прямую до совмещения со II прямой, против часовой
стрелки, вокруг их точки пересечения.
Тогда угол между этими прямыми
определяют по формуле:
k 2  k1
tg 
1  k1  k 2
(2)
l2

l1
1
Если, при нахождений угла между двумя
прямыми не указан порядок в котором они
рассматриваются, то можно установить порядок
произвольно, изменение порядка повлечет за
собой изменение знака для тангенса угла.
0


180



Так, если бы находили угол 1 ,то 1
тогда tg1  tg(1800   )   tg
т.е. формулу (2), можно записать в виде:

k 2  k1
tg 
1  k1  k 2
2)
(3)
3)
(4)
y
y
l2
l2
l1
l1
x
x

Пример 1. Для прямой 3х+2у-4=0 найти
параллельную и перпендикулярную.
(5)
Ax  By  C  0
Теорема. Всякое уравнение первой степени
,
Ax  By  C  0
где А и В не обращаются в нуль одновременно, представляет
собой уравнение некоторой прямой линии на плоскости .

Доказательство: Преобразуем уравнение (5):
Ax  By  C  0  Ву   Ах  С  у  
Обозначим: k  
А
С
;b  
В
В
А
С
х
В
В
(*)
,подставим в (*), получим:
y  k  x  b - уравнение прямой с угловым коэффициентом.
Вывод: доказали, что всякое уравнение первой степени задает
на плоскости прямую, т.к. оно приводится к уравнению прямой
с угловым коэффициентом.
Частные случаи общего уравнения прямой Ax  By  C  0
1. При С=0 =>
Ах  Ву  0  y  
A
x
B
- прямая проходит через начало координат.
2. При А=0 =>
Ву  С  0  y  
C
b
– параллельна оси оси ОХ .
B
C
3. При B=0=> Ах  С  0  x   A  a - параллельна оси ОУ
4. При B=C=0
=> Ax=0
5. При А=С=0
=>
=> x = 0 – ось ОУ.
By = 0 => y = 0 – ось ОХ.
l
Определение 3. Вектор n А; В 
перпендикулярный прямой l,
называется её нормальным вектором.


Замечание. Коэффициенты А и В
уравнении прямой Ax  By  C  0
координатами нормального вектора
n
в общем
являются
. Пример 2. Найти координаты нормального

вектора для прямой у=-5х+1/3
Решение. Приведем к общему виду
Ах+By+C=0: 5х +у - 1/3=0  n

5 ;1

Пусть даны прямые: А1х+В1у+С1=0; А2х+В2у+С2=0,
где n1 А1;В1  - нормальный вектор для прямой l1;
n2  А2 ; В2 нормальный вектор для l2.

1) Угол между прямыми:
cos 
 ( A1 A2  B1 B2 )
A1  B1  A2  B2
2) Условие параллельности :
А1 В1

А2 В2


(7)
2
2
2
2
(6)
3) Условие перпендикулярности:
А1  А2  В1  В2  0
(8)

ПРИМЕР 2. Установить какие прямые
параллельные, какие перпендикулярные?
1)2х-3у+5=0;
2) 4х-6у+8=0;
3)2у+3х+1=0
Прямые заданы уравнениями
в общем виде:
с угловым
коэффициентом:
A1x + B1y + C1 =0 ,
y=k1x + b1
A2x + B2y + C2 =0
y=k2x + b2
Угол 
прямыми
между
двумя
Прямые параллельны
(условие параллельности)
Прямые перпендикулярны
(условие
перпендикулярности)
cos 
 ( A1 A2  B1 B2 )
A1  B1  A2  B2
2
2
A1
B
 1
A2 B2
A1∙A2 + B1∙B2=0
2
2
tg 
k 2  k1
1  k1  k 2
k1=k2
k1  
1
k2
Пусть прямая АВ отсекает на осях координат
определенные отрезки a и b
x y
 1
a b
(11)
B(0;b)
b
A(a;0)
а
ПРИМЕР 3. Построить прямые, приведя их к виду в отрезках на
осях:а) 2х+4у-4=0; б) 3х-2у+6=0
Пусть прямая проходит через данную точку М0(х0;у0) и
имеет угловой коэффициент k
y  y0  k  x  x0 
(9)
Определение . Совокупность всех прямых,
проходящих через некоторую точку плоскости,
называется пучком прямых, а общая их точка –
центром пучка.
Пример 5. Написать уравнение пучка прямых,
проходящих через точку А(3;-2) и выбрать из пучка
прямую параллельную прямой у=2х-1.
4) Уравнение прямой, проходящей через две точки
Пусть прямая проходит через две данные точки
M1x1, y1  и M 2 x2 , y2  ;
x  x1
y  y1

x2  x1 y2  y1
(10)
Пример 6. Составить уравнение прямой, проходящей через
точки А(-1;2); В(1;-3)
5) Уравнение прямой в отрезках на осях
Пусть прямая АВ отсекает на осях координат
определенные отрезки a и b
x y
 1
a b
(11)
B(0;b)
b
A(a;0)
а
Пример 7. Построить прямую 2х+4у-4=0
№
п/п
Название
уравнения
Вид уравнения
Угловой
коэффициент
1
Общее
k= 
Ax + By + C = 0
n = (A; B);
A
B M (x ; y ) прямой
0 0
0
2
с угловым
коэффициентом
3
в отрезках
4
5
проходящей в данном
направлении
через
данную точку
проходящей через две
данные точки
y = kx + b
x y
 1
a b
y – y0 = k (x – x0)
коэффи-циент
при х
k 
Необходимые
данные
b
a
коэффи-циент
при
b – величина отрезка
на ОУ;
k = tgα, α - угол
наклона прямой к
оси ОХ
а – отрезок на ОХ;
b – отрезок,
отсекаемый на ОУ
M0(x0;y0) прямой
(х - х0)
y  y1
x  x1

y 2  y1 x 2  x1
k
y 2  y1
x 2  x1
M1(x1;y1), M2(x2;y2)
лежат на прямой
=>

Определение. Расстоянием от точки М(х0;у0) до прямой, заданной
уравнением Ах+Ву+С=0 называется длина перпендикуляра d=
/MN/ , опущенного из точки М на данную прямую и вычисляемая по
формуле:
M(x0; y0)
d 
| Ax0  By 0  C |
A B
2
2
(12)
N




O
Пример 9. Определить расстояние между параллельными
прямыми: 3х – 4у –6=0 и 6х – 8у +28=0;
,

,

,
Чтобы найти точку пересечения двух непараллельных прямых, нужно
решить совместно их уравнения:
 A1x  B1 y  C1  0;
 A1 x  B1 y  C1;
=>


A
x

B
y

C

0
;
2
2
 2
 A2 x  B2 y  C2 .
Решение данной системы можно найти по формулам Крамера:

x

где ,







A1
B1
A2
B2
x

x 
y
 C1
B1
 C2
B2
y

y 
A1
 C1
A2
 C2
Причем если: а) ∆ ≠ 0, то прямые имеют точку пересечения;
б) ∆ = 0, а ∆х≠0 или ∆у≠0, то прямые параллельны ;
в) ∆=∆х=∆у=0, то прямые совпадают.
Пример 10. Найти точку пересечения прямых х+7у –6=0
и х + у –2=0.







Пример 8. Даны координаты вершин
треугольника АВС: А(4;3), В(16;-6), С(20;16).
Найти: 1) длину стороны АВ;
2) уравнение сторон АВ и АС, их угловые
коэффициенты;
3) уравнение высоты СД;
4) уравнение медианы АМ;
5) длину высоты СД;
6) уравнение окружности с центром в точке С и
радиусом, равным половине длины отрезка АВ.


Определение 1. Кривой второго порядка на
плоскости OXY называется геометрическое место
точек, координаты которых удовлетворяют
уравнению второй степени относительно x и y:
Ax 2  Bxy  Cy 2  Dx  Ey  F  0 , где A,B,D
одновременно в нуль не обращаются.
Таких линии три: эллипс (частным случаем
является окружность), гипербола, парабола. Они
играют большую роль в математике,
естествознании и технике. Начнем их
рассмотрения с окружности.

Определение 2. Окружностью называется
геометрическое место точек равноудаленных от точки
С(a;b), называемой центром на расстоянии R – радиус.
Каноническое уравнение окружности имеет вид:
( x  a ) 2  ( y  b) 2  R 2


(12)
Уравнение второй степени относительно текущих
координат x и y является уравнением окружности тогда
и только тогда, когда в этом уравнении коэффициенты
при квадратах координат равны, а член с 2
2
произведением координат отсутствует – Ax  Cy  Dx  Ey  F  0
В этом случае говорят, что окружность задана общим
уравнением.
Замечание: Если центром окружности является
начало координат О(0;0), то уравнение окружности
примет вид:x 2  y 2  R 2

Для определения координат центра и радиуса окружности,
заданной общим уравнением, надо с помощью метода
дополнения до полного квадрата привести к виду
( x  a) 2  ( y , b) 2  R 2
с помощью формулы:
(1)
.
(a  b)  a  2ab  b
2
2
2
y
C(-3;1)
1
-3
О
Рисунок 8

Определение 3.
Эллипс есть геометрическое множество
точек, сумма расстояний которых от двух
фиксированных точек, называемых
фокусами эллипса, есть величина
постоянная (2а), большая, чем расстояние
между фокусами (2с).
М ( х; у )
F1 (с;0)
F2 (с;0)
| MF1 |  | MF2 | 2a
M
F1
F2
(2)
B2 (b;0)
b
A1 (а;0)
F1 (с;0)
a
c
F2 (с;0)
B1 (b;0)
A2 (а;0)
(рис.11)
Рисунок 11
Рисунок 12
(рис.12)
|| MF1 |  | MF2 || 2a
M
F1
F2
(4)
B2 (b;0)
М ( х; у )
a
F1 (с;0) A1 (а;0)
A2 (а;0)
b
B1 (b;0)
F2 (с;0)
(рис.14)
14
Рисунок 14
(14)
(14)
(14)
4
-3
3
-4
Рисунок 14

Определение 5. Параболой называется
геометрическое множество точек,
равноудаленных от данной точки,
называемой фокусом, и данной прямой,
называемой директрисой параболы.


Величина p, равная расстоянию от фокуса до
директрисы, называется параметром параболы;
прямая, проходящая через фокус параболы
перпендикулярно ее директрисе, называется
осью, а точка пересечения параболы с ее осью
– вершиной параболы.
Простейшее уравнение параболы получается,
если координатная система расположена
следующим образом: за одну из координатных
осей берется ось параболы, а за другую –
прямая, перпендикулярная оси параболы и
проведенная посередине между фокусом и
директрисой.
| FM || NM |
K ( p / 2;0)
p/2
F ( p / 2;0)
p/2
N
M ( x; y )
Рисунок 15
(рис.16)
Рисунок 16

Определение 5. Параболой называется
геометрическое множество точек,
равноудаленных от данной точки,
называемой фокусом, и данной прямой,
называемой директрисой параболы.
z=
.







Определение
1. Поверхностью называется
геометрическое место точек, координаты
которых удовлетворяют уравнению:
F (х; у; z)=0 или z= f ( х; у )
Пример
поверхности.
Сферическая
поверхность (или сфера) с центром в точке
(х0; у0; z0 ) радиусом R задаётся уравнением:
(х –х0)2 + (у – у0)2 + (z – z0)2 = R2.
Если уравнение поверхности переменные
х, у, z содержит только в первой степени и не
содержит
их
произведений,
то
такая
поверхность называется плоскостью.












1) Уравнение плоскости, заданной точкой М0(х0;у0;z0)
и нормальным вектором n =( А;В;С):
А (х – х0) + В (у – у0) + С (z –z0) =0
(1)
1) Возьмем на прямой
произвольную точку
М(x;y;z)
М(х;у;z) и рассмотрим
вектор М 0 М х  х0 ; у  у0 ; z  z0 
n
М
2) Векторы М 0 М и nА; В; С
перпендикулярны,
следовательно их скалярное произведение равно
нулю (сумма произведений соответствующих
координат равна нулю)
0
А (х – х0) + В (у – у0) + С (z –z0) =0.

Дано: А (3;-15) , В(7;1;1),С(4;-1;3)

1. Составить уравнение плоскости Q1 ,
проходящей через точку А
перпендикулярно вектору АВ;

2.Уравнение плоскости через три данные точки:
М 1 ( x1 ; y1 ; z1 ), M 2 ( x2 ; y2 ; z2 ), M 3 ( x3 ; y3 ; z3 )
М3
1)Возьмем точку на плоскости
произвольную точку М (х; у; z )
2) Рассмотрим три вектора:
М2
М1
М
М 1М , М 2 М 1 , М 3 М 1
Найдем координаты векторов:
М1М 2 х2  х1 ; у2  у1; z2  z1 М1М 3 х3  х1 ; у3  у1 ; z3  z1 М М х  х ; у  у ; z  z 
1
1
1
1
3)
Векторы лежат в одной плоскости, следовательно
компланарны, их смешанное произведение равно нулю, т.е.
определитель равен нулю:
x  x1
y  y1
z  z1
x2  x1
x3  x1
y2  y1
y3  y1
z 2  z1  0
z3  z1

Дано: А (3;-15) , В(7;1;1),С(4;-1;3)

2.Составить уравнение плоскости,
проходящей через точки А,В,С;


3) Уравнение плоскости в отрезках на осях:
где a, b, c – отрезки, отсекаемые плоскостью
соответственно на осях ОХ, ОУ, ОZ z
с
х у z
  1
а b с
а
b
x
y


4) Общее уравнение плоскости:
Ах+Ву+Сz+D=0


(4)
Частные случаи общего уравнения плоскости Ах+Ву+Сz+D=0:
1. D=0 Ах+Ву+Сz=0

2. а) А=0
– проходит через начало координат.
Ву+Сz+ D =0 – плоскость параллельна оси ОХ,
б) В=0
Ах+Сz+ D =0 – плоскость параллельна оси ОУ;
в) С=0
Ах+Ву+ D =0 – плоскость параллельна оси ОZ.




4) Общее уравнение плоскости:
Ах+Ву+Сz+D=0

Частные случаи общего уравнения плоскости
Ах+Ву+Сz+D=0:

3. а) А= D =0 Ву + Сz = 0
проходит через ось ОХ,
– плоскость



б) В= D =0 Ах+Сz=0
проходит через ось ОУ,
– плоскость
в) С= D =0 Ах+Ву=0
проходит через ось ОZ.
– плоскость





(4)


4) Общее уравнение плоскости:
Ах+Ву+Сz+D=0
















4.
а)В=С=0
(4)
Ах+D=0 х= 
D
А
– плоскость параллельна
координатной плоскости УОZ,
D

б)А=С=0 Ву+D=0 у=
–плоскость параллельна
В
плоскости ХОZ,
в) А=В=0 Сz+D=0 z=  – плоскость параллельна
С
плоскости ХОУ.
D
5.
а) В=С=D=0 Ах=0
б) А=С=D=0 Ву=0
в) А=В=D=0 Сz=0
х=0 – уравнение плоскости УОZ,
у=0 – уравнение плоскости ХОZ,
z=0 – уравнение плоскости ХОУ.



Дано: А (3;-15) , В(7;1;1),С(4;-1;3)
3.Составить уравнение плоскости Q2
через точку В и ось ОХ;
4.Построить плоскости Q1 , Q2 и Q3







Построить плоскости:
1) 2х + 6у + 16z – 10 = 0;
2) 3х + 6z – 6 = 0;
3) 2y – 5 = 0;
4) х – 3у + 6z = 0;
5) 6у – z = 0.






. Вывод векторного уравнения прямой.
Положение прямой L в пространстве определяется
однозначно, если на ней заданы точка М0 (х0; у0; z0 ),
принадлежащая прямой, и ненулевой вектор s = (m;n;p)
(m2+n2+p2≠0), параллельный этой прямой.
Вектор s называется направляющим вектором прямой.
ВЫВОД:
1) Возьмем на прямой произвольную
М
точку М(х;у) и рассмотрим вектор М 0 М
М0
s





2) Векторы М 0 М и s
коллинеарные,
по условию коллинеарности, получим:
М 0М  t S
- векторное уравнение прямой.






1. Уравнения прямой, проходящей через точку
М0 (х0; у0; z0 ) с направляющим вектором s =(m;n;p)
:
а) канонические уравнения прямой:
х  х0 у  у0 z  z0


m
n
p
(1)
б) параметрические уравнения прямой:
 х  х0  mt;

 у  у0  nt;
 z  z  pt.
0

(2)



2.Уравнения прямой, проходящей через две
заданные точки: М1(х1; у1 ; z1 ) и М2(х2; у2 ; z2 ):
х  х1
у  у1
z  z1


х2  х1 у2  у1 z2  z1
.
(3)
3. Общие уравнения прямой (в виде
пересечения двух плоскостей):
 А1х  В1 у  С1z  D1  0;

 А2 х  В2 у  С2 z  D  0.

(4)

Дано: А (3;-15) , В(7;1;1),С(4;-1;3)

5.Составить уравнение прямой L1,

проходящей через точку С,
перпендикулярно плоскости Q1;
6.Составить общее уравнение прямой L2,
как линию пересечения плоскостей Q1 и
Q3, привести уравнение к каноническому
виду.












Пусть плоскости и заданы общими уравнениями:
1. A1x  B1 y  C1z  D1  0
,
2. A2 x  B2 y  C2 z  D2  0
.
где n1{A1;B1;C1}, n2{A2;B2;C2} – координаты нормальных
векторов.
а) Угол между плоскостями.
При пересечении плоскости образуют четыре попарно
равных двугранных угла.
n2
Углом между двумя плоскостями
n1
называется любой из этих

P2
двух смежных двугранных углов.
Один из углов между плоскостями
P1
равен углу между их
нормальными векторами n 1 и n2, нахождение угла из
скалярного произведения.
cos 
n1  n2

n1  n2
A1 A2  B1B2  C1C2
A12  B12  C12  A22  B22  C22

б) условие параллельности - условие
коллинеарности n1 и n2
n  A , B , C 
1
А1 В1 С1


А2 В2 С2


1
1
n 2   A2 , B 2 , C 2 
p1
p2
в) условие перепендикулярности - скалярное
произведение векторов n1 и n2 равно нулю
А1А2+В1В2+С1С2=0
n1   A1 , B1 , C1 


1
n 2   A2 , B 2 , C 2 
p1
p2

Пусть
x  x0 y  y 0 z  z 0
l1 :


,
m1
n1
p1
l2 :
x  x1 y  y1 z  z1


,
m2
n2
p2

где s1  m1 , n1 , p1 , s 2  m2 , n2 , p2 – направляющие
векторы прямых l1 и l2 соответственно.

а) угол между прямыми равен углу между

направляющими векторами этих прямых, т.е.

cos  
s1  s 2
s1  s 2

m1m2  n1n2  p1 p2
m n  p  m n  p
2
1
2
1
2
1
2
2
2
2
2
2
.

б) условие параллельности::
l1 // l 2  s1 // s 2 ,

m1 n1
p1
l1 // l 2 


;
m2 n2 p2
в) условие перепендикулярности:

l1  l2  s1  s 2  m1m2  n1n2  p1 p2  0;




x  x0 y  y 0 z  z 0


а) условие параллельности: прямая
m
n
p
параллельна плоскости Ax  By  Cz  D  0 тогда и только тогда,
когда направляющий вектор прямой s  m, n, p 
n   A, B, C  , т.е.

перпендикулярен нормали плоскости

их скалярное произведение равно нулю:


sn  0
n
l
или
Am  Bn  Cp  0
s

б) условие перпендикулярности: прямая
перпендикулярна плоскости при условии:


A
B
C


m
n
p
в) угол между прямой и плоскостью: называется
любой из двух смежных углов, образованных
прямой и ее проекцией на плоскость.
cos   cos(90   )  sin  
Аm  Вn  Сp
s
n
A2  B 2  C 2  m 2  n  p
2
2


l







1) Точка пересечения плоскости и прямой.
Если условия параллельности прямой и плоскости
х  х0 у  у0 z  z0
не выполняются, то прямая m  n  p
и плоскость Ах+Ву+Сz+D=0 пересекаются. Чтобы
найти их точку пересечения, надо решить систему
трех уравнений с тремя неизвестными:
 х  х0 у  у0 z  z0


;

n
p
 m
 Ах  Ву  СZ  D  0.
2) Расстояние от точки до плоскости:
Расстояние d от точки А (х0; у0; z0) до плоскости
Ах+Ву+Сz+D=0 находится по формуле:


d=
Ах0  Ву 0  Сz0  D
А2  В 2  С 2

Условие
Две плоскости с
нормальными
векторами
n1 (А1;В1;С1);
сos 
параллельности
 ( A1 A2  B1B2  C1C2 )
A1  B1  C1  A2  B2  C2
2
2
2
2
2
2
m1 n1
p

 1
m2 n2
p2
Две прямые с
направляющими
векторами
s1 (m1;n1; p1),
сos 
А В C


m n
p
m1m2+n1n2+p1p2=0
n2 (А2;В2;С2)
Аm+Вn+Сp=0
А1 В1 С1


А2 В2 С2
 (m1m2  n1n2  p1 p2 )
m1  n1  p1  m2  n2  p2
2
2
2
2
2
2
s2 (m ;n ; p ).
2 2
2
Прямая
(направляющий вектор s (m;n;p))
и
плоскость
(нормальный вектор n (А;В;С))
sin  
Аm  Вn  Сp
A  B C  m n  p
2
2
2
2
2
2
перпендикулярности
А1А2+В1В2+С1С2=0
Угол







Дано: А (3;-15) , В(7;1;1),С(4;-1;3)
7.Исследовать
взаимное
расположение
плоскостей: Q1 и Q3.
8.Выяснить взаимное расположение прямых L1 и
L2.
9.Исследовать взаимное расположение прямой
L1 и плоскости Q2, их точку пересечения;
10.Найти расстояние от точки С до плоскости
Q1;

ПРИМЕР 2.

Дано: А (3;-15) , В(7;1;1),С(4;-1;3)















1. Составить уравнение плоскости Q1 , проходящей через точку А
перпендикулярно вектору АВ;
2.Составить уравнение плоскости, проходящей через точки А,В,С;
3.Составить уравнение плоскости Q2 через точку В и ось ОХ;
4.Построить плоскости Q1 , Q2 и Q3
5.Составить уравнение прямой L1, проходящей через точку С,
перпендикулярно плоскости Q1;
6.Составить общее уравнение прямой L2, как линию пересечения
плоскостей Q1 и Q3, привести уравнение к каноническому виду.
7.Исследовать взаимное расположение плоскостей: Q1 и Q3.
8.Выяснить взаимное расположение прямых L1 и L2.
9.Исследовать взаимное расположение прямой L1 и плоскости Q2,
их точку пересечения;
10.Найти расстояние от точки С до плоскости Q1;

















ПРИМЕР 2.
Дано:
1. Составить уравнение плоскости Q1 , проходящей через точку А
перпендикулярно вектору АВ;
2.Составить уравнение плоскости Q2 через точку В и указанную ось
координат;
3.Составить уравнение плоскости, проходящей через точки АВС;
4.Построить плоскости Q1 , Q2 и Q3
5.Составить уравнение прямой L1, проходящей через точку С,
перпендикулярно плоскости Q1;
6.Составить общее уравнение прямой L2, как линию пересечения
плоскостей Q1 и Q3, привести уравнение к каноническому виду.
7.Исследовать взаимное расположение плоскостей: Q1 и Q3.
8.Выяснить взаимное расположение прямых L1 и L2.
9.Исследовать взаимное расположение прямой L1 и плоскости Q2,
их точку пересечения;
10.Найти расстояние от точки С до плоскости Q1;