Раздел 1. Задание 1
Введение
Пусть две величины x и y связаны табличной зависимостью,
полученной, например, из опытов.
x
x1
x
x
y
y1
У2
yn
n
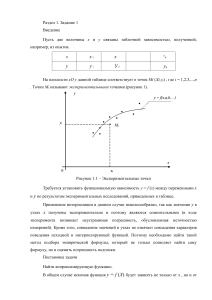
На плоскости xO y данной таблице соответствует n точек Mi (Xi,yt) , где i = 1,2,3,...,n
. Точки Mt называют экспериментальными точками (рисунок 1).
Рисунок 1.1 – Экспериментальные точки
Требуется установить функциональную зависимость y = f (x) между переменными x
и y по результатам экспериментальных исследований, приведенных в таблице.
Применение интерполяции в данном случае нецелесообразно, так как значения y в
узлах x получены экспериментально и поэтому являются сомнительными (в ходе
эксперимента
возникает
неустранимая
погрешность,
обусловленная
неточностью
измерений). Кроме того, совпадение значений в узлах не означает совпадения характеров
поведения исходной и интерполирующей функций. Поэтому необходимо найти такой
метод подбора эмпирической формулы, который не только позволяет найти саму
формулу, но и оценить погрешность подгонки.
Постановка задачи
Найти аппроксимирующую функцию.
В общем случае искомая функция y
= f (X) будет зависеть не только от x , но и от
2
некоторого количества параметров:
y = f (x, a, b,...)
( 1.1 )
такую, чтобы в точках x= xi она принимала значения по возможности близкие к
табличным, то есть график искомой функции должен проходить как можно ближе к
экспериментальным точкам. Вид функции (1) может быть известен из теоретических
соображений или определяться характером расположения экспериментальных точек M
i
на плоскости xOy.
Для отыскания коэффициентов a, b,... в функции (1.1) применяется метод
наименьших квадратов, который состоит в следующем. Между искомой функцией и
табличными значениями в точках x наблюдаются отклонения. Обозначим их
(1.2)
где i = 1,2,3,...,n .
Выбираем значения коэффициентов a,b,... так, чтобы сумма квадратов отклонений
принимала минимальное значение:
(1.3)
Сумма S (a,b,...) является функцией нескольких переменных. Необходимый
признак экстремума функции нескольких переменных состоит в том, что обращаются в
нуль частные производные:
(1.4)
План решения задачи
1. Выбираем функцию y = f (X,a,b,...) .
2. Для отыскания коэффициентов a,b,... составляем системууравнений ( 1.4 ) .
3. Решая систему уравнений (3), находим значения коэффициентов a,b,... .
4. Подставляя a,b,... в уравнение (1), получаем искомую функцию y
= f (X,a,b,...') .
5. По достаточному признаку экстремума функции нескольких переменных следует
убедиться в постоянстве знака дифференциала второго порядка этой функции:
d2S > 0 при любых приращениях аргументов da, db,... .
Такая проверка делается в теоретической части метода наименьших квадратов и на
практике не повторяется.
Обычно рассматривают несколько видов функций y = f (x, a, b,...) и выбирают ту
3
функцию, для которой суммарная погрешность окажется наименьшей:
(1.5)
Задание №1
Исходные данные
№ Вар.
7
1
2
3
4
5
6
7
8
9
10
11
x
0,01
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
y
1
1,22
1,48
1,78
2,12
2,5
2,92
3,38
3,88
4,42
5
Решение задачи 1
Решение производилось в Microsoft Excel. Само решение представлено ниже.
Нам дана таблица значений некоторой функциональной зависимости, полученной
из n = 11 опытов.
1.1 Найдем зависимость y от x в виде линейной функции y = ax + b.
Выберем значения коэффициентов a и b так, чтобы сумма квадратов отклонений была
минимальной.
(1.6)
Функция S(a, b) будет принимать минимальное значение, если обращаются в нуль
частные производные:
(1.7)
Преобразуем уравнения системы:
4
(1.8)
При этом:
11
11
11
∑ 𝑥𝑖 = 5,51 ,
∑ 𝑦𝑖 =
𝑖=1
𝑖=1
29,7 , ∑ 𝑥𝑖2
𝑖=1
11
= 3,8501 , ∑ 𝑥𝑖 ∗ 𝑦𝑖 = 19,26
𝑖=1
Тогда система уравнений примет вид:
{
3,8501𝑎 + 5,51𝑏 = 19,26
}
5,51𝑎 + 11𝑏 = 29,7
Решим систему уравнений по формулам Крамера:
3,8501
∆= |
5,51
5,51
| = 11,991
11
19,26 5,51
∆1 = |
| = 48,213
29,7
11
3,8501
∆2 = |
5,51
19,26
| = 8,2254
29,7
Тогда
𝑎=
∆1 48,213
∆2 8,2254
=
= 4,02; 𝑏 =
=
= 0,69.
∆
11,991
∆
11,991
Следовательно, искомая линейная функция будет иметь вид:
𝑦 = 4,02𝑥 + 0,69.
1.2 Найдем зависимость y от x в виде степенной функции 𝑦 = 𝛽 ∗ 𝑥 𝛼 .
Прологарифмируем равенство y = β ∗ x a .по основанию e и получим lny = a ∗
lnx + lnβ.
Обозначим Y = lny, X = lnx, b = lnβ.
Тогда получим линейную функцию Y = aX + b, где переменные и связаны
следующей табличной зависимостью.
Система имеет вид:
(1.9)
Найдем коэффициенты системы.
5
11
11
11
11
2
∑ 𝑙𝑛𝑥𝑖 = −12,5266 ,
∑ 𝑙𝑛𝑦𝑖 = 9,5761 , ∑ 𝑙𝑛 𝑥𝑖 = 32,3184 , ∑ 𝑙𝑛𝑥𝑖 ∗ 𝑙𝑛𝑦𝑖 = −4,5476
𝑖=1
𝑖=1
𝑖=1
𝑖=1
Система уравнений будет иметь вид:
32,3184𝑎 − 12,5266𝑏 = −4,5476
{
}
−12,5266𝑎 + 11𝑏 = 9,5761
Решим систему уравнений по формулам Крамера:
32,3184 −12,5266
∆= |
| = 198,5868
−12,5266
11
−4,5476 −12,5266
∆1 = |
| = 69,9322
9,5761
11
32,3184 −4,5476
∆2 = |
| = 252,5179
−12,5266 9,5761
Тогда
∆1
69,9322
∆2 252,5179
𝑎=
=
= 0,35; 𝑏 =
=
= 1,27.
∆
198,5868
∆
198,5868
Находим 𝛽 = 𝑒 𝑏 = 𝑒 1,27 = 3,57.
Получаем искомую степенную функцию 𝑦 = 3,57𝑥 0,35 .
1.3
Найдем зависимость y от x в виде показательной функции 𝑦 = 𝛽 ∗ 𝑒 𝑎𝑥 .
Для этого требуется прологарифмировать равенство 𝑦 = 𝛽 ∗ 𝑒 𝑎𝑥 по основанию e.
Получим 𝑙𝑛𝑦 = 𝑎𝑥 + 𝑙𝑛𝛽.
Тогда получим линейную функцию 𝑌 = 𝑎𝑋 + 𝑏, где переменные и связаны
следующей табличной зависимостью.
Тогда система имеет вид:
(1.10)
Найдем коэффициенты системы.
11
11
11
11
2
∑ 𝑥𝑖 = 5,51 ,
∑ 𝑙𝑛𝑦𝑖 = 9,5761 , ∑ 𝑥𝑖 = 3,8501 , ∑ 𝑥𝑖 ∗ 𝑙𝑛𝑦𝑖 = 6,5571
𝑖=1
𝑖=1
Система уравнений имеет вид:
𝑖=1
𝑖=1
3,8501𝑎 + 5,51𝑏 = 6,5571
{
}
5,51𝑎 + 11𝑏 = 9,5761
Решим систему уравнений по формулам Крамера:
3,8501
∆= |
5,51
5,51
| = 11,991
11
6,5571
∆1 = |
9,5761
5,51
| = 19,3637
11
3,8501
∆2 = |
5,51
6,5571
| = 0,7394
9,5761
6
Тогда
𝑎=
∆1 19,3637
∆2 0,7394
=
= 1,61; 𝑏 =
=
= 0,06.
∆
11,991
∆
22,405
Находим 𝛽 = 𝑒 𝑏 = 𝑒 0,7394 = 1,06.
Искомая показательная функция 𝑦 = 1,06𝑒1,61𝑥 .
1.4
Найдем зависимость y от x в виде квадратичной функции y = ax2 + bx + c.
Выберем коэффициенты a , b и c так, чтобы сумма квадратов отклонений была
минимальной.
(1.11)
Функция S (a, b, c) будет принимать минимальное значение, если частные
производныеS’a (a, b, c), S’b (a, b, c), S’c (a, b, c) обращаются в нуль.
(1.12)
Преобразуем выражение выше.
(1.13)
11
11
∑ 𝑥𝑖4
= 2,5333 ,
𝑖=1
∑ 𝑥𝑖3
11
=
3,025 , ∑ 𝑥𝑖2
𝑖=1
11
∑ 𝑥𝑖2
𝑖=1
11
= 3,8501 , ∑ 𝑥𝑖 = 5,51
𝑖=1
11
∗ 𝑦𝑖 = 14,9667 ,
𝑖=1
11
∑ 𝑥𝑖 ∗ 𝑦𝑖 = 19,26 , ∑ 𝑦𝑖 = 29,7
𝑖=1
𝑖=1
Тогда система уравнений примет вид:
2,5333𝑎 + 3,025𝑏 + 3,8501с = 14,9667
{ 3,025𝑎 + 3,8501𝑏 + 5,51𝑐 = 19,26 }
3,8501𝑎 + 5,51𝑏 + 11с = 29,7
Решим систему уравнений по формулам Крамера:
2,5333 3,025 3,8501
∆= | 3,025 3,8501
5,51 | = 0,9938
3,8501
5,51
11
7
14,9667 3,025 3,8501
∆1 = | 19,26
3,8501
5,51 | = 1,9528
29,7
5,51
11
2,5333 14,9667 3,8501
∆2 = | 3,025
19,26
5,51 | = 2,0318
3,8501
29,7
11
2,5333 3,025 14,9667
∆3 = | 3,025 3,8501
19,26 | = 0,9821
3,8501
5,51
29,7
Тогда
𝑎=
∆1 1,9528
∆2 2,0318
∆3 0,9821
=
= 1,96; 𝑏 =
=
= 2,04; 𝑐 =
=
= 0,99.
∆
0,9938
∆
0,9938
∆
0,9938
Следовательно, искомая квадратичная функция будет иметь вид:
𝑦 = 1,96𝑥 2 + 2,04𝑥 + 0,99.
2.
Построим
в
плоскости
графики
полученных
функций
и
нанесем
экспериментальные точки xOy.
x
y
0,01
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
y1
y2
1
1,14
1,36
1,66
2,04
2,5
3,04
3,66
4,36
5,14
6
y3
0,73
1,09
1,49
1,89
2,29
2,70
3,10
3,50
3,90
4,30
4,71
0,70
1,59
2,02
2,33
2,58
2,79
2,98
3,15
3,30
3,44
3,57
y4
1,08
1,25
1,47
1,73
2,03
2,38
2,80
3,29
3,87
4,55
5,35
1,01
1,21
1,48
1,78
2,12
2,50
2,92
3,38
3,88
4,42
5,00
7
6
5
y
4
y1
y2
3
y3
2
y4
1
0
0
0,2
0,4
0,6
0,8
1
1,2
Рисунок 1.2 - Графики аппроксимирующих функций и экспериментальные точки
8
3. Сравним полученные результаты. Для этого найдем соответствующие суммарные погрешности.
2
𝑆(𝑎, 𝑏) = ∑11
𝑖=1(∆𝑦𝑖 )
(1.14)
Значения S1, S2, S3, S4 найдем с использованием Excel.
Значения S1
Значения S2
Значения S3
Значения S4
0,074983073
0,08726418
0,006547148
7,83876E-05
0,002699994
0,198217931
0,012100159
0,005227191
0,016929936
0,440188329
0,011896213
0,013382749
0,053912959
0,454316872
0,004426477
0,01401077
0,064652318
0,294714399
0,000118476
0,006455981
0,038551264
0,086450913
0,013287589
2,65651E-06
0,00341305
0,003684726
0,056328354
0,013874627
0,025440928
0,264713836
0,134069263
0,077235271
0,209238151
1,130096885
0,23901481
0,229187519
0,697807971
2,901696765
0,348642737
0,518773854
1,672553641
5,92209912
0,426578144
1,004976308
Вывод
В данной задаче лучшей аппроксимирующей функцией является показательная
функция: y3 = 1,06𝑒 1,61𝑥 .
Раздел 2. Задание 2
Таблица 2.1 – Исходные данные задания 2
№вар.
Интервалы (0,2)
(2,4)
(4,6)
(6,8)
(8,10)
(10,12)
значений
7
Число
8
11
32
28
10
11
попаданий
Произведем оценку ряда. Для этого составим таблицу в Microsoft Excel и найдем
совокупность показатели.
9
Рисунок 2.1 – Расчеты для задания 2
Средняя взвешенная (выборочная средняя)
𝑥̅ =
∑ 𝑥𝑖 ∗ 𝑓𝑖 8 ∗ 1 + 11 ∗ 3 + 32 ∗ 5 + 28 ∗ 7 + 10 ∗ 9 + 11 ∗ 11 608
=
=
= 6,08.
∑ 𝑓𝑖
100
100
Мода - наиболее часто встречающееся значение признака у единиц данной
совокупности. В симметричных рядах распределения значение моды и медианы
совпадают со средней величиной, а в умеренно асимметричных они соотносятся таким
образом: 3(xср-Me) ≈ xср-Mo
Среднее значение изучаемого признака по способу моментов.
𝑥̅ =
𝑥𝑖 ∗ 𝑓𝑖
∗ ℎ + 𝐴.
∑ 𝑓𝑖
А – условный нуль, равный варианте с максимальной частотой (середина интервала
с максимальной частотой), h – шаг интервала.
𝑥𝑖. =
𝑥𝑖 − 𝐴 𝑥𝑖 − 5
=
ℎ
2
Средний квадрат отклонений по способу моментов.
𝐷=
Тогда
[𝑥𝑖 ]2 ∗𝑓𝑖
∑ 𝑓𝑖
∗ ℎ2 + (𝑥̅ − 𝐴)2
(2.1)
54
𝑥̅ =
∗ 2 + 5 = 6,08.
100
210 2
𝐷=
∗ 2 + (6,08 − 5)2 = 7,234.
100
Найдём среднее квадратическое отклонение.
𝜎 = √𝐷 = √7,234 = 2,69.
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями
признака первичного ряда.
𝑅 = 𝑥𝑚𝑎𝑥 − 𝑥𝑚𝑖𝑛 = 12 − 0 = 12
Дисперсия - характеризует меру разброса около ее среднего значения (мера
рассеивания, т.е. отклонения от среднего).
∑(𝑥𝑖 − 𝑥̅ )2 ∗ 𝑓𝑖 218,16
𝐷=
=
= 2,182.
∑ 𝑓𝑖
100
10
Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная
дисперсия).
𝑆2 =
∑(𝑥𝑖 − 𝑥̅ )2 ∗ 𝑓𝑖 723,36
=
= 7,307.
∑ 𝑓𝑖 − 1
99
Каждое значение ряда отличается от среднего значения 6,08 в среднем на 2,69.
Оценка среднеквадратического отклонения.
𝑠 = √𝑆 2 = √7,307 = 2,703.
Показатели формы распределения.
Относительный показатель квартильной вариации –
𝐾𝑞 =
4,375
∗ 100% = 73,68%.
5,938
Степень асимметрии.
Симметричным является распределение, в котором частоты любых двух вариантов,
равностоящих в обе стороны от центра распределения, равны между собой.
Наиболее точным и распространенным показателем асимметрии является
моментный коэффициент асимметрии.
(2.2)
где M3 - центральный момент третьего порядка; s - среднеквадратическое
отклонение.
170,34
= 1,7.
100
1,7
𝐴𝑆 =
= 0,0996.
2,693
𝑀3 =
Положительная величина указывает на наличие правосторонней асимметрии
Оценка существенности показателя асимметрии дается с помощью средней
квадратической ошибки коэффициента асимметрии:
𝑠𝐴𝑠 = √6 ∗
𝑛−2
(𝑛 + 1) ∗ (𝑛 + 3)
Расчет необходимых компонентов произведем в электронной таблице:
11
Рисунок 2.3 – Продолжение расчетов задания 2
𝑠𝐴𝑠 = √6 ∗
6−2
= 0,617.
(6 + 1) ∗ (6 + 3)
В анализируемом ряду распределения наблюдается несущественная асимметрия
(0,0876/0,617 = 0,14 < 3).
Применяются также структурные показатели (коэффициенты) асимметрии,
характеризующие асимметрию только в центральной части распределения, т.е. основной
массы единиц, и независящие от крайних значений признака. Рассчитаем структурный
коэффициент асимметрии Пирсона:
𝐴𝑠𝑝 = 𝑥 −
Другой
показатель
𝑀0 6,08 − 5,68
=
= 0,15.
𝜎
2,69
асимметрии,
предложенный
шведским
математиком
Линдбергом, исчисляется по формуле:
𝐴𝑠 = П − 50
(2.3)
где П – процент тех значений признака, которые превышают величину средней
арифметической; 50 – процент вариант, превосходящих среднюю арифметическую ряда
нормального распределения..
49
∗ 100 − 50 = −1
100
распределений рассчитывается
𝐴𝑠 =
Для
симметричных
показатель
эксцесса
(островершинности). Эксцесс представляет собой выпад вершины эмпирического
распределения вверх или вниз от вершины кривой нормального распределения.
Чаще всего эксцесс оценивается с помощью показателя:
(2.4)
Для распределений более островершинных (вытянутых), чем нормальное,
показатель эксцесса положительный (Ex > 0), для более плосковершинных (сплюснутых) отрицательный (Ex < 0), т.к. для нормального распределения M4/s4 = 3.
12
𝑀4 =
𝐸𝑥 =
13553,71
= 135,54.
100
135,54
− 3 = 2,5903 − 3 = −0,41.
2,694
Число 3 вычитается из отношения μ4/ σ4 потому, что для нормального закона
распределения μ4/ σ4 = 3. Таким образом, для нормального распределения эксцесс равен
нулю. Островершинные кривые обладают положительным эксцессом, кривые более
плосковершинные - отрицательным эксцессом.
Ex < 0 - плосковершинное распределение
Для приближенного определения величины эксцесса может быть использована
формула Линдберга:
Es=П-38,29
(2.5)
где П – процент количества вариант, лежащих в интервале, равном половине
среднего квадратического отклонения (в ту и другую сторону от величины средней); 38,29
– процент количества вариант, лежащих в интервале, равном половине среднего
квадратического
отклонения,
в
общем
количестве
вариант
ряда
нормального
распределения.
60
∗ 100 − 38,29 = 21,71.
100
Чтобы оценить существенность эксцесса рассчитывают статистику Ex/sEx
𝐸𝑠 =
где sEx - средняя квадратическая ошибка коэффициента эксцесса.
(2.6)
Если отношение Ex/sEx > 3, то отклонение от нормального распределения считается
существенным.
Ex/sEx = -0.41/0,597 = 0.687.
Поскольку sEx < 3, то отклонение от нормального распределения считается не
существенным.
Построим гистограмму распределения в Microsoft Excel.
13
Рисунок 2.4 – Гистограмма задания 2
Проверка гипотез о виде распределения
1. Проверим гипотезу о том, что Х распределено по нормальному закону с
помощью критерия согласия Пирсона.
(2.7)
где
pi —
вероятность
попадания
в
i-й
интервал
случайной
величины,
распределенной по гипотетическому закону
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа
(2.8)
где
s = 2,703, xср = 6,08
Теоретическая (ожидаемая) частота равна fi = fpi, где f = 100
Вероятность попадания в i-й интервал: pi = Ф(x2) - Ф(x1). Расчеты приведены в
электронной таблице.
Рисунок 2.5 – Определение вероятностей
Определим границу критической области.
Так как статистика Пирсона измеряет разницу между эмпирическим и
теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем
сильнее довод против основной гипотезы. Поэтому критическая область для этой
14
статистики всегда правосторонняя: [Kkp;+∞). Её границу Kkp = χ2(k-r-1;α) находим по
таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры
xcp и s оценены по выборке).
𝐾𝑘𝑝 = 𝜒 2 (6 − 2 − 1; 0,05) = 7,81473; 𝐾набл = 10,7407.
Наблюдаемое значение статистики Пирсона попадает в критическую область:
Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Справедливо
предположение о том, что данные выборки распределены не по нормальному закону.
Проверим гипотезу о том, что Х распределено по нормальному закону с помощью
показателей As и Ex.
В случае нормального распределения справедливо следующее условие: |As| < 3S As;
|A| < 3SAs; |E| < 3SEx
Проверим выполнение этого условия для заданного варианта.
𝑆𝐴𝑠 = 0,6172, 𝑆𝐸𝑥 = 0,5968
𝐴𝑠 = 0,0876, 𝐸𝑥 = −0,41
|0,0876| < 3 ∗ 0,6172 = 1,8516
| − 0,41| < 3 ∗ 0,5968 = 1,7905
Условия выполняются.
Проверку выборочной совокупности на близость ее к нормальному распределению
можно производить, используя статистики χ2, As и Ex.
Сначала вычислим статистику χ2 по формуле:
(2.9)
Затем при заданном уровне значимости α и числе степеней свободы k = 2
(используют в расчетах две статистики As и Ex) для распределения χ2 Пирсона находят χкр2.
Если выполняется неравенство χ2 < χкр2, то гипотезу о нормальном распределении
выборочной совокупности принимают. В противном случае, т.е. когда χ2>χкр2, гипотезу о
нормальном распределении выборки отвергают. Проверим гипотезу о том, что Х
распределено по нормальному закону с помощью правила 3-х сигм. Если случайная
величина распределена нормально, то абсолютная величина её отклонения от
математического
ожидания
не
превосходит
утроенного
среднеквадратического
отклонения, т.е. все значения случайной величины должны попасть в интервал:
(𝑥̅ − 3 ∗ 𝜎; 𝑥̅ + 3 ∗ 𝜎)
В нашем случае этот интервал составит:
(6,08 − 3 ∗ 2,69; 6,08 − 3 ∗ 2,69) = (−1,99; 14,15)
Все значения величин попадают в интервал, так как x min=0; xmax=12
2. Проверим гипотезу о том, что Х распределено по закону Пуассона
15
где
pi —
вероятность
попадания
в
i-й
интервал
случайной
(2.10)
величины,
распределенной по гипотетическому закону.
а) Находим по заданному эмпирическому распределению выборочную среднюю
(xВ = 6,08).
б) Принимаем в качестве оценки параметра λ распределения Пуассона выборочную
среднюю xср = 6,18. Следовательно, предполагаемый закон Пуассона имеет вид:
𝑝𝑖 =
6,18𝑖
∗ 𝑒 −6,08
𝑖!
в) Найдем по формуле Пуассона вероятности Pi, появления ровно i событий в n
испытаниях. Находим теоретические частоты
𝑖 = 0: 𝑝0 = 0,00229, 𝑛𝑝0 = 0,23
𝑖 = 1: 𝑝1 = 0,0139, 𝑛𝑝1 = 1,39
𝑖 = 2: 𝑝2 = 0,0423, 𝑛𝑝2 = 4,23
𝑖 = 3: 𝑝3 = 0,0857, 𝑛𝑝3 = 8,57
𝑖 = 4: 𝑝4 = 0,13, 𝑛𝑝4 = 13,03
𝑖 = 5: 𝑝5 = 0,16, 𝑛𝑝5 = 15,84
в) Вычисляем слагаемые статистики Пирсона по формуле
(2.11)
Рисунок 2.6 – Расчет слагаемых статистики Пирсона В ВИДЕ ТАБЛИЦЫ!
Определим границу критической области. Так как статистика Пирсона измеряет
разницу между эмпирическим и теоретическим распределениями, то чем больше ее
наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы.
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения γ2 и заданным
значениям s, k (число интервалов), r=1 (параметр λ).
𝐾𝑘𝑝(0,05; 4) = 9,48773; 𝐾набл = 558,87
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл >
Kkp, поэтому есть основания отвергать основную
16
гипотезу. Данные выборки
распределены не по закону Пуассона.
3. Проверка гипотезы о показательном распределении генеральной совокупности.
Для того чтобы при уровне значимости а проверить гипотезу о том, что
непрерывная случайная величина распределена по показательному закону, надо:
1. Найти по заданному эмпирическому распределению выборочную среднюю х cp.
Для этого находят середину i-го интервала xcπ = (xi+xi+1)/2, составляют последовательность
равноотстоящих вариант и соответствующих им частот.
2. Принять в качестве оценки параметра Х показательного распределения
величину, обратную выборочной средней:
𝜆 = 1/𝑥̅
(2.12)
3. Найти вероятности попадания X в частичные интервалы (xi,xi+1) по формуле:
𝑃𝑖 = 𝑃(𝑥𝑖 < 𝑋 < 𝑥𝑖+1 ) = 𝑒 −𝜆∗𝑥𝑖 − 𝑒 −𝜆∗𝑥𝑖+1
(2.13)
4. Вычислить теоретические частоты:
𝑛𝑖 = 𝑛 · 𝑃𝑖
(2.14)
5. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона,
приняв число степеней свободы k = s-2, где s - число первоначальных интервалов
выборки; если же было произведено объединение малочисленных частот, следовательно,
и самих интервалов, то s - число интервалов, оставшихся после объединения.
Среднее значение равно 6,08. Следовательно, параметр
1
= 0,16.
6,08
Таким образом, плотность предполагаемого показательного распределения имеет
𝜆=
вид:
𝑓(𝑥) = 0,16𝑒 − 0,16𝑥, 𝑥 ≥ 0
Найдем вероятности попадания X в каждый из интервалов по формуле:
Pi = P(xi < X < xi+1 ) = e−λ∗xi − e−λ∗xi+1
(2.15)
P1 = P(0 < 𝑋 < 2) = 1 − 0,7197 = 0,2803, ni = 100 ∗ 0,2803 = 28,03.
P2 = P(2 < 𝑋 < 4) = 0,7197 − 0,5179 = 0,2017, ni = 100 ∗ 0,2017 = 20,17.
P3 = P(4 < 𝑋 < 6) = 0,5179 − 0,3728 = 0,1452, ni = 100 ∗ 0,1452 = 14,52.
P4 = P(6 < 𝑋 < 8) = 0,3728 − 0,2683 = 0,1045, ni = 100 ∗ 0,1045 = 10,45.
P5 = P(8 < 𝑋 < 10) = 0,2683 − 0,1931 = 0,0752, ni = 100 ∗ 0,0752 = 7,52.
P6 = P(10 < 𝑋 < 12)
17