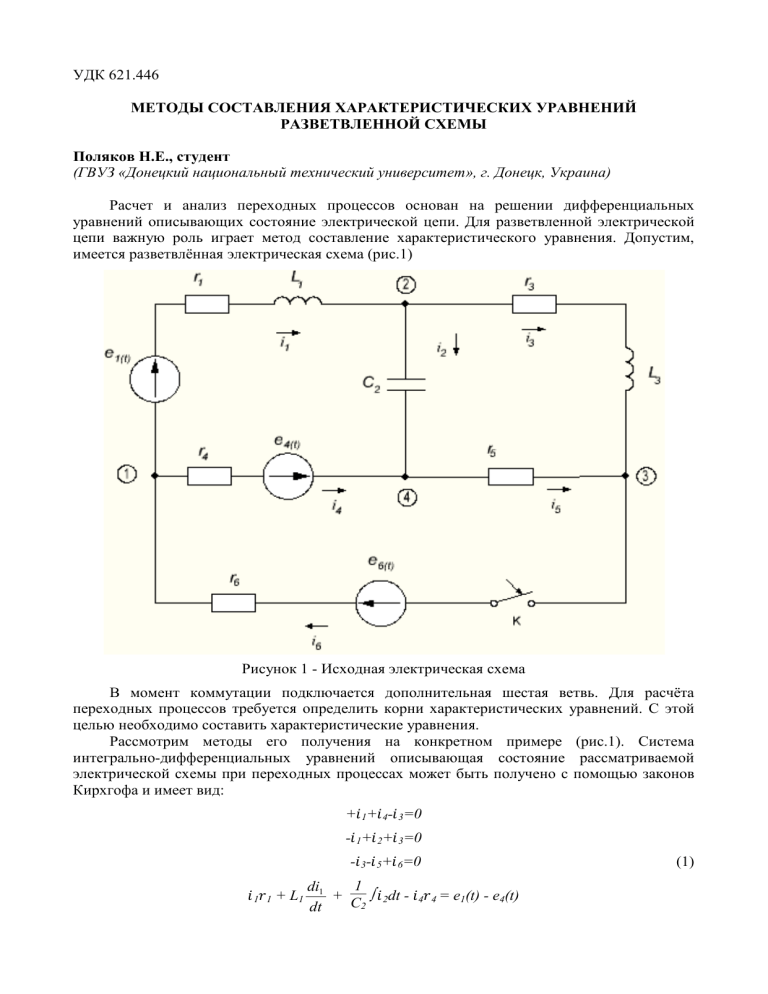
УДК 621.446 МЕТОДЫ СОСТАВЛЕНИЯ ХАРАКТЕРИСТИЧЕСКИХ УРАВНЕНИЙ РАЗВЕТВЛЕННОЙ СХЕМЫ Поляков Н.Е., студент (ГВУЗ «Донецкий национальный технический университет», г. Донецк, Украина) Расчет и анализ переходных процессов основан на решении дифференциальных уравнений описывающих состояние электрической цепи. Для разветвленной электрической цепи важную роль играет метод составление характеристического уравнения. Допустим, имеется разветвлённая электрическая схема (рис.1) Рисунок 1 - Исходная электрическая схема В момент коммутации подключается дополнительная шестая ветвь. Для расчёта переходных процессов требуется определить корни характеристических уравнений. С этой целью необходимо составить характеристические уравнения. Рассмотрим методы его получения на конкретном примере (рис.1). Система интегрально-дифференциальных уравнений описывающая состояние рассматриваемой электрической схемы при переходных процессах может быть получено с помощью законов Кирхгофа и имеет вид: +𝑖 1+𝑖 4-𝑖 3=0 -𝑖 1+𝑖 2+𝑖 3=0 -𝑖 3-𝑖 5+𝑖 6=0 𝑖 1𝑟1 + L1 1 di1 + C ∫ 𝑖 2dt - 𝑖 4𝑟4 = e1(t) - e4(t) 2 dt (1) 𝑖 3𝑟3 + L3 1 di3 - 𝑖 5𝑟5 - C ∫ 𝑖 2dt =0 2 dt 𝑖 4𝑟4 + 𝑖 5𝑟5 + 𝑖 6𝑟6 = e4(t) + e6(t) Составим систему уравнений для свободных составляющих. При этом принимаем во внимание, что свободные составляющие не зависят от внешних сил, поэтому ЭДС и токи источников равны нулю. Токи в произвольной k-той ветви равны 𝑖𝑘 = 𝐴𝑘 𝑒 𝑝𝑡 (𝐴𝑘 -постоянная интегрирования, 𝑝 -корень характеристические уравнения. Исходя из вышеизложенного напряжения на индуктивных элементах и емкостях соответственно равны. uL1св = L1 uL3 = L3 di1 св = L1pA1ept = pL1𝑖1св dt di3св dt = L3pA3ept=pL3𝑖3св (2) 1 1 1 uC2 = C ∫ 𝑖 2свdt = C P A2ept = C P 𝑖2св 2 2 2 Тогда система уравнений для свободных составляющих будет иметь вид: 𝑖1св + 𝑖6св - 𝑖св = 0 -𝑖1св + 𝑖2св + 𝑖3св = 0 -𝑖3св - 𝑖5св + 𝑖св = 0 – 1 𝑖1св r1 + pL1𝑖1св + C2P 𝑖2св + 0 - 𝑖св r = 0 (3) 1 𝑖 + 𝑖3св r3 + pL3𝑖3св - 𝑖5св r5 = 0 C2P 2св 𝑖4св r4 + 𝑖3св r3 + 𝑖5св r5 = 0 Определитель системы уравнений (3) имеет вид: ∆(p) = -1 0 0 1 0 -1 -1 1 1 0 0 0 0 0 -1 0 -1 1 (r1+ pL1) 1 C2 P 0 1 C2 P 0 0 0 r4 0 0 =0 (r3+ pL3) 0 r5 0 0 r5 r6 r5 (4) Так как правая часть системы уравнений (3) равна нулю, то и определитель системы 𝛥(𝑝) = 0. После раскрытия определителя получаем характеристическое уравнение системы. Оно имеет вид: p3L1L3C2+p2C2(R2(L1+L3)+R1L3+R3L1)+p(L1+L3+C2R2(R1+R3)+R1+R3=0, где R1=r1+ r4 r6 r4 + r6 + r5 (5) r4 r5 r4 + r6 + r5 R2= R3=r3+ r5 r6 r4 + r6 + r5 Полученное характеристическое уравнение третьего порядка, что соответствует количеству реактивных элементов исходной схемы. В результате получаем кубическое уравнение (третий порядок), что соответствует (5) и, следовательно после его решения имеем три корня. Недостатком известного вышесказанного способа является трудность раскрытия определителя высокого порядка, который имеет место для разветвлённых цепей. Ниже приводятся методы составления характеристических уравнений, в которых используется определитель более низкого порядка. На рис.2 приведена схема, составленная в соответствии с системой уравнений для свободных составляющих (3). Рисунок 2 – Схема для свободных составляющих В приведенной схеме (рис.2) ключ k ставят в положение, занимаемое после коммутации (замкнутое), источники питания заменяют их внутренними сопротивлениями, индуктивности 1 представляем сопротивлениями в виде pL, а ёмкости C P . При применении метода 2 контурных токов (МКТ) имеем: 1 1 𝑖𝐼св (r1+ pL1+ P +r4) - 𝑖𝐼𝐼св P - 𝑖𝐼𝐼𝐼св r4 = 0 C2 C2 A 1 1 -𝑖𝐼св C P + 𝑖𝐼𝐼св(C P + r3+ pL3+r5) - 𝑖𝐼𝐼𝐼свr5 = 0 2 2 A E A A E A -𝑖𝐼св r4- 𝑖𝐼𝐼свr5+𝑖𝐼𝐼𝐼св(r4+r5+r6) = 0 (6) Определитель полученной системы уменьшаем до третьего порядка, и он имеет вид: 1 (r1+ pL1+C P +r4) 2 A ∆(p) = 1 –C P 2 A E E 1 –C P 2 A A E -r4 A 1 ( C P + r3+ pL3+r5) 2 A A E -r4 -r5 A r5 =0 (7) (r4+r5+r6) После его раскрытия получим характеристически теоретическое уравнение, совпадающее с ранее полученным.Полученный определитель уменьшился до третьего порядка и после его раскрытия получаем характеристическое уравнение, совпадающее с ранее полученным (5). Для получения характеристического уравнения можно воспользоваться и методом узловых потенциалов (МУП). Принимая φ4св=0 имеем: 1 1 1 1 1 φ1св(r1+ pL1 + r4 + r6) – φ2свr1+ r4 – φ3свr6 = 0 1 1 1 1 –φ1свr1+ pL1 + φ2св(r1+ pL1 + r3+ pL3 + C2p) – φ3свr3+ pL3 = 0 1 1 1 1 1 (8) –φ1свr6 – φ2свr3+ pL3 + φ3св(r1+ pL1 + r5 + r6) = 0 Определитель полученной системы имеет вид: 1 ∆(p) = 1 1 (r1+ pL1 + r4 + r6) 1 – r1+ pL1 1 – r6 1 1 1 – r1+ r4 1 (r1+ pL1 + r3+ pL3 + C2p) 1 –r3+ pL3 – r6 1 1 – r3+ pL3 1 =0 (9) 1 (r1+ pL1 + r5 + r6) Выводы: Таким образом, используя МКТ и МУП можно уменьшить порядок определителя и тем самым существенно облегчить полученное характеристическое уравнениеВ схеме для свободных составляющих можно осуществлять эквивалентные преобразования с целью получения более простых схем, например треугольник сопротивлений r4,r5 и r6 заменяем эквивалентной звездой сопротивлений. В этом случае схема будет иметь три ветви и два узла. При применении МКТ получим определитель второго порядка, а по МУП одно уравнение Перечень ссылок 1. Зевеке Г.В., Ионкин П.А., Нетушил А.В. Основы теории цепей. – М. : Энергия, 1989.- 530 с.