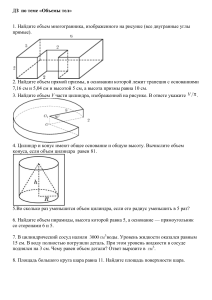
Общая цилиндрическая поверхность, её направляющая L и образующая m L m Общее определение цилиндрического тела 1 m Наклонный круговой цилиндр круг Н Прямой круговой цилиндр основание О1 боковая поверхность образующая О ось цилиндра С 2R R О1 О1 H So R 2 Sб 2R H О S п 2R H 2R 2R ( H R) 2 О R Сечение цилиндра плоскостью, параллельной его оси О1 Сечение цилиндра плоскостью, перпендикулярной его оси О1 А1 О2 О О А Цилиндрическая гастрономия Цилиндрическая архитектура Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см) указаны на рисунке. Решение. 1) Если дно шляпы опустить на плоскость её полей, то получим круг радиуса R = r1+ 10 = 20 cм. r1=10 10 10 2) Площадь этого круга So R2 400 (см2 ). 3) Найдем площадь боковой поверхности цилиндрической части Sб Сокр h 2 r1 h 2 10 10 200 (см2 ). 4) Найдем площадь шляпы Sшляпы 2 (Sкруга Sб ) 2 (400 200 ) 1600 (см2 ). Ответ: 1600 (см2). №523 Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см. Найдите: а) высоту цилиндра; б) So цилиндра Решение. B C 1. Проведем диагональ АС сечения АВСD. 2. ADC – равнобедренный, прямоугольный, АD=DC, h = 2r, 45 20 CAD = ACD=45, тогда 2 h AC cos 45 20 10 2 . 2 3. Найдем радиус основания 45 A D 4. Найдем площадь основания Ответ: а )10 2 ; б )50 . h 10 2 r 5 2. 2 2 2 So r 5 2 50 . 2 Площадь осевого сечения цилиндра равна 10 м2, а площадь основания – 5 м2. Найдите высоту цилиндра. №525 C Решение. 1. Площадь основания – круг, B So r 2 , тогда r S 5 . 2. Площадь сечения – прямоугольник, Sc AB BC h 2r , D A r тогда Sc 5 h 10 2 5 5 . 2r 5 Ответ: 5 . №527 В Концы отрезка АВ лежат на разных основаниях цилиндра. Радиус цилиндра равен r, его высота – h, расстояние между прямой АВ и осью цилиндра равно d. Найдите: a) высоту, если r = 10, d = 8, AB = 13. 1. Построим отрезок АВ. Решение. 2. Проведем радиус АО. 3. Построим отрезок d. 4. Отрезок ОК – искомое расстояние. 5. Из прямоугольного АОК находим: a AK r 2 d 2 100 64 6, С К А значит АС = 12. 6. Из прямоугольного АВС находим: d r ВС АВ 2 АС 2 169 144 5. r Итак, h = 5. Ответ: 5. №532 Через образующую АА1 цилиндра проведены две секущие плоскости, одна из которых проходит через ось цилиндра. Найдите отношение площадей сечений цилиндра этими плоскостями, если угол между ними равен . Решение. В A 1) Сделаем чертеж, построим плоскости АА1В1В и АА1С1С. 2) Составим отношение площадей AA1 AB AB сечений S ABB1 A1 C S ACC1 A1 AA1 AC AC . 3) Построим плоскость ВВ1С1С. В1 А1 1 Ответ: . cos 4) Заметим, что АВ диаметр основания цилиндра, значит АСВ=90, тогда AC AB cos . C1 5) Итак, S ABB1 A1 S ACC1 A1 AB AB 1 . AC AB cos cos Плоскость , параллельная оси цилиндра, отсекает от окружности основания дугу AmD с градусной мерой . Радиус цилиндра равен a, высота равна h, расстояние между осью цилиндра ОО1 и плоскостью равно d. 1) Докажите, что сечение цилиндра плоскостью есть прямоугольник. 1) Составьте план вычисления площади сечения по данным , h, d. 2) Найдите AD, если a = 10 см, = 60. 2) Найдите AD, если a = 8 см, = 120. Ответ: 10 Ответ: 8 3 Домашнее задание Повторить стр.130-132, гл. 1, п.59-60, №530, № 537. Рефлексия Что нового вы узнали на уроке? Чему вы научились? Какое у вас настроение в конце урока? Можете ли вы объяснить решение данных задач однокласснику, пропустившему урок сегодня?