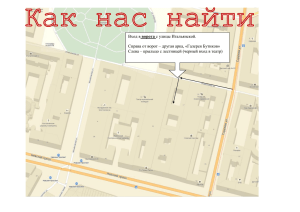
1. Понятие логической переменной, способы задания функций алгебры логики. Логические переменные принимают два значения: истина и ложь. Логическая переменная — это электрический сигнал, принимающий два различных значения, известные как состояния ИСТИНА и ЛОЖЬ. Логической функцией называется функция f (x 1, x 1,...,x n) , которая, так же как и ее аргументы, может принимать только два значения (0 и 1). Различают несколько способов задания ФАЛ, основными из которых являются: табличный, аналитический, цифровой, таблично-графический, геометрический. Табличный способ предусматривает задание ФАЛ таблицей истинности, в которой указывают, какие из двух возможных значений «0» или «1» принимает функция на каждом наборе аргументов. Наборы, на которых значение ФАЛ равно «1» называются рабочими. Наборы, на которых функция принимает нулевое значение, называются запрещёнными. Аналитический способ задания предполагает запись функции в виде формализованного выражения, составленного с использованием математического аппарата алгебры логики. Например Цифровой способ задания ФАЛ реализуется посредством записи функции в виде совокупности рабочих, запрещённых и условных наборов аргументов. Условными наборами аргументов называются наборы, на которых значение функции не определено или нас не интересует. При цифровом способе задания функции f, будут записаны в виде: Таблично-графический или координатный способ предусматривает задание ФАЛ в виде координатных карт состояний, называемых картами Карно. При наличии n переменных карты Карно состоят из полей и представляют собой прямоугольные таблицы, на пересечении строки и столбца которых записывают значение функции при соответствующем наборе аргументов. При составлении карты необходимо следить, чтобы наборы аргументов в соседних полях (клетках) таблицы отличались только значением одной переменной. Каждое поле карты соответствует одной строчке таблицы истинности, при табличном способе задания функции. 2. Полностью и не полностью определенные функции алгебры логики. Функция является полностью заданной, если указаны ее значения для всех наборов. Сопоставляя каждому набору значение функции можно задать функцию с помощью таблицы, называемой таблицей истинности или таблицей соответствия. Функция является не полностью заданной, если не указаны ее значения для некоторых наборов. 3. Функции алгебры логики одной переменной. Рассмотрение понятия функции в алгебре логики (АЛ) можно начать с функций одной переменной. Нетрудно видеть, что таких функций можно построить четыре набора. Продолжая этот ряд получим таблицу, показывающую, что количество логических функций вычисляется как два в степени количества возможных входных наборов. 4. Функции алгебры логики двух переменных Таблица истинности функции двух переменных Y=f(X1,Х2) содержит 4 строки, а число функций двух переменных равно 16. 1. Логическое ИЛИ (логическое сложение, дизъюнкция): Y= X1 + X2 = X1VX2 Техническая реализация этой функции - два параллельно соединенных ключа: Таблица истинности логического ИЛИ имеет вид: Логический элемент ИЛИ обозначается на схемах следующим образом: 2. Логическое И (логическое умножение, конъюнкция, схема совпадений): Y = X1X2 = X1&X2 Техническая реализация этой функции - два последовательно соединенных ключа: Таблица истинности логического И имеет вид: Логический элемент И обозначается на схемах следующим образом: 5. Основные свойства функций алгебры логики В алгебру логики установлен целый ряд законов, с помощью которых возможно преобразование логических функций (ЛФ): коммутативный (переместительный) ассоциативный (сочетательный) Эти законы полностью идентичны законам обычной алгебры; дистрибутивный (распределительный) Закон поглощения. В дизъюнктивной форме ЛФ конъюнкция меньшего ранга, т.е. с меньшим числом переменных, поглощает все конъюнкции большего ранга, если ее изображение содержится в них. Это же справедливо и для конъюнктивных форм: Закон склеивания Закон свёртки . Правило де Моргана где F - логическая функция общего вида, не зависящая от переменной х. 6. Функционально полные системы, понятие базиса. Функционально полной системой булевых функций (ФПСБФ) называется совокупность таких булевых функций (f1, f2, ... fk), что произвольная булева функция f может быть записана в виде формулы через функции этой совокупности. Функционально полная система логических функций представляет собой набор логических функций, с помощью которых можно записать любую, сколь угодно сложную функцию. В этом случае говорят, что этот набор образует базис. Функционально полными являются 3 базиса: 1) "И-ИЛИ-НЕ" (базис конъюнкции, дизъюнкции, инверсии) 2) "И-НЕ" (базис Шеффера) 3) "ИЛИ-НЕ" (базис Пирса или функция Вебба). Элементы, реализующие операцию "И-НЕ", “ИЛИ-НЕ” и “Исключающее ИЛИ” на принципиальных и структурных схемах изображаются так: 7. Минимизация функций алгебры логики, постановка задачи. На основе ФАЛ осуществляется построение схем различных ДУ. Поэтому актуальной задачей является преобразование ФАЛ к виду, обеспечивающему наиболее простую по количеству используемых логических элементов, схемную реализацию. Решение этой задачи в полном объёме сопряжено со значительными трудностями, обусловленными необходимостью учёта индивидуальных особенностей используемой элементной базы. Однако существуют методы, позволяющие преобразовывать ФАЛ к виду, содержащему минимальное число термов. Под минимизацией логической функции понимается выполнение преобразований с целью получения наиболее простого представления ФАЛ. Преобразование логических функций с целью упрощения их аналитического представления называются минимизацией. Существуют два направления минимизации: 1. Кратчайшая форма записи (цель – минимизировать ранг каждого терма). При этом получаются кратчайшие формы КДНФ, ККНФ, КПНФ. 2. Получение минимальной формы записи (цель – получение минимального числа символов для записи всей функции сразу). Метод последовательного перебора основан на простом переборе всех возможных вариантов алгебраического выражения ФАЛ. Метод последовательного упрощения аналитического выражения базируется на преобразовании ФАЛ с использованием основных законов и тождеств АЛ. Достоинством метода является возможность его применения для минимизации любых ФАЛ, представленных в виде аналитического выражения. Метод, основанный на применении карт Карно, предусматривает задание ФАЛ в виде координатных карт состояний. После записи ФАЛ в карту Карно сразу можно записать минимальную форму функции, что существенно уменьшает вероятность появления ошибки. 8. Алгебраический метод минимизации. Алгебраический подход. Минимизация как упрощение формул в булевой алгебре (как и в любой другой алгебре) производится на основе эквивалентных преобразований , опирающихся на основные законы, тождества и правила. 9. Табличный метод минимизации. Карта Карно́ — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Исходной информацией для работы с картой Карно является таблица истинности минимизируемой функции. Таблица истинности содержит полную информацию о логической функции, задавая её значения на всех возможных 2N наборах входных переменных X1 ... XN. Карта Карно также содержит 2N клеток, каждая из которых ассоциирцется с уникальным набором входных переменных X1 ... XN. Таким образом, между таблицей истинности и картой Карно имеется взаимно однозначное соответствие, и карту Карно можно считать соответствующим образом отформатированной таблицей истинности. 10. Метод существенных переменных. Возьмем произвольную функцию f, M1(f) – единичное множество. Проще говоря, множество наборов переменныx, на которых функция обращается в верное высказывание. Построить таблицу истинности. Выписать все гиперкубы из M1(f) и импликанты. Взять простые импликанты. Построить таблицу накрытия. Из оставшихся простых импликантов создать тупиковую ДНФ. Построим таблицу истинности для нее: Выпишем все гиперкубы, лежащие в M1(f) и соответствующие им импликанты: Выбираем простые импликанты и строим таблицу их накрытия: Поскольку импликанта yz перекрывается другими, ее можно изъять из выражения. Выходит, что тупиковая ДНФ функции имеет вид: 11.Типы цифровых устройств, комбинационные и последовательностные цифровые устройства. Цифровые устройства можно разделить на комбинационные и последовательностные. В комбинационных – значения Y в течение каждого такта определяются только значениями X в этом же такте. Такие устройства состоят из логических элементов. В последовательностных – значения Y определяются значениями X, как в течение рассматриваемого такта, так и существовавшими в ряде предыдущих тактов. Для этого в последовательностных устройствах, кроме логических должны быть еще и запоминающие элементы. а б Запоминающее устройство может хранить информацию не бесконечно большого, а только ограниченного числа тактов, поэтому цифровые устройства с памятью называют конечными автоматами, к которым относят все ЭВМ. Цифровые устройства можно разделить на асинхронные и синхронные. В асинхронных изменение входных сигналов сразу же вызывает изменение выходных сигналов. В синхронных изменение выходных сигналов, соответствующее новому сочетанию входных, происходит только после подачи синхронизирующих (тактовых) импульсов, управляющих работой автомата. Период синхроимпульсов является, таким образом, минимальным временем между выполнением автоматом двух последовательных микроопераций, т.е. служит единицей машинного времени, называемой тактом. В зависимости от структуры автомата за один такт могут выполняться одна или несколько микроопераций, если они совмещены во времени. В асинхронных устройствах отсутствуют синхронизирующие сигналы, поэтому в их структуры обычно включаются специальные схемы, которые после окончания каждой микрооперации вырабатывают сигнал готовности к выполнению следующей микрооперации. 12. Преобразователи кода. Микросхемы преобразователей кодов (англ. сonverter) служат для преобразования входных двоичных кодов в выходные двоично-десятичные и наоборот - входных двоично-десятичных кодов в выходные двоичные. Преобразователи кодов служат для перевода одной формы числа в другую. Их входные и выходные переменные однозначно связаны между собой. Эту связь можно задать таблицами переключений или логическими функциями. Шифратор преобразует одиночный сигнал в n-разрядный двоичный код. Наибольшее применение он находит в устройствах ввода информации для преобразования десятичных чисел двоичную систему счисления. Предположим, на пульте десять клавишей с гравировкой от 0 до 9. При нажатии любой из них на вход шифратора подаётся единичный сигнал (ХО-Х9). Дешифратор преобразует код, поступающий на его входы, в сигнал только на одном из его выходов. Дешифраторы широко применяются в устройствах управления, в системах цифровой индикации, для построения распределителей импульсов по различным цепям и т. д. 13. Дешифраторы, двоичные дешифраторы. Дешифратор преобразует код, поступающий на его входы, в сигнал только на одном из его выходов. Дешифраторы широко применяются в устройствах управления, в системах цифровой индикации, для построения распределителей импульсов по различным цепям и т. д. Двоичный дешифратор работает по следующему принципу: пусть дешифратор имеет N входов, на них подано двоичное слово xN − 1xN − 2...x0, тогда на выходе будем иметь такой код, разрядности меньшей или равной 2N, что разряд, номер которого равен входному слову, принимает значение единицы, все остальные разряды равны нулю. Очевидно, что максимально возможная разрядность выходного слова равна 2N. Такой дешифратор называется полным. Если часть входных наборов не используется, то число выходов меньше 2N, и дешифратор является неполным. Часто дешифраторы дополняются входом разрешения работы. Если на этот вход поступает единица, то дешифратор функционирует, в ином случае на выходе дешифратора вырабатывается логический ноль вне зависимости от входных сигналов. Функционирование дешифратора описывается системой конъюнкций: ………………………………………………………… Дешифраторы. Это комбинационные схемы с несколькими входами и выходами, преобразующие код, подаваемый на входы в сигнал на одном из выходов. На выходе дешифратора появляется логическая единица, на остальных — логические нули, когда на входных шинах устанавливается двоичный код определённого числа или символа, то есть дешифратор расшифровывает число в двоичном, троичном или k-ичном коде, представляя его логической единицей на определённом выходе. Число входов дешифратора равно количеству разрядов поступающих двоичных, троичных или k-ичных чисел. Число выходов равно полному количеству различных двоичных, троичных или k-ичных чисел этой разрядности. Для n-разрядов на входе, на выходе 2n, 3n или kn. Чтобы вычислить, является ли поступившее на вход двоичное, троичное или k-ичное число известным ожидаемым, инвертируются пути в определённых разрядах этого числа. Затем выполняется конъюнкция всех разрядов преобразованного таким образом числа. Если результатом конъюнкции является логическая единица, значит на вход поступило известное ожидаемое число. 14. Мультиплексоры и демультиплексоры. Мультиплексор является устройством, которое осуществляет выборку одного из нескольких входов и подключает его к своему выходу. Мультиплексор имеет несколько информационных входов (D0, D1, ...), адресные входы (А0 А1, ...), вход для подачи стробирующего сигнала С и один выход Q. Каждому информационному входу мультиплексора присваивается номер, называемый адресом. При подаче стробирующего сигнала на вход С мультиплексор выбирает один из входов, адрес которого задается двоичным кодом на адресных входах, и подключает его к выходу. Демультиплексор имеет один информационный вход и несколько выходов. Он представляет собой устройство, которое осуществляет коммутацию входа к одному из выходов, имеющему заданный адрес (номер). Объединяя мультиплексор с демультиплексором, можно построить устройство, в котором по заданным адресам один из входов подключается к одному из выходов. Таким образом, может быть выполнена любая комбинация соединений входов с выходами. 15. Цифровые компараторы. Компаратор цифровой – это устройство, осуществляющее сравнение двух многоразрядных двоичных чисел. В общем случае, на рисунке показан компаратор, который получает на выходе логическую ‘1’ при равенстве двух многоразрядных двоичных чисел. Два многоразрядных числа равны, если в одноименных разрядах цифры одинаковые. Цифровые компараторы выполняют сравнение двух чисел, заданных в двоичном коде. Они могут определять равенство двух двоичных чисел А и В с одинаковым количеством разрядов либо вид неравенства А>В или А<В. Цифровые компараторы имеют три выхода. Схема одноразрядного компаратора представляет собой структуру логического элемента «исключающее ИЛИ–НЕ» Из анализа схемы следует, что если А = В, то F = 1, в противном случае, т. е. при А ≠ В, F = 0. Если А > В, т. е. А = 1, В = 0, то С = 1, а если А < В, т. е. А = 0, В = 1, то D = 1. Если попарно равны между собой все разряды двух n-разрядных двоичных чисел, то равны и эти два числа А и В. Применяя цифровой компаратор для каждого разряда, например, четырехзначных чисел, и определяя значения F1, F2, F3, F4 логических переменных на выходах компараторов, факт равенства А = В установим в случае, когда F = F1 · F2 · F3 · F4 = 1. Если же F = 0, то А ≠ В. Неравенство А> В обеспечивается (для четырехразрядного числа) в четырех случаях: или А4 > В4, или А4 = В4 И А3> В3, или А4 = В4, А3 =В3 и А2 > В2, или А4 = В4, А3 = В3, А2 = В2 и А1 > В1, где А4 и В4 – старшие разряды чисел А и В). Очевидно, что если поменять местами A i и Bi то будет выполняться неравенство А < В. Цифровые компараторы выпускают, как правило, в виде самостоятельных микросхем. Так, микросхема К564ИП2 (рис. 1.24) является четырехразрядным компаратором, в котором каждый из одноразрядных компараторов аналогичен рассмотренной ранее схеме. Данная микросхем а имеет расширяющие входы А<В, А=В, А>В, что позволяет наращивать разрядность обоих чисел. Для этого компараторы соединяют каска дно или параллельно (пирамидально ). 16. Сумматоры двоичных кодов чисел. Сумматор — логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учёт знаков чисел, выравнивание порядков слагаемых и тому подобное. Указанные операции выполняются в арифметическо-логических устройствах (АЛУ) или процессорных элементах, ядром которых являются сумматоры. Сумматор - устройство, выполняющее операции арифметического сложения над двоичными числами. Сумма двух нулей есть нуль, сумма нуля и единицы есть единица, сумма двух единиц есть нуль. Одноразрядный цифровой сумматор имеет три входа: два входа слагаемых и вход переноса (от предыдущего сумматора). При этом правила сложения чуток усложняются. Одноразрядный сумматор обозначается так: Сумматор имеет входы А и В - слагаемые, С - вход переноса, S - выход суммы, Р - выход переноса. Табличка истинности: Входы Выходы Слагаемые Вход переноса Сумма Выход переноса А B C S P 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 0 0 1 0 0 1 1 0 0 1 1 0 1 1 0 1 0 1 1 1 1 1 1 На выходе S представляется сумма сложения трех переменных - А, В, С. При переполнении сумматора, т. е. когда в результате сложения формируется единица в старшем разряде выходного числа, на выходе переноса Р формируется уровень лог. 1, который подается на вход переноса С следующего сумматора. В принципе, старшим разрядом суммы является выход переноса Р. В целом работу сумматора полностью иллюстрирует таблица. Из таких одноразрядных сумматоров составляются многоразрядные сумматоры (обычно 4-х разрядные), которые бывают последовательного и параллельного действия. Сумматоры последовательного действия обладают более низким быстродействием. 17. Устройства вычитания двоичных чисел. Со сложением двоичных чисел все понятно. Как же осуществить на микросхемах-сумматорах операции вычитания двоичных чисел? Допустим необходимо выполнить вычитание: 11 - 5 = 6. В двоичных эквивалентах произведем операцию сложения числа 1011 (число 11) иобратный код числа 5, равный 1010 (прямой код 0101). Итак: Если отбросить единицу в старшем (пятом) разряде, то получится код 0101, который соответствует числу 5. Но это не число 6. Значит к результату необходимо прибавить единицу. Кстати, операция увеличения какого-либо числа на единицу называется инкрементом, уменьшения на единицу декрементом. На рисунке 2 показана схема четырехразрядного вычитателя. Инверторы микросхемы DD1 формируют обратный код числа В. Число А поступает на входы А1-А4 сумматора DD2, обратный код числа В - на входы В1-В4 сумматора. На вход переноса Р0 подан уровень лог. 1, что обеспечивает прибавление к результату сложения единицы (т. е. инкремент результата). На выходах S1-S4 сумматора в итоге получается разность между числами А и В. 18. Двоично-десятичные сумматоры. Чаще приходится суммировать десятичные числа. Ниже на рисунке приведена схема сумматора двоично-десятичных чисел на основе двоичных сумматоров. Операцию сложения выполняет сумматор DD1. При сумме большей или равной десяти на выходе микросхемы DD2, которая является схемой сравнения входов, формируется сигнал переноса Р10. На второй вход (Y1-Y4) микросхемы DD2 подается двоичный эквивалент числа 9 (1001). Сумматор DD3 осуществляет десятичную коррекцию результата суммирования. При отсутствии сигнала переноса на выходе микросхемы DD3 повторяется код числа, который был на выходе DD1, поскольку на входы В поданы лог. 0. При наличии сигнала переноса Р10=1 на входах В2-В3 устанавливаются лог. 1, что соответствует коду числа 6. Допустим есть числа А=8 и В=4. На выходе сумматора DD1 появляется код числа 12 (8+4=12). На выходе DD2 формируется сигнал переноса, сумматор DD3 выполняет операцию 12+6=18. Числу 18 соответствует код 10010. На выходах S сумматора DD3 устанавливается код 0010 (собственный перенос микросхемы DD3 не учитывается). Поскольку на выходе Р10 число 10, на выходах сумматора число 2 (0010), то в результате получается число 12. 19. Триггеры, типы триггеров. Триггеры-это логические устройства с памятью. Их выходные сигналы в общем случае зависят не только от сигналов, приложенных к входам в данный момент времени, но и от сигналов, воздействовавших на них ранее. В зависимости от свойств, числа и назначения входов триггеры можно разделить на несколько видов. Типы триггеров. Все современные серии цифровых микросхем, как правило включают различные типы триггеров, представляющих устройство с двумя устойчивыми состояниями, содержащее бистабильный запоминающий элемент (собственно триггер) и схему управления. Входы, как и сигналы, подаваемые на них делятся на информационные и вспомогательные. Информационные сигналы через соответствующие входы управляют состоянием триггера. Сигналы на вспомогательных входах служат для предварительной установки триггера в заданное состояние и его синхронизации. Вспомогательные входы могут при необходимости выполнить, роль информационных. По способу приема информации триггеры подразделяют тактируемые и нетактируемые триггеры. Изменение состояния нетактируемого (асинхронного) триггера происходит сразу же после соответствующего изменения потенциалов на его управляющих входах. В тактируемом (синхронном) триггере изменение состояния может произойти только в момент присутствия соответствующего сигнала на тактовом входе. Тактирование может осуществляться импульсом (потенциалом) или фронтом (перепадом потенциала). В первом случае сигналы на управляющих входах оказывают влияние на состояние триггера только при разрешающем потенциале на тактовом входе. Во втором случае воздействие управляющих сигналов проявляется только в момент перехода единица - нуль или нуль - единица на тактовом входе. Существуют также универсальные триггеры, которые могут работать как в тактируемом, так и в нетактируемом режиме. Основные типы триггеров в интегральном исполнении носят следующие названия: D-триггеры, Ттриггеры, RS-триггеры и JK-триггеры. RS-триггер. Асинхронный триггер RS-типа имеет два информационных входа R и S. Входы S и R названы по первым буквам английских слов set - установка и reset - сброс. При S=1 и R=0 на выходах триггера появляются сигналы: на прямом выходе Q=1, на инверсном Q=0. При S=0 и R=1 выходные сигналы триггера принимают противоположные состояния (Q=0, Q=1). Этот триггер не имеет тактового входа. Простейший RS-триггер можно реализовать на логических элементах ИЛИ-НЕ или И-НЕ, как показано на рисунке 1. Проиллюстрировать работу такого асинхронного триггера можно с помощью таблиц истинности или временных диаграмм. Обратите внимание, что простейший триггер при S=1 и R=0 устанавливается в состояние логического нуля (и наоборот). Здесь Q – состояние выхода до установки входных сигналов (режим хранения). На элементах ИЛИ-НЕ На элементах И-НЕ Вход S Вход R Прям. Q Инвер. Q Вход S Вход R Прям. Q Инвер. Q 0 0 Q Q 0 0 1 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 1 1 0 0 1 1 Q Q При одновременном поступлении сигнала 1 или 0 на входы R и S выходные сигналы триггера не определены, поэтому в устройствах на основе RS-триггера необходимо исключать такие режимы (запрещенное состояние). Существуют разновидности RS-триггера, носящие название Е-, R- и Sтриггеров, для которых сочетание S=1 и R=1 не является запрещенным. Синхронный одноступенчатый RS-триггер рис. 2 отличается от асинхронного наличием С-входа для синхронизирующих тактовых импульсов. Синхронный триггер состоит из асинхронного RS-триггера и двух логических элементов на его входе. а б в Рис. 2. Синхронный RS-триггер. а - структурная схема; б - условное обозначение в - временные диаграммы Переключение этого триггера происходит только при появлении высокого уровня на тактовом входе С, что хорошо видно на временной диаграмме, рис. 2. Триггер RS используется как устройство памяти в других типах триггеров. D-триггер. или триггер задержки (от английского delay-задержка), при разрешающем сигнале на тактовом входе устанавливается в состояние, соответствующее потенциалу на входе D. Если обозначать выходной сигнал триггера буквой Q, то для D-тригтера можно написать следующее равенство: Qn=Dn-1. Индексы n и n-1 указывают на то, что выходной сигнал Q изменяется не сразу после изменения входного сигнала D, а только с приходом разрешающего тактового сигнала. Тактирование D-триггера может о существляться импульсом или фронтом. В тактируемом фронтом D-триггере изменение потенциала на входе D, синхронное с тактовыми импульсами, повторяется на выходе Q с задержкой на один период тактовых импульсов (отсюда и название-триггер задержки). На рисунке 3 показаны: структурная схема, условное обозначение и временная диаграмма D-триггера. Он состоит из синхронного RS-триггера и инвертора. Благодаря инвертору невозможно запрещенное соотношение сигналов на входах S и R. Из временной диаграммы (рис. 3в) видно, что D-триггер осуществляет задержку установки Q на время, отделяющее момент из менения сигнала D от начала очередного тактового импульса, причем выходной сигнал Q сохраняется до прихода очередного тактового импульса. Dn Qn+1 0 0 1 1 а. б. в. г. Рис. 3. D-триггер: а- таблица истинности б - структурная схема; в - условное обозначение г - временные диаграммы Тактирование D-триггера может осуществляться уровнем или фронтом. Более простым является Dтриггер первого типа, который реализуется на основе RS-триггера (рис. 3). Он состоит из синхронного RS-триггера и инвертора. Благодаря инвертору невозможно запрещенное соотношение сигналов на входах S и R. Рис. 4. D-триггер синхронизируемый уровнем (статическое управление). Условное обозначение и временные диаграммы На анализ работы и временная диаграмма (рис. 4) показывают, что сигнал с входа D проходит на выход Q только при условии высокого уровня на тактовом входе C. Рис. 5. D-триггер синхронизируемый фронтом (динамическое управление). Условное обозначение и временные диаграммы. В тактируемом фронтом D-триггере (рис.5) изменение потенциала на входе D, синхронное с тактовыми импульсами, повторяется на выходе Q по перепаду уровня (в данном случае с низкого на высокий) с задержкой относительно тактовых импульсов. Выходной сигнал Q сохраняется до прихода очередного тактового импульса. При чем эта информация хранится в D-триггере, пока не придет следующий бит (0 или 1) информации. По сути это ячейка памяти. Если вход D замкнуть с инверсным выходом, то останется только один вход С. При подаче на вход С импульсов триггер переключается в противоположное состояние. Таким образом, триггер осуществляет деление частоты входных импульсов на 2. В таком режиме D-триггер работает счетным или Т-триггером. Т-триггер, или счетный триггер, срабатывает только по соответствующему фронту на тактовом входе, т. е. Т-триггеры бывают только тактируемые фронтом. Кроме тактового входа, Т-триггер может иметь один управляющий вход - Т-вход. Сигнал на этом входе разрешает (если Т=1) или запрещает (если Т=0) срабатывание триггера от фронтов импульсов, приходящих на тактовый вход. Для такого триггера Qn= (QT+QT)n-1. Из этого уравнения следует, что при Т=1 соответствующий фронт сигнала на тактовом входе переводит триггер в противоположное состояние (из нуля в единицу и наоборот). Частота изменения потенциала на выходе Т-триггера в два раза меньше частоты импульсов на его тактовом входе (при Т=1). Это свойство Т-триггеров позволяет строить на их основе двоичные счетчики. Поэтому эти триггеры и называются счетными. Если в Т-триггере отсутствует управляющий вход, то он срабатывает на каждый соответствующий перепад на тактовом входе, т.е. ведет себя как Т-триггер с управляющим входом при Т=1. Tn Qn+1 0 Qn 1 Qn+1 а. б. в. г. Рис. 6. T-триггер: а-таблица истинности б - структурная схема в - условное обозначение г - временные диаграммы JK-триггер имеет также два управляющих входа J и K. Подобно RS-триггеру, в JK-триггере J и K-это входы установки триггера в единицу и нуль. В отличие от RS-триггера в JK-триггере наличие двух единичных управляющих сигналов (J=K=1) приводит к переходу триггера в противоположное состояние, т. е. в данном случае JK-триггер работает как T-триггер. JK-триггеры тактируются только перепадом потенциала на тактовом входе, те он всегда тактируемый или уровнем, или фронтом. Находят применение также JK-триггеры, которые изменяют свои состояния под воздействием перепадов сигналов на входах J и K. Уравнение для JK-триггера выглядит следующим образом: Qn=( JQ + KQ )n-1. На рис.4 указаны основные принципы построения и обозначения JK-триггеров. Рис. 4 Принципы построения (а, в, г) и обозначения (б, д) JK-триггеров. Практические микросхемы триггеров обычно содержат различные вспомогательные входы. В качестве примера на рис. 4 д показана схема триггера К155ТВ1. Здесь кроме тактируемых входов J и K имеются также нетактируемые инверсные входы S и R. Для того чтобы упростить построение счетчиков, в этих триггерах предусмотрено по три входа J и К, объединенных посредством ячеек И (J=J1J2J3. K=K1K2K3). В таблице ниже перечислены режимы работы JK-триггера. Напоминаем, что переключение происходит только при поступлении тактового импульса на вход C. J K Q Режим работы 0 0 Q Хранение 1 0 1 Установка в 1 0 1 0 Сброс в 0 1 1 Qinv Счет 20. Делители частоты, формирователи цифровых сигналов. Счетчиками в цифровой технике называются специальные элементы, позволяющие подсчитывать число поступивших на вход импульсов. Понятие «счетчик импульсов» тесно связано с понятием «делитель частоты». По сути дела, это одно и то же устройство.. В качестве простейшего делителя частоты может выступать рассмотренный в предыдущей главе Жтриггер. Для того, чтобы этот триггер работал как делитель, нужно на оба входа J и К подать высокий логический уровень. Теперь, если на вход С подать импульсный сигнал некоторой постоянной частоты, то по спаду каждого входного импульса триггер будет переключаться в противоположное состояние. В результате на выходе JK-триггера мы получим другой сигнал с частотой следования импульсов в два раза меньшей, чем частота импульсов на его входе. Этот процесс наглядно показан на рис. 1.20. Как видно из рисунка, период сигнала на выходе делителя ровно в два раза больше периода входного сигнала. А частота выходного сигнала, соответственно, в два раза ниже входного. Второй вариант делителя частоты приведен на рис. 1.21. Он построен на основе D-триггера. Для того, чтобы перевести D-триггер в_счетный режим, нужно соединить инверсный выход триггера Q с его Dвходом, так как это показано на рис. 1.21. Теперь, если подать сигнал на вход С, такая схема тоже будет работать как делитель. Выходной сигнал такого делителя снимается с выхода Q триггера. Рассмотрим подробнее работу этой схемы. Предположим, что после включения триггер установился в единичное состояние. Это означает, что на инверсном выходе триггера (Q) присутствует логический ноль. Этот ноль поступает на D-вход. Подадим на вход делителя некоторый цифровой сигнал, такой же, как мы подавали и в предыдущем случае (см. рис. 1.20). По спаду первого входного импульса D-триггер перейдет в нулевое состояние, так как на его D-входе сигнал логического нуля. После этого на инверсном выходе триггера устанавливается логическая единица. Поэтому по спаду следующего входного импульса триггер переключится в единичное состояние. И так далее. Результат работы делителя на D-триггере точно такой же, как и делителя на JK-триггере, и выходной сигнал нового варианта так же полностью соответствует рис. 1.20. Следует заметить, что в настоящее время Ж-триггеры применяются довольно редко. Гораздо большее распространение благодаря своей простоте и универсальности получили D-триггеры. Делители широко используются в цифровой технике. Цепочка последовательно соединенных Dтриггеров позволяет получить сигналы требуемой частоты путем деления импульсов задающего генератора. 21. Регистры последовательного и параллельного типа. Регистры Регистром называется последовательное или параллельное соединение триггеров. Регистры обычно строятся на основе D триггеров. При этом для построения регистров могут использоваться как динамические D триггеры, так и статические триггеры. Параллельные регистры Параллельный регистр служит для запоминания многоразрядного двоичного (или недвоичного) слова. Количество триггеров, входящее в состав параллельного регистра определяет его разрядность. Схема четырёхразрядного параллельного регистра приведена на рисунке 1, а его условно-графическое обозначение - на рисунке 2. . В условно-графическом обозначении возле каждого входа D указывается степень двоичного разряда, который должен быть запомнен в этом триггере регистра. Точно таким же образом обозначаются и выходы регистра. То, что микросхема является регистром, указывается в центральном поле условнографического обозначения символами RG. В приведённом на рисунке 2 условно-графическом обозначении параллельного регистра инверсные выходы триггеров не показаны. В микросхемах регистров инверсные выходы триггеров часто не выводятся наружу для экономии количества выводов корпуса. При записи информации в параллельный регистр все биты (двоичные разряды) должны быть записаны одновременно. Поэтому все тактовые входы триггеров, входящих в состав регистра, объединяются параллельно. Для уменьшения входного тока вывода синхронизации C на этом входе в качестве усилителя часто ставится инвертор. Следует помнить, что назначение разрядов является условным. Если по каким либо причинам (например, с точки зрения разводки печатной платы) удобно изменить нумерацию разрядов, то это можно свободно сделать. При перенумерации входов регистров нужно не забывать, точно таким же образом, изменить номера выходов параллельного регистра. Для реализации параллельного регистра можно использовать как триггеры с статическим, так и с динамическим входом синхронизации. В переводной литературе при использовании для построения параллельного регистра триггеров-защелок этот регистр, в свою очередь, называют регистромзащелкой. Последовательные регистры Кроме параллельного соединения триггеров для построения регистров используются последовательное соединение этих элементов. Последовательный регистр (регистр сдвига) обычно служит для преобразования последовательного кода в параллельный и наоборот. Применение последовательного кода связано с необходимостью передачи большого количества двоичной информации по ограниченному количеству соединительных линий. При параллельной передаче разрядов требуется большое количество соединительных проводников. Если двоичные разряды последовательно бит за битом передавать по одному проводнику, то можно значительно сократить размеры соединительных линий на плате (и размеры корпусов микросхем). Принципиальная схема последовательного регистра, собранного на основе D-триггеров и позволяющего осуществить преобразование последовательного кода в параллельный, приведена на рисунке 3. В этом регистре триггеры соединены последовательно, то есть выход первого соединён с входом второго и т.д. Условно-графическое изображение рассмотренного последовательного регистра приведено на рисунке 4. Входы синхронизации в последовательных регистрах, как и в параллельных, объединяются. Это обеспечивает одновременность смены состояния всех триггеров, входящих в состав последовательного регистра. Преобразование последовательного кода в параллельный производится следующим образом. Отдельные биты двоичной информации последовательно подаются на вход D0. Каждый бит сопровождается отдельным тактовым импульсом, который поступает на вход синхронизации C. После поступления первого тактового импульса логический уровень, присутствующий на входе D0, запоминается в первом триггере и поступает на его выход, а так как он соединён с входом второго триггера, то и на его вход. После поступления второго тактового импульса логический уровень, присутствующий на входе второго триггера, запоминается в нем и поступает на его выход, а так как он соединён с входом третьего триггера, то и на его вход. Одновременно следующий бит запоминается в первом триггере. После поступления четвертого тактового импульса в триггерах регистра будут записаны уровни бит, которые последовательно присутствовали на входе D0. Теперь этими битами можно воспользоваться, например, для отображения на индикаторах. 22. Сдвиговые регистры. Регистры сдвига или сдвиговые регистры (англ. shift register) представляют собой последовательно соединенную цепочку триггеров. Основной режим их работы - это сдвиг разрядов кода, записанного в эти триггеры, То есть по тактовому сигналу содержимое каждого предыдущего триггера переписывается в следующий по порядку в цепочке триггер. Код, хранящийся в регистре, с каждым тактом сдвигается на один разряд в сторону старших разрядов или в сторону младших разрядов, что и дало название регистрам данного типа. В связи с названием направления сдвига в сдвиговых регистрах часто возникает путаница. Сдвиг бывает двух видов: вправо (основной режим, который есть у всех сдвиговых регистров) и влево (этот режим есть только у некоторых, реверсивных сдвиговых регистров). Названия эти отражают внутреннюю структуру регистров сдвига и перезапись сигналов последовательно по цепочке триггеров. При этом триггеры, вполне естественно, нумеруются слева направо, например, от 0 до 7 (или от 1 до 8) для 8разрядных регистров. В результате сдвиг информации регистром вправо представляет собой сдвиг в сторону разрядов, имеющих большие номера, а сдвиг информации регистром влево - это сдвиг в сторону разрядов, имеющих меньшие номера. Однако, как известно, в любом двоичном числе слева расположены старшие разряды, а справа младшие разряды. Поэтому сдвиг двоичного числа вправо будет сдвигом в сторону младших разрядов, а сдвиг влево - сдвигом в сторону старших разрядов. В стандартные серии цифровых микросхем входит несколько типов сдвиговых регистров, отличающихся возможными режимами работы, режимами записи, чтения и сдвига, а также типом выходных каскадов (2С или 3С). Большинство регистров сдвига имеет восемь разрядов. 23. Регистры последовательного приближения. Регистр последовательных приближений работает следующим образом. По сигналу Пуск или по приходу первого тактового импульса старший разряд регистра устанавливается в единичное состояние, а все остальные разряды - в нулевое. К приходу следующего тактового сигнала на управляющий вход Глодается корректирующий сигнал, выработанный соответствующим устройством. Если этот корректирующий сигнал равен 1, то подтверждается правильность введения единицы в старший разряд, и эта единица сохраняется; если он равен 0, то единица в старшем разряде заменяется на нуль. Кроме того, с приходом тактового импульса в регистр записывается единица в следующий за старшим разряд. Регистр последовательных приближений II состоит из сдвигающего регистра на /) - триггерах и регистра памяти на Л5 - триггерах. Он выполняет функцию поразрядного сдвига логической 1 в направлении от старшего разряда к младшим, который осуществляется с появлением каждого нового тактового импульса. Регистр памяти в РПП предназначен для хранения результата преобразования и выполнения поразрядной записи текущих состояний КН. Схема делителя двух чисел с использованием регистра последовательных приближений. На регистр последовательных приближений CARG поступает сигнал Пуск, обнуляющий его разряды. Микросхемы представляют собой двенадцатиразрядный регистр последовательного приближения 24. Накапливающий сумматор. Накапливающий сумматор (НС) обычно представляет собой совокупность сумматора комбинационного типа и регистра (который хранит результаты суммирования как текущие, так и окончательные). Работает такой сумматор по формуле Si = Si-1 + A, ( формула 1.1) где Si –текущая сумма, Si-1 –предыдущая(на предыдущем цикле суммирования), А – очередное текущее слагаемое. Результат замещает старое значение суммы. Очередное прибавление слагаемого тактируется синхроимпульсами. Учитывая такие особенности функцио-нирования накапливающие сумматоры называются иногда аккумуляторами. На схемах сумматоры обозначаются SM. В российских сериях интегральных микросхем(ИМС), соответственно – ИР(например-К155ИМ3). В американских сериях они отдельно не обозначаются: SN40S08N. Интегральные микросхемы содержат,как правило, четырехразрядные комбинационные сумматоры. Чаще всего применяют четырехразрядные сумматоры комбинационного типа. Помимо выходных разрядов суммы и выхода переноса в сумматорах предусмотрен вход расширения С для обьединения сумматоров с целью повышения разрядности. Многоразрядные сумматоры можно построить, прибегнув к обьединению синхронизирующих входов, а также соединению соответствующих входов и выходов переноса нескольких базовых сумматоров. Эти сумматоры являются ядром арифметико-логических устройств(АЛУ) , без которых, в свою очередь, не было бы процессоров. По сути, эти устройства является интегральными микросхемами, без которых не обходится ни один компьютер в целом, ни сколько-нибудь сложное цифровое устройство. где необходимо выполнять арифметичесие операции. Накапливающие сумматоры применяются также, например, для формирования адреса ОЗУ, в генераторах сигналов произвольной формы. 25. Кольцевой счетчик. Первая схема, которую мы рассмотрим - это схема кольцевого счётчика. Такой счётчик можно построить на основе сдвигового регистра. Схема кольцевого счётчика приведена на рисунке 1. Рисунок 1. Схема кольцевого счетчика. Рассмотрим работу этой схемы. Пусть первоначально в счетчике записано число 002. После первого же тактового импульса состояние счётчика станет равным 102, после второго - 112. Временные диаграммы этой схемы приведены на рисунке 2. В результате анализа временных диаграмм можно определить, что коэффициент деления схемы кольцевого счётчика будет равен: Кд = 2*n. В качестве преимущества схемы кольцевого счётчика можно отметить то, что её быстродействие зависит только от времени задержки одного триггера. Это означает, что на кольцевых счётчиках можно реализовывать самые быстродействующие делители частоты. То, что коэффициент деления пропорционален не степени количества триггеров, а только сумме является недостатком данной схемы. Это означает, что при увеличении коэффициента деления сложность схемы неоправданно возрастает по сравнению со схемой двоичного счётчика. Ещё одним недостатком схемы является то, что в результате воздействия помехи в регистр может быт записано число 012. В результате коэффициент деления схемы изменится, а это является недопустимым. Ещё одним недостатком схемы кольцевого счётчика является то, что при количестве триггеров большем трёх, в результате воздействия помехи в регистр может быт записано число, содержащее несколько единиц. В результате коэффициент деления схемы изменится, а это является недопустимым. 26. Счетчик Джонсона. Счетчик Джонсона.. Так часто называют кольцевой счетчик, который тоже строится на основе замкнутого регистра сдвига, но с одной перекрестной (инверсной) связью. На рис. 6 показана схема построенного таким путем счетчика, имеющего коэффициент пересчета 10. Рисунок 6. Схема счетчика Джонсона. Здесь регистр сдвига К155ИР1 дополнен D-триггером. Вход D-триггера соединен с выходом четвертого разряда регистра, а на информационный вход I регистра подан сигнал не с прямого, а с инверсного выхода этого триггера. За счет этого и реализуется перекрестная связь в кольце. В отличие от простейших кольцевых счетчиков счетчик Джонсона имеет коэффициент пересчета вдвое больший числа составляющих его триггеров. В частности, счетчик рис. 6 под воздействием счетных импульсов n последовательно проходит следующие состояния: n 0 1 2 3 4 5 6 7 8 9 Q1 0 1 1 1 1 1 0 0 0 0 Q2 0 0 1 1 1 1 1 0 0 0 Q3 0 0 0 1 1 1 1 1 0 0 Q4 0 0 0 0 1 1 1 1 1 0 Q5 0 0 0 0 0 1 1 1 1 1 Как видно, при счете сначала от первого разряда до последнего распространяется волна единиц, а затем волна нулей. В счетчике Джонсона, как и в других кольцевых счетчиках, возможны сбои в виде лишних волн нулей или единиц. Для предотвращения их в десятичном счетчике простая цепь связи инверсного выхода последнего и входа первого разряда I=Q5 может быть заменена логической ячейкой, реализующей функцию I=Q1Q4+Q5. Связи, соответствующие этой ячейке, показаны штриховыми линиями на рис. 6. Подобная ячейка обеспечивает переход счетчика под воздействием входных импульсов из любой запрещенной комбинации в одну из разрешенных. На основе регистра с одной перекрестной связью может быть построен счетчик с любым четным коэффициентом пересчета. Если же нужен нечетный коэффициент пересчета 2N-1, то используется N-разрядный регистр сдвига, но на вход 1-го разряда подается сигнал неQN, a QNQN-i. При этом по сравнению с обычным счетчиком Джонсона пропускается одна кодовая комбинация, полностью составленная из нулей. 27. Двоичные счетчики. Счётчики используются для построения таймеров или для выборки инструкций из ПЗУ в микропроцессорах. Они могут использоваться как делители частоты в управляемых генераторах частоты (синтезаторах). При использовании в цепи ФАП счётчики могут быть использованы для умножения частоты как в синтезаторах, так и в микропроцессорах. Двоичные асинхронные счётчики Простейший вид счётчика - двоичный может быть построен на основе T-триггера. T-триггер изменяет своё состояние на прямо противоположное при поступлении на его вход синхронизации импульсов. Для реализации T-триггера воспользуемся универсальным D-триггером с обратной связью, как это показано на рисунке 1. Рисунок 1 Реализация счетного T-триггера на универсальном D-триггере. Так как эта схема, как мы уже рассматривали ранее, при поступлении на вход импульсов меняет свое состояние на противоположное, то её можно рассматривать как счётчик, считающий до двух. Временные диаграммы сигналов на входе и выходах T-триггера приведены на рисунке 2. Рисунок 2 Временные диаграммы сигналов на входе и выходах T-триггера. Обычно требуется посчитать большее количество импульсов. В этом случае можно использовать выходной сигнал первого счетного триггера как входной сигнал для следующего триггера, то есть соединить триггеры последовательно. Так можно построить любой счётчик, считающий до максимального числа, кратного степени два. Схема счётчика, позволяющего посчитать любое количество импульсов, меньшее шестнадцати, приведена на рисунке 3. Количество поступивших на вход импульсов можно узнать, подключившись к выходам счётчика Q0 … Q3. Это число будет представлено в двоичном коде. Рисунок 3 Схема четырёхразрядного счётчика, построенного на универсальных D-триггерах. Для того чтобы разобраться, как работает схема двоичного счётчика, воспользуемся временными диаграммами сигналов на входе и выходах этой схемы, приведёнными на рисунке 4. Рисунок 4 Временная диаграмма четырёхразрядного счётчика. Пусть первоначальное состояние всех триггеров счётчика будет нулевым. Это состояние мы видим на временных диаграммах. Запишем его в таблицу 1. После поступления на вход счётчика тактового импульса (который воспринимается по заднему фронту) первый триггер изменяет своё состояние на противоположное, то есть единицу. Запишем новое состояние выходов счётчика в ту же самую таблицу. Так как по приходу первого импульса изменилось состояние первого триггера, то этот триггер содержит младший разряд двоичного числа (единицы). В таблице поместим его значение на самом правом месте, как это принято при записи любых многоразрядных чисел. Здесь мы впервые сталкиваемся с противоречием правил записи чисел и правил распространения сигналов на принципиальных схемах. Подадим на вход счётчика ещё один тактовый импульс. Значение первого триггера снова изменится на прямо противоположное. На этот раз на выходе первого триггера, а значит и на входе второго триггера сформируется задний фронт. Это означает, что второй триггер тоже изменит своё состояние на противоположное. Это отчётливо видно на временных диаграммах, приведённых на рисунке 4. Запишем новое состояние выходов счётчика в таблицу 1. В этой строке таблицы образовалось двоичное число 2. Оно совпадает с номером входного импульса. Продолжая анализировать временную диаграмму, можно определить, что на выходах приведённой схемы счётчика последовательно появляются цифры от 0 до 15. Эти цифры записаны в двоичном виде. При поступлении на счётный вход счётчика очередного импульса, содержимое его триггеров увеличивается на 1. Поэтому такие счётчики получили название суммирующих двоичных счётчиков. 28. Счетчики с произвольным и управляемым модулем счета. Счетчики с произвольным коэффициентом счета. Принцип построения подобного класса счетных устройств состоит в исключении нескольких состояний обычного двоичного счетчика, являющихся избыточными для счетчиков с коэффициентом пересчета, отличающимися от двоичных. При этом избыточные состояния исключаются с помощью обратных связей внутри счетчика. Число избыточных состояний для любого счетчика определяется из следующего выражения: М = 2m - Ксч, где М - число запрещенных состояний, Ксч - требуемый коэффициент счета; 2m - число устойчивых состояний двоичного счетчика. Задача синтеза счетчика с произвольным коэффициентом счета заключается в определении необходимых обратных связей и минимизации их числа. Требуемое количество триггеров определяется из выражения n= [log2 Ксч], где [log2 Ксч] - двоичный логарифм заданного коэффициента пересчета Ксч, округленный до ближайшего целого числа.