Кольцов В.Б. Кондратьева О.В. - Теоретические основы защиты окружающей среды - 2018

В.Б. Кольцов, О.В. Кондратьева ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЗАЩИТЫ ОКРУЖАЮЩЕЙ СРЕДЫ Учебник для вузов под редакцией В.Б. Кольцова МОСКВА 2018 УДК 628.5 ББК 20.1 К626 Авторы: Кольцов Владимир Борисович — доктор химических наук, профессор института перспективных материалов и технологий (ИПМ) Национального исследовательского университета МИЭТ; Кондратьева Ольга Владимировна — кандидат технических наук, доцент кафедры информационных технологий в строительстве строительного факультета ФГБОУ ВО Российского государственного аграрного университета — МСХА имени К.А. Тимирязева. Рецензенты: Шубов Л. Я. — доктор технических наук, профессор, заведующий лабораторией научно-исследовательского центра по проблемам управления ресурсосбережением и отходами; Рощин В. М. — доктор технических наук, профессор, заведующий кафедрой общей и физической химии Национального исследовательского университета МИЭТ. К626 Кольцов, Владимир Борисович. Теоретические основы защиты окружающей среды : Учебник для вузов / В.Б. Кольцов, О.В. Кондратьева. — М. : «Прометей», 2018. — 734 с. ISBN 978-5-906879-79-0 В учебнике излагаются теоретические основы инженерной защиты окружающей среды от загрязнений. Материал книги систематизирует и обобщает современные практические и теоретические знания по технологиям очистки атмосферного воздуха, промышленных сточных вод, переработки, утилизации и обезвреживания твердых отходов производства и потребления. Рассмотрены примеры решения задач по основным разделам книги. Приведены задания для самостоятельной работы студентов. Соответствует Федеральному государственному образовательному стандарту высшего образования четвертого поколения (ФГОС-3++). Для студентов, обучающихся по программе бакалавриата по направлению «Техносферная безопасность». Может быть использован при изучении смежных дисциплин, связанных с безопасностью жизнедеятельности и техническими системами, а так же работниками природоохранных служб промышленных предприятий. ISBN 978-5-906879-79-0 © В.Б. Кольцов, 2018 © Издательство «Прометей», 2018 ǒǍƞǋǌƞǎǑƝǎ Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 Глава 1. Проблемы защиты окружающей среды . . . . . . . . . . . . . . . 21 1.1. Экологическая ситуация в мире . . . . . . . . . . . . . . . . . . . . . . . . 21 1.2. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 Глава 2. Фундаментальные законы природы и их применение при анализе процессов окружающей среды . . . . . . . . . . . . . . . . . . . 35 2.1. Закон сохранения массы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 2.1.1. Применение закона сохранения массы к технологическому процессу . . . . . . . . . . . . . . . . . . . . . . . . . . 35 2.1.2. Пример расчета фрагмента технологической схемы процесса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40 2.2. Законы термодинамики . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 2.2.1. Первый закон (начало) термодинамики (закон сохранения энергии). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 2.2.2. Второй закон (начало) термодинамики. Фазовое равновесие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 2.2.3. Третий закон (начало) термодинамики . . . . . . . . . . . . . . 54 2.2.4. Применение законов термодинамики для расчета энергетического и теплового баланса процесса . . . . . . . . 55 2.3. Законы переноса массы и энергии . . . . . . . . . . . . . . . . . . . . . . 60 2.3.1. Законы Фика и Фурье. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62 2.3.2. Перенос количества движения. Вязкость . . . . . . . . . . . . . 66 2.3.3. Баланс количества движения (импульса). . . . . . . . . . . . . 72 2.3.4. Поле температур в движущейся среде. . . . . . . . . . . . . . . . . 75 2.3.5. Поле концентраций в движущейся среде . . . . . . . . . . . . . . 77 2.4.Инженерные методы защиты окружающей среды . . . . . . . . . 78 2.4.1.Энергоэнтропийная концепция защиты окружающей среды и риск-ориентируемое мышление . . . . . . . 78 2.4.2. Принцип существования и возрастания энтропии . . . 79 2.4.3. Энергоэнтропийная концепция защиты окружающей среды . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88 — 3 — ǣƼǁǪǫǁǬǃǀǬ 2.4.4. Оценка энтропии опасностей, термодинамического техногенного риска в технических системах и окружающей среде . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93 2.4.4. Теоретические оценки опасности и риска в природных и техногенных системах. . . . . . . . . . . . . . . . . 96 2.5. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99 2.6. Примеры решения задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100 2.7. Пример выполнения курсовой работы . . . . . . . . . . . . . . . . . . 107 2.8. Задачи для самостоятельного решения . . . . . . . . . . . . . . . . . 113 Глава 3. Общие (основные) принципы математического описания процессов природной среды. . . . . . . . . . . . . . . . . . . . . . . . 115 3.1. Аналогия процессов переноса количества движения, энергии и массы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115 3.2. Моделирование типовых процессов . . . . . . . . . . . . . . . . . . . . 117 3.3. Основы физического моделирования (теория подобия) . . . . 122 3.3.1. Подобие гидромеханических процессов. . . . . . . . . . . . . . . .125 3.3.2. Подобие тепловых процессов. . . . . . . . . . . . . . . . . . . . . . . . . .131 3.3.3. Тепловые процессы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .134 3.3.4. Подобие процессов массопереноса . . . . . . . . . . . . . . . . . . . . .135 3.4. Метод анализа размерностей . . . . . . . . . . . . . . . . . . . . . . . . . 137 3.5. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 141 3.6. Примеры решения задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145 3.7. Задачи для самостоятельного решения . . . . . . . . . . . . . . . . . 146 Глава 4. Неоднородные (двухфазные) системы . . . . . . . . . . . . . . . 147 4.1. Классификация неоднородных (двухфазных) систем. . . . . . 147 4.2. Методы обезвоживания твердого материала и удаления твердых частиц из газового потока . . . . . . . . . . . . . . . . . . . . 148 4.3. Формы связи воды с твердым телом. Энергия связи различных форм воды с твердым телом . . . . . . . . . . . . . . . . . 150 4.4. Влагоудерживающая способность твердых тел. Влияние основных факторов на степень обезвоживания . . . . . . . . . . . 152 4.5. Характеристики аэродисперсных систем . . . . . . . . . . . . . . . 153 4.5.1. Конденсационное образование аэродисперсных систем . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156 4.5.2. Закономерности распределения частиц. . . . . . . . . . . . . .156 4.5.2.1. Геометрические параметры частиц. . . . . . . . . . . . . . . . . 156 4.5.2.2. Размеры пылевидных частиц . . . . . . . . . . . . . . . . . . . . . . . . 157 4.5.2.3. Дисперсный состав частиц . . . . . . . . . . . . . . . . . . . . . . . . . . 158 4.5.3. Физико-химические характеристики пыли . . . . . . . . . .159 4.6. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 163 4.7. Примеры решения задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 166 4.8. Задачи для самостоятельного решения . . . . . . . . . . . . . . . . . 167 — 4 — ǣƼǁǪǫǁǬǃǀǬ Глава 5. Теоретические аспекты отделения твердых частиц от жидкости или газа под действием механических методов . . . 168 5.1. Теоретические закономерности отделения твердых частиц от газа. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 168 5.1.1. Осаждение крупной пыли в гравитационном поле. . . .169 5.1.2. Инерционное осаждение. (Применение центробежной силы при осаждении). . . . . . . . . . . . . . . . . . 172 5.1.3. Очистка газов от пыли методом фильтрации . . . . . . .173 5.2. Теоретические закономерности отделения твердых частиц от жидкости. Характеристика суспензий.. . . . . . . . . . . . . . . 176 5.2.1. Обезвоживание кускового материала дренированием. Гидродинамика течения жидкости под влиянием | собственного веса в порах осадка . . . . . . . . . . . . . . . . . . . . . 176 5.2.2. Отстаивание под действием силы тяжести. Основные понятия. Классификация суспензий . . . . . . . 179 5.2.3. Способы выражения и расчета концентрации твердого в суспензии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 183 5.2.3.1. Исследование скорости расслоения суспензий I-го и II-го классов методом длинной трубки . . . . . . . . . . . . .184 5.2.3.2. Качественное описание процесса расслоения суспензий III и IV классов . . . . . . . . . . . . . . . . . . . . . . . . . . . .185 5.2.3.3. Расчет удельной поверхности сгущения по методу Коу и Клевенжера . . . . . . . . . . . . . . . . . . . . . . . . . .189 5.2.3.4. Расчет удельной поверхности по методу Кинча . . . . 190 5.3. Применение центробежной силы при обезвоживании. Основные понятия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191 5.3.1. Основные закономерности разделения суспензий в осадительных центрифугах. Индекс производительности . . . . . . . . . . . . . . . . . . . . . . . . . 192 5.4. Фильтрование. Основные понятия. Классификация . . . . . . 194 5.4.1. Физические основы фильтрации с образованием осадка. Гидродинамика течения жидкости через пористые и зернистые слои . . . . . . . . . . . . . . . . . . . . . 196 5.4.2. Основные уравнения фильтрации. . . . . . . . . . . . . . . . . . . . .199 5.4.3. Применение уравнения фильтрации. Определение удельного сопротивления осадка и его сжимаемости . . . . . . . . . . . . . . . . . . . . . . . . . . . . 202 5.4.4. Физические основы разделения суспензий в фильтрующих центрифугах . . . . . . . . . . . . . . . . . . . . . . . . 205 5.5. Отделение твердых частиц из газовой среды в электрическом поле . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 207 5.6. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 207 5.7. Примеры решения задач. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 209 5.7.1. Осаждение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .209 — 5 — ǣƼǁǪǫǁǬǃǀǬ 5.7.2. Фильтрование . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .211 5.7.3. Центрифугирование . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .214 5.8. Задачи для самостоятельного решения . . . . . . . . . . . . . . . . . 217 5.8.1. Осаждение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .217 5.8.2. Фильтрование . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .218 5.8.3. Центрифугирование . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .218 Глава 6. Агрегирование. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 220 6.1. Теория процесса агрегирования. Механизмы встреч частиц друг с другом. Понятие о расклинивающем давлении. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 220 6.1.1. Теория процесса агрегирования. . . . . . . . . . . . . . . . . . . . . . . .220 6.1.2. Два механизма соударения или встречи частиц . . . . .221 6.2. Три слагающие поверхностных сил (расклинивающего давления). Двучленный закон взаимодействия . . . . . . . . . . 223 6.3. Силы Ван-дер-Ваальса. Слагающие сил Ван-дер-Ваальса. Вандерваальсовское взаимодействие между молекулами и конденсированными фазами. . . . . . . . . . . . . . . . . . . . . . . . 227 6.3.1. Силы Ван-дер-Ваальса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .227 6.3.2. Вандерваальсовское взаимодействие конденсированных фаз . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 228 6.3.3. Электромагнитная теория взаимодействия конденсированных фаз . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 229 6.4. Природа ионно-электростатических сил. Закономерность изменения их вглубь раствора . . . . . . . . . . 230 6.5. Гидратационная слагаемая поверхностных сил (расклинивающего давления). . . . . . . . . . . . . . . . . . . . . . . . . 234 6.6. Три механизма агрегирования: коагуляция, флокуляция, мостиковая флокуляция . . . . . . . . . . . . . . . . . 235 6.7. Основные принципы селективной агрегации частиц в суспензии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 238 6.8. Коагуляция в аэродисперсных системах . . . . . . . . . . . . . . . . 241 6.8.1. Тепловая коагуляция . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .242 6.8.2. Градиентная коагуляция . . . . . . . . . . . . . . . . . . . . . . . . . . . . .243 6.8.3. Турбулентная коагуляция . . . . . . . . . . . . . . . . . . . . . . . . . . . .244 6.8.4. Кинематическая коагуляция . . . . . . . . . . . . . . . . . . . . . . . . .245 6.8.5. Акустическая коагуляция. . . . . . . . . . . . . . . . . . . . . . . . . . . . .246 6.8.6. Электрическая коагуляция . . . . . . . . . . . . . . . . . . . . . . . . . . .246 6.9. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 247 6.10. Примеры решения задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . 248 6.11. Задачи для самостоятельного решения . . . . . . . . . . . . . . . . 249 — 6 — ǣƼǁǪǫǁǬǃǀǬ Глава 7. Процессы массопередачи в системах с неподвижной границей раздела фаз применительно к процессам защиты окружающей среды . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 250 7.1. Физические основы процессов массопередачи . . . . . . . . . . . 251 7.1.1. Уравнение массоотдачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .252 7.2. Растворение твердых тел . . . . . . . . . . . . . . . . . . . . . . . . . . . . 256 7.2.1. Расчет процесса растворения в каскаде последовательно соединенных аппаратов. . . . . . . . . . . . 261 7.3. Кристаллизация. Физико-химические основы и принципы расчета процессов кристаллизации . . . . . . . . . 262 7.4. Процессы экстракции в системах твердое тело — жидкость (процесс выщелачивания) . . . . . . . . . . . . . . . . . . . 268 7.4.1. Равновесие и скорость выщелачивания . . . . . . . . . . . . . . .270 7.5. Процесс сушки. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 274 7.5.1. Расчет процессов сушки. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .276 7.5.2. Равновесное содержание влаги при сушке. Кинетика сушки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 277 7.5.3. Основные параметры влажного воздуха . . . . . . . . . . . . . .281 7.5.4. J-X-диаграмма влажного воздуха . . . . . . . . . . . . . . . . . . . . .284 7.5.5. Сушка топочными газами . . . . . . . . . . . . . . . . . . . . . . . . . . . .287 7.6. Адсорбция. Общие сведения . . . . . . . . . . . . . . . . . . . . . . . . . . 288 7.6.1. Характеристики адсорбентов и их виды. . . . . . . . . . . . .289 7.6.2. Равновесие при адсорбции . . . . . . . . . . . . . . . . . . . . . . . . . . . . .293 7.6.3. Кинетика адсорбции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .301 7.6.4. Расчет процесса адсорбции в неподвижном слое адсорбента . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 302 7.6.5. Адсорбция в кипящем слое . . . . . . . . . . . . . . . . . . . . . . . . . . . . .305 7.6.6. Очистка сточных вод методом адсорбции . . . . . . . . . . .306 7.6.7. Десорбция после адсорбции . . . . . . . . . . . . . . . . . . . . . . . . . . . .307 7.7. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 309 7.8. Примеры решения задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 311 7.9. Задачи для самостоятельного решения . . . . . . . . . . . . . . . . . 315 Глава 8. Процессы массопередачи в системах с подвижной границей раздела фаз применительно к процессам защиты окружающей среды . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 317 8.1. Абсорбция (общие сведения) . . . . . . . . . . . . . . . . . . . . . . . . . 319 8.1.1. Равновесие при абсорбции (равновесие между фазами) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 320 8.1.2. Скорость процесса. Скорость физической абсорбции. .326 8.2. Десорбция после абсорбции, дегазация, дезодорация . . . . . 330 8.2.1. Десорбция . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .330 8.2.2. Дезодорация . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .331 8.2.3. Дегазация. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .333 — 7 — ǣƼǁǪǫǁǬǃǀǬ 8.3. Дистилляция . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 335 8.3.1. Расчет процессов дистилляции в емкостных аппаратах (периодический процесс) . . . . . . . . . . . . . . . . . 337 8.4. Ректификация. Физико-химические основы . . . . . . . . . . . . 339 8.5. Экстракция . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 342 8.5.1. Процессы экстракции в системах жидкость — жидкость . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 342 8.5.2. Равновесие в системах жидкость — жидкость . . . . . .344 8.5.3. Равновесие в бинарных системах . . . . . . . . . . . . . . . . . . . . .348 8.5.4. Равновесие в тройных системах. Треугольная диаграмма . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 350 8.5.5. Изотермы экстракции (кривые равновесия) . . . . . . . . .352 8.5.6. Методы экстракции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .354 8.5.7. Многоступенчатая экстракция при перекрестном токе . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 360 8.6. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 362 8.7. Примеры решения задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 363 8.8. Задачи для самостоятельного решения . . . . . . . . . . . . . . . . . 368 Глава 9. Явление осмоса и его использование при очистке сточных вод . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9.1. Осмотическое давление . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9.2. Биологическая роль осмотического давления . . . . . . . . . . . 9.3. Законы осмотического давления . . . . . . . . . . . . . . . . . . . . . . 9.4. Термодинамика осмотического давления . . . . . . . . . . . . . . . 9.5. Очистка сточной воды ультрафильтрацией и обратным осмосом . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9.6. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9.7. Примеры решения задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9.8. Задачи для самостоятельного решения . . . . . . . . . . . . . . . . . 379 383 383 384 Глава 10. Флотация . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10.1. Общие сведения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10.2. Теоретические основы процесса флотации . . . . . . . . . . . . . 10.2.1. Процессы смачивания . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10.3.Флотационные реагенты и их классификация. . . . . . . . . . . 10.4. Механизм действия собирателей . . . . . . . . . . . . . . . . . . . . . 10.5. Реагенты-депрессоры . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10.6. Реагенты-активаторы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10.7. Реагенты — регуляторы среды . . . . . . . . . . . . . . . . . . . . . . . 10.8. Реагенты-пенообразователи . . . . . . . . . . . . . . . . . . . . . . . . . 10.9. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10.10.Примеры решения задач . . . . . . . . . . . . . . . . . . . . . . . . . . . 10.11. Задачи для самостоятельного решения . . . . . . . . . . . . . . . 386 386 388 389 402 404 408 416 419 421 426 426 427 — 8 — 369 369 372 374 377 ǣƼǁǪǫǁǬǃǀǬ Глава 11. Химические и биологические методы очистки сточных вод . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 429 11.1.Нейтрализация. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 430 11.1.1. Нейтрализация смешением . . . . . . . . . . . . . . . . . . . . . . . . .431 11.1.2. Реагентная нейтрализация . . . . . . . . . . . . . . . . . . . . . . . .431 11.1.3. Нейтрализация кислых сточных вод путем их фильтрования через нейтрализующие материалы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .432 11.1.4.Нейтрализация щелочных сточных вод кислыми газами. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .433 11.2. Окислительный метод очистки сточных вод . . . . . . . . . . . . 433 11.2.1. Окисление реагентами, содержащими активный хлор . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .434 11.2.2. Окисление пероксидом водорода . . . . . . . . . . . . . . . . . . . . .436 11.2.3. Окисление кислородом воздуха . . . . . . . . . . . . . . . . . 437 11.2.4. Озонирование . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .437 11.2.5. Окисление перманганатом калия. . . . . . . . . . . . . . . . . . .438 11.2.6. Радиационное окисление . . . . . . . . . . . . . . . . . . . . . . . . . . . .439 11.3. Очистка восстановлением . . . . . . . . . . . . . . . . . . . . . . . . . . . 439 11.4. Реагентные методы выделения загрязняющих веществ в виде малорастворимых и нерастворимых соединений . . . 442 11.5. Ионно-обменная очистка сточных вод . . . . . . . . . . . . . . . . . 446 11.6. Биологические методы очистки сточных вод . . . . . . . . . . . 449 11.6.1. Основные показатели . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .449 11.6.2. Закономерности распада органических веществ . . .450 11.6.3. Очистка сточных вод в природных условиях . . . . . . .458 11.6.4. Анаэробные методы биохимической очистки . . . . . 459 11.7. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 461 Глава 12. Физические основы электродных процессов при очистке сточных вод от примесей . . . . . . . . . . . . . . . . . . . . . . . . 463 12.1. Явления электролиза, поляризации и перенапряжения . . 463 12.1.1. Электролиз. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .463 12.1.2. Кривая напряжения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .465 12.1.3. Электродвижущие силы разложения . . . . . . . . . . . . . . .467 12.1.4. Потенциалы разложения . . . . . . . . . . . . . . . . . . . . . . . . . . .468 12.1.5. Концентрационная поляризация . . . . . . . . . . . . . . . . . . .470 12.1.6. Деполяризация . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .471 12.1.7. Перенапряжение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .472 12.2. Электрокапиллярные явления. . . . . . . . . . . . . . . . . . . . . . . 473 12.2.1. Зависимость поверхностного натяжения от заряда . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 473 12.2.2.Электрокапиллярная кривая . . . . . . . . . . . . . . . . . . . . . . .475 — 9 — ǣƼǁǪǫǁǬǃǀǬ 12.2.3. Влияние адсорбции на электрокапиллярную кривую . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 477 12.2.4. Проблема абсолютных потенциалов. . . . . . . . . . . . . . .480 12.3. Электрокинетические явления. . . . . . . . . . . . . . . . . . . . . . . 482 12.3.1. Диффузионный двойной слой и электрокинетический потенциал . . . . . . . . . . . . . . . .482 12.3.2. Емкость двойного слоя . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .485 12.3.3. Электроосмос. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .486 12.3.4. Потенциал течения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .489 12.3.5. Электрофорез . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .489 12.3.6. Потенциалы осаждения . . . . . . . . . . . . . . . . . . . . . . . . . . . .491 12.4. Электрохимические методы очистки сточных вод . . . . . . . 492 12.4.1. Анодное окисление и катодное восстановление . . . .493 12.4.2. Электрокоагуляция . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .496 12.4.3. Электрофлотация . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .497 12.4.4. Электродиализ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .498 12.5. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 498 12.6. Примеры решения задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . 500 12.7. Задачи для самостоятельного решения . . . . . . . . . . . . . . . . 502 Глава 13. Физико-химические основы процессов переработки твердых отходов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 503 13.1. Классификация твердых отходов. . . . . . . . . . . . . . . . . . . . . 504 13.2. Подготовка твердых отходов к последующей переработке. 504 13.3. Дробление и измельчение твердых отходов. . . . . . . . . . . . . 505 13.3.1. Назначение операций дробления и измельчения . . . .505 13.3.2. Степень дробления и измельчения . . . . . . . . . . . . . . . . . .507 13.3.3. Стадийность и схемы дробления и измельчения . . .509 13.3.4. Удельная поверхность диспергированного материала . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .512 13.3.5. Современные представления о разрушении твердого материала . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .513 13.3.6. Дефекты кристаллической структуры . . . . . . . . . . .514 13.3.7. Механические свойства твердых тел при простых видах деформации . . . . . . . . . . . . . . . . . . . .518 13.3.8. Анизотропные свойства природных материалов . .521 13.3.8.1. Масштабный фактор . . . . . . . . . . . . . . . . . . . . . . . . . . . . 522 13.3.8.2. Твердость природного материала . . . . . . . . . . . . . . . . 522 13.3.8.3. Общий коэффициент крепости материала. . . . . . 523 13.3.9. Законы дробления . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .524 13.3.10. Способы дробления, классификация машин для дробления и измельчения. . . . . . . . . . . . . . . . . . . . . . .527 13.4. Процесс грохочения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 530 13.4.1. Основные понятия и назначение грохочения. . . . . . . .530 — 10 — ǣƼǁǪǫǁǬǃǀǬ 13.4.2. Просеивающая поверхность. . . . . . . . . . . . . . . . . . . . . . . . .534 13.4.3. Способы определения гранулометрического состава . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .534 13.4.4. Ситовой анализ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .535 13.4.5. Характеристика крупности . . . . . . . . . . . . . . . . . . . . . . .535 13.4.6. Аналитическое представление характеристик крупности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .539 13.4.7. Дифференциальные функции распределения по крупности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .545 13.4.8. Вычисление поверхности и числа частиц по уравнениям суммарной характеристики крупности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .547 13.4.9. Эффективность процесса грохочения . . . . . . . . . . . . . . .548 13.4.10. «Легкие», «трудные» и «затрудняющие» частицы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .551 13.4.11. Факторы, влияющие на процесс грохочения . . . . . . .552 13.4.12. Кинетика процесса грохочения . . . . . . . . . . . . . . . . . . . .553 13.5. Электромагнитная сепарация. Физические основы процесса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 553 13.6. Электродинамическая сепарация. . . . . . . . . . . . . . . . . . . . . 557 13.7. Электросепарация . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 557 13.8. Аэросепарация. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 560 13.8.1.Теоретические основы процесса . . . . . . . . . . . . . . . . . . . . .561 13.9. Сепарация твердых материалов по коэффициенту трения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 564 13.10. Сепарация на основе явления смачиваемости . . . . . . . . . . 567 13.11. Переработка твердых отходов методом окисления в промышленное сырье . . . . . . . . . . . . . . . . . . . . . . . . . . . . 569 13.11.1. Сжигание отходов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .569 13.11.2. Пиролиз и газификация . . . . . . . . . . . . . . . . . . . . . . . . . .569 13.12. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 571 Глава 14. Теоретические основы защиты окружающей среды от энергетических воздействий . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 573 14.1. Общая характеристика энергетических воздействий . . . . . 574 14.1.1. Шум и вибрации . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .574 14.1.2. Электромагнитные поля и излучения . . . . . . . . . . . . .580 14.2. Обобщенное защитное устройство . . . . . . . . . . . . . . . . . . . . 590 14.3. Методы и средства защиты от шума и вибрации . . . . . . . . . 593 14.4. Методы и средства защиты от электромагнитных полей . . 598 14.5. Средства защиты от инфракрасного, ультрафиолетового, лазерного и ионизирующего излучений . . . . . . . . . . . . . . . 602 14.6. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 604 14.7. Примеры решения задач. . . . . . . . . . . . . . . . . . . . . . . . . . . . 605 — 11 — ǣƼǁǪǫǁǬǃǀǬ 14.8. Задачи для самостоятельного решения . . . . . . . . . . . . . . . . 607 Глава 15. Диффузионные процессы в атмосфере и гидросфере. Рассеивание и разбавление примесей . . . . . . . . . . . . . . . . . . . . . . . . 609 15.1. Физические основы рассеивания выбросов загрязняющих веществ в атмосфере.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 609 15.1.1. Структура и состав атмосферы . . . . . . . . . . . . . . . . . . .609 15.1.2. Классификация загрязняющих атмосферу веществ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .611 15.1.3. Загрязнение атмосферы транспортом и промышленностью . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .616 15.1.4. Последствия загрязнения атмосферы . . . . . . . . . . . . . .617 15.1.5. Химические превращения веществ в атмосфере. . . .623 15.1.6. Перенос загрязнений в атмосфере . . . . . . . . . . . . . . . . . .625 15.1.7. Метеорологические параметры переноса примесей и их учет . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .627 15.1.8. Методика ОНД-86 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .634 15.1.9. Анализ существующих средств автоматизации в сфере экологии и защиты воздушной среды . . . . . . .636 15.2. Физические основы распространения примесей в водной среде . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 638 15.2.1. Источники загрязнения природных вод. . . . . . . . . . . . .645 15.2.2. Вторичное загрязнение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .645 15.2.3. Методы анализа воды. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .645 15.2.4. Оценка качества воды . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .646 15.2.5. Состав и расчет выпусков (сбросов) сточных вод . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .649 15.2.6. Модели распространения загрязнений в воде . . . . . . .651 15.3. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 656 15.4 Примеры решения задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . 657 15.5. Задача для самостоятельного решения . . . . . . . . . . . . . . . . 660 Список использованной литературы . . . . . . . . . . . . . . . . . . . . . . . . . 661 Приложение. Фонд оценочных средств по дисциплине «Теоретические основы защиты окружающей среды» . . . . . . . . . 664 — 12 — ǌǌǎƚǎǑƝǎ Грандиозные масштабы производственной деятельности человека привели к большим позитивным изменениям в мире — созданию мощного промышленного и сельскохозяйственного потенциала, мелиорации больших земельных площадей и, как следствие, создание систем искусственного климата. Однако вместе с этим в XXI — веке резко ухудшилось состояние окружающей среды, которое выражается в глобальном загрязнении атмосферы, водоемов и почвы твердыми, жидкими и газообразными отходами различных производств. Кроме того, происходит истощение невозобновляемых природных ресурсов и в первую очередь это касается полезных ископаемых и пресной воды. Поэтому защита окружающей среды от загрязнений стала одной из насущных проблем человечества. Для сокращения выбросов загрязнений в биосферу и поддержания качества окружающей среды на должном уровне академиками Н. Н. Семеновым и И. В. Соколовым-Петряновым выдвинута концепция безотходной (малоотходной) технологии. Эта технология подразумевает такое производство, при котором минимизируется объем газообразных, жидких, твердых и тепловых отходов в процессах переработки природного сырья. Это связано в первую очередь с разработкой таких процессов переработки сырья, в которых используется замкнутая система водооборота, а также полная рекуперация (улавливание и использование) газообразных отходов производства. — 13 — ǝǫǬƽǬǃǀǬ Под «окружающей природной средой» или «окружающей средой» понимается совокупность естественных и измененных природных условий обитания человека и производственной деятельности общества. В процессе бытовой и производственной деятельности человеческое общество неизбежно влияет на окружающую среду, которая немедленно или через определенный промежуток времени реагирует на это влияние и оказывает обратное положительное либо отрицательное действие. Развитие мирового общественного производства идет все ускоряющимися темпами, и размеры ущерба, наносимого окружающей среде, увеличиваются при этом так, что их уже невозможно, как раньше, преодолеть естественным путем, без использования глубоко продуманного комплекса законодательных и технологических мероприятий, затрагивающих все сферы производственной деятельности человека. Промышленные отходы (ПО) и загрязнения, выделяющиеся в технологических циклах предприятий и при очистке производственных сточных вод, представляют наибольшую опасность, прежде всего для населения крупных промышленных центров и окружающих их регионов, создают трудности в работе городских коммунальных служб. В связи с этим в дальнейшем необходимо внедрение технологических процессов, дающих минимальные выбросы, при которых самоочищающаяся способность природы в достаточной степени будет препятствовать возникновению необратимых экологических изменений. Под безотходной технологией понимается идеальная модель производства, в результате деятельности которого не происходит выбросов в окружающую среду, но в большинстве случаев она не может быть реализована в полной мере. Безотходное производство можно характеризовать всемерно возможной утилизацией образовавшихся в прямых технологических процессах отходов. Малоотходная технология представляет собой промежуточную ступень безотходной технологии и отличается от нее тем, что обеспечивает получение готового продукта с не полностью утилизируемыми отходами. Отходы представляют собой побочные продукты промышлен— 14 — ǝǫǬƽǬǃǀǬ ного производства, выделяющиеся в процессе производства основных видов продукции и характеризующиеся определенными физико-химическими свойствами. отходы производства и потребления, пригодные для переработки в товарную продукцию, относятся к вторичным материальным ресурсам. При создании и реализации малоотходной и безотходной технологии используются различные методы и технологические процессы инженерной экологии, включая механические, физико-химические, химические, термические и биологические процессы: осаждения и разделения гетерогенных систем, коагуляции и электрокоагуляции, флокуляции, сорбции, катализа, конденсации, флотации, экстракции, ионного обмена, окисления и восстановления, биохимического окисления и разложения, пиролиза, огневого обезвреживания и др. Теоретические основы технологических процессов охраны окружающей среды — это комплексная научно-техническая дисциплина инженерной экологии, изучающая основы создания ресурсосберегающих технологий, экологически безопасных промышленных производств, реализации инженерно-экологических решений по рациональному природопользованию и охране окружающей среды. Целью курса «Теоретические основы защиты окружающей среды» является формирование у бакалавров современных представлений о природе и закономерностях основных технологических процессов защиты окружающей среды, основах технологий очистки пылегазовых выбросов, жидких сбросов, утилизации и переработки твердых отходов, о физических принципах защиты окружающей среды от энергетических воздействий. В основе подавляющей массы технологий лежат физические и химические превращения. В физических процессах изменяются лишь форма, размеры, агрегатное состояние и другие физические свойства веществ. Их строение и химический состав сохраняются. Физические процессы доминируют при дроблении, измельчении полезных ископаемых, в различных способах обработки металлов давлением, при сушке и в других аналогичных случаях. — 15 — ǝǫǬƽǬǃǀǬ Химические процессы изменяют физические свойства исходного сырья и его химический состав. С их помощью получают металлы, спирты, удобрения, сахар и т.п., которые в чистом виде в сырье не присутствуют. Химические процессы являются основой производства в металлургии, химической промышленности, промышленности строительных материалов, целлюлозно-бумажной промышленности и во множестве других отраслей народного хозяйства. Химические явления в технологических процессах зачастую получают развитие под влиянием внешних условий (давление, объем, температура и т.д.), в которых реализуется процесс. При этом имеют место нестехиометрические превращения одних веществ в другие, изменение их поверхностных, межфазных свойств и ряд других явлений смешанного (физического и химического) характера. Совокупность взаимосвязанных химических и физических процессов, происходящих в веществе, получила название физико-химических, пограничных между физическими и химическими. Физико-химические процессы широко применяются в обогащении полезных ископаемых, металлургии, технологиях основных химических производств, органическом синтезе, энергетике, но особенно в природоохранных технологиях (пыле- и газоулавливании, очистке сточных вод и др.). Специфическую группу составляют биохимические процессы — химические превращения, протекающие с участием субъектов живой природы. Биохимические процессы составляют основу жизнедеятельности всех живых организмов растительного и животного мира. На их использовании построена значительная часть сельскохозяйственного производства и пищевой промышленности, например биотехнология. Продуктом биотехнологических превращений, протекающих с участием микроорганизмов, являются вещества неживой природы. Задачами данной дисциплины являются получение необходимого объёма знаний в области теоретических основах — 16 — ǝǫǬƽǬǃǀǬ защиты окружающей среды и формирование умений по применению этих знаний в будущей профессиональной деятельности, освоение физико-химических и технологических основ методов предотвращения загрязнения окружающей среды выбросами в атмосферу, сбросами сточных вод и твердыми отходами. Предмет «Теоретические основы защиты окружающей среды» входит в состав базовой части математических и естественных дисциплин подготовки специалистов по специальности «инженерная защита окружающей среды» и изучается после прохождения курсов «Физики», «Общей экологии», «Физической химии». Базовые знания о природных естественных процессах на Земле лежат в основе более полного освоения таких программных учебных дисциплин, как «Мониторинг окружающей среды», «Экологическая экспертиза и оценка воздействия на окружающую среду», «Промышленная экология», «Экологический аудит», «Управление охраной окружающей среды» и др. Учебник предназначен для студентов высшего профессионального образования для углубленного изучения материала курса, а также для выполнения практических и лабораторных работ по расчету средств защиты от опасных и вредных факторов техносферы и природной среды. Процесс изучения дисциплины «Теоретические основы защиты окружающей среды» по направлению подготовки 20.03.01 Техносферная безопасность разработан на основе нового стандарта ФГОС-3++. В результате изучения данной дисциплины студент должен обладать следующими компетенциями: как универсальными, так и общепрофессиональными, которые приведены в таблицах 1 и 2 Весь материал учебника написан В.Б. Кольцовым в соавторстве с О.В. Кондратьевой, за исключением главы 14, которая написана В.Б. Кольцовым в соавторстве с доктором технических наук, профессором В.И. Каракеяном. — 17 — ǝǫǬƽǬǃǀǬ Таблица 1 Универсальные компетенции Наименование категории (группы) универсальных компетенций Код и наименование универсальной компетенции выпускника программы бакалавриата Системное и критическое мышление УК-1. Способен осуществлять поиск, критический анализ и синтез информации, применять системный подход для решения поставленных задач Разработка и реализация проектов УК-2. Способен определять круг задач в рамках поставленной цели и выбирать оптимальные способы их решения, исходя из действующих правовых норм, имеющихся ресурсов и ограничений Командная работа и лидерство УК-3. Способен осуществлять социальное взаимодействие и реализовывать свою роль в команде Коммуникация УК-4. Способен осуществлять деловую коммуникацию в устной и письменной формах на государственном языке Российской Федерации и иностранном(ых) языке(ах) Межкультурное взаимодействие УК-5. Способен воспринимать межкультурное разнообразие общества в социально-историческом, этическом и философском контекстах Самоорганизация и саморазвитие (в том числе здоровьесбережение) УК-6. Способен управлять своим временем, выстраивать и реализовывать траекторию саморазвития на основе принципов образования в течение всей жизни — 18 — ǝǫǬƽǬǃǀǬ Наименование категории (группы) универсальных компетенций Код и наименование универсальной компетенции выпускника программы бакалавриата УК-7. Способен поддерживать должный уровень физической подготовленности для обеспечения полноценной социальной и профессиональной деятельности Безопасность жизнедеятельности УК-8. Способен создавать и поддерживать безопасные условия жизнедеятельности Таблица 2 Общепрофессиональные компетенции Наименование категории (группы) общепрофессиональных компетенций Код и наименование общепрофессиональной компетенции выпускника программы бакалавриата ОПК-1. Способен учитывать современные тенденции развития техники и технологий в области техносферной безопасности, измерительной и вычислительной техники, информационных технологий при решении типовых задач в области профессиональной деятельности, связанной с защитой окружающей среды и обеспечением безопасности человека. ОПК-2. Владеет культурой безопасности и рискориентированным мышлением, при котором в безопасности человека и сохранения окружающей природной среды рассматриваются — 19 — ǝǫǬƽǬǃǀǬ Наименование категории (группы) общепрофессиональных компетенций Код и наименование общепрофессиональной компетенции выпускника программы бакалавриата в качестве важнейших приоритетов в личной жизни и профессиональной деятельности. ОПК-3. Способен осуществлять профессиональную деятельность с учетом государственных требований в области обеспечения безопасности В учебнике использованы работы таких известных экологов, химиков-технологов, инженеров-металлургов и инженеров-обогатителей, как А.Г. Касаткин, К.Ф. Павлов, П.Г. Романков, А.А. Носков, Н.Н. Моисеев, В.Б. Коган, В.М. Глазов, А.И. Бродский, В.В. Крапухин, С.Б. Старк, Л.Я. Шубов, А.И. Родионов, В.Н. Клушин, В.Г. Систер, П.П. Кукин, В.Д. Самыгин, Н.Ф. Пантелеева и других. Ссылки на использованные источники приводятся в конце учебника. — 20 — ǍưǙǚǙÍ Í Í ǓǔǒƙƞǎǐƥÍƜǋƣƝǖƥÍ Í ǒǏǔƟƛǋƨƣǎ֏ÍǕǔǎƚƥ В результате освоения главы 1 бакалавр должен: Знать: – причины экологического кризиса в XI веке – современную экологическую ситуацию в мире; Уметь: пользоваться действующими законодательно-правовыми актами, положениями и инструкциями в области безопасности и охраны окружающей среды; Владеть: комплексным организационно-правовым подходом к решению проблемы безопасности природной среды. ϭ͘ϭ͘ˑ̸̶̡̨̨̡̛̛̛̛̣̖̭̭̯̱̥̬̖̐̌́̌́̏ За 4 млрд. лет существования планеты Земля пришли в равновесие происходящие в природе процессы. Установился кругооборот основных элементов органического мира (С, О, Н, N) и многих других. На высоте 20–25 км сформировался озоновый слой, защищающий биологический мир от ультрафиолетового излучения. Однако появление человека и его жизнедеятельность внесли дисбаланс в установившееся термодинамическое равновесие. Нарушение равновесия связано, прежде всего, с ростом численности населения планеты в XX веке и в начале XXI с 1,5 до 7 млрд. человек. Кроме того, каждые 15 лет происходит удвоение объемов производства. Растет номенклатура используемых элементов. Если в 1869 г. было известно 62 элемента, из которых использовали лишь 35, — 21 — ǞǁǪǫǪÐ ÐǤ͠ǮƻǁǬǂǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐÐ то к 2013 г. число открытых элементов выросло до 111, из них находят применение уже 90. В настоящее время объем производства определяется получением различных металлов (примерно 800 млрд. тонн в год), добычей полезных ископаемых (примерно 100 млрд. тонн), производством синтетических материалов (около 60 млрд. тонн). На поля ежегодно вывозится до 500 тыс. тонн химических удобрений, из них 40 тыс. тонн — вредных для здоровья человека, а 12 тыс. тонн — ядовитых. Кроме того, в мире производится большое количество энергии, которое удваивается каждые 12 лет. Это приводит к тепловыделению порядка 1013 Вт (для сравнения: излучение Солнца составляет 1017 Вт). Большое тепловыделение, наряду с выбросом в атмосферу около 12 млрд. тонн двуокиси углерода влияет на климат Земли и приводит к появлению так называемого парникового эффекта. Последнее грозит таянием гренландских ледников и затоплением земной поверхности. Использование атомной энергии связано с опасностью радиоактивного заражения в результате различных аварий, подобных аварии на ПО Маяк (СССР-1957), Чернобыльской (СССР-1986) и аварии на атомной станции в городе Фукусима (Япония-2011 г.). При этом обостряется проблема захоронения радиоактивных отходов. В результате жизнедеятельности человека ежегодно в атмосферу выбрасывается: – 250 млн. тонн пыли; – 200 млн. тонн окиси углерода; – 50 млн. тонн оксидов азота; – 50 млн. тонн различных углеводородов. Из-за выброса фреона реальна возможность нарушения озонового слоя, что может привести к массовой гибели организмов под действием жесткого ультрафиолета. Большое количество выбросов возвращается на Землю вместе с осадками в виде так называемых «кислотных дождей», загрязняющих водоемы. Большое значение в жизни человека имеет вода. Около 13 % речных вод потребляет человек. Однако в результате его — 22 — ÐƸǭǮǁǮƼǀǆǬǯǭǪǎÐǯǀǰǱǪǅǀǎÐǫÐǂǀ͠Ǭ жизнедеятельности в водоемы сбрасывается 700 млрд. м3 сточных вод, загрязненных ядовитыми веществами (тяжелыми металлами, кислотами и органическими соединениями). Кроме того, в воды ежегодно сбрасывается 17 млрд. т твердых отходов, которые уносятся в моря и океаны. Водоемы пересыхают, засоряются и засоляются (Аральское море, Азовское море, Байкал, залив Кара-Богаз-Гол). Серьезной проблемой является низкий коэффициент использования природного сырья. Так, при производстве металла 2/3 добытого сырья уходит в отходы. Причем даже из произведенной стали 25 % также уходит в отходы. В ухудшение экологии свою лепту вносит и производство материалов электронной техники. Используемые вредные вещества As, P, Hg, Pb, Cd, Te и их соединения, HCl и другие кислоты, органические растворители, к сожалению, нередко попадают в среду обитания человека. Сегодня экологическую ситуацию в мире можно охарактеризовать, как близкую к критической. Среди глобальных экологических проблем можно отметить следующие: – уничтожены и продолжают уничтожаться тысячи видов растений и животных; – в значительной мере истреблен лесной покров; – стремительно сокращается имеющийся запас полезных ископаемых; – мировой океан не только истощается в результате уничтожения живых организмов, но и перестает быть регулятором природных процессов; – атмосфера во многих местах загрязнена до предельно допустимых размеров, а чистый воздух становится дефицитом; – частично нарушен озоновый слой, защищающий от губительного для всего живого космического излучения. Экологические проблемы городов мира, главным образом наиболее крупных из них, связаны с чрезмерной концентрацией на сравнительно небольших территориях населения, транспорта и промышленных предприятий, с образованием антропогенных ландшафтов, очень далеких от состояния экологического равновесия. — 23 — ǞǁǪǫǪÐ ÐǤ͠ǮƻǁǬǂǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐÐ Темпы роста населения мира в 1,5–2,0 раза ниже роста городского населения, к которому сегодня относится 40% людей планеты. За период 1972–2012 гг. население крупных городов выросло в 4, средних — в 3 и малых — в 2 раза (судя по всем сайтам, тенденция роста урбанизированных зон за последние годы остается на том же уровне). Социально-экономическая обстановка привела к неуправляемости процесса урбанизации во многих странах. Процент городского населения в отдельных странах на 2011 г. по данным The United Nations Department of Economic and Social Affairs равен: Аргентина — 92,6, Уругвай — 92,6, Австралия — 89,3, США — 82,6, Япония — 67, Германия — 74, Швеция — 84,8. Помимо крупных городов-миллионеров, быстро растут городские агломерации или слившиеся города. Таковы Вашингтон — Бостон и Лос-Анжелес — Сан-Франциско в США; города Рура в Германии; Москва, Донбасс и Кузбасс в СНГ. Круговорот вещества и энергии в городах значительно превосходит таковой в сельской местности. Средняя плотность естественного потока энергии Земли — 180 Вт/м2, доля антропогенной энергии в нем — 0,1 Вт/м2. В городах она возрастает до 30–40 и даже до 150 Вт/м2 (Манхэттен). Над крупными городами атмосфера содержит в 10 раз больше аэрозолей и в 25 раз больше газов. При этом 60–70% газового загрязнения дает автомобильный транспорт. Более активная конденсация влаги приводит к увеличению осадков на 5–10%. Самоочищению атмосферы препятствует снижение на 10–20% солнечной радиации и скорости ветра. При малой подвижности воздуха тепловые аномалии над городом охватывают слои атмосферы в 250–400 м, а контрасты температуры могут достигать 5–6 градусов. С ними связаны температурные инверсии, приводящие к повышенному загрязнению, туманам и смогу. Города потребляют в 10 и более раз больше воды в расчете на 1 человека, чем сельские районы, а загрязнение водоемов достигает катастрофических размеров. Объем сточных вод достигают 1м3 в сутки на одного человека. Поэтому практически все крупные города испытывают дефицит водных ресурсов и многие из них получают воду из удаленных источников. Водоносные горизонты под городами сильно истощены — 24 — ÐƸǭǮǁǮƼǀǆǬǯǭǪǎÐǯǀǰǱǪǅǀǎÐǫÐǂǀ͠Ǭ в результате непрерывных откачек скважинами, колодцами, а кроме того загрязнены на значительную глубину. Коренному преобразованию подвергается и почвенный покров городских территорий. На больших площадях, под магистралями и кварталами он физически уничтожается, а в зонах рекреаций — парки, скверы, дворы — сильно уничтожается, загрязняется бытовыми отходами, вредными веществами из атмосферы, обогащается тяжелыми металлами, обнаженность почв способствует водной и ветровой эрозии. Растительный покров городов обычно практически полностью представлен «культурными насаждениями» — парками, скверами, газонами, цветниками, аллеями. Структура антропогенных фитоценозов не соответствует зональным и региональным типам естественной растительности. Поэтому развитие зеленых насаждений городов протекает в искусственных условиях, постоянно поддерживается человеком. Многолетние растения в городах развиваются в условиях сильного угнетения. Самое опасное загрязнение всей окружающей среды — радиоактивное. Известно, что в начале 60-х годов фон искусственной радиоактивности, вызванной испытаниями ядерного оружия, достиг угрожающего уровня. Страшные последствия проявляются уже сейчас. Для получения электроэнергии конструкторы ядерных реакторов создают достаточно надежную защиту от выделения радиоактивных элементов в окружающую среду. Однако проблему захоронения радиоактивных отходов все еще нельзя считать решенной. К важнейшим экологическим проблемам относится загрязнение водоемов промышленными и бытовыми стоками. Потребление загрязненной воды служит источником 3/4 всех болезней и 1/3 всех смертных случаев. Особенно остро проблема чистой питьевой воды стоит в тропических странах, где водоемы часто служат средой размножения паразитов. Очистка сточных вод в подавляющем большинстве государств мира отличается крайним несовершенством. Особенно много «проскакивает» через очистные сооружения неорганических соединений азота, фосфора, калия, минеральных солей, в том числе и солей высо— 25 — ǞǁǪǫǪÐ ÐǤ͠ǮƻǁǬǂǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐÐ котоксичных металлов. В Англии 90%населения пользуются водой сомнительного качества. Ряд рек имеет воду плохого качества по бактериальным и химическим показателям. Особенно загрязнена река Темза, в которую сбрасываются все сточные воды Лондона. К наиболее загрязненным рекам мира относятся также Нил, Амазонка, Дон, Нигер, Миссисипи, Миссури, Конго, Москва-река и др. Основным загрязнителем морей (Средиземное море наиболее загрязненное в этом плане), значение которого быстро возрастает, является нефть. Этот вид загрязнителя попадает в море разными путями: при спуске воды после промывки цистерн из-под нефти, при аварии судов, в особенности нефтевозов, при бурении морского дна и авариях на морских нефтепромыслах. О масштабах загрязнения можно судить по следующим показателям. В Мировой океан сбрасывается более 5% транспортируемой нефти — примерно 10 млн. т в год. Резкий рост потребления в последние десятилетия во всем мире привел к существенному увеличению объемов образования твердых бытовых отходов. В настоящее время масса потока ТБО, ежегодно поступающего в техносферу, достигла почти геологического масштаба и составляет около 400 млн т в год. Влияние потока ТБО уже остро сказывается на глобальных геохимических циклах ряда биофильных элементов, в частности органического углерода. Так, масса этого элемента, поступающего в окружающую среду с отходами, составляет примерно 85 млн т в год, в то время как общий естественный приток углерода в почвенный покров планеты составляет немногим более 40 млн т в год. К настоящему времени сложилась следующая система классификации отходов, производимых цивилизацией: – отходы производства — материалы, образующиеся в процессах производства продукции и выполнения услуг, не находящие применения на том предприятии, где они были получены; – отходы потребления — материалы или изделия, утратившие свои потребительские свойства в процессе эксплуатации| – твердые бытовые отходы (ТБО) — отходы потребления образующиеся в населенных пунктах в результате жизне— 26 — ÐƸǭǮǁǮƼǀǆǬǯǭǪǎÐǯǀǰǱǪǅǀǎÐǫÐǂǀ͠Ǭ деятельности населения. ТБО образуются, главным образом, в жилых зданиях, учреждениях и предприятиях общественного назначения (общественного питания, учебных и зрелищных комплексах, гостиницах детских садах и т.п.). К ТБО относятся также отходы от отопительных устройств, уличный мусор, опавшие листья, собираемые с дворовых территорий, канализационные отходы, осадки сточных вод н т.п. В последние годы эти отходы стали выделять в особую группу так называемых «муниципальных отходов; – опасные отходы — отходы, содержащие в своем составе вещества, обладающие хотя бы одним опасным для людей и окружающей среды (ОС) (токсичностью, инфекционностью, взрыво- или пожароопасностью и т.п.), и присутствующие в таком количестве и в таком виде, в которых они представляют непосредственную или потенциальную опасность для здоровья людей или состояния ОС как самостоятельно, так и при вступлении в контакт с другими веществами или объектами ОС; – вторичное сырье — отходы производства и потребления, собранные и подготовленные к повторному использованию при условии экологической безопасности применяемых технологий их переработки. Источниками городских отходов являются домашнее хозяйство, коммерческие (конторы, магазины, рестораны) и муниципальные (школы, больницы) учреждения. По характеру использования бывших в употреблении товаров ТБО делятся на отходы товаров длительного (бытовая техника, мебель) и краткосрочного (газеты, одежда, пищевые отходы) пользования, а также различных видов упаковочных материалов. По качественному составу бытовые отходы подразделяются на бумагу (картон), пищевые отходы, дерево, металл черный, металл цветной, текстиль, кости, стекло, кожу и резину, камни, полимерные материалы, прочие компоненты и отсев (мелкие фрагменты, проходящие через 1,5-сантиметровую сетку). Академик Б.Н. Ласкорин предлагает классифицировать отходы по направлениям переработки на группы, в которые попадают ТБО, подлежащие, соответственно: — 27 — ǞǁǪǫǪÐ ÐǤ͠ǮƻǁǬǂǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐÐ – ликвидации без дополнительной обработки (сжигание, санитарные свалки и т.д.); – повторному использованию в том или ином производстве после дополнительной обработки (разделение фаз, извлечение отдельных элементов, химическая обработка и т.д.); – захоронению или складированию с необходимой предварительной обработкой. К опасным ТБО относятся: отходы, содержащие батарейки и аккумуляторы, электроприборы, лаки и краски, косметика, удобрения и ядохимикаты, бытовая химия, медицинские отходы, ртутьсодержащие термометры, барометры, тонометры, лампы. Проблема твердых отходов появилась вместе с человеком, но в древности это, в основном, была проблема домашнего мусора. Около 1450 г. до н. э. Моисей обязал свой народ возвращать отбросы обратно в землю [Второзаконие, гл. 23, ст. 12–13]. Природа была в состоянии справляться с отходами, когда население было немногочисленным и отбросы были невелики, а человек продолжал вести натуральное хозяйство. Лишь позднее к ТБО добавились твердые отходы производства, к которым принято относить и отходы сельского хозяйства. История этой проблемы тесно связана с историей развития городов. Население древних городов увеличивалось в ограниченном крепостными стенами пространстве. Будущие горожане переселялись из деревень вместе с живностью, что увеличивало скученность в городе и загрязненность его территории отходами жизнедеятельности людей и животных. Приблизительно около 500 г. до н.э. в Афинах был издан первый известный эдикт, запрещающий выбрасывать мусор на улицы и предусматривающий организацию специальных свалок. Согласно закону мусорщикам предписывалось сбрасывать отходы не ближе чем за милю от города. У римлян в Кодексе Юстиниана I были записаны меры, ограждающие граждан от скопления отбросов. Однако, подобно многим античным изобретениям, практика утилизации отходов была забыта в средние века. Средне— 28 — ÐƸǭǮǁǮƼǀǆǬǯǭǪǎÐǯǀǰǱǪǅǀǎÐǫÐǂǀ͠Ǭ вековые города утопали в грязи и отбросах, а главными санитарами были кошки, собаки, свиньи и вороны. В жаркое время года отбросы быстро разлагались и, попадая в почву и водоёмы, порождали тяжёлые болезни, а зачастую и эпидемии, такие как чума, холера. К тому же обилие не убираемых бытовых отходов создавало благоприятную среду для быстрого размножения насекомых и грызунов — переносчиков инфекций. Жители продолжали выбрасывать мусор в окна вплоть до XIV в. По мнению некоторых историков, одна из наиболее жестоких эпидемий чумы 1348–1350 гг., уничтожившая почти треть населения стран от Исландии до Индии, была вызвана именно этими загрязнениями. Лишь со временем, когда была установлена прямая связь между отходами и эпидемиями различных болезней, мусор стали собирать и вывозить за пределы городов. В 1297 г. в Лондоне был принят закон, приказывающий домовладельцам содержать дом и тротуар перед домом в чистоте. Закон 1354 г. обязывал жителей убирать грязь на улице ежедневно. Появилась профессия мусорщика и специальные повозки. Указ 1407 г. обязывал лондонцев сохранять накопившийся у них мусор в доме до прихода мусорщика. Во Франции в XVI в. издаётся ряд вердиктов, предписывающих горожанам собирать мусор в корзины, но они как не выполнялись горожанами, так и не контролировались городскими властями. В связи с тем, что проблема мусора и нечистот приобретала всё большую остроту; в 1789 г. власти Парижа предложили установить в определённых местах города каменные столбы, огороженные железными решётками, куда надлежало сбрасывать бытовые отходы. Во второй половине XIX в. уже были изданы указы, согласно которым на каждом этаже устанавливалось ведро или ёмкость для нечистот. Постепенно европейские муниципалитеты оформили ответственность за сбор и утилизацию отходов в законах. Мусор вывозили за городские ворота и просто складировали в различных хранилищах в сельской местности. В результате роста городов свободные площади в их окрестностях уменьшались, а неприятные запахи и возросшее количество крыс, вызван— 29 — ǞǁǪǫǪÐ ÐǤ͠ǮƻǁǬǂǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐÐ ные свалками, стали невыносимыми. В результате отдельно стоящие свалки были во многих местах заменены ямами для хранения мусора. Попытки частичного использования твердых отходов относятся к концу XVIII в., когда перед помещением отходов на свалку в г. Эдинбурге (Шотландия) производилась их ручная сортировка, и часть повторно использовалась или продавалась. Первое систематическое использование мусорных печей было опробовано в Ноттингеме (Англия) в 1874 г. Сжигание сокращало объем мусора на 70...90 %, в зависимости от состава. Поэтому оно быстро нашло применение по обе стороны Атлантики. Густонаселенные и наиболее значимые города вскоре внедрили экспериментальные печи, но не везде смогли оправдать затраты на их эксплуатацию. Большие затраты были уместны тогда, когда не было дешевого способа захоронения. Кроме того, многие города, которые применили сжигательные печи, вскоре отказались от них из-за ухудшения состава воздуха. Проблема отходов становилась все острее не только из-за изменения состава, но и в связи с ростом их массы на одного человека и с общим увеличением населения городов. Первые шаги к переработке мусора были сделаны в Нью-Йорке в 1895–1898 гг. по инициативе Дж. Варинга — комиссара отдела очистки улиц. Им были установлены разные по форме и цвету мусорные ящики для составляющих отходов. Это позволило использовать большую часть отходов — для этого была построена специальная фабрика. Но первый завод по переработке твердых отходов (с глубокой сортировкой) был введен в действие лишь в 1932 г. в Голландии. В середине 80-х гг. прошлого века в мире работало более тысячи мусоросжигательных заводов и в несколько раз меньше — перерабатывающих. Но в последнее десятилетие XX в. это соотношение резко изменилось в пользу переработки. Тем не менее, однако, и до сих пор основным способом удаления отходов является их депонирование на свалках или полигонах. Это приводит к тому, что среда обитания человека становится опасной. Экология — 30 — ÐƸǭǮǁǮƼǀǆǬǯǭǪǎÐǯǀǰǱǪǅǀǎÐǫÐǂǀ͠Ǭ и технический прогресс должны быть системно связаны между собой, иначе неизбежно приближение экологической катастрофы. Создание и применение ресурсосберегающих технологий, базирующихся на комплексном использовании сырья, экономии ресурсов, минимизации количества образующихся отходов (в ряде случаев — предотвращение их образования), максимально возможном вовлечении вторичных ресурсов в хозяйственный оборот, переработке и утилизации отходов производства и потребления, является генеральным стратегическим направлением обеспечения экологической безопасности без снижения темпов научно-технического прогресса. В перспективе базовой основой производства должно стать использование техногенного сырья — отходов производства и потребления. Естественно, при этом должен активно проводиться поиск альтернативных, нетрадиционных источников энергии, новых направлений использования вторичных ресурсов. По своей природе техногенное сырье может быть использовано как ВМР и ВЭР (вторичные материальные и энергетические ресурсы). Вместе с тем в настоящее время в хозяйственный оборот вовлекается всего около 10% образующихся твердых отходов. Это очень мало. И в то же время 100%-ная утилизация отходов в данных технико-экономических условиях невозможна. Наука и практика отстают от требований времени. Проблема отходов для своего решения требует больших капиталовложений и должна решаться поэтапно, но обязательно целенаправленно и непрерывно. Важнейшую роль при этом играют комплексный подход, подготовка специалистов, принятие научно-обоснованных решений, своевременное финансовое и научно-техническое обеспечение. Понять природу экологического кризиса в целом и в отдельных ее проявлениях и сделать выводы из допущенных просчетов развития, скорректировать развитие экономики, политики и культуры — вот основные задачи, которые должны решать люди всей планеты. В противном случае экологический кризис перерастет в необратимую экологическую катастрофу с полным разрушением биосферы. — 31 — ǞǁǪǫǪÐ ÐǤ͠ǮƻǁǬǂǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐÐ Крайне неблагополучное состояние природопользования диктует необходимость уделять этому вопросу особое внимания в жизнедеятельности человека. В различных странах разработаны соответствующие законодательные документы, регулирующие хозяйственную деятельность человека, создан общественный контроль (например, движение «зеленых»). В России существует Комитет по охране природы, в задачу которого входит контроль за действующим производством, апробация внедряемых новых производств. Составляется экологический паспорт производства (газовые, жидкие и твердые отходы, их количество и состав). За выбросы вредных веществ предприятие обязано платить значительные суммы. При создании предприятия составляется его экологическая карта или паспорт, в котором указываются: 1. общие сведения о предприятии; 2. природно-климатическая характеристика района расположения предприятия; 3. цеха и производственные объекты, которые производят выбросы запрещенных веществ, объемы продукции, технологические схемы с указанием видов и количеств отходов, материального баланса; 4. использование земельных ресурсов, здания, проезды и склады; 5. расход сырья и вспомогательных материалов по видам продукции; 6. расход энергоресурсов по видам продукции; 7. характеристика выбросов в атмосферу, методы их улавливания и утилизации; 8. характеристика водопотребления, водоснабжения и очистки сточных вод на предприятии; 9. характеристика твердых отходов, образующихся на предприятии; 10. характеристика полигонов и накопителей, предназначенных для захоронения (складирования) отходов; 11. рекультивация земель; 12. транспортируемая продукция; 13. плата за выбросы. — 32 — ÐƸǭǮǁǮƼǀǆǬǯǭǪǎÐǯǀǰǱǪǅǀǎÐǫÐǂǀ͠Ǭ ɋɵɪɶɟ ɉɪɨɢɡɜɨɞɫɬɜɨ Ɂɚɝɪɹɡɧɟɧɢɟ ɚɬɦɨɫɮɟɪɵ Ɂɚɝɪɹɡɧɟɧɢɟ ɝɢɞɪɨɫɮɟɪɵ ɉɪɨɞɭɤɰɢɹ Ɉɬɯɨɞɵ Ⱥɷɪɨɡɨɥɢ Ƚɚɡɵɢɩɚɪɵ ɋɭɯɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ⱥɛɫɨɪɛ ɰɢɨɧɧɵɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ ɗɥɟɤɬɪɢ ɱɟɫɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ ³Ɇɨɤɪɵɟ´ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ʉɚɬɚɥɢɬɢ ɱɟɫɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ⱥɞɫɨɪɛ ɰɢɨɧɧɵɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ʉɨɧɜɟɤ ɰɢɨɧɧɵɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ɂɚɝɪɹɡɧɟɧɢɟ ɥɢɬɨɫɮɟɪɵ ɋɬɨɱɧɵɟɜɨɞɵ ɇɟɪɚɫɬɜɨ ɪɢɦɵɟ ɬɜɟɪɞɵɟɢ ɠɢɞɤɢɟ ɩɪɢɦɟɫɢ Ƚɢɞɪɨ ɦɟɯɚɧɢ ɱɟɫɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ɏɢɡɢɤɨ ɯɢɦɢɱɟɫ ɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ɍɜɟɪɞɵɟɨɬɯɨɞɵ Ɋɚɫɬɜɨ ɪɢɦɵɟ ɩɪɢɦɟɫɢ ɋɛɨɪɢ ɯɪɚɧɟɧɢɟ ɇɟɨɪɝɚ ɧɢɱɟɫɤɢɟ Ɉɪɝɚɧɢ ɱɟɫɤɢɟ ɏɢɦɢ ɱɟɫɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ ɪɟɚɝɟɧɬ Ɏɢɡɢɤɨ ɯɢɦɢɱɟɫ ɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ɏɢɡɢɤɨ ɯɢɦɢɱɟɫ ɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ȼɢɨɯɢ ɦɢɱɟɫɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ɍɟɪɦɢ ɱɟɫɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ɍɟɪɦɢ ɱɟɫɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ƚɚɡɨ ɨɛɪɚɡɧɵɟ Ɏɢɡɢɤɨ ɯɢɦɢɱɟɫ ɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ɇɟɯɚɧɢ ɱɟɫɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ɏɢɡɢɤɨ ɯɢɦɢɱɟɫ ɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ Ɍɟɪɦɢ ɱɟɫɤɢɟ ɦɟɬɨɞɵ ɨɱɢɫɬɤɢ 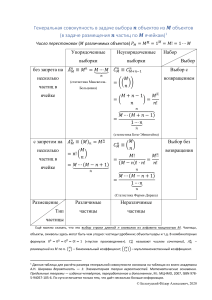Рис.1.1. Схема обезвреживания и переработки промышленных отходов В настоящее время все инженерные методы защиты окружающей среды в целом могут быть проиллюстрированы схемой, в которой представлены все основные способы очистки отходов производства от опасных и вредных веществ (рис. 1.1). Научные успехи человечества на сегодняшний день, прежде всего, связанны с существенным углублением физических и физико-химических представлений о механизме процессов, их математизацией и компьютеризацией. Ускорение промышленного развития в мире обусловлено остро вставшими энергетическими, сырьевыми и экологическими проблемами, а так же появившимися возможностями интенсификации и совмещения технологических процессов, оптимизации проектирования, управления аппаратурой и реализацией ряда новых технологий. В соответствии с общеобразовательным стандартом выпускник по направлению «Техносферная безопасность» должен хорошо представлять себе, что человек — это часть природы, и в этом — 33 — ǞǁǪǫǪÐ ÐǤ͠ǮƻǁǬǂǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐÐ отношении является неправомерным противопоставление природы и человека, как внешних сил по отношению друг к другу. А раз это так, то и появление в недрах человеческого общества техники — закономерное явление в процессе эволюции планеты Земля. Поэтому главные усилия инженера-эколога на сегодняшний день должны быть направлены на гармоничное развитие природы и техники, которое возможно только в результате научно-обоснованного компромисса между объектами природы и социальной деятельностью человека. Ответственность за такой компромисс лежит на инженерной экологии — этой многопрофильной области знания о законах природосберегающего формирования техносферы планеты и её сбалансированного безопасного экологического развития. ϭ͘Ϯ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏ 1. Назовите основные виды антропогенного воздействия на среду обитания. 2. Как влияет загрязнение окружающей среды на здоровье человека, фауну и флору нашей планеты? 3. В чем заключается организация защиты окружающей среды? 4. Какие экологические проблемы существуют в крупных городах? 5. Какие экологические проблемы в настоящее время существуют в сельской местности? 6. Каковы последствия загрязнения атмосферы? 7. Каковы последствия загрязнения гидросферы? 8. Каковы последствия загрязнения литосферы? 9. Почему главными загрязнителями природы являются твердые отходы потреблениями? 10. Какое, по вашему мнению, существует решение проблемы твердых отходов? 11. Перечислите самые распространенные процессы лежащие в основе инженерной защиты окружающей среды от загрязнений. 12. Что изучает предмет «Теоретические основы защиты окружающей среды»? — 34 — ǍưǙǚǙÍ Í Í ǗƟǑƚǋǐǎǑǖǋƞƦǑƥǎÍƜǋǏǒǑƥÍ ǓǔƝǔǒƚƥÍƝÍƝǘÍǓǔƝǐǎǑǎǑƝǎÍǓǔƝÍ ǋǑǋƞƝƜǎÍǓǔǒƠǎǕǕǒǌÍƜǋƣƝǖƥÍ ǒǏǔƟƛǋƨƣǎ֏ÍǕǔǎƚƥ В результате освоения главы 2 бакалавр должен: Знать: – фундаментальные законы природы и их применение к процессам защиты окружающей среды. Уметь: – применять основные законы природы при описании процессов обезвреживания биосферы от загрязняющих веществ. Владеть: – методами расчета материального и энергетического (теплового) баланса отдельного процесса, а также совокупности последовательных процессов (технологическая схема производства). Ϯ͘ϭ͘ʯ̵̡̨̨̛̦̭̬̦̖̦̥̭̭̼̌̌́̌ Закон сохранения массы — один из фундаментальных законов природы был впервые открыт М. В. Ломоносовым. При анализе технологических и природных процессов закон сохранения массы применяется к системе в целом или отдельным ее частям (в том числе и к бесконечно малым). Кроме — 35 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ того, он может применяться ко всей массе участвующих в процессе веществ или к отдельному компоненту. Закон сохранения массы применим к веществам, находящимся в любом агрегатном состоянии. Согласно современной интерпретации [9] изменение массы вещества в некотором объеме V вызывается притоком ее из окружающей среды или отводом из рассматриваемого объема в окружающую среду: Gâõ − Gâûõ = VDr (2.1) где Gвх, Gвых — количество вещества поступающего в систему и выходящего из нее, соответственно; ∆ρ — изменение плотности. Для произвольного компонента i закон сохранения массы с учетом химических реакций записывается в виде: Gi вх − Gi вых + riv Vt = VDri (2.2) где riv — масса компонента i, образующегося в единице объема за единицу времени (скорость реакции); τ — время; ∆ρi — изменение массы компонента i в единице объема системы. Так как в результате химических процессов общая масса всех веществ остается постоянной, то n ∑riv = 0 i =1 где n — число компонентов в системе. При отсутствии в системе химических превращений, riv = 0 и уравнение (2.2) становится аналогичным уравнению (2.1) Gâõ − Gâûõ = V ∆ρi (2.3) Если плотность вещества в процессе не меняется (∆ρ = 0), то Gâõ = Gâûõ (2.4) При периодических процессах величины G и V — масса и объем соответственно, а при непрерывных процессах — G и V массовый и объемный расходы. Рассмотрим применение закона сохранения массы к элементарному объему dxdydz жидкости (газа) (рис. 2.1). Скорость движения ω и плотность жидкости ρ в общем случае изменяются в пространстве и во времени ω = f ( x, y, z, τ ) (2. 5) ρ = ϕ ( x, y, z, τ ) — 36 — ÐƭǪǭǮǃÐǯǮǲ͠ǪǃǬǃǀǎÐǂǪǯǯǊ Рис.2.1. Распределение скоростей в бесконечно малом объеме движущейся жидкости или газа. Изменение количества вещества в элементарном объеме, обусловленное движением жидкости, можно рассматривать как сумму изменений по осям координат. Скорости движения в направлении осей х, у и z определяются проекциями ωx, ωv и ωz вектора скорости ω. Изменение массы вещества в рассматриваемом элементарном объеме в направлении оси х равн о разности между массой, входящей через поверхность dy dz, расположенную на расстоянии х от начала координат, и массой, выходящей через такую же поверхность, отстоящую от первой на расстоянии dx. Количество поступающего за единицу времени вещества равно ρωxdydz. На расстоянии dx от мест а входа в соответствии с (2.5) меняются как скорость, так и плотность. Количество вещества, покидающего элементар ∂ (ρω x )  ный объем за единицу времени, равно ρω x + dx  dydz . ∂x   Таким образом, изменение количества вещества в единицу времени за счет движения жидкости (газа) в направлении оси х:   (ρω x ) dx  dydz = − (ρω x ) dxdydz dGx = ρω x − ρω x +  x x     Аналогично для направлений у и z имеем: ρω y (σω z ) dxdydz . dGy = − dxdydz ; dGz = y z ( ) — 37 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Суммарное изменение количества вещества за счет его переноса жидкостью или газом запишется в виде:  ∂ (ρω ) ∂ ρω y ∂ (σω )  x z  dV dG = dGx + dGy + dGz = −  + + x y z ∂ ∂ ∂    ∂ (ρω ) dG x Получаемая отсюда производная = − + dV  ∂x ρω y ∂ (σω z )   при dV → 0 выражает отнесенное к единице + + ∂y ∂z   объема изменение количества вещества за счет переноса движущейся жидкостью или газом в точке с координатами x, y, z. Вследствие этого переноса происходит изменение плот∂ρ ности в времени . По закону сохранения массы ∂τ ∂ρ ∂ (ρω x ) ∂ ρω y ∂ (σω z ) + + + =0 ∂τ ∂x ∂y ∂z В общем случае ρ, ωx, ωy и ωz — переменные величины. Дифференцируя три последних слагаемых в уравнении (1.6), получаем ∂ω y ∂ω z   ∂ω ∂ρ ∂ρ ∂ρ ∂ρ (2.7) + ωx + ωy + ωz + ρ x + + =0 ∂τ ∂x ∂y ∂z ∂y ∂z   ∂x Учитывая, что координаты рассматриваемого элементарного объема х, у и z меняются во времени, сумма первых четырех слагаемых в уравнении (1.7) представляет собой полную производную к плотности по времени. Действительно, по правилу дифференцирования функции нескольких переменных ( ( ) ) ( ) dρ ∂ρ ∂ρ dx ∂ρ dy ∂ρ dz ∂ρ ∂ρ ∂ρ ∂ρ (2.8) = + + + = + ωx + ωy + ωz dτ ∂τ ∂x dτ ∂y dτ ∂z dτ ∂τ ∂x ∂y ∂z dx dy dz = ωx; = ωy; = ω z . Принимая во внимание поскольку dτ dτ dτ (2.8), уравнение (2.6) можно преобразовать к виду: ∂ω y ∂ω z   ∂ω dρ + ρ x + + =0 dτ ∂y ∂z   ∂x — 38 — (2.9) y ÐƭǪǭǮǃÐǯǮǲ͠ǪǃǬǃǀǎÐǂǪǯǯǊ Сумма частных производных компонентов вектора скорости ωx, ωv и ωz по соответствующим им направлениям называется расхождением, или дивергенцией, вектора скорости и обозначается div ω. Уравнение (2.9), записанное в виде 1 dρ (2.10) + divω = 0 ρ dτ известно в аэро- гидродинамике как уравнение неразрывности потока. Изменение плотности вещества обусловлено процессами расширения или сжатия вследствие изменения температуры или давления. Различают несжимаемые и сжимаемые среды. К несжимаемым средам относятся материальные тела, находящиеся в жидком состоянии (капельные жидкости). При небольших изменениях температуры или давления их объем остается практически неизменным. К сжимаемым средам относятся газы, объем которых сильно зависит от температуры и давления, а также капельные жидкости при высоких и сверхвысоких давлениях. Для несжимаемых жидкостей (ρ=const) и уравнение (2.10) упрощается, т.е.: divω = 0 (2.11) Приведенные уравнения формулируют закон сохранения массы системы в произвольной точке. Для произвольного компонента вместо плотности ρ в этих уравнениях должна фигурировать плотность ρi, численно равная его массовой концентрации сi (в кг/м3). Следует также учесть скорость образования вещества в результате химических превращений riv. Уравнение (2.9) для компонента записывается в виде: dci + ci divω = rvi dτ или ∂ω y ∂ω z   ∂ω ∂ci ∂c ∂c ∂c + ω x i + ω y i + ω z i + ci  x + + =r x ∂τ ∂x ∂y ∂z ∂ ∂x ∂x  iv  (2.12) Процессы, в которых свойства участвующих в них веществ изменяются только в пространстве, но не во времени, называ— 39 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ ются установившимися (стационарными). Для них уравнение (2.12) имеет вид ∂c ∂c ∂c ω x i + ω y i + ω z i + cidivω = riv (2.13) ∂x ∂y ∂z При отсутствии химических превращений компонента i (riv=0) ∂c ∂c ∂c ω x i + ω y i + ω z i + ci divω = 0 (2.14) ∂x ∂y ∂z Если и концентрации отдельных компонентов не меняются, т. е. ci=const, то из (2.14) следует divω=0. Это означает, что при неизменном составе поведение жидкости или газа в целом и отдельных их компонентов подчиняется одинаковым закономерностям. Ϯ͘ϭ͘ϭ͘ʿ̵̡̨̨̛̛̛̬̥̖̦̖̦̖̦̭̬̦̖̦̥̭̭̼̌̌̌́̌̚ ̵̸̶̡̨̨̡̨̨̛̯̖̦̣̖̭̥̱̪̬̖̭̭̱̐͘ Материальный баланс для любого технологического процесса или части его при статических условиях составляется на основании закона сохранения массы вещества: (2.15) ∑ G исх = ∑ G кон где ΣGисх — сумма масс исходных продуктов процесса; ΣGкон — сумма масс конечных продуктов процесса в тех же единицах измерения. Таким образом, если в какой-либо технологический узел поступает GА кг продукта А, GВ кг продукта В и т.д., а в результате переработки их получается GС кг продукта С, GD кг продукта Д и т.д., а также если в конечных продуктах остается часть начальных продуктов А (GА кг), В (GВ кг) и т.д., то при этом должно сохраниться равенство (2.16) GA + GB +… = GA ′ + GB′ + GC + GD +…∆G где ∆G — производственные потери продукта. Определение массы вводимых компонентов и полученных продуктов производится отдельно для твердой, жидкой и газообразных фаз согласно уравнению ' (2.17) Gг + Gж + Gт = G'г + Gж + Gт' — 40 — ÐƭǪǭǮǃÐǯǮǲ͠ǪǃǬǃǀǎÐǂǪǯǯǊ В процессе не всегда присутствуют все фазы, в одной фазе может содержаться несколько веществ, что приводит к упрощению или усложнению уравнения (2.17). При составлении полного баланса обычно решают систему уравнений с несколькими неизвестными. При этом могут быть использованы соответствующие формулы для определения равновесного и фактического выхода продукта, скорости процесса и т. д. Теоретический материальный баланс рассчитывается на основе стехиометрического уравнения реакции и молекулярной массы компонентов. Практический материальный баланс учитывает состав исходного сырья и готовой продукции, избыток одного из компонентов сырья, степень превращения, потери сырья и готового продукта и т. п. Основой для составления материального баланса отдельного процесса или всего производства служит технологическая схема. Совокупность и последовательность операций, которым подвергается материал при переработке либо очистке позволяет составить технологическую схему процесса, которую принято изображать графически. В зависимости от назначения схемы могут быть качественными, количественными и шламовыми (этот термин пришел из обогащения и означает присутствие жидкой фазы). 1. В качественной схеме процесса изображается путь движения материала последовательно по стадиям с указанием некоторых данных о качественных изменениях материала по стадиям. Качественная схема дает представление о стадийности процесса, количестве операций, о виде процесса, способе обработки промежуточных продуктах и возможном количестве продуктов. 2. Если на качественной схеме указывать количество переработанных продуктов, получаемых в отдельных операциях и содержание в них каких-либо компонентов, то схема уже будет называться количественной. Выход продуктов по операциям определяют, как правило, в процентах от исходного продукта. 3. Если в схеме имеются данные о количестве жидкой фазы, применяемой в процессе, то количество жидкости ука— 41 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ зывается в соотношении Т:Ж или в процентах, например столько-то % твердого, тогда такая схема процесса называется шламовой. Эффективность любого процесса оценивается качественно-количественными технологическими показателям: выходом продукта (γ), содержанием полезного компонента (γ) и извлечением полезного компонента (ε). В частности для процесса разделения — выход продукта γ количество продукта разделения, выраженное в процентах от количества материала, принятого за 100%. Суммарный выход всех продуктов разделения равен 100%. Уравнение баланса выходов имеет вид: ∑ γ i = 100% (2.18) При разделении материала на два конечных продукта — фракцию 1 с выходом γk и фракцию 2 с выходом γx — уравнение баланса имеет вид: γ k + γ x = 100% (2.19) Содержание компонента — β весовая доля того или иного компонента (минерала или химического соединения) в материале или продукте разделения. Содержание полезного компонента в материале обозначается буквой α. Суммарное количество любого компонента, содержащегося в конечных продуктах разделения, соответствует количеству этого компонента в общем количестве материала. Уравнение баланса для содержания имеет вид: (2.20) ∑ γ iβi = γ исх β исх = 100α Если при разделении получены два конечных продукта — фракция 1 и фракция 2, то уравнение баланса записывается следующим равенством: γ kβk + γ xβx = 100α (2.21) Извлечение ε — величина, показывающая, какая часть всего количества того или иного компонента, содержащегося в материале, перешла в данный продукт разделения. Вычисляется как отношение массы компонента в данном продукте к его массе в материале и выражается в процентах или долях единицы: γβ ε i = i i , 100% (2.22) αi — 42 — ÐƭǪǭǮǃÐǯǮǲ͠ǪǃǬǃǀǎÐǂǪǯǯǊ Сумма извлечений компонента в конечных продуктах равна извлечению в материале, то есть (2.23) ∑ ε i = ε исх = 100% Материальный баланс составляется для каждого химического элемента исходных материалов и продуктов производства, включая и отходы. Материальный баланс технологического процесса или всего производства какого-либо материала необходим для: – знания распределения исходных элементов в технологическом процессе между его продуктами; – определения выхода конечного продукта в процессе его получения; – определения расхода сырья для получения единицы готового продукта; – расчета количества и состава отходов производства для решения вопроса об их улавливании и переработки с целью создания безотходного, экологически чистого производства; – составления экологического паспорта производства; – получения исходных данных для расчета оборудования. На рис. 1.2 приведен фрагмент технологической схемы разделения при процессе обогащения железной руды на концентрат и хвосты. Рис.2.2. Фрагмент технологической схемы разделения при процессе обогащения железной руды. — 43 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ В полной технологической схеме указываются последовательность проводимых технологических процессов, загружаемые материалы и продукты процесса. По результатам расчетов составляется таблица материального баланса. Материальный баланс технологического процесса или нескольких процессов, последовательно используемых для получения какого-либо продукта, представляет собой учет всех поступивших с исходными материалами элементов и полученными в результате проведения технологического процесса (или ряда процессов). Материальный баланс позволяет определить количество и состав отходов производства, представляющих экологическую опасность. Отходы группируются по фазовому составу (газы, жидкости и твердые тела) и по возможным методам улавливания и переработки. Ϯ͘ϭ͘Ϯ͘ʿ̸̴̛̬̥̖̬̬̭̖̯̬̥̖̦̯̌̌̌̐̌ ̵̸̵̶̨̨̡̨̨̛̯̖̦̣̖̭̜̭̖̥̼̪̬̖̭̭̐̌͘ Задача: При обогащении руды, содержащей 31% железа, получен магнетитовый концентрат, содержащий 68,5% железа. Выход концентрата составил 39%. Производительность по руде (Qисх) — 2100 т/час. Определить технологические показатели обогащения. Решение: Выход хвостов определяем по уравнению баланса (2.18): γx =100 — γк=100–31 = 61% Извлечение железа в магнетитовый концентрат рассчитываем по формуле (2.22): εi = γiβi / αi ,% = 39*68,5/31 = 86,18% Извлечение железа в хвосты (потери железа) определяем по уравнению баланса (1.22,1.23): εк = 100 — εк=100*86,18 = = 13,82% С другой стороны, извлечение железа в хвосты равно εк = = γхβх / α Следовательно, содержание железа в хвостах определяется, как βх= εк α/γх = 13,82*31/61 = 7,02% — 44 — ÐƭǪǭǮǃǊÐǰǬ͠ǂǮƽǀǃǪǂǀǭǀ Производительность по концентрату составляет: Ок = Оисхγк=2100•0,39 = 819 т/час. Количество хвостов определяется по разнице: Ох= Оисх – – Ок – 2100 – 819 = 281 т/час Показатели обогащения оформляются в виде таблицы (табл. 2.1). Таблица 2.1. Результаты обогащения железной руды. Продукты обогащения Проиводительность, т/ч Выход γ, % Содержание железа,% Извлечение железа,% Концентрат 819 39,0 68,5 86,18 Хвосты 1281 61,0 7,02 13,82 Руда 2100 100 31,0 100 Ϯ͘Ϯ͘ʯ̡̨̨̡̛̛̛̦̼̯̖̬̥̦̥̌̔̌͘ Ϯ͘Ϯ͘ϭ͘ʿ̡̨̖̬̼̜̦̏̌̚;̸̨̦̣̌̌Ϳ̨̡̛̛̛̯̖̬̥̦̥̔̌ ;̵̡̨̨̛̛̛̦̭̬̦̖̦̦̖̬̌̌́̾̐̚Ϳ͘ Первый закон (начало) термодинамики является частным случаем закона сохранения материи и рассматривает сохранение энергии при различных превращениях одних форм движения материи в другие. В начале развития термодинамики в ней, в основном, рассматривались взаимные переходы теплоты и работы, и была установлена их эквивалентность. Позднее была установлена эквивалентность теплоты и многих других видов энергии. Закон сохранения энергии, как и закон сохранения массы, был впервые сформулирован М.В. Ломоносовым (1748 г.). В установлении современной формулировки первого начала термодинамики большую роль сыграли работы Г.И. Гесса, Майера, Джоуля и Гельмгольца. В частности, Гельмгольц писал: «Энергия в природе не уничтожается и не возникает вновь, а лишь переходит из одного вида в другой. — 45 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Следовательно, если в каком-либо процессе энергия одного вида исчезает, то взамен ее появляется энергия в другой форме и встрого эквивалентном количестве». Любой процесс связан с различными превращением материальных тел и взаимным превращением различных форм движения материи. Мерой движения материи является энергия. Поэтому различные формы движения соответствуют различным видам энергии. По форме перехода энергии от одного тела, к другому процессы можно разделить на две группы: 1. Процессы, связанные с перемещением макроскопических количеств вещества (например, процессы сжатии и расширения газа, поднятия груза, перемещения жидкости и т. д.). Мерой такой формы передачи движения от одного тела к другому является работа. 2. Процессы, в которых переход энергии вызывает изменение движения микрочастиц, из которых состоит рассматриваемое тело. Так, при нагревании газа в замкнутом пространстве возрастает скорость, и энергия движущихся микрочастиц, в результате чего повышаются температура и давление. Мерой такой формы передачи энергии является теплота. Под системой обычно понимают совокупность материальных тел, изменение свойств которых существенно для данного процесса. Взаимодействующие с ними тела рассматриваются как окружающая среда. Такое разделение, конечно, условно и определяете конкретной задачей. Например, если задача процесса — сжатие газа, то системой целесообразно считать газ. Тогда устройство, производящее сжатие, — окружающая среда. Если предметом исследования является состояние устройства, производящего сжатие, то в качестве системы рассматривается это устройство, а окружающей средой является газ. Если от окружающей среды системе передается некоторое количество энергии в форме теплоты δQ, то лишь часть ее расходуется на производство работы δA. Другая часть идет на увеличение энергии системы dE. Следовательно (2.24) δQ − δA = dE — 46 — ÐƭǪǭǮǃǊÐǰǬ͠ǂǮƽǀǃǪǂǀǭǀ Уравнение (1.24) формулирует первый закон термодинамики — закон сохранения энергии. При переходе из одного энергетического состояния в другое энергия Е изменяется на определенную величину независимо от пути перехода. Поэтому значение энергии Е характеризует энергетическое состояние системы. В противоположность этому δQ и δA характеризуют не систему, а процессы ее взаимодействия с окружающей средой; следовательно, они не являются полными дифференциалами. Чтобы подчеркнуть эту их особенность, приращения Q и А обозначены через δQ и δА. В большинстве процессов приходится иметь дело с потоками жидкости или газа, ограниченными твердыми стенками. Поэтому работу δA, производимую движущейся, жидкостью или газом, можно рассматривать как сумму работы против сил, действующих со стороны стенок (δAc), и работы против сил, действующих в объеме газа или жидкости (δAж). Если стенки неподвижны, то единственная сила, определяющая значение δAс, — сила трения, направленная по касательной к поверхности. Когда стенки подвижны, появляется дополнительная внешняя работа (например, при движении жидкости (газа) в каналах между лопастями турбины). При движении жидкости (газа) в канале на элемент объема длиной dx в произвольном поперечном сечении площадью F действует сила pF, обусловленная давлением р. Работа этой силы за время dτ равна pFωdτ, где ω — скорость жидкости (газа). В общем случае по длине канала изменяются все величины (р, F, ω). Работа сил давления в сечении с координатой х + dx равна [pFω + d(pFω)]dτ. Следовательно, окружающая жидкость (газ) производит над элементом объема работу — d(pFω)dτ; элемент же объема производит над жидкостью (газом) работу d(pFω)dτ. Произведение Fω равно объемному расходу жидкости (газа) V, который можно выразить как произведение массового расхода G на удельный объем жидкости (газа) v. Тогда при G = const получаем: d(pFω)dτ = Gd(pv)dτ и δА = δAc + Gd(pv). Величина δАс зависит от характера процесса, произведение же pv является функцией состояния жидкости (газа). Величина d(pv) = pdv + + vdp состоит из двух слагаемых: pdv — работы расширения эле— 47 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ мента объема на величину dv и vdp — работы элемента против гидромеханических сил, например силы трения в объеме жидкости (газа). При отсутствии трения работа vdp расходуется на ускорение элемента объема и увеличение его кинетической энергии. Энергия тела (в рассматриваемом примере — жидкости или газа) складывается из механической энергии тела как целого (внешней энергии) и энергии образующих его микрочастиц (внутренней энергии). Внешняя механическая энергия является суммой кинетической энергии, пропорциональной ω2/2, и потенциальной энергии (энергии положения), пропорциональной gh, где h — высота над уровнем, принятым за начало отсчета, a g — ускорение свободного падения. Под внутренней энергией понимается энергия движения микрочастиц, образующих тело, а также энергия их взаимодействия друг с другом. Таким образом, равенство (2.24) можно записать в следующем виде, относя все величины к единице массы жидкости:  ω2  (2.25) δQ = dU + d ( pv ) + d   + gdh + δAc  2 В этом уравнении дифференциалы dU и d(pv) отражают изменение внутреннего состояния системы. Их сумму dU + + d(pv) можно рассматривать как полный дифференциал функции, называемой энтальпией. (2.26) H = U + pv С учетом этого уравнение (2.25) преобразуется к виду:  ω2  (2.27) δQ = dH + +d   + gdh + δAc  2 При движении жидкости (газа) в горизонтальной (dh = 0) теплоизолированной трубе (δQ — 0), когда можно пренебречь трением о стенки (δAc = 0), имеем:  ω2  (2.28) dH + d   = 0  2 Это означает, что возможные адиабатические изменения состояния движущейся жидкости (газа) приводят к перерас— 48 — ÐƭǪǭǮǃǊÐǰǬ͠ǂǮƽǀǃǪǂǀǭǀ пределению энтальпии и кинетической энергии жидкости (газа). Сумма же этих видов энергии остается неизменной. Очевидно, возможно множество сочетаний значений H и ω, удовлетворяющих условию (2.28), соотношение между которыми зависит от условий проведения процесса. Для находящейся под постоянным давлением (dp=0) покоящейся системы, не производящей над окружающей средой никакой работы, кроме работы расширения, d(ω2/2) = 0, dh = 0 и δAc = 0. Поэтому закон сохранения энергии (2.25) записывается в виде: δQ = dU + pdv (2.29) Если заменить dU с помощью (1.26), dU = dH − pdv − vdp , то δQ = dH − vdp При постоянном давлении dH = δQ, т. е. приращение величины Н равно подведенной теплоте. При постоянном объеме, как следует из (2.29), δQ = dU. Изменение энергии системы при отсутствии фазовых превращений приводит к изменению температуры, что можно выразить следующим образом: при постоянном объеме  ∂U  (2.30) cv =   ∂T  v при постоянном давлении  ∂H  (2.31) cP =   ∂T  p где сv, ср — теплоемкости. Величины cv и ср зависят от природы вещества и температуры. Значения их для различных веществ приводятся в справочной литературе. В соответствии с определениями (2.30) и (2.31) dU = cvdT (при v = const); dH = cpdT (при р = const) Для движущихся систем в выражение (2.29) надо ввести дополн ительную величину dEд, учитывающую изменение внутренней энергии системы, обусловленное движением, например за счет внутреннего трения в жидкости, связанного с ее вязкостью. Следовательно δQ = dU + pDV − dE∂ — 49 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Постановка этого выражения δQ в (2.25) приводит к несколько иной формулировке закона сохранения энергии  ω2  d   + gdh + vdp + dEä + δAñ = 0  2 или, поскольку удельный объем v обратно пропорционален плотности v = 1/ρ  ω2  dp + dEä + δAñ = 0 d   + gdh + (2.33) ρ 2   Для идеальной жидкости, под которой понимается жидкость, движущаяся без трения, Eд= 0 и Ас = 0. При этом уравнение (2.33) может быть записано в интегральной форме: ω2 p (2.34) + gh + = const 2 ρ Это — уравнение Бернулли, выражающее энергетический баланс потока идеальной жидкости. Ϯ͘Ϯ͘Ϯ͘ʦ̨̨̡̨̯̬̜̦̌̚;̸̨̦̣̌̌Ϳ̨̡̛̛̛̯̖̬̥̦̥̔̌͘ ˇ̨̨̨̛̖̬̦̖̭̖̌̏̌̏̏̚͘ Целью любых технологических процессов является направленное изменение макроскопических свойств веществ. Обычно в технологических процессах участвуют массы веществ, состоящие из большого числа частиц. Макроскопические свойства вещества определяются энергией и числом частиц и рассматриваются в статическом смысле, т.е., как результат усреднения состояния всех частиц. В отдельных объемах системы число частиц может меняться вследствие их перемещения с различными скоростями. Энергия частиц зависит от скорости движения. Перенос массы и энергии происходит принудительно (под воздействием внешних источников), а также самопроизвольно (вследствие «теплового» движения и соударений частиц). Пределом является состояние динамического равновесия, которое для изолированной системы, не обменивающейся с окружающей средой массой и энергией, характеризуется неизменностью макроскопических — 50 — ÐƭǪǭǮǃǊÐǰǬ͠ǂǮƽǀǃǪǂǀǭǀ свойств вещества во времени и в пространстве. То есть через любую выделенную в объеме системы площадку конечных размеров в прямом и обратном направлениях перемещается одинаковое количество массы и энергии. Поскольку в общем случае каждое свойство можно рассматривать как функцию координат и времени, то математически условия равновесия можно сформулировать как равенство нулю полного дифференциала параметров состояния, определяющих свойства вещества, т. е. dT = 0;dp = 0;dci = 0 (2.35) Равенство dT = 0 выражает условие термического равновесия, dp = 0 — механического равновесия, dci = 0 — химического равновесия. Все самопроизвольные процессы проходят в направлении приближения состояния системы к равновесному. Изменение состояния системы в противоположном направлении возможно лишь под воздействием окружающей среды, заключающемся в подводе к системе вещества или энергии. Согласно второму закону термодинамики, все самопроизвольные процессы сопровождаются увеличением энтропии системы. В изолированной системе энтропия в состоянии равновесия достигает максимального значения. Поэтому для состояния равновесия справедливо равенство dS = 0 (2.36) Таким образом, равновесие системы определяется условиями (2.35) и (2.36). При их соблюдении в системе не происходит изменение макроскопических свойств ни во времени, ни в пространстве. Для открытой системы (способной обмениваться с окружающей средой массой и энергией) равновесное состояние может быть устойчивым лишь при ее равновесии с окружающей средой. В противном случае состояние системы будет изменяться. Так, если температура окружающей среды выше температуры системы, то к системе будет передаваться энергия в форме теплоты, при различии давлений будет происходить процесс расширения или сжатия, при различии концентраций возникнет поток вещества. Отсюда следует, что движущая — 51 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ сила процессов, приводящих к изменению макроскопических свойств системы, возникает вследствие отклонения от равновесия в самой системе или в окружающей среде. Чем меньше отклонение от состояния равновесия, тем медленнее протекает процесс. В предельном случае бесконечно малой движущей силы, т. е. при равновесии системы с окружающей средой, процессы с равной вероятностью могут протекать как в прямом, так и в обратном направлениях (обратимые процессы). В этом случае δQ = TdS, δА = pdV и закон сохранения энергии (2.29) для системы объемом V записывается в виде: dU = TdS − pdV (2.37) Для количественного описания изменения энергетического состояния систем в технологических процессах вместо внутренней энергии U используют другие характеристические функции — энтальпию, определяемую выражением (2.26), и энергию Гиббса G: G = H − TS = U + pV − TS (2.38) По правилам дифференцирования функции нескольких переменных изменения U и G с учетом (2.37) выражаются соотношениями: dH = dU + pdV + Vdp = TdS + Vdp (2.39) dG = dH − TdS − SdT = −SdT + Vdp (2.40) Из уравнений (2.35) — (2.40) следует, что для системы, находящейся в равновесии, dU = 0, dH = 0 и dG = 0. Эти равенства также можно рассматривать как условия равновесия. Величины U, Н и G являются характеристическими функциями в том смысле, что их значения характеризуют состояние системы. Каждая из них выражается в зависимости от определенных параметров, рассматриваемых как независимые переменные. Все термодинамические свойства системы можно определить через производные характеристических функций по соответствующим им независимым переменным. Для внутренней энергии U такими независимыми переменными, согласно (2.37), являются энтропия S и объем V, для энтальпии — энтропия S и давление р, для энергии Гиббса — — 52 — ÐƭǪǭǮǃǊÐǰǬ͠ǂǮƽǀǃǪǂǀǭǀ температура Т и давление р. Если система представляет собой смесь нескольким компонентов, то помимо указанных параметров значения U, Н и G зависят от чисел молей всех компонентов Ni. Поэтому можно написать U = f(S,V,Ni), H = f(S,p,Ni), i= 2, 3, ..., n (n — число компонентов). Полные дифференциалы U, Н и G равны: ∂U ∂U ∂U ∂U ∂U dU = dS + dV + dN1 + dN2 + ! + dNn ∂S ∂V ∂N1 ∂N2 ∂Nn dH = ∂H ∂H ∂H ∂H ∂H dS + dV + dN1 + dN2 + ! + dNn ∂S ∂V ∂N1 ∂N2 ∂Nn dG = ∂G ∂G ∂G ∂G ∂G dT + dp + dN1 + dN2 + ! + dNn ∂T ∂p ∂N1 ∂N2 ∂Nn (2.41) Частные производные характеристических функций по числам n компонентов при всех других постоянных параметрах состояния называются химическими потенциалами этих ∂U ∂H ∂G компонентов. Обозначив = = = µ i уравнения (2.41) ∂Ni ∂Ni ∂Ni представить следующим образом: n ∂U ∂U dU = dS + dV + ∑µ i dNi ∂S ∂V i =1 dH = dG = n ∂H ∂H dS + dp + ∑µ i dNi ∂S ∂p i =1 n ∂G ∂G dT + dp + ∑µ i dNi ∂T ∂p i =1 (2.42) сопоставив (1.42) с (1.37), (1.39) и (1.40), нетрудно установить, что  ∂U   ∂H   ∂U  = = T;  = − p;     ∂V  S,N ∂S V ,N  ∂S  p,N i i i  ∂H   ∂G   ∂G  = −S = = V;   ∂p    ∂T  p,N  p ∂ S,N T,N i i i — 53 — (2.43) ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Здесь индексы — параметры состояния, при постоянных значениях которых берутся производные. С учетом (2.43) условия равновесия системы будут иметь вид n dU = TdS − pdV + ∑µ i dNi = 0 i =1 n dH = TdS + Vdp + ∑µ i dNi = 0 i =1 n dG = −SdT + Vdp + ∑µ i dNi = 0 i =1 (2.44) Ϯ͘Ϯ͘ϯ͘˃̡̨̛̬̖̯̜̦̌̚;̸̨̦̣̌̌Ϳ̨̡̛̛̛̯̖̬̥̦̥̔̌ Третий закон (начало) термодинамики, согласно Нернсту В.Ф.Г. [2], может быть сформулирован так: «Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система». или lim S,(T,x2 ) − S (T,x1 ) = 0 (2.45)  ∂S  lim   = 0 ∂x  T (2.46) T →0 K  T →0 K  где x — любой термодинамический параметр. Третье начало термодинамики относится только к равновесным состояниям. Поскольку на основе второго начала термодинамики энтропию можно определить только с точностью до произвольной аддитивной постоянной (то есть, определяется не сама энтропия, а только её изменение): δQ (2.47) T — третье начало термодинамики может быть использовано для точного определения энтропии. При этом энтропию равновесной системы при абсолютном нуле температуры считают равdS = — 54 — ÐƭǪǭǮǃǊÐǰǬ͠ǂǮƽǀǃǪǂǀǭǀ ной нулю. Третье начало термодинамики позволяет находить абсолютное значение энтропии, что нельзя сделать в рамках классической термодинамики (на основе первого и второго начал термодинамики). В классической термодинамике энтропия может быть определена лишь с точностью до произвольной аддитивной постоянной S0, что не мешает термодинамическим исследованиям, так как реально измеряется разность энтропий (∆S) в различных состояниях. Согласно третьему началу термодинамики, при Tĺ0 значение ∆Sĺ0. Из третьего начала термодинамики следует, что температура не может достичь абсолютного нуля ни в каком конечном процессе, связанном с изменением энтропии, к нему можно лишь асимптотически приближаться, поэтому третье начало термодинамики иногда формулируют как принцип недостижимости абсолютного нуля температуры. Из третьего начала термодинамики вытекает ряд термодинамических следствий: при Tĺ0 должны стремиться к нулю теплоёмкости при постоянном давлении и при постоянном объёме, коэффициенты теплового расширения и некоторые аналогичные величины. Справедливость третьего начала термодинамики одно время подвергалась сомнению, но позже было выяснено, что все кажущиеся противоречия (ненулевое значение энтропии у ряда веществ при T=0) связаны с метастабильными состояниями вещества, которые нельзя считать термодинамически равновесными. Ϯ͘Ϯ͘ϰ͘ʿ̸̡̨̨̨̡̛̛̛̛̛̬̥̖̦̖̦̖̦̯̖̬̥̦̥̣̬̭̖̯̌̏̔̌̔́̌̌̚ ̸̶̡̨̨̨̨̨̨̛̛̦̖̬̖̯̖̭̯̖̪̣̣̦̭̪̬̖̭̭̾̐̐̏̐̍̌̌̌̌͘ Как было показано выше при расчете энергетического баланса процесса необходимо использовать формулу (2.25). Изменение тепловой энергии системы можно описать уравнением теплового баланса: ∑ Qн + ∑ Qр = ∑ Qк + ∑ Qпот (2.48) где ∑ Qн , ∑ Qк — теплота, поступающая в процесс с исходными материалами и теплота, отводимая из процесса с конечными — 55 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ продуктами; ∑ Qр — тепловой эффект процесса; ∑ Qпот — потери теплоты в окружающую среду. Применительно к тепловому балансу закон сохранения энергии формулируется следующим образом: приход теплоты в данном процессе (или производственной операции) должен быть равен расходу теплоты в том же процессе (или операции). Для процессов непрерывного действия тепловой баланс, как правило, составляют на единицу времени, а для процессов периодического действия — на время цикла (или отдельного периода) обработки. Тепловой баланс рассчитывают по данным материального баланса с учетом тепловых эффектов (экзотермических и эндотермических) химических реакций и физических превращений (испарение, конденсация и т.п.), происходящих в процессе с учетом подвода теплоты извне и отвода ее с продуктами реакции. Тепловой баланс, как и материальный баланс, выражают в виде таблиц, диаграмм, а для расчета используют следующее уравнение Qт + Qж + Qг + Q ф + Qр + Qп = Qт' + Q'ж+ Q'г + Q'ф+ Q'р + Q'п (2.49) где Qт, Qж, Qг — количество теплоты, вносимое в процесс твердыми, жидкими и газообразными веществами соответственно; Q߰т, Q߰ж, Q߰г — количество теплоты, уносимое из процесса выходящими продуктами и полупродуктами реакции и не прореагировавшими исходными веществами в твердом, жидком и газообразном виде; Qф и Q߰ — теплота физических процессов, ф происходящих с выделением и поглощением (Q߰ ) теплоты; Qр, ф и Q߰ — количество теплоты, выделяющееся в результате экзор и эндотермических реакций (Q߰ ); Q — количество теплоты, р п подводимое в процесс извне (в виде дымовых газов, нагретого воздуха, сжигания топлива, электроэнергии и т.п.); Q߰ — потеп ри тепла в окружающую среду. Величины Qт, Qж, Qг, Q߰ , Q߰ , Q߰г рассчитывают для кажт ж дого вещества, поступающего в процесс и выходящего из него по формуле: Q = Gct — 56 — (2.50) ÐƭǪǭǮǃǊÐǰǬ͠ǂǮƽǀǃǪǂǀǭǀ где G — количество вещества, с — средняя теплоемкость этого вещества; t — температура, отсчитанная от какой-либо точки (обычно от 00С). Теплоемкости газов в Дж/(кмоль-К), участвующих в процессе, для данной температуры в °С (или Т К) можно подсчитать, пользуясь формулой: (2.51) C = a0 + a1T + a2T 2 Коэффициенты а0, а1, а2 — приведены в справочниках. Чаще всего приходится иметь дело со смесями веществ. Поэтому в формулу (2.50) подставляют теплоемкость смеси ссм, которая может быть вычислена по закону аддитивности. Так, для смеси трех веществ в количестве G1, G2 и G3, имеющих теплоемкости с1, с2 и с3 (2.52) cсм = (G1c1 + G2c2 + G3c3 ) / (G1 + G2 + G3 ) Суммарная теплота физических процессов, происходящих в аппаратах, может быть рассчитана по уравнению: Qô = G1r1 + G2r2 + G3r3 (2.53) где r1, r2 и r3 — теплота фазовых переходов; G1, G2 и G3 — количества компонентов смеси, претерпевших фазовые переходы в данном аппарате. Количество членов в правой части уравнения (2.53) должно соответствовать числу индивидуальных компонентов, изменивших в аппарате свое фазовое состояние. Аналогично рассчитывается расход теплоты на физические процессы, которые идут с поглощением теплоты (Q߰ ): деф сорбция газов, парообразование, плавление, растворение и т.п. Тепловые эффекты химических реакций могут быть рассчитаны на основе теплот образования или теплот сгорания веществ, участвующих в реакции. Так, по закону Гесса тепловой эффект реакции определяется как разность между теплотами образования всех веществ в правой части уравнения и теплотами образования всех веществ, входящих в левую часть уравнения. Например, для модельной реакции: A + B = D + F + q p изобарный тепловой эффект будет: — 57 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ ( qр− = qобрD + qобрF − qобрA + qобрB ) (2.54) Изобарные теплоты образования из элементов различных веществ qр− (или –∆Н0) приведены в справочниках физико-химических, термохимических или термодинамических величин. При этом в качестве стандартных условий приняты: температура 250С, давление 1,01 u 105Па и для растворенных веществ концентрация 1 моль на 1 кг растворителя. Газы и растворы предполагаются идеальными. Тепловой эффект реакции также равен сумме теплот образования исходных веществ за вычетом суммы теплот образования продуктов реакции: ( ∆H = Σ ∆Hобр ) исх ( − Σ ∆H обр ) (2.55) прод Для определения зависимости теплового эффекта реакции от температуры применяется уравнение Нернста:  1   1  (2.56) qр = q −р + ∆a0T +  − ∆a1T 2  +  − ∆a2T 3   2   3  где ∆a0 , ∆a1, ∆a2 — разности соответственных коэффициентов уравнения (1.56) для продуктов реакции и исходных веществ. Значения этих коэффициентов для отдельных реакций приведены в справочниках. Подвод теплоты в процесс Qп можно учитывать по потере количества теплоты теплоносителя, например, греющей воды Gв и св) Qп = Gвcв (tнач− tкон) (2.57) (2.58) Gr и пара Qп = G или же по формуле теплопередачи через греющую стенку: kT F (tr − tx ) τ (2.59) Qп = G где kT — коэффициент теплопередачи; F — поверхность теплообмена; tr — средняя температура греющего вещества (воды, пара); tx — средняя температура нагреваемого вещества в аппарате; r — теплота испарения; τ — время. По этой и другим формулам теплопередачи можно также рассчитать отвод теплоты от реагирующей смеси или потерю — 58 — ÐƭǪǭǮǃǊÐǰǬ͠ǂǮƽǀǃǪǂǀǭǀ теплоты в окружающую среду QԠп. Эту статью расхода теплоты часто вычисляют по изменению количества теплоты хладагента, например, охлаждающей воды или воздуха. Теплоту, получаемую при сжигании топлива или при превращении электрической энергии в тепловую, подсчитывают по формулам: для пламенных печей (2.60) Qп = BQнр (2.61) для электрических печей Qп = Nβ где В — расход топлива, м3/с или кг/с; Qíð — низшая теплота сгорания топлива, дж/м3 или Дж/кг; N — мощность печи, Вт; β — размерный коэффициент. При подсчетах теплоты сгорания топлива по его элементарному составу в технических расчетах чаще всего используют формулу Менделеева Qíð = 339,3C + 1256H − 109 ( O − S ) − 25,2(9H + W ) (2.62) Где С, Н, О, S — соответственно содержание углерода, водорода, кислорода и серы, % масс.; W — содержание влаги в рабочем топливе (с учетом содержания в нем А% золы, N% азота), % масс. Высшая теплота сгорания Qâð вычисляется при условии, что вся вода, образовавшаяся при сгорании, влага, первоначально содержащаяся в топливе, конденсируется из отходящих газов в жидкость и охлаждается до первоначальной температуры, с которой поступает топливо в топку, определяется по формуле: Qíð = Qïð + 25,2(9H + W ) (2.63) На основе элементарного состава топлива, теоретический расход воздуха G кг на 1 кг топлива рассчитывается по уравнению Gòåîð = 0,116C + 0,348H + 0,0135( S − O ) (2.64) Количество тепла, вносимого влажным воздухом, Iвозд, можно подсчитать по формуле: Iâîçä = αGòåîð (1,02 + 1,95x ) tâîçä — 59 — (2.65) ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ где Gтеор — теоретический расход воздуха (в кг), идущего на сжигание 1 кг рабочего топлива; α — коэффициент избытка воздуха (практически обычно для твердого топлива а берется от 1,3 до 1,7); 1,02 — удельная теплоемкость воздуха; 1,95 — удельная теплоемкость водяных паров; х — влагосодержание воздуха (в кг) на 1 кг сухого воздуха; tвозд — температура воздуха, поступающего на сгорание. Ϯ͘ϯ͘ʯ̡̨̨̛̛̛̦̼̪̖̬̖̦̭̥̭̭̼̦̖̬̌̌̌̾̐͘ Молекулярный перенос массы и энергии происходит вследствие беспорядочного теплового движения микрочастиц. Перенос массы по такому механизму называется диффузией, а энергии — теплопроводностью. Макроскопические количества массы и энергии переносятся лишь при наличии движущей силы, т. е. при отклонении системы от состояния равновесия. Условием материального равновесия фазы является постоянство состава, а условием теплового равновесия — постоянство температуры во всем объеме фазы. Для многофазных систем условием материального равновесия является равенство химических потенциалов каждого компонента в сосуществующих фазах. Для однородной среды движущей силой переноса некоторого компонента можно считать разность его концентраций сi а движущей силой переноса энергии — разность температур t в разных точках системы. Распределение этих величин в объеме рассматриваемой среды выражается функциями сi = f(х, у, z, τ) и t = φ(х, у, z, τ), определяющими поля величин сi и при сi = const и t = const эти функции описывают, соответственно, поверхности равных концентраций и температур. Вектор потока энергии q между двумя точками двух изотермических поверхностей (рис. 2.3) можно разложить на две составляющие — нормальную qн и касательную qк. При сближении поверхностей касательная составляющая стремится к нулю, так как на изотермической поверхности нет разности температур и, следовательно, отсутствует перенос теплоты. Поэтому можно считать, что теплота передается в направлении нормали к поверхности постоянной — 60 — ÐƭǪǭǮǃǊÐ͟Ǭ͠ǬǃǮǯǪÐǂǪǯǯǊÐǀÐǌǃǬ͠Ƽǀǀ температуры. То же относится и к переносу массы. Таким образом, в качестве движущей силы процессов переноса массы и энергии можно рассматривать градиент концентрации и градиент температуры, соответственно. Рис. 2.3. Разложение вектора потока энергии. На основе экспериментальных данных по диффузии и теплопроводности, было обнаружено, что количество переносимого вещества пропорционально градиенту его концентрации, а количество теплоты — градиенту температуры. Первое положение известно как закон диффузии Фика, второе — как закон теплопроводности Фурье. В математической формулировке они имеют вид: ∂ci (2.66) ∂n ∂t (2.67) q = −λ ∂n где ji — поток компонента i, отнесенный к единице по верхности, кмоль/(м2с); ci — концентрация, кмоль/м3; q — поток теплоты, отнесенный к единице поверхности, Вт/м2; t — температура, К. Знак минус в уравнениях (2.66) и (2.67) означает, что потоки направлены, соответственно, в сторону уменьшения концентрации и температуры. Очевидно, что потоки компонента i и теплоты через заданную поверхность пропорциональны ее проекции на плоскость, перпендикулярную к направлению потока (F), т. е. ji = − Di — 61 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ ∂ci (2.68) ∂n ∂t (2.69) Q = −λF ∂n где Gi — поток компонента i, кмоль/с; Q — поток теплоты, Вт. Коэффициент диффузии Di (в м2/с) и коэффициент теплопроводности λ (в Вт/м-К) являются свойствами вещества. Величина Di определяет скорость переноса (транспорта) частиц компонента i в объеме рассматриваемого вещества, а величина λ — скорость переноса теплоты в этом объеме. В последнее время эти свойства вещества принято называть коэффициентами переноса. Gi = − Di F Ϯ͘ϯ͘ϭ͘ʯ̡̨̦̼̌ˇ̡̛̛̌ˇ̱̬̖̽͘ Законы Фика и Фурье можно рассматривать как частные случаи применения общего принципа описания физических процессов, заключающегося в раздельном рассмотрении движущей силы переноса и его кинетических характеристик. Наличие движущей силы определяет возможность протекания процесса. Скорость же процесса (его кинетические характеристики) зависит от свойства системы. Общий для разных процессов методический прием заключается в том, что поток массы, энергии или количества движения принимается прямо пропорциональным движущей силе процесса. При этом коэффициент пропорциональности характеризует свойства переноса рассматриваемого вещества и является мерой возникающего в нем сопротивления переносу материальных частиц или энергии. Достоинство такого приема заключается в том, что влияние движущей силы, зависящей главным образом от условий проведения процесса, и кинетических факторов, зависящих в основном от свойств системы, на результаты процесса учитывается раздельно. Особенно это удобно в тех случаях, когда кинетические коэффициенты и движущая сила процесса взаимно независимы. Напри— 62 — ÐƭǪǭǮǃǊÐ͟Ǭ͠ǬǃǮǯǪÐǂǪǯǯǊÐǀÐǌǃǬ͠Ƽǀǀ мер, в ограниченном температурном интервале коэффициент теплопроводности можно считать постоянным, не зависящим от температуры. Коэффициенты переноса меняются с изменением параметров состояния (температуры, давления и состава), поскольку они зависят от природы вещества. Поэтому их можно считать постоянными лишь в ограниченном интервале изменения параметров состояния системы (с учетом допустимой погрешности расчетов). Особенно существенное значение имеет зависимость свойств переноса смесей от их состава. Как показывают опытные данные, эти свойства могут сильно изменяться с составом. В случае зависимости коэффициентов переноса от движущей силы достоинства рассмотренного принципа описания явлений переноса в значительной степени утрачиваются. Однако использовать его все же полезно, так как зависимость коэффициентов переноса от движущей силы не всегда велика и в расчет могут вводиться усредненные величины. Следует учитывать, что: выделение движущей силы процессов дает возможность сопоставления и оценки различных вариантов их проведения. Рис.2.4. Диффузионный перенос вещества через бесконечно малый элемент объема. Закономерности процессов молекулярного переноса выявляются на основе применения законов сохранения к элементарному объему рассматриваемой среды dv = dxdydz (рис. 2.4). [9] Расход вещества i, обусловленный диффузией в направле— 63 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ нии оси х, через поверхность dydz, находящуюся на расстоянии х от начала координат, равен: ∂c Gix = − Di i dydz ∂x На расстоянии dx от данной поверхности концентрация вещества i вследствие ее изменения в пространстве равна ∂c ci + i dx . Расход этого вещества через поверхность dydz, на∂x ходящуюся на расстоянии х + dx от начала координат, выражается соотношением: ∂c ∂y   Gi(x+dx) = − Di ci + i dx dydz  ∂x  ∂x  Следовательно, за счет изменения концентрации сi в направлении оси х в рассматриваемый элементарный объем поступает в единицу времени количество вещества i равное ∂ 2c dGx = Gix − Gi(x+dx) = Di 2i dxdydz ∂x Аналогично, для двух других направлений получаем: ∂2ci ∂2ci dGiy = Di dxdydz;dGiz = Di dxdydz 2 ∂xy ∂xz2 Таким образом, в элементарный объем в единицу времени поступает следующее количество компонента:  ∂2 c ∂2 c ∂2 c  dGi = dGix + dGiy + dGiz = Di  2i + 2i + 2i  dxdydz ∂y ∂z   ∂x Сумма вторых частных производных некоторой величины по координатам называется оператором Лапласа и обозначается ∇2 . Следовательно dGi = Di ∇2cidv Изменение количества вещества i в рассматриваемом объеме dv может происходить также в результате его образования или расходования за счет химических процессов. Если вещество образуется, то имеется источник этого вещества, — 64 — ÐƭǪǭǮǃǊÐ͟Ǭ͠ǬǃǮǯǪÐǂǪǯǯǊÐǀÐǌǃǬ͠Ƽǀǀ а при расходовании — сток. При скорости образования вещества, отнесенной к единице объема riv, количество получаемого в единицу времени вещества равно rivdv. За счет притока в элементарный объем вещества i изменяется его концентрация во времени. По закону сохранения массы ∂c Di ∇2cidv + rivdv = i dv ∂τ или ∂c (2.70) Di ∇2ci + riv = i ∂τ Это выражение описывает закономерности массопереноса путем молекулярной диффузии и иногда называется вторым законом диффузии Фика, хотя, как было показано, оно является следствием закона Фика (2.69) и закона сохранения массы. Уравнение (2.70) определяет поле концентраций компонента i в рассматриваемой среде. Аналогичным образом описывается процесс распространения теплоты теплопроводностью. В соответствии с уравнением () поток теплоты, поступающей в элементарный объем в направлении оси х за счет теплопроводности, равен:  ∂t ∂  ∂t ∂ 2t  dQx = −λ  − dx  dydz = λ 2 dxdydz  t + ∂x   ∂x  ∂x ∂x Для двух других направлений ∂2 t ∂2 t dQy = λ 2 dxdydz; dQz = λ 2 dxdydz ∂y ∂z Общий поток: dQ = dQx + dQy + dQz = λ∇2tdv Изменение количества теплоты в элементарном объем, помимо переноса путем теплопроводности, возможно за счет химических процессов — внутреннего источника (для экзотермических реакций — положительного, для эндотермических — отрицательного). Если мощность источника теплоты, отнесенная к единице объема, равна qr, то приток теплоты — 65 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ в элементарный объем dv составляет qrdv. За счет притока теплоты в результате теплопроводности и химических процессов температура элементарного объема изменяется во времени. По закону сохранения энергии ∂t λ∇2tdv + qr dv = c pρ dv ∂τ или q ∂t (2.71) a∇2t + r = c p ρ ∂τ где ср — теплоемкость; ρ = плотность; a = λ — коэффициент c pρ температуропроводности. Величина а является мерой скорости изменения температуры рассматриваемого вещества и характеризует его теплоинерционные свойства. Выражение (2.71) называется уравнением Фурье. Оно определяет закономерности распространения теплоты путем теплопроводности и описывает поле температур в рассматриваемой системе. Уравнения (2.70) и (2.71) аналогичны по структуре. Коэффициенты Di и а имеют одинаковые размерности и единицу измерения (м2/с). При отсутствии источников и стоков (riv = 0 и qr = 0) для стационарных процессов, т. е. при неизменяющихся во време∂c ∂t ни распределениях концентраций и температур ( i = 0; = 0 ), ∂τ ∂τ уравнения (2.70) и (2.71) становятся математически идентичными: (2.72) ∇2ci = 0; ∇2t = 0 Соотношение вида (2.72) называется уравнениями Лапласа. Ϯ͘ϯ͘Ϯ͘ʿ̸̨̡̨̛̛̛̖̬̖̦̭̣̖̭̯̙̖̦̏̌̔̏́͘ʦ̡̨̭̯́̽̚͘ В движущейся жидкости (газе) взаимодействие молекул проявляется в виде сопротивления изменению формы (трения). Поэтому для поддержания движения к жидкости (газу) — 66 — ÐƭǪǭǮǃǊÐ͟Ǭ͠ǬǃǮǯǪÐǂǪǯǯǊÐǀÐǌǃǬ͠Ƽǀǀ необходимо подводить энергию. Жидкость (газ), движущиеся в канале под действием внешней силы, на разных расстояниях от стенок имеет вследствие трения разные скорости. Отсюда следует, что жидкостное трение вызывает появление градиента скорости в направлении, перпендикулярном, направлению потока. Мерой жидкостного трения является касательное напряжение στ, равное силе трения, приходящейся на единицу поверхности. Закономерности жидкостного трения, выявленные экспериментально, формулируются законом Ньютона, согласно которому касательное напряжение пропорционально градиенту скорости: dω σ τ = −µ (2.73) dn Жидкости, для которых соблюдается эта закономерность, называются ньютоновскими. Коэффициент пропорциональности μ носит название динамического коэффициента вязкости (динамической вязкости или просто вязкости) и является свойством жидкости. Единицей измерения вязкости служит Па-с. В справочной литературе для μ часто используется единица измерения, называемая пуазом П [1П = 1 г/(см-с) = 10 Па-с]. Помимо динамического коэффициента вязкости широко используется кинематический коэффициент вязкости ν, определяемый выражением µ (2.74) ν= ρ где ρ — плотность жидкости. Единица измерения кинематического коэффициента вязкости та же, что и коэффициентов диффузии и температуропроводности, т. е. м2/с. Рассмотрим элементарный объем жидкости (газа) в потоке, движущемся в направлении оси х (рис. 2.5). Будем считать нижнюю поверхность неподвижной. Для поддержания градиента скорости в направлении нормали n на верхнюю поверхность действует напряжение στ, которое за время dx вызовет — 67 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ деформацию объема, в результате которой боковые грани поворачиваются на угол dφ. Рис.2.5. Схема деформации бесконечно малого объема жидкости под действием касательного напряжения. dx , где dx — расстояdn ние, на которое смещается верхняя поверхность элементарного объема за время dτ. Знак минус означает, что с увелиdω чением dx угол φ уменьшается. Очевидно, что dx = dndτ , dn При малых деформациях dϕ = − a dϕ = − dx dω dn = − dτ . dn dn dϕ dω . Производная dφ/dτ опреде= dτ dn ляет скорость деформации объема жидкости (газа) путем сдвига. Таким образом, в соответствии с (2.73) Отсюда следует, что − dω dϕ , (2.75) −µ dτ dτ т. е. касательное напряжение пропорционально скорости деформации жидкости (объема газа). Появление градиента скорости жидкости (объема газа) обусловлено взаимодействием с твердыми поверхностями. Если канал неподвижен, то непосредственно на стенке скорость движения жидкости (объема газа) равна нулю. Тормозящее влияние стенки уменьшается по мере удаления от нее. В свяσ τ = −µ — 68 — ÐƭǪǭǮǃǊÐ͟Ǭ͠ǬǃǮǯǪÐǂǪǯǯǊÐǀÐǌǃǬ͠Ƽǀǀ зи с этим градиент скорости, а, следовательно, и касательное напряжение имеют наибольшее значение на границе жидкости (газа) с твердой поверхностью. Механизм жидкостного (вязкого) трения, согласно молекулярно-кинетической теории, заключается в следующем. Скорость движения молекул в потоке жидкости можно рассматривать как сумму усредненной скорости движения молекул, зависящей от температуры, и скорости потока в рассматриваемой точке. Следовательно, в слоях жидкости (газа), движущихся с большей скоростью, находятся более «быстрые» молекулы. При наличии градиента скорости соударение «быстрых» и «медленных» молекул вызывает перенос некоторого количества движения от первых ко вторым. При отсутствии внешней силы такой процесс приводил бы к замедлению «быстрых» и ускорению «медленных» молекул до тех пор, пока не произойдет усреднения скорости во всем объеме, т. е. пока не наступит состояние равновесия. Чтобы поддерживать градиент скорости, без которого невозможно движение жидкости (газа), необходимо приложить внешнюю силу. В движущейся жидкости (газе) за счет этой силы создается касательное напряжение. Согласно второму закону Ньютона, сила f равна производной количества движения mω по времени: d (mω ) (2.76) f= dτ f выражает количество движения, переF носимое через единицу поверхности F в единицу времени в направлении перпендикулярном движению жидкости, т. е. поток количества движения. Этот поток создается соударяющимися молекулами и подобен потоку энергии, обусловленному молекулярным механизмом переноса, т. е. теплопроводностью. По описанному механизму вязкость обусловлена исключительно молекулярным взаимодействием (молекулярная вязкость). Такой механизм возможен лишь в том случае, когда поток жидкости (газа) представляет собой струи, которые движутся не смешиваясь. Этот вид движения называется Величина σ τ = — 69 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ струйным, или ламинарным. Траектория каждой частицы при ламинарном режиме движения жидкости (газа) в некотором канале представляет собой непрерывную линию, форма которой подобна форме канала. Например, при движении жидкости (газа) в прямой трубе траектории всех частиц — прямые линии, параллельные стенкам трубы. При определенных условиях, однако, ламинарное движение становится неустойчивым и переходит в турбулентное, характеризующееся тем, что каждая частица жидкости (газа) беспорядочно отклоняется от основного направления потока. Эти отклонения можно рассматривать как пульсации в направлении, перпендикулярном направлению потока (турбулентные пульсации). Условия перехода от ламинарного режима к турбулентному определяются условиями движения и свойствами среды. При турбулентном режиме перенос количества движения и энергии происходит не только по описанному молекулярному механизму, но главным образом за счет переноса макроколичеств жидкости (газа) из более «быстрых» частей потока в более «медленные» и наоборот. Такой механизм подобен рассмотренному механизму молекулярной вязкости с той разницей, что вместо микрочастиц перенос количества движения осуществляется макрочастицами, в результате чего в жидкости (газе) возникает дополнительное трение. Подобно тому, как при ламинарном режиме движения трение в жидкости связывают с молекулярной вязкостью, при турбулентном режиме его характеризуют турбулентной вязкостью. Для турбулентного режима движения жидкости формула (2.73) записывается в виде: dω (2.77) σ τ = − (µ + µ τ ) dn где μτ — коэффициент турбулентной вязкости. Энергия, затрачиваемая на перемещение жидкости, расходуется по механизму жидкостного трения на увеличение скорости «быстрых» частиц по сравнению с «медленными», т. е. превращается в теплоту. Явление перехода энергии упорядоченного движения (механической) в энергию неупорядоченного движения молекул в потоке жидкости (тепло— 70 — ÐƭǪǭǮǃǊÐ͟Ǭ͠ǬǃǮǯǪÐǂǪǯǯǊÐǀÐǌǃǬ͠Ƽǀǀ вую) называют диссипацией энергии. (Диссипация энергии лат. dissipatio — рассеяние — переход части энергии упорядоченных процессов (кинетической энергии движущегося тела, энергии электрического тока и т. п.) в энергию неупорядоченных процессов, в конечном счёте — в теплоту). Для несжимаемой жидкости поток диссипируемой энергии, отнесенный к единице объема жидкости εдν, определяется выражением: dω εдν = −σ τ (2.78) dτ Знак минус здесь означает, что поток энергии направлен в сторону уменьшения скорости. С учетом уравнения (2.73) получаем: εдν = µ  dω   dn  2 (2.79) За счет диссипации энергии движущаяся жидкость нагревается. В большинстве случаев нагрев невелик (температура повышается на несколько тысячных или сотых долей градуса) и может не приниматься во внимание. Однако при больших градиентах скорости повышение температуры жидкости за счет диссипации энергии может быть весьма значительным. Так как динамический коэффициент вязкости зависит от строения молекул и их взаимодействия, а интенсивность последнего сильно изменяется с температурой, то μ является также функцией температуры. Все жидкости делят на две группы: 1) ньютоновские, для которых значение μ не зависит от градиента скорости и постоянно при данной температуре; 2) неньютоновские, для которых касательное напряжение выражается зависимостями более сложными, чем (2.73). К ньютоновским жидкостям относятся газы и жидкости с относительно небольшими молекулярными массами («нормальные» жидкости), к неньютоновским — жидкие полимеры, растворы высокомолекулярных полимеров, суспензии и т. д. — 71 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Ϯ͘ϯ͘ϯ͘ʥ̸̡̨̛̛̛̣̦̭̣̖̭̯̙̖̦̌̌̏̌̔̏́;̛̥̪̱̣̭̽̌Ϳ͘ Перенос количества движения связан с переносом энергии, поэтому уравнение баланса количества движения составляется так же, как уравнение энергетического баланса. Согласно соотношению (2.76), сумма потоков количества движения равна равнодействующей приложенных внешних сил. Это положение одинаково справедливо для системы в целом и для любой ее части. Рассмотрим элементарный объем dv = dxdydz в одномерном потоке несжимаемой жидкости, движущемся вдоль оси z (см. рис. 2.1). Через нижнюю площадь dxdy поступает поток количества движения GMωz, где GM — массовый расход жидкости. Очевидно, что GM = ρωzdxdy. Через противоположную площадь dxdy, отстоящую от первой на расстоянии dz, удаляется поток количества движения GMωz + d(GMωz). Здесь d(GMωz) — приращение потока количества движения при перемещении жидкости на расстояние dz. Для системы, изолированной от окружающей среды, GM=const и приращение потока количества движения обусловливается только изменением скорости, т. е. d(GMωz)= GMdωz. В общем случае скорость движения изменяется во времени и в пространстве. Поэтому ∂ω z ∂ω dω z = dz + z dτ ∂z ∂τ Для одномерного потока dτ =  ∂ω 1 ∂ω \  dz ;dω z =  z + dz ωz  ∂z ω z ∂τ  Следовательно dτ =  ∂ω 1 ∂ω z  dz dz ;dω z =  z + ωz  ∂z ω z ∂τ   ∂ω 1 ∂ω z  d (GM ω z ) = ρω z  z +  dxdydz ∂ ω z  z ∂τ  (2.80) На жидкость (газ) действуют внешние силы (сила тяжести, давления и т. д.) и внутренние (обусловленные вязким тре— 72 — ÐƭǪǭǮǃǊÐ͟Ǭ͠ǬǃǮǯǪÐǂǪǯǯǊÐǀÐǌǃǬ͠Ƽǀǀ нием). За счет этого скорость движения жидкости (газа) ωz изменяется как в направлении оси х, так и в направлении оси у. На боковую поверхность dydz, перпендикулярную оси х и находящуюся на расстоянии х от оси z, действует сила трения, ∂ω равная σ zxdydz = −µ z dydz , а на поверхность, отстоящую ∂x от первой на расстоянии dx, — противоположно направленная  ∂ω ∂  ∂ω z   сила (σ zx + dσ zx ) dydz = −µ  z +   dx  dydz . Аналогич ∂x ∂x  ∂x   ным образом выражаются силы трения, действующие на поверхности dxdz и перпендикулярные оси у: σ zydxdz = −µ ∂ω z dxdz; σ zy + dσ zy dxdz = ∂y ( )  ∂ω ∂  ∂ω   = −µ  z +  z  dy  dxdz y y  ∂y   ∂ ∂  Равнодействующая этих сил определяется выражением:  ∂2 ω z ∂2 ω z  µ + dxdydz 2 ∂y2   ∂x Из внешних сил ограничимся учетом только силы тяжести и силы, обусловленной давлением в направлении движения жидкости. Сила тяжести равна gp dxdydz. Сила давления р на нижнюю площадь dxdy составляет pdxdy. На расстоянии dz от нижней площади сила давления уменьшается на величину ∂p dz за счет жидкостного трения. Следовательно, сила давле∂z ∂p   ния на верхнюю площадь dxdy равна  p − dz dxdy . Равно ∂z  действующая внешних сил: ∂p    gρ −  dxdydz ∂z — 73 — dy ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Равнодействующая всех сил, действующих на элементарный объем жидкости (газа):   ∂2 ω z ∂2 ω z   ∂p + µ + (2.81)  gp −  dxdydz 2 ∂z ∂y2    ∂x  Приравнивая в соответствии с (2.76) выражения (2.80) и (2.81), получаем:  ∂2 ω z ∂2 ω z  ∂ω z ∂ω 1 ∂ρ + ωz z = g − + ν + 2 ∂τ ∂z ρ ∂z ∂y2   ∂x (2.82) Это — уравнение баланса количества движения для одномерного потока жидкости вдоль оси z. Первое слагаемое левой части уравнения (2.82) выражает ускорение жидкости, возникающее вследствие изменения скорости во времени, а второе слагаемое — ускорение, возникающее в результате изменения скорости в пространстве, т. е. при переходе из одной точки пространства в другую, отстоящую от первой на расстоянии dz. Члены правой части уравнения (2.82) выражают силы, отнесенные к единице массы жидкости: первый — силу вязкого трения, второй — силу тяжести и третий — силу, возникающую в результате давления, приложенного к жидкости. Сила вязкого трения определяется свойствами жидкости и условиями ее движения, а сила внешнего давления градиентом давления в жидкости; сила же тяжести пропорциональна массе жидкости (силы, обладающие такой особенностью, называют массовыми). Уравнение (2.82) выведено для одномерного движения в направлении оси z. В более общем случае, трехмерного движения, при котором изменяются проекции скорости по всем осям координат, уравнение баланса количества движения вдоль оси z имеет вид: ∂ω z ∂ω ∂ω z ∂ω 1 ∂ρ (2.83) + ωx z + ωy + ω z z = ν∇2ω z + Z − ∂τ ∂x ∂y ∂z ρ ∂z — 74 — ÐƭǪǭǮǃǊÐ͟Ǭ͠ǬǃǮǯǪÐǂǪǯǯǊÐǀÐǌǃǬ͠Ƽǀǀ ∂2 ω z ∂2 ω z ∂2 ω z — оператор Лапласа; Z — проек+ + ∂ x2 ∂y 2 ∂z2 ция массовой силы, отнесенной к единице массы жидкости, на ось z. В уравнении (2.82) Z = g. Аналогичный вид имеют уравнения баланса количества движения вдоль осей х и у: ∂ω x ∂ω ∂ω x ∂ω 1 ∂ρ + ωx x + ωy + ω z x = ν∇2ω x + X − (2.83a) ∂τ ∂x ∂y ∂z ρ ∂x где ∇2ω z = ∂ω y ∂ω y ∂ω y ∂ω y 1 ∂ρ = ν∇2ω y + Y − (2.83б) ∂τ ∂x ∂y ∂z ρ ∂y где X и Y — компоненты массовой силы по осям х и у. Система уравнений (2.83) описывает закономерности ламинарного движения вязкой жидкости и носит название — уравнения Навье — Стокса. + ωx + ωy + ωz Ϯ͘ϯ͘ϰ͘ʿ̨̛̣̖̯̖̥̪̖̬̯̱̬̙̱̺̖̜̭̭̬̖̖̌̏̔̏́̔͘ Различают два механизма переноса энергии: 1) молекулярный 2) конвективный По первому механизму передача энергии осуществляется путем молекулярной теплопроводности, т. е. в результате соударений микрочастиц (электронов, ионов, молекул и т. д.). При этом изменяется кинетическая энергия микрочастиц. Скорость молекулярного переноса зависит от физических свойств среды. По второму механизму энергия переносится макроскопическими количествами движущейся жидкости. Скорость конвективного переноса энергии тоже является функцией свойств среды, но основную роль при этом играют условия движения. Вывод уравнения, описывающего перенос энергии в движущейся среде, аналогичен выводу уравнений движения, и сводится к составлению энергетического баланса для элементарного объема жидкости. — 75 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Тепловой баланс можно записать следующим образом: ρc p   ∂t ∂t ∂t ∂t   + ωy + ω z   dv + qr dv dv =  λ∇2t − ρc p  ω x  ∂τ ∂ ∂ ∂ x y z   или  ∂t ∂t ∂t ∂t  q (2.84) = a∇2t −  ω x + ωy + ωz  + r  ∂τ ∂x ∂y ∂z  ρc p где a — коэффициент температуропроводности. Выражение (2.84), называемое уравнением Фурье — Кирхгофа, описывает процесс распространения теплоты в движущейся среде. Решением этого уравнения является функция t = f(x,y,z,τ), определяющая поле температур, т. е. распределение температуры в пространстве и во времени. Для установившегося процесса, когда поле температур не изменяется во времени, dt/dτ = 0 и уравнение (2.84) преобразуется к виду: ωx q ∂t ∂t ∂t + ωy + ωz = a∇2t + r ∂x ∂y ∂z ρc p (2.85) Для неподвижной среды (wx=wy=wz=0) поле температур определяется только молекулярной теплопроводностью (уравнение (2.71)). При отсутствии источников теплоты для установившегося процесса справедливо уравнение Лапласа, которое описывает поле температур при отсутствии конвективного переноса энергии. ∂ 2t ∂ 2t ∂ 2t (2.86) + + =0 ∂x2 ∂y2 ∂z2 Из выведенных уравнений следует, что в движущихся средах распространение теплоты зависит от поля скоростей. Поэтому математическое описание таких процессов, кроме уравнения Фурье — Кирхгофа (2.84), включает уравнения движения (2.83). Чтобы решить эту систему уравнений, нужно из уравнений движения найти составляющие скорости wx, wy и wz как функции координат и времени, подставить их в уравнение Фурье — Кирхгофа и решить его относительно температуры. — 76 — ÐƭǪǭǮǃǊÐ͟Ǭ͠ǬǃǮǯǪÐǂǪǯǯǊÐǀÐǌǃǬ͠Ƽǀǀ Ϯ͘ϯ͘ϱ͘ʿ̶̶̨̡̨̛̛̣̖̦̖̦̯̬̜̙̱̺̖̜̭̭̬̖̖̌̏̔̏́̔͘ Вывод уравнений переноса вещества в движущейся среде, аналогичен выводу уравнений, описывающих перенос количества движения и энергии, и сводится к составлению материального баланса произвольного i-гo компонента смеси для элементарного объема жидкости. Вследствие этого получаем уравнение материального баланса по компоненту i для элементарного объема несжимаемой жидкости: ∂ci ∂c ∂c ∂c   = Di ∇2ci −  ω x i + ω y i + ω z i  + riv  ∂τ ∂x ∂y ∂z  (2.87) Уравнение (1.87) описывает перенос произвольного компонента в движущейся среде. Для установившегося процесса ∂c ( i = 0 ) оно приобретает вид: ∂τ ωx ∂ci ∂c ∂c + ω y i + ω z i = Di ∇2ci + riv ∂x ∂y ∂z (2.88) Решения уравнений (2.87) и (2.88) получаются, соответственно, в виде функций ci = f ( x, y,z, τ ) и ci = ϕ ( x, y,z) , описывающих поле концентраций. Из изложенного следует, что скорость переноса вещества в движущейся среде, подобно скорости переноса энергии, зависит не только от поля концентраций и свойств среды, но и условий движения, т. е. от гидродинамической обстановки, в которой протекает процесс. Для системы, состоящей из n компонентов, можно написать n–1 независимое уравнение (1.87) для n–1 компонента. Очевидно, уравнение для n-го компонента не является независимым вследствие очевидного услоn вия ∑ci = ρ , где ρ — плотность смеси. Эти уравнения должны i =1 быть дополнены уравнениями Навье — Стокса (2.83), определяющими поле скоростей жидкости или газа. — 77 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Ϯ͘ϰ͘ʰ̨̨̡̛̦̙̖̦̖̬̦̼̖̥̖̯̼̺̯̼̬̱̙̺̖̜̭̬̖̼̔̌̌̀̔̚͘ В теоретических основах защиты окружающей среды, базирующихся на общих законах физики, физической и коллоидной химии, термодинамики, гидро- и аэродинамики, изучается физико-химическая сущность основных процессов экобиозащитных технологий. Такой системный подход позволяет сделать обобщения по теории процессов защиты среды и применить к ним единый методологический подход. В зависимости от основных закономерностей, характеризующих протекание процессов защиты среды, последние, как мы указывали выше, подразделяют на физические; механические; гидромеханические; массообменные, химические; физико-химические; тепловые; биохимические; процессы, осложненные химической реакцией. Кроме того анализ состояния окружающей среды на основе фундаментальных законов природы позволяет оценить деградацию природной среды и разработать энергоэнтропийную концепцию защиты окружающей среды, а также риск-ориентируемое мышление человека. Ϯ͘ϰ͘ϭ͘ˑ̶̶̨̨̡̨̨̡̛̛̛̦̖̬̦̯̬̪̜̦̦̖̪̺̯̼̬̱̙̺̖̜̐̾̌́́̌̌̀̚ ̡̛̛̭̬̖̼̬̭̔Ͳ̨̨̛̛̛̬̖̦̯̬̱̖̥̖̥̼̹̣̖̦̖͘ Первого начала термодинамики недостаточно для полного описания термодинамических процессов. Оно позволяет точно найти энергетический баланс этих процессов, но не дает никаких указаний об их направлении и о возможности их протекания. Общей закономерностью, позволяющей находить направление и устанавливать возможность или невозможность этих процессов, является второе начало термодинамики. Некоторые из формулировок второго начала, как мы показали выше, наглядны и непосредственно связаны с опытом, другие более абстрактны, но являются более удобными для математического развития теории. Одной из наиболее удачных является формулировка Томсона. «Различные виды энергии стремятся переходить в теплоту, а теплота, в свою очередь, стремится рассеяться, т.е. распределиться между всеми телам наиболее рав— 78 — ÐƮǃƾǬǃǬ͠ǃǊǬÐǂǬǰǮƽǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊ номерным образом». В этой формулировке содержится представление о том, что в природе происходит процесс рассеяния тепловой энергии, вследствие чего второе начало термодинамики называют законом рассеяния или деградации тепловой энергии. Ϯ͘ϰ͘Ϯ͘ʿ̶̨̨̨̛̛̛̛̛̛̛̬̦̪̭̱̺̖̭̯̦̬̭̯̦̦̯̬̪̏̏̌́̏̌̌́̾̚͘ Происхождение и развитие понятия «энтропия» нельзя рассматривать вне эволюции естественнонаучных представлений о втором начале термодинамики. Более того, существует точка зрения, что второй закон термодинамики есть не что иное, как закон об энтропии. В частности, Гиббс отождествлял представление о функции энтропии с представлением о втором начале термодинамики. Он характеризовал энтропию как величину, само понятие о которой связано со вторым началом термодинамики. Клаузиус определил содержание второго начала следующим образом: «Невозможен процесс, единственным конечным результатом которого был бы переход теплоты от тела с данной температурой к телу с более высокой температурой». По мнению Кельвина, «невозможен процесс, единственным конечным результатом которого будет превращение в работу теплоты, извлеченной из источника, имеющего всюду одинаковую температуру». Оба эти принципа эквивалентны и основаны на анализе круговых процессов машины Карно. Введем теперь представление об обратимых и необратимых, самопроизвольных и несамопроизвольных процессах. Выше мы показали, что обратимым может быть только такой процесс, в котором система последовательно проходит через ряд положений равновесия. Это достигается только в тех случаях, когда процесс совершается бесконечно медленно или квазистатически. Следовательно, обратимый процесс — это такой процесс, который может протекать в обратном направлении, уменьшая какую-либо независимую переменную на бесконечно малую величину. Однако, как известно, обратимые процессы являются идеализацией реальных процессов и практически нереали— 79 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ зуемы. Но абстрактное представление об обратимых процессах является в термодинамике необходимой основой для расчетов, поскольку все ее количественные соотношения имеют смысл для обратимых процессов. Поэтому чисто реальные процессы представляют как ряд обратимых стадий. Кроме того, чтобы провести тот или иной процесс обратимо, необходимо бесконечно большое время. Однако, некоторые процессы, происходящие в тех или иных системах, не могут быть обратимыми ни при каких условиях. Например, образование тепла при трении, переход тепла от одного тела к другому при конечной разности температур путем теплопроводности или излучения, самопроизвольная диффузия и т.п. Эти процессы внутренне необратимы. Помимо обратимых и необратимых процессов, различают самопроизвольные и несамопроизвольные процессы. Под самопроизвольным, понимают такой процесс, который доходит до конца, т.е. до положения равновесия, без внешнего воздействия. Очевидно, что всякий самопроизвольный процесс можно использовать для превращения энергии в работу, что и производится на практике. В абсолютном большинстве в процессе жизнедеятельности человека его не устраивают результаты самопроизвольных процессов, поэтому в систему извне вводится энергия с целью проведения процесса несамопроизвольно, т.е. над системой совершается работа, чтобы получить конечный результат. Конечным результатом может быть перекачка воды в гору, электролиз, сжатие газа и т.д. Во всех таких случаях используют энергию других, уже самопроизвольных процессов. Другими словами, всю жизнедеятельность человека можно характеризовать как то или иное сочетание самопроизвольных и несамопроизвольных процессов. Все реально протекающие процессы являются необратимыми, но это не значит, что их нельзя проводить обратимо. Достаточно приложить такое сопротивление, чтобы переход был бы очень медленным, и процесс в любое время мог бы пойти в обратном направлении при конечно малом изменении противодействующих сил. Следовательно, самопроизвольные процессы совсем не исключают обратимости при квазистационарных условиях. — 80 — ÐƮǃƾǬǃǬ͠ǃǊǬÐǂǬǰǮƽǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊ Однако, необходимо отметить, что невозможно получить максимальную работу ни в одной из систем с реальной машиной из-за потерь на трение и из-за того, что истинный обратимый процесс должен протекать бесконечно медленно. Поэтому реальные процессы в какой-то степени всегда необратимы, и полученная работа меньше максимально возможной. Действительно, КПД тепловой машины с необратимым циклом меньше, чем КПД машины с обратимым циклом, но и в последнем случае он всегда меньше 1. Это и является следствием фундаментального различия между двумя видами энергии в процессе ее передачи — теплотой и работой. Именно это различие составляет основное содержание второго принципа термодинамики. Опыт показывает, что если различные виды работы могут быть полностью обращены в теплоту, то обратимое эквивалентное преобразование в круговых циклах невозможно. Если превращение работы в теплоту может ограничиваться только изменением термодинамического состояния рабочего тела, то при превращении тепла в работу только часть его затрачивается на совершение рабочим телом положительной работы, часть же тепла идет на изменение термодинамического состояния одного из обязательных элементов тепловой машины — холодильника. КПД идеальной тепловой машины Карно вычисляется по известным формулам Q − Q2 (2.89) η= 1 Q1 где Q1 — количество теплоты, соответственно полученное от нагревателя, а Q2 — отданное холодильнику. T −T (2.90) η= 1 2 T1 где T1 — температура нагревателя, а T2 — температура холодильника. Откуда, Q1 T1 (2.91) = Q2 T2 — 81 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Очевидно, что Q2 = Если обозначить Q1 ∆T2 T1 (2.92) Q1 = S , то T1 Q2 = ST2 (2.93) Следовательно, отданное рабочим телом холодильнику тепло тем больше, чем меньше S при температуре Т2. Другими словами, чем выше энтропия рабочего тела, тем большая доля тепла в идеальном круговом процессе оказывается непревращенной в тепло и передается холодильнику. Поэтому энтропия определяет степень обесценивания тепла, его деградацию в круговом процессе. При фиксированной температуре холодильника наибольшая эффективность тепловой машины достигается путем увеличения температуры источника, что ведет к снижению энтропии рабочего тела, а значит к повышению ценности тепла, переданного источником, поскольку снижается доля рассеянной или переданной холодильнику энергии. Q Q Из соотношения (2.93) следует, что 1 = 2 , или T1 T2 Q1 T1 − =0 Q2 T2 (2.94) Или Q =0 T (2.95) А подынтегральная функция, подчиняющаяся соотношению (2.95), обладает свойством полного дифференциала, откуда ൏δ ൏dS = 0 (2.96) Интегрирование уравнения (2.96) по замкнутому циклу, отражающему обратимое изменение температуры системы от T1 до T2, позволяет определить соответствующее изменение энтропии — 82 — ÐƮǃƾǬǃǬ͠ǃǊǬÐǂǬǰǮƽǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊ T2 ∆S = S2 − S1 = ∫ δ T1 Q T (2.97) Однако реально существующая необратимость процессов вносит коррективы в приведенные соотношения, потому что в реальной тепловой машине непроизводительное тепло Q не ограничено величиной отданного холодильнику тепла и включает в себя другие непроизводительные затраты. Следовательно, равенство (2.94) должно быть заменено неравенством Q2 Q1 (2.98) > T2 T1 т.е. приведенное тепло, полученное рабочим телом от нагревателя, меньше приведенной теплоты, отданной холодильнику, в необратимой машине Карно. Если обобщить неравенство (2.98) на необратимый круговой процесс, то Q (2.99) ൏ i ≤0 Ti где знак равенства относится к обратимым процессам, а знак неравенства — к необратимым, если считать тепло, полученное рабочим телом, положительным, а отданное холодильником отрицательным. Возрастание количества теплоты Q2 под влиянием необратимости вызывает еще одно следствие, которое содержится в выражении (1.99). Так как тепло передается холодильнику при температуре Т2, то его величина выражается произведением Т2∆S, так что увеличение Q2 вызывает соответствующее возрастание энтропии. Для обратимого цикла ∆S = S2 — S1. А для необратимого цикла ∆S = S’2 – S’1, причем S’2 > S’1. Поэтому можно считать, что при необратимости ∆S > 0, т.е. возрастание энтропии при необратимом процессе связано с необратимостью самого процесса. Следовательно, энтропия замкнутой системы остается постоянной, если в ней происходят обратимые процессы, и увеличивается при необратимых процессах. Ни при каких процессах энтропия замкнутой системы не уменьшается. Таким образом, когда энтропия — 83 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ достигает максимума — система оказывается в положении равновесия. Отметим, что термодинамическому равновесию соответствует состояние с максимумом энтропии. Энтропия может иметь не один, а несколько максимумов. Равновесие, которому соответствует наибольший максимум, называется абсолютно устойчивым или стабильным. С учетом первого начала термодинамики дифференциальное определение энтропии принимает вид 1 (2.100) dS = (dU + pdV ) T Откуда энтропия представляет собой термодинамический потенциал при выборе в качестве независимых переменных внутренней энергии U и объема V. Частные производные энтропии связаны с Т и Р соотношениями 1  ∂S  (2.101) =  T  ∂U  V P  ∂S  (2.102) =  T  ∂V  U которые определяют уравнения состояния системы — первое калорическое, а второе — термическое. Понятно, что формула (2.97) определяет энтропию лишь с точностью до аддитивной постоянной. Абсолютное значение энтропии можно установить лишь с помощью третьего начала термодинамики, основываясь на котором, за начальную точку отсчета энтропии принимают S = 0 при Т = 0 К. Статистическая физика, как известно, связывает энтропию с вероятностью осуществления данного макроскопического состояния системы. Энтропия определяется через логарифм статистического веса или через плотность состояний. (2.103) S = KlnΩ ( ε, N ) где Ω ( ε,N ) — число квантовомеханических уровней в узком интервале энергий ∆ε вблизи значения энергии ε системы из N частиц в статистической физике, а Ω — величина объема в фазовом пространстве системы при заданных N и ε. — 84 — ÐƮǃƾǬǃǬ͠ǃǊǬÐǂǬǰǮƽǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊ В отличие от термодинамики, статистическая физика рассматривает особый класс процессов — флуктуации, при которых система переходит из более вероятного состояния в менее вероятное, и ее энтропия уменьшается. Наличие флуктуации показывает, что закон возрастания энтропии выполняется только в среднем для большого промежутка времени. Термодинамика неравновесных процессов позволяет более детально исследовать процесс возрастания энтропии и вычислить количество энтропии, образующейся в единице объема в единицу времени, вследствие отклонения от термодинамического равновесия. В термодинамике неравновесных процессов принимается, что энтропия элемента объема (локальная энтропия) является такой же функцией внутренней энергии и удель1 ного объема v = , где ρ — плотность, и концентрации ск, как ρ и в состоянии полного равновесия, и, следовательно, для этих величин справедливы обычные термодинамические равенства. Эти положения вместе с законами сохранения массы, количества движения (импульса) и энергии позволяют найти уравнения баланса энтропии. dS (2.104) ρ = −divJS + σ dt где Js — плотность потока энтропии, выражающаяся через плотность потока теплоты, диффузного потока и т.п., а σ — локальное производство энтропии на единицу объема в единицу времени. Производство энтропии определяется только необратимыми процессами (например, диффузией, теплопроводностью и др.) и равно n σ = ∑Ji xi (2.105) i =1 где Ji — потоки, а xi — сопряженные им термодинамические силы, т.е. градиенты термодинамических параметров. При малых отклонениях системы от термодинамического равновесия возникающие потоки линейно зависят от термоди— 85 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ намических сил и описываются феноменологическими уравнениями типа (2.106) Ji = ∑Lik xk k где Lik — кинетические коэффициенты или коэффициенты переноса. Однако необходимо отметить, что процессы переноса могут быть как прямыми, так и перекрестными. При прямом переносе термодинамическая сила xk вызывает поток Jk (например, градиент температуры вызывает поток тепла), однако термодинамическая сила xk может вызвать и поток вещества Ji и при ik (например, термодиффузия). С учетом этого производство энтропии равно σ = ∑xi Lik ≥ 0 (2.107) i,k Энтропия, в отличие от массы, энергии и импульса, не сохраняется, а возрастает со временем, как это следует из уравнения (2.104), в элементе объема вследствие необратимых процессов. Скорость возрастания энтропии мы обозначили значком σ. Положительность производства энтропии σ > 0 означает закон возрастания энтропии. Особо отметим гетерогенные системы, в которых термодинамические параметры изменяются скачком, например, газы, соединенные капилляром или мембраной. В стационарном состоянии величина σ минимальна при заданных временных условиях, препятствующих достижению равновесия (Теорема Пригожина). В состоянии равновесия σ = 0 (Теорема Онсангера). Соотнося это к мероприятиям по защите окружающей среды, раскрывая смысл этих мероприятий, можно отметить, что смысл жизнедеятельности человека — это свести величину dS/dt к минимуму или к нулю, что соответствовало бы вечной жизни. Кроме того, энтропия может изменяться вследствие втекания ее в элемент объема или вытекания из него. Это дает основу для исследования открытых систем, т.е. позволяет объяснить различные неравновесные процессы природы и общества. Энтропия в физике тесно связана с информацией. В этом случае энтропия служит мерой неопределенности сообщений. Пусть сообщения описываются множеством величин и вероятностей P1, P2, ..., Pn появления этих величин в сообщении. — 86 — ÐƮǃƾǬǃǬ͠ǃǊǬÐǂǬǰǮƽǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊ Для определенного дискретного статистического распределения вероятностей Рк информационная энтропия равна n H = − ∑Pk ln Pk при k =1 n ∑Pk = 1 (2.108) k −1 Нк = 0, если какое-либо из Рk = 1, а остальные нулю, т.е. информация достоверна, и неопределенность отсутствует. С другой стороны, энтропия принимает наибольшее значение, когда все Рk одинаковы. Заметим, из вероятностной трактовки информационной энтропии могут быть выведены основные законы распределения статистической физики — каноническое распределение Гиббса — распределение, соответствующее максимальному значению информационной энтропии при заданной средней энергии, а также большое каноническое распределение Гиббса — при заданных средней энергии и числе частиц в системе. Однако необходимо отметить, что последовательное применение информационной энтропии при описании процессов физики, химии, истории, экологии требует количественных способов оценки порядка и беспорядка. Если рассматривать процессы фазовых переходов, связанных с разупорядочением (плавление, сублимация), как меру потери информации о внутренней структуре системы, то в ряде случаев наблюдается корреляция между, скажем, энтропией плавления и степенью порядка в жидкости. Весьма важным свойством энтропии является свойство ее аддитивности. Это свойство эквивалентно утверждению, что при разделении данной системы на подсистемы полная энтропия равна сумме энтропий отдельных частей системы. Отмечу, что аддитивность энтропии следует из ее определения и свойств аддитивности внутренней энергии и объема. В частности, если говорить о таком разупорядочении твердого тела, как плавление, то энтропия плавления будет складываться из трех составляющих — позиционной, колебательной и электронной (2.109) ∆Sпл = ∆Sпоз + ∆Sкол + ∆Sэл — 87 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Ϯ͘ϰ͘ϯ͘ˑ̶̶̨̨̡̨̛̛̦̖̬̦̯̬̪̜̦̦̖̪̐̾̌́́ ̨̡̛̺̯̼̬̱̙̺̖̜̭̬̖̼̌̌̀̔̚͘ Решение проблем производственно-экологической безопасности невозможно без принятия единой научно обоснованной методологии, созданной на основе объективных представлениях о факторах и закономерностях аварийности, травматизма в техносфере и в окружающей природной среде. Такая методология должна обосновать выбор объекта, предмета и основных методов исследования и совершенствования безопасности производственных и технологических процессов. Более того, она может стать специфичным инструментарием познания и преобразования действительности в других сферах человеческой жизнедеятельности. Считается, что принимаемая методология должна иметь эмпирическую основу в форме проверенной практикой совокупности утверждений и концептуальных высказываний, используемых при выборе необходимых методов в качестве исходных постулатов и аксиом. Их введение позволяет внести ясность в последующие рассуждения, избежать произвольного толкования используемых терминов, обосновать объект исследования и совершенствования. Такой подход в наибольшей степени обеспечивает истинность принятых предпосылок, а значит обоснованность и плодотворность основанных на них построений. При формулировании исходных утверждений, касающихся природы аварийности и травматизма в техносфере и в охране окружающей среды мы будем исходить из следующих представлений. Суть этих представлений состоит в сложном, стохастическом характере событий рассматриваемых явлений, их причинной обусловленности большим числом факторов, проявляющихся в объективном стремлении энергетических потенциалов к выравниванию, и противодействии им со стороны разного рода защитных механизмов. Эти идеи соответствуют современным представлениям и позволяют сформулировать энергоэнтропийную концепцию и классификацию объективно существующих в техносфере и окружающей среде опасностей. При этом сущность такой концепции может быть представлена следующими основными утверждениями. — 88 — ÐƮǃƾǬǃǬ͠ǃǊǬÐǂǬǰǮƽǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊ 1. Производственная деятельность потенциально опасна, так как связана с проведением технологических процессов, а последние — с энергопотреблением (выработкой, хранением, преобразованием тепловой, механической, электрической, химической и других видов энергии). 2. Техногенная опасность проявляется в результате несанкционированного или неуправляемого выхода энергии, накопленной в технологическом оборудовании и вредных веществах, непосредственно, как в самих работающих так и, во внешней относительно их и техники среде. 3. Несанкционированный или неуправляемый выход больших количеств энергии или вредных веществ приводит к происшествиям с гибелью и травмированием людей, повреждениями технологического оборудования, загрязнением окружающей природной среды. 4. Возникновение техногенных происшествий является следствием появления причинной цепи предпосылок, приводящих к потере управления технологическим процессом, несанкционированному высвобождению используемой при этом энергии (рассеиванию вредных веществ) и их разрушительному воздействию на людей, объекты производственного оборудования и природной среды. 5. Инициаторами и звеньями причинной цепи каждого такого происшествия являются ошибочные и несанкционированные действия работающих, неисправности и отказы технологического оборудования, а также неблагоприятное влияние на них внешних факторов. 6. Ошибочные и несанкционированные действия персонала обусловлены его недостаточной технологической дисциплинированностью и профессиональной неподготовленностью к работам, связанных с потенциально опасной технологией и конструктивными несовершенствовами используемого производственного оборудования. 7. Отказы и неисправности технологического и производственного оборудования вызваны его собственной низкой надежностью, а также несанкционированными или ошибочными действиями работающих. — 89 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ 8. Нерасчетные (неожиданные или превышающие допустимые пределы) внешние воздействия связаны с недостаточной комфортностью рабочей среды для человека, ее агрессивным воздействием на технологическое оборудование, а также с не благоприятными климатическими или гидрогеологическими условиями дислокации производственного объекта. Сущность только что сформулированной концепции проиллюстрирована на рис. 2.6, а ее правомерность обусловлена, прежде всего, эмпирическим характером сделанных выше утверждений. Это объясняется тем, что опыт (корректная статистика) есть результат проявления объективно существующих факторов. Рис. 2.6. Иллюстрация природы опасностей. Другим аргументом, подтверждающим справедливость только что сформулированной концепции, является ее непро— 90 — ÐƮǃƾǬǃǬ͠ǃǊǬÐǂǬǰǮƽǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊ тиворечивость фундаментальным законам энтропии, в частности ее объективнoмy стремлению к самопроизвольному росту в условиях техносферы. Согласно второму началу термодинамики, например, получение синтетических веществ и химически чистых элементов, выработка и аккумулирование энергии, очистка и обогащение природных материалов являются «противозаконными», так как влекут за собой снижение энтропии. Вот почему большое число технологических процессов, включая транспортировку материальных ресурсов, являются потенциально опасными, поскольку содержат в себе неестественные с точки зрения энтропии преобразования. Учитывая необходимость в более тщательной проверке принятой здесь концепции, поясним последнюю особенность исследуемых процессов подробнее. Для этого напомним, что законы энтропии обычно играют как бы роль бухгалтера природы, следящего за балансом количества энергии (первый), и диспетчера, указывающего направление соответствующих преобразований (второй). Более того, они предписывают и конечный результат таких преобразований в закрытых системах: для вещества — это пыль, для информации — шум и для энергии — тепло. В частности, в последнем случае имеется в виду стремление любой энергии постепенно переходить в тепло, равномерно распределяемое среди окружающих тел. При этом оказывается, что энтропия любой системы обратно пропорциональна величине эксэргии — той свободной части энергии, которая способна к дальнейшим превращениям. В силу этого каждая предоставленная самой себе система неминуемо переходит в состояние с максимальной энтропией, характеризуемое отсутствием энергетических потенциалов — такое равновесное состояние, которое соответствует наибольшей степени дезорганизации, т.е. хаосу. Вот почему любые попытки вывести систему из таких состояний требуют преодоления естественных энергетических барьеров и рассматриваются как приводящие ее в неустойчивое, а стало быть, опасное состояние. Можно показать также, что потенциально опасной является не только произ— 91 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ водственная (физическая) деятельность, но и творческая или познавательная, связанная с добычей нематериальных ценностей, а информации. Дело в том, что интеллектуальная работа направлена на уменьшение энтропии, т. е. степени неопределенности, но уже в информационном смысле: поиск внутренней структуры и организованности вещей, выяснение закономерностей появления и предупреждения событий, создание моделей объектов и процессов, конструирование новых образцов технологического оборудования. Рассматриваемая деятельность человека требует интеллектуальных усилий, вызванных необходимостью преодоления «стремления природы к сокрытию своих тайн», а поэтому сопровождается усталостью или перенапряжением анализаторов человека, возможностью ухудшения состояния его здоровья в результате профессиональных заболеваний. С учетом сделанных замечаний энергоэнтропийная концепция может быть обобщена с целью описания не только техногенных происшествий, но и остальных неблагоприятных событий, происходящих в других средах обитания человека. Для этого необходимо скорректировать сделанные выше утверждения на предмет замены энергии энтропией, а опасности — вредностью. Например: в первом утверждении необходимо слово «опасна» поменять на «вредна», а всю его оставшуюся часть, начиная со слова «энергопотребление» — на «понижение энтропии и получение различных видов информации»; во втором — сменить слово «опасность» на «вредность», а выражение «несанкционированного и неуправляемого выхода энергии...» на «постепенного расходования той части свободной энергии, которая накоплена в технологическом процессе ...»; в третьем — перейти от всей фразы «несанкционированный или неуправляемый выход энергии» к фразе «несвоевременный рост энтропии организма человека и других биологических особей может сопровождаться увеличением их заболеваемости, повышенной смертностью и сокращением естественного разнообразия природы». Если продолжить подобные дальнейшие обобщения, то можно формулировать более общую концепцию, касающуюся уже природы всех объективно существующих опасностей — 92 — ÐƮǃƾǬǃǬ͠ǃǊǬÐǂǬǰǮƽǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊ не только в техносфере, но и в окружающей среде и повседневной жизни человека. Приведенные выше соображения подтверждают правомерность энергоэнтропийной концепции, раскрывающей природу объективно существующих опасностей и позволяющей дать их наиболее общую классификацию. Действительно, исходя из неадекватности потоков энергии, вещества и информации, все опасности можно делить на следующие три класса: 1. природно-экологические, вызванные нарушением естественных циклов миграции вещества, в том числе по причине природных катаклизмов; 2. техногенно — производственные, связанные с возможностью нежелательных выбросов энергии и вредного вещества, накопленных в созданных людьми технологических объектах; 3. антропогенно-социальные, обусловленные умышленным сокрытием и (или) искажением информации. Ϯ͘ϰ͘ϰ͘ʽ̶̡̨̨̨̛̛̖̦̦̯̬̪̪̭̦̭̯̖̜͕̌̾̌ ̸̵̨̡̨̨̨̨̨̡̛̛̛̯̖̬̥̦̥̖̭̯̖̦̖̦̦̬̭̔̌̐̐̐̌ ̵̸̵̵̡̨̡̛̛̛̛̯̖̦̖̭̭̭̯̖̥̬̱̙̺̖̜̭̬̖̖̏̌̌̀̔͘ Представленная выше энергоэнтропийная концепция опасностей позволяет оценить термодинамический техногенный риск в технических системах и окружающей природной среде. При проведении данных оценок мы, основываясь на энергоэнтронийной концепции защиты окружающей среды, будем предполагать, что в результате действия различных опасностей уменьшается упорядоченность среды обитания, а с нарастанием беспорядка увеличивается энтропия. Рассмотренная концепция, как мы отмечали выше, основана на экспериментальных данных и не противоречит второму началу термодинамики, которое формулируется следующим образом: естественные процессы сопровождаются возрастанием энтропии Вселенной (принцип энтропии). Если предложить, что вся энергия, сбрасываемая в окружающую среду при действии опасности приводит к повыше— 93 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ нию беспорядка (хаоса) в ней (то есть увеличивает ее термодинамическую энтропию), несложно дать количественную оценку опасности в энергетических единицах. Рис.2.7. Действие опасности на систему. Из второго начала термодинамики следует, что полное изменение энтропии (∆Sполн.) в результате химического или физического превращения определяется выражениями (2.112– 2.113): ∆Sполн = ∆Sсистема + ∆Sокружение (2.110) Для любых самопроизвольных процессов ∆Sполн > 0 . Уравнение (2.110) можно переписать в следующим виде: ∆H ∆Sполн = ∆Sсистема − (2.111) T где ∆H — изменение энтальпии. Умножаем последнее уравнение на (– T): −T∆Sполн = ∆H − T ∆Sсистема (2.112) Член (–T ∆Sполн) определяет изменение свободной энергии рассматриваемой системы: ∆G = −T∆Sполн (2.113) где ∆G — изменение свободной энергии системы или изменение энергии Гиббса. Из выражения (2.113) следует, что: ∆G ∆Sполн = − (2.114 ) T Используя последнее выражение, можно определить полное изменение энтропии в рассматриваемой системе и ее окружении при действии опасности. — 94 — ÐƮǃƾǬǃǬ͠ǃǊǬÐǂǬǰǮƽǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊ Рассмотрим теперь, как практически вычисляется ∆G. Если при действии опасности на систему и ее окружение температура и давление остаются постоянным (или изменение этих параметров пренебрежимо мало), то для процессов со стационарным потоком энергии полная работа, которая направлена на разрушение среды обитания и к увеличению ∆Sполн, может быть оценена величиной изменения свободной энергии, происходящей при переходе системы из состояния 1 в состояние 2 (2.113): (2.115) −∆G = G1 − G2 где ∆G — изменение свободной энергии Гиббса при переходе системы из состояния 1 в состояние 2; G1 — свободная энергия системы в состоянии 1; G2 — свободная энергия системы в состоянии 2. Отрицательный знак при ∆G означает, что система сама производит работу над внешней средой (окружением), а положительный знак указывает, что над системой работа производится извне. Обозначив максимальную работу символом Wвн, можем записать ее связь с ∆G (2.115): (2.116) ∆G = −Wвн −∆G = Wвн (2.117) В том случае, если система самопроизвольно совершает работу над окружающей средой (G< 0), то Wвн положительна; в противном случае она отрицательна. На рис.2.7. показано действие опасности на систему, которое заключается в совершении работы, направленной на ее разрушение. Примем эту работу равной полной энергии опасности, выбрасываемой в окружающую среду. Объединяя выражение (2.114) и (2.116) получаем: W (2.118) ∆S полн = вн T Wвн можно охарактеризовать как работу разрушения системы и ее окружения. Используя выражение, мы можем количественно оценивать действие опасности на рассматриваемую систему, предполагая, что работа, совершаемая ею, полностью идет на разрушение системы и ее окружения, что может быть — 95 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ выражено величиной ∆Sполн. Таким образом, осуществлена количественная энергоэнтропийная оценка опасностей. Рассмотрим далее, как провести термодинамическую оценку риска. Как известно, математически риск можно определить по формуле: R= Nнж Nобщ (2.119) где Nнж — число нежелательных событий за определенный период времени (обычно за год); Nобщ — общее число событий за тот же период времени. Из последней формулы следует, что риск — это вероятность появления нежелательных событий за определенный промежуток времени. Учитывая это определение, мы предлагаем термодинамически оценивать риск, как вероятную величину изменения полной энтропии системы и ее окружения, возникающей в результате действия опасности (работы разрушения) за определенный промежуток времени: RWвн (2.120) RT = ∆Sполн R = T где RT — термодинамический риск; T — температура в градусах Кельвина. Размерность термодинамического риска [Дж/Кτ], где τ — рассматриваемый период времени (обычно — год).В этом случае размерность риска Дж/Кτ. Ϯ͘ϰ͘ϱ͘˃̸̶̨̡̨̡̨̨̡̛̛̛̛̛̛̖̬̖̯̖̭̖̖̦̪̭̦̭̯̬̭̌̌ ̵̵̵̵̨̨̛̛̛̪̬̬̦̼̯̖̦̖̦̦̼̭̭̯̖̥̏̔̐̌͘ 1) Землетрясение. Энергия землетрясения может быть рассчитана по формуле: ) E = 10( Дж (2.121) где М — магнитуда — мощность землетрясения, измеренная в баллах по Ч. Рихтеру (0–9 баллов). 5,24+1,44 M — 96 — ÐƮǃƾǬǃǬ͠ǃǊǬÐǂǬǰǮƽǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊ Предполагая, что вся энергия землетрясения затрачивается на производство работы разрушения Wвн. С помощью Sполн. мы можем дать термодинамическую оценку опасности при возникновении землетрясений различной мощности. Полученные результаты представлены в табл.2.2. Таблица 2.2. Результаты оценки опасности землетрясения различной мощности. Мощность землетрясения М Работа разрушения Wвн, кДж S0 298 полн, кДж/ град 0 0,17 · 103 0,57 1 3 4,79 · 10 16,07 2 0,13 · 10 6 0,44 · 103 3 3,63 · 106 12,18 · 103 5 2,75 · 109 9,23 · 106 9 1,58· 1015 5,30· 1012 2) Цунами. Определим опасность действия цунами, энергия которого оценивается в 1013 Дж. Проведем расчет по формуле (2.114) при Т = 298 К: Wп 1013 0 ∆S298 = = = 3,36⋅ ≤ 107 кДж/град (2.122) полн 298 298 Сравнивая полученную величину с результатами оценки опасности землетрясения, можно утверждать, что по порядку величин, опасность цунами превосходит опасность землетрясения мощностью 5 баллов. 3) Шум. Рассмотрим шум на частоте f = 1000 Гц, уровень интенсивности звука, дб I L1 = 10lg 1 I0 2 где I1 — интенсивность звука, Вт/м ; I0— интенсивность звука, соответствующая порогу слышимости человеческого уха (I0= const; I0 = 10–12 Вт/м2 при f = 1000 Гц). — 97 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ I1 = 10L1/10 ; I1 = I010L1/10 I0 при L1 = 120 дб I = 10−12 ⋅ ≤ 1012 = 1 Вт/м2 Звуковая энергия, проходящая через площадку с поверхностью 1 м2 , расположенную перпендикулярно фронту распространения звуковой волны за 1 с, равна Вт Езв = Wвн = 1 2 i1м 2 i1с = 1Дж м 1 0 = 0,34i10−2 Дж/град S298 полн = 298 4) Электромагнитное излучение представлено на примере микроволновой печи. Интенсивность этого воздействия по данным работы составляет I1= 15 Вт/м2. Переходя от интенсивности к энергии по аналогии с расчетом Eзв, имеем: Вт 2 Е эми = Wвн = 15 2 i1м i1с = 15 Дж м где Eэми — энергия электромагнитного излучения, Дж. 15 0 = 0,05 Ä Дж/град S298 полн = 298 5) Ионизирующее излучение. 1 Рентген (1Р) рентгеновского или γ- излучения в 1 кг сухого воздуха, 1 Р = 87,7 Дж/кг. 87,7 = 0,29 Дж/град 298 В 1 кг биологической ткани при поглощении 1 зиверта (1 Зв) энергии рентгеновского или γ- излучения ( 1 Зв = 1 Дж/кг): 0 S298 полн = 1 = 0,34<10−2 Дж/град 298 Используя полученные результаты по формуле (2.120) легко рассчитать термодинамический риск любого происшествия за определенный период времени. 0 S298 полн = — 98 — ÐǠǮǃǰ͠ǮǁǋǃǊǬÐǫǮ͟͠ǮǯǊ Предложим, что в данной местности вероятность (риск) 5-балльного землетрясения — R = 10–2 в год. 10−2 i2,75i109 Тогда RT = = 9,23i104 кДж/град iгод. 298 Данный подход может быть уточнен, если при действии опасности совершается полезная работа, например, при действии направленного взрыва, используемого при строительных работах. В этом случае из энергии, сбрасываемой в окружающую среду, должна быть вычтена величина полезной работы, и именно эта разность должна быть использована при расчете энтропии и термодинамического риска. Ϯ͘ϱ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏͘ 1. Напишите выражение закона сохранения массы. 1) в статических условиях 2) при условии, если в процессе протекает химическая реакция. 3) в движущихся средах 4) в движущихся средах, при условии протекания химической реакции 2. Как на основе закона сохранения массы получить уравнение материального баланса процесса? 3. Напишите выражение закона сохранения энергии. 1) в статических условиях 2) при условии, если в процессе протекает химическая реакция. 3) в движущихся средах 4) в движущихся средах, при условии протекания химической реакции. 4. Как на основе закона сохранения энергии получить уравнение энергетического баланса процесса? 5. Чем отличается энергетический баланс процесса от теплового баланса процесса? 6. Напишите выражение, которое с точки зрения энтропии является критерием обратимости процесса в идеальной системе. — 99 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ 7. Напишите выражение, которое с точки зрения энтропии является критерием необратимости процесса в идеальной системе. 8. Как формулируется третий закон термодинамики? 9. В чем заключается физический смысл уравнения Навье-Стокса? К каким процессам движения жидкости или газа применимо это уравнение? 10. К какой величине стремится энтропия системы при стремлении температуры к абсолютному нулю? 11. Напишите уравнение баланса энтропии для неравновесного процесса. 12. Как записывается уравнение для энтропии системы в статистической физике? 13. Что происходит с энтропией системы, когда система стремится к хаосу? 14. Как энтропия связана с процессами деградации окружающей среды: в техническом, экологическом, социальном и историческом плане? 15. Почему основой описания процессов защиты окружающей среды является энергоэнтропийная концепция. Ϯ͘ϲ͘ʿ̸̛̛̬̥̖̬̼̬̖̹̖̦́̌̔̌̚͘ Задача 1. Монооксид углерода («угарный газ») — опасный загрязнитель атмосферы. Он снижает способность гемоглобина крови к переносу кислорода, вызывает болезни сердечно-сосудистой системы, снижает активность работы мозга. Из-за неполного сжигания природного топлива ежегодно на Земле образуется 500 млн. т CO. Определите, какой объем (при н.у.) займет угарный газ, образующийся на Земле по этой причине. Решение. Запишем условие задачи в формульном виде: m(CO) = 500 млн. т = 5 . 1014 г M(CO) = 28 г/моль VM = 22,4 л/моль (н.у.) V (CO) = ? (н.у.) В решении задачи используются уравнения, связывающие между собой количество вещества, массу и молярную массу: — 100 — Ǥ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ m(CO) / M(CO) = n(CO), а также количество газообразного вещества, его объем и молярный объем: V (CO) / VM = n(CO) Следовательно: m(CO) / M(CO) = V (CO) / VM, отсюда: V(CO) = {VM . m(CO)} / M(CO) = {22,4 . 5 . 1014} / 28 [{л/моль} . г / {г/моль}] = 4 . 1014 л = 4 . 1011 м3 = 400 км3 Ответ. 4 . 1014 л, или 4 . 1011 м3, или 400 км3. Задача 2. В процессах фотосинтеза зеленые растения усваивают из воздуха газообразный оксид углерода, относительная плотность которого по водороду составляет 22. Какова формула этого оксида углерода? Решение. Чтобы установить формулу оксида углерода CXOY, который усваивается растениями при фотосинтезе, надо знать молярную массу этого соединения. Известные нам оксиды углерода состава CO и CO2 имеют молярные массы, равные соответственно 28 и 44 г/моль. Запишем условие задачи в формульном виде: D(H2) = 22 M(H2) = 2 г/моль M(CXOY) = ? Запишем уравнение, связывающее между собой молярную массу газа M(CXOY), относительную плотность его по водороду D(H2) и молярную массу водорода M(H2): M(CXOY) = M(H2) . D(H2) = 2 . 22 [г/моль] = 44 г/моль Молярная масса, равная 44 г/моль, отвечает диоксиду углерода CO2. Ответ. Формула оксида углерода — CO2. Задача 3. Расчёт материального баланса технохимического процесса. Рассмотрим в качестве примера уравнение, лежащее в основе производства фосфора в электропечах: Ca3 ( PO4 )2(т) + Cт + SiO2(т) ↔ P4 + CO + CaSiO3 — 101 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Обозначим вступающие во взаимодействие вещества: приход как — x1, а образующиеся продукты — расход как х. Тогда реакцию х1Са3(РО4)2(т) + х2С + х3SiO2 ļ х4Р4 + х5СО + х6Са SiO3 можно представить в виде таблицы: Элемент Приход Расход Линейное уравнение Сa –3x1 x6 x6=3x1 P –2x1 4x4 4x4=2x1 O –8x1; –2x3 x5+3x6 x5+x6=8x1+2x3 C –x2 x5 x5=x2 Si –x3 x6 x6=x3 Итого –13x1; –3x3–x2 4x4+2x5+5x6 4x4+2x5+5x6= =13x1+3x3+x2 Из системы линейных уравнений следует: x6=3x1=x3; x1=2x4; x5=x2; x5+3x1=8x+2x3; x5=5x1+2x3; x6=x3; x2=5x1+2x3 Предположим, что х4 (коэффициент 1-го продукта реакции) равен 1, тогда из уравнения х1 = 2х4 находим х1 = 2, а из уравнения х6 = 3x1 = х3 получим х6 = 6 и х3 = 6. Коэффициенты х5 = х2 находим из уравнения х5 + Зх1, = = 8x1 + 2х3, откуда х5 = 8 · 2 + 2 · 6 – 3 · 6 = 16 + 12 –18 = 10. Таким образом, x1 x2 x3 x4 x5 x6 2 10 6 1 10 6 Уравнение как основа материального баланса: 2Са3(РО4)2(T) + 10С(т) + 6SiO2(T) ļ Р4(T)+ 10СО(Г) + 6СаSiO3 Упрощенный вид материального баланса производства фосфора путем восстановления и возгонки его в электрической печи из шихты, состоящей из фосфата кальция (апатит или фосфорит), кокса и песка приведен в табл. 1,3. — 102 — Ǥ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ По математическому балансу определяют расход получаемых продуктов, полупродуктов и отходов, отнесенных к заданной единице продукции (Р4). Исходные данные Сырье — апатитовая руда, содержащая 61,2 % фосфата кальция. Реагенты: кокс, содержащий 80 % углерода, песок, содержащий 95 % SiO2. Основной продукт: фосфор 1000 кг. Побочные продукты: шлак (CaSiO3); оксид углерода (СО). Рассчитаем массу руды, кокса и песка, необходимую для получения 1,000 т фосфора (Р4). Опорные справочные данные: Вещество Р4 Са3(РО4)2 С SiO2 М, г/моль 123,9 310,2 12,01 60,08 По стехиометрическому уравнению на 1 моль Р4 приходится 2 моль Са3(РО4)2, 10 моль С, 6 моль SiO2, следовательно, Масса основных исходных веществ: 2 ⋅ 310,2 ⋅1000 m(Са3(РО4 )2) = = 5007 êкг 123,9 10 ⋅12á 01 ⋅1000 = 969,3 кг 123,9 6 ⋅ 60,08 ⋅1000 = 2909 кг m(SiO2) = 123,9 m(С) = Масса апатитовой руды (61,2% Са3(РО4)2): 5007 ⋅100 m(руды) = = 8181 кг 61,2 — 103 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ m(кокса) = 969,3 ⋅100 = 1212 кг 80,0 Масса песка (95 % SiO2): 2909 ⋅100 m(песка) = = 3062 кг 95,0 Масса продуктов реакции: Опорные справочные данные: Вещество СО CaSiO3 М, г/моль 28,01 116,2 m(СО) = 10 ⋅ 28,01 ⋅1000 = 2261 кг 123,9 6 ⋅116,2 ⋅1000 = 5627 кг 123,9 Масса остатков (отходов производства): m(CaSiO3) = mƍ(руды) = 8181(100 − 61,2) = 3174 кг 61,2 mƍ(кокса) = 969,3(100 − 20) = 242,3 кг 80,0 mƍ(песка) = 2909 (100 − 95) = 153,1 кг 95,0 Таблица 2.3. Материальный баланс производства фосфора Вещество Масса, кг Апатитовая 8181 руда (61,2 % Са3(РО4)2) ω, % Вещество Масса, кг ω, % 65,69 фосфор (Р4) 1000,0 8,03 — 104 — Ǥ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ Приход Расход Кокс(80 %С) 1212 9,73 Оксид углерода (СО) 2261 18,15 Песок (95 % SiO2) 3062 24,58 Шлак (СаSiO3) 5625 45,2 Остаток руды 3174 25,45 Остаток кокса 242,0 1,94 Остаток песка 153,0 1,23 Итого 12455 100,00 Итого 12455 100,00 Задача 4. Расчет теплоты химического превращения. Определить теоретическую теплотворную способность углистого колчедана, содержащего 45%S и 5%С в кДж/кг, зная, что 1 кг чистого колчедана при сгорании дает 7060кДж/ кг, а 1 кг чистого углерода — 32700 кДж/кг. 4FeS2 +11O2 → 2Fe2O3 +SO2 +Q C+O2 → CO2 +Q1 Решение. Чистый колчедан (пирит) содержит 64 • 100/120 = 53.35% S (120 — мол. масса FеS2). Следовательно, рассматриваемая руда содержит: Колчедан 45/53.35 = 0.842 кг, углерод 0.05 кг, пустая порода 0.108 кг. Итого: 1 кг. Q = 7060 • 0.842 + 32700 • 0.05 = 5940 + 1635 = 7575 кДж/ кг Задача 5. Расчет теплового баланса промышленного процесса частичного окисления SO2. Подсчитать тепловой баланс контактного аппарата для частичного окисления SO2 производительностью 25000 м3/ч, — 105 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ если состав газовой смеси: SO2–9%(об), O2–11%(об), N2– 80%(об). Степень окисления 88%. Температура входящего газа 4600С; выходящего — 5800С. Средняя теплоемкость смеси (условно считаем ее неизменной) с = 2052 кДж/(м3 /град). Потери тепла в окружающую среду принимаем 5% от прихода теплоты. Решение. 1 SO2 + O2 → SO3 + 94207 кДж 2 Состав газа приведен в таблице. Исходный После аппарата газ м3/ч газ м3/ч SO2 SO3 N2 O2 2250 – 20000 2750 SO2 2250 0,88=1980 SO3 2250–1980=270 N2 O2 2750-(1980/2)=1760 1980 270 20000 1760 Итого 25000 24010 Приход теплоты. Физическая теплота газа: Q1 = 25000 • 2.052 • 460 = = 23598000 кДж Теплоты реакции: Q2 = 94207 • (22650/22.4) • 0.83 = = 8290216 кДж Всего ΣQпр=31888216 кДж Расход теплоты. Теплота, уносимая отходящими газами Q3 = 24010 • 2.052 • • 580 = 8564000 кДж Qпот = 31888 • 103 • 0.05 = 1594400 кДж Всего ΣQрасх = 30158400 кДж Следовательно, необходимо отвести теплоты: ΣQпр — ΣQрасх=31888216 – 30158400 = 1729816 кДж Данные теплового баланса сведены в таблицу. — 106 — ÐǤ͠ǀǂǬ͠ÐǫǊ͟ǮǁǃǬǃǀǎÐǭǱ͠ǯǮǫǮ֬Ð͠ǪƻǮǰǊ Приход Расход Исходные данные кДж % Конечные данные кДж % Q1 Q2 23598000 829026 73,9 26,1 Q3 Qпот Qотв 28564000 1594400 1729816 89,6 5 5 Итого 31888216 100 Итого 31888216 100 Ϯ͘ϳ͘ʿ̨̡̨̨̨̛̛̬̥̖̬̼̪̣̦̖̦̱̬̭̜̬̯̼̦̯̖̥̱̏́̏̌̍̌͗ ʺ̸̡̡̨̡̨̨̛̛̛̛̯̖̬̣̦̼̜̦̖̬̖̯̖̭̜̣̦̭̦̬̖̯̦̌̌̽̾̐̍̌̌̐ ̨̨̛̪̬̭̯̏̔̏̌̚;̨̨̛̼̬̯̖̥̼̦̱̭̥̯̬̖̦̖̭̯̱̖̦̯̏̍̌̔̌Ϳ͘ Для правильного выбора способов очистки окружающей среды от отходов производства необходимо, прежде всего, провести анализ возможности возникновения отходов в реальном процессе и составить уравнение материального баланса. Например, для изготовления эпитаксиальных кремниевых пластин широко используется водородное восстановление трихлорсилана по уравнению: 2SiHCl3(г)+2H2(г)o2Si(тв)+6HCl. Рассмотрим процесс получения трихлорсилана и составим схему материального баланса производства. Трихлорсилан — это бесцветная дымящаяся и легкозагорающаяся на воздухе жидкость плотностью 1,35 г/см3, кипящая при 31,8 °С и кристаллизирующаяся при –127 °С. Для получения трихлорсилана производится обработка технического кремния хлористым водородом: Si(тв)+3HCl(ж)=SiHCl3(г)+H2(г) Общая технологическая схема получения трихлорсилана приведена на рис.2.8. Реакция проводится обычно при температуре 300 ÷ 400 °С с использованием измельченного кремния. Выход трихлорсилана возрастает при добавлении к хлористому водороду чистого водорода. — 107 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Рис. 2.8. Общая схема получения трихлорсилана Очень важна хорошая очистка поступающей газовой смеси от кислорода и водяного пара, присутствие которых вызывает осаждение продуктов реакции гидролиза на кремний и снижение его реакционной способности. Общая по этапам схема получения трихлорсилана с учетом потерь α на каждой операции приведена на рис. 2.8 продуктов реакции, например, получения 100 кг кремния в табл.2.4. расчет по уравнениям (2.1) и (2.2). Материальный баланс Для получения трихлорсилана производится обработка 100 кг технического кремния хлористым водородом: Si(тв)+3HCl(ж)=SiHCl3(г)+H2(г). Первоначально из 100 кг кускового кремния на фильтрацию тратится 1%, т.е.: — 108 — ÐǤ͠ǀǂǬ͠ÐǫǊ͟ǮǁǃǬǃǀǎÐǭǱ͠ǯǮǫǮ֬Ð͠ǪƻǮǰǊ Таблица 2.4. Материальный баланс процесса получения трихлорсилана (из 100 кг Si) Наименование Количество, кг Cl Si % кг % кг 78,3 335 1. Трихлорсилан 428 21 89,81 2. Твердые отходы синтеза 19,8 30 5,94 3. Кубовой остаток ректификации 13,9 10 1,39 4. Газы при ректификации 93,0 2 1,86 Итого: 100 100 кг 100% →x = 1 кг x кг 1% На синтез SiHCl3 поступает (100–1) = 99 кг кремния. Из них, на твердые отходы синтеза теряется 6%, т.е. 99 кг x кг 100% 6 ⋅ 99 →x = = 5,94 кг 100 6% Оставшиеся (99–5,94) = 93,06 кг поступает на ректификацию, где 2% кремния расходуется на газовые отходы, т.е. 93,06 кг x кг 100% 93,06⋅2 →x = = 5,94 кг 100 2% а 1,5% — на кусковой остаток, т.е. 93,06 кг 100% → x = 1,3959 кг x кг 1,5% — 109 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Следовательно, масса кремния в полученном трихлорсилане составляет (93,06 – 1,8612 – 1,3959) = 89,8 кг. Таблица 2.5. Cl Si Наименование Количество, кг % кг % кг 1 2 3 4 5 6 1. Трихлорсилан 428 21 89,8 78,3 335 2. Твердые отходы синтеза 19,8 30 5,94 – – 3. Кубовой остаток ректификации 13,9 10 1,396 50,22 6,98 4. Газы при ректификации 93,0 2 1,86 7,5 6,98 Итого: 100 348,96 По таблице 2.5 масса хлора в трихлорсилане равна 335 кг, что составляет 96% от первоначальной массы хлора, т.е. x кг 335 кг 100% 335 ⋅100 →x = = 348,96кг 96 96% Из них 2% составляет кусковой остаток, т.е. 348,96 кг x кг 100% 348,96 ⋅ 2 →x = = 6,98 кг 100 2% и 2% (6,98 кг) — газовый отходы при ректификации. Рассчитаем процентное содержание хлора (для табл.1) в кубовом остатке ректификации: 13,9 кг 100% 6,98 ⋅100 →x = = 50,22 кг 13,9 6,98кг x% в газах при ректификации: — 110 — ÐǤ͠ǀǂǬ͠ÐǫǊ͟ǮǁǃǬǃǀǎÐǭǱ͠ǯǮǫǮ֬Ð͠ǪƻǮǰǊ 93,0 кг 100% 6,98 ⋅100 →x = = 7,5 кг 93,0 x% 6,98 кг Энергетический баланс Таблица 2.6 ∆H кДж/моль ∆S Дж/мольК ∆G кДж/моль T, К интервал температур 0 18,83 0 298–1685 HCl(ж) –92,31 186,79 –95,30 298–2000 SiHCl3(г) –657,52 330,95 –617,62 298–1000 0 130,50 0 298–3000 Элемент (вещество) 0 298 Si(тв) H2(г) m (кг) 0 298 100 0 298 428 Si(тв)+3HCl(ж)=SiHCl3(г)+H2(г) М (г/моль) 28,1 36,51 135,61 2,02 Масса трихлорсилана: m(SiHCl3) = m(Si)+m(H)+m(Cl3) => m(H) = = 428–89,81–335 = 3,19 кг Т.к. потерь водорода в реакции нет, то масса выделившегося водорода: m(H2)=3,19Â2 = 6,38 кг. Следовательно, m(HCl) = 3[m(H) + m(Cl)] = 3Â(3,19 + 335/3) = = 344,5 кг Количество вещества: ν(Si) = 100/28,1 = 3,559 моль, ν(HCl) = 344,5/36,51 = 9,436 моль, ν(SiHCl3) = 428/135,61 = 3,156 моль, ν(H2) = 6,38/2,02 = 3,158 моль. — 111 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Энтальпия реакции: 0 0 ∆S =  ν (SiHCl3 ) ⋅ ∆S298 ( H2 ) − (SiHCl3 ) + ν( H2 ) ∆S298 0 0 −  ν ( Si ) ∆S298 (Si ) + ν( HCl ) ∆S298 ( HCl ) = = [3.156 ⋅ 330.95 + 3.158 ⋅130.50] − [9.436 ⋅186.79 + 3.559 ⋅18.83] = = 1456.5972 − 1829.5663 = −372.9691 Дж/моль⋅К Энтропия реакции: 0 0 ∆G =  ν (SiHCl3 ) ⋅ ∆G298 ( H2 ) − (SiHCl3 ) + ν( H2 ) ∆G298 0 0 −  ν ( Si ) ∆G298 (Si ) + ν( HCl ) ∆G298 ( HCl ) = = 3,156 ( −617.652) − 9,436 ( −95,30) = −1049,9579 Свободная энергия Гиббса: кДж/моль Вывод: Т.к. энтальпия данной реакции ∆H < 0, то, следовательно, реакция получения трихлорсилана является экзотермической, т.е. протекает с выделением тепла. Т.к. энтропия реакции ∆S < 0, то, следовательно, данный процесс обратим. Т.к. свободная энергия Гиббса так же ∆G < 0, то это свидетельствует о том, что данная реакция идет. ˇ̸̨̨̨̨̡̨̨̨̛̬̥̪̬̖̭̯̣̖̦̯̖̯̪̱̬̭̜̬̯̖̌̔̌̏́̌̏̌̍͘ Отчёт выполняется по результатам выполнения курсовой работы, тема работы (технологический процесс) должна быть согласована с преподавателем. Отчет должен содержать: 1. Качественную технологическую схему выбранного процесса (если с участием жидкой фазы, то вместо качественной технологической схемы необходимо представить шламовую схему процесса), на которой должен быть указан выход продукта в том или ином агрегатном состоянии на той или иной технологической операции с указанием возможных технологических потерь продукта. 2. Расчет материального и энергетического баланса конкретного технологического процесса с использованием совре— 112 — ÐƭǪƽǪǆǀÐƽǁǎÐǯǪǂǮǯǰǮǎǰǬǁǋǃǮƼǮÐ͠ǬǇǬǃǀǎ менной классификации процессов химической технологии. 3. Количественную схему, разработанную на основе проведенных расчетов материального и энергетического баланса, избранного технологического процесса. 4. Выводы с необходимыми пояснениями и обоснованиями. Ϯ͘ϴ͘ʯ̸̨̨̨̨̛̛̣̭̥̭̯̯̖̣̦̬̖̹̖̦̌̔̌̔́̌́̽̐́͘ Задача 1. Первая стадия получения серной кислоты в промышленности, дающая наибольшее количество вредных выбросов в атмосферу — обжиг пирита, минерала, отвечающего формуле FeS2. Определите массовые доли (в процентах) железа и серы в пирите. Рассчитайте массу серы, которая содержится в 1 т пирита. Задача 2. Рассчитайте объем, который занимает (при н.у.) порция газа, необходимого для дыхания, если в этой порции содержится 2,69 . 1022 молекул этого газа. Какой это газ? Задача 3. Определить количество теплоты, выделяющейся при обжиге 1 т FеS2, содержащего 38% серы, если степень выгорания серы из колчедана х=0.96. Процесс горения колчедана описывается следующим суммарным уравнением FеS2 + 11О2 = 2Fе20з + 8SO2 + Q Теплоты образования в кДж/моль: Fе203–821.3; S02– 296.90; FеS2–177.4. Чистый FеS2 содержит 53.35% серы и 46.65% железа. Задача 4. Составить тепловой баланс генератора водяного газа при газификации 1 т кокса, содержащего 93% (масс.) С; 4% (масс.) золы и 3% (масс.) Н20 и подаче 1575 кг водяного газа на 1 т кокса. При этом образуется 2190 кг водяного газа, содержащего 89.9% (масс.) СО, 1.94% (масс.) С02 и 8.16% (масс.) Н2. Температура водяного газа на выходе из генератора 1000°С, температура подаваемого кокса 250С и водяного пара 1000С. — 113 — ǞǁǪǫǪÐ ÐǨǱǃƽǪǂǬǃǰǪǁǋǃǊǬÐƿǪǭǮǃǊÐ͟͠ǀ͠ǮƽǊÐǀÐǀǲÐ͟͠ǀǂǬǃǬǃǀǬ Задача 5. Рассчитать материальный и энергетический баланс процесса получения эпитаксиальных слоев кремния парофазной эпитаксией с химическим осаждением (ПФЭХО). Технологическая схема процесса представлена на рисунке 2.9: Рис.2.9. Технологическая схема процесса парофазной эпитаксии. — 114 — ǍưǙǚǙÍ Í Í ǒƙƣƝǎÍ̢ǒǕǑǒǌǑƥạ̌ÍǓǔƝǑƠƝǓƥÍ ǐǋǖǎǐǋǖƝơǎǕǏǒǍǒÍǒǓƝǕǋǑƝƩÍ ǓǔǒƠǎǕǕǒǌÍǓǔƝǔǒƚǑǒ֏ÍǕǔǎƚƥ В результате освоения главы 3 бакалавр должен: Знать: – основные принципы математического моделирования процессов природной среды (теорию подобия, метод анализа размерностей). Уметь: – выбирать адекватную математическую модель для описания процессов защиты окружающей среды от загрязнений. Владеть: – методами теории подобия и методом анализа размерностей при теоретическом рассмотрении процессов природной среды. ϯ͘ϭ͘ʤ̶̸̨̨̨̨̡̨̛̛̛̛̦̣̪̬̖̭̭̪̖̬̖̦̭̣̖̭̯̙̖̦͕̌̐́̏̌̏̌̔̏́ ̛̛̛̦̖̬̥̭̭̼̾̐̌͘ Цель проведения процессов любой технологии — это изменение свойств перерабатываемых материальных тел за счет взаимодействия между собой и окружающей природной средой. Это взаимодействие приводит к перераспределению массы и энергии между отдельными частями системы и между системой и окружающей средой. Конкретные формы таких взаимо— 115 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð действий неодинаковы для различных процессов и определяются их физической природой. При расчете любого технологического процесса согласно[5.6.9] необходимо определить потоки количества движения, энергии и массы между отдельными частями системы и окружающей средой. Напишем уравнения переноса количества движения (3.1), энергии (3.2) и массы (3.3) в виде: ∂ω ∂ω z ∂ω ∂ω z 1 ∂p + ωx z + ωy + ω z z = ν∇2ω z + Z − ∂x ∂y ∂z ∂τ ρ ∂z (3.1) ∂2 ω z ∂2 ω z ∂2 ω z — оператор Лапласа, Z — проек+ + ∂ x2 ∂y 2 ∂z2 ция массовой силы, отнесенной к единице массы жидкости или газа, на ось z, ν — вязкость жидкости или газа, p — давление жидкости или газа.  ∂t ∂t ∂t  q ∂t = a∇2t −  ω x + ωy + ωz  + r (3.2)  ∂τ ∂x ∂y ∂z  ρc p где ∇2ω z = где a — коэффициент температуропроводности, cp — теплоемкость жидкости или газа при постоянном давлении, qr — мощность источника теплоты на единицу объема жидкости или газа, ρ — плотность жидкости или газа. ∂ci ∂c ∂c ∂c   = Di ∇2ci −  ω x i + ω y i + ω z i  + riυ  ∂τ ∂x ∂y ∂z  (3.3) где Di — эффективный коэффициент диффузии, ci — концентрация компонента в смеси, riv — скорость образования компонента i в единице объема. Приведенные уравнения тождественны по форме. Первые слагаемые в правой части этих уравнений, заключенные в круглые скобки, определяют, соответственно, скорость переноса количества движения, энергии и массы за счет конвективного механизма, вторые — за счет молекулярного механизма, а третьи характеризуют мощность внешнего источника. Одинаковая форма уравнений, описывающих рассматриваемые процессы, указывает на аналогию полей скоростей, темпера— 116 — ÐǡǮƽǬǁǀ͠ǮǫǪǃǀǬÐǰǀ͟ǮǫǊǲÐ͟͠ǮǅǬǯǯǮǫ тур и концентраций в движущихся средах. Различие этих полей обусловливается разными мощностями внешних источников (если они имеются), а также значениями коэффициентов переноса v, a, D для рассматриваемой среды. При отсутствии внешних источников количества движения, энергии и массы и численном равенстве коэффициентов переноса (ν = а = D) уравнения становятся идентичными. Это означает, что при идентичных начальных и граничных условиях поля скоростей, температур и концентраций совпадают. При отсутствии внешних источников во всех случаях имеет место подобие полей концентраций и температур в неподвижных средах (ωx = = ωy = ωz = 0), поскольку получающиеся при этом уравнения отличаются только значениями коэффициентов а и D. Эти обстоятельства используются для изучения процессов переноса массы и энергии с помощью методов электродинамической и электротепловой аналогии. Существенно, что конвективные члены уравнений переноса идентичны. Чем интенсивнее движение жидкости или газа, тем меньше вклад молекулярного переноса по сравнению с конвективным. Поэтому с увеличением скорости движения жидкости или газа различие между полями скоростей, температур и концентраций, обусловленное различием коэффициентов молекулярного переноса, должно убывать. Из данного факта можно сделать фундаментальный вывод, что имеется глубокая аналогия процессов переноса количества движения, энергии и массы. Рассмотрим количественно интерпретацию этой аналогии. ϯ͘Ϯ͘ʺ̵̶̨̨̨̨̨̛̛̛̖̣̬̦̖̯̪̼̪̬̖̭̭̔̏̌̏̏͘ Рассмотренные уравнения описывают явления переноса количества движения, энергии и массы в произвольной точке подвижной среды. Они не содержат никаких специальных ограничений относительно конкретных особенностей процессов или физических свойств участвующих в них материальных объектов кроме тех, которые вытекают из использованных при их выводе линейных соотношений (3.4), (3.5) и (3.6). — 117 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð dω (3.4) dn στ — касательное напряжение, равное силе трения, приходящейся на единицу поверхности, μ, ω, n — динамический коэффициент вязкости жидкости (газа), скорость потока жидкости или газа и направление нормали соответственно, тогда dω/dn — градиент скорости σ τ = −µ ∂ci (3.5) ∂n ∂t (3.6) q = −λ ∂n где ji — поток компонента, отнесенный к единице поверхности, кмоль/(м2с), ci — концентрация, кмоль/м3, q — поток теплоты, отнесенный к единице поверхности, Вт/м2, t — температура, К. Следовательно, эти уравнения применимы к любым процессам. При практическом использовании уравнений переноса на изменения переменных величин налагаются ограничения, вытекающие из свойств рассматриваемого конкретного процесса. Так, любой процесс протекает в системе с определенной геометрической характеристикой. Обычно обрабатываемая среда и объекты заключены в аппарат, размеры которого ограничивают пределы изменения координат в уравнениях переноса. Определяющими факторами являются также физические характеристики системы. Они могут быть заданы в виде чисел — значений соответствующих физических констант или в виде уравнений, выражающих зависимость физических свойств от влияющих на них параметров. Перечисленные параметры определяют геометрические и физические свойства системы. Кроме них должны быть заданы условия взаимодействия системы с окружающей средой на границах системы (граничные условия) и условия, характерные для того момента, который принимается за начало отсчета (начальные условия). Если объектом процесса является жидкость или газ, а границей системы — стенки аппарата, в котором проводится процесс, то неji = − Di — 118 — ÐǡǮƽǬǁǀ͠ǮǫǪǃǀǬÐǰǀ͟ǮǫǊǲÐ͟͠ǮǅǬǯǯǮǫ обходимо определить условия взаимодействия жидкости или газа со стенками. Это означает, что условия, определяющие перенос количества движения, энергии и массы от жидкости или газа к стенке (или в противоположном направлении), должны быть заданы в виде чисел или зависимостей. Начальные условия включают значения всех существенных параметров в момент, принимаемый за начало отсчета. Геометрические и физические характеристики системы совместно с граничными и начальными условиями содержат комплекс сведений, выделяющих данный конкретный процесс из класса процессов, описываемых соответствующими уравнениями переноса. Так, если объектом исследования или расчета является движение жидкости; в трубе, то должны быть заданы диаметр, длина трубы и ее форма (геометрические характеристики), свойства жидкости (физические характеристики), граничные условия (для вязкой жидкости — равенство нулю составляющих скорости на границе со стенкой) и начальные условия (например, профиль скоростей на входе в трубу). Дифференциальные уравнения переноса, геометрические и физические характеристики системы, граничные и начальные условия составляют математическое описание процесса. Его можно использовать для расчета конкретного процесса. Такой расчет заключается в интегрировании соответствующего уравнения переноса (или системы уравнений) с учетом перечисленного выше комплекса сведений, характеризующих данный конкретный объект. Вследствие сложности уравнений переноса их интегрирование представляет большие трудности, однако оно возможно за счет упрощения этих уравнений путем исключения из них членов малой значимости и использования методов численного интегрирования с помощью персональных компьютеров. Результатом расчетов является получение числовых значений искомых величин. Специфика инженерных задач заключается в том, что они редко бывают определенными, т. е. обычно число величин, которые должны быть найдены в результате расчета, превышает число уравнений связи между переменными. В связи с этим, чтобы сделать задачу определенной, рядом величин прихо— 119 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð дится задаваться. Такая процедура связана с принятием «волевых» решений, поскольку указанные величины чаще всего могут изменяться в значительных пределах. Между тем в области допустимых значений рассматриваемых величин имеется лишь определенное их сочетание, обеспечивающее наилучшие условия проведения процесса. Чтобы найти это сочетание, необходимо проделать серию расчетов при изменении параметров процесса в области их допустимых значений. Исследование влияния параметров процесса на его результаты, осуществляемое путем решения уравнений, составляющих математическое описание процесса, называется математическим моделированием. Математическое описание воспроизводит наиболее существенные стороны процесса. Поэтому представляется возможным, варьируя отдельные параметры, получать расчетным путем сведения о влиянии этих вариаций на показатели процесса. Так, например можно изменять параметры технологического режима (температуру, давление, состав, скорость движения материальных потоков и т. д.), получая сведения об их влиянии на ход процесса. Кроме того, можно варьировать размеры аппарата. Это дает возможность выяснить, как изменяются показатели процесса при переходе от небольшого аппарата к большому (от модели к крупному объекту). Поскольку расчеты связаны с трудоемкими вычислениями, моделирование выполняется с помощью специальных компьютерных программ. Метод математического моделирования позволяет исследовать процессы в широком диапазоне изменения влияющих на них параметров и определять оптимальные условия их проведения. Благодаря большой познавательной силе этого метода математическое моделирование и оптимизация процессов любой технологии выделилась в самостоятельную научную дисциплину. Важными достоинствами метода математического моделирования также являются возможность изучения сложных процессов без создания дорогостоящих и трудоемких в обслуживании опытных установок и возможность исследования режимов, которые нельзя или трудно реализовать, исходя из требований техники безопасности, а также по экономическим соображениям. — 120 — ÐǡǮƽǬǁǀ͠ǮǫǪǃǀǬÐǰǀ͟ǮǫǊǲÐ͟͠ǮǅǬǯǯǮǫ При исследовании сложных процессов необходимо иметь в виду, что различные явления переноса оказывают влияние друг на друга, которое часто весьма трудно учесть расчетным путем с достаточной точностью. Так, изменение температуры в процессе переноса теплоты приводит к изменению физических свойств жидкости, что влияет на поле скоростей. Изменение же поля скоростей влияет на поле температур. Это существенно усложняет математическое описание процесса. В связи с этим при математическом моделировании сложного процесса приходится пренебрегать некоторыми факторами, а затем в результаты вносить соответствующие коррективы, что не всегда просто сделать. Другая возможность заключается в. использовании для описания некоторых свойств моделируемого объекта закономерностей, полученных на физических моделях и учитывающих факторы, которые иным путем учесть затруднительно или невозможно. По изложенным соображениям в современных технологиях применяются как методы математического, так и физического моделирования. Под методом физического моделирования понимается изучение свойств объектов на моделях. Применение физического моделирования обусловлено необходимостью создания новых крупных промышленных производств. Чем крупнее создаваемая установка, тем больше риск принятия ошибочного или неточного решения и тем, следовательно, более надежной должна быть информация, используемая при математическом описании объекта. Такую информацию должен давать метод физического моделирования. Относительная роль и взаимосвязь методов физического и математического моделирования при исследованиях — в определенной мере вопрос неоднозначный, зависящий от уровня развития вычислительной техники, прикладной математики и техники экспериментальных исследований. Еще сравнительно недавно (20–30 лет назад до всеобщей компьютеризации) физическое моделирование было основным методом перехода «от пробирки к заводу». Исследование процесса — 121 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð на более или менее крупных опытных и опытно-промышленных установках являлось необходимым этапом создания новых производств. Между тем, физическое моделирование не всегда обеспечивает соблюдение необходимых условий создания уменьшенных моделей, точно воспроизводящих свойства сложных процессов. Это было причиной многих затруднений при создании и освоении новых производств. Однако, на современном этапе развития науки таких трудностей в значительной мере можно избежать благодаря использованию физического моделирования в комбинации с математическим, причем роль последнего непрерывно возрастает в связи с прогрессом вычислительной техники и прикладной математики. ϯ͘ϯ͘ʽ̴̸̨̡̨̨̨̨̛̛̛̛̭̦̼̖̭̥̖̣̬̦̏̐̔̏̌́̚ ;̨̨̨̛̛̯̖̬̪́̔̍́Ϳ͘ Экспериментальные исследования процессов и аппаратов, в которых эти процессы проводятся, выполняются обычно на моделях, а не на натурных объектах. Поэтому необходимо знать, каким условиям должна удовлетворять модель и как должны проводиться эксперименты, чтобы обеспечивалось получение результатов, адекватно отражающих свойства изучаемого объекта. На эти вопросы отвечает теория подобия. Исходной предпосылкой теории подобия является то, что подобные явления должны описываться одинаковыми уравнениями. Общие закономерности различных классов процессов описываются, как известно, уравнениями переноса. Так, процессы, связанные с движением ньютоновских жидкостей, описываются уравнениями Навье — Стокса и неразрывности. Следовательно, эти уравнения должны входить в математическое описание любого аэро-гидромеханического процесса. Математическое описание тепловых процессов, в которых участвуют текучие среды, включает уравнение Фурье — Кирхгофа, уравнения Навье — Стокса и уравнения неразрывности. Описание закономерностей процессов массопереноса включает уравнения переноса массы, движения и неразрывности. Наконец, — 122 — ÐǣǯǃǮǫǊÐǄǀƿǀǆǬǯǭǮƼǮÐǂǮƽǬǁǀ͠ǮǫǪǃǀǎÐǰǬǮ͠ǀǎÐ͟ǮƽǮƻǀǎ математическое описание процессов, в которых одновременно происходит перенос энергии и массы (процессы тепломассопереноса), включает все перечисленные уравнения. Однако эти уравнения описывают общие закономерности процессов соответствующих классов. В практике же всегда приходится иметь дело с конкретными объектами моделирования. Поэтому прежде всего необходимо сформулировать условия однозначности — условия, выделяющие рассматриваемое явление из общего класса явлений. К ним относится геометрическая форма и размеры системы существенные для рассматриваемого процесса, физические свойства жидкости или газа, начальные условия (начальные скорости, температуры и т. д.), а также граничные условия, характеризующие свойства жидкости или газа на границах системы. Группа подобных явлений должна, очевидно, иметь подобные условия однозначности, т. е. геометрическая форма систем должна быть одинаковой, а их размеры, физические свойства жидкостей, газов, скорости и другие существенные величины должны находиться в постоянных соотношениях. Кроме того, в постоянных соотношениях должны находиться все характеристики потоков (физические свойства, скорости) в сходственных точках образца и модели. Это значит, что между образцом и моделью должно быть геометрическое подобие, подобие полей физических величин, а также начальных и граничных условий. Соотношения между сходственными величинами для образца и модели характеризуются значениями констант подобия. Константа подобия — это отношение однородных сходственных величин для образца и модели. Так, константа геометрического подобия представляет собой отношение сходственных геометрических размеров образца и модели. Например, если рассматривается движение жидкости в трубах, то l′ D′ , где l’ и l’’, D’ и D’’ — длины и диаметры образца al = = l ′′ D ′′ и модели (здесь и ниже одним штрихом обозначены величины, относящиеся к образцу, а двумя — к модели). Константа подобия физических величин определяет отношение значений физических констант в сходственных точках — 123 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð образца и модели в соответственные моменты времени. Наприρ′ µ′ - константа подобия плотностей, aµ = — конмер, aρ = ρ′′ µ′′ станта подобия вязкостей. При моделировании процессов, связанных с изменением свойств системы во времени, должно соблюдаться временное подобие. Это значит, что частицы в образце модели, находящиеся в сходственных точках, проходят геометрически подобные траектории за промежутки времени, находящиеся в постоянτ′ ных соотношениях, т. е. aτ = τ′′ При геометрическом и временном подобии соблюдается подобие полей скоростей, температур, концентраций и других ω′ c′ t′ ;a = ;a = физических величин, т. е. aω = — константы. ω′′ c c ′′ t t ′′ Для двух сравниваемых подобных систем каждая константа подобия имеет постоянное значение. Константы подобия показывают масштаб соответствующих величин в образце по сравнению с моделью. Из сформулированных выше условий подобия вытекает идентичность отношений двух значений какого-либо свойства образца и двух значений этого же свойства модели для сходственных условий. Так, для двух подобных труб одинаково D ′ D ′′ отношение их длин к диаметрам, т. е. = = Гi, где Гi — l′ l ′′ инвариант, называемый также симплексом геометрического подобия. С помощью все подобные геометрические размеры выражаются в относительных величинах, например по отношению к длине. Аналогичный смысл имеют инварианты физического, временного и других видов подобия. При изменении размеров и свойств модели инварианты подобия, в противоположность константам подобия, не изменяются. С помощью констант подобия все величины, характеризующие образец, могут быть выражены через соответствующие величины для модели: — 124 — ÐǣǯǃǮǫǊÐǄǀƿǀǆǬǯǭǮƼǮÐǂǮƽǬǁǀ͠ǮǫǪǃǀǎÐǰǬǮ͠ǀǎÐ͟ǮƽǮƻǀǎ l ′ = all ′′;ρ′ = aρρ′′;µ ′ = aµ µ ′′; τ ′ = aτ τ ′′ (3.7) и т. д. Рассмотренные условия подобия геометрических, физических и других характеристик образца и модели являются необходимыми, но недостаточными условиями для создания модели. Достаточные условия выявляются, исходя из того, что процессы в образце и модели должны описываться одними и теми же дифференциальными уравнениями. Рассмотрим основные положения теории подобия на примере гидромеханических процессов. ϯ͘ϯ͘ϭ͘ʿ̵̸̵̶̨̨̨̡̨̨̛̛̛̛̖̬̥̖̦̖̭̪̬̖̭̭̔̍̐̔̌̏͘ Для любого процесса данного класса при ламинарном движении жидкости справедливо уравнения Навье — Стокса (3.1). Поскольку при моделировании какого-либо аэро-гидромеханического процесса в модели может использоваться иная жидкость или газ, чем в образце, то числовые коэффициенты в уравнениях Навье — Стокса, вообще говоря, получаются различными. Между тем подобие процессов в образце и модели требует, чтобы уравнения, описывающие эти процессы, были одинаковыми. Для выяснения того, при каких условиях это возможно, напишем уравнения Навье — Стокса для образца и модели (так как уравнения движения вдоль осей координат х, у и z идентичны, рассмотрим только уравнения, относящиеся к движению вдоль оси x):  ∂2 ω ′ ∂ω x′ ∂ω x′ ∂ω x′ ∂ω x′ ∂2 ω x′ ∂2 ω x′  1 ∂ρ′ x  + g′ − + ω x′ + ω y′ + ω z′ = ν′  + + 2 2 2 ∂x ′ ∂y ′ ∂z ′ ρ ′ ∂x ′ ∂τ ′  ∂ ( x ′ ) ∂(y′) ∂ ( z ′ )  (3.8)  ∂2 ω ′′ ∂ω′′x ∂ω ′′ ∂ω ′′ ∂ω ′′ ∂2 ω x′′ ∂2 ω x′′  1 ∂ρ′′ x  + g ′′ − + ω x′′ x + ω y′′ x + ω z′′ x = ν′′  + + 2 2 2 ∂τ′′ ∂x ′′ ∂y ′′ ∂z ′′ ρ′′ ∂x ′′  ∂ ( x ′′ ) ∂ ( y ′′ ) ∂ ( z ′′ )  (3.9) Примем, что единственной массовой силой является сила тяжести. Поэтому вместо величины X, входящей в уравнение (3.1), подставлено ускорение свободного падения g. Заме— 125 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð нив теперь все величины в уравнении (3.8) на соответствующие величины для модели с помощью соотношений (3.7), получаем: ∂ω ′′ ∂ω x′′ ∂ω ′′  aω ∂ω x′′ aω2  + ω ′′ x + ω ′′y + ω z′′ x  = ∂y ′′ ∂z′′  aτ ∂τ ′′ al  x ∂x′′  ∂2ω ′′ a p 1 ∂ρ′′ ∂2ω x′′ ∂2ω x′′  x (3.10)   + ag g ′′ − + + 2 2 2 a pal ρ′′ ∂x′′  ∂ ( x′′ ) ∂ ( y ′′ ) ∂ ( z′′ )  Чтобы уравнения (3.10) и (3.9) были одинаковы, все числовые коэффициенты, содержащие константы подобия, должны быть равны, т. е. ap aω aω2 aνaω = = 2 = ag = aρal aτ al al = aνaω al2 Разделив все члены этого равенства на aω2 имеем: al ap a a al a = g2 l = = ν =1 aω aτ aω aρaω2 aω al Все соотношения в последнем выражении — безразмерные величины. После подстановки в них значений констант подобия, находим: (ω ′′ ) ; p′ = p′′ ; ω ′l ′ = ω ′′l ′′ ω ′τ ′ ω ′′τ ′′ ( ω ′ ) = = ; (3.11) l′ l ′′ g ′l ′ g ′′l ′′ ρ′ ( ω ′ )2 ρ′′ ( ω ′′ )2 ν′ ν′′ Выполненное преобразование уравнения (3.8) называется подобным. Физический смысл полученного результата (3.11) заключается в том, что для обеспечения подобия двух гидродинамических процессов недостаточно геометрического подобия и подобия полей всех существенных величин; эти величины должны, кроме того, находиться в таких соотношениях, чтобы обеспечивалось равенство безразмерных комплексов, определяемых выражениями (3.11). Следовательно, эти комплексы являются критериями подобия. Они имеют ωτ определенные обозначения и названия: = Ho — критерий l 2 2 — 126 — ÐǣǯǃǮǫǊÐǄǀƿǀǆǬǯǭǮƼǮÐǂǮƽǬǁǀ͠ǮǫǪǃǀǎÐǰǬǮ͠ǀǎÐ͟ǮƽǮƻǀǎ гомохронности; p ω2 = Eu — кри= Fr — критерий Фруда; gl ρω2 ωl = Re — критерий Рейнольдса. Наиболее упоν требляемые критерии подобия приведены в табл.3.1. Согласно (3.11), для обеспечения подобия критерии подобия для образца и модели (и таким образом, для всей группы подобных процессов или явлений) должны быть численно одинаковы. Это положение составляет содержание первой теоремы подобия, которая утверждает, что подобные между собою явления имеют одинаковые критерии подобия. Чтобы уяснить физический смысл критериев подобия, следует обратить внимание на то, что все члены исходного уравнения (3.8) имеют размерность [м/с2] и выражают действующие в жидкости силы, отнесенные к единице массы жидкости [м/с2 = =(кг м/с2)/кг=Н/кг]. Первый член dω’/dr’ в левой части уравнения (3.8) пропорционален инерционной силе, обусловленной изменением скорости во времени, а последующие три члена определяют инерционные силы, обусловленные изменением скоростей в пространстве. Первый член в правой части уравнения (3.8) характеризует силу вязкого трения в жидкости, второй — силу тяжести, а третий — силу давления. Поэтому отношения констант подобия и следующие из них критерии подобия (3.11) представляют собой отношения сил, действующих в жидкости: критерий Но — отношение инерционных сил, обусловленных нестационарностью процесса, к инерционным силам, обусловленным изменением скоростей в пространстве; критерий Fr — отношение силы инерции к силе тяжести; критерий Eu — отношение сил давления и инерции; критерий Re — отношение инерционной силы к силе вязкого трения. Условие подобия, заключающееся в равенстве критериев подобия для образца и модели, означает, следовательно, подобие силовых полей. Таким образом, теория подобия гидромеханических процессов требует, чтобы кроме соблюдения геометрического подобия и подобия физических свойств в любых сходственных точках образца и модели было бы одинаковым терий Эйлера; — 127 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð отношение инерционной силы — к силе вязкого трения, инерционной силы — к силе тяжести и т. д. Для группы подобных явлений, протекающих в геометрически подобных системах, критерии подобия имеют конкретные числовые значения. Критерии подобия, относящиеся к другой группе подобных явлений, имеют иные постоянные значения. Это обусловлено различием геометрических, физических и режимных параметров. Так, можно выделить группу подобных явлений, моделирующих процесс движения воды в трубопроводе определенных размеров. Данная группа характеризуется определенными значениями критериев Но, Fr, Eu, Re и симплекса геометрического подобия Гl. Если вместо воды в рассматриваемом трубопроводе будет транспортироваться другая жидкость, т. е. при прочих равных условиях изменятся физические свойства жидкости, то такой процесс будет характеризоваться иным набором числовых значений критериев подобия. Эти значения определяют новую группу подобных процессов. Аналогичная ситуация возникнет, если изменить размеры трубопровода или скорость движения жидкости. При этом также получится новый набор значений критериев подобия и симплекса геометрического подобия. Отсюда следует, что изменение любого свойства моделируемого объекта (размеров, формы, физических свойств, скоростей и т. д.) приводит к изменению числовых значений критериев подобия для данного объекта и всей группы ему подобных. Однако вид дифференциальных уравнений, описывающих явления в объекте при указанных изменениях, остается одинаковым. На этом основании можно утверждать, что математическое описание указанных явлений может быть представлено в форме функциональной зависимости между критериями подобия: f ( Ho, Fr, Eu, Re, Γ l ) = 0 (3.12) Иными словами, решение дифференциальных уравнений, описывающих процесс и связывающих влияющие на этот процесс переменные величины, можно представить в виде зависимости между критериями подобия. Это положение известно как вторая теорема подобия. Конкретный вид зависимости — 128 — ÐǣǯǃǮǫǊÐǄǀƿǀǆǬǯǭǮƼǮÐǂǮƽǬǁǀ͠ǮǫǪǃǀǎÐǰǬǮ͠ǀǎÐ͟ǮƽǮƻǀǎ между критериями подобия определяется геометрическими, физическими и режимными характеристиками моделируемого объекта и обычно устанавливается на основе обобщения опытных данных. Таким образом, для любых гидромеханических процессов вместо функциональной зависимости между отдельными физическими величинами, входящими в уравнения Навье — Стокса, рассматривается связь между критериями подобия. Критерии подобия используются здесь в качестве обобщенных переменных величин. Это имеет очень важное практическое значение, поскольку для экспериментального определения зависимости (3.12) в явном виде можно варьировать критерии подобия, а не все физические величины в отдельности. Практические задачи обычно сводятся к определению одних свойств системы по известным другим ее свойствам. Например, требуется определить перепад давления ∆р в трубопроводе определенных размеров при заданных физических свойствах и скорости движения жидкости. При такой постановке задачи в условия однозначности включаются размеры трубопровода, свойства жидкости и скорость ее движения. Эти величины входят в критерии Re, Fr и Но, а также в симплекс геометрического подобия. Критерии подобия, составленные из величин, которые содержатся в условиях однозначности, называются определяющими. В критерий Eu входит искомая величина ∆р, отсутствующая в условиях однозначности. Такие критерии подобия называются определяемыми. В рассматриваемом примере определяемым является критерий Eu, поэтому зависимости (3.12) следует придать вид: Eu = f ( Fr, Re, Ho, Γ l ) (3.13) При известных Re, Fr, Но и Гl из зависимости (3.13) однозначно определяется значение Eu. Таким образом, для обеспечения подобия достаточно равенства определяющих критериев, относящихся к образцу и модели. Это положение составляет сущность третьей теоремы подобия. При численно одинаковых определяющих критериях равенство определяемых критериев получается как следствие. — 129 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð Положения, устанавливаемые тремя теоремами подобия, справедливы для любых процессов. Они используются как для постановки экспериментальных исследований, так и для математического описания процессов. В практических задачах определяющие критерии имеют различную значимость. Это является следствием неодинакового влияния сил, действующих, например, в жидкости, на конкретный процесс. Например, при установившемся движении жидкости по горизонтальному трубопроводу из перечисленных выше — см. зависимость (3.13) — определяющих критериев наибольшую роль играют Re и Гl, так как основное значение в данном случае имеют инерционные силы и силы вязкого трения, отношение которых входит в критерий Re, а Гl характеризует размеры трубопровода. Критерий Но может быть исключен, поскольку движение установившееся, а критерием Fr можно пренебречь вследствие того, что сила тяжести мала по сравнению с силами инерции и вязкого трения. Таким образом, зависимость (3.13) сводится к виду: Eu = f ( Re, Γ l ) = 0 Моделирование на основе приведенной зависимости является приближенным. Однако погрешность, возникающая за счет пренебрежения влиянием критерия Fr, невелика и приемлема для технических целей. В рассматриваемом случае задача экспериментального исследования сводится к установлению для объектов заданной формы (Гl = const) явного вида зависимости Eu = f(Re). Такое исследование на модели можно проводить с той же жидкостью, что и в прототипе, изменяя соответственно скорость. Для моделирования необходимо равенство значений Re и Гl, относящихся к образцу и модели. Из равенства значений Re вытекает условие, что поля скоростей в образце и модели должны быть связаны соотношением ω ′ l ′ ν′ = . Следовательно, вязкости жидкостей, используемых ω ′′ l ′′ν′′ в образце и модели, и скорости их движения должны находиться в определенных соотношениях, зависящих от размеров образца и модели. Если модель является 0,01 частью натуры — 130 — ÐǣǯǃǮǫǊÐǄǀƿǀǆǬǯǭǮƼǮÐǂǮƽǬǁǀ͠ǮǫǪǃǀǎÐǰǬǮ͠ǀǎÐ͟ǮƽǮƻǀǎ (l’/l’’ = 100), то при одинаковых скоростях ω’ = ω’’ кинематический коэффициент вязкости жидкости в модели должен быть в 100 раз меньше, чем в образце, а при использовании одной и той же жидкости (ν’ = ν’’) скорость в модели должна быть в 100 раз больше, чем в образце. Такие условия не всегда могут быть выполнены точно, поэтому часто моделирование является приближенным. Кроме приведенных выше критериев подобия в ряде случаев оказывается целесообразным использовать их сочетания — производные критерии подобия. Например, чтобы учесть влияние силы тяжести и силы вязкого трения, из критериев Re2 gl3 Fr и Re можно получить критерий Галилея, Ga = = 2 , Fr ν в который не входит скорость. Если действие силы тяжести обусловливается различием плотности жидкости, то в критерий Галилея вводится безразмерное отношение изменения плотности ∆ɏ к ее значению ɏ и получается новый критерий подобия — критерий Архимеда: ∆ρ gl3 ∆ρ (3.14) Ar = Ga = 2 ρ ν ρ Под величиной l, входящей в критерии Re, Fr и Но понимается так называемый определяющий размер, т. е. такой размер системы, который определяющим образом влияет на распределение скоростей в объеме жидкости. Выбор его для конкретных систем будет рассмотрен ниже. ϯ͘ϯ͘Ϯ͘ʿ̵̶̨̨̨̨̨̛̖̯̖̪̣̼̪̬̖̭̭̔̍̏̏͘ Критерии подобия тепловых процессов выводятся из уравнения Фурье — Кирхгофа так же, как критерии подобия гидромеханических процессов из уравнения Навье — Стокса. При отсутствии источников теплоты уравнения Фурье — Кирхгофа для образца и модели имеют вид:  ∂2 t ′ ∂t ′ ∂t ′ ∂t ′ ∂t ′ ∂2 t ′ ∂2t ′  (3.15)  + ω x′ + ω y′ + ω z′ = a′  + + 2 2 2 ∂τ ′ ∂x ′ ∂y ′ ∂z ′  ∂ ( x ′ ) ∂(y′) ∂ ( z ′ )  — 131 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð  ∂2t ′′ ∂t ′′ ∂t ′′ ∂t ′′ ∂t ′′ ∂2t ′′ ∂2t ′′   + ω x′′ + ω y′′ + ω z′′ = a ′′  + + 2 2 2 ∂τ ′′ ∂x ′′ ∂y ′′ ∂z ′′  ∂ ( x ′′ ) ∂ ( y ′′ ) ∂ ( z ′′ )  Выражая величины, относящиеся к образцу (обозначены одним штрихом) через величины, относящиеся к модели (обозначены двумя штрихами) с помощью констант подобия и преобразуя уравнение (3.15), имеем:  ∂2t ′′ at ∂t ′′ aω at  ∂t ′′ ∂t ′′ ∂t ′′  aa at ∂2t ′′ ∂2t ′′   + ω x′′ + ω y′′ + ω z′′ = 2 a ′′  + +   2 2 2 ∂x ′′ ∂y ′′ ∂z ′′  aτ ∂τ ′′ al  at  ∂ ( x ′′ ) ∂ ( y ′′ ) ∂ ( z ′′ )  Отсюда условие подобия тепловых процессов: at aω at aaat = = 2 aτ al al Из равенства at aaat aa = 2 получаем a 2 t = 1 или aτ al al a ′τ ′ ( L′ ) 2 = a′′τ ′′ ( L′′ )2 = FoT (3.16) т. е. критерий Фурье, характеризующий условия распространения теплоты теплопроводностью при изменении температуры во времени. Используя равенство aa at aaat = 2 , имеем a 2 t = 1 или aτ al al ω ′t ′ ω ′′t ′′ = = PeT a′ a′′ (3.17) Критерий подобия тепловых процессов Рет называется критерием Пекле и представляет собой отношение скоростей переноса теплоты в движущейся среде за счет течения жидкости (конвективный механизм) и теплопроводности (молекулярный механизм). Он аналогичен критерию Рейнольдса, который можно рассматривать как отношение скоростей переноса количества движения по конвективному и молекулярному механизмам. Поскольку на конвективный перенос теплоты влияют условия движения жидкости, то условия подобия те— 132 — ÐǣǯǃǮǫǊÐǄǀƿǀǆǬǯǭǮƼǮÐǂǮƽǬǁǀ͠ǮǫǪǃǀǎÐǰǬǮ͠ǀǎÐ͟ǮƽǮƻǀǎ пловых процессов помимо равенства критериев; Пекле и Фурье для образца и модели должны включать равенство критериев гидродинамического подобия. Поэтому в соответствии со второй теоремой подобия тепловые процессы описываются обобщенной зависимостью: (3.18) f ( Ho, Fr, Re, FoT , PeT , Γ l ) = 0 Критерий Эйлера не включен в эту зависимость, так как обычно он не является определяющим. Для установившихся процессов из зависимости (3.18) исключаются критерии гомохронности и Фурье и она приобретает вид: f ( Fr, Re, PeT , Γ l ) = 0 Поскольку в эти критерии входит скорость, вместо Fr и Рет используются производные критерии подобия. Сочетанием критериев Fr и Re, как это было сделано ранее, получается критерий Архимеда (3.14), который не cодержит величины скорости. В тепловых процессах изменение плотности жидкости происходит вследствие различия температуры в разных точках, т. е. за счет термического расширения. Поэтому ∆ρ = β æ ∆t , где βж — коэффициент объемного расширения жидρ кости. После подстановки этого значения ∆ɏ/ɏ в выражение (3.14) получается критерий Грасгофа gl3 (3.19) Gr = 2 β æ ∆t ν характеризующий отношение силы тяжести, обусловленной термическим расширением, к силе вязкого трения. Критерий Пекле преобразуется также путем сочетания с критерием Рейнольдса. В результате получаем критерий Прандтля, который содержит только те величины, которые характеризуют физические свойства жидкости. Как было показано выше, значения кинематического коэффициента вязкости и коэффициента температуропроводности определяют поля скоростей и температур. Поэтому по физическому смыслу критерий Рrт — величина, показывающая, в каком соотноше— 133 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð нии находятся поля скоростей и температур в рассматриваемой жидкости. ϯ͘ϯ͘ϯ͘˃̶̨̨̖̪̣̼̖̪̬̖̭̭̼̏͘ Тепловые процессы обычно протекают при передаче энергии системе от окружающей среды (нагревание) или при передаче энергии от системы окружающей среде (охлаждение). Если рассматривается нагревание какой-либо жидкости, то роль окружающей среды играют стенки аппарата или граница раздела с другой жидкостью, т. е. любая (подвижная или неподвижная) граница, через которую происходит перенос энергии. Из условия физического подобия очевидно, что для подобных процессов должно осуществляться подобие граничных условий. Граничные условия, определяющие процесс передачи энергии на границе системы, задаются обычно в виде, соотношений, вытекающих из принципа линейности. Тепловой поток на границе системы можно выразить с помощью уравнения Фурье:  ∂t  q = −λ   (3.20а)  ∂n  г где (dt/dn)г — градиент температуры на границе системы. Его значение определяется распределением температуры в рассматриваемой жидкости и может быть найдено, если известно поле температур. Тепловой поток можно также выразить в виде линейной зависимости от разности температур на границе (стенке) и в объеме жидкости (tст – tж): (3.20б) Q = α (tст − tж) = α∆t Величина ∆t при этом рассматривается как движущая сила процесса переноса теплоты, а величина α, называемая коэффициентом теплоотдачи, является кинетической характеристикой переноса энергии от стенки в объем жидкости или в противоположном направлении. Согласно (3.20а) и (3.20б)  ∂t  −λ   = α∆t (3.21)  ∂n  ãг — 134 — ÐǣǯǃǮǫǊÐǄǀƿǀǆǬǯǭǮƼǮÐǂǮƽǬǁǀ͠ǮǫǪǃǀǎÐǰǬǮ͠ǀǎÐ͟ǮƽǮƻǀǎ Условие подобия граничных условий в образце и модели находится путем подобного преобразования этого соотношения. Получаем: aλ at a a α ′l ′ α ′′l ′′ (3.22) = aα at ; α l = 1; = = Nu λ′ λ ′′ al aλ где l’, l’’ — определяющий размер образца и модели, соответственно. . Безразмерный комплекс Nu = аl/λ, характеризующий подобие граничных условий, называется критерием Нуссельта. Его можно рассматривать как безразмерный коэффициент теплоотдачи. Равенство критериев Нуссельта для образца и модели — следствие подобия геометрических и физических характеристик, а также подобия полей скоростей и температур. Поэтому критерий Нуссельта не является определяющим. С учетом изложенного обобщенную зависимость, описывающую кинетику переноса теплоты в движущихся средах, можно представить в виде: Nu =f (Re, Gr, PrT, Но, FoT, Гl) (3.23) Для установившихся процессов из зависимости (3.23) исключаются критерии Но и FoT содержащие время. Таким образом, имеем: Nu=f(Re, Gr, Ргт, Гl) ϯ͘ϯ͘ϰ͘ʿ̶̨̨̨̨̨̨̛̖̪̬̖̭̭̥̭̭̪̖̬̖̦̭̔̍̏̌̌͘ Процессы массопереноса описываются уравнением (3.3), поэтому критерии их подобия находятся путем подобного преобразования данного уравнения. Так как процессы в образце и модели должны описываться одинаковыми дифференциальными уравнениями, условием a a a a a подобия являются равенства c = ω c = D2 c , из которых слеaτ al al дует ac aDac aDaτ D ′τ ′ D ′′τ ′′ = 2 ; 2 = 1; = = Foäд (3.24) aτ al al (l′ )2 (l′′ )2 — 135 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð aω ac aDac aω al ω ′l ′ ω ′′l ′′ = 2 ; = 1; = = Peäд al aD D′ D ′′ al (3.25) ωl Dτ — диффузионный критерий Фурье; Peäд = — D l2 диффузионный критерий Пекле. Для подобия процессов массопереноса необходимо равенство значений критериев Foд и Ред для образца и модели. Критерий Ред аналогичен по смыслу критериям Рейнольдса и Прандтля для тепловых процессов. Он выражает отношение количеств вещества, переносимых в подвижной среде по конвективному (движущейся жидкостью) и молекулярному (диффузией) механизмам. Подобно тому, как это было сделано выше для тепловых процессов, критерий Ред можно преобразовать, разделив на Re: Peд ν = = Prд Re D В результате получается производный критерий, называемый диффузионным критерием Прандтля. Как и тепловой критерий Прандтля, он содержит только те величины, которые характеризуют свойства вещества — транспортные коэффициенты, являющиеся мерой скорости переноса по молекулярному механизму количеств движения и вещества. Следовательно, критерий определяет, в каком соотношении находятся поля скоростей и концентраций в рассматриваемой подвижной среде. Перенос массы вещества происходит через подвижную или неподвижную границу раздела. Поэтому при соблюдении подобия, геометрических характеристик, полей физических величин, а также равенства определяющих критериев подобия (Foд и Рrд) в образце и модели должно обеспечиваться подобие граничных условий, которые выражаются так же, как и для тепловых процессов ( уравнение (3.21)), т. е. где Foäд =  ∂c  j = − D   = β∆c  ∂n  г — 136 — (3.26) ÐǡǬǰǮƽÐǪǃǪǁǀƿǪÐ͠ǪƿǂǬ͠ǃǮǯǰǬ֬ где j — поток вещества, отнесенный к единице поверхности; D — коэффициент диффузии; (дс/дп)г — градиент концентрации переносимого вещества на границе раздела с окружающей средой; β — коэффициент массоотдачи, характеризующий скорость переноса вещества от границы раздела в объем жидкости или в противоположном направлении (по смыслу аналогичен коэффициенту, теплоотдачи α); ∆с = сг–сж — разность концентраций на границе раздела и в объеме жидкости. Подобное преобразование уравнения (3.26) приводит к равенствам: aβal aDac β′l ′ β′′l ′′ (3.27) = aβac ; = 1; = = Nuä al aD D′ D ′′ βl Безразмерный комплекс Nuд = — диффузионный криD терий Нуссельта, аналогичный по смыслу тепловому критерию Нуссельта (3.22). Величину Nuд можно рассматривать как безразмерный коэффициент массоотдачи. Равенство критериев для образца и модели — следствие подобия протекающих в них процессов. Таким образом, критерий NuH не является определяющим. Обычно в расчетах кинетики процессов массоотдачи Nuд — искомая величина. Поэтому обобщенную зависимость, описывающую процессы массопереноса в подвижных средах, можно представить в виде: Nuд = f (Re, Аr, Но, Рrд, Fод, Гl) (3.28) Критерии Re, Аr и Но входят в зависимость (3.28) в связи с тем, что для подобия процессов массопереноса в подвижных средах необходимо подобие полей скоростей или, иными словами, подобие гидродинамической обстановки в образце и модели. Для установившихся процессов критерии Но и Foд исключаются из зависимости (3.28), и она приобретает вид: Nuд = f (Re, Аr, Рrд, Гг) (3.29) ϯ͘ϰ͘ʺ̨̨̛̖̯̦̣̬̥̖̬̦̭̯̖̜̔̌̌̌̌̚̚͘ Для сложных явлений (процессов) не всегда удается составить описывающие их дифференциальные уравнения, а сле— 137 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð довательно, отсутствует возможность подобным преобразованием уравнений выявить критерии подобия. Используемый в таких случаях метод анализа размерностей основан на том, что любое уравнение должно быть размерно однородным (размерности левой и правой частей уравнения одинаковы). Вначале устанавливаются все физические величины, оказывающие существенное влияние на рассматриваемый процесс. Постулируется степенная зависимость между ними, и затем путем сопоставления размерностей членов правой и левой частей уравнений находится связь между показателями степени. Пусть, например, требуется найти перепад давления ∆р (в Па) при движении жидкости в горизонтальной трубе. Величина Ар должна зависеть от скорости движения жидкости ω (м/с), ее плотности ɏ (кг/м3) и динамического коэффициента вязкости μ (Па с), а также от длины трубы L (м). Для горизонтальной трубы действием силы тяжести можно пренебречь. Следовательно, функциональная зависимость ∆р от влияющих на него факторов имеет вид: ∆p = f (ω, ρ, µ, L) (3.30) Связь между величинами, входящими в уравнение (3.30), можно записать следующим образом: ∆p = kω aρb µ c Ld (3.31) где а, b, с, d и k — числовые коэффициенты. В системе международных единиц СИ в качестве основных единиц измерения используют кг, м и с. Выразив размерности рассматриваемых величин в этих единицах, получаем: a b c  кг   м   кг   кг  d =  мс 2   с   м 3   м·с  [ м ]         Из условия размерной однородности показатели степеней при одинаковых основных единицах измерения в левой и правой частях уравнения должны быть равны: 1 = b + c ; –1=a–3b–c+d ; −2 = −a –c Полученная система уравнений содержит четыре неизвестные величины, три из которых могут быть выражены через четвертую. Так, выражая а, b и с через d, имеем: — 138 — ÐǡǬǰǮƽÐǪǃǪǁǀƿǪÐ͠ǪƿǂǬ͠ǃǮǯǰǬ֬ a=2+d; b=1+d; c=–d Подстановка найденных значений а, b и с в уравнение (3.32) дает:  ωLρ  ∆p = kω2ρ   µ  d Разделив левую и правую части этого выражения на ω2ɏ, получаем: d  ωLρ  ∆p = k или Eu =f(Re) (3.32)  µ  ρω2 Таким образом, при использовании метода анализа размерностей исходная зависимость между пятью величинами сводится к зависимости между двумя безразмерными комплексами. Этот результат является частным случаем так называемой π-теоремы теории подобия: любая зависимость, связывающая некоторые величины, может быть выражена в виде функции безразмерных комплексов, число которых меньше числа исходных величин на число основных единиц измерения. Так как основных единиц измерения три, то соотношение (3.30), включающее пять физических величин, преобразуется к соотношению (3.32), связывающему два безразмерных комплекса. Если число величин, рассматриваемых как независимые переменные, превышает четыре, то безразмерные комплексы утрачивают однозначность, характерную для приведенного выше частного случая, поскольку можно составить ряд таких комплексов из различных величин. Обычно для преодоления указанных затруднений безразмерные комплексы выбираются так, чтобы каждый из них учитывал действие только одного какого-либо фактора. Рассмотрим, например, вывод безразмерных комплексов для описания распределения давления в жидкости, движущейся с большой скоростью. В общем случае помимо учтенных выше факторов на движение жидкости в горизонтальной трубе оказывают влияние силы тяжести, поверхностного натяжения и сжимающие усилия, возникающие при скоростях, близких к скорости звука. Поэтому — 139 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð 'р = f(ω, ρ, µ, L, g, σ, ωз) (3.32) где g — ускорение свободного падения, м/с2; σ — поверхностное натяжение, Н/м; ω3 — скорость звука, м/с. Длина трубы L, скорость и плотность жидкости всегда оказывают влияние на рассматриваемый процесс движения. Они и учитывались при выводе соотношения (3.32). Если же вместо силы вязкого трения учитывается сила поверхностного натяжения, то вместо зависимости (3.30) получится: ∆p = f (ω, ρ, L, σ) a или b  кг   м   кг  c  кг   м · с 2  =  с   м3  [ м ]  с2          d Из полученной системы уравнений находим: а = 2 — 2d, b = 1 — d, с = –d. Таким образом 2 Lω2ρ  ∆p = kρω   σ  −d (3.33) Здесь а, b, с, d и k — числовые коэффициенты, аналогичные рассмотренным выше. Из (3.33) получается зависимость: Eu = f (We) где We — безразмерный комплекс, представляющий собой отношение инерционных сил к силам поверхностного натяжения (критерий Вебера) We = Lωгр/σ (3.34) Если же в зависимость (3.30) вместо ц ввести ω3, то имеем: a b  кг   м   кг  c  кг   м · с 2  =  с   м3  [ м ]  с2          d Из этой системы уравнений находим: а = 2–d, b= 1, с = 0. В результате ω  ∆p = kσω2  ç   ω d После преобразований получаем новый безразмерный комплекс — критерий Маха Ма = ω/ω3 (3.35) — 140 — ÐǠǮǃǰ͠ǮǁǋǃǊǬÐǫǮ͟͠ǮǯǊ учитывающий эффекты, возникающие при больших скоростях (сжимаемость жидкости). Аналогичным образом выводится критерий Фруда Fr = ω2/(gl), учитывающий действие силы тяжести. Следовательно, с помощью метода анализа размерностей вместо зависимости (3.32), содержащей восемь величин, получается следующая зависимость между пятью безразмерными комплексами: Eu = f(Re, Fr, We, Ма). Необходимо отметить, что метод анализа размерностей уступает в познавательном отношении теории подобия в связи с указанными выше элементами неопределенности при установлении факторов, влияющих на ход процесса, и при выводе безразмерных комплексов, когда число неизвестных в исходной зависимости превышает пять. Тем не менее метод анализа размерностей дает полезные результаты при анализе сложных явлений. ϯ͘ϱ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏͘ 1. Какие теоретические и технологические обобщения положены в основу общепринятой классификации процессов? 2. Что является движущей силой гидромеханических процессов? 3. Что является движущей силой тепловых процессов? 4. Что является движущей силой диффузионных (массообменных) процессов? 5. Скорость каких процессов определяется по законам физики твердого тела? 6. Какие процессы описываются закономерностями химической кинетики? 7. В чем заключается физический смысл теории подобия? 8. Какой математический аппарат лежит в основе теории подобия? 9. Что такое числа и критерии подобия? 10. В чем заключается сходство и различие между числами подобия и критериями подобия? — 141 — № Наименовап/п ние 1 Число Рейнольдса Обозначение — 142 — Re = ωl υ Fr = ω2 gl Eu = ∆p ρω2 Сопоставляемые эффекты Примечание Силы инерции и трения (или перенос количества движения конвекции и внутренним трением) Силы инерции и гравитации ω — скорость, l — длина, ɓ — кинематическая вязкость g — ускорение свободного падения Сила давления и инерция ∆p — перепад давлений, ρ — плотность τ — время 2 Число Фруда 3 Число Эйлера 4 Число Струхала str = ωτ l Конвективные и локальные изменения величины 5 Число Лагранжа La = ∆pl µω Силы давления и трения µ — динамическая вязкость 6 Число Архимеда Подъемные силы и сила трения ∆ρ — разность плотностей 7 Число Рэлея Ar = Ra = gl3 ∆ρ υ2ρ Термическая подъемная сила α — коэффициент темgl3β∆T α и сила трения при полученном пературопроводности 2 υ режиме течения ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð Таблица 3.1 Безразмерные комплексы химической технологии. № Наименовап/п ние 8 Число Кирхгофа Обозначение Сопоставляемые эффекты 3 gl β∆T υ2 Термическая подъемная сила и сила трения течения W a Скорость движения и распространение возмущений ∝l Nu = λ Перенос теплоты конвекцией и теплопроводностью через подвижный слой жидкости Gr = — 143 — Число Маха 10 Число Нуссельда 11 Число Шервуда 12 Число Пекле 13 Число Стептона st = 14 Критерий Био Bi = 15 Число Фурье F0 = M= βl D ωl Pe = a Sh = Перенос массы конвекцией и диффузией β — коэффициент объемного расширения T — температура а — скорость света α — коэффициент теплоотдачи λ — теплопроводность жидкости β — коэффициент массоотдачи Перенос теплоты конвекцией и теплопроводностью Радиальный и оксиальный тепловой поток cp — изобарная теплоемкость ∝ l0 λ Внутреннее и внешнее сопротивления ∝τ l2 Изменение температуры в окружающей среде или внутри тела λ — теплопроводность, l0 — определяющий размер α — коэффициент теплоотдачи ∝ ρc p ω ÐǠǮǃǰ͠ǮǁǋǃǊǬÐǫǮ͟͠ǮǯǊ 9 Примечание Обозначение Pr = υ a sh = υ D — 144 — 17 Критерий Шмитта 18 19 Число Какутеладзе Число Бонда 20 Число Вебера 21 Критерий гомохронности ρlω2 σ ωτ Ho = L 22 Критерий Ньютона Ne = 23 Критерий Лященко Ly = ω 3ρ µ∆ρg 24 Критерий Стокса Stk = d2wρ÷ 18l0 K= r c p ∆T Bo = g ∆pl2 σ We = fτ mω Сопоставляемые эффекты Перенос количества движения и массы по средством молекулярного механизма Перенос количества движения и массы по средствам молекулярного механизма Теплота фазового перехода и нагрева жидкости Гравитационная подъемная сила и сила поверхностного натяжения Сила инерции поверхностного натяжения Примечание D — коэффициент диффузии r — теплота парообразования σ — коэффициент поверхностного натяжения Неустановившийся характер движения жидкости или газа Сила действующая на частицу m — масса частицы и сила инерции f — сила действующая на частицу Эффекты осаждения и вязкого ߂ɏ — разность плотнотечения жидкости стей Силы инерции и сопротивления среды l0 -определяющий размер твердого элемента ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð № Наименовап/п ние 16 Критерий Прандля ÐǤ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ 11. Назовите основные безразмерные комплексы используемые в технике защиты окружающей среды. 12. Какие фундаментальные законы природы лежат в основе общих принципов расчетов процессов? 13. Какое соотношение можно составить по данным о равновесии? 14. Как называется уравнение учитывающее изменение тепловой энергии? 15. Что лежит в основе физического моделирования процесса? ϯ͘ϲ͘ʿ̸̛̛̬̥̖̬̼̬̖̹̖̦́̌̔̌̚͘ Задача 1. Найти единицу измерения динамического коэффициента вязкости в СИ. Уравнение Ньютона для силы трения Р между параллельно движущимися слоями жидкости имеет вид: dω P = µF dy где μ — динамический коэффициент вязкости; F — площадь dω трения; — градиент скорости. dy Решив это уравнение относительно µ, получаем следующую единицу измерения μ: Pdy Н iсi м Нi с кг iмiс кг [µ ] =  Fdω  = м2м = м2 = Паiс = с2м2 = мi с   Задача 2. Найти единицу измерения коэффициента теплопроводности в СИ. Для установления теплового потока Q через однородную λ плоскую стенку можно написать: Q = F ∆t , где λ — коэффиδ циент теплопроводности; δ — толщина стенки; F — поверхность, через которую передается теплота; ∆t — разность температур по обе стороны стенки. — 145 — ǞǁǪǫǪÐ ÐǣƻǈǀǬÐǮǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǂǪǰǬǂǪǰǀǆǬǯǭǮƼǮÐǮ͟ǀǯǪǃǀǎÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀ͠ǮƽǃǮ֬Ðǯ͠ǬƽǊ Ð Решив это уравнение относительно λ, получим: Джм  Qδ  λ = = [ ]  F ∆t  мс2 К = мВт iК   ϯ͘ϳ͘ʯ̸̨̨̨̨̛̛̣̭̥̭̯̯̖̣̦̬̖̹̖̦̌̔̌̔́̌́̽̐́͘ Задача 1. Найти соотношение между единицами измерения динамического коэффициента вязкости в системах единиц СИ и СГС. Задача 2. Установить соотношение между единицами измерения коэффициента теплопроводности ккал и Вт . мiчi°С мiК — 146 — ǍưǙǚǙÍ Í Í ǑǎǒƚǑǒǔǒƚǑƥǎÍ̢ƚǌƟǘǗǋƜǑƥạ̌Í ǕƝǕǖǎǐƥ В результате изучения главы 4 бакалавр должен: Знать: – основные физико-химические свойства двухфазных систем, а также закономерности их образования. Уметь: – классифицировать двухфазные системы, исходя из дисперсного состава твердых или жидких частиц. Владеть: – основными методами и методиками теоретического анализа двухфазных систем. ϰ͘ϭ͘ʶ̴̶̵̡̨̨̨̛̛̛̣̭̭̦̖̦̬̦̼̌̌́̔̔;̵̴̵̱̦̼̔̏̌̚Ϳ̛̭̭̯̖̥͘ При обезвоживании и пылеулавливании, согласно [1, 16–19, 22], приходится отделять твердые частички материала от воды или газа. Гетерогенные системы, содержащие вещества в двух различных агрегатных состояниях, называют двухфазными. При обезвоживании имеют дело с двухфазной системой, состоящей из твердых частиц материала и жидкости, а при пылеулавливании — с системой, состоящей из твердых частиц материала и газа. Гидродинамические закономерности (т.е. зависимость скорости расслоения на отдельные фазы) для этих двух систем имеют много общего. А именно, аналогичны математический — 147 — ǞǁǪǫǪÐ ÐǢǬǮƽǃǮ͠ǮƽǃǊǬÐƽǫǱǲǄǪƿǃǊǬÐǯǀǯǰǬǂǊ Ð аппарат и вид полученных многих закономерностей. Коренное отличие этих двух систем обуславливается большей вязкостью жидкости, чем газа (примерно в 50 раз), и более сильным взаимодействием жидкости с поверхностью твердых частиц. ϰ͘Ϯ͘ʺ̨̨̨̨̨̛̛̛̖̯̼̖̙̦̯̖̬̥̯̖̬̣̔̍̏̏̌́̏̔̐̌̌̌̚ ̵̸̶̨̨̨̨̨̡̛̛̛̛̱̣̖̦̯̖̬̼̭̯̪̯̔̌́̏̔̌̐̌̏̐̌̚̚͘ Поведение двухфазных систем в основном определяется концентрацией твердой фазы и размером частиц. Чем меньше размер частиц и их концентрация, тем ближе свойства двухфазных систем к однофазным — жидкостям и газам. В настоящие время отсутствует какое-либо единое уравнение, описывающие свойства двухфазных систем в широком диапазоне концентраций и размеров твердых частиц. Однако в продуктах различных производств подлежащих обезвоживанию и пылеулавливанию, встречается самый широкий набор размеров частиц от 10 мм до десятых и сотых долей микрона. В настоящее время двухфазные системы принято разбивать на ряд подсистем в зависимости от размера частиц и их концентрации (рис. 4.1). На рисунке также показаны основные методы обезвоживания и движущие силы процессов. Дренаж — свободное вытекание жидкости под действием собственного веса из крупнозернистого осадка по каналам большого диаметра. При грохочении к силе тяжести воды добавляется сила вибрации и небольшая центробежная сила. Сгущение происходит под действием сил тяжести, но по сравнению с дренажом происходит не вытекание жидкости, а осаждение частиц, обладающих большей плотностью, чем вода. Для ускорения первоначального обезвоживания, например шламов и коллоидов приходится вводить в действие центробежные силы или укрупнять частицы за счет, как коагуляции, так и флокуляции, применяя для этого специальные реагенты. — 148 — ÐǡǬǰǮƽǊÐǮƻǬƿǫǮƾǀǫǪǃǀǎÐǰǫǬ͠ƽǮƼǮÐǂǪǰǬ͠ǀǪǁǪÐǀÐǱƽǪǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǀƿÐƼǪƿǮǫǮƼǮÐ͟ǮǰǮǭǪ ɫʉʚʜʛ ʇʎʔʢʌGʘʏʘʙʌʓʢ ʙʉGRGʍʏʋʑʕʌ ʙʉGRGʊʇʎ ʤʒʌʑʙʗʕT ʛʏʒʣʙʗʢ ʛʏʒʣʙʗʇʝʏʦGGGGGʉGʋʌʐʘʙʉʚʥʠʏʐGʘʒʏʉGGGG ʢ ʕʔ ʑʒ ʝʏ ɱʕʒʒʕʏʋʔʢʌ ɩʎʉʌʘʏSGʖʢʒʏ ɸʚʘʖʌʔʎʏʏ ɧʤʗʕʎʕʒʏ ʘʏʘʙʌʓʢ ʗʇʎʓʌʗGeGWSXGʓʑ ¡ GeGWSXGʓʑ ʋʏʇʓʌʙʗGʞʇʘʙʏʝ ¡GcGWSXGʓʑ ɸʙʉUGʋʕG[WGTG\WGL ɸʙʉUGʋʕGXGTGYGL ʑʕʔʝʌʔʙʗʇʝʏʦGXGTGYGL GcGWSXGʓʑ Z ɽʌʔʙʗ ʏʛ ɪʗʚʈʢʌGʘʚʘʖʌʔT ʚʊʏ ɫʗʌʔʇʍ ʎʏʏbGʑʚʘʑʕT ʘʏʒʇGʙʦʍʌʘʙʏ ʉʢʐGGʓʇʙʌʗʏʇʒ ¡ dGTXWGRGYGʓʓ UdGXGOʉʕʋʇP GGGGGʕʘʇʋʑʏS GGʑʌʑʏSGʖʇʘʙʢ ɵʘʇʋʑʏ ɪʗʕʜʕʞʌʔʏʌ ɱʗʚʖʔʕʎʌʗʔʏʘTGRGʘʏʒʇ ʙʢʌGʘʚʘʖʌʔʎʏʏ OʉʏʈʗʇʝʏʐGʏ ɸʙʉGdG_WGTG_\GL ¡ GdGTYGRGWS\ʓʓ ʝʌʔʙʗʕʈʌʍʔʇʦP ɸʙʉGdG\WGTG]WGL ʔʌʙGʊʗʇʉʏʙʇʝʏʕʔT ʔʕʐSGʞʇʘʙʏʞʔʕ ɵʙʘʙʇʏʉʇʔʏʌ Gʚʋʇʒʌʔʇ ʊʏʋʗʕʝʏʑʒʕT ɳʌʒʕʑʕʎʌʗʔʏʘT ʑʇʖʖʏʒʦʗʔʇʦ ʔʏʗʕʉʇʔU ɺʋʇʒʦʌʙʘʦGʔʇ ʙʢʌGʘʚʘʖʌʔʎʏʏ ʉʒʇʊʇ ʋʌʐʘʉUGʘʏʒʇGd ]\GTG_WGLGʊʗʇʉʏT ¡GdGTWS\Gʓʓ GRGZ ʙʇʝʏʕʔʔʇʦGʉʒʇʊʇS ɸʚʟʑʇ ɵʙʘʙʇʏʉʇʔʏʌ ʕʘʙʇʒʣʔʢʌGʉʏʋʢ ɸʙʉGdG`ZGTG`\GL ʉʒʇʊʏGʕʘʙʇʥʙʘʦ ʊʏʋʗʕʝʏʑʒʕT ʔʌʙGʊʗʇʉʏʙʇʝʏʕʔT Gɿʒʇʓʢ ʔʏʗʕʉUGʘGʖʗʏT ʔʕʐGʏGʑʇʖʏʒʒʦʗT ¡GdGTWS\Gʓʓ ʓʌʔʌʔʏʌʓ ʔʕʐGʉʒʇʊʏ ʛʒʕʑʚʒʦʔʙʕʉU ʋʌʘʙʉUGʘʏʒʇGd GRGZY Рис.4.1. Классификация двухфазных систем. Механические методы обезвоживания легче описать с помощью двух физических процессов: 1) оседания частиц в жидкости с переменной вязкостью 2) фильтрации воды через поры Первый метод применяют для сгущения материала содержащего до 50% твердой фазы (т:ж = 1:1), исходя из закона Стокса. При этом необходимо учитывать направление и скорость потоков в сгустителях. — 149 — ǞǁǪǫǪÐ ÐǢǬǮƽǃǮ͠ǮƽǃǊǬÐƽǫǱǲǄǪƿǃǊǬÐǯǀǯǰǬǂǊ Ð Процесс отделения воды из двухфазной системы, содержащей более 50% твердого, легче представить себе как фильтрацию через пористый и сжимаемый во времени осадок. ϰ͘ϯ͘ˇ̨̨̨̛̬̥̼̭̼̭̯̖̬̼̥̯̖̣̥̏́̏̔̏̔̚͘ ˑ̸̵̴̨̨̨̛̛̛̦̖̬̭̬̣̦̼̬̥̼̭̯̖̬̼̥̯̖̣̥̐́̏́̌̏̔̏̔̚̚͘ На практике нельзя достичь необходимого обезвоживания за счет лишь одного приема или другими словами — применением одного метода обезвоживания. Это связано с тем, что влага на поверхности частиц и в каналах осадка удерживается различными силами — химическими или физическими (капиллярными). В зависимости от природы действующих сил между жидкостью и твердым телом различают следующие типы связей. Химически связанную воду, например, в гидроокисях Fe(OH)2, Ca(OH)2 называют конституционной. Влага из этих соединений удаляется, как правило, при высокой температуре, порядка 500–1000°С. Fe(OH)2 → FeO + H2O Ca(OH)2 → CaO + H2O Координационно-химически связанную воду в кристаллогидратах (CuSO4 × 5H2O) называют кристаллизационной водой. Физически адсорбированную воду на поверхности твердых тел часто называют пленочной и гигроскопической. Гигроскопичность можно связать с поглощением паров за счет их конденсации в микропорах. Увеличение адсорбции жидкости, например воды, в тонких ° вызвано перекрыванием полей сил Ван-дер-Вапорах менее 10А альса от противоположных стенок, что способствует возрастанию сил притяжения по сравнению с плоской поверхностью. Давление паров воды, которое зависит от кривизны поверхности раздела жидкость-газ и с радиусом пор, может быть описано уравнением Кельвина: ln P 2σVM = cosϕ P0 rRT — 150 — (4.1) ÐǨǮ͠ǂǊÐǯǫǎƿǀÐǫǮƽǊÐǯÐǰǫǬ͠ƽǊǂÐǰǬǁǮǂ ÐƸǃǬ͠ƼǀǎÐǯǫǎƿǀÐ͠ǪƿǁǀǆǃǊǲÐǄǮ͠ǂÐǫǮƽǊÐǯÐǰǫǬ͠ƽǊǂÐǰǬǁǮǂ где Р и Р0 — давление паров воды, соответственно, над искривленной и плоской поверхностями; σ — поверхностное натяжение; VM — молярный объем адсорбированной воды; ϕ — краевой угол смачивания; r — радиус пор; R — универсальная газовая постоянная; Т — абсолютная температура, К. ° , имеющиеся Если вода смачивает поры больше, чем 10А в твердом теле или осадке, то она будет задерживаться в них капиллярными силами. Влага, удерживаемая в порах осадка капиллярными силами, называется капиллярной. Вода имеет конечную скорость вытекания из капилляра. Скорость эта падает по мере уменьшения гидростатического напора при вытекании. Поэтому вода не успевает вытечь из пористой системы за время ее удаления в каком-либо аппарате. Влага, остающаяся в осадке по этой причине, называется гравитационной. Она не удерживается ни поверхностными, ни капиллярными силами. Гравитационная влага обычно содержится в обводненных продуктах, когда количество воды настолько велико, что мениски в капиллярах отсутствуют. Энергию связи воды с поверхностью твердого тела можно оценить. Энергия связи конституционной воды равна тепловому эффекту реакции разложения гидроксида металла до его окисла, что в среднем составляет около 100–200 ккал/моль. Тепловой эффект реакции при удалении кристаллизационной воды составляет десятки килокалорий на моль. Дифференциальные теплоты адсорбции q паров воды зависят от степени заполнения поверхности. При малых заполнениях q = 2–3L (L — это скрытая теплота конденсации). В тонких порах (диаметром менее 1 Ангстрема), где удерживается гигроскопическая влага, дифференциальная теплота адсорбции почти не уменьшается для второго и третьего слоев. Энергию удаления капиллярной удерживаемой влаги можно оценить по величине работы перемещения объема жидкости с высоты, соответствующей капиллярному поднятию, до уровня жидкости в широком сосуде. Энергия удаления гравитационной влаги аналогично оценивается по необходимому перепаду давления (работа против сил вязкости). — 151 — ǞǁǪǫǪÐ ÐǢǬǮƽǃǮ͠ǮƽǃǊǬÐƽǫǱǲǄǪƿǃǊǬÐǯǀǯǰǬǂǊ Ð Для строгого проведения такого рода расчетов необходимо точно знать величины поверхностей твердых частиц, размер пор, а также диаметр капилляров, образующихся в осадке. Эти величины, как правило, неизвестны. ϰ͘ϰ͘ʦ̵̨̨̨̨̛̣̱̖̬̙̺̭̪̭̦̭̯̯̖̬̼̯̖̣̌̐̔̏̌̀̌́̍̽̏̔͘ ʦ̵̴̨̨̡̨̨̨̨̛̛̛̛̣̦̖̭̦̦̼̯̬̦̭̯̖̪̖̦̖̙̦́̏̌̏̌̽̍̏̏̌́̚͘ Влагоудерживающая способность материалов в первую очередь определяется гранулометрическим составом частиц и величиной смачиваемости их поверхности жидкостью, а также наличием пор в самых твердых частицах. При уменьшении размера частиц отделение их от жидкости затрудняется по следующим причинам: падает скорость осаждения, уменьшается сила веса, вязкость суспензии быстрее увеличивается при наличии в ней мелких частиц, капилляры в осадке образуются более тонкие, что затрудняет вытекание из них жидкости. Возрастает роль капиллярных сил и доля влаги, удерживаемой ими. Возрастает также величина поверхности частиц и, следовательно, доля адсорбционно удерживаемой жидкости. Мелкие частицы могут также закупоривать капилляры, имеющиеся между крупными частицами в осадке. С ростом смачиваемости поверхности жидкостью, например, водой доля адсорбционно связанной воды возрастает. Обычно эту влагу нецелесообразно удалять даже при сушке, так как адсорбционная влага находится в равновесии с парами воды атмосферного воздуха. Степень гидратации поверхности определяется величиной смачиваемости и оказывает сильное влияние на агрегирование частиц. Гидратные слои препятствуют агрегированию частиц, а в отсутствии агрегирования скорость осаждения твердой фазы всегда меньше. В случае образования агрегатов из частиц осаждение значительно ускоряется. Влагоудерживающая способность также определяется пористостью самих твердых частиц. Материалы по степени пористости условно разделяют на три класса: макропористые (размер пор — 152 — ÐǩǪ͠ǪǭǰǬ͠ǀǯǰǀǭǀÐǪǌ͠Ǯƽǀǯ͟Ǭ͠ǯǃǊǲÐǯǀǯǰǬǂ более 2,10–4 мм), переходные (размер пор 6,10–6 ÷ 2,10–4 мм) и микропористые (размер пор 2,10–6 ÷ 6,10–6 мм). Степень пористости материалов определяет величину внутренней поверхности, а также сказывается на характере адсорбции воды. Удельная внутренняя поверхность макропор относительно мала, поэтому на их стенках адсорбируется незначительное количество воды. На поверхности переходных пор удерживается большое количество адсорбированной влаги. Размеры микропор, как уже отмечалось, приближаются к размерам адсорбируемых молекул воды и адсорбция в микропорах приводит к заполнению их объема. Такие тела обычно называют гигроскопичными, и они удерживают значительное количество влаги. В больших порах диаметром более 2,10–4 мм и малых порах, сравниваемых с диаметром молекул воды, явление капиллярной конденсации отсутствует. Уравнение Кельвина применимо, следовательно, не только к капиллярным системам, образуемым в каналах межзеренного пространства в осадке, а также и к самим твердым частицам, если последние имеют поры переходного размера. К микропористым материалам относятся цеолиты, которые представляют собой алюмосиликаты катионов элементов первой и второй групп периодической системы Д.И. Менделеева. Цеолиты применяются даже как адсорбенты. Сульфидные материалы можно отнести к макропористым материалам. Сведения о степени пористости большинства материалов в настоящее время отсутствуют. ϰ͘ϱ͘ˈ̵̡̡̨̛̛̛̛̛̬̯̖̬̭̯̬̭̪̖̬̭̦̼̭̭̯̖̥̌̌̌̾̔͘ Газы, в том числе и воздух, содержащие взвешенные частицы, относятся к аэродисперсным системам. Дисперсными принято называть системы, состоящие из мелкораздробленных частиц (дисперсная фаза), распределенных в какой-либо дисперсионной среде (воде, растворителе, воздухе). Аэродисперсными называют системы, в которых дисперсионной средой является газ, а дисперсной фазой — твердые — 153 — ǞǁǪǫǪÐ ÐǢǬǮƽǃǮ͠ǮƽǃǊǬÐƽǫǱǲǄǪƿǃǊǬÐǯǀǯǰǬǂǊ Ð или жидкие частицы. Пылегазовый поток — это аэродисперсная система, образующаяся в технологическом процессе. Аэродисперсные системы могут образовываться: 1) при измельчении твердых тел; 2) при пересыпании и транспортировании сыпучих материалов; 3) в процессе обжига или нагрева кускового материала, приводящего к растрескиванию и измельчению; 4) при барботировании газа (воздуха) через расплавленный металл, при выделении газов (водорода, хлора и др.) в ходе процесса, когда мелкие частицы уносятся отходящими газами; 5) при конденсации паров или в ходе химических реакций. В зависимости от концентрации дисперсной фазы аэродисперсные системы делят на аэрозоли и аэровзвеси. К аэровзвесям относят потоки с высокой концентрацией частиц, имеющей место в пневмотранспорте пылевидного материала. К аэрозолям принято относить потоки с концентрацией дисперсных частиц, не превышающей нескольких граммов на кубический метр объема газа. В практике пыли, образующиеся в результате конденсации или при химических реакциях, называют возгонами. Пыли, образовавшиеся в результате перечисленных выше первых четырех процессов, называют механическим уносом. Аэрозоли могут быть естественного и так называемого антропогенного, т.е. обусловленного деятельностью человека, происхождения. Природные аэрозоли очень разнообразны. Это туманы, облака, пыли и дым, возникающие при извержении вулканов, лесных пожарах, пыльных бурях и т.д. Аэрозоли промышленного происхождения являются индикаторами технического развития общества. В зависимости от процесса, в результате которого возникает система, аэрозоли делят на диспергационные и конденсационные. Диспергационные аэрозоли образуются в результате измельчения твердых или жидких материалов или распыления порошков под действием тока воздуха или вибрации. — 154 — ÐǩǪ͠ǪǭǰǬ͠ǀǯǰǀǭǀÐǪǌ͠Ǯƽǀǯ͟Ǭ͠ǯǃǊǲÐǯǀǯǰǬǂ Конденсационные аэрозоли образуются при конденсации пересыщенных паров или в результате химического взаимодействия газов с образованием нелетучего продукта. Различие между этими аэрозолями заключается также в том, что размер частиц в конденсационных аэрозолях менее 0,5 мкм в диаметре, а в диспергационных размер частиц значительно больше, а распределение по размерам — шире. Если диспергированная фаза твердая, то в состав такого аэрозоля входят индивидуальные или в незначительной степени агрегированные (т.е. связанные между собой) частицы неправильной формы. В конденсационных аэрозолях твердые частицы представляют собой непрочные агрегаты из очень большого числа отдельных частиц правильной кристаллической или сферической формы. Различают три типа аэрозолей: − пыль (диспергационный аэрозоль с твердыми частицами); − дым (конденсационный аэрозоль с твердой и жидкой дисперсными фазами); − туман (конденсационные и диспергационные аэрозоли с жидкой дисперсной фазой). Встречаются также системы смешанного типа, например аэрозоли промышленных городов (смог). В зависимости от дисперсности различают аэрозоли: − высокодисперсные (с диаметром частиц от 10–3 до 1 мкм); − тонкодисперсные (с диаметром частиц 1–10 мкм); − грубодисперсные (с диаметром частиц от 20 до 100 мкм). По тому же принципу аэровзвеси делят на тонкие — с частицами от 0,2 до 1 мм и грубые — с частицами более 1 мм. Если дисперсная фаза состоит из частиц одинаковой величины, то система называется монодисперсной, если же она состоит из частиц разного размера — полидисперсной. Как уже отмечалось выше, по способу образования аэрозоли делятся на конденсационные и диспергационные. От способа образования зависят не только форма и размеры частиц, но и многие свойства аэрозолей. При диспергировании и конденсации образуются новые поверхности, следовательно, эти процессы, за исключением самопроизвольного диспергирования, требуют затрат энергии. — 155 — ǞǁǪǫǪÐ ÐǢǬǮƽǃǮ͠ǮƽǃǊǬÐƽǫǱǲǄǪƿǃǊǬÐǯǀǯǰǬǂǊ Ð ϰ͘ϱ͘ϭ͘ʶ̶̨̨̨̨̨̛̛̦̖̦̭̦̦̖̬̦̖̔̌̍̌̏̌̚ ̵̨̛̛̬̭̪̖̬̭̦̼̭̭̯̖̥̌̾̔͘ Процесс конденсации предполагает образование новой фазы на уже имеющихся поверхностях (стенках, частицах посторонних веществ) — ядрах конденсации или на поверхностях зародышей, возникающих самопроизвольно в результате флуктуаций плотности и концентрации вещества в системе. В первом случае конденсация называется гетерогенной, а во втором — гомогенной. Как правило, конденсация происходит на поверхности ядер конденсации или зародышей очень малых размеров. Чтобы сконденсированное вещество не возвращалось в первоначальную фазу, и конденсация продолжалась, необходимо наличие пересыщения в системе, иначе в результате испарения или растворения зародыши конденсации будут исчезать. ϰ͘ϱ͘Ϯ͘ʯ̸̶̡̨̨̨̛̛̛̦̥̖̬̦̭̯̬̭̪̬̖̖̣̖̦̭̯̌̌̔́̌͘ ϰ͘ϱ͘Ϯ͘ϭ͘ʧ̸̸̶̨̡̛̛̛̖̥̖̯̬̖̭̖̪̬̥̖̯̬̼̭̯̌̌̌͘ Взаимодействие газов с твердыми телами и жидкостями происходит на поверхности этих тел. Площадь поверхности раздела фаз является одним из основных геометрических параметров. Удельная поверхность Sуд, т.е. отношение площади поверхности S к объему тела V, связана с линейными размерами тела. Для куба со стороной а удельная поверхность 6a2 6 = a a3 (4.2) 6 πδ2 = 3 πδ / 6 δ (4.3) Sóä = а для сферы диаметром d Sóä = С учетом формы тела можно записать: 1 Sóä = K = KD* a — 156 — (4.4) ÐǩǪ͠ǪǭǰǬ͠ǀǯǰǀǭǀÐǪǌ͠Ǯƽǀǯ͟Ǭ͠ǯǃǊǲÐǯǀǯǰǬǂ где К — коэффициент формы, равный 2 — для пластины, 4 — для бруска, 6 — для куба; D* = 1/а или 1/δ, называемый показателем дисперсности. При дроблении и измельчении тел показатель дисперсности и удельная поверхность увеличиваются. Другим геометрическим параметром является кривизна поверхности Н, которая определяется производной площади поверхности по объему частицы: H= dS 2dV (4.5) Для сферических частиц Н = 2D*, а для волокон Н = D*. ϰ͘ϱ͘Ϯ͘Ϯ͘ˀ̵̸̶̛̛̥̖̬̼̪̼̣̖̦̼̭̯̌̏̔̌̚͘ При измельчении тел образуются частицы различных размеров, т.е. все реальные порошковые и пылевидные материалы полидисперсны. Кроме того, частицы имеют различную форму — сферы, чешуйки, волокна и т.д. Частицы удобнее представлять сферическими или близкими к ним по форме. Размер частицы обычно характеризуют радиусом или диаметром. Эквивалентным диаметром частицы δэ называется диаметр шара, равного с ней объема, или диаметр круга, площадь которого равна площади проекции частицы. Седиментационным или стоксовским диаметром частицы δs называется диаметр шара, для которого скорость осаждения и плотность равны скорости осаждения и плотности частицы. При этом δs представляет собой либо измеренный диаметр, либо длину стороны ячейки сита, через которое осуществляется рассев порошкообразного материала, либо размер проекции частицы. В некоторых случаях для так называемых монодисперсных частиц используется средний диаметр δср, например, средний арифметический δñð = ∑ (nδ i ) ∑n где n – номер фракции. — 157 — (4.6) ǞǁǪǫǪÐ ÐǢǬǮƽǃǮ͠ǮƽǃǊǬÐƽǫǱǲǄǪƿǃǊǬÐǯǀǯǰǬǂǊ Ð Фракция порошка — группа частиц, размер которых находится в некоторых установленных для нее пределах. ϰ͘ϱ͘Ϯ͘ϯ͘ʪ̸̶̨̛̛̭̪̖̬̭̦̼̜̭̭̯̭̯̌̏̌͘ содержание, % Дисперсный состав может быть задан тремя способами: таблицей, графиком или аналитически в виде функции распределения. Для характеристики дисперсности монодисперсных частиц служит одна величина — средний размер δ ср. Для характеристики полидисперсных частиц, кроме среднего размера, необходимо знать еще и функцию распределения их по размерам (рис. 4.3) диаметр, мкм Рис. 4.2. Графическое изображение дисперсного состава пыли: распределение по фракциям. Кривые, выражающие функцию плотности распределения числа частиц по размерам f(δ) или массы частиц по размерам g(δ), называются дифференциальными кривыми распределения или кривыми плотности распределения (рис. 4.3). Величина f(δ) характеризует долю частиц, относящихся к определенному размеру, а g(δ) — долю общей массы частиц для этого же размера. Обе функции распределения связаны между собой: g ( δ ) = K1mf ( δ ) (4.7) — 158 — ÐǩǪ͠ǪǭǰǬ͠ǀǯǰǀǭǀÐǪǌ͠Ǯƽǀǯ͟Ǭ͠ǯǃǊǲÐǯǀǯǰǬǂ где m – масса частицы размером δ; К1 — нормирующий множитель, равный 1/mср; mср — средняя масса частицы. Рис.4.3. Кривые дифференциального (числа f(δ) и массы g(δ)) и интегрального (числа F и массы (G) распределения частиц по их размерам). При ситовом анализе дисперсного состава пыли, а также при определении степени улавливания частиц в пылеулавливающем аппарате пользуются кривыми интегрального распределения (рис. 4.4.). Функцию распределения определяют опытным путем, например, производя рассев на специальных ситах и строя затем гистограмму. ϰ͘ϱ͘ϯ͘ˇ̡̨̛̛̚Ͳ̵̸̵̡̡̡̛̛̛̛̛̛̛̥̖̭̖̬̯̖̬̭̯̪̼̣̌̌͘ Каждому производству или отдельному технологическому процессу соответствует определенный химический состав пыли. Если пыли, образующиеся при механической обработке, по химическому и вещественному составу почти не отличаются от исходного материала, то этого нельзя сказать о возгонах. При высоких температурах технологического процесса могут одновременно испаряться как металлы, так и флюсы. В процессе конденсации этих паров образуются частицы, которые могут содержать несколько веществ. Таким образом, возгоны по химическим свойствам отличаются от исходного материала и механической пыли. — 159 — ǞǁǪǫǪÐ ÐǢǬǮƽǃǮ͠ǮƽǃǊǬÐƽǫǱǲǄǪƿǃǊǬÐǯǀǯǰǬǂǊ Ð Плотность пыли. Различают истинную плотность пыли, плотность насыпной массы пыли и кажущуюся плотность пыли. Истинная плотность обусловлена химическим составом материала, из которого она создана, и измеряется отношением массы пыли к занимаемому ею объему. В большинстве случаев в процессе очистки газа имеют дело с пылью, которая после выделения из газа собирается в определенной емкости и образует насыпную массу. В этой массе между частицами пыли содержится воздух. Таким образом, плотность насыпной массы учитывает наличие воздушных зазоров между отдельными частицами пыли и объем их закрытых пор и изменяется в зависимости от способа заполнения (уплотнения) пыли в заданном объеме. Чем меньше размеры частиц пыли, тем меньше поверхность их соприкосновения, тем большее количество пустот окажется между отдельными частицами и тем меньше, по сравнению с истинной, будет насыпная масса. Кажущаяся плотность пыли представляет собой отношение массы пыли к занимаемому ею объему, включая имеющиеся в ней поры и пустоты. Величина объема пор и пустот зависит от формы и размеров частиц. Чем больше плотность частиц пыли, тем более полно они осаждаются в очистительных аппаратах. Коагуляция пыли (укрупнение) заключается в способности ее мелких частиц слипаться между собой и образовывать более крупные частицы. Коагуляция частиц размером более 0,1 мкм происходит вследствие их сталкивания во время движения. Мелкая пыль (в том числе и возгоны) склонна к самопроизвольной коагуляции. Частицы пыли размером более 100 мкм почти не коагулируют в газовом потоке. Пыли, образованные в результате механических процессов, коагулируют меньше пылей, возникших при термических и химических процессах. Чем выше скорость газов, тем больше вероятность столкновения частиц пыли, и тем быстрее они коагулируют. Частицы пыли разного размера лучше коагулируют, тем частицы одинакового размера. Форма скоагулированной пыли может быть шарообразной, бесформенной и в виде цепочки. Укрупнение — 160 — ÐǩǪ͠ǪǭǰǬ͠ǀǯǰǀǭǀÐǪǌ͠Ǯƽǀǯ͟Ǭ͠ǯǃǊǲÐǯǀǯǰǬǂ находящихся в газовом потоке капель жидкости называют коалесценцией. Слипаемость пыли — это ее способность налипать на стенки газоходов и аппаратов газоочистки, что приводит к частичному или полному забиванию их пылью. Слипаемость пыли зависит от свойств ее материала, а также от крупности частиц, влажности, температуры, наличия неслипающихся включений. В зависимости от степени слипаемости пыли делят на четыре группы: неслипающиеся, слабослипающиеся, среднеслипающиеся и сильнослипающиеся. К первой группе относится глиноземная, сухая шлаковая и коксовая пыль. Ко второй группе — доменная пыль (после пылеуловителя), коксовая и апатитная сухая пыли, летучая зола с недожегом и при слоевом сжигании любых сортов углей. К третьей группе относятся пыли концентратов цветной металлургии и железного колчедана, предварительно скоагулировавшиеся окиси свинца, олова, цинка, торфяная пыль, летучая зола без недожега и др. К четвертой группе — зола антрацитового штыба с недожегом, пыли асбеста, цемента, глины, каолина, алебастра, цементная пыль с большим влагосодержанием. Смачиваемостью пыли называют поверхностное адсорбирование влаги ее частицами. Чем меньше размер частиц пыли, тем меньше способность их смачиваться. Смачиванию препятствует газовая оболочка, которая образуется вокруг частиц пыли. Чем крупнее частицы и чем круглее их форма, тем слабее силы, удерживающие газовую оболочку вокруг поверхности частиц, и, следовательно, тем больше их способность смачиваться. Смоченные частицы лучше отделяются от газа в аппаратах газоочистки. По характеру смачивания все твердые тела разделяют на три основные группы: 1) гидрофильные материалы — хорошо смачиваемые: кальций, кварц, большинство силикатов и окисленных минералов, галогениды щелочных металлов; — 161 — ǞǁǪǫǪÐ ÐǢǬǮƽǃǮ͠ǮƽǃǊǬÐƽǫǱǲǄǪƿǃǊǬÐǯǀǯǰǬǂǊ Ð 2) гидрофобные материалы — плохо смачиваемые: графит, уголь, сера; 3) абсолютно гидрофобные: парафин, тефлон, битумы. Гигроскопичность частиц. Способность пыли впитывать влагу зависит от химического состава, размера, формы и степени шероховатости поверхности частиц. Гигроскопичность способствует их улавливанию в аппаратах мокрого типа. Воспламенение и взрываемость пыли. Чем меньше размеры частиц, тем пористее их структура, тем больше их удельная поверхность и тем выше их физическая и химическая активность. Высокая химическая активность некоторых видов пыли вызывает ее взаимодействие с кислородом воздуха, что, как правило, сопровождается повышением температуры. Поэтому в местах скопления пыли возможно ее самовоспламенение и взрыв. Более склонны к возгоранию возгоны — из-за большой удельной поверхности и наличия в них неокисленных металлов, углерода и серы. Взрывоопасность пыли увеличивается с уменьшением ее зольности и влажности. Большое значение при проектировании и эксплуатации электрофильтров имеет электрическая проводимость частиц пыли. Этот показатель оценивается по удельному электрическому сопротивлению слоя пыли ρсл, которое зависит от свойств отдельных частиц (от поверхностной и внутренней электропроводности, формы и размеров частиц), а также от структуры слоя и параметров газового потока. Электрическая заряженность частиц. Знак заряда частиц зависит от способа их образования, химического состава, а также от свойств веществ, с которыми они соприкасаются. Этот показатель оказывает влияние на эффективность улавливания в газоочистных аппаратах (мокрых пылеуловителях, фильтрах и др.), на взрывоопасность и адгезионные свойства частиц. Абразивная (истирающая) способность пыли оказывает большое влияние на прочность систем газоочистки при больших скоростях движения газа. Абразивная способность зависит от твердости пыли, формы и размеров частиц, их плотности. — 162 — ÐǠǮǃǰ͠ǮǁǋǃǊǬÐǫǮ͟͠ǮǯǊ Оптические свойства пыли (способность отражать и поглощать лучи света) имеют значение при визуальной оценке работы пылеулавливающих аппаратов и при использовании приборов для автоматического контроля запыленности газов. Токсичность пыли зависит от материала, из которого она образована (например, мышьяк, свиней и др.), и размеров частиц. Чем мельче частицы пыли, тем больше их способность проникать вместе с воздухом в органы дыхания человека и вызывать различные заболевания. Выбор типа аппарата газоочистки, а также поведение аэрозольной системы определяется свойствами аэрозолей. Свойства аэрозолей отражают свойства газа и взвешенных в нем частиц и определяются дисперсностью (т.е. степенью измельчения материала) и концентрацией частиц, функцией распределения частиц по размерам и т.д. Другим отличительным свойством аэрозоля является его многофазность, т.е. гетерогенность, которая приводит к взаимодействию двух разных фаз и сопровождается поверхностными явлениями (испарение, конденсация, сорбция и др.), отражающими особые свойства аэрозолей, их устойчивость и химическую активность. ϰ͘ϲ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏͘ 1. Какие системы называются двухфазными? 2. Чем определяется поведение двухфазных систем? 3. При каких условиях двухфазная система приближается к однофазной? 4. При помощи каких процессов обезвоживают суспензии различных классов? 5. Можно ли достичь 100 % обезвоживания с применением только одного способа обезвоживания? Если да, то почему? Если нет, то почему? 6. Дайте определения химически связанной воды, координационно-химически связанной воды, влаги на поверхности твердых тел, воды остающейся в осадке. 7. Чему равна энергия связи конституционной воды? — 163 — ǞǁǪǫǪÐ ÐǢǬǮƽǃǮ͠ǮƽǃǊǬÐƽǫǱǲǄǪƿǃǊǬÐǯǀǯǰǬǂǊ Ð 8. Чему равен тепловой эффект реакции при удалении кристаллизационной воды? 9. Чему равна дифференциальная теплота адсорбции паров и от чего она зависит? 10. Как можно оценить энергию удаления капиллярно-удерживаемой влаги? 11. Чему равна энергия удаления гравитационной влаги? 12. Как определить энергию связи воды с поверхностью твердого тела? 13. Что такое макропористые материалы? 14. Какой размер пор имеют материалы, относящиеся к переходному классу? 15. Какой размер пор имеют микропористые материалы? 16. Что определяет степень пористости материалов? 17. Что такое пористость и что такое порозность материала? В чем различия между понятиями? 18. Какие вещества называют гигроскопичными? 19. В каких порах отсутствуют явления капиллярной конденсации? 20. Что включает в себя комбинированная очистка пылегазового потока? 21. Какие системы называют дисперсными? 22. Какие системы называют аэродисперсными? 23. Перечислите способы образования аэродисперсных систем. 24. Какие потоки относят к аэровзвесям? 25. Какие пыли называют возгонами? 26. В результате каких процессов образуются диспергационные аэрозоли? 27. В результате каких процессов образуются конденсационные аэрозоли? 28. Перечислите типы аэрозолей и дайте их определение. 29. Что называют дисперсностью материала? 30. Из каких составляющих складывается работа, необходимая для диспергирования материала? 31. В каких случаях можно пренебречь работой образования новой поверхности при диспергировании материала? — 164 — ÐǠǮǃǰ͠ǮǁǋǃǊǬÐǫǮ͟͠ǮǯǊ 32. В каких случаях можно пренебречь работой объемного деформирования при диспергировании материала? 33. С использованием каких веществ можно облегчить разрушение материалов? Как происходит этот процесс? 34. В чем заключается сущность гомогенного и гетерогенного конденсационного образования аэродисперсных систем? 35. Перечислите основные геометрические параметры частиц. 36. Какими величинами характеризуют размеры частиц? Дайте их определения. 37. Что называется фракцией порошка? 38. Какими способами можно задать дисперсный состав пыли? 39. Охарактеризуйте исходный и конечный химический состав пылей, образующихся при механической обработке материалов и при их конденсационном образовании. 40. Какие виды плотности пыли различают? В чем их отличие? 41. В чем заключается сущность процесса коагуляции пыли? 42. Как влияет скорость пылегазового потока на процесс коагуляции пыли? 43. Как влияет размер частиц на процесс коагуляции пыли? 44. На какие группы делят пыли в зависимости от степени слипаемости? Приведите примеры пылей для этих групп. 45. Что называется смачиваемостью пыли? Как влияет на эту характеристику размер частиц пыли? 46. Какие параметры и как влияют на возможность воспламенения и взрываемости пыли? 47. От каких параметров зависит абразивная способность пыли? 48. В каких случаях необходимо учитывать оптические свойства пыли? 49. От чего зависит токсичность пыли? — 165 — ǞǁǪǫǪÐ ÐǢǬǮƽǃǮ͠ǮƽǃǊǬÐƽǫǱǲǄǪƿǃǊǬÐǯǀǯǰǬǂǊ Ð ϰ͘ϳ͘ʿ̸̛̛̬̥̖̬̼̬̖̹̖̦́̌̔̌̚͘ Задача 1. В сосудах диаметр капель эмульсии масла зависит от способа приготовления и при ручном взбалтывании составляет 20 мкм, а при машинном перемешивании 4 мкм. Определить дисперсность, удельную поверхность дисперсной фазы, а также отношение этих величин, если плотность масла равна 1.1–103 кг/м3. Решение. Определяем дисперсность по формуле: Dìàø = 1 1 = = 2,5<105 ì −1 a 4<10−6 Dðó÷ = 1 1 = = 5<104 ì −1 a 20<10−6 Рассчитываем удельную поверхность: 6 6 ìàø = = = 13,6<102 ì 2 Sóä −6 ρ 4<10 <1,1<103 ðó÷ = Sóä 6 6 = = 2,72<102 ì 2 ρ 20<10−6 <1,1<103 ìàø Sóä Dìàø 2,5<105 13,6<102 = = = =5 5 ; ðó÷ Dðó÷ Sóä 5<104 2,72<102 Задача 2. Массовая концентрация мучной пыли в воздухе рабочих зон помещения мукомольных предприятий составляет 4.2 мг/м3 . Определить численную концентрацию мучной пыли, если средний диаметр частиц составляет 3.7мкм, а их плотность 1.1–103 кг/м3 . Решение. V1 = V 4 3 4,2<10−6 πr ; V÷ = 1 = = 1,44<108 ì 2 ρ 4 3 3 −6 3 <3,14 1,85<10 1,1<10 3 ( ) В 1 м3 воздуха содержится 14400 млн. частиц, или в 1 см3 14400 частиц. — 166 — ÐƭǪƽǪǆǀÐƽǁǎÐǯǪǂǮǯǰǮǎǰǬǁǋǃǮƼǮÐ͠ǬǇǬǃǀǎ ϰ͘ϴ͘ʯ̸̨̨̨̨̛̛̣̭̥̭̯̯̖̣̦̬̖̹̖̦̌̔̌̔́̌́̽̐́͘ Задача 1. На пакетах молока указано, что содержание жира составляет 3.2%. Определить объем дисперсной фазы в упаковке вместимостью 1 литр и численную концентрацию дисперсной фазы, если диаметр жировых капель равен 85 мкм. Чему равна численная концентрация в расчете на 1 м3 . Задача 2. Суспензия кварца содержит сферические частицы, причем 30% объема приходится на частицы, имеющие радиус 1–10–5м, а объем остальных — на частицы радиуса 5–10–5м. Какова удельная поверхность кварца? — 167 — ǍưǙǚǙÍ Í Í ǖǎǒǔǎǖƝơǎǕǏƝǎÍǋǕǓǎǏǖƥÍ ǒǖƚǎƞǎǑƝƩÍǖǌǎǔƚƥǘÍơǋǕǖƝƠÍ ǒǖÍƛƝƚǏǒǕǖƝÍƝƞƝÍǍǋƜǋÍǓǒƚÍ ƚǎ֏ǕǖǌƝǎǐÍǐǎǘǋǑƝơǎǕǏƝǘÍƝƞƝÍ ƧƞǎǏǖǔƝơǎǕǏƝǘÍǐǎǖǒƚǒǌ В результате изучения главы 5 бакалавр должен: Знать: – основные физические законы и механизмы отделения твердых частиц от жидкости или газа. Уметь: – в зависимости от размера твердых частиц дезинтеграции и механизма их отделения от сплошной среды обоснованно выбирать соответствующие процессы разделения. Владеть: – основными физическими методами и законами для описания отделения твердых частиц от жидкости или газа механическими методами. ϱ͘ϭ͘˃̸̨̡̡̨̨̨̨̛̛̛̛̖̬̖̯̖̭̖̦̥̖̬̦̭̯̯̖̣̖̦̌̔́̚ ̵̸̶̨̛̯̖̬̼̭̯̯̏̔̌̐̌̌̚͘ Для отделения аэрозолей (пыли) используются различные механические и электрические методы разделения в зависимости от размера сепарируемых частиц, химического — 168 — ǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐƿǪǭǮǃǮǂǬ͠ǃǮǯǰǀÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƼǪƿǪ состава газа, его температуры и требуемой эффективности процесса. ϱ͘ϭ͘ϭ͘ʽ̶̡̨̨̨̨̛̛̛̛̭̙̖̦̖̬̱̪̦̜̪̼̣̬̯̦̦̥̪̣̖̌̔̏̐̌̏̌͘ Аэрозоль (пыль) диаметром более 100 мкм образуется при обработке твердого материала дробления, измельчения, просева в металлургическом и химическом производствах, в производстве строительных материалов. По составу пыль может значительно отличаться, Однако, в большинстве своем пыль относится к минеральным веществам, плотность которых около 2 г/см3. Пыль находится в воздушной среде, плотность которой ~ 1,3–10–3 г/см3. Различие плотностей почти в 1000 раз приводит к тому, что под действием гравитационного поля Земли происходит осаждение частиц пыли. Рис.5.1. Силы, действующие на твердую частицу в газовой среде. На частицу пыли (рис. 5.1) будут действовать следующие силы: • сила тяжести G = V ρò g = c1 D3ρò g • подъемная сила Архимеда Ar = c1d3ρã g ∂ωîñ ∂ω = c2d2 îñ , где V — объем ча∂n ∂n стицы представлен величиной, пропорциональной кубу ее ли• сила трения, R = Sη — 169 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ нейного размера d; с1, c2 — коэффициенты пропорциональности; ρт , ρг — плотность материала твердой частицы и газа, соответственно; g — ускорение силы тяжести; S — поверхность частицы пыли; η — коэффициент динамической вязкости газа; ωoc — скорость осаждения частицы; п — нормаль к поверхности частицы. По законам механики равнодействующая всех сил, действующих на тело, равна произведению массы на ускорение ∂ωîñ ∂ωîñ (5.1) = c1d3ρò ∂n ∂n В полученном выражении первый член характеризует статическую силу, второй — силу трения, третий — силу инерции. Используя теорию подобия, из полученного уравнения находятся безразмерные числа, описывающие осаждение частиц. Отношение силы инерции к силе трения определяет безразмерное число Рейнольдса. Заменяя бесконечно малые величины конечными и умножая на ρг/ρт, получим значение числа Рейнольдса осаждения: c d3ρò ω ρã dωîñ (5.2) Reîñ = 1 2 îñ < ò = ν tc2d ηωîñ ρ ( ) c1d3 ρò − ρã g − c2d2 Таким образом, получаем обычное выражение числа Рейнольдса, но в него входят размер частиц пыли, скорость осаждения частиц и коэффициент кинематической вязкости газовой среды, в которой происходит осаждение. Взяв соотношение статических сил и сил инерции и умножив на квадрат числа Рейнольдса осаждения и соотношение плотностей твердых частиц и газа, получим безразмерное число Архимеда, характеризующее подъемную силу Архимеда: Ar = ( ) ( c1d3 ρò − ρã gt ρò gd3 ρò − ρã 2 = Re < îñ c1d3ρò ωîñ ρã ν2ρã ) (5.3) Для определения скорости осаждения частиц пыли используется безразмерное уравнение (5.4) Reîñ = aAr n — 170 — ǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐƿǪǭǮǃǮǂǬ͠ǃǮǯǰǀÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƼǪƿǪ где а и п — определяются из эксперимента в зависимости от значения числа Рейнольдса осаждения. Практически найдено, что при Reoc < 1,85; Reoc = Аr /18; при 1,85 < Reoc < 500; Reос = 0,152 Ar0,715; при Reoc >500; Reoc = = 1,74 Ar0,5. Зная число Архимеда, в которое входят величины, характеризующие расчетную часть, находят число Рейнольдса осаждения, из которого определяется скорость осаждения частиц: Reîñ ν (5.5) d В расчетные уравнения входит размер частиц пыли, определение которого представляет определенную трудность. На основе приведенных уравнений используется метод оценки размера частиц путем наблюдения за скоростью осаждения частиц в жидкости с известным значением коэффициента кинематической вязкости. Полученное значение эффективного диаметра частиц используется при расчете пылеосадительных устройств. Часто пыль имеет частицы различного размера. Поэтому важно знать гранулометрический состав пыли. Его представляют в виде гистограммы, по которой можно судить о соотношении частиц разного размера. Распределение часто описывается нормальным логарифмическим законом. Концентрация пыли в воздухе оценивается по массе пыли в единице объема (г/м3). В особо чистых помещениях (гермозонах), используемых в электронной промышленности, содержание пыли оценивается числом пылинок в единице объема. Оценка эффективности оборудования, используемого для улавливания пыли производится по коэффициенту полезного действия установки (КПД), %: V ã (cíà÷ − cêîí )  c  =  1 − êîí  100% ÊÏÄ = cíà÷  V ã cíà÷  (5.6) где снач и скон — начальная и конечная концентрации пыли в атмосфере. ωîñ = — 171 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ В зависимости от крупности частиц пыли и ее количества используется различное улавливающее оборудование. Осаждение крупной (грубой) пыли происходит в осадительных камерах. ϱ͘ϭ͘Ϯ͘ʰ̶̨̨̨̛̛̦̖̬̦̦̖̭̙̖̦̖̌̔͘ ;ʿ̶̨̨̨̛̛̛̛̛̛̬̥̖̦̖̦̖̖̦̯̬̖̙̦̜̭̣̼̪̬̭̙̖̦̍̌̔Ϳ͘ Центробежная сила при инерционном осаждении частиц пыли применяется в циклонах. В этих аппаратах газ с большой скоростью подается тангенциально в верхнюю часть цилиндрической камеры. При вращении газа внутри цилиндра частицы пыли испытывают центробежное ускорение в сторону внешней стенки цилиндра. Сталкиваясь со стенкой, частица теряет скорость и под действием силы тяжести опускается в нижнюю часть цилиндра (бункер), откуда при его наполнении периодически выгружается. Газ, сделав несколько витков внутри корпуса циклона, удаляется через внутренний цилиндр. Центробежная сила, действующая на частицу пыли, определяется массой частицы т, угловой скоростью вращения газа ωг и расстоянием частицы от центра вращения (радиуса вращения) r и находится из уравнения mω2ã (5.7) = mω2r r где ω — угловая скорость вращения. Скорость осаждения может быть найдена по формуле dr (5.8) ωîñ = dt где t — время осаждения. Общее время, необходимое для перемещения частицы на расстояние от внутреннего цилиндра до внешнего: Gö = r2 tîñ = dr ∫ ωîñ (5.9) r1 По времени осаждения частицы находится необходимый объем камеры циклона. — 172 — ǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐƿǪǭǮǃǮǂǬ͠ǃǮǯǰǀÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƼǪƿǪ Для определения скорости осаждения можно воспользоваться зависимостью, полученной для пылевых камер, используя критерии подобия Re и Аr При этом значение числа Аг находится заменой ускорения силы тяжести g на величину центробежного ускорения Архимеда Arц = ( ω2ã или ω2r . Тогда значение числа r ω2г d3 ρ т − ρ г 2 г ) = ω rd (ρ 2 3 т − ρг 2 г rν ρ νρ ) (5.10) Для сферических частиц при значении Аrц <35 можно воспользоваться зависимостью Rц = Аrц. Тогда время осаждения r 18νρг (5.11) tос = 2 2 т ln 2 r1 ω d ρ − ρг ( ) Необходимый объем камеры циклона при этом определяется по формуле (5.12) Vц = Qt ос = π r22 − r12 Hр ( ) где Q — расход очищаемого газа, м /с. При заданных значениях r2 и r1 находят рабочую высоту циклона Нр. Циклоны позволяют улавливать пыль размером > 15 мкм при КПД до 80 %. 3 ϱ͘ϭ͘ϯ͘ʽ̸̡̨̨̛̛̭̯̯̪̼̣̌̐̌̏̚ ̴̶̨̨̛̛̛̥̖̯̥̣̯̬̔̽̌͘ Для улавливания более тонкой пыли (< 15 мкм) используется метод фильтрования. Принципиальная схема фильтровальной перегородки приведена на рис. 5.2. Загрязненный газ поступает на фильтрацию через под давлением p1, проходит, через слой осевшей пыли 2 и фильтрующего материала 3, выходит под давлением р2. Проходя через фильтровальную перегородку и осевший на нем слой уловленной пыли (гидравлическое сопротивление), происходит потеря давления, поэтому p2 < p1 — 173 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ Рис.5.2. Принципиальная схема фильтра (а) и движения газа через фильтрующий слой (б). Для определения скорости фильтрации (ωф) воспользуемся феноменологическим законом (аналогично законам Ома, Фика и др.): плотность потока равна отношению движущей силы (∆р = р1– р2) к сопротивлению фильтрации (Rф). Тогда p1 − p2 ∆p = ωф = (5.13) R ф rф lф + (rсл l сл ) ср где Rф и rсл — сопротивление единицы поверхности фильтровальной перегородки и слоя пыли; lф и lсл — толщины фильтровальной перегородки и слоя пыли (для слоя пыли берется среднее значение за время фильтрации). Необходимую поверхность фильтровальной перегородки F для фильтрации потока газа Q находим по формуле F= Q ωф (5.14) Для определения скорости фильтрации будем использовать критериальное уравнение вида  1  Eu = aRe −n   d экв  — 174 — m (5.15) ǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐƿǪǭǮǃǮǂǬ͠ǃǮǯǰǀÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƼǪƿǪ ∆p — безразмерное число Эйлера, представляющее г ω 2ρ собой отношение потери давления в фильтрующем слое (∆р) к скорости движения газа в порах фильтра (ω) и плотности газа ωd экв (ρг); Re = — число Рейнольдса; dэкв — эквивалентный диг ν аметр пор; ν — кинематическая вязкость газа; а — коэффициент. 110 1 i При значении Re < 35 эта зависимость имеет вид Eu = Re dэкв Тогда скорость газа в порах фильтра ω при высоте фильтрующего слоя l = 1; где Eu = ω= 2 ∆pdэкв 110νρг (5.16) Для определения эквивалентного диаметра пор воспользуемся понятием гидравлического диаметра, который находится из зависимости d экв = 4ε fф (5.17) где ε — пористость материала, определяемая отношением объема пор к общему объему материала; fф — удельная поверхность частиц в объеме фильтрующего слоя. Связь скорости движения газа над фильтрующим слоем ωф с найденной скоростью движения газа в порах фильтра ω находится из зависимости ωф = ωu (5.18) Приведенные зависимости позволяют определить необходимую площадь, зная объем фильтруемого газа, перепад давления и характеристику фильтрующего слоя. — 175 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ ϱ͘Ϯ͘˃̸̵̸̶̨̡̡̨̨̨̨̛̛̛̛̛̖̬̖̯̖̭̖̦̥̖̬̦̭̯̯̖̣̖̦̯̖̬̼̭̯̌̔́̏̔̌̚ ̨̡̨̛̛̯̙̭̯̔͘ˈ̡̡̛̛̛̬̯̖̬̭̯̭̱̭̪̖̦̜̌̌̌̚͘ ϱ͘Ϯ͘ϭ͘ʽ̨̡̡̨̨̨̛̛̛̖̙̦̖̱̭̥̯̖̬̣̍̏̏̌̏̐̌̌̌̚ ̨̛̛̬̖̦̬̦̖̥̔̏̌͘ʧ̸̨̡̡̨̛̛̛̛̛̛̬̦̥̯̖̖̦̙̭̯̔̔̌̌́̔ ̵̨̨̨̨̨̨̡̛̛̪̣̦̖̥̭̭̯̖̦̦̖̭̪̬̭̔̏́̍̏̐̏̌̏̌̌̔̌͘ Дренированием называют операцию обезвоживания за счет стекания жидкости под влиянием собственного веса по капиллярам осадка. Такой процесс проходит эффективно, когда размер частиц осадка, как правило, более 2 мм. Количество вытекающей жидкости по капилляру определяется режимом течения. Режимы течения, как известно, бывают трех типов: ламинарное, турбулентное и промежуточное. Характер течения в капиллярах осадка можно определить по числу: ϑD Re = v где D — диаметр капилляра, см; ϑ — скорость течения, см/сек; ν — кинематическая вязкость для воды равна 0,01см2/сек При Re > 20 ÷ 50 ламинарный режим переходит в турбулентный. Размер пор в осадке оценивают из диаметра частиц. Задаваясь формой и упаковкой частиц в осадке, рассчитывают радиус межчастичного или межзеренного пространства. При плотной укладке шарообразных зерен эффективный радиус межзеренных каналов (Rэф) составляет Rýô = 0.31rçåð , где rçåð — радиус зерна (частицы). При других упаковках, которые чаще встречаются для сы+ Rmin R . пучих материалов, Rэф принимает величину Rýô = max 2 При этом Rmax = 0.41 dзер — 2 для кубической, Rmin = dзер — ромбоэдрической упаковки, где dзер — средний 2 диаметр зерна (частицы). = 0.41 — 176 — ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐƿǪǭǮǃǮǂǬ͠ǃǮǯǰǀÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀ Считается, что более вероятна упаковка с числом соседей, равным шести. По данным опытов в каждом сечении осадка имеется распределение размеров каналов. При этом для осадков с полидисперсными зернами Dmin близок к нулю. Удельный расход жидкости определяется также величиной гидравлического уклона «i» (перепад давления по длине осадка), который является движущей силой процесса. Величина гидравлического уклона «i» рассчитывается как hγ + Lγ H i= = (5.19) L γL где γ — плотность жидкости; h и L — высоты, соответственно уровня воды над осадком и осадка; H=h+L. Как следует из расчета числа Рейнольдса, при дренировании чаще всего наблюдается переходный режим течения жидкости по капиллярам осадка. Скорость вытекания жидкости для переходного режима определяется по формуле: ε2 gd2i 2 (1 − ε ) (5.20) ϑ= 3  ε  3 gd i 4ν A − 15 B + 2B   1 − ε  ( ) где ε — пористость осадка; g — ускорение силы тяжести, 981 см/см2; d — диаметр зерна в осадке, см; i — гидравлический уклон; v — кинематическая вязкость, см2/сек; А и В — коэффициенты, зависящие от формы зерен и незначительно от природы материала: Таблица 5.1. Коэффициенты, зависящие от формы зерен материала. Форма зерна A B Округлая 50 0,75 Обычная (смешанная) 75 1,05 Остроугольная 105 1,30 — 177 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ При ламинарном течении уравнение (5.20) переходит в закон Дарси (5.22). При этом: 1800ν2 i≤ (5.21) 3  ε  3   gd 1− ε ϑ= ε (1 − ε ) 2 < gd2i 4 Aν т.е. ϑ = Kфi , (5.22) где Кф — коэффициент сопротивления движению жидкости через осадок. В условиях, когда вязкость не играет роли (v = 0), выражение переходит в закон квадратичного сопротивления (инерционная сила больше силы вязкости) ϑ= ε2 gdi < 1 − ε 2B (5.23) т.е. ϑ = Kф i (5.24) Для того чтобы определить режим течения при дренировании по значению числа Рейнольдса необходимо подсчитать диаметр капилляров в осадке и экспериментально определить скорость течения жидкости. В соответствии с числом Рейнольдса выбрать формулу для расчета и проверить ее соответствие экспериментальным данным. Приведем пример расчета: dзер= 4 мм, dкап = 0,4 × 0,28 = 0,112 см. Определенная экспериментально средняя скорость движения жидкости по капиллярам осадка составила: 1.50.1 = 15 0.01 Т.е. наиболее вероятен переходный режим движения. Поэтому расход жидкости следует рассчитывать по формуле (5.21) для переходного режима. Режим течения можно также оценить по выражению (5.24). Обычно гидравлический уклон «i» при дренировании ϑср=1,5 см/сек или — 178 — Re = ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐƿǪǭǮǃǮǂǬ͠ǃǮǯǰǀÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀ равен 2÷3. Пористость можно оценить по удельной средней (ρ) и объемной ρ0 массе ρ − ρ0 2,3 − 1,9 0,4 ε= = = ≈ 0,174 2,3 2,3 ρ 1800 (0,01) 2 i= 3 3  0,174    981(0,112) 1 − 0,174  = 0,616 Поскольку i > 0,616, то режим вытекания жидкости из кускового материала со средним диаметром зерна 0,4 см можно считать переходным. Следовательно, определение режима течения по межзерновым каналам осадка по значению Re и по формуле (5.2) дают идентичные результаты. Чтобы рассчитать значение критерия Рейнольдса, нужно знать средний диаметр каналов в осадке и скорость течения жидкости по ним, а для расчетов режима течения по формуле (5.20) нужно иметь значения среднего диаметра каналов в осадке и его пористость (или удельную и объемную массу сухого осадка). Необходимо отметить, что турбулентный режим течения при дренировании маловероятен. Вытекание воды из осадка, состоящего из кускового материала, на самом деле будет происходить по двум режимам: в начале при переходном и в конце — при ламинарном, так как значение гидравлического уклона по мере обезвоживания будет уменьшаться. Поэтому на практике существует оптимальное время обезвоживания, после которого скорость дренирования резко падает. ϱ͘Ϯ͘Ϯ͘ʽ̨̛̛̛̛̛̯̭̯̦̖̪̖̜̭̯̖̥̭̣̼̯̙̖̭̯̌̏̌̔̔̏́͘ ʽ̨̨̛̭̦̦̼̖̪̦̯̏́́͘ʶ̴̶̡̛̛̛̛̣̭̭̭̱̭̪̖̦̜̌̌́̚͘ Отстаиванием называется процесс обезвоживания, происходящий при расслоении суспензии за счет осаждения частиц материала под влиянием собственного веса. Процесс отстаивания можно разделить на сгущение и осветление. Основной целью сгущения является увеличение концентрации твердой — 179 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ фазы, а цель осветления — удаление вещества из относительно разбавленной суспензии (смесь мелких частиц с жидкостью, в основном с водой). Подобно осаждению твердых частиц в газовой среде осаждение твердых частиц в жидкости подчиняется закону Стокса т ж 3  gdпр ρ −ρ   . Скои характеризуется числом Архимеда  Ar = ж2 ж  ν ρ   ω ос d пр рость осаждения находится по числу Рейнольдса Re = νж ( ( ) ) как функция числа Архимеда. Поскольку (ρт — ρж) << (ρт — ρг), a νж >> νг, то осаждение в жидкости будет более медленным. Большое влияние на скорость осаждения, как и в газовой фазе оказывает приведенный диаметр частиц (dпр). Однако, строго говоря, в настоящее время не существует строго количественных методов расчета этих процессов, которые бы основывались на свойствах двухфазных систем. Например, нет аналитического вида функций типа G Vðàññëîåíèÿ = f còâ ;ròâ ; γ òâ ;µñóñï ; ϑ (5.25) ( ) äâóõôàçíîé ñèñòåìû rтв и их где ств — концентрация твердого с размером частиц G удельной массой γтв; μсусп — вязкость суспензии; ϑ скорость жидкости относительно твердого. Большое влияние на скорость осаждения оказывает также и агрегация частиц. Закон Стокса применим, когда ств не более 0,1–1%, размер частиц rтв не выходит из диапазона 0–100 мкм; G µ = const, а ϑ не превышает ее значение для ламинарного потока. В системе не происходит также агрегирование частиц. При осаждении вязкость суспензии изменяется, т.к. она зависит от концентрации твердого тела по законам вида (уравнения Эйнштейна): μсусп = μ0 ( 1 + 2,5ϕ ) при ϕ < 10% (5.26а) μсусп = μ0 ( 1 + 4,5ϕ ) при ϕ > 10% (5.26б) — 180 — ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐƿǪǭǮǃǮǂǬ͠ǃǮǯǰǀÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀ где µсусп и µо — вязкость соответственно суспензии и воды; ϕ — объемная концентрация твердой фазы. Эти формулы применимы для таких концентраций твердой фазы, при которых суспензия еще обладает текучестью. При большой концентрации суспензии расстояние между частицами настолько мало, что они приходят в соприкосновение. Вследствие этого, наряду с внутренним трением жидкости, возникают силы трения частиц друг о друга, и тогда гидравлическое течение переходит в пластическое, для которого формулы не применимы. Как указывалось выше, жидкости, в которых величина вязкости постоянная и не зависит от скорости ее течения, называются ньютоновскими, а жидкости, для которых величина вязкости изменяется, называются неньютонов скими. В концентрированных суспензиях более мелкие частицы тормозят движение более крупных, а частицы больших размеров увлекают за собой мелкие частицы, ускоряя их движение. В результате наблюдается тенденция к сближению скоростей осаждения частиц различных размеров; возникает коллективное или солидарное осаждение частиц с близкими скоростями в каждом сечении аппарата, но различными скоростями по его высоте. Уменьшение скорости частиц при уплотнении суспензии объясняется не только возрастанием вязкости, а также тормозящим действием жидкости, вытесняемой осаждающимися частицами и движущейся в направлении, обратном движению частиц. В настоящее время ряд эмпирических методов позволяет в той или иной степени оценить зависимость типа (5.25). При проведении исследований ставятся две задачи. Первая задача — определение площади, необходимой для получения чистого слива; вторая — определение объема сгустителя, необходимого для получения осадка требуемой плотности. Типы суспензий, встречающиеся на практике, и методы расчета скорости их расслоения можно классифицировать следующим образом — табл. 5.2. — 181 — Классификация отстаиваемых суспензий и методы испытаний Суспензия Описание начала процесса отстаивания Примеры Метод определения площади осаждения Методы определения высоты уп-лотненной зоны — 182 — I класс — разбавленная. Независимое осаждение частиц до 5% твердого Частицы или хлопья осаждаются независимо друг от друга. Границы осаждения нет. Скорость осаждения зависит от размеров частиц и хлопьев Метод длинМутная вода, ной трубки ил, фугаты, фильтраты, сливы — оборотная вода Метод Коу и Клевенжера, метод Робертса II класс — промежуточная. Фазовое осаждение до 15% твердого Верхняя зона — свободное осаждение частиц. Нижняя — осаждение коагулированных частиц. Нет резкой линии раздела Химические и металлургические пульпы, сточные воды, хлопья пыли III класс — концентрированная 15–25% твердого массовое осаждение Метод Клевен- То же Заметна определенная гра- Химические ница осаждения. Скорость и металлургиче- жера и Кинга ские пульпы осаждения уменьшается с увеличением концентрации тв. частиц IV класс — компактная; стесненное осаждение Хлопья или частицы осаж- Все пульпы даются в тесном соприкосновении друг с другом благодаря уплотнению То же Метод длинной трубки, метод Клевенжера, Кинга То же То же ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ Таблица 5.2. ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐƿǪǭǮǃǮǂǬ͠ǃǮǯǰǀÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀ ϱ͘Ϯ͘ϯ͘ˁ̸̨̨̛̛̪̭̼̼̬̙̖̦̬̭̖̯̍̏̌́̌̌ ̶̶̡̨̨̨̛̛̛̛̦̖̦̯̬̯̖̬̭̱̭̪̖̦̌̏̔̐̏̚͘ Перед тем, как приступить к описанию картины осаждения твердого материала из суспензии, рассмотрим основные методы определения и расчета концентрации твердого в суспензии. На практике для определения содержания твердого в материале суспензии, а также отношения Т:Ж отбирают мерной кружкой определенный объем суспензии и взвешивают его вес. Зная вес и объем суспензии, составляют два балансных уравнения и из них рассчитывают все необходимые величины: (5.27) Mï = Mòâ + Mæ Vï = Vòâ + Væ = Mòâ Mæ + ρòâ ρæ (5.28) Уравнение (4.27) говорит о том, что масса суспензии (Mп) равен сумме масс твердого (Mтв) и жидкого (Mж), а уравнение (4.28) отражает баланс объемов: объем суспензии (Vп) равен сумме объемов твердого (Vтв) и жидкого (воды) (Vтв). Объемы Vтв и Vж далее выражают через массу и плотность твердого (ρтв ) и жидкого (ρж). Решение системы уравнений относительно массы твердого имеет вид: M ρ − Vï ρòâ ρæ (5.29) Mòâ = ï òâ ρòâ − ρæ Обычно Vп =1000см3, ρж =1г/см3; а для веса воды: V ρ ρ − Mï ρæ Mæ = ï òâ æ ρòâ − ρæ отсюда Т:Ж равно: M ρ − Vï ρòâ ρæ l = (Ò : Æ ) = Mòâ : Mæ = ï òâ Vï ρòâ ρæ − Mï ρæ (5.30) (5.31) а разжижение R = Ж:Т- выразится обратным соотношением. M M Учитывая, что Væ = æ и Vòâ = òâ найдем их значения: ρæ ρòâ — 183 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ Vòâ = Mï ρòâ − Vï ρòâ ρæ Mï − Vnρæ = ρòâ (ρòâ − ρæ ) ρòâ − ρæ Væ = Vï ρòâ Mï ρòâ − ρæ (5.32) (5.33) Зная массу твердого и объем жидкости, легко найти концентрацию M M ρ − Vï ρòâ ρæ (5.34) ñ = òâ = ï òâ ã / ñì 3 Vï Vï (ρòâ − ρæ ) Для того, чтобы было соответствие в размерности между объемом и плотностью, объем необходимо в формулах подставлять в (см3), плотность в (г/см3), массу в (г), а концентрацию в (г/см3). Переход от концентрации к разжижению (Ж:Т): ρ ( V ρ − Mï ) R = æ ï òâ (5.35) cVï (ρòâ − ρæ ) Если концентрация выражена в процентах, то разжижение рассчитывают обычно, как 100 − b R= (5.36) b где b — содержание твердого в суспензии или пульпе, %. Зная разжижение, можно определить содержание твердо100 . го b = R +1 ϱ͘Ϯ͘ϯ͘ϭ͘ʰ̨̡̨̨̨̛̛̛̛̭̭̣̖̦̖̭̬̭̯̬̭̭̣̖̦̭̱̭̪̖̦̜̔̏̌̌́̚ /Ͳ̨̛̐//Ͳ̨̡̨̨̨̨̡̛̛̣̭̭̥̖̯̥̣̦̦̜̯̬̱̐̌̏̔̔̍͘ Все суспензии I-го класса и многие суспензии II-го класса при отстаивании не дают четкой границы раздела «твердое — жидкость». Расслоение таких суспензий анализируют по зависимости изменения концентрации твердого в сливе от времени осаждения. Для определения потерь твердого со сливом проводятся опыты в стеклянной трубке диаметром 25–30 мм с рабочей дли— 184 — ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐƿǪǭǮǃǮǂǬ͠ǃǮǯǰǀÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀ ной 1,8 м (для ускорения работы лучше иметь несколько таких трубок). Каждый конец трубки плотно закрывается пробкой и трубка устанавливается вертикально. В трубку до отметки 1,8 м заливается суспензии, через определенный промежуток времени, например, после 15 минут отстаивания суспензии, сифоном отбирается столб слива высотой 0,3м, а после этого до первоначальной отметки доливается свежая суспензии. С принятым интервалом вся операция неоднократно повторяется в течение первого часа. В течение второго часа операция производится с интервалом, например, в 30 минут. Последующие опыты можно проводить с интервалом в один и несколько часов. Отсифоненные сливы фильтруют, осадок высушивают и определяют вес сухого материала. По результатам опытов определяют потери твердого со сливом при разной площади сгущения. Пример расчетов приведен в табл.5.3. ϱ͘Ϯ͘ϯ͘Ϯ͘ʶ̸̶̨̨̨̛̛̖̭̯̖̦̦̖̪̭̦̖̪̬̖̭̭̌̏̌̌ ̨̛̛̬̭̭̣̖̦̭̱̭̪̖̦̜̌́̚///̛/ṣ̡̨̭̭̌̏͘ Сгущению подвергаются суспензии III и IV типов. Оседание частиц в таких суспензиях происходит в стесненных условиях и хорошо видна граница расслоения. Как ранее отмечалось, для скорости расслоения суспензии на твердую и жидкую фазы пока нет аналитических формул, поэтому последнюю определяют экспериментально. Суспензию равномерно перемешивают в цилиндре, а затем дают отстояться. По прошествии определенного времени можно заметить границу раздела между осветленной зоной и суспензией. В концентрированных суспензиях граница, как правило, бывает четкой (рис.5.3). Выше границы осаждения находится осветленная зона «А». При внимательном рассмотрении в суспензии также можно выделить и другие зоны — в первую очередь осадка из крупных частиц (зона уплотнения «D»), а над ней небольшую, менее уплотненную и несколько рыхлую переходную зону «С». Оставшаяся зона «В» в суспензии называется зоной свободного — 185 — 0.5 2.30 0.299 0.6 14.4 7.82 2.5 1.95 5.76 0.17 1 0.60 0.147 0.3 7.2 4.08 2.5 1.02 2.88 0.35 2 0.27 0.147 0.15 3.6 1.84 2.5 0.46 1.44 0.70 3 0.18 0.147 0.10 2.4 1.22 2.5 0.31 0.96 1.05 4 0.14 0.147 0.175 1.8 0.95 2.5 0.24 0.72 1.40 q= Vó .ñë F F 24 c = ρòâ Vï Q= Потери со сливом % Vn объем пробы, л Удельная площадь сгущения, м2/сутки 1 т f — 186 — Pтв Удельная нагрузка, т/м2 сутки qn Количество слива с 1 т твердого, Q м3/т Содержание твердого в сливе, кг/м3 Удельная производительность по сливу, м3/м2 сутки Скорость удаления слива, м/ч 0,3м/∆t=ࠓу.сп. Интервал времени между сливами, ∆t часы. Вес твердого в отобранном сливе, г Rï Rê Потери q = cQ = c<1 qï = Q ρæ c<10−3100% = % = 10−1 cQ f= 1 qí ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ Таблица 5.3. Результаты по сгущению суспензии (внутренний диаметр трубки 25мм, отношение Ж:Т в исходном 3,5:1. (Отбиралось 0,30 м или объем 0,147 л = Vn) ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐƿǪǭǮǃǮǂǬ͠ǃǮǯǰǀÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀ падения. Из нее в первую очередь выпали крупные частицы, которые частично захватили и более мелкие, и образовали нижележащие зоны «С» и «D». Поэтому концентрация частиц в зоне «В» значительно уменьшилась. В ряде случаев для расчета скорости осаждения частиц в зоне «В» можно применять закон Стокса. Рис.5.3. Процесс сгущения пульпы в стеклянном цилиндре: I – исходное состояние, II, III, IV – промежуточное состояние, V – критическое состояние и VI — уплотнение осадка. В дальнейшем частицы из зоны «В» переходят в зоны «С» и «D». Зона «В» уменьшается, зона «С» вообще исчезает. Высота, при которой зоны «В» и «С» исчезнут, а останутся только зоны «А» и «D», называется критической, а время ей соответствующее — критическим. Дальнейшее сгущение суспензии считается нецелесообразным, так как уплотнение суспензии происходит очень медленно, а сам процесс скорее напоминает «выжимание губки» под действием гидростатического столба жидкости. Процесс сгущения можно условно охарактеризовать 4-мя этапами — начальными, промежуточными, критическими и «уплотнение осадка». Если построить график, где на вертикальной оси отложить высоту осветленного слоя в мм, а на горизонтальной оси — соответствующее ей время, то получится — 187 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ Рис. 5.4. Кривая процесса сгущения. кривая, характеризующая процесс сгущения. Высоту осветленной зоны отсчитывают от границы раздела « суспензия — газ», рис.5.4. Через точки, нанесенные на графике, можно провести три прямые, соответствующие трем зонам в сгустителе. Первая от начала координат АВ — характеризует скорость свободного падения или скорость осветления, а соответствующая ей высота H1 = HКР — высоте «зоны свободного падения». Прямая ВС соответствует зоне уплотнения или зоне сжатия, а соответствующая ей высота H2 — высоте зоны уплотнения. Прямая DC, проведенная параллельно оси абсцисс через точку, соответствующую продолжительности осаждения (24 часа), характеризует конечное сжатие суспензии, а H3 — высоту осадка. Точка В соответствует критическому или оптимальному сгущению. По кривой процесса сгущения можно определить скорости осаждения твердых частиц: а) оптимальная скорость H ϑ0 = 1 (5.37) têð — 188 — ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐƿǪǭǮǃǮǂǬ͠ǃǮǯǰǀÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀ б) средняя скорость при заданной степени сгущения суспензии H (5.38) ϑi = i ti Практически не всегда можно наблюдать указанные зоны. Важно наблюдать за изменением зоны А и замерять ее в каждый период изменения скорости осаждения твердых частиц. Резкое уменьшение скорости осаждения дает возможность определить критическую точку В. ϱ͘Ϯ͘ϯ͘ϯ͘ˀ̸̵̨̨̨̛̛̭̖̯̱̖̣̦̜̪̖̬̦̭̯̭̱̺̖̦̌̔̽̏̐́ ̨̨̪̥̖̯̱̔ʶ̨̛̱ʶ̣̖̖̦̙̖̬̏̌͘ В методе Коу и Клевенжера удельная поверхность f рассчитывается по формуле f= Rn − RÊ ρæ ν0 K1 [м2 ·сутки/т] (5.39) где Rn и RK — Ж:Тв — исходное и конечное разжижение; ρж = = 1г/см3 или 1 т/м3 , a v0 — скорость осаждения, м/сут R − RÊ  ки. То есть предполагается, что количество воды  n   ρ æ с 1 тонны твердого должно удаляться со скоростью осаждения v0. Поскольку на практике возможны колебания в производительности, вводится коэффициент надежности К1 = 0,7 ÷ 0,8. Для того чтобы определить оптимальную скорость осаждения ࠓ0, проводятся опыты в мерных цилиндрах по расслоению пульпы при различных ее плотностях, начиная от исходной, которая может поступать в сгуститель, и кончая наибольшей плотностью в зоне свободного осаждения. Для каждой плотности получают кривую осаждения, из первоначального угла наклона которой рассчитывают скорость осаждения: ν0 = h0 − h1 [м/сутки] têð − t0 — 189 — (5.40) ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ где h0 — первоначальная высота суспензии; h1 — высота суспензии в момент времени tk; t0 — начало отсчета, t0 = 0; tкр — время осветления. По экспериментальным значениям v0 рассчитывается удельная площадь, необходимая для сгущения материала при различных разжижениях. Разжижение, соответствующее максимальному значению fmax считается критическим. По максимальному значению удельной площади сгущения fmах рассчитывается общая площадь сгустителя и его диаметр: F = fmax Q [м2] (5.41) где Q — производительность, т/ч ( π D2 − d 2 ) [м2] (5.42) 4 где D и d — диаметры соответственно сгустителя и питающего патрубка 4fQ + d2 [м] D= (5.43) π F= ϱ͘Ϯ͘ϯ͘ϰ͘ˀ̸̵̨̨̨̨̨̛̭̖̯̱̖̣̦̜̪̖̬̦̭̯̪̥̖̯̱̌̔̽̏̔ʶ̸̛̦̌͘ В методе Кинча f рассчитывается по формуле вида tp f = 695 [м2 · сутки/т] (5.44) c0h0 где 695 — переходный коэффициент от одних единиц измерения к другим; tp — расчетное время сгущения, мин: c0 — содержание твердого в исходной суспензии, г/л; h0 — исходная высота, мм. При использовании данного метода расчета отпадает необходимость в постановке опытов по определению скорости осаждения при различных плотностях суспензии. Кривую осаждения строят по результатам одного опыта, проведенного при средней плотности поступающего на сгущение продукта, tP соответствует времени достижения критической точки осаждения (рис.5.5). — 190 — ÐǤ͠ǀǂǬǃǬǃǀǬÐǅǬǃǰ͠ǮƻǬƾǃǮ֬ÐǯǀǁǊÐ͟͠ǀÐǮƻǬƿǫǮƾǀǫǪǃǀǀ ÐǣǯǃǮǫǃǊǬÐ͟Ǯǃǎǰǀǎ Точку В находят как пересечение кривой осаждения с биссектрисой угла, образованного касательной, проведенной к зоне свободного осаждения, и линией песков. Рис.5.5. Определение tp по методу Кинча Положение линии песков находится из состояния, h0C0 = = hПCП, где СП — желаемая степень сгущения. Желательно, чтобы положение линии hП было несколько ниже критической точки. ϱ͘ϯ͘ʿ̶̨̨̨̨̛̛̛̛̛̛̛̬̥̖̦̖̦̖̖̦̯̬̖̙̦̜̭̣̼̪̬̖̙̦̍̍̏̏̌̚͘ ʽ̨̨̛̭̦̦̼̖̪̦̯̏́́͘ Центробежная сила развивается в гидроциклонах и центрифугах. В первом случае вращательное движение суспензии происходит за счет подачи по касательной в аппарат цилиндрической формы, а во втором — за счет вращения суспензии в роторе центрифуги. Величина центробежной силы F зависит от радиуса: mν2 mπ2n2 R (5.45) = mω2 R = F= R 900 где m — масса; v — линейная скорость; ω — угловая скорость; n — число оборотов; R — текущий радиус. — 191 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ Поэтому аналитическое описание процессов расслоения осложняется. Центробежная сила в современных аппаратах может превышать силу тяжести в сотни и тысячи раз. Отношение центробежной силы к силе тяжести называется фактором разделения: π2n2 R (5.46) K= 900g Следовательно, в аппаратах, в которых развивается центробежная сила, процессы разделения ускоряются и происходят более полно. ϱ͘ϯ͘ϭ͘ʽ̨̡̨̨̨̛̛̛̭̦̦̼̖̦̥̖̬̦̭̯̬̖̣̖̦̭̱̭̪̖̦̜̏̌̌̔́̚̚̚ ̵̶̴̵̨̛̛̭̯̖̣̦̼̖̦̯̬̱̏̌̔̽̐̌͘ʰ̡̨̨̨̛̛̛̦̖̭̪̬̯̖̣̦̭̯̔̏̔̽̚͘ Скорость осаждающейся частицы под действием ценробежной силы не достигает предельного значения, как это имеет место при осаждении в поле тяжести. Дифференциальное уравнение движения частицы относительно жидкости, находящейся в поле центробежных сил, имеет вид: m dv πd3 2 λRe2µ2 = <ω r = 6 dt ρæ (5.47) где m — масса частицы, кГ; v — относительная скорость радиального движения частицы, м/сек; d — диаметр частицы, см; ∆ = ρтв — ρж , г/см; r — радиус вращения частицы; ω — угловая скорость, рад/сек; µ — вязкость кг/(м.сек); λ — коэффициент сопротивления. При Re < 0,2, когда имеем ламинарный закон движения частицы и сила сопротивления (второй член уравнения 4.47) определяется законом Ньютона: F = 6πµr ν , решение уравнения приобретает вид: w2rd2 (5.47) ì /ñ 18 Данное выражение аналогично закону Стокса, в котором g заменено на ω2 r. ν= — 192 — ÐǤ͠ǀǂǬǃǬǃǀǬÐǅǬǃǰ͠ǮƻǬƾǃǮ֬ÐǯǀǁǊÐ͟͠ǀÐǮƻǬƿǫǮƾǀǫǪǃǀǀ ÐǣǯǃǮǫǃǊǬÐ͟Ǯǃǎǰǀǎ Производительность по твердому можно приблизительно оценить по формуле: VdVw2r 3 (5.49) Qтв = м /с 9µh где V — объем суспензии в роторе центрифуги; h — толщина осадка; r — радиус трубчатого ротора центрифуги. Задавшись Qтв из этого уравнения, можно оценить граничный диаметр частиц, уходящих в слив. Уравнение для расхода часто записывают в виде: Qтв = 2Ug Σ м3/с (5.50) где Ug — предельная скорость осаждения в поле силы тяжести, м/сек; Σ — индекс производительности центрифуги. Он показывает во сколько раз нужна большая площадь в м2 ротора в отсутствии центробежного ускорения, обеспечивающего такое же осаждение частиц, как и в центрифуге. Индекс производительности Σ можно определить через фактор разделения Кр, как: Σ = FK p (для ламинарного движения) Σ = FK 0,785 (в переходном режиме) p Σ = FK 0,5 (в турбулентном режиме) p где F — площадь цилиндрической поверхности осаждения. При увеличении значения Re происходит замедление роста эффективности действия центрифуг. Для цилиндрической центрифуги значения Кр и F можно рассчитать по формулам: 2 K= πD2 w2r  2πn  r n2 D ≈ , F= l   g g 1800 60 4 (5.51) где l — длина цилиндрической части ротора; D — его диаметр; n — число оборотов ротора. На практике жидкость находится на расстоянии, равном не диаметру центрифуги, а (D – h) , где h — толщина слоя осадка. Поэтому величину фактора разделения относят к среднему диаметру (D – h) и выражения для Кр и F — 193 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ примут вид: K p = ( D − h)n2 , F = 2πr0l 1800 где r0 — радиус свободной поверхности жидкости; l — длина ротора. Подставив значение для F и Кр, получим:  ( D − h )2 n2  (5.52)  Σ = FK np = πl   1800  Σ — для трубчатых: 120–2520, Σ — для тарельчатых: 6300–12400, Σ — со шнековой выгрузкой: 560–600. ϱ͘ϰ͘ˇ̨̛̛̣̯̬̦̖̽̏̌͘ʽ̨̨̛̭̦̦̼̖̪̦̯̏́́͘ ʶ̴̶̡̛̛̛̣̭̭̌̌́͘ Фильтрование — это процесс отделения нерастворимых твердых частиц от раствора с пористых перегородок, которые пропускают жидкость и задерживают твердые частицы. Процессы фильтрования и фильтры классифицируют по ряду признаков: 1. По характеру процесса с образованием осадка и без него с закупориванием пор (без осадка). Целью первого процесса является получение товарного продукта в виде осадка, а второго — фильтрата. В первом случае содержание твердого в исходной суспензии обычно не менее 50,0% (объемных), а во втором — не более 0,1 ÷ 1,0%. В каналах осадка преимущественно задерживаются твердые частицы более 1 ÷ 2 мкм. Частицы менее 1 мкм можно отделить только фильтрованием с закупориванием пор или ультра фильтрованием. При обогащении, полезных ископаемых, в химической промышленности, металлургии имеет место фильтрация с образованием осадка, так как даже в случае осветления оборотных вод чаще всего получаются осадки. На практике часто оба вида фильтрования протекают одновременно. Однако преимущественно в каждом конкретном случае наблюдается либо первый, либо второй. Смена типов фильтрования может происходить во времени. — 194 — ÐǨǀǁǋǰ͠ǮǫǪǃǀǬ ÐǣǯǃǮǫǃǊǬÐ͟Ǯǃǎǰǀǎ ǠǁǪǯǯǀǄǀǭǪǅǀǎ 2. По способу создания разности давлений — под вакуумом или под избыточным давлением. Отделение жидкости за счет собственного веса — дренирование и за счет центробежных сил — центробежное фильтрование. 3. По взаимному направлению действия силы тяжести и движения фильтрата в фильтрах (рис.4.1). 4. По свойствам осадка. Накапливающийся в фильтре осадок может быть как сжимаемым, так и почти несжимаемым. Под несжимаемыми понимают такие осадки, в которых пористость ε, то есть отношение объема пор (V) к объему осадка (Vос), не уменьшается при увеличении разности давлений. Пористость сжимаемых осадков уменьшается, а их гидравлическое сопротивление потоку жидкой фазы возрастает с увеличением давления. 5. К числу практически несжимаемых можно отнести осадки, состоящие из относительно крупных кристаллических частиц более 70 ÷ 100 мкм. К сильно сжимаемым относятся аморфные осадки гидроокисей металлов, а также осадки, состоящие из легко деформируемых агрегатов, которые образуются из первичных мелких частиц. По этой причине флокулированные суспензии не всегда быстрее обезвоживаются при фильтровании, и, вероятно, необходимо в ряде случаев уменьшать давление. Фильтрация с применением вспомогательного вещества, которое препятствует проникновению твердых частиц в поры фильтровальной перегородки. В качестве вспомогательных веществ используют доломит, перлит, асбест, целлюлозу, активированный уголь, древесную муку. Слой вспомогательного вещества наносят на фильтровальную перегородку толщиной не более 50 мм или добавляют в суспензию в количестве не более 1% веса суспензии. При непрерывном съеме осадка срезается небольшой слой около 0,1 мм вспомогательного вещества и поэтому процесс идет как бы с самоочищающейся разделительной перегородкой. Добавление вспомогательного вещества к разделяемой суспензии способствует повышению ее концентрации и переходу из процесса с закупориванием пор к процессу с образованием — 195 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ осадка. Предполагается, что образуются сводики над входами в поры фильтровальной перегородки, что предотвращает их закупоривание. В производственных условиях под фильтрованием понимают не только операцию разделения суспензии на фильтрат и осадок, но и последующие операции промывки, продувки и сушки осадка на фильтре. Все эти операции и процесс загрузки и снятия осадка называют вспомогательными. ϱ͘ϰ͘ϭ͘ˇ̸̴̶̡̨̨̛̛̛̛̛̛̖̭̖̭̦̼̣̯̬̏̽̌̚ ̨̨̨̡̛̭̬̦̖̥̭̍̌̏̌̌̔̌̚͘ʧ̸̨̡̛̛̛̛̬̦̥̯̖̖̦̔̔̌̌́ ̸̡̨̨̨̛̛̛̛̛̛̙̭̯̖̬̖̪̬̭̯̼̖̖̬̦̭̯̼̖̭̣̔̚̚͘ В самом общем виде скорость течения жидкости через пористый или зернистый слой — осадок, как было показано выше, определяется размерами пор и перепадом давления: lρ W 2 (5.53) ∆p = λ ж 2d где ∆р — перепад давлений; ρж — удельная масса воды; W — скорость течения воды; l — длина капилляров в осадке; dэ — эквивалентный диаметр, соответствующий суммарному поперечному сечению каналов в зернистом слое; λ — общий коэффициент сопротивления. Коэффициент сопротивления отражает не только влияние сопротивления трению, но и дополнительных местных сопротивлений. Значение коэффициента λ зависит от режима течения жидкости. Для всех режимов движения применимо, в частности, обобщенное уравнение: 133 (5.54) λ= + 2,34 Re Характерной особенностью движения жидкости через зернистый слой является более раннее наступление переходного режима, чем при течении по трубам, так как поры в осадке не гладкие и способствуют образованию вихрей. Ламинарный ражим практически существует примерно при Rе < 50. Необхо— 196 — ÐǨǀǁǋǰ͠ǮǫǪǃǀǬ ÐǣǯǃǮǫǃǊǬÐ͟Ǯǃǎǰǀǎ ǠǁǪǯǯǀǄǀǭǪǅǀǎ димо отметить, что при течении жидкости в осадке нет резких границ между режимами. При больших значениях числа Re коэффициент сопротивления λ практически постоянен: λ ≅ 2,34 . Эквивалентный диаметр dэ находят через основные характеристики зернистого слоя. К ним относятся: величина удельной поверхности — а (м2/м3) и пористость — ε осадка. Удельная поверхность а (м2/м3) представляет собой поверхность зерен или частиц осадка, находящихся в единице объема. Величина а определяется экспериментально. Долю свободного объема или пористость находят по формуле: V − V0 ρ − ρ0 (5.55) ε= = ρ V где V — общий объем осадка;V0 — объем, занимаемый только частицами; ρ и ρ0 — удельная и насыпная массы. Рис.5.6. Взаимные направления действия силы тяжести и движения фильтрата в фильтрах: а — направления совпадают; б — направления противоположны; в — направления перпендикулярны; сплошные стрелки — направление действия силы тяжести; пунктирные стрелки — направление движения фильтрата; 1 — фильтровальная перегородка; 2 — осадок; 3 — суспензия; 4 — фильтрат; 5 — чистая жидкость — 197 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ Эквивалентный диаметр равен отношению: 4S 4Sос ε 4ε (5.56) = = П Sос a a где S — площадь сечения каналов; П — периметр сечения; Sос — геометрическая поверхность осадка. Удельную площадь можно выразить через пористость: dэ = 6 (1 − ε ) (5.57) Фd где d — диаметр частиц; Ф — фактор формы, характеризующий степень отклонения формы частицы от сферической. Тогда с учетом (5.1) dэ выразится: 2Фεd dэ = (5.58) 3(1 − ε ) Поскольку на практике скорость прохождения воды через осадок W0 определяют как частное от деления объема воды V на геометрическую поверхность осадка, а в формулу входит истинная скорость течения жидкости по каналам осадка, то ее можно найти как: W V W= 0 = (5.59) S ос εt ε где t — время фильтрации объема V. Необходимо еще отметить, что длина пор в осадке l, как правило, больше высоты осадка Н. Это различие учитывается коэффициентом кривизны к, так как кН = l. Очевидно, что к > 1. Однако эту кривизну не учитывают, так как она не существенна. Теперь основное уравнение течения жидкости через пористую среду можно записать в виде: H  W0  λ ρ 3H (1 − ε ) ρжW02 2Фεd ж  ε  (5.60) ∆p = = λ 2 4d Фε2 3(1 − ε ) a= При фильтровании через пористую среду часто имеет место ламинарный режим течения жидкости. В этом случае можно принять, что: — 198 — ÐǨǀǁǋǰ͠ǮǫǪǃǀǬ ÐǣǯǃǮǫǃǊǬÐ͟Ǯǃǎǰǀǎ ǠǁǪǯǯǀǄǀǭǪǅǀǎ λ= 133 Wdж ρж 2W0dρ жФ , а Re = = Re 3µ (1 − ε ) µ Тогда уравнение (4.60) после простых преобразований примет вид: 2 ϕ (1 − ε ) µHW0 (5.61) ∆p = 150 ф ε 2d 2 где φф — коэффициент формы, связанный с фактором формы соотношением: ϕ ф = 1 Ф2 Как видно, перепад давления пропорционален скорости течения жидкости в первой степени. Коэффициент пропорциональности называют коэффициентом сопротивления осадка: ∆p ∆p = µRос W0 ; W0 = µRос 150ϕ ф (1 − ε ) H 2 (5.62) ε 2d 2 Как видно Rос обратно пропорционально d2 частиц, поэтому размер частиц в осадке в первую очередь определяет его сопротивление течению жидкости. Rос = ϱ͘ϰ͘Ϯ͘ʽ̴̶̨̛̛̛̛̭̦̦̼̖̱̬̦̖̦̣̯̬̏̌̏́̽̌͘ Скорость процесса пропорциональна движущей силе (∆P) и обратно пропорциональна сопротивлению. В общем случае в процессе фильтрования значения разности давлений и гидравлического сопротивления слоя осадка с течением времени изменяются. Переменную скорость фильтрования выражают в дифференциальной форме: dV (5.63) W= Sdτ где V — объем жидкости, прошедший через поверхность осадка S за время τ. При описании процесса фильтрации принято общее сопротивление движению жидкости представлять в виде сум— 199 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ мы сопротивлений осадка Rос и фильтрованной перегородки R фп = Rос + R фп. В общем виде дифференциальное уравнение R фильтрации примет вид dV ∆P = W= (5.64) sDτ µ ( Rос + R фп ) Гидравлическое сопротивление осадка Rос в среднем можно считать постоянным, хотя оно нередко меняется по ходу процесса фильтрования из-за засорения пор мелкими частицами, а также некоторого сжатия осадка. Считается, что диапазон изменения пористости вследствие засорения и сжатия осадка при постоянных условиях фильтрации более или менее одинаков. Поэтому целесообразно в ряде случаев оперировать с величинами удельных сопротивлений осадков. Значение Rос с увеличением толщины осадка изменяется от нуля в начале фильтрования до максимального значения в конце процесса. Объем осадка пропорционален объему пульпы. Если этот коэффициент равен x0, а его объем равен V, то высота осадка составляет xV (5.65) H= 0 S Удельное и полное сопротивления между собой связаны выражение Rос = r0 H = r0x0 V S С учетом этого выражения дифференциальное уравнение фильтрации примет вид ∆P dV (5.66) = W= V Sdτ   µ  r0x0 + R фп    S При допущении постоянства удельного сопротивления осадка дифференциальное уравнение фильтрации можно проинтегрировать в трех предельных случаях: 1) когда ∆P = const; dV 2) когда = const; dτ dV 3) когда ∆P и = const. dτ — 200 — ÐǨǀǁǋǰ͠ǮǫǪǃǀǬ ÐǣǯǃǮǫǃǊǬÐ͟Ǯǃǎǰǀǎ ǠǁǪǯǯǀǄǀǭǪǅǀǎ На практике процесс фильтрации, как правило, протекает при постоянной разности давлений. В этом случае после интегрирования получим следующее уравнение: V   (5.67) S0τ µ  r0x0 + Rфп  dV = S0τ ∆PSdτ   S Или V2 (5.68) + µRфпV = ∆PSτ 2S Разделив обе части последнего уравнения на µr0x0 2S , окончательно получим 2Rôï S ∆PS2 (5.69) τ V2 + V =2 r0x0 µr0x0 Поскольку при ∆P = const величины r0 и x0 обычно постоянны, то это уравнение применимо для сжимаемых и несжимаемых осадков. При постоянной скорости фильтрации, т.е. когда скорость подачи суспензии равна скорости фильтрации, дифференциал V τ можно заменить отношением конечных величин и уравнение фильтрации примет вид V2 V (5.70) ∆P = µr0x0 2 + µRôï Sτ S τ V = const, можно записать: а учитывая, что W = Sτ (5.71) ∆P = µr0x0W 2 + µRôï W Из уравнения видно, что для увеличения скорости фильтрации необходимо повысить давление. Это уравнение применимо только к несжимаемым осадкам, так как с ростом давления осадок сжимается и увеличивается его удельное сопротивление r0. Если жидкость фильтруется сквозь осадок постоянной толщины, то ∆Р = const, W = const и дифференциальное уравнение фильтрации упрощается: ∆PSτ V= (5.72) µ r0 H + Rôï µr0x0 ( — 201 — ) ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ Так как H постоянна, то в последнем выражении величиV на x0 заменяется на H. S Данное уравнение применимо при фильтрации оборотных вод через пористые фильтры. Оно применимо для сжимаемых и несжимаемых осадков, так как ∆Р = const. ϱ͘ϰ͘ϯ͘ʿ̴̶̛̛̛̛̛̛̬̥̖̦̖̦̖̱̬̦̖̦̣̯̬̌̏́̽̌͘ ʽ̨̨̨̨̛̛̛̪̬̖̖̣̖̦̖̱̖̣̦̭̪̬̯̣̖̦̔̔̽̐̏́ ̨̡̨̨̛̛̛̭̖̭̙̥̖̥̭̯̌̔̌̐̌͘ Уравнение фильтрования редко используется для практических расчетов производительности фильтровального оборудования, но оно необходимо при объяснении результатов лабораторных опытов, нахождении оптимальных условий фильтрования и определения влияний действующих факторов на процесс. Поскольку константы r0 и Rфп сильно зависят от свойств суспензий, то перенесение данных, полученных в одних условиях, на другие условия фильтрования даже одинаковых суспензий, но несколько различающихся гранулометрическим составом, часто дает большие ошибки. Поэтому полученные данные характеризуют фильтрацию пульпы в определенных условиях. Уравнение фильтрования применяется для нахождения r0 и Rфп и изучения влияния различных факторов (условий перемешивания, концентрации и природы реагентов — флокулянтов, температуры и др.). Для этого проводится фильтрование при постоянных давлении, температуре и концентрации твердой фазы в суспензии, определяется количество фильтрата, прошедшее за время фильтрации. Типичный вид установки показан на рис 5.7. Поскольку основное уравнение фильтрования при ∆P = = const в координатах τ/V и V представляет уравнение прямой линии, которую строят по опытным данным, 1 µr0x0 V µRôï τ + = 2 ∆P S2 S∆P V (5.73) — 202 — ÐǨǀǁǋǰ͠ǮǫǪǃǀǬ ÐǣǯǃǮǫǃǊǬÐ͟Ǯǃǎǰǀǎ ǠǁǪǯǯǀǄǀǭǪǅǀǎ Рис.5.7. Лабораторная фильтровальная вакуум-установка: 1 — ванна для пульпы; 2 — фильтрующая воронка; 3 — сборник фильтрата; 4 — вакуум-насос; 5 — ртутный манометр Рис.5.8. К определению удельного сопротивления осадка и сопротивления фильтровальной перегородки. — 203 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ то из прямой М и отрезка, отсекаемого на оси абсцисс (рис.5.8.), можно рассчитать искомые величины r0 и Rфп: ∆PS 2∆PS2 (5.74) r0 = M ; Rôï = N µx0 µ Влияние различных факторов на r0 и Rфп определяют из результатов опытов, поставленных при P = const и равном давлении в нулевом опыте. Для определения эффекта изменения давления необходимо провести опыты при различных давлениях и вычислить описанным способом соответствующие значения r0 и Rфп. Экспериментально установлено, что удельное сопротивление осадка r0 с увеличением давления измеряется по зависимости типа (5.75) r0 = r0′PS — постоянная, зависящая в значительной степени от разгде r0′P мера частиц, образующих осадок; S – коэффициент сжимаемости осадка, изменяющийся от 0 для совершенно несжимаемых осадков до 1,0 для сильно сжимаемых. Для большинства промышленных осадков значение S колеблется в пределах 1,0 ÷ 0,8. Рис. 5.9. Определение сжимаемости осадка из опытных данных. — 204 — ÐǨǀǁǋǰ͠ǮǫǪǃǀǬ ÐǣǯǃǮǫǃǊǬÐ͟Ǯǃǎǰǀǎ ǠǁǪǯǯǀǄǀǭǪǅǀǎ Поэтому при нанесении полученных данных в координатах lgr0–lgP и lgRфпílgP часто получают прямые линии, на основании которых можно вычислить S и r0 (рис.5.9). Для многих случаев Rфп не изменяется сколько-нибудь заметно при увеличении давления, поэтому можно принять среднее значение Rфп для всего диапазона давлений тонкодисперсных частиц. ϱ͘ϰ͘ϰ͘ˇ̸̡̨̨̛̛̛̛̛̖̭̖̭̦̼̬̖̣̖̦̭̱̭̪̖̦̜̏̌̔́̚̚̚ ̴̵̶̴̵̛̛̛̣̯̬̱̺̖̦̯̬̱̏̽̀̐̌͘ Процесс центробежного фильтрования сложнее, чем фильтрование под влиянием силы тяжести или под давлением. В данном случае поверхность фильтрования и движущая сила процесса возрастают с увеличением радиуса слоя осадка. Существенно может измениться и удельное сопротивление осадка в зависимости от толщины слоя. Выбор центрифуг подачи всегда производится на основании предварительных лабораторных опытов. Когда образовавшийся в центрифуге осадок затоплен жидкостью, скорость протекания через него фильтрата примерно соответствует величинам, найденным при фильтровании под соответствующим давлением. В случае несжимаемых или почти несжимаемых осадков скорость фильтрования может быть вычислена по уравнению: Q= ( ρж ω2 r22 − r12 ) [м3/сек ] (5.76)  αm т Rср  2µ  + Sф   S ср. лог. Sср. ар. где Q — объемная скорость вытекающей жидкости, м3/сек; ω — угловая скорость вращения, рад/сек; ρж — удельная масса жидкости, кг/м3; r1 и r2 — радиус поверхности жидкости и внутренний радиус ротора, м; µ — вязкость жидкости, кг/(м·сек); α — удельное сопротивление осадка, м/кг; mт — масса твердого осадка в роторе, кг; Sср. лог. и Sср. ар. — среднелогарифмическое и среднеарифметическое значения площади осадка, м2; Rср — удельное сопротивление фильтра, м−1; Sср — площадь фильтра, м2. — 205 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ Средние площади осадка определяются из уравнений: Sср. лог. = 2πh (r2 − r1 ) r ln 2 r1 (5.77) Sср. ар. = (r2 − r1 ) πh (5.78) где h — высота осадка; ri — радиус внутренней поверхности осадка, м. Определить заранее необходимую продолжительность центрифугирования и конечную влажность осадка в роторе центрифуги несколько сложнее, чем предсказать скорость фильтрования. Время фильтрации может колебаться от 10 ÷ 20 сек до 5 ÷ 15 мин. Влажность осадка после центрифугирования значительно меньше, чем после фильтрования, даже если осадок продут воздухом. После центрифугирования остается 40–60 % от количества жидкости, содержащейся в осадке после фильтрования. Остается жидкость, которая удерживается исключительно капиллярными и молекулярными силами. При повышении скорости вращения ротора в некоторых случаях остаточная влажность снижается очень незначительно, а в других — на очень значительную величину. Максимальное значение коэффициента разделения Кр ограничивается тем, что напряжение давления жидкости на стенки ротора центрифуги возрастает быстрее, чем величина центробежной силы: ( ) 2 [кгс / см2] P = 1,36i10−3 n2ρж D2p − Dвн где P — давление жидкости на стенки ротора; n — число оборотов ротора в минуту; ρж — плотность жидкости; Dр — диаметр ротора, см; Dвн — внутренний диаметр слоя жидкости, см. Величина напряжений пропорциональна D2, а центробежная сила (m·ω2·D/2) только диаметру в первой степени. Поэтому трудно выработать конструкционный материал, который выдержал бы возрастающее давление жидкости. — 206 — ÐǠǮǃǰ͠ǮǁǋǃǊǬÐǫǮ͟͠ǮǯǊ ϱ͘ϱ͘ʽ̵̸̶̨̨̛̛̛̯̖̣̖̦̖̯̖̬̼̭̯̜̭̬̖̼̔̏̔̌̐̌̏̔̚̚ ̸̡̡̨̨̛̣̖̯̬̖̭̥̪̣̖̏̾͘ Для отделения твердых частиц из газовой среды в настоящее время широко используют электрофильтры. В электрофильтрах применяется метод ионизации частиц пыли и осаждения их в электрическом поле. Коронирующий электрод соединен с источником постоянного тока высокого напряжения и расположен внутри металлической трубы, являющейся осадительным электродом. Осадительный электрод, как правило, соединен с отрицательным полюсом источника высокого напряжения. Газ находящийся между коронирующим и осадительным электродами, ионизируются. Положительные ионы адсорбируются на частицах пыли, придавая им положительный заряд. Заряженные частицы притягиваются отрицательным или зарядом осадительного электрода, теряют при этом свой заряд и оседают на стенках трубы. Слой пыли со стенки трубы ссыпается в накопительный бункер металлического корпуса фильтра. Металлическая конструкция фильтра позволяет работать при повышенной температуре очищаемого газа. Различают сухие и мокрые электрофильтры. Сухие электрофильтры применяют для очистки газов от пыли, а мокрые — от мельчайших капелек жидкости, взвешенных в газе. Кроме того мокрые электрофильтры можно применять для улавливания туманообразных веществ. В электрофильтрах улавливается пыль размером от 0,01 до 100 мкм при малых затратах электроэнергии. КПД фильтра при этом до 99%, однако, он значительно снижается при частицах малого размера из-за малой вероятности адсорбции на них положительных ионов. ϱ͘ϲ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏͘ 1. Как определить степень очистки газа при гравитационном осаждении? 2. От каких факторов зависит степень очистки газа при гравитационном осаждении? — 207 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ 3. Как работают пылеуловители, основанные на использовании силы инерции ? 4. Как составить дифференциальное уравнение, описывающее работу циклона? 5. От каких факторов зависит степень очистки газа в циклоне? 6. Какое физическое явление лежит в основе фильтрации? 7. Какие физические механизмы возможны при прохождение газа через пористую среду? 8. Какие пористые перегородки используют в фильтрах для отчистки газов и каковы принципы их выбора? 9. Как классифицируются современные фильтры в зависимости от назначения и величины входной и выходной концентрации? 10. Как устроен и для каких целей используется электрофильтр? 11. Какое физическое явление лежит в основе работы электрофильтра? 12. Почему электрофильтр не всегда позволяет убрать наиболее мелкие частицы из газового потока? 13. Какие основные факторы влияют на эффективность работы электрофильтра? 14. Отстаивание под действием силы тяжести. Классификация суспензий. 15. Как определить среднюю скорость осаждения частиц в сгустителе. 16. Какие зоны проходит частица по высоте в сгустителе. Как эти зоны характеризуются по плотности суспензии. 17. При какой начальной плотности суспензии скорость осаждения материала будет больше при Т:Ж=1:8 или Т:Ж=1:12? Дайте Ваши соображения. 18. Какое практическое значение имеют полученные результаты по обезвоживанию материала методом сгущения. 19. Ламинарный и турбулентный режим движения жидкости. Характеристика твердых частиц в зависимости от их размеров. — 208 — ÐǤ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ 20. Для какого режима течения жидкости число Рейнольдса; концентрация твердого, крупность частиц, скорость осаждения частиц списывается законом Стокса. 21. Процесс фильтрования, его разновидности и основные механизмы. 22. Процесс фильтрования при постоянной разности давлений. Область применения данного процесса. Понятие о сжимаемых и несжимаемых осадках. 23. Основное уравнение фильтрации и его решение. 24. Применение основного уравнения фильтрации. Определение удельного сопротивления осадка и его сжимаемости. 25. Какие, по вашему, факторы влияют на скорость фильтрации? 26. Сопротивлении осадка. Факторы влияющие на величину сопротивления осадка. 27. Применение центробежной силы при обезвоживании. 28. Основные закономерности силы при обезвоживании. 29. В чем сходство и в чем различие осаждения частицы под воздействием центробежной силы по сравнению с осаждением под действием силы тяжести. 30. Что такое фактор разделения? От каких величин он зависит? Как выбрать режим центробежного фильтрования. 31. Провести сравнение методов механического обезвоживания, выявив основные достоинства и недостатки методов. Можно ли на Ваш взгляд добиться полного обезвоживания продукта механическими методами? ϱ͘ϳ͘ʿ̸̛̛̬̥̖̬̼̬̖̹̖̦́̌̔̌̚͘ ϱ͘ϳ͘ϭ͘ʽ̛̭̙̖̦̖̌̔͘ Задача 1. Найти верхний предел (т. е. наибольший диаметр частиц) применимости формулы Стокса к частицам кварца плотностью 2650 кг/м3, осаждающимся в воде при 20 °С. Решение. Формула Стокса строго применима при Аr <3,6. Поэтому наибольшая частица кварца, осаждение которой может быть рассчитано по формуле Стокса, должна иметь диаметр: — 209 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ d=3 3.6<12 <10−6 = 60<10−6 м = 60 мкм (2650 − 1000)1000<9.81 Задача 2. Найти скорость осаждения в воде частиц кварцевого песка шарообразной формы диаметром 0,9 мм, если плотность песка 2650 кг/м3, а температура воды 20 °С. Решение. Определяем критерий Аr: d3 (ρ − ρc ) ρc g 0,93 <10−9 (2650 − 1000)1000<9,81 = = 1,18<104 Ar = 12 <10−6 µ2c где для воды μc= 1 10–3 Па с Рис. 5.10. Зависимость критериев Re и Ly от критерия Аr для осаждения одиночном частицы в неподвижной среде. — 210 — ÐǤ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ По значению Ar = 1,18–104 из рис. 5.10 находим Re = 140. Скорость осаждения частиц кварцевого песка шарообразной формы диаметром 0,9 мм определяем из выражения: Reµ c 140<1<10−3 ω oc = = = 0,15 0,0009<1000 dρc Задача 3. Определить размер наименьших частиц, осаждающихся в газоходе квадратного сечения длиной 16 м и высотой 2 м при линейной скорости газа 0,5 м/с. Вязкость газа 0,03–10–3 Па •с, плотность газа 0,8 кг/м3, плотность частиц 4000 кг/м3. Решение. Газ проходит канал в течение 16 τ= = 32 с 0,5 За это время успеют полностью осесть только те частицы, действительная скорость осаждения которых не меньше, чем 2 ω ос = = 0,062 м/с 32 Определим диаметр шарообразных частиц, теоретическая скорость осаждения которых вдвое больше, т. е. равна 0,124 м/с. Вычислим значение критерия Ly по формуле: ω2 ρ2 0,12430,83 Ly = oc c = = 1,035<10−3 µ cρg 0,03<10−3 ⟩4000<9,81 По графику (рис. 5.10) находим значение Re = 0,14, откуда d= Reµ c 0,14i3i10−2 i10−3 = = 4,24i10−5 м = 42,4 мкм 0,124i0,8 ω ocρc ϱ͘ϳ͘Ϯ͘ˇ̨̛̛̣̯̬̦̖̽̏̌͘ Задача 1. Вывести формулу, дающую зависимость между массой сухого осадка на 1 м3 фильтрата, плотностью фильтрата, концентрацией суспензии и влажностью осадка. — 211 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ Решение. Уравнение материального баланса процесса фильтрования: Gсусп + Gф = Gвл.ос где Gсусп, Gф и Gвл.ос — масса суспензии, фильтрата и влажного осадка, соответственно. Разделим это уравнение на Gсух-массу сухого вещества, содержащегося в суспензии: G сусп Gф G вл.ос = + G сух G сух G сух Массу фильтрата заменим произведением объема фильтрата на его плотность:Gф = Vф ρ Введем обозначения: G кг влажного осадка ; m = вл.ос кг сухого вещества Gсух кг сухого вещества кг сухого вещества G G ; с = сух x = сух м 3 фильтрата кг суспензии Gф G сусп Тогда уравнение можно переписать так: Откуда c = ρx 1 − mx 1 ρ = +m x c Задача 2. Определить продолжительность фильтрования 10 дм3 жидкости через 1 м2 фильтра, если при предварительном испытании фильтра с 1 м2 было собрано фильтрата: 1 дм3 через 2,25 мин и 3 дм3 через 14,5 мин после начала фильтрования. Решение. По опытным данным находим экспериментальные константы К и С в уравнении фильтрования: V 2 = 2VC = Kτ Для этого составляем два уравнения с двумя неизвестными: 12 + 2<1<C = K <2,25 ; 32 + 2<3<C = K <14,5 откуда К = 0,77 дм6/(м4-мин) и С = 0,37 дм3/м2. Для определения искомой продолжительности фильтрования полученные значения констант и заданный объем фильтрата подставляем в уравнение фильтрования: 102 + 2<10<0,37 = 0,77τ, откуда τ= 140 мин или 2 ч 20 мин. — 212 — ÐǤ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ Задача 3. Во время опытного фильтрования водной суспензии с содержанием 13,9% карбоната кальция при 20 °С на лабораторном фильтрпрессе с F = 0,1 м2 и толщиной осадка 50 мм были получены данные, приведенные в таблице. Определить константы фильтрования: К (в м2/ч) и С (в м3/м2). При избыточном давлении Собрано фильтрата, дм3 Время от начала опыта Па Кгс/см2 3,43 ·104 0,35 2,92 146 10,3 ·104 1,05 7,80 888 2,45 50 9,80 660 Решение. Численные значения констант фильтрования найдем из уравнения (3.13): V 2 = 2VC = Kτ При избыточном давлении 3,43–104 Па (0,35 кгс/см2) результаты опытов дают: 146 2,92 = 0,0405 ч = 2,92<10−2 м3/м2 ; τ1 = V1 = 3600 1000<0,1 V2 = 7,8 888 = 7,8<10−2 м3/м2 ; τ2 = = 0,246 ч 1000<0,1 3600 Подставляем пересчитанные величины в уравнение и решаем систему уравнений: (2,92<10 ) + 2<2,92<10 С = К<0,0405 (7,8<10 ) + 2<7,8<10 С = КÊ <0,246 −2 2 −2 2 −2 −2 откуда К = 278–10–4 м2/ч; С = 4,7·10–3 м3/м2. Аналогичным образом вычисляем константы К и С для избыточного давления 10,3–104 Па (1,05 кгс/см2). Получаем следующие значения констант фильтрования: К = 560–10–4 м2/ч; С = 3,78 10–3 м3/м2. — 213 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ ϱ͘ϳ͘ϯ͘ˉ̴̨̛̛̛̖̦̯̬̱̬̦̖̐̏̌͘ Задача 1. Центрифуга периодического действия имеет барабан с внутренним диаметром 1200 мм, высотой 550 мм, толщиной стенок 10 мм и массой 120 кг. Число отверстий в стенке барабана по вертикали 12, диаметр отверстий 5 мм. На барабан надеты три стальных обруча сечением 15 u 30 мм2 каждый. Материал барабана — сталь с временным сопротивлением на разрыв 4500 кгс/см2. Масса загрузки 400 кг, толщина слоя 200 мм. Найти предельно допустимую частоту вращения центрифуги, если запас прочности не должен быть менее 5. Решение. Для данной стали допускаемое напряжение на разрыв 4500i9,81i104 Kz = = 8,83i102 Па или 900 кгс2 см 5 Площадь сечения стенки барабана и обручей за вычетом отверстий: f = 55<1 − 12<1<0,5 + 3<3<1,5 = 6,25<10−3 м2 Из формулы следует, что максимально допустимая центробежная сила: C1 + C2 = 8,83<107 <2<6,25<10−3 = 1,1<106 H Расстояние от центра тяжести полукольца стенки барабана до оси вращения находим по формуле: 4  0,613 − 0,63  =0,387 Rб = 3<3,14  0,612 − 0,62  Центробежная сила, развиваемая половиной барабана, согласно уравнению C1 = 0,011<60<0,387n2 = 0,253n2 H Расстояние от центра тяжести полукольца загрузки до оси вращения  0,63 − 0,43  4 = 0,32 м Rз =  3 ⊗ 3,14  0,62 − 0,42  Центробежная сила, развиваемая полукольцом загрузки C2 = 0,011<200<0,32n2 H = 0,697n2 H Общая центробежная сила C1 + C2 = 0,253n2 + 0,697n2 = = 0,950n2 H . — 214 — ÐǤ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ Выше было найдено, что центробежная сила не должна превышать 1,1–106 Н. Следовательно, максимально допустимая частота вращения центрифуги: n= 1,1<106 =1070 об/мин=1738 об/с 0,950 Задача 2. Определить часовую производительность (по питанию) автоматической осадительной центрифуги АОГ8ОО при работе ее на водной суспензии гидроксида магния. Плотность частиц ρ = 2525 кг/м3. Температура суспензии 30 °С. Наименьший диаметр частиц 3 мкм. Характеристика центрифуги: диаметр барабана 800 мм; длина барабана 400 мм; диаметр борта 570 мм; частота вращения 1200 об/мин. Цикл работы центрифуги составляет 20 мин; из них 18 мин — подача суспензии, 2 мин — разгрузка осадка. Решение. Производительность определяем по формуле: Vч = 25,3ηLn2 R02ω î ñk Скорость осаждения частиц находим по формуле Стокса: ω ос = d2 (ρ − ρc ) g 18µ c = 32 (2525 − 1000)9,81 1012 i18i0,8i10−3 0,935i10−5 м /с Динамический коэффициент вязкости воды при 30 °С μс = = 0,8–10–3 Па-с Определяем скорость осаждения под действием центробежной силы: R n2 0,285i12002 ω = ω ос 0 0,935i10−5 = 4,26i10−3м /с 900 900 Проверяем режим осаждения: ωdρc 4,26<10−3 <3<10−6 <103 Re = = = 1,6<10−2 µc 0,8<10−3 т. е. режим ламинарный. Далее находим: k= 18/20 = 0,9. Производительность центрифуги, принимая η = 0,45: Vч = 25,.3<0,450,4<12002 <0,2852 <0,935<10−5 <0,9 = 4,46 м2/ч — 215 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ Задача 3. Определить, какую производительность может обеспечить трубчатая сверхцентрифуга СГО-150 с трехлопастной крыльчаткой, работающая на осветлении минерального масла. Плотность масла ρc = 900 кг/м3. Динамический коэффициент вязкости масла при температуре центрифугирования 3–10–3 Па с. Плотность твердых частиц ρ = 1400 кг/м3. Диаметр частиц 1 мкм. Техническая характеристика центрифуги: внутренний диаметр барабана 150 мм, диаметр сливного порога 50 мм, длина барабана 750 мм, частота вращения 13 000 об/мин. Решение. Производительность определяем по формуле ωVж . V≤ h Так как частицы очень малы, то режим осаждения их будет, вероятно, ламинарным. Воспользуемся формулой Стокса с последующей проверкой режима осаждения: d2 (ρ − ρ с ) 12 (1400 − 900)9,81 ω ос = = = 9,06i10−8м /с 18µ с 1012 i18i3i10−2 Скорость осаждения под действием центробежной силы: ω = ω oc f = 9,06<10−8 <4700 = 4,26<10−4 м /с Здесь f = n2 R0 132 <106 <0,025 = = 4700 900 900 Проверяем режим осаждения: ωdρc 4,26<1<900 1,42 Re = = 4 = µc 10 <106 <3<10−3 104 Найдем полезный объем барабана центрифуги: ( ) ( ) Væ = FL = 0,785 D2 − D02 L = 0,785 0,152 − 0,052 0,75 = 0,0118ì 3 D − D0 0,15 − 0,05 Глубина потока в барабане: h = = = 0,05 ì 2 2 ωVæ 4,26<0,0118 3600 = 3600 = 0,368 ì 3 /÷ Тогда V ≤ h 104 <0,05 — 216 — ÐƭǪƽǪǆǀÐƽǁǎÐǯǪǂǮǯǰǮǎǰǬǁǋǃǮƼǮÐ͠ǬǇǬǃǀǎ Проверяем режим потока и барабане центрифуги: ω dρ Reïîò = ïîò ý µ 1,05 V 0,368 1,05 3 = = 0,0067 ì / ñ V = = ì /ñ F 104 <0,0157 3600 104 ; F = 0,785 D2 − D02 = 0,785 0,152 − 0,052 = 0,0157ì 2 ωïîò = ( ) ( ) Для центрифуги с трехлопастной крыльчаткой: ( ) ( ) 2 2 3,14 0,152 − 0,052 F 4π D − D0 = = 0,0815 ì dý = 4 = Ï 4 ( πD + 6h ) 3,14<0,15 + 6<0,05 0,0067<0,0815<900 = 161 < 350 310−3 т. e. режим ламинарный. Reïîò = ϱ͘ϴ͘ʯ̸̨̨̨̨̛̛̣̭̥̭̯̯̖̣̦̬̖̹̖̦̌̔̌̔́̌́̽̐́͘ ϱ͘ϴ͘ϭ͘ʽ̛̭̙̖̦̖̌̔͘ Задача 1. Найти соотношение диаметров частиц свинцового блеска (ρ = 7800 кг/м8) и кварца (ρ = 2600 кг/м3), осаждающихся с одинаковой скоростью: а) в воздухе; б) в воде, считая, что осаждение происходит при Re < 0,2. Задача 2. С какой скоростью будут осаждаться шарообразные частицы кварца (ρ = 2600 кг/м8) диаметром 10 мкм; а) в воде при 15 °С; б) в воздухе при 15 и 500 °С? Задача 3. Через пылевую камеру с расстоянием между полками 100 мм проходят 2000 м3/ч запыленного газа плотностью 1,6 кг/м3 (расход и плотность даны при нормальных условиях). Температура газа 400 °С. Динамический коэффициент вязкости газа при этой тeмпepaтype 0,03–10–3 Па-с. Плотность пыли 3700 кг/м3. Длина камеры 4,55 м, ширина 1,71 м, высота 4 м. Какого размера частицы пыли будут улавливаться в камере, если считать, что действительная скорость осаждения вдвое меньше теоретической? — 217 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǪǯ͟ǬǭǰǊÐǮǰƽǬǁǬǃǀǎÐǰǫǬ͠ƽǊǲÐǆǪǯǰǀǅÐǮǰÐƾǀƽǭǮǯǰǀÐǀǁǀÐƼǪƿǪ ϱ͘ϴ͘Ϯ͘ˇ̨̛̛̣̯̬̦̖̽̏̌͘ Задача 1. Какое количество влажного осадка будет собрано на фильтре в результате фильтрования 10 м3 суспензии относительного удельного веса 1,12, содержащей 20% (масс.) твердой фазы? Влажность осадка 25%. Задача 2. Время фильтрования 20 м3 раствора на рамном фильтрпрессе 2,5 ч. Найти ориентировочное время промывки осадка 2 м3 воды, полагая приближенно, что скорость промывки в 4 раза меньше скорости фильтрования в конечный момент. Сопротивлением ткани пренебречь. Динамические коэффициенты вязкости фильтрата и промывной воды одинаковы. Задача 3. Как изменится производительность фильтра, если: 1) вдвое увеличить фильтрующую поверхность; 2) вдвое увеличить давление (при однородном несжимаемом осадке); 3) вдвое увеличить концентрацию твердого вещества в фильтруемой суспензии;4) вдвое уменьшить (повышая температуру) вязкость фильтрата; 5) вдвое увеличить время полного оборота фильтра (т. е. увеличить толщину слоя осадка)? ϱ͘ϴ͘ϯ͘ˉ̴̨̛̛̛̖̦̯̬̱̬̦̖̐̏̌͘ Задача 1. Определить удельное давление на стенки барабана центрифуги, если толщина слоя жидкости 10 см, внутренний диаметр барабана 1 м, частота вращения 500 об/мин. Плотность жидкости 1100 кг/м3. Задача 2. Найти частоту вращения центрифуги, если известно, что высота барабана Н = 0,5 м. Давление у стенок барабана должно быть 5 кгс/см2 (~0,5 МПа). Загружено 400 кг суспензии. Задача 3. Как изменится производительность фильтрующей центрифуги, если увеличить частоту ее вращения вдвое? — 218 — ÐƭǪƽǪǆǀÐƽǁǎÐǯǪǂǮǯǰǮǎǰǬǁǋǃǮƼǮÐ͠ǬǇǬǃǀǎ Осадок однородный несжимаемый. Сопротивлением фильтрующей ткани пренебречь. Задача 4. Осаждение частиц какого диаметра обеспечит центрифуга НОГШ-230, если на разделение подавать 3 м3/ч водной суспензии каолина при 35 °С? Техническая характеристика центрифуги: диаметр сливного цилиндра 180 мм; длина его 164 мм; частота вращения барабана 1600 об/мин. — 219 — ǍưǙǚǙÍ Í Í ǋǍǔǎǍƝǔǒǌǋǑƝǎ В результате изучения главы 6 бакалавр должен: Знать: – основные физико-химические закономерности процессов агрегирования и их классификацию; сущность процессов пептизации. Уметь: – применять определенные реагенты для инициирования процессов агрегирования или пептизации. Владеть: – основными методами и методиками для проведения процессов агрегирования суспензий, коагуляции твердых частиц в газовой среде. ϲ͘ϭ͘˃̶̨̨̨̛̛̛̖̬̪̬̖̭̭̬̖̬̦́̌̌̐̐̏̌́͘ʺ̵̸̛̖̦̥̼̭̯̬̖̌̏̚ ̸̶̨̛̭̯̬̱̭̬̱̥̌̔̐̔̐͘ʿ̨̨̡̛̛̛̛̛̦̯̖̬̭̣̦̺̖̥̣̖̦́̌̏̌̀̔̌̏͘ ϲ͘ϭ͘ϭ͘˃̶̨̨̨̛̛̛̖̬̪̬̖̭̭̬̖̬̦́̌̌̐̐̏̌́͘ В реальном процессе сгущения частицы менее 5 микрон частично уходят со сливом. Чистого слива практически не бывает. Осаждение суспензий, содержащих большое количество мелких частиц, ускоряют процесс агрегирования частиц, т.е. образование агрегатов, состоящих, как из некоторого числа мелких частиц, так и крупных. Часто процессы агрегирования называют коагуляцией и флокуляцией. — 220 — ÐǧǬǮ͠ǀǎÐ͟͠ǮǅǬǯǯǪÐǪƼ͠ǬƼǀ͠ǮǫǪǃǀǎ ÐǡǬǲǪǃǀƿǂǊÐǫǯǰ͠ǬǆÐǆǪǯǰǀǅÐƽ͠ǱƼÐǯÐƽ͠ǱƼǮǂ В дальнейшем этим понятиям дадим четкие определения. Процессы образования флокул (от лат. flocculus — клочок, пушинка, рыхлое образование) можно представить состоящим из двух последовательных стадий — соударения или встречи частиц друг с другом и прилипания. Но не каждое соударение частиц друг с другом приводит к прилипанию. Число соударений или встреч в основном определяется гидродинамическим режимом перемешивания суспензии, а доля прилипших частиц друг к другу или эффективность встреч — поверхностными силами. Необходимо отметить, что такое разграничение в некоторой степени условно, так как поверхностные силы в зоне их действия способствуют соударению, а механические силы, возникающие при перемешивании, разрушают флокулы, т.е. уменьшают эффективность встреч. Однако такое последовательное рассмотрение позволяет выявить основные закономерности агрегирования частиц. ϲ͘ϭ͘Ϯ͘ʪ̵̸̸̶̨̛̛̛̛̛̛̥̖̦̥̭̱̬̖̦̣̭̯̬̖̭̯̏̌̌̌̔̌́̏̌̚͘ В зависимости от гидродинамического режима течения суспензии или перемешивания, а также от соотношения размеров соударяющихся частиц различают следующие механизмы встреч частиц друг с другом: инерционный и диффузионный механизмы. Диффузионный механизм встреч в свою очередь делится на молекулярно- и турбулентно-диффузионный механизмы. Чтобы четко представить различия в механизме встреч частиц друг с другом, полидисперсную суспензию условно представляют состоящей как бы из частиц только двух сортов — мелких и крупных. Мелкими частицами называют такие, которые подвержены хаотическому движению под влиянием тепловой энергии — (КТ) или турбулентному перемешиванию. Такие частицы не имеют собственных траекторий движения относительно жидкости. Крупными частицами называют такие, которые имеют собственные траектории относительно жидкости за счет сил инерции. — 221 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð Коллоидные частицы могут быть распределены по всему объему жидкости даже без перемешивания за счет броуновского движения или молекулярной диффузии. Рис. 6.1. Механизмы встреч частиц. Величина произвольного смещения частицы ∆Х за время t за счет броуновского движения определяется по закону Эйнштейна-Смолуховского. ∆X = 2DT (6.1) KTC , где К — 6πµr постоянная Больцмана; T — абсолютная температура; r — радиус частиц; µ — вязкость (пуазы); C — поправка Кеннигема, учитывающая повышение подвижности частиц при очень малых размерах, соизмеримых с длиной свободного пробега газовых молекул, С = (1+0,86 10–5/r). Для частиц менее 0,1 микрона скорость осаждения по закону Стокса составит порядка 1·10–6 см/сек, а смещение ∆Х — 1·10–5 см за 1 сек, т.е. броуновское движение не дает осесть частицам такого размера. В хаотическом движении, аналогичном броуновскому, находятся мелкие частицы при турбулентном режиме перемешивания суспензии. Частицы, диаметр которых меньше внутреннего масштаба турбулентных пульсаций λ, полностью увлекаются турбулентными пульсациями l λ=− (6.2) 3/4 2  R 2πn   ν60  где D — коэффициент диффузии, равный D = — 222 — Ðǧ͠ǀÐǯǁǪƼǪǍǈǀǬÐ͟ǮǫǬ͠ǲǃǮǯǰǃǊǲÐǯǀǁÐÐ͠ǪǯǭǁǀǃǀǫǪǍǈǬƼǮÐƽǪǫǁǬǃǀǎ где l — диаметр камеры, где перемешивается суспензия; R — µ радиус импеллера; n — число оборотов импеллера; ν = — ρ0 кинематическая вязкость и плотность жидкости. Внутренний масштаб турбулентности — это средний размер объема жидкости, который совершает беспорядочное движение. Частицы диаметром D = 2r ≤ λ , находящиеся в турбулентном потоке, так же, как и коллоидные, условно называют мелкими. Частицы больших размеров, которые имеют собственные траектории относительно жидкости, называют крупными. Мелкие частицы могут сталкиваться друг с другом только за счет диффузионного механизма. Мелкие с крупными сталкиваются за счет инерционного и диффузионного механизмов. Крупные с крупными — только по инерционному механизму. Относительное значение обоих механизмов при различном гидродинамическом режиме можно оценить по формуле Nèíåð Näèô = ρ r ρc λ (6.3) где r и ρ — средний радиус частиц и их удельная масса. Расчеты показывают, что число соударений, обусловленное инерционным механизмом (Nинер), может быть в десятки и сотни раз больше, чем за счет диффузионного (Nдиф). Поэтому полидисперсные суспензии должны агрегироваться быстрее, чем суспензии, состоящие только из мелких частиц. ϲ͘Ϯ͘˃̵̵̨̨̛̛̛̬̭̣̺̖̪̖̬̦̭̯̦̼̭̣̌̐̌̀̏ ;̡̨̛̛̛̬̭̣̦̺̖̣̖̦̌̏̌̀̐̔̌̏́Ϳ͘ ʪ̸̡̨̨̛̛̱̣̖̦̦̼̜̦̥̖̜̭̯̏̌̏̌̔̏́̚̚͘ Прилипание частиц друг к другу так же, как и к пузырьку воздуха при флотации, обуславливается поверхностными силами, которые количественно и качественно характеризуются величиной и знаком расклинивающего давления. Расклинивающее давление проявляется только в тонких пленках — 223 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð и показывает, какое дополнительное давление по отношению к гидростатическому оказывают поверхностные силы на твердые тела. Понятие расклинивающего давления разберем на примере взаимодействия двух пластин, помещенных в жидкость. При сближении пластин под действием силы q, начиная с определенной толщины, разделяющей пленки, возникает дополнительная сила, препятствующая или способствующая вытеканию жидкости из зазора. Поскольку, начиная с толщины h, химический потенциал в пленке µc отличен от его объемного значения µ∞, то для выравнивания значений µc и µ∞ необходимо произвести работу по перемещению жидкости (рис.6.2). Если µ∞ > µс, то жидкость для выравнивания значения химических потенциалов (под действием давления Р) будет втекать в зазор между телами, а при µ∞< µс — будет вытекать. Рис.6.2. Схема возникновения расклинивающего давления. Следовательно, чтобы препятствовать втеканию (утолщение пленки) или вытекание (утончение пленки) жидкости из зазора, нужно приложить нагрузку Р в соответствующем направлении и по величине, очевидно, равной µ − µc P= ∞ Vm µ ∞ − µ c = PVm или (6.4) где Р — давление; Vm — молярный объем. — 224 — Ðǧ͠ǀÐǯǁǪƼǪǍǈǀǬÐ͟ǮǫǬ͠ǲǃǮǯǰǃǊǲÐǯǀǁÐ͠ǪǯǭǁǀǃǀǫǪǍǈǬƼǮÐƽǪǫǁǬǃǀǎ Поэтому можно рассматривать, что граничный слой (пленка) как бы оказывает воздействие на ограничивающие его тела. Поскольку первоначально возникновение этого давления было привлечено Б.В. Дерягиным для объяснения расклинивающего действия тонких пленок, то его и назвали расклинивающим давлением. Положительное расклинивающее давление стремится раздвинуть ограничивающие твердые тела. При отрицательном значении стремится их сблизить. Расклинивающее давление Р(h) слагается из трех составляющих: P (h) = N (h) − A (h) + S (h) (6.5) где N(h) — слагающая, обусловленная электростатическими зарядами и возникающая за счет перекрытия (или деформации) ионных атмосфер, расположенных на обеих фазовых поверхностях смачивающей пленки; A(h) — удельное (на см2) притяжение, являющееся результирующим молекулярных взаимодействий молекул водной пленки как с частицей, так и между собой, т.е. характеризует притяжение за счет Ван-дер-Ваальсовских сил; S(h) — сольватационная слагающая, зависящая от степени гидратированности поверхностей. Энергия взаимодействия двух атомов или двух твердых частичек, в зависимости от расстояния их друг от друга, как известно, хорошо иллюстрируется общеизвестной кривой с потенциальной ямой (рис. 6.3). Кривые с потенциальной ямой характерны для любой системы взаимодействующих частиц, в которых действуют как силы отталкивания, так и притяжения. Любой кристалл, любое тело сопротивляется и сжатию и растяжению. Известно, что силы, препятствующие сжатию, возрастают сильнее с уменьшением расстояния между атомами или молекулами, чем силы притяжения. Силы притяжения и сжатия имеют разные знаки. Первым (силам приближения) приписывается отрицательный знак, а вторым (силам отталкивания) — положительный. Поскольку силы отталкивания возрастают (при сближении двух тел) или убывают (при их уда— 225 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð Рис.6.3. Потенциальная энергия (а) и сила взаимодействия (б) двух частиц в зависимости от расстояния между частицами. лении) быстрее, чем силы притяжения, то радиус их действия меньше. Положение равновесия возникает при равенстве этих сил на определенном расстоянии между частицами (атомами или телами), равном r0. Математически полную энергию взаимодействия тел можно записать в виде двучленного уравнения A B V=− m + n (6.6) r r А для силы взаимодействия, соответственно  A B d − m + n   r dV r  mA nB (6.7) = = m +1 − n+1 F= dr dr r r Первый член выражает силу отталкивания, а второй — притяжения, причем m < n. Работа диссоциации измеряется глубиной «потенциальной ямы» Umin, которую легко найти из равенства силы F нулю при r = r0 , nB = mAr0n−m или U=− A rm  m  r  n −m  1 −  0   nr   — 226 — (6.8) ÐǦǀǁǊÐǝǪǃ ƽǬ͠ ǝǪǪǁǋǯǪ ÐÐǦǁǪƼǪǍǈǀǬÐǯǀǁÐǝǪǃ ƽǬ͠ ǝǪǪǁǋǯǪ Минимум энергии соответствует состоянию равновесия при r = r0 , A m (6.9) Umin = − m  1 −   n r0 Двучленный закон для изменения энергии и силы с расстоянием, как отмечалось выше, носит общий характер, который отражает взаимодействие двух тел за счет любых сил притяжения и отталкивания. В случае кристаллов — это силы химических связей, действующие между атомами и молекулами. В случае взаимодействия двух частиц — это поверхностные силы. Роль сил отталкивания в расклинивающем давлении играют, как правило, электростатические силы, когда частицы одноименно заряжены и всегда силы гидратных оболочек. Роль сил притяжения в данном случае играют силы Ван-дер-Ваальса. Характер взаимодействия частиц — прилипание или отталкивание зависит от того, какие силы преобладают и как они (по какому закону) меняются с расстоянием от поверхности. Рассмотрим подробнее закономерности изменения поверхностных сил с расстоянием. ϲ͘ϯ͘ˁ̛̣̼ʦ̦̌Ͳ̖̬̔Ͳʦ̣̭̌̌̽̌͘ ˁ̛̛̣̺̖̭̣̌̐̌̀ʦ̦̌Ͳ̖̬̔Ͳʦ̣̭̌̌̽̌͘ ʦ̨̡̨̨̛̛̦̖̬̣̭̭̖̥̖̜̭̯̖̥̖̙̱̌̔̏̌̌̽̏̏̌̔̏̔̚ ̴̨̡̡̨̨̛̛̛̛̛̥̣̖̱̣̥̦̖̦̭̬̦̦̼̥̥̌̔̏̌̌̌̚͘ ϲ͘ϯ͘ϭ͘ˁ̛̣̼ʦ̦̌Ͳ̖̬̔Ͳʦ̣̭̌̌̽̌͘ Как известно, силы Ван-дер-Ваальса точно передают взаимодействие отдельных молекул между собой и имеют три слагаемых: ориентационное, индукционное и дисперсионное. Энергия взаимодействия соответственно имеет вид νν  1  2 P2 P2 3h U = 6  1 2 + P12d2 + P22d1 + d1d2 1 2  (6.10) ν1 + ν2  2 r  3 kT ( ) где Р1 и Р2 — дипольные моменты молекул 1 и 2; d1 и d2 — их поляризуемость; ν1 и ν2 — их собственные главные частоты; — 227 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð h — постоянная Планка; К — постоянная Больцмана; Т — абсолютная температура, °К. Как видно, энергия притяжения между двумя молекула1 ми убывает обратно пропорционально 6 независимо от типа r взаимодействия. Первый член отражает ориентационное взаимодействие молекул, у которых есть постоянные “жесткие” диполи. В индукционном взаимодействии основную роль играет поляризуемость молекул, т.е. появление наведенных зарядов. Природа дисперсионного взаимодействия (третий член) — излучательная и связана с одновременным появлением мгновенных диполей в молекулах. ϲ͘ϯ͘Ϯ͘ʦ̨̡̨̨̛̛̦̖̬̣̭̭̖̥̖̜̭̯̖̌̔̏̌̌̽̏̏̌̔̏̚ ̵̴̡̨̨̛̦̖̦̭̬̦̦̼̔̏̌̌̚͘ Характерной особенностью сил Ван-дер-Ваальса является то, что они в отличие от валентных химических сил не насыщаются. Поэтому взаимодействия между твердыми и жидкими телами, которые называют конденсированными фазами и которые состоят из множества атомов, можно в первом приближении рассматривать, как сумму независимых аддитивных взаимодействий между парами молекул или атомов, входящих в состав тел. Силы взаимодействия между конденсированными фазами увеличиваются, так как они являются суммой атомных и молекулярных взаимодействий. В зависимости от геометрической формы взаимодействующих твердых частичек закон изменения сил Ван-дер-Ваальса с расстоянием имеет вид: для двух шаров одинакового радиуса R она составляет AR AR ; для плоскости и шара F = − ; для двух бесF=− 2 6H 2 12H A , где А – константа Гамакера 12πH 3 для индивидуального вещества. конечных плоскостей F = — 228 — ÐǦǀǁǊÐǝǪǃ ƽǬ͠ ǝǪǪǁǋǯǪ ÐǦǁǪƼǪǍǈǀǬÐǯǀǁÐǝǪǃ ƽǬ͠ ǝǪǪǁǋǯǪ Для расстояний между телами Н больших, чем длина основной волны поглощения атомов — λ, их образующих, энергия и сила притяжения убывают для этих случаев с расстоянием на порядок быстрее. Энергия вандерваальсовского взаимодействия зависит не только от формы твердого тела, а также и от его размеров. При δ = Н (U ≈ 0.5 U∞) энергия взаимодействия частиц конечного размера примерно вдвое меньше энергии взаимодействия двух бесконечных полупространств. Поэтому сила прилипания к крупным частицам больше и, следовательно, повышение полидисперсности системы должно приводить к более интенсивной агрегации. Интересно отметить, что аналогичный вывод был получен, когда рассматривали первую стадию образования агрегатов — стадию соударений. Основная трудность практического использования этих формул заключается в том, что не известны константы А и А1. ϲ͘ϯ͘ϯ͘ˑ̡̨̨̨̛̛̛̛̣̖̯̬̥̦̯̦̯̖̬̥̖̜̭̯̌̐̌́́̏̌̔̏́̚ ̵̴̡̨̨̛̦̖̦̭̬̦̦̼̔̏̌̌̚͘ К настоящему времени Лившицем и Питаевским развит более общий подход к рассмотрению взаимодействия конденсированных фаз. Они рассматривают взаимодействие твердых тел, как обмен квантами энергии электромагнитного излучения, наподобие обменных валентных сил с той разницей, что электромагнитное поле носит случайный характер, вызванный флуктуацией энергии, а квант энергии hν имеет малое абсолютное значение. Важно отметить то обстоятельство, что сила взаимодействия и в этом подходе обратно пропорциональна величине Н3 или Н4, а само взаимодействие определяется только диэлектрическими свойствами тел. Препятствие для применения этой теории — это отсутствие данных по изменению диэлектрической постоянной в большой области частот. Этот подход позволяет представить универсальную зависимость энергии взаимодействия двух тел (в виде кубиков — 229 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð с площадью 1 см2) от величины статической диэлектрической постоянной. У твердых диэлектриков в большинстве случаев ε0 изменяется от 2 до 10. Таким образом, их энергия взаимодействия не превышает 1·10–19 эрг/см3. Максимальная сила притяжения должна быть для металлов, так как для них ε0 можно считать равной бесконечности. Экспериментально этот факт подтверждается. Металлы наиболее гидрофобны и легко флокулируют, а также флотируются, особенно в тех случаях, когда с их поверхности удалена окисная пленка. Сила, действующая на два твердых тела, которые разделены жидкой прослойкой для случая H < λ, имеет вид: F= ∞ (ε1 − ε3 )(ε2 − ε3 ) dξ hω ω = , а ∫ 2 3 ε + ε3 )( ε2 + ε3 ) 8π H 0( 1 (6.11) где ε1, ε2 — мнимая часть диэлектрической проницаемости для твердых тел 1 и 2; ε3 — для разделяющей жидкой прослойки. Из формулы видно, что в случае одинаковых тел (ε1 = ε2), а разности (ε1 – ε2) имеют одинаковый знак, тогда сила F > 0, т.е. всегда существует притяжение. В случае тел различной природы, для которых разности (ε1 – ε3) и (ε2 – ε3) имеют разные знаки, F < 0, следовательно, возможно отталкивание. Например, для системы металл (ε2 = ∞ ), вода (ε3 = 80) и диэлектрик (ε1 = 10) (10 – 80)= –70, ( ∞ — 80) = + ∞ и F < 0, т.е. диэлектрик не притягивается силами Ван-дер-Ваальса к металлу в среде, где его ε1 < ε3 жидкости. ϲ͘ϰ͘ʿ̨̨̨̛̛̬̬̦̦̔̌Ͳ̸̵̡̨̡̛̛̛̣̖̯̬̭̯̯̖̭̭̣̾̌͘ ʯ̵̡̨̨̨̨̛̛̛̦̥̖̬̦̭̯̥̖̦̖̦̣̱̬̭̯̬̌̽́̏̐̍̽̌̏̌̚͘ На границе раздела твердое тело — жидкость, как известно, всегда возникает двойной электрический слой. Механизм его возникновения связан: а) с преимущественным появлением катиона или электрона у металлов, аниона или катиона у солей и окислов; б) с преимущественной адсорбцией катионов или анионов из раствора; — 230 — ÐǤ͠ǀ͠ǮƽǪÐǀǮǃǃǮ ǌǁǬǭǰ͠ǮǯǰǪǰǀǆǬǯǭǀǲÐǯǀǁ ÐƭǪǭǮǃǮǂǬ͠ǃǮǯǰǋÐǀƿǂǬǃǬǃǀǎÐǀǲÐǫƼǁǱƻǋÐ͠ǪǯǰǫǮ͠Ǫ в) с направленной ориентацией диполей полярных молекул в пограничном слое; г) с образованием полярных химических связей. Рис. 6.4. Зависимость энергии притяжения двух параллельных плоскостей от статической диэлектрической постоянной. Электростатическое взаимодействие связано с перекрытием внешних (диффузионных) обкладок двойного электрического слоя. Результаты теоретических расчетов для трех практически важных случаев: 1) когда заряды взаимодействующих поверхностей противоположны; 2) когда заряды одноименны, но сильно отличаются по своей величине; 3) когда заряды одноименные и примерно одинаковые по своей величине, можно качественно проиллюстрировать ходом кривых зависимости расклинивающего давления от расстояния между частицами (рис. 6.5). В первом случае, естественно, электростатические силы являются силами притяжения, а во втором — силами отталкивания. Не тривиален третий случай. До расстояния Но одноименно заряженные поверхности, но с сильно различающимися величинами зарядов, отталкиваются, а, начиная с расстояния не менее Но — притягиваются. Рмах на расстоянии Нмах — характеризует величину энергетического барьера, который должны преодолеть такие частицы, чтобы прилипнуть друг к другу. — 231 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð Рис. 6.5. Зависимость ионно-электростатической слагающей расклинивающего давления в трех случаях: а) противоположные знаки зарядов поверхностей; б) одноименно заряженные поверхности, заряды примерно одинаковые; в) одноименно заряженные поверхности, заряды сильно отличаются. Чаще всего электростатические силы выступают в роли сил отталкивания по причине одинакового заряда поверхностей и близости абсолютных значений их зарядов. Главной особенностью электростатических сил является то, что радиус действия их является функцией концентрации электролита. При отсутствии электролита или при малой его концентрации вторая обкладка двойного электрического слоя носит диффузионный характер из-за теплового размытия, и скачок межфазного потенциала распределен по всей толщине двойного слоя. Радиус действия электростатических сил можно оценить по толщине ионной атмосферы, параметра, вводимого в теорию сильных электролитов Дебая-Хюккеля. ε 0 kT 1 (6.12) = X 4πe2 ∑ zi2ni где е — заряд электрона; zi — валентность i иона; ni — частичная концентрация i-го электролита, которая с молярной концентрацией связана соотношением n 1000 (6.13) C= i N где N — число Авогадро; εо — диэлектрическая проницаемость; k — постоянная Больцмана. — 232 — ÐǤ͠ǀ͠ǮƽǪÐǀǮǃǃǮ ǌǁǬǭǰ͠ǮǯǰǪǰǀǆǬǯǭǀǲÐǯǀǁ ÐƭǪǭǮǃǮǂǬ͠ǃǮǯǰǋÐǀƿǂǬǃǬǃǀǎÐǀǲÐǫƼǁǱƻǋÐ͠ǪǯǰǫǮ͠Ǫ Для одновалентного электролита зависимость приобретает простой вид: 1 10−8 =2 X C (6.14) где С — концентрация в г — экв/л. Из этого уравнения следует, что для раствора 0,01N 1/Х=10–7 см. Так как ионный радиус — величина порядка 10–8 см, то толщина ионной атмосферы будет в 10 раз больше, чем радиус иона r. При 0,0001N 1/X=100 и т.д. В растворе концентрации 1N толщина ионной атмосферы сравнима с радиусом иона. Все эти размеры являются оценками толщины диффузионного облака и двойного электрического слоя. В случае большого заряда поверхностей механизмы коагуляции при прибавлении электролита можно объяснить сжатием двойного электрического слоя. В этом случае увеличением или снижением заряда поверхности, вследствие адсорбции ионов, можно пренебречь. На рис. 5.6 видно, что прилипание обусловлено уменьшением радиуса действия электростатических сил отталкивания при сжатии двойного слоя. Радиус действия сил притяжения не зависит от концентрации электролита. В случае малого заряда поверхностей на коагуляцию оказывает влияние не только сжатие двойного слоя при прибавлении электролита, а также снижение заряда при адсорбции противоионов. При этом адсорбирующиеся молекулы могут полностью компенсировать заряд поверхности, и, следовательно, ослабить действие электростатических сил. Следовательно, в точке нулевого заряда коагуляция должна быть максимальной. Сила коагулирующего действия электролитов в большой мере определяется валентностью ионов. Экспериментально установленное правило Шульца-Гарди nZ6 = const было выведено теоретически Ландау-Дерягиным. Концентрация электролита, необходимая для достижения порога коагуляции, в Z6 раз меньше для многовалентных электролитов. — 233 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð Рис. 6.6. Схема действия электростатической и вандерваальсовской слагающих расклинивающего действия: а — при малой; б — при большой концентрации электролита. Например, ионов Ва+2 нужно добавить в 64 = 26 раз меньше, чем ионов Na+1 при коагуляции коллоидов. Это правило лучше всего выполняется для сильноразреженных коллоидных частиц, когда прибавляется неабсорбирующий электролит. В общем случае произвольного заряда поверхности и учете адсорбции электролита критерий коагуляции имеет более сложный вид. ϲ͘ϱ͘ʧ̶̵̵̨̨̨̛̛̛̬̯̦̦̭̣̖̥̪̖̬̦̭̯̦̼̭̣̔̌̌̌́̌̐̌̌́̏ ;̡̨̛̛̛̬̭̣̦̺̖̣̖̦̌̏̌̀̐̔̌̏́Ϳ͘ Слагающее расклинивающего давления S(h) проявляется при перекрытии сольватных оболочек соприкасающихся тел. Природа сил гидратации определяется взаимодействием молекул воды с поверхностью твердого тела и связана с подвижностью иона водорода (протона). Степень смещения протона обуславливает силу связи. В некоторых случаях она явно носит водородный характер. Например, при взаимодействии H2O с атомом кислорода, находящимся на поверхности окисла. H Si — OH . . . O H — 234 — Ðǧ͠ǀÐǂǬǲǪǃǀƿǂǪÐǪƼ͠ǬƼǀ͠ǮǫǪǃǀǎÐǭǮǪƼǱǁǎǅǀǎ ÐǄǁǮǭǱǁǎǅǀǎ ÐǂǮǯǰǀǭǮǫǪǎÐǄǁǮǭǱǁǎǅǀǎ Si – O . . . H —— O —— H Однако же чаще взаимодействие молекул воды с катионами (Ме+n) и анионами (A-n) происходит по схемам H Me+n - - - - O и A–n - - - H - O - H H Сила взаимодействия ионов с молекулами воды во многом зависит от отношения заряда иона к его радиусу, а энергетически точнее всего характеризуется теплотами гидратации ионов. Современная теория жидкого состояния не позволяет определить закон изменения S(h) с расстоянием от поверхности. Однако можно предположить, что эти силы не дальнодействующие, т.к. обуславливают наличие только ближнего порядка в жидкостях. В некоторых случаях известно образование толстых полимолекулярных сольватных пленок, обладающих особыми свойствами. ϲ͘ϲ͘˃̵̨̛̛̛̛̬̥̖̦̥̬̖̬̦̌̌̌̐̐̏̌́͗̚ ̶̴̶̴̶̡̨̨̡̨̡̨̨̡̛̛̛̛̱̣͕̣̱̣͕̥̭̯̣̱̣̌̐́́́́̏̌́́́͘ Первый механизм — коагуляционный наблюдается при добавлении электролита, в результате чего уменьшается радиус действия электростатических сил отталкивания и снижается заряд поверхности. Образующие агрегаты, как правило, рыхлые. Частицы друг с другом слабо связаны, так как им мешает наличие сольватных слоев воды, если, конечно, исходные частицы не были природно гидрофобны. Второй механизм — флокуляция — наблюдается при искусственной гидрофобизации, происходящей при адсорбции реагентов типа флотационных собирателей. Образующие агрегаты гидрофобны, так как гидрофобизирующие реагенты частично или полностью разрушают сольватную оболочку воды. Частицы друг с другом связаны довольно прочно и полностью не разрушаются даже при турбулентном режиме перемешивания. — 235 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð Третий механизм — мостиковый, который часто тоже называют флокуляцией. Мостиковая флокуляция наблюдается при применении высокомолекулярных полимерных веществ, активные группы которых, расположенные в одной молекуле, одновременно закрепляются на разных частицах. Образуются, как правило, большие агрегаты, которые чаще всего имеют вид хлопьев. Флокулы непрочные и быстро разрушаются при турбулентном режиме перемешивания. Эффективность действия высокополимерных веществ определяется двумя факторами: сродством их активных групп к поверхности материала, прочностью и структурой образующихся в суспензии полимерных молекул. Часто отмечается, что величина адсорбции молекул полимеров во многом определяется знаком и величиной заряда поверхности минеральных частиц. Разноименные заряды на поверхности и в молекуле полимера способствуют адсорбции. Механизм действия этого класса соединений рассмотрим подробнее на примере полиакриламина (ПАА), следуя гипотезе, развиваемой Г.Р. Бочкаревым. Полиакриламин представляет собой соединение типа: [ — CH2 — CH2 — ] CONH2 Группы —СОNH2 частично могут гидролизоваться до гидроксильных групп СООН. ПАА обычно характеризуют степенью полимеризации или молекулярным весом, а также степенью гидролиза. Исследования Г.Р. Бочкарева показали, что ПАА в растворе представлен пространственно-сетчатой структурой, состоящей из переплетающихся нитевидных образований и центров стяжений в местах их переплетения, являющихся участками концентрированных молекулярных форм ПАА разных размеров и степени концентрации. В 0,2% растворах в центрах стяжений наблюдается наиболее концентрированные ассоциаты молекул. При концентрации ПАА ниже 0,001% часто сетчатая структура ПАА при— 236 — Ðǧ͠ǀÐǂǬǲǪǃǀƿǂǪÐǪƼ͠ǬƼǀ͠ǮǫǪǃǀǎÐǭǮǪƼǱǁǎǅǀǎ ÐǄǁǮǭǱǁǎǅǀǎ ÐǂǮǯǰǀǭǮǫǪǎÐǄǁǮǭǱǁǎǅǀǎ нимает локализованный характер, связи между стяжениями рвутся. Нити сетчатой структуры представляют собой разветвленные молекулярные пачки различной толщины и длины. Связывание частиц сетками полиакриламина доказывали следующими опытами. В растворы ПАА вносили небольшое количество слабо концентрированной суспензии из тонких частиц кварца и магнетита и воздействовали на систему переменным магнитным полем. При этом наблюдали под оптическим микроскопом, что частицы не осаждаются на дно сосуда, а система стабилизируется, а при воздействии переменным магнитным полем происходит синхронное колебание частиц кварца и магнетита. Аналогичные опыты с растворами менее 0,05%-ной концентрации показали, что растворы обладают менее прочной и более редкой сетчатой структурой, так как крупные частицы осаждаются беспрепятственно, средние стабилизируются, а наиболее мелкие находятся в движении. При воздействии переменным магнитным полем не наблюдается синхронное колебание частиц кварца и магнетита. Эти опыты доказывают, что по мере растворения ПАА или уменьшения его концентрации изменяется его структура. Наблюдение кинетики растворения ПАА под оптическим микроскопом выявило ряд интересных качественных особенностей. При контакте ПАА с водой в воду устремляются мелкие глобулы раствора ПАА, но они не исчезают сразу в массе воды, а совершают 3–4 возвратно — поступательных движения. Такие этапы визуально наблюдаются до полного исчезновения глобул, за время от 10 до 25 сек. Между глобулами и массой раствора ПАА, а также между глобулами первых двух-трех рядов имеются очень тонкие нитеобразные связи. Возвратно-поступательное движение и объясняется этими связями. Перемешивание суспензии способствует дальнейшему растворению и распространению флокулянта по всему объему. В зависимости от интенсивности перемешивания и неравномерности самой структуры ПАА, некоторые свернутые или полусвернутые молекулярные пачки в сетчатой структуре — 237 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð флокулянта растягивается, разворачивается; при этом увеличивается площадь соприкосновения с твердыми частицами. Некоторые связи в молекулах, растянутых до предела, рвутся, захватив на себя определенное количество частиц, т.е. флокул, которые быстро осаждаются. При разрыве тонких молекулярных пачек концы их стремятся вновь присоединиться к сетчатой массе флокулянта или свернуться на себя. Время сворачивания пачек определяет количество частиц, попавших в эти своеобразные сетчатые мешки (вроде сеток). Поскольку ПАА неравномерно распределен в растворе, наблюдается несколько форм взаимодействия ПАА с частицами. Большинство флокул образовано в результате взаимодействия частиц с слабоупорядоченными, плотносетчатыми структурными формами. Флокула такого рода имеет вид плотных агрегатов. В меньшем количестве наблюдаются флокулы, скрепленные редкосетчатыми формами ПАА. Такая флокула обычно рыхлая и меньшего размера. Встречаются отдельные частицы, имеющие на себе поверхностный слой ПАА с нитеобразными ответвлениями молекулярных пачек. Таким образом, следует, что при взаимодействии ПАА с суспензией основная масса образующихся флокул возникает за счет связывания частиц сетчатыми структурами ПАА, а не отдельными молекулярными пачками. ϲ͘ϳ͘ʽ̶̶̨̡̨̛̛̛̛̛̭̦̦̼̖̪̬̦̪̼̭̖̣̖̯̦̜̬̖̏̏̌̐̐̌ ̸̶̛̛̛̭̯̭̱̭̪̖̦̌̏̚͘ Для селективной агрегации частиц чаще всего применяется флокуляция собирателями или флокулянтами, а также их сочетаниями. Электролиты употребляются в качестве модификаторов, способствующих селективному закреплению реагентов — флокулянтов. Селективная флокуляция наблюдается в условиях селективной адсорбции собирателя. Качественно зависимости степени флокуляции и извлечения материала от значения рН аналогичны (рис. 6.7). — 238 — ÐǣǯǃǮǫǃǊǬÐ͟͠ǀǃǅǀ͟ǊÐǯǬǁǬǭǰǀǫǃǮ֬ÐǪƼ͠ǬƼǪǅǀǀÐǆǪǯǰǀǅÐǫÐǯǱǯ͟Ǭǃƿǀǀ Рис.6.7. Зависимость адсорбции Г, извлечения Е и степени флокуляции Ф суспензии галенита от значения рН Однако критические концентрации, необходимые для начала флотации и флокуляции различны. Флокуляция галенита бутиловым ксантогенатом прекращается при рН = 8, а абсорбция — при рН=10,5. При значениях рН больших, чем 8, флокуляция переходит в пептизацию, т.е. распадаются флокулы, которые имелись в суспензии и флокулы из собирателя. Критическое значение рН для анионоактивного собирателя, когда прекращается его флокулирующее действие или даже наблюдается пептизация, можно вычислить из соотношения Kx − ( OH − ) x =C (6.15) Вид этого уравнения аналогичен уравнению Барского для критического значения рН. Если для ряда материалов критические значения рН флокуляции отличается, то можно один из минералов сфлокулировать, а другой нет (рис. 6.8). — 239 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð Из рисунка видно, что при рН = 7,0 бутиловый спирт ксантогенат калия (25 мг/л) флокулирует галенит и пептизирует (пирит). Следовательно, первым и основным правилом поведения селективной флокуляции является селективная адсорбция флокулянта на поверхности частиц. При этом необходимо учитывать, что процесс флокуляции флотационными собирателями обратим, т.е. флокулированную суспензию можно пептизировать, например, добавками соды или извести повышая рН, и наоборот (понижая рН). Рис. 6.8. Зависимость степени флокуляции сульфидных минералов ксантогенатом от значения рН. При применении высокомолекулярных флокулянтов процесс агрегации необратим. Например, флокуляция суспензии галенита наблюдается независимо от порядка подачи реагента (рис. 5.9). А при подаче полиакриламида и щелочи уменьшение флокуляции не наблюдается, как при обратном порядке подачи. Поэтому в случае применения высокомолекулярных флокулянтов рекомендуется первоначально суспензию спептизировать, а потом один из материалов, входящих в нее, сфлокулировать. Обратный порядок проведения процесса обречен на неудачу из-за необратимости действия ПАА. — 240 — ÐǠǮǪƼǱǁǎǅǀǎÐǫÐǪǌ͠Ǯƽǀǯ͟Ǭ͠ǯǃǊǲÐǯǀǯǰǬǂǪǲ Селективность процесса флокуляции во многом зависит от соосаждения с флокулами механически захваченных мелких частиц пептизированного материала. Чем крупнее и рыхлее флокула, тем больше неселективных захватов. Соосаждение резко возрастает с ростом концентрации суспензии. При концентрации суспензии более 5–10% твердого селективность процесса полностью нарушается из-за осаждения. Селективность процесса можно также регулировать режимом перемешивания, подобрав его так, чтобы слабосвязанные флокулы распадались, а сильносвязаные — оставались. Процесс селективной флокуляции — пептизации, как правило, применяется при обесшламливании железных руд. Сочетание крахмала с Са(ОН)2 пептизирует мелкие частицы кварца и флокулирует мелкие частицы магнетита. При хорошо подобранном реагенте потери железосодержащих материалов со сливом уменьшаются в 1,5–2 раза по сравнению с потерями при дешламации без реагентов. В настоящее время процесс селективной флокуляции интенсивно развивается, в особенности для выделения частиц менее 5 микрон, которые при обычной флотации селективно не флотируются. Рис. 6.9. Зависимость флокулирующего действия бутилового ксантогената (а) и ПАА (б) от порядка подачи реагентов. ϲ͘ϴ͘ʶ̶̵̵̨̨̛̛̛̱̣̬̭̪̖̬̭̦̼̭̭̯̖̥̌̐́́̏̌̾̔̌͘ Коагуляция — это укрупнение частиц в аэродисперсных системах при их соприкосновении друг с другом. Это явление — 241 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð уменьшает степень дисперсности аэрозолей и приводит к снижению поверхностной энергии, облегчая тем самым осаждение частиц в газоочистных аппаратах. Коагуляция взвешенных частиц может происходить за счет броуновского движения (тепловая коагуляция), а также под действием аэро-гидродинамических, гравитационных, акустических, электрических и других сил. Если причиной коагуляции является броуновское движение, то процесс называется самопроизвольной коагуляцией, при воздействии остальных внешних сил, перечисленных выше, — вынужденной коагуляцией. Скорость коагуляции аэрозольных частиц подчиняется закону 1 1 (6.16) − = Kê τ n n0 где n — концентрация частиц в некоторый момент времени τ; n0 — начальная концентрация частиц; Кк — константа коагуляции. Скорость убывания счетной концентрации частиц в результате процесса коагуляции может быть определена из выражения dn (6.17) N=− − Kê n2 dτ где N — скорость коагуляции — величина, соответствующая числу встреч частиц в единице объема в единицу времени. Согласно (5.20) в начальный момент времени, когда счетная концентрация велика, коагуляция протекает с большой скоростью, но затем скорость ее быстро падает. Рассмотрим основные виды коагуляции подробнее. ϲ͘ϴ͘ϭ͘˃̶̨̡̨̛̖̪̣̱̣̏̌́̌̐́́͘ Константу тепловой коагуляции Кбр рассчитывают по формуле 4k T Káð = á ã (6.18) 3µã — 242 — ÐǠǮǪƼǱǁǎǅǀǎÐǫÐǪǌ͠Ǯƽǀǯ͟Ǭ͠ǯǃǊǲÐǯǀǯǰǬǂǪǲ где kб — постоянная Больцмана, равная 1,38 × 10–23 Дж/К; Тг – абсолютная температура газов, К. Если средняя длина пробега газовых молекул соизмерима с размерами частиц, в выражение (6.21) вводится поправка Кенингема-Милликена: 4k T C (6.19) Káð = á ã ê 3µã Установлено, что, как и в случае суспензий, полидисперсные аэрозоли коагулируют быстрее монодисперсных. Особенно быстро происходит поглощение мелких частиц крупными, однако увеличение скорости коагуляции за счет полидисперсности не превышает 10 %. Скорость броуновской коагуляции Nбр рассчитывается по формуле (6.20) Náð = 8πD÷ n02 где Dч — коэффициент диффузии частиц, характеризующий интенсивность броуновского движения. Таким образом, с увеличением абсолютной температуры газов скорость коагуляции растет. Однако эта зависимость не прямо пропорциональная, т.к. с увеличением температуры растет и вязкость газов. Скорость коагуляции малых частиц возрастает также с понижением давления. Броуновская коагуляция играет существенную роль в начальный момент образования высокодисперсного аэрозоля, т.к. способствует практически мгновенному укрупнению частиц. ϲ͘ϴ͘Ϯ͘ʧ̶̡̨̛̛̬̖̦̯̦̱̣̌̔̌́̌̐́́͘ При наличии поперечного градиента скорости газов в потоке происходит градиентная коагуляция. Например, частица у стенки движется с меньшей скоростью, чем частица, расположенная дальше от нее. Если при этом расстояние между ними меньше суммы их размеров, то частицы должны встретиться. Скорость градиентной коагуляции определяют по выражению — 243 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð 32n02Ã d÷3 3 где Г — градиент скорости, 1/с. Для монодисперсного аэрозоля Nãðàä 4Ã d÷4 = Náð 3πD÷ Nãðàä = (6.21) (6.22) При dч = 1 мкм и Г = 20 с–1 отношение Nград /Nбр = 0,4×10–2, то есть эффект градиентной коагуляции ничтожен. У грубодисперсных аэрозолей (dч = 20 мкм) при том же значении градиента концентрации Nград /Nбр = 16, т.е. коагуляция происходит даже при небольшом градиенте. Градиентная коагуляция ограничена тонким пристенным слоем, интенсивна при турбулентном движении газового потока по длинным каналам при развитой поверхности контакта. ϲ͘ϴ͘ϯ͘˃̶̡̨̛̱̬̱̣̖̦̯̦̱̣̍̌́̌̐́́͘ При турбулентном движении газового потока возможны два механизма протекания коагуляции. Первый имеет место при полном увлечении частиц аэрозоля турбулентными пульсациями. Он наблюдается при плотности частиц, мало отличающейся от плотности потока. Если плотность частиц примерно в 103 раз больше плотности газов, полного увлечения не происходит. Второй механизм — механизм ускорения — имеет наибольший коагуляционный эффект. Он осуществляется благодаря наличию разности между плотностью газового потока и плотностью частиц аэрозоля. Из-за различия в этом случае скоростей движения частиц происходят встречи этих частиц и затем их коагуляция. При первом механизме скорость коагуляции ε  Nò ~ 1,3  ò   νã  0,5 d÷3n02 (6.23) где εт — величина, характеризующая турбулентный поток, равная νг3/L, а L — линейный параметр (для трубы диаметр трубы). — 244 — ÐǠǮǪƼǱǁǎǅǀǎÐǫÐǪǌ͠Ǯƽǀǯ͟Ǭ͠ǯǃǊǲÐǯǀǯǰǬǂǪǲ Скорость коагуляции по второму механизму определяется по формуле Nóñê ~ ω2/4 3/4 Dòð (6.24) Механизм ускорений преобладает, в основном, у крупных частиц. ϲ͘ϴ͘ϰ͘ʶ̸̶̡̡̨̛̛̛̦̖̥̯̖̭̱̣̌̌́̌̐́́͘ Процесс кинематической коагуляции протекает при относительном движении частиц различного размера, возникающем под действием внешних сил и происходящем при разных скоростях, например, осаждение частиц на каплях, падающих под действием силы тяжести (гравитационная коагуляция). Теория кинематической коагуляции различна для крупных и мелких частиц, причем для крупных можно пренебречь диффузией. Рассмотрим процесс свободного падения крупной шарообразной капли со скоростью vс. Капля падает через аэрозоль, состоящий из мелких частиц, скорость падения которых незначительна. Тогда число мелких частиц, захваченных в одну секунду крупной каплей, может быть найдено по уравнению I÷ = n0 πηç dê2 νñ 4 (6.25) где ηз — коэффициент захвата частиц (определяется графически); dк — диаметр капли; νс — вязкость среды. На явлении кинематической коагуляции основано осаждение частиц распыленной водой в мокрых пылеуловителях. При этом капли либо движутся через аэрозоль под действием только силы тяжести (полые форсуночные скрубберы), либо вводятся в аэрозоль со скоростью, превосходящей скорость их седиментации (скрубберы Вентури). — 245 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð ϲ͘ϴ͘ϱ͘ʤ̸̶̡̡̡̨̛̛̱̭̯̖̭̱̣̌́̌̐́́͘ При воздействии звуковых и ультразвуковых волн на промышленные газы, содержащие взвешенные частицы, можно при определенных условиях добиться такого колебательного движения частиц, при котором значительно увеличится столкновение частиц друг с другом, в результате чего частицы слипаются, образуя крупные агрегаты. При таких воздействиях на взвешенные частицы оказывают влияние три основных фактора: – совместное колебание частиц и газовой среды; – динамические силы между соседними частицами; – давление акустической радиации. В зависимости от условий взвешенная частица либо участвует в колебании среды, либо нет. Промышленные газы содержат частицы разного диаметра, поэтому в акустическом поле частицы будут колебаться с разными фазами и разными амплитудами. Число столкновений будет увеличиваться, в результате чего произойдет коагуляция. ϲ͘ϴ͘ϲ͘ˑ̸̶̡̡̡̨̛̛̣̖̯̬̖̭̱̣̌́̌̐́́͘ В процессе дробления, при трении или контакте с поверхностью оборудования, движении через раскаленную среду частицы пыли могут приобретать заряд. Дымы заряжаются при движении через раскаленные среды в результате ионизации в пламени, термоэлектронной и фотоэлектрической эмиссии электронов. Туманы заряжаются в результате распыления при барботировании газов через жидкости. Взвешенные частицы могут заряжаться в результате химических реакций, под действием рентгеновского излучения, электрической индукции. Естественный электрический заряд взвешенных частиц называется трибозарядом. Электрические заряды взвешенным частицам можно сообщать и искусственно (воздействием ионизаторов, электрофильтрами. Чаще всего неметаллические взвешенные частицы — 246 — ÐǠǮǃǰ͠ǮǁǋǃǊǬÐǫǮ͟͠ǮǯǊ в естественных условиях заряжаются положительно, металлические частицы — отрицательно; заряд солей зависит от их химического состава. Между электрически заряженными взвешенными частицами, между заряженными и незаряженными частицами развиваются силы взаимодействия, приводящие их к сталкиванию и образованию укрупненных агрегатов. Это могут быть силы притяжения или отталкивания (кулоновские силы); сила индукции между заряженной частицей и индуцированным зарядом на соседней незаряженной частице; сила взаимодействия между заряженной частицей и другими частицами, заряженными униполярно; сила внешнего электрического поля напряженностью Е. ϲ͘ϵ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏͘ 1. Теория процесса агрегирования. Механизмы встреч частиц друг с другом. 2. Опишите три слагающие поверхностных сил (расклинивающее давление). Какой их физический смысл? 3. Природа электростатических сил. Закономерности их изменения вглубь раствора. 4. Основные механизмы агрегирования: коагуляция, флокуляция и мостиковая флокуляция. В чем их сходство и в чем различие? 5. По какому механизму происходит слипание мелких и крупных частиц? Какой механизм преобладает? 6. Агрегирование суспензий полимерами. 7. Почему полиэлектролит по сравнению с низкомолекулярным электролитом обеспечивает значительно большую скорость осаждения частиц твердой фазы и более чистый слив сгустителя? 8. Какой процесс называется коагуляцией? 9. Под действием каких сил может происходить коагуляция взвешенных частиц? 10. В каких случаях коагуляция называется самопроизвольной, вынужденной? — 247 — ǞǁǪǫǪÐ ÐǜƼ͠ǬƼǀ͠ǮǫǪǃǀǬ Ð 11. Записать закон, которому подчиняется скорость коагуляции аэрозольных частиц. 12. Какие виды коагуляции различают? Дайте их характеристику. 13. Какие факторы оказывают воздействие на частицы при акустической коагуляции? 14. В результате протекания каких процессов может происходить акустическая коагуляция? 15. Какой заряд частиц называется трибозарядом? ϲ͘ϭϬ͘ʿ̸̛̛̬̥̖̬̼̬̖̹̖̦́̌̔̌̚͘ Задача 1. Время половинной коагуляции золя иодида серебра при исходном содержании частиц в 1 м3, равном 3,2 u 1014, составляет 11,5 с. Определите константу скорости коагуляции. Решение. Для расчета используют формулу, связывающую константу скорости коагуляции с временем половинной коагуляции: 1 1 1   = = 2,8<10−16  k=  ÷àñòèö <ñ  n0t1/2 3,2<1014 <11,5 Задача 2. Определите вид коагуляции (быстрая или медленная) путем сопоставления констант скорости коагуляции, полученных расчетными и экспериментальным путем, для золя серы, коагулируемого раствором хлорида алюминия (при Т = 293 К). Время коагуляции: Время коагуляции. τ 0 1 4 10 Частичная концентрация, 10–17 м3 16 1,78 0,5 0,2 Решение. Рассчитаем теоретические значения константы скорости коагуляции: — 248 — ÐƭǪƽǪǆǀÐƽǁǎÐǯǪǂǮǯǰǮǎǰǬǁǋǃǮƼǮÐ͠ǬǇǬǃǀǎ kòåîð = 4RT 4<8,314<293 = = 5,4<10−18 ì 3 / ñ 3N A 3<10−336,022<1023 Рассчитаем экспериментальные значения по формуле: (16 − 1,78)1017 = 5<10−18 ì 3 / ã ; k = (16 − 0,5)1017 = k1 = 4 16<1017 <1,78<1017 16<1017 <0,5<1017 <4 = 4,8<10−18 ì 3 / ã ;k6 = (16 − 0,2)1017 16<1017 <0,2<1017 <10 = 4,9<10−18 ì 3 / ã k1 + k4 + k6 (5 + 4,8 + 4,9)10−18 = = 4,9<10−18 ì 3 / ã 3 3 т.е. коагуляция медленная kýêñï = kýêñï < kòåîð ϲ͘ϭϭ͘ʯ̸̨̨̨̨̛̛̣̭̥̭̯̯̖̣̦̬̖̹̖̦̌̔̌̔́̌́̽̐́͘ Задача 1. Рассчитайте время половинной коагуляции аэрозоля с дисперсностью 0.25 нм-1 и концентрации 1.5–10–3 кг/ м3, если константа быстрой коагуляции по Смолуховскому, равна 3 u10–6 м3/с. Плотность частиц аэрозоля примите равной 2.2 г/см3. Задача 2. Рассчитайте число первичных частиц гидрозоля золота при коагуляции электролитом к моменту времени T = 150 с, если первоначальное число частиц в 1 м3 составляет X0 = 1.93 1014 , а константа скорости быстрой коагуляции равна 0.2 u 10–17 м3/с. — 249 — ǍưǙǚǙÍ Í Í ǓǔǒƠǎǕǕƥÍǐǋǕǕǒǓǎǔǎƚǋơƝÍ ǌÍǕƝǕǖǎǐǋǘÍǕÍǑǎǓǒƚǌƝƛǑǒ֏Í ǍǔǋǑƝƠǎ֏ÍǔǋƜƚǎƞǋÍǗǋƜÍ ǓǔƝǐǎǑƝǖǎƞƦǑǒÍǏÍǓǔǒƠǎǕǕǋǐÍ ƜǋƣƝǖƥÍǒǏǔƟƛǋƨƣǎ֏ÍǕǔǎƚƥ В результате изучения главы 7 бакалавр должен: Знать: – какие процессы, при защите окружаюшей среды от опасных и вредных факторов, являются процессами массопередачи в системах с неподвижной границей раздела. – основные физико-химические закономерности процессов массопередачи в системах с неподвижной границей раздела. Уметь: – обоснованно выбирать процессы для извлечения примесей из газового потока и из загрязненных сточных вод, при массопередаче в системах с неподвижной границей раздела фаз. Владеть: – основными методами и законами физической химии для описания процессов массопередачи в системах с неподвижной границей раздела. К этой группе относятся процессы, в ходе которых скоростью перемещения поверхности раздела фаз по сравнению со скоростью — 250 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀ движения фаз можно пренебречь. Таковы процессы растворения твердых тел, кристаллизации, экстракции из твердых тел и сушки твердых материалов. ϳ͘ϭ͘ˇ̸̶̸̡̨̨̨̨̨̛̛̛̛̖̭̖̭̦̼̪̬̖̭̭̥̭̭̪̖̬̖̏̏̌̔̌̚͘ Трудности чисто теоретического анализа и расчета массопереноса обусловлены сложностью механизма переноса к границе раздела фаз посредством молекулярной и турбулентной диффузии и недостаточной изученностью гидродинамических закономерностей турбулентных потоков, особенно вблизи границы раздела фаз. Рассмотрим процесс массопередачи между жидкостью и газом (паром) или между двумя жидкостями, которые движутся с некоторой скоростью друг относительно друга и разделены поверхностью раздела. Процесс массопередачи теснейшим образом связан со структурой турбулентного потока в каждой фазе. Как известно из термодинамики, при турбулентном движении потока у твердой стенки образуется ламинарный пограничный слой. Поэтому для каждой фазы различают ядро, или основную массу фазы, и пограничный слой у границы фазы. В ядре вещество переносится преимущественно турбулентными пульсациями, и концентрация распределяемого вещества в ядре фазы практически постоянна. В пограничном слое происходит постепенное затухание турбулентности. Это выражается все более резким изменением концентрации по мере приближения к поверхности раздела. Непосредственно у поверхности перенос сильно замедляется, т.к. его скорость уже будет определяться скоростью молекулярной диффузии. В этой области наблюдается наиболее резкое, близкое к линейной, изменение концентрации по мере приближения к поверхности раздела (рис.7.1). Такой характер изменения концентрации объясняется тормозящим действием сил трения между фазами и сил поверхностного натяжения на границе раздела фаз. В настоящее время существует множество моделей массопереноса. В основу большинства моделей положены следующие допущения: — 251 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Рис. 7.1. Схема распределения концентраций в фазах в процессе массопереноса. 1. Общее сопротивление переноса из фазы в фазу складывается из сопротивления двух фаз и сопротивления поверхности раздела фаз. Однако сопротивление на поверхности раздела можно в большинстве случаев считать равным нулю. Тогда, принимая, что процесс переноса в пределах каждой фазы протекает независимо от другой, общее сопротивление переносу можно рассматривать как сумму фазовых сопротивлений (правило аддитивности). 2. На поверхности раздела фазы находятся в равновесии, причем равновесие на границе фазы устанавливается значительно быстрее изменения средней концентрации в ядре фазы. ϳ͘ϭ͘ϭ͘˄̸̨̨̛̛̬̦̖̦̖̥̭̭̯̌̏̌̔̌͘ Ввиду сложности механизма процессов массоотдачи в фазах, для практических целей принимают, что скорость массоотдачи пропорциональна движущей силе, равной разности концентраций в ядре и на границе фазы. Если распределяемое вещество переходит из фазы Фу в фазу Фх, то основное — 252 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀ уравнение массоотдачи, определяющее количество вещества М, переносимого в единицу времени в каждой из фаз (к границе раздела или в обратном направлении), выражается следующим образом: Фаза Фу : M = β y F y − yãð (7.1) Фаза Фх : ( M = β F (x x ãð ) − x) (7.2) Коэффициенты βу и βх называются коэффициентами массоотдачи, которые показывают, какое количество вещества переходит от поверхности раздела фаз в ядро (или в обратном направлении) через единицу поверхности в единицу времени при движущей силе, равной единице. Коэффициент массоотдачи является не физической константой, а кинетической характеристикой, зависящей от физических свойств фазы и определяемой конструкцией и размерами массообменного аппарата, т.е. критериями подобия. Уравнение массопередачи — описывает процесс переноса распределяемого вещества через поверхность раздела фаз. Учитывая это, основное уравнение массопередачи определяет количество вещества, переносимого из фазы в фазу в единицу времени, т.е. ( M = K F (x ) − x) M = Ky F y − y* * x (7.3) (7.4) где y*, x* — равновесные концентрации в данной фазе, соответствующие концентрациям распределяемого вещества в основной массе (ядре) другой фазы; Ky , Kx — коэффициенты массопередачи, выраженные через концентрации фаз Фу и Фх. Отметим, что концентрация фаз изменяется при движении их вдоль поверхности раздела. Поэтому в уравнения (6.3; 6.4) для упрощения расчетов вводят величину средней движущей силы. M = Ky F ∆yñð (7.5) M = Kx F ∆xñð (7.6) — 253 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Зависимость между коэффициентами массоотдачи и массопередачи. Пусть распределяемое вещество переходит из фазы Фу в фазу Фх, а движущая сила массопередачи выражается в концентрациях фазы Фу. Для простоты рассмотрим случай, когда равновесная зависимость между концентрациями фаз линейна, т.е. y* = mx , где m — тангенс угла наклона линии равновесия. Выразим движущую силу в уравнении массоотдачи (7.1) в концентрациях фазы Фу, принимая, что концентрации вещества непосредственно у границы (хгр, угр) равновесны друг другу. Из уравнения линии равновесия следует: xãð = yãð / m ; x = y* / m (7.7) y* — концентрация фазы Фу, равновесная с концентрацией х фазы Фх. Подставляя эти значения в уравнение (7.2), получим: yãð − y* M = βx F (7.8) m Откуда yãð − y* = Mm βx F (7.9) Вместе с тем из уравнения массоотдачи (7.1) имеем M y − yãð = (7.10) βy F Складывая выражения (7.9) и (7.10), исключаем неизвестную нам концентрацию на границе раздела фаз: M 1 m +  , y − y* = (7.11)  F  β y βx  а из уравнения массопередачи получим y − y* = M 1 < F Ky (7.12) Откуда следует, что 1 1 m = + Ky β y βx — 254 — (7.13) ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀ аналогичные рассуждения приводят к зависимости 1 1 1 = + Kx βx β ym (7.14) Левые части уравнений представляют собой общее сопротивление переноса вещества из фазы в фазу, т.е. сопротивление массопередачи, а правые части — сумму сопротивлений массоотдачи в фазах. Уравнения аддитивности были выведены для линейной равновесной зависимости, но они остаются в силе и для криволинейной линии равновесия. Коэффициенты массоотдачи и массопередачи часто относят не к поверхности контакта F, а к рабочему объему аппарата V, который связан с поверхностью зависимостью V = F / a , где a — удельная поверхность контакта фаз, отнесенная к единице рабочего объема аппарата, мг/м3. Тогда уравнения массоотдачи запишутся ( V (x ) − x) ( V (x ) − x) M = β yV V y − yãср M = βxV Уравнения массопередачи ср (7.15) (7.16) M = KyV V y − y* M = KxV * (7.17) (7.18) Средняя движущая сила массопередачи выражается уравнением: ∆yср = (y н ) ( − y*н − y к − y*к y − yн* ln н yк − yк* ) = ∆y − ∆yм ∆y 2,3lg б ∆yм б (7.19) где величина ∆y б обозначает выраженную в общем виде движущую силу процесса массопередачи на том конце аппарата, где она больше, а величина ∆yм — на другом конце аппарата, где она меньше. Аналогично, в концентрациях другой фазы (фазы Фх) имеем: — 255 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ ∆xср = (x * н ) ( − xн − x*к − x к x* ln н* xк − xн − xк ) = ∆x − ∆xм ∆x б 2,3lg ∆xм б (7.20) При ∆yб / ∆yм ≤ 2 с достаточной для технических расчетов точностью средняя движущая сила может быть рассчитана как среднеарифметическая: ∆y + ∆yм ∆yср = б (7.21) 2 ∆xñð = ∆xá + ∆xì 2 (7.22) ϳ͘Ϯ͘ˀ̵̨̛̭̯̬̖̦̖̯̖̬̼̯̖̣̌̏̏̔͘ Растворение твердых веществ в жидкостях можно рассматривать как процесс, состоящий из следующих стадий: 1. переноса молекул растворителя из объема жидкой фазы к поверхности твердого тела; 2. перехода молекул твердого тела в соприкасающуюся с ними жидкость; 3. переноса растворенных молекул от поверхности твердого тела в объем жидкой фазы. Чаще всего лимитирующей является последняя стадия. Это означает, что наибольшее сопротивление массопереносу при растворении твердого тела создает диффузионный пограничный слой на его поверхности. При этом можно считать, что на границе с твердым телом раствор насыщен. Тогда движущей силой процесса является разность содержания растворенного вещества в насыщенном растворе и объеме жидкой фазы. Кинетику процесса можно описать уравнением dM (7. 23) = βF c p − cæ dτ где М — масса растворенного вещества; τ — время; F — площадь поверхности твердого тела; ср и сж — содержание растворенного вещества в единицах массы на единицу объема чисто- ( — 256 — ) ÐǥǪǯǰǫǮ͠ǬǃǀǬÐǰǫǬ͠ƽǊǲÐǰǬǁ го растворителя в насыщенном растворе и в объеме жидкости, соответственно; β — коэффициент массоотдачи в жидкой фазе. Как было показано, коэффициент массоотдачи зависит от гидродинамической обстановки процесса. Обычно растворы приготовляют из предварительно измельченных твердых тел и значение β определяется формой и размерами частиц и условиями обтекания их жидкостью. Поскольку при обтекании частицы (особенно, неправильной формы), структура потока весьма сложна, поверхность частицы неоднородна в кинетическом отношении. Кроме того, отдельные частицы обычно различаются по форме и размерам. В связи с этим значение β в соотношении (7.23) имеет смысл величины, усредненной по поверхности частиц. Наиболее простые соотношения, описывающие кинетику растворения, получаются для сферических частиц. Для одиночной сферической частицы радиусом r можно написать dM = ρò Fdr , и уравнение (7.23) приобретает вид: − ρò dr = c p − cò dτ = ∆cdτ β ( ) (7. 24) Коэффициент массоотдачи β является функцией размера частицы, который в процессе растворения уменьшается. В случае мелких частиц, для которых Re 0,2, значение β определяется из условия Nu = βd = 2 , из которого следует, что D 2D D = , где D — коэффициент диффузии растворяемого веd r щества в растворителе. Подстановка этого значения β в уравнение (7.24) и интегрирование при условии постоянства ∆с дают: β= r = rí2 − 2D∆cτ , где rн — начальный радиус частицы. ρò Отсюда следует, что время полного растворения (r = 0) составляет: τ p = ρò rí2 . 2D∆c — 257 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ При Re > 0,2 диффузионный критерий Нуссельта зависит от критерия Рейнольдса, для определения значения которого нужно знать скорость относительного движения частицы и жидкости. Ее можно считать равной скорости осаждения. Принятое при интегрировании уравнения (7.24) условие постоянства ∆с означает, что при растворении частицы состав раствора не меняется, т. е. частица растворяется в бесконечно большом объеме жидкости. В реальных процессах содержание растворенного вещества в жидкой фазе увеличивается. Связь состава раствора с количеством твердой фазы определяется условиями материального баланса. При идеальном перемешивании или прямотоке: Mí − M = V (c − cí ) где Мн и М — количество твердой фазы в начале процесса и в произвольный момент времени τ, соответственно; V — объем растворителя; с и сí — содержание растворенного вещества в момент τ и в начале процесса, соответственно. Содержание растворенного вещества в жидкой фазе связано с размером частиц: 4 Mí − M = π rí3 − r 3 ρò N = V (c − cí ) (7.25) 3 где N — число частиц; V — объем растворителя. V r Путем введения новых переменных y = и m = — 4 3 r πrí ρò N 3 объема растворителя, приходящегося на единицу массы растворяемого вещества, уравнение (7.25) преобразуется к виду: (7.26) y3 = 1 − m (c − cí ) ( ) При противотоке твердой и жидкой фаз: 4 Mí − M = V (cê − c ) ; π rí3 − r 3 ρò N = V (cê − c ) 3 где ск конечное содержание растворенного вещества в жидкой фазе. Имеем: y3 = 1 + m (c − cê ) ( — 258 — ) ÐǥǪǯǰǫǮ͠ǬǃǀǬÐǰǫǬ͠ƽǊǲÐǰǬǁ Для мелких частиц противоточное движение фаз трудно реализовать вследствие уноса частиц жидкостью. Чаще всего растворение твердых тел проводится в аппаратах с мешалками, структура потока в которых приближается к модели идеального перемешивания. Поэтому процесс растворения однородных сферических частиц описывается системой уравнений (7.24) и (7.26). После преобразования уравнения (7.24) путем введения у вместо r, получаем систему уравнений dy β c p − c ; y3 = 1 − m c − c − = dτ ρ r из которой после исключения величины с следует: 1 dy 1  3  0β c −c −  p н m 1− y    τ = ρт rн ∫ ( ) (7.27) D r D βd 2rβ . = =2 β= < í = D D r rí yrí Подставляя это значение β в уравнение (7.27), получаем: 1 ρ r 2m ydy τ= ò í ∫ (7.28) D 0 m∆c − 1 + y3 где ∆c = c p − cí — при заданных условиях проведения процесса постоянная величина, определяющая максимальное количество вещества, способного раствориться в единице объема растворителя. Количество исходного твердого вещества, приходящегося на единицу объема растворителя, равно 1/m. Если ∆с > 1/m, то все твердое вещество способно перейти в раствор. Если же ∆с < 1/m, то при достаточной длительности процесса (теоретически за бесконечно большое время) получится насыщенный раствор и останется некоторое количество твердой фазы, рав1  ное  − ∆c V . При ∆с > 1/m время растворения определяется m  интегрированием выражения (6.28). В практике приходится иметь дело с частицами, различающимися не только размерами, но и формой. Расчет кинетики При Nuä = — 259 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ процессов растворения в таких системах представляет чрезвычайно большие трудности и не может дать достаточно точных результатов. Поэтому с целью получения данных для проектирования промышленных установок кинетику растворения исследуют экспериментально. Обычно эксперименты проводят с тем же материалом и по возможности при такой же гидродинамической обстановке, как в реальном процессе. Определяется доля твердого вещества в суспензии М/Мн в зависимости от его содержания в растворе с, продолжительности процесса растворения τ, температуры t и факторов, характеризующих гидродинамическую обстановку процесса (Г). По опытным данным получается кинетическая функция M = γ (c, τ, t,Ã ) , Mí с помощью которой можно найти скорость растворения: dγ − = f (c, τ, t,Ã ) . dτ При обработке опытных данных удобно вместо времени растворения τ ввести безразмерное время Θ = τ/τр, где τр — время полного растворения твердого вещества. Величина τр является функцией кинетических факторов (состава раствора, размеров частиц, гидродинамической обстановки и т. д.). В результате обработки экспериментальных данных часто получается единая кинетическая функция γ(Θ), инвариантная относительно условий проведения процесса. При периодическом проведении процесса оборудование рассчитывается по времени полного растворения, найденному экспериментально. При непрерывном проведении процесса в аппарате с мешалкой необходимо учесть неодинаковое время пребывания частиц суспензии. Если функция распределения времени пребывания f(x) известна, то доля нерастворившихся частиц, находящихся в аппарате в интервале времени от τ до τ+dτ, составит γ τ = γ (c, τ, t,Ã ) f ( τ ) dτ — 260 — ÐǥǪǯǰǫǮ͠ǬǃǀǬÐǰǫǬ͠ƽǊǲÐǰǬǁ а средняя доля нерастворившегося вещества от первоначально загруженного τ γ = ∫γ (c, τ, t,Ã ) f ( τ ) dτ 0 или, если кинетическая функция представлена зависимостью γ = f (Θ ) Θ γ = ∫ γ ( Θ ) f ( Θ ) dτ (7.29) 0 При этом функция времени пребывания f(τ) должна быть соответствующим образом пересчитана для получения функции f(Θ). В связи с неодинаковым временем пребывания частиц в одном аппарате непрерывного действия полное растворение всех частиц невозможно. Поэтому непрерывные процессы растворения проводят в каскаде аппаратов, работающих по принципу прямотока или противотока. При противотоке достигается большая движущая сила процесса, чем при прямотоке, однако из-за сложности разделения жидкой и твердой фаз после каждого аппарата, чаще применяется прямоток. При этом, естественно, движущая сила процесса растворения постепенно понижается. ϳ͘Ϯ͘ϭ͘ˀ̸̶̨̨̡̡̛̭̖̯̪̬̖̭̭̬̭̯̬̖̦̭̖̌̌̌̏́̏̌̌̔ ̵̨̨̨̨̨̛̪̭̣̖̯̖̣̦̭̖̦̖̦̦̼̪̪̬̯̔̏̌̽̔̌̌̌̏͘ Расчет проводится последовательно для каждого аппарата, начиная от первого. Все параметры потоков на входе в первый аппарат известны. Для него, очевидно, γ=1. Вначале принимается некоторое значение γi на выходе из первой ступени и по уравнению материального баланса (7.25) рассчитывается состав раствора: M − M1 M  M  M = cí + í  1 − 1  = cí + í (1 − γ i ) (7.30) c1 = cí + í V V  Mí  V По экспериментально найденной зависимости γ (c, τ, t,Ã ) определяется время полного растворения τр и величина Θ при — 261 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ полученном из предыдущего уравнения значении с1. Потом с помощью соотношения (7.29) вычисляется доля нерастворившегося материала γi и она сравнивается с принятой в начале расчета. При необходимости расчет повторяется до получения значений γi совпадающих с необходимой степенью точности. Затем аналогичным образом выполняется расчет второй ступени, для которой входными параметрами являются выходные параметры первой ступени. Таким же образом рассчитываются последующие ступени. Функция распределения времени пребывания частиц f(Θ) зависит от конструкции и режима работы аппарата. Для одноступенчатого аппарата идеального смешения:  Θ  1 f (Θ ) = exp  −  Θñð  Θñð  Здесь Θср = τср/τр — среднее время пребывания в аппарате, отнесенное к времени полного растворения τр. Среднее время пребывания в аппарате равно отношению V его рабочего объема Vа к объемному расходу жидкости τñð = a . Væ При расчете числа ступеней n необходимых для обеспечения достаточно полного растворения (значение γn для последней ступени должно быть известно из технологических требований), приходится задаваться значением τср. Это равносильно тому, что при заданном расходе растворителя Vж, принимается определенный размер аппарата. Для выбора аппаратурно-технологического оформления процесса такой расчет следует выполнить для ряда значений τср (или Va) и затем найти оптимальный вариант по экстремальному значению критерия оптимальности. ϳ͘ϯ͘ʶ̶̛̛̛̬̭̯̣̣̌̌́̚͘ˇ̡̨̛̛̚Ͳ̵̸̡̨̨̛̛̛̥̖̭̖̭̦̼̏ ̶̸̶̶̨̨̡̛̛̛̛̛̛̛̪̬̦̪̼̬̭̖̯̪̬̖̭̭̬̭̯̣̣̌̌̏̌̌̚͘ Кристаллизация — это процесс выделения твердых веществ из насыщенных растворов или расплавов. В процессе — 262 — ÐǠ͠ǀǯǰǪǁǁǀƿǪǅǀǎ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǀÐ͟͠ǀǃǅǀ͟ǊÐ͠ǪǯǆǬǰǪÐ͟͠ǮǅǬǯǯǮǫÐǭ͠ǀǯǰǪǁǁǀƿǪǅǀǀ кристаллизации используется различие составов равновесных твердой и жидкой фаз. Проведение процесса кристаллизации из растворов основано либо на использовании зависимости растворимости твердого вещества от температуры, либо на удалении растворителя из насыщенного раствора путем его выпаривания. Чаще всего, растворимость твердых веществ с понижением температуры уменьшается, поэтому при проведении процесса по первому способу раствор необходимо охлаждать. По второму способу кристаллизация проводится при практически постоянной температуре. Процесс кристаллизации путем охлаждения раствора обычно сочетается с выпариванием раствора, оставшегося после выделения твердой фазы (маточного раствора), для его концентрирования до первоначального состава. Кристаллизация — это процесс, обратный растворению. В связи с этим тепловой эффект процесса кристаллизации равен по величине и противоположен по знаку тепловому эффекту растворения: вещества, растворяющиеся с поглощением теплоты, кристаллизуются с выделением теплоты, и наоборот. Процесс периодической кристаллизации состоит из стадий образования зародышей кристаллов и их последующего роста. При непрерывном проведении процесса обе стадии протекают одновременно. Образование новой фазы в существующей возможно только при ее пересыщении, поскольку этот процесс требует расхода энергии на образование поверхности раздела фаз. Для процесса образования зародышей твердой фазы степень пересыщения раствора связана с радиусом зародыша r и удельной энергией поверхности раздела фаз следующей зависимостью: x 2σv ln ï = (7.31) x p rRT где хр и хп — содержание кристаллизирующегося вещества в насыщенном и перенасыщенном растворах, соответственно; v — мольный объем твердой фазы. Степень пересыщения возрастает с уменьшением размеров зародышей твердой фазы. Поэтому, подобно другим про— 263 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ цессам фазовых переходов, образование зародышей твердой фазы происходит не во всем объеме раствора или расплава, а в особых точках — центрах кристаллизации. Их роль играют механические примеси или шероховатости поверхностей аппаратов. Для ускорения образования зародышей и во избежание отложения твердой фазы на стенках аппаратов в них вводят затравку — мелкие частицы кристаллизующегося вещества. Особенно это полезно для растворов или расплавов, склонных к пересыщению. Чем мельче частицы, тем менее уравновешены их поверхностные силы и тем в большей степени они склонны к взаимодействию. Результатом этого является агрегирование мелких частиц. С увеличением размера частиц быстро (по экспоненте) уменьшается равновесная степень пересыщения. Можно считать, что для кристаллов таких размеров, какие получаются в промышленных кристаллизаторах, равновесная степень пересыщения пренебрежимо мала, т. е. на поверхности кристалла находится насыщенный раствор. При этом движущей силой переноса молекул из объема раствора или расплава является разность содержаний кристаллизующегося вещества в пересыщенном растворе, образующем жидкую фазу хп и в насыщенном растворе хр. Кинетику процесса кристаллизации можно описать таким же уравнением, что и кинетику растворения: dM = βF xï − xð dτ где dM/dτ — скорость увеличения массы кристаллов M; F — площадь поверхности кристаллов; β — коэффициент массоотдачи. Применение этого соотношения для инженерных расчетов затруднительно, поскольку величины F, хп и коэффициент массоотдачи β зависят от многих факторов, плохо поддающихся учету. Некоторые качественные закономерности выявляются из рассмотрения физической природы процесса кристаллизации и анализа имеющихся опытных данных. Так, увеличение интенсивности перемешивания при кристаллизации повыша- ( — 264 — ) ÐǠ͠ǀǯǰǪǁǁǀƿǪǅǀǎ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǀÐ͟͠ǀǃǅǀ͟ǊÐ͠ǪǯǆǬǰǪÐ͟͠ǮǅǬǯǯǮǫÐǭ͠ǀǯǰǪǁǁǀƿǪǅǀǀ ет ее скорость за счет возрастания коэффициента массоотдачи и способствует равномерному росту кристаллов, но они получаются более мелкими. К увеличению скорости процесса приводит повышение температуры, поскольку уменьшается вязкость жидкой фазы. С увеличением движущей силы процесса степени пересыщения (∆х = хп – хр) за счет более быстрого выпаривания растворителя или более быстрого охлаждения суспензии скорость кристаллизации повышается в связи с быстрым возрастанием числа зародышей, но частицы твердой фазы получаются также более мелкими. Кроме того, при быстрой кристаллизации ухудшается однородность кристаллов — в них может «защемляться» маточный раствор. Цель процесса кристаллизации — получение твердого продукта с определенными химическими и физическими свойствами (в частности, определенного гранулометрического состава). Поэтому при создании установки для проведения кристаллизации должны быть обеспечены все необходимые для этого условия. В связи с практической невозможностью расчетного определения кинетики роста кристаллов она исследуется экспериментально. Опытные данные представляются dr в виде функции = λ ( ∆x,r ) , выражающей скорость изменеdτ ния линейного размера кристалла r в зависимости от степени пересыщения ∆х = хп – хр и размера частицы r. Математическое описание процесса непрерывной кристаллизации основывается на уравнениях материального и теплового балансов: Lí = G + Lê + Lâ Lí xí = Gy + Lê xê Lí cí tí + Gqê + Q = Gcò tê + Lê cê tê + Lâ iâ Где Lн и Lк — расходы исходного и конечного растворов; Lв — расход удаляемого растворителя; G — расход получаемой твердой фазы; хн, хк, у — содержания кристаллизующегося вещества в исходном и конечном растворах и в твердой фазе, соответственно; сн, ск, ст — теплоемкости начального и конечного — 265 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ раствора и твердой фазы, соответственно; tн — начальная температура раствора; tк — температура кристаллизации; qк — теплота кристаллизации; (iв — энтальпия удаляемого растворителя; Q — расход теплоты, подводимой при выпаривании растворителя (Q > 0) и отводимой (Q < 0) при охлаждении раствора. При установившемся непрерывном процессе кристаллизации объем находящейся в кристаллизаторе суспензии, число частиц и их распределение по размерам остаются неизменными. Функцию распределения частиц по размерам f(r) можно установить, исходя из следующих соображений. Число зародышей размером rз образующихся в аппарате, равно числу частиц N, выводимых из него. Если рассмотреть частицы с интервалом размеров от r до r + dr, то их число увеличивается за счет роста более мелких частиц со скоростью λ = dr/dτ. Число таких частиц в единицу времени равно N  λf (r )r . За то же время за пределы рассматриваемого интервала вырастает N  λf (r )r +dr частиц. Часть частиц размером от r до r + dr выводится из аппарата вместе с отбираемой суспензией с расхоV дом, равным Nf (r )r dr æ ; Vж — объемный расход отбираемой Và суспензии, Va — объем суспензии в аппарате). При установившемся процессе V N  λf (r )r = N  λf (r )r +dr + Nf (r )r dr æ Và Или, поскольку Và = τñð — среднее время пребывания суVæ спензии в аппарате 1  λf r  r =  λf r  r +dr + τ f r r dr (7.32) Величину,  λf (r )r +dr являющуюся функцией r, можно разложить в ряд Тейлора. Если ограничиться слагаемыми первого порядка малости, то d  λf (r )r (7.33)  λf (r )r +dr =  λf (r )r + dr dr — 266 — ÐǠ͠ǀǯǰǪǁǁǀƿǪǅǀǎ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǀÐ͟͠ǀǃǅǀ͟ǊÐ͠ǪǯǆǬǰǪÐ͟͠ǮǅǬǯǯǮǫÐǭ͠ǀǯǰǪǁǁǀƿǪǅǀǀ Подстановка в соотношение (7.32) дает: d  λf (r )r 1 dr + f (r )r dr .  λf (r )r =  λf (r )r + τ dr ñð d  λf (r )r 1 dr . =− τñð λ  λf (r )r Нижний предел интегрирования по r определяется разИли  1 мером зародыша r3. Следовательно λf (r ) = Cexp  −  τñð r   C 1 dr и f (r ) = exp  − .  τñð r∫ λ  λ r ∫ rç dr   λ  ç Постоянная интегрирования С находится из условия нормирования функции плотности распределения на единицу. Поскольку величина f(r) dr определяет долю частиц размером от r до r + dr от общего количества частиц, то с учетом выражения, определяющего f (r), получаем: ∞ ∞  1 ∞ dr  1 ∫ f (r )dr = 1 = C ∫ λ exp  − τñð ∫ λ    rç rç rç 1  1 1 ∫ rç λ exp  − τñð Таким образом Отсюда C = ∞ dr  ∫ rç λ  . ∞  1 r dr  exp  − ∫   τñð rç λ  f (r ) = (7.34)  1 ∞ dr  ∞ 1 λ∫ exp  − ∫  rç λ  τñð rç λ  Из этого выражения следует, что вид функции распределения частиц по размерам зависит от вида функции λ, определяющей скорость роста кристаллов. Эта функция находится экспериментально. Когда скорость роста кристаллов не зависит от их размеров (λ = const), то из уравнения (7.32) имеем — 267 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ  r − rç  1 (7.35) exp  −  λτñð  λτñð  Средний размер частиц при этом равен rñð = rç + λτñð Суммарный объем образующейся в аппарате твердой фазы, определяется соотношением: f (r ) = ∞ Vт = N ∫ Φr 3f (r ) dr rз Здесь Ф — коэффициент (фактор) формы, равный отношению объема частицы к кубу половины ее размера. Для шара Ф = 4/3π, для куба Ф = 8 и т. Д. Если принять, что все частицы имеют одинаковую форму, то после подстановки значения f(r) из (7.35) и интегрирования получаем: 2 3 Vт = NΦ rз3 + 3rз2 λτ ср + 6rз λτ ср + 6 λτ ср  = Nv   Где v — средний объем частицы. Число частиц, образующихся в единице объема раствора за единицу времени J, связано с числом частиц, отводимых из аппарата N, зависимостью: N = J (Và − Vò ) τñð = J (Và − Nv ) τñð ( Отсюда N = JVà τñð 1 + Jv τñð ) ( ) . Величина J является функцией степени пересыщения раствора и определяется эспериментально. ϳ͘ϰ͘ʿ̶̶̵̨̡̡̨̨̛̛̛̬̖̭̭̼̭̯̬̭̭̯̖̥̯̖̬̖̯̖̣̾̌̏̌̏̔Ͷ ̡̨̛̙̭̯̔̽;̶̸̨̛̛̪̬̖̭̭̼̺̖̣̦̏̌̏̌́Ϳ͘ Растворение твердых частиц в жидкостях — один из широко применяемых основных процессов химической технологии (производство органических полупродуктов и красителей, минеральных удобрений и многие другие). Растворение является предпосылкой для ускорения различных химико-технологических процессов, так как в растворенном и в значительной мере — 268 — ÐǤ͠ǮǅǬǯǯǊÐÐǌǭǯǰ͠ǪǭǅǀǀÐǫÐǯǀǯǰǬǂǪǲÐǰǫǬ͠ƽǮǬÐǰǬǁǮÐèÐƾǀƽǭǮǯǰǋÐ͟͠ǮǅǬǯǯÐǫǊǈǬǁǪǆǀǫǪǃǀǎ диссоциированном состоянии увеличиваются подвижность и химическая активность молекул растворенного вещества. В промышленности применяется растворение практически чистых твердых веществ, перевод которых в раствор позволяет ускорить проведение последующих химических реакций или диффузию растворенных веществ, а также растворение, происходящее в результате химического взаимодействия твердых частиц и жидкости, например с целью извлечения металлов из руд. Ниже рассмотрены процессы избирательного (селективного) растворения одного или нескольких веществ из твердых тел, являющихся смесью различных компонентов. Такие процессы растворения, представляющие собой диффузионное извлечение растворителем компонента (или компонентов) из пористого твердого материала, называются экстракцией в системе твердое тело — жидкость, или выщелачиванием. В качестве избирательных растворителей при выщелачивании используют в основном воду или водные растворы некоторых минеральных кислот и щелочей. Выщелачивание является, в частности, первой стадией химической переработки сырья, из которого этим путем извлекаются ценные компоненты, отделяемые от инертного материала. Процессы выщелачивания часто сопровождаются последующими процессами фильтрования, выпаривания и кристаллизации. Любой процесс выщелачивания заключается в том, что жидкость, проникая в поры твердого тела, растворяет извлекаемый компонент или вступает с ним в реакцию; вещество, перешедшее в раствор (или продукт реакции), диффундирует к поверхности твердого тела и переходит в основную массу жидкости. Иногда извлекаемое вещество содержится в порах твердого тела в растворенном виде, и в этом случае оно непосредственно переходит в растворитель путем диффузии. На перенос вещества при выщелачивании значительное влияние оказывает, помимо формы, размера и химического состава частиц твердого тела, его внутреннее строение, в том числе размеры, расположение и вид пор (сквозные или закрытые с одного конца). От структуры пористого твердого тела зависит — 269 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ его диффузионная проводимость, которая может оказывать значительное, а иногда и определяющее влияние на скорость выщелачивания. В некоторых случаях растворение происходит в результате гетерогенной реакции на поверхности раздела фаз, протекание которой сопровождается образованием не только растворимых, но и нерастворимых (или частично растворимых) твердых, а также газообразных продуктов реакции. Выделение твердых и газообразных продуктов может приводить к образованию пористой пленки или оседанию пузырьков газа на поверхности твердого материала. Твердая фаза может также образовываться и оседать на поверхности исходного твердого материала вследствие кристаллизации при пресыщении раствора. Все эти явления могут существенно уменьшать поверхность материала, доступную для взаимодействия с растворителем, и соответственно снижать скорость процесса. ϳ͘ϰ͘ϭ͘ˀ̸̨̡̨̨̛̛̛̛̦̖̭̖̭̬̭̯̼̺̖̣̦̌̏̏̽̏̌̏̌́͘ Равновесие при экстракции в системе твердое тело — жидкость наступает тогда, когда химический потенциал растворенного вещества становится равным величине его химического потенциала в исходном твердом материале. Достигаемая при этом предельная концентрация раствора соответствует насыщению последнего и называется растворимостью. Данные о растворимости различных веществ в зависимости от температуры приводятся в справочниках. Движущей силой процессов экстракции жидкостью из твердых материалов является разность между концентрацией растворяющегося вещества у поверхности твердого тела сгр и его средней концентрацией с0 в основной массе раствора. Обычно вблизи поверхности твердого тела равновесие устанавливается очень быстро. Поэтому концентрация на границе твердой фазы может быть принята равной концентрации насыщенного раствора снас, а движущая сила — выражена разностью снас – со. — 270 — ÐǤ͠ǮǅǬǯǯǊÐÐǌǭǯǰ͠ǪǭǅǀǀÐǫÐǯǀǯǰǬǂǪǲÐǰǫǬ͠ƽǮǬÐǰǬǁǮÐèÐƾǀƽǭǮǯǰǋÐ͟͠ǮǅǬǯǯÐǫǊǈǬǁǪǆǀǫǪǃǀǎ Соответственно при большой скорости межфазного перехода скорость процесса, определяемая количеством вещества, dM , где М — масса растворяющегося за время dτ, и равная dτ растворяющегося твёрдого вещества в момент времени τ, определяется по уравнению массоотдачи (7.23) Изменение концентрации растворяющегося вещества упрощенно представлено на рис. 7.2. Из него видно, что наиболее резко падение концентрации происходит в области диффузионного пограничного подслоя толщиной δ. Соответственно наиболее медленной и лимитирующей стадией процесса является перенос растворяющегося вещества в этом подслое путем молекулярной диффузии. Поэтому согласно первому закону Фика: c − c0 dM = DF íàñ (7.36) dτ δ где D — коэффициент молекулярной диффузии. Сопоставляя уравнение (7.23) и (7.36), получим, что β = и уравнение (7.23) может быть записано в виде M D = Fñð (cíàñ − c0 ) = βFñð (cíàñ − c0 ) , τ δ D δ (7.37) M — количество вещества, растворяющегося в единицу τ времени; Fср — средняя во времени поверхность растворения. Кинетическое уравнение (7.37) было впервые получено А.Н. Щукаревым в результате обработки опытных данных по растворению. Если принять, что δ ≈ D1 3 , то из уравнения (7.37) следует, что коэффициент массоотдачи β при растворении твердых частиц пропорционален D2 3 . Обобщение опытных данных, с учетом этого, позволило получить для расчета β уравнение: где Nu ′ = 0,8 3 Pr ′ Re — 271 — , ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Рис. 7.2. Изменение концентрации растворяющегося вещества вблизи поверхности твердого тела. βd ν ωd , Pr ′ = , Re = , причем d — диаметр твердой ν D D частицы, v — кинематическая вязкость жидкости, обтекающей частицу, ω — скорость обтекания. Из уравнения (7.37) видно, что коэффициент массоотдачи D/δ обратно пропорционален толщине δ диффузионного пограничного слоя, которая, в свою очередь, зависит от гидродинамической обстановки вблизи растворяющихся твердых частиц. Чем быстрее движение жидкости относительно твердой частицы, тем тоньше диффузионный пограничный слой и тем больше коэффициент массоотдачи. Поэтому перемешивание жидкости, позволяющее уменьшить величину δ и равномерно распределить твердые частицы в жидкости, дает возможность существенно ускорить растворение. Другим фактором, ускоряющим растворение и выщелачивание, является температура, так как с повышением ее возрастает величина снас и при прочих равных условиях увеличивается движущая сила. Кроме того, при повышении температуры возрастает значение коэффициента диффузии D вследствие уменьшения вязкости жидкой фазы, что также способствует увеличению скорости процесса. где Nu ′ = — 272 — ÐǤ͠ǮǅǬǯǯǊÐÐǌǭǯǰ͠ǪǭǅǀǀÐǫÐǯǀǯǰǬǂǪǲÐǰǫǬ͠ƽǮǬÐǰǬǁǮÐèÐƾǀƽǭǮǯǰǋÐ͟͠ǮǅǬǯǯÐǫǊǈǬǁǪǆǀǫǪǃǀǎ В случае проведения процесса выщелачивания при атмосферном давлении температура процесса должна быть ниже температуры кипения жидкости, приближаясь к ней как к пределу. Использование избыточных давлений позволяет проводить выщелачивание при температурах, превышающих температуру кипения жидкости при атмосферном давлении. Избыточное давление, создаваемое насосом, дает возможность осуществлять процесс при значительно более высоких скоростях жидкости, обрабатывая более мелко измельченные твердые пористые материалы и преодолевая при этом возросшее гидравлическое сопротивление системы. В результате процессы выщелачивания под давлением протекают с большей скоростью. Степень измельчения твердого материала также оказывает значительное влияние на скорость выщелачивания. Измельчение приводит к увеличению поверхности соприкосновения фаз, а также позволяет сократить путь вещества, диффундирующего из глубины пор к поверхности твердого материала. Однако практически степень измельчения ограничена ввиду того, что ее увеличение сопровождается возрастанием расхода энергии на измельчение, и является экономически целесообразным лишь до определенного предела. Степень измельчения лимитируется также необходимостью проведения фильтрования после процесса выщелачивания. Рис. 7.3. К определению скорости выщелачивания. — 273 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ В отличие от простого растворения в процессе выщелачивания, доступная для взаимодействия с жидкостью поверхность извлекаемого компонента перемещается вглубь пор твердого материала. Это приводит к значительному падению скорости выщелачивания, когда скорость процесса начинает лимитироваться скоростью внутренней диффузии из глубины куска (зерна) твёрдого материала к его поверхности. В соответствии со схемой на рис 7.3, скорость выщелачивания меньше скорости растворения и определяется по уравнению dM DF = (c − c0 ) (7.38) dτ δ + h íàñ где h — глубина выщелоченного материала. В связи с этим различные факторы, указанные выше, далеко не в равной мере влияют на скорость простого растворения и выщелачивания. Так, перемешивание не может оказать существенного влияния на скорость внутренней диффузии при выщелачивании и поэтому дает меньший эффект, чем в процессе простого растворения. Вместе с тем измельчение твердого материала, приводящее, как отмечалось, наряду с увеличением поверхности соприкосновения фаз, к уменьшению пути растворяемого вещества при его внутренней диффузии, является относительно более эффективным фактором ускорения процессов выщелачивания. ϳ͘ϱ͘ʿ̶̨̡̛̬̖̭̭̭̱̹͘ Согласно [1–6,9,10,22,28] сушка является последней стадией при обезвоживании различных материалов. Удаление влаги из материала производят испарением за счет подвода тепла. Следовательно, при сушке одновременно протекают два, процесса: массо- и теплообмена. Различают три основных вида сушки по способу подвода тепла к сушильному материалу, подвергающемуся данному процессу: — 274 — ÐǤ͠ǮǅǬǯǯÐǯǱǇǭǀ 1. Конвективная сушка — путем непосредственного соприкосновения высушиваемого материала с сушильным агентом, в качестве которого обычно используют нагретый воздух или топочные газы (как правило, в смеси с воздухом). 2. Контактная сушка — путем передачи тепла от теплоносителя к материалу через разделяющую их стенку. 3. Радиационная сушка — путем передачи тепла инфракрасными лучами. При сушке большинства материалов чаще всего применяют конвективный способ с применением в качестве сушильного агента топочных газов. Этот вид сушки применим для многих материалов, независимо от их крупности в начальной влажности. Схема установки для сушки дымовыми газами (рис.7.4) включает следующие основные операций: 1) получение сушильного агента при сжигании топлива в отдельной топке 1, куда поступает необходимый для горения воздух 2) установление необходимой температуры сушильного агента с добавлением атмосферного воздуха к топочным газам в камере смешения 2; 3) высушивание материала в сушилке 3, которая, как правило, представляет собой полую вращающуюся трубу, в которую непрерывно поступает и из которой также непрерывно выводится материал; 4) улавливание пыли из отобранного сушильного агента с помощью специальных устройства вентилятора 6. В некоторых случаях отработанный газ частично возвращается в камеру смещения для повторного использования. При этом сокращается расход топлива на полученные сушильного агента. Целью сушки является получение материала с конечной влажностью Wконечн. При этом должно испариться жидкости в количестве W. Как видно из схемы, конечная влажность материала Wкон. зависит от следующих параметров, с помощью которых: регулируется процесс: — 275 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Рис. 7.4. Схема установки для сушки дымовыми газами 1 — топка; 2 — камера смещения; 3 — сушилка; 4,5 — устройство для обеспыливания дымовых газов; 6-вентилятор 1) времени сушки — τ чаc; L êã âîçäóõà W êã âîäû B êêàë 3) удельного расхода топлива q = 0 W êã âîäû 4) исходной влажности материала Wисх%; 5) количества влажного материала WG, кг. В свою очередь время сушки, расход топлива и воздуха зависят от свойств высушиваемого материала и сушильного агента (смеси топочных газов и воздуха). Рассмотрим эти свойства более подробно. 2) удельного расхода воздуха l = ϳ͘ϱ͘ϭ͘ˀ̸̶̨̨̡̛̭̖̯̪̬̖̭̭̭̱̹̌̏͘ Материальный баланс процесса сушки можно представить равенствами: (7.39) W = Gí − Gê = L (x2 − x0 ) — 276 — ÐǤ͠ǮǅǬǯǯÐǯǱǇǭǀ где W — количество влаги, удаленной из высушиваемого материала; Gн И Gк — начальное и конечное количества материала, соответственно; L — расход воздуха, считая на абсолютно сухой; х2 и х0 — конечное и начальное влагосодержание воздуха, соответственно. Отсюда определяется расход воздуха l, необходимый для удаления из материала единицы массы влаги L 1 = l= W x2 − x0 Тепловой баланс процесса выражается соотношением: LI0 + Gí cí tí + Qê + Qä = LI2 + Gê cê tê + Qòð + Qïîò (7.40) Здесь Qк и Qд — количества теплоты, сообщаемой воздуху перед входом в сушилку (в калорифере) и дополнительно в сушилке, соответственно; сн и tн — теплоемкость и температура исходного материала, ск, tк — теплоемкость и температура высушенного материала, I0 и I2 — энтальпии исходного и отработавшего воздуха, соответственно; Qтp — расход теплоты на нагревание устройств для транспортировки материала в сушилке; Qпот — потери теплоты в окружающую среду. ϳ͘ϱ͘Ϯ͘ˀ̨̨̨̡̛̛̛̦̖̭̦̖̭̖̬̙̦̖̣̪̬̭̱̹̖̌̏̏̔̌̏̌̐͘ ʶ̡̡̛̛̛̦̖̯̭̱̹̌͘ Если материал находится в контакте с влажным воздухом (или сушильным агентом), то принципиально возможны два процесса: 1) сушка (десорбция или испарение влаги из материала) при парциальном давлении пара над поверхностью материала Рм, превышающем его парциальное давление в сушильном агенте Рn, т.е. при Рм >Рп; 2) увлажнение (сорбция) при Рм <Рп. В процессе сушки величина Рм уменьшается и становится равной Рn . Влажность материала, соответствующая динамическому равновесию, называют равновесной Wp. Равновесная влажность зависит от парциального давления водяного пара над материалом Рп или пропорциональной — 277 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ ему величины относительной влажности воздуха ϕ, равной P ϕ = ï , где РH. — давление насыщенного водяного пара при PÍ данной температуре °С и общем давлении P. Зависимостъ Wp = f ( ϕ ) устанавливается экспериментально. Для этой цели навеска высушиваемого материала помещается в среду с различной относительной влажностью φ при термостатировании и периодически взвешивается. Влажность материала при достижении им постоянной массы является равновесной. Обычно навески доводят до постоянной массы в эксикаторе с растворами серной кислоты различной концентрации и получают зависимость WP от ϕ. Кроме адсорбционной связанной влаги, которую для сокращения называют просто «связанной влагой», в материале содержатся так называемая свободная влага, которая не удерживается ни поверхностными, ни капиллярными силами. Применительно к процессу сушки под свободной влагой понимают влагу, скорость испарения которой из материала равна скорости испарения жидкости, как правило, воды со свободной поверхности. Изменение влажного материала в процессе сушки показано на рис.7.5, из которого видно, что, начиная с точки А, конечная возможная или равновесная влажность материала при сушке определяется только относительной влажностью сушильного агента. Обычно говорят, что материал находится во влажном состоянии, когда его влажность находится в пределах от Wнач. до WГ. Точка А называется гигроскопической, а соответствующая ей влажность WГ — гигроскопической влажностью. В точке А Рм = Рп и ϕ = 100%. Другой важной характеристикой, устанавливаемой экспериментально, является скорость сушки. Скорость сушки определяют по изменению влагосодержания материала после его нагревания при данной температуре через определенные промежутки времени. — 278 — ÐǤ͠ǮǅǬǯǯÐǯǱǇǭǀ Рис. 7.5. Изменение влажности материала в процессе сушки. Рис.7.6. Кривая сушки материала Характерный ход кривой такой зависимости представлен на рис.7.6, из которого видно, что кривая состоит как бы из трех участков. На первом участке АВ тепло преимущественно расходуется на нагревание материала, и скорость сушки мала. На прямолинейном участке ВС все тепло расходуется только на испарение влаги. В этот период, называемый периодом постоянной скорости сушки, устанавливается динамическое равновесие между скоростью теплопередачи к материалу и ско— 279 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ ростью удаления пара от поверхности. При этом температура материала не изменяется, а скорость испарения из материала равна скорости испарения с открытой поверхности жидкости. Эта постоянная температура называется температурой мокрого термометра tм.т.. В этот период скорость испарения не зависит от природы твердого материала. Давление пара над материалом равно давлению насыщенного пара РН при данной температуре над жидкостью. Влажность в точке «С» перехода первого периода сушки во второй, более замедленный, называется первой критической влажностью Wкр1. Во втором периоде сушки уменьшение влажности материала выражается некоторой кривой Ск, которая в общем случае состоит из двух участков различной кривизны (отрезки ДЕ и ЕК). Точка перегиба «Д» соответствует второй критической влажности Wкр2. В конце второго периода сушки влажность материала асимптотически приближается к равновесной Wр, при которой прекращается дальнейшее испарение влаги. Скорость сушки определяется из кривой сушки путем графического дифференцирования по тангенсу угла наклона касательной, проведенной к точке кривой, отвечающей влажности материала. В точке «С» (при первой критической влажности Wкр1) влажность на поверхности материала становится равной гигроскопической. С этого момента начинается испарение связанной влаги. Точка «D» (вторая критическая влажность) соответствует достижению равновесной влажности на поверхности материала (Wкр1=Wкр2). Внутри материала влажность превышает равновесную. Начиная с этого момента и вплоть до установления равновесной влажности во всей толще материала, скорость сушки определяется скоростью внутренней диффузии влаги из глубины материала к его поверхности. Из-за высыхания все меньшая поверхность остается доступной для испарения влаги в окружающую среду и скорость сушки падает непропорционально уменьшению влажности материала. На участке «СD» скорость сушки упала из-за уменьшения парциального давления пара над материалом РП менее PН насыщенного пара. Продолжительность испарения или сушки зависит от скорости сушки на всех этапах. К сожалению теоретические расчеты скорости — 280 — ÐǤ͠ǮǅǬǯǯÐǯǱǇǭǀ сушки сложны и не точны и в практических расчетах применяются редко. Чаще при расчете конвективных сушилок их объем находят приближенно, пользуясь средней опытной величиной напряжения объема сушилки по влаге А (кг/см3-час) — параметром, выражающим количество влаги, удаляемой при подобных условиях в единице объема сушильной камеры. При этом рабочий объем сушилки определяется простой зависимостью W Q ( R1 − R2 ) = Vp = (7.41) A A где W — общее количество влаги, удаляемой за весь процесс сушки; Q — производительность сушильного отделения (по весу твердой фазы в материале подвергающимся сушке), кг/ час; R1 и R2 — весовые отношения Ж:Т соответственно в поступающем и выходящей из сушилки материале WÍ WÊ R1 = è R2 = 100 − WÍ 100 − WÊ Следовательно, объем сушилки определяется эмпирически на основании значений А из опытных данных. Дальнейшие расчеты упрощаются, так как исключается две переменные — время сушки и количество материала. Для того, чтобы провести дальнейшие расчеты, необходимо познакомится с основными параметрами влажного воздуха. ϳ͘ϱ͘ϯ͘ʽ̵̨̨̨̨̭̦̦̼̖̪̬̥̖̯̬̼̣̙̦̱̏̌̌̏̌̐̏̔̌̚͘ При конвективной сушке сушильный агент передает материалу тепло и уносит влагу, испаряющуюся из материала за счет этого тепла. Таким образом сушильный агент играет роль тепло- и массоносителя. Влажный газ является смесью сухого газа и водяного пара. В дальнейшем под влажным газом будем подразумевать только влажный воздух, учитывая, что физические свойства топочных газов и влажного воздуха отличаются лишь количественно. — 281 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Влажный воздух как влаго- и теплоноситель, характеризуется следующими основными параметрами: абсолютной и относительной влажностью, влагосодержанием и энтальпией (теплосодержанием). Абсолютная влажность определяется количеством водяного пара в кг, содержащегося в I м3 влажного воздуха. Можно считать, что пар занимает весь этот объем и поэтому абсолютная влажность равна плотности пара ρн (кг/м3) при температуре влажного воздуха и парциальном давлении Pн. Относительной влажностью или степенью насыщения воздуха φ называется отношение массы водяного пара в I м3 влажного воздуха ρп при данных условиях (температуре и общем барометрическом давлении) к максимально возможной ρ массе водяного пара в I м3 воздуха ρn; ϕ = ï , поскольку ρп и ρH ρÍ по уравнению Менделеева — Клапейрона выражаются как Pµ p µ ρï = ï ï è ρÍ = Í Í RT RT Р и Pн — парциальное давление соответственно пара в данных условиях и насыщенного пара; μ — масса I кг/моль водяного пара, равная 18 · 10–3г/моль; R — универсальная газовая постоянная, равная 8314 (кДж)/кмоль.град. или 1,99 ккал/кмоль. град. Подставляя эти значения в уравнения для ϕ, получим: P ϕ= ï PÍ Значения Рп водяного пара для температур менее 100 °С берутся из стандартных таблиц давления водяного пара при данной температуре воздуха. Если температура воздуха выше температуры кипения (насыщения), то максимально возможное давление водяного пара будет равно общему или барометрическому давлению Рб. В этих условиях P ϕ= n Pб С ростом температуры Рн растет и поэтому φ уменьшается вплоть до t = 100 °С. Далее Pп = Pб = const и, следовательно, — 282 — ÐǤ͠ǮǅǬǯǯÐǯǱǇǭǀ ϕ также постоянна. В процессе сушки воздух отдает тепло, охлаждается и забирает влагу. Величина ϕ увеличивается вплоть до ϕ =1 т.е. до насыщения воздуха. Поскольку объем воздуха в процессе сушки изменяется с изменением его температуры, то пользоваться в расчетах значением его абсолютной влажности неудобно. Количество водяного пара (в кг), содержащегося во влажном воздухе и приходящегося на I кг абсолютно сухого воздуха, называется влагосодержанием воздуха: ρ m x= ï = ï mñ .â ρñ .â где mп, и mc.в — масса водяного пара и масса абсолютно сухого воздуха в данном объеме влажного воздуха, кг; ρc.в — плотность абсолютно сухого воздуха, кг/м3.Связь между ϕ и x устанавливается с помощью уравнения Менделеева-Клапейроиа. PM P M Mï Pï P = 0,622 ï x = ï ï : ñ .â ñ .â = RT RT Mñ .â Pñ .â Pñ .â где Mс.в — масса I кг/моль абсолютно сухого воздуха, равная 29 · 10–3г /моль. По закону Дальтона Pc.в равно разности общего давления влажного воздуха Р и парциального давления пара в нем PÑ .Â = P − PÏ но так как Pп = ϕPп, получим: X = 0,622 ϕPÏ P − lPÏ Теплофизический параметр влажного воздуха — энтальпия или теплосодержание J влажного воздуха относится к I кг абсолютно сухого воздуха и определяется при данной температуре воздуха (t°С), как сумма энтальпий абсолютно сухого воздуха Сс.вt и водяного пара xiп (Дж/кг). J = Cñ .â t + xiï (7.42) где Сс.в — средняя удельная теплоемкость сухого воздуха, которая может быть принята приближенно равной 1000 дж/кг. град или 0,24 ккал/кг. град; iп— энтальпия водяного пара. — 283 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Из этого уравнения хорошо видно, что воздух при сушке может отдавать тепло только за счет охлаждения (уменьшается член (Сс.вt), так как влагосодержание воздуха X при сушке возрастает, поэтому произведение xiп должно возрастать. Водяной пар находится в процессе сушки в перегретом состоянии в смеси с воздухом. Обозначим энтальпию водяного пара при 0°С через r0 ( r0 = 2493.103 дж/кг или 595 ккал/кг) и примем среднюю удельную теплоемкость перегретого водяного пара Сn = 1,97.103 дж/кг.град. Тогда энтальпия перегретого пара (0,47 кал/кг.град.) iï = r0 + Cï t = 2493<103 + 1,97<100 чим Подставив значения iп и Cс.в в основное уравнение, полу- ( ) J = 1000 + 1,97<103 X t + 2493<103 X ϳ͘ϱ͘ϰ͘:ͲyͶ̵̨̨̨̛̬̥̥̣̙̦̱̔̌̐̌̌̏̌̐̏̔̌̚͘ Основные свойства влажного воздуха можно с достаточной для технических расчетов точностью определять с помощью J-x диаграммы, впервые разработанной Л. К. Рамзиным. Диаграмма J-x построена для постоянного давления Р = 745 мм.рт.ст. (рис.7.7) Диаграмма имеет угол 135° между осями координат, причем по оси ординат отмечены в определенном масштабе энтальпии, а на наклонной оси абсцисс — влагосодержание X, значения которых для удобства пользования диаграммой спроектированы на вспомогательную ось, перпендикулярную оси ординат. На диаграмме нанесены: – линии постоянного влагосодержания (x = const) вертикальные прямые, параллельные оси ординат; – линии постоянной энтальпии (J = const) — прямые, параллельные оси абсцисс, т.е. идущие под углом в 135° к оси абсцисс; – линии постоянных температур, или изотермы (t = const) – линии постоянной относительной влажности (ϕ = const) — 284 — ÐǤ͠ǮǅǬǯǯÐǯǱǇǭǀ – линия парциальных давлений водяного пара Pn во влажном воздухе, значения, которых отложеныа в масштабе на кривой оси ординат диаграммы. Линия ϕ = 100% соответствует насыщению воздуха водяным паром при данной диаграмме J-x это состояние изобразится точкой А, которая является пересечением двух прямых x0 и t0 = const или x0 и ϕ0 = const (рис.7.8). Известна также температура воздуха (t1) на выходе из калорифера. Тогда процесс нагревания воздуха в калорифере изобразится на диаграмме J-x точкой В, которая является пересечением линий x0 и t1 =const . Поскольку каждой точке на диаграмме соответствуют четыре параметра влажного воздуха, а для построения процесса нагревания (отрезка АВ) необходимо знать только три параметра, то остальные параметры считывают с диаграммы. Например, если для точки А были известны t0 и ϕ0, то из диаграммы находим другие два параметра — J01 и x0. Для точки В, зная только t1, легко считывают из диаграммы значения J1 и ϕ1. При охлаждении воздуха из точки А возможно два варианта, когда tk > tp и когда tк < tp , где tp — температура точки росы. В первом случае изображение процесса охлаждения ничем не отличается от изображения процесса нагревания. Точка В получается, как пересечение двух линий tk и x0. Во втором случав (tk < tp), когда линия х0 пересекается с линией ϕ = 100%, воздух полностью насыщается паром и при дальнейшем его охлаждении из него конденсируется влага. Температура, соответствующая этому процессу, называется температурой точки росы. Конечное состояние воздуха в этом случае находится как точка пересечения линий tk’ , и ϕ = 100%. В этом случае, как видно из диаграммы, в конечном состоянии влагосодержание воздуха уменьшается до величины x1’. Остальные параметры находятся аналогично. Поскольку при сгорании топлива в топках происходит не только нагревание воздуха, но и увеличение его влагосодержания за счет образования водяных паров при сгорании водорода, содержащегося в топливе (в некоторых случаях дают для — 285 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Рис.7.7. Диаграмма J-x для влажного воздуха. интенсификации горения острый пар), то этот процесс на диаграмме J-x изображается прямой В, где точка В получается как пересечение линий tT= const и x2 = const, где x2 — влагосодержание в топочных газах на выходе из топки, а tT — их температура. В этом заключается особенность изображения процесса нагревания при применении топочных газов. Ранее мы отмечали, что в первом периоде сушки все подводимое, тепло расходуется только на испарение влаги, т.е. теплосодержание воздуха не изменяется, так как уменьше— 286 — ÐǤ͠ǮǅǬǯǯÐǯǱǇǭǀ Рис.7.8. Изображение процессов сушки на J-x диаграмме: а — теоретическая сушилка; б — действительная сушилка. ние члена Cс.xt полностью компенсируется возрастанием члена xin(yp). Процесс без изменения теплосодержания называется адиабатическим. Этот процесс при J = const также называется теоретическим процессом сушки, т.к. нет излишних потерь тепла и изображается на диаграмме J-x линией J = const например, отрезками BС и В’С’, где точка С’ получена, как пересечение линий J = const с tck = const1, где tck — температура газа, покидающего сушильную камеру. ϳ͘ϱ͘ϱ͘ˁ̸̡̨̨̛̛̱̹̯̪̦̼̥̥̌̐̌̌̚͘ В настоящее время все более широкое распространение приобретает сушка топочными газами, т.к. их влагопоглощающая способность велика вследствие их большой температуры. В качестве сушильного агента применяют газы, полученные либо сжиганием в топках твердого, жидкого или газообразного топлива, либо отработанные газы котельных, промышленных печей или других установок. Газы для сушки не должны содержать золы и сажи, загрязняющие высушиваемый материал в условиях конвективной сушки. С этой целью газы подвергаются сухой или мокрой очистке перед поступлением в сушилку. Обычно температура топочных газов превы— 287 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ шает предельно допустимую для высушиваемого материала и поэтому их разбавляют воздухом для получения сушильного агента с требуемой температурой. ϳ͘ϲ͘ʤ̶̨̛̭̬̔̍́͘ʽ̛̛̺̖̭̖̖̦̍̏̔́͘ Под адсорбцией мы понимаем[5,6,9] процесс поглощения одного или нескольких компонентов из газовой смеси или раствора твердым веществом — адсорбентом. Поглощаемое вещество носит название адсорбата или адсорбтива. Процессы адсорбции (как и другие процессы массопередачи) избирательны и обычно обратимы. Благодаря их обратимости становится возможным выделение поглощенных веществ из адсорбента, или проведение процесса десорбции. Адсорбция применяется главным образом при небольших концентрациях поглощаемого вещества в исходной смеси жидкостей или газов, когда требуется достичь практически полного извлечения удаляемого вещества. В тех случаях, когда концентрация поглощаемого вещества в исходной смеси велика, обычно выгоднее использовать абсорбцию. Процессы адсорбции широко применяются в промышленности при очистке и осушке газов, очистке и осветлении растворов, разделении смесей газов или паров, в частности при извлечении летучих растворителей из их смеси с воздухом или другими газами (рекуперация летучих растворителей) и т.д. Еще сравнительно недавно адсорбция применялась в основном для осветления растворов и очистки воздуха в противогазах; в настоящее время ее используют для очистки аммиака перед контактным окислением, осушки природного газа, выделения и очистки мономеров в производствах синтетического каучука, смол и пластических масс, выделения ароматических углеводородов из коксового газа и для многих других целей. В ряде случаев после адсорбции поглощенные вещества выделяют (десорбируют) из поглотителя. Процессы адсорбции часто сопутствуют гетерогенному катализу, когда исходные реагенты адсорбируются на катализаторе, а продукты реакции десорбируются, например при каталитическом окислении двуокиси — 288 — ÐǜƽǯǮ͠ƻǅǀǎ ÐǣƻǈǀǬÐǯǫǬƽǬǃǀǎ серы в трехокись на поверхности платинового катализатора и др. Значение адсорбционных процессов сильно возросло за последнее время вследствие расширения потребности в веществах высокой чистоты. Различают физическую и химическую адсорбцию. Физическая адсорбция обусловлена взаимным притяжением молекул адсорбата и адсорбента под действием сил Ван-дер-Ваальса и не сопровождается химическим взаимодействием адсорбированного вещества с поглотителем. При химической адсорбции, или хемосорбции, в результате химической реакции между молекулами поглощенного вещества и поверхностными молекулами поглотителя возникает химическая связь. При поглощении паров адсорбция иногда сопровождается заполнением, пор адсорбента жидкостью, образующейся в результате конденсации паров (капиллярная конденсация). Конденсация происходит вследствие понижения давления пара над вогнутым под действием сил поверхностного натяжения мениском жидкости в капиллярах. ϳ͘ϲ͘ϭ͘ˈ̵̡̡̨̨̛̛̛̛̛̛̬̯̖̬̭̯̭̬̖̦̯̼̌̌̌̔̍̏̏̔͘ В качестве адсорбентов применяются пористые твердые вещества с большой удельной поверхностью, обычно относимой к единице массы вещества. Адсорбенты имеют различные по диаметру капиллярные каналы — поры, которые условно могут быть разделены на макропоры (более 2 ·10–4 мм), переходные поры (6 ·10–6 – 2 10–4 мм), микропоры (2 · 10–6 – 6 · 10–6 мм). Характер процесса адсорбции определяется размером пор. Удельная поверхность макропор относительно очень мала, поэтому на их стенках адсорбируется ничтожное количество вещества. Макропоры играют роль лишь транспортных каналов для адсорбируемых молекул. На поверхности переходных пор, размеры которых обычно значительно превышают размеры адсорбируемых молекул, в процессе адсорбции образуются слои поглощенного вещества. Возможно образование слоев толщиной в одну молекулу — 289 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ (мономолекулярная адсорбция) и в несколько молекул (полимолекулярная адсорбция). Размеры микропор приближаются к размерам адсорбируемых молекул и адсорбция в микропорах приводит к заполнению их объема. Вследствие этого предположение об образовании слоев поглощенного вещества на поверхности микропор не имеет физического смысла. Обычно микропоры пересекаются макро- и переходными порами, что сокращает путь, проходимый адсорбируемыми молекулами, и приводит к ускорению адсорбции. В больших порах диаметром более 2 · 10–4 мм и малых порах, сравнимых с диаметром молекул поглощаемого вещества, явление капиллярной конденсации отсутствует. Адсорбенты характеризуются своей поглотительной, или адсорбционной, способностью, определяемой концентрацией адсорбтива в единице массы или объема адсорбента. Поглотительная способность адсорбента по отношению к данному веществу зависит от температуры и давления, при которых производится адсорбция, и от концентрации поглощаемого вещества. Максимально возможная при данных условиях поглотительная способность адсорбента условно называется его равновесной активностью. В промышленности в качестве поглотителей применяют главным образом активные угли и минеральные адсорбенты (силикагель, цеолиты и др.), а также синтетические ионообменные смолы (иониты). Активные угли. Высокопористые активные угли получают путем сухой перегонки различных углеродсодержащих веществ (дерева, костей и др.) и активирования полученных углей для повышения их пористости. Активирование осуществляют прокаливанием угля при температурах 900°С, а также другими способами, например удалением из пор угля смол и некоторых других продуктов сухой перегонки путем их экстрагирования органическими растворителями, окислением кислородом воздуха и др. Для повышения активности углей в них часто перед обугливанием вводят активирующие добавки (растворы хлористого цинка, кислот, щелочей и др.). — 290 — ÐǜƽǯǮ͠ƻǅǀǎ ÐǣƻǈǀǬÐǯǫǬƽǬǃǀǎ Удельная поверхность активных углей колеблется от 600 до 1700 м2/г. Размер гранул некоторых стандартных марок активных углей для адсорбции газов и паров составляет 1–5 мм (уголь БАУ) и 1,5–2,7 мм (уголь СКТ). Насыпная плотность углей этих марок равна 350 и 380–450 г/м3 соответственно. Применение углей того или иного вида зависит от разновидности процесса адсорбции, в котором они используются (поглощение газов, рекуперация летучих растворителей и т. д.). Активные угли лучше поглощают пары органических веществ, чем воды, однако с повышением содержания влаги в активных углях их способность поглощать пары органических веществ снижается. Они применяются обычно для рекуперации летучих растворителей. Недостатком активных углей является их горючесть. Силикагели. Эти адсорбенты представляют собой продукты обезвоживания геля кремневой кислоты, получаемые путем обработки раствора силиката натрия (растворимого стекла) минеральными кислотами или кислыми растворами их солей. Удельная поверхность силикагелей изменяется от 400 до 770 м2/г. Размер гранул колеблется от 0,2 до 7 мм, насыпная плотность составляет 100–800 кг/л3. Силикагели применяются главным образом для осушки газов. Поглотительная способность силикагелей по отношению к парам органических веществ сильно снижается в присутствии влаги. Достоинством силикагелей является их негорючесть и большая механическая прочность, чем у активных углей. Цеолиты. Эти адсорбенты представляют собой природные или синтетические минералы, которые являются водными алюмосиликатами катионов элементов первой и второй групп периодической системы Д. И. Менделеева. В качестве промышленных адсорбентов применяются главным образом искусственные (синтетические) цеолиты. Относительно недавно были получены цеолиты, обладающие весьма однородной структурой пор, размеры которых соизмеримы с размерами адсорбируемых молекул. Эти цеолиты проявляют молекулярно-ситовое действие, которое заключается в их способности — 291 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ не поглощать молекулы, диаметр которых больше диаметра пор. Молекулярно-ситовыми свойствами обладают также некоторые природные цеолиты, например натролит. Молекулярно-ситовое действие цеолитов часто используют в промышленной практике для разделения некоторых веществ, например нормальных и изопарафиновых углеводородов. Цеолиты отличаются высокой поглотительной способностью по отношению к воде и являются высокоэффективными адсорбентами для осушки и очистки газов и жидкостей, в частности для глубокой осушки газов, содержащих небольшие количества влаги. Размер гранул цеолитов составляет от 2 до 5 мм. Иониты. Эти адсорбенты представляют собой как природные, так и синтетические неорганические и органические вещества. К природным ионитам относятся цеолиты, глинистые минералы, ископаемые угли и др. Синтетическими ионитами являются плавленые цеолиты и молекулярные сита (цеолиты с правильной кристаллической структурой), ионообменные смолы, активированные минералы и органические вещества и др. Иониты практически нерастворимы в воде, а также в обычных растворителях и обладают подвижными ионами, способными обмениваться на эквивалентное количество ионов (с зарядом того же знака) из раствора электролита, с которым поглотитель взаимодействует. Иониты, содержащие кислые активные группы и обменивающиеся с раствором электролита подвижными анионами, называются анионитами, а иониты, содержащие основные активные группы и обменивающиеся подвижными катионами, í катионитами. Существуют так же амфотерные иониты, способные к катионному и анионному обмену одновременно. Типичные реакции ионного обмена: 1. Реакция анионного обмена 2RCl + Na2SO4 ļ R2S04 + 2NaCl где R — молекула ионита, связанная с подвижным ионом. 2. Реакция катионного обмена 2NaR + СаСl2 ļ CaR2 + 2NaCl причем в обоих уравнениях выделены формулы веществ, составляющих твердую фазу. — 292 — ÐǜƽǯǮ͠ƻǅǀǎ ÐǣƻǈǀǬÐǯǫǬƽǬǃǀǎ Механизм ионного обмена обусловлен структурой и свойствами ионита. Так, например, иониты с кристаллической решеткой содержат в ее углах ионы, удерживаемые электростатическими силами; под действием этих сил и происходит в основном ионный обмен. Свойства многих ионитов связаны с их способностью к набуханию в водных растворах; набухание обычно сопровождается весьма значительным повышением давления. Ионообменные смолы обладают большой обменной емкостью, избирательностью к отдельным ионам, химической стойкостью и механической прочностью. Поэтому сейчас они являются наиболее распространенными ионитами, практически вытеснившими в промышленных условиях иониты других типов. Изменением состава активных групп при синтезе ионообменных смол можно получить иониты с весьма разнообразными свойствами. ϳ͘ϲ͘Ϯ͘ˀ̶̨̨̛̛̛̛̦̖̭̖̪̬̭̬̌̏̏̌̔̍͘ Количество вещества, адсорбированное единицей массы или объема данного поглотителя при достижении состояния равновесия, зависит от температуры и концентрации поглощаемого вещества в парогазовой смеси или растворе. Соответственно зависимость между равновесными концентрациями фаз при адсорбции имеет вид X * = f ( Y,T ) (7.43) или при постоянной температуре * X * = f1 ( Y ) (7.44) где X — относительная концентрация адсорбтива в адсорбенте (называемая также величиной адсорбции), равновесная с концентрацией адсорбтива в газовой или жидкой фазе, кг адсорбтива кг адсорбента; — относительная концентрация адсорбтива в фазе, из которой адсорбируется вещество, кг адсорбтива/кг носителя газовой смеси или раствора. — 293 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Концентрация Y поглощаемого вещества может быть заменена его парциальным давлением р в паро-газовой смеси. Тогда X * = f ( p) (7.45) Зависимости (7.43) и (7.44) представляют собой выраженные в самом общем виде уравнения линии равновесия при адсорбции, или изотермы адсорбции. Изотермы адсорбции определяются опытным путем. Вид изотермы адсорбции зависит от многих факторов: удельной поверхности адсорбента, объема пор, их распределения по размерам и других характеристик структуры адсорбента, свойств поглощаемого вещества, а также от температуры процесса. Адсорбция сопровождается уменьшением давления пара поглощаемого компонента в исходной смеси и заметным выделением тепла. Поэтому, в соответствии с принципом Ле-Шателье, количество адсорбированного вещества возрастает с понижением температуры и повышением давления. Таким образом, повышение температуры и понижение давления отрицательно влияют на процесс адсорбции, способствуя десорбции поглощенного вещества из адсорбента. Количество выделяющегося при адсорбции тепла определяется экспериментально; теплоты адсорбции различных веществ приводятся в справочной литературе. При отсутствии опытных данных о равновесии (или данных, полученных путем обработки эмпирических уравнений) построение изотермы равновесия возможно при использовании уравнений, выведенных на основе того или иного механизма, или теории процесса адсорбции. Предложенные теории адсорбции исходят как из представлений о химическом взаимодействии между адсорбируемым веществом и поглотителем и мономолекулярной адсорбции (Ленгмюр), так и допущения о притяжении молекул поглощаемого вещества к поверхности адсорбента с силой, пропорциональной адсорбционному потенциалу ε в данной точке (потенциальная теория Эйкена и Поляни). При этом величина ε выражает работу, совершаемую адсорбционными силами при — 294 — ÐǜƽǯǮ͠ƻǅǀǎ ÐǣƻǈǀǬÐǯǫǬƽǬǃǀǎ перемещении одной молекулы поглощаемого вещества из бесконечности в данную точку адсорбционного пространства. Таким образом, ε = f(x), где х — расстояние от поверхности адсорбента. Потенциальная теория рассматривает процессы поглощения веществ адсорбентами как полимолекулярную адсорбцию. Эта теория позволяет вычислить изотерму адсорбции пара любого вещества по известной изотерме адсорбции пара некоторого стандартного вещества (например, бензола). Пределом адсорбции является полное насыщение адсорбента. Предел адсорбции, т.е. количество адсорбированных молекул, которое приходится на единицу поверхности при предельно плотной упаковке молекул в мономолекулярном слое, зависит от размера молекул. Равновесную адсорбцию характеризуют зависимостью количества адсорбата от равновесного давления (или концентрации) при постоянной температуре. График такой зависимости называется изотермой адсорбции Ленгмюра. Теория Ленгмюра основывается на следующих положениях: – адсорбционная поверхность насыщается по мере увеличения концентрации адсорбирующегося вещества; – адсорбция локализована (молекулы не перемещаются на поверхности) на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбата — образуется мономолекулярный слой; – адсорбционные центры энергетически эквивалентны; – адсорбированные молекулы не взаимодействуют друг с другом. Для описания монослойного покрытия поверхности адсорбента используют общий вид изотермы Ленгмюра (рис. 7.9). Кривая изотермы имеет три характерных участка: 0–1 — участок, выражающий пропорциональную зависимость адсорбции от давления; 1–2 — криволинейный переходный участок, отвечающий промежуточной стадии заполнения поверхности; 2–3 — прямолинейный, почти горизонтальный участок, соответствующий при больших давлениях (или концентрациях) полному насыщению поверхности адсорбатом. — 295 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Рис. 7.9. Изотерма адсорбции Ленгмюра. Уравнение адсорбции, которое называют уравнением изотермы адсорбции по Ленгмюру, будет иметь вид V= Vm bp 1 + bp (7.46) величина b является мерой поверхностной активности или константой равновесия адсорбции; V, Vm — объем адсорбированного газа при равновесном давлении р и такой же объем газа, при котором вся поверхность будет покрыта монослоем молекул, соответственно. В начальной стадии процесса, когда давление р еще мало, уравнение (7.46) преобразуется в уравнение Генри: (7.47) V = Vm bp Это уравнение описывает линейную зависимость объема от давления (см. рис. 7.9). В конечной стадии процесса, когда давление велико и bp >> 1, уравнение (7.46) сводится к виду (7.48) V = Vm Это значит, что адсорбция уже не зависит от давления; этому соответствует горизонтальный участок изотермы адсорбции на рис. 7.9. — 296 — ÐǜƽǯǮ͠ƻǅǀǎ ÐǣƻǈǀǬÐǯǫǬƽǬǃǀǎ Для мономолекулярной адсорбции при равновесии концентрация газа в адсорбенте уравнение Ленгмюра в другом виде может быть записано как xi0 = abpi 1 + bpi (7.49) где а — емкость монослоя газа на адсорбенте; b — константа равновесия процесса адсорбции, определяемая отношением скоростей прямой и обратной реакций. pi → 0 Для предельных случаев получаем: при xi0 = abpi = mpi — уравнение Генри; при pi → ∞ , xi0 = a — предельное значение при занятии всех оборванных связей на поверхности адсорбента. Согласно теории Эйкена и Поляни, как мы указывали выше, располагая изотермой адсорбции пара стандартного вещества для температуры Т1 можно вычислить изотерму адсорбции другого при температуре Т2. Величины адсорбции находят по формуле a1V1 (7.50) V2 a1 и a2 — ординаты изотермы соответственно стандартного (обычно бензола) и исследуемого вещества, кг/кг или кмоль/г, V1 и V2 — молярные объемы стандартного исследуемого вещества, м3. Молярные объемы определяют по формуле: a2 = M (7.51) ρ M — молекулярная масса, кг/кмоль, ρ- плотность жидкости, кг/м3. Давление находят из выражения: V= lgp2 = lgps1 − β T1 ps2 lg T2 p1 (7.52) p1 , p2 — парциальные давления стандартного и исследуемого вещества, кПа; ps2 — давление насыщенного пара исследуемого вещества при температуре T1 , кПа; β — коэффициент аффинности, равный отношению молярных объемов: — 297 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ (7.53) β = V2 / V1 При расчете точек изотермы исследуемого пара координаты a1 и p1 берутся по кривой стандартного вещества, а значения p1 , p2 , ps1 , ps2 — из таблиц давления насыщенного пара. Обычно изотерму адсорбции при периодическом процессе, как мы описывали выше, можно разделить на три области: первая p характеризуется отклонением ≤ 0,17 (по бензолу); для втоps p p ≈ 0,17 ÷ 0,5 ; для третьей < 0,5 . ps ps Для первой области, где изотерма адсорбции считается прямолинейной, можно пользоваться формулой: рой τ= a0 a0 H −b β yc0 wc0 (7.54) τ — продолжительность адсорбции, с; w — скорость паро-газового потока; H — высота слоя адсорбента; c0 — начальная концентрация адсорбированного вещества в парогазовом потоке; a0 — количество адсорбируемого вещества, равновесное с концентрацией потока c0 (кг/м3) берется по изотерме адсорбции в (кг/кг) и умножается на насыпную плотность адсорбента (кг/м3); β y - коэффициент массоотдачи, с–1 Для второй области изотермы адсорбции применяют уравнение:   c0 0  w1  c0  (7.55) τ=  H −  ln  − 1 + ln − 1   wC0  c β y  p p  c   p p = c0 / c* , где c* — содержание вещества в газовом потоке, равновесное с половинным количеством, от максимально адсорбируемого данным адсорбентом, кг/м3. Для третьей области изотермы адсорбции: τ= a0  w  c0  − 1  ln H −  wc0  βY  c — 298 — (7.56) ÐǜƽǯǮ͠ƻǅǀǎ ÐǣƻǈǀǬÐǯǫǬƽǬǃǀǎ Теплота адсорбции, как известно, складывается из теплоты конденсации и теплоты смачивания. Практически можно принять, что величина теплоты адсорбции органических веществ не зависит от температуры. Зависимость удельной теплоты адсорбции q (Дж/кг) адсорбента от количества поглощаемого пара определяется по формуле: q = man (7.57) a — количество адсорбируемого пара, дм3/кг; m, n — константы. Поглощение газов и паров, как правило, проводится в динамических условиях — из потока газа-носителя. В этом случае слой сорбента характеризуется величиной динамической адсорбционной активности aд — количеством поглощенного вещества (сорбтива) слоем адсорбента до момента появления за слоем притока сорбтива. (7.58) aä = c0 wτ aä — динамическая адсорбционная активность слоя адсорбента, кг/м3; c0 — исходная концентрация сорбтива в газовом потоке, кг/м3; w — скорость паро-газовой смеси, отнесенная к полному сечению аппарата, м/с; τ — время защитного действия, с. При низком давлении газа равновесие в системе для i-то компонента газа записывается в виде уравнения Генри: (7.59) xi0 = mpi где хi0 — равновесная концентрация газа в адсорбенте; pi — парциальное давление i-го газа над адсорбентом. На рис. 7.10 эта зависимость представлена прямой 1. Более универсальной является разработанная М. М. Дубининым теория объемного заполнения микропор, получившая широкое признание. По Дубинину, процесс адсорбции микропористыми адсорбентами рассматривается как процесс объемного заполнения микропор поглощаемым веществом. Полученные на основе этой теории уравнения изотермы адсорбции для газов и паров отражают зависимость равновесия от структуры пор адсорбента и пригодны для широкого диапазона температур. — 299 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Рис. 7.10. Равновесные зависимости концентрации адсорбированного газа в адсорбенте от парциального его давления: 1 — зависимость по закону Генри; 2 и 3 — реальные зависимости. Для иллюстрации сложной зависимости величины адсорбции от различных факторов приведем уравнение изотермы адсорбции, полученное М. М. Дубининым для микропористых адсорбентов и паров при любых температурах ниже критической T < Têð : ( ) a* = 2  W T2  P   exp − B 2 lg    VM β A  p    (7.60) где W — суммарный объем пор адсорбента; Vм — объем адсорбированного вещества в жидком состоянии; В — константа, зависящая от структурного типа адсорбента; βА — коэффициент аффинности, равный отношению мольных объемов в жидком состоянии или парахоров данного и стандартного веществ и определяемый по справочнику; Т — абсолютная температура пара; Р и р — давление насыщенного пара и парциальное давление пара адсорбируемого вещества соответственно (при температуре Т адсорбции).Уравнения изотерм адсорбции приводятся в литературе, посвященной вопросам физической химии сорбционных процессов, а также в справочной литературе. — 300 — ÐǜƽǯǮ͠ƻǅǀǎ ÐǣƻǈǀǬÐǯǫǬƽǬǃǀǎ ϳ͘ϲ͘ϯ͘ʶ̶̡̨̛̛̛̛̦̖̯̭̬̌̌̔̍͘ Скорость процесса адсорбции зависит от условий транспорта адсорбируемого вещества и поверхности (внешний перенос) и переноса его внутри зерен адсорбента (внутренний перенос). Скорость внешнего переноса определяется гидродинамической обстановкой процесса, а внутреннего — структурой адсорбента и физико-химическими свойствами системы. Гидродинамическая обстановка зависит от условий проведения процесса. Процессы адсорбции проводятся в основном двумя способами — в плотном и псевдоожиженном слоях адсорбента. В первом случае поток в пространстве между частицами приближается по структуре к модели поршневого движения, во втором — к модели идеального смешения. Кинетика внешнего переноса описывается уравнением: da = β (c − cÏ ) (7.61) dτ где с и сП — содержание поглощаемого вещества в объеме смеси и на поверхности адсорбента, соответственно; β — коэффициент массоотдачи. В зависимости от пористой структуры адсорбента и свойств системы перенос вещества внутри зерен адсорбента может протекать по разным механизмам, причем чаще всего перенос осуществляется одновременно двумя или более способами. Так, наряду с диффузией при адсорбции из газовых смесей возможно кнудсеновское и гидродинамическое течение, диффузионный перенос вещества в жидком состоянии сопровождается перемещением под действием капиллярных сил и т. д. В связи со сложностью установления доли переноса вещества по каждому механизму принятый метод описания кинетики внутреннего переноса заключается в использовании так называемого эффективного коэффициента диффузии DЭ, суммарно учитывающего все существенные факторы. Значения DЭ находятся экспериментально. Таким образом, кинетика внутреннего переноса описывается уравнением молекулярной диффузии — 301 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ  ∂2ñ ∂2ñ ∂2ñ  ∂c = DÝ  2 + 2 + 2  , ∂τ ∂y ∂z   ∂x (7.62) которое должно быть проинтегрировано с учетом граничных и начальных условий. Процесс заполнения зерен адсорбента является нестационарным. Он осложняется неравноценностью условий, в которых находятся отдельные зерна в промышленных аппаратах. Учесть это расчетным путем чрезвычайно сложно. Поэтому в расчетах обычно принимают, что все зерна адсорбента имеют одинаковую форму и размеры и находятся в одинаковых условиях. Отклонение от этих допущений в реальных процессах учитывается путем введения поправок на основании опытных данных. В связи с тем, что скорость процесса переноса внутри зерен адсорбента обычно много меньше скорости внешнего переноса, содержание адсорбируемого вещества на границе с поверхностью адсорбента чаще всего принимается равным содержанию адсорбируемого вещества в объеме смеси, которое зависит от условий проведения процесса. При интегрировании уравнения диффузионного переноса считают, что коэффициент эффективной диффузии в течение всего процесса остается постоянным. Решения, описывающие кинетику диффузионного переноса внутри частиц различной формы, были приведены выше. ϳ͘ϲ͘ϰ͘ˀ̸̶̶̨̨̛̛̭̖̯̪̬̖̭̭̭̬̌̌̌̔̍ ̨̨̨̨̛̦̖̪̙̦̥̭̣̖̭̬̖̦̯̏̔̏̌̔̍̌͘ При проведении процесса адсорбции в неподвижном слое адсорбента по мере удаления от входа в слой содержание поглощаемого вещества в потоке уменьшается. На некоторой длине, называемой длиной работающего слоя, происходит практически полное поглощение рассматриваемого вещества. В этом слое формируется определенное поле концентраций поглощаемого вещества. Перпендикулярное к направлению потока сечение адсорбента, отвечающее заданному минимальному содержанию поглощаемого вещества в потоке, называется фронтом — 302 — ÐǜƽǯǮ͠ƻǅǀǎ ÐǣƻǈǀǬÐǯǫǬƽǬǃǀǎ адсорбции. По мере насыщения ближайших к входу слоев адсорбента фронт адсорбции перемещается вдоль слоя. По достижении им границы слоя наблюдается повышение содержания поглощаемого вещества в потоке — проскок. При этом процесс адсорбции заканчивается и проводится десорбция поглощенного вещества, цель которой — выделить это вещество и регенерировать адсорбент. Таким образом, процесс адсорбции в слое — полунепрерывный. Распределение содержания поглощаемого вещества в работающем слое адсорбента можно выявить, исходя из дифференциального уравнения материального баланса, которое для одномерного потока, движущегося в направлении оси x, в соответствии с ∂ci ∂c ∂c ∂c   = Di ∇2ci −  ω x i + ω y i + ω z i  + riυ  ∂τ ∂x ∂y ∂z  имеет вид: ∂a ∂c ∂c ∂ 2c + +ω + DÏ ∂τ ∂τ ∂x ∂ x2 (7.63) где а — масса вещества, поглощенного единицей объема адсорбента; с — масса поглощаемого вещества в единице объема подвижной фазы; ω — средняя скорость движения; DП — коэффициент продольной диффузии. При отсутствии продольного перемешивания уравнение (7.63) принимает вид: ∂a ∂c ∂c + +ω =0 ∂τ ∂τ ∂x (7.64) Величины а и с взаимосвязаны, т. е. a = f (c ) . Если процесс протекает при условиях, близких к равновесным, то функция a = f (c ) представляет собой изотерму адсорбции. Следователь∂a но, = ∂τ ∂f ( c ) ∂c , и после подстановки в (7.63) получаем: ∂c ∂τ — 303 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ  ∂f ( c )  ∂c ∂c  ∂c + 1 ∂τ + ω ∂x = 0 или ∂c ∂c + ωa =0 ∂τ ∂x (7.65) ω . ∂f ( c ) +1 ∂c Величина ω a выражает скорость движения сечения поля концентраций, соответствующего определенному значению с. ∂f ( c ) Поскольку > 0 , то скорость движения адсорбируемого ве∂c щества в слое адсорбента меньше средней скорости подвижной фазы. Если изотерма адсорбции линейна, т. е. фазовое равновесие описывается законом Генри a = Γc (Г — константа Генри), ∂f ( c ) то f (c ) = Γc и = Γ . В этом случае ∂c где ω a = ω (7.66) 1+ Γ Чем больше константа Генри, т. е. чем лучше адсорбируется вещество, тем медленнее оно движется в слое адсорбента. На использовании этой закономерности основана адсорбционная газовая хроматография, широко используемая как метод определения состава смесей. В поток инертного газа, движущегося через слой адсорбента, вводится анализируемая проба, и фиксируется выход отдельных компонентов из слоя путем изменения теплопроводности, плотности или иных свойств газовой смеси. Полученные этим методом данные позволяют количественно определять содержание отдельных компонентов. ωa = — 304 — ÐǜƽǯǮ͠ƻǅǀǎ ÐǣƻǈǀǬÐǯǫǬƽǬǃǀǎ ϳ͘ϲ͘ϱ͘ʤ̶̨̡̨̛̛̭̬̪̺̖̥̭̣̖̔̍́̏́͘ При прохождении газа через слой сыпучего материала в зависимости от скорости движения газа наблюдается различное состояние слоя (рис. 7.11). При малой скорости движения газа он фильтруется через слой, оставляя его неподвижным (участок 1). С увеличением скорости газа, сопротивление слоя возрастает. Рис. 7.11. Зависимость перепада давления в слое адсорбента от скорости движения газа. При достижении скорости ωmin частицы начинают интенсивно перемешиваться, напоминая жидкость в состоянии кипения. Перепад давления остается постоянным (участок 2). Такое состояние сохраняется в интервале изменения скорости от ωmin до ωmax. Дальнейшее увеличение скорости приводит к уносу частиц с газом (участок 5) — это режим витания. Из рассмотренной закономерности следует, что для интенсификации процесса массообмена между газом и частицами адсорбента целесообразно процесс проводить в режиме кипящего слоя. Расчет скоростей начала образования кипящего слоя и перехода частиц в состояние витания проводится по уравнениям: Ar ; Remin = 1400 + 5,22 Ar 0,5 Remax = Ar 18 + 0,61 Ar 0,5 (7.67) Числа Рейнольдса и Архимеда находят по формулам: — 305 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Re = ( 3 dýêâ g ρò − ρã ωdýêâ = Ar ; νã ν2ρã ) (7.68) где ω — скорость газа в свободном (полном) сечении реактора; ρт, ρг — плотности газа и материала адсорбента соответственно; νг — кинематическая вязкость газа; g — ускорение силы тяжести; dэкв — эквивалентный диаметр канала в слое адсорбента, 4ε , где ε — пористость кипяопределяемый по формуле dýêâ = f щего слоя; f — поверхность зерен адсорбента в единице его объема. Все расчеты проводятся при температуре процесса. Коэффициент массоотдачи в кипящем слое находят из зависимости числа Шервуда от числа Рейнольдса: βdýêâ = 46,25<10−6 Re0,67 (7.69) D где D — коэффициент диффузии в газовой фазе. По количеству примеси, переходящей в адсорбент, находят его расход, а объем реактора определяют по необходимому времени пребывания адсорбента в адсорбере из условия массопередачи в кипящем слое. Sh = ϳ͘ϲ͘ϲ͘ʽ̸̸̵̶̡̨̨̨̨̨̛̛̛̭̯̭̯̦̼̥̖̯̥̭̬̌̏̔̔̌̔̍͘ Очистка сточных вод адсорбцией используется для удаления растворенных примесей, таких как фенолы, гербициды, ароматические вещества, красители. Метод основан на распределении примеси между водой и адсорбентом. Так, при очистке сточных вод от фенолов адсорбцией активными углями при содержании фенолов в воде менее 0,5г/л равновесие описывается зависимостью: a = 15,85c0,22 (7.70) где a — количество фенолов, адсорбированных активным углем, % от массы угля; c — равновесное содержание фенолов в воде, г/л. — 306 — ÐǜƽǯǮ͠ƻǅǀǎ ÐǣƻǈǀǬÐǯǫǬƽǬǃǀǎ Равновесная зависимость находиться обычно по данным эксперимента. ϳ͘ϲ͘ϳ͘ʪ̶̶̨̨̨̛̛̛̖̭̬̪̭̣̖̭̬̍́̌̔̍͘ Извлечение адсорбированного вещества из твердого поглотителя (десорбция) является необходимой составной частью всех технологических процессов адсорбции, проводимых в замкнутом цикле. Стоимость десорбции оказывает большое влияние на общую экономичность проведения процессов разделения и очистки веществ адсорбционными методами. К числу основных методов десорбции (регенерации адсорбента) относятся: – вытеснение из адсорбента поглощенных компонентов посредством агентов, обладающих более высокой адсорбционной способностью, чем поглощенные компоненты; – испарение поглощенных компонентов, обладающих относительно высокой летучестью, путем нагрева слоя адсорбента. В некоторых случаях для удаления из адсорбента смолообразных и других продуктов, образующихся в результате побочных процессов, окончательную очистку адсорбента осуществляют выжиганием этих компонентов (окислительная регенерация адсорбента). Выбор того или иного способа десорбции производится на основе технико-экономических соображений, причем часто указанные выше способы применяются в комбинации друг с другом. На практике процессы десорбции обычно осуществляют путем пропускания пара или газа, не содержащего адсорбтива, через слой адсорбента после завершения прямого процесса (адсорбции). Для повышения скорости извлечения десорбцию проводят наиболее часто при повышенных температурах, например, пропуская через слой адсорбента предварительно нагретый десорбирующий агент. В качестве десорбирующих агентов используют острый насыщенный или перегретый водяной пар, пары органических веществ, а также инертные газы. После проведения процесса — 307 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ десорбции слой адсорбента обычно подвергают сушке и охлаждению. Десорбцию острым водяным паром наиболее часто применяют в процессах рекуперации летучих растворителей на активном угле. При этом основная масса поглощенного вещества выделяется из поглотителя вначале десорбции. По мере приближения к концу процесса скорость его значительно снижается, а расход водяного пара на единицу десорбируемого продукта сильно возрастает. Поэтому из технико-экономических соображений адсорбируемое вещество извлекают из поглотителя не полностью, оставляя некоторое количество его в адсорбенте. Часть водяного пара, называемая греющим паром, расходуется при десорбции на нагревание всей системы, десорбцию поглощенных веществ из угля и компенсацию тепловых потерь в окружающую среду. Греющий пар полностью конденсируется в аппарате. Некоторая часть пара расходуется на компенсацию отрицательной теплоты смачивания угля водой и также полностью конденсируется в адсорбере. Десорбированные из угля вещества выдуваются из угольного слоя динамическим паром, который, не конденсируясь, выходит из реактора в смеси с парами десорбированных веществ. Расходы греющего пара и пара, идущего на компенсацию теплоты смачивания, находятся расчетом. Расход динамического пара зависит от условий проведения процесса и с достаточной надежностью определяется лишь опытным путем. При ориентировочных расчетах расход динамического пара можно принимать в среднем 3–4 кг на 1 кг десорбируемого вещества. Регенерацию цеолитов наиболее часто проводят путем продувания сквозь слой адсорбента нагретого сухого газа, причем удаление поглощенных веществ из цеолитов обычно более затруднительно, чем из активных углей. Процессы десорбции, подобно процессам собственно адсорбции, осуществляют не только в неподвижном, но также в движущемся и кипящем слоях адсорбента. — 308 — ÐǠǮǃǰ͠ǮǁǋǃǊǬÐǫǮ͟͠ǮǯǊ ϳ͘ϳ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏͘ 1. Чем характеризуются процессы массопередачи с неподвижной границей раздела фаз? 2. Что такое процесс массоотдачи и процесс массопередачи? Какая между ними разница? 3. Как записывается уравнение массоотдачи? 4. Как записывается уравнение массопередачи? 5. Какая существует взаимосвязь между коэффициентами массоотдачи и массопередачи? 6. Как можно охарактеризовать с позиции молекулярно-кинетической теории процесс растворения твердого тела? 7. Для частиц какой формы можно математически описать кинетику растворения твердого тела? 8. Какой по знаку тепловой эффект наблюдается при растворении твердого тела? 9. Какой по знаку тепловой эффект наблюдается при процессе кристаллизации раствора или расплава? 10. Что является движущей силой процесса кристаллизации? 11. Можно ли математически описать процесс кристаллизации? 12. Зачем при процессе кристаллизации нужна «затравка»? 13. Что такое процесс экстракции в широком понимании этого слова? 14. Как в химической технологии и обогащении называется процесс экстракции из . твердых тел? 15. В чем сущность процесса выщелачивания? 16. Из каких основных стадий состоит процесс выщелачивания? 17. Что является движущей силой процесса экстракции в системе твердое тело-жидкость? 18. Какие основные факторы влияют на скорость выщелачивания? 19. Как степень измельчения материала влияет на скорость выщелачивания? 20. Сушка. Основные понятия. Параметры, подлежащие расчету. — 309 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ 21. Равновесное содержание влаги при сушке. Кинетика сушки. 22. Основные параметры влажного воздуха. 23. J-x диаграмма влажного воздуха. Её описание. 24. Как можно изобразить процесс изменения состояния воздуха на J-x диаграмме? 25. Равновесие при сушке. Материальный и тепловой баланс сушки. Определение расходов воздуха и тепла на сушку. 26. Варианты процесса сушки. Скорость сушки. Специальные виды сушки. 27. Какие два основных процесса протекают при сушке материала? 28. Какие основные виды сушки различают в настоящее время? 29. Какой из видов сушки в настоящее время наиболее предпочтителен? 30. Что такое влагосодержание материалов? 31. Какой пар называют насыщенным? 32. Какой пар называют ненасыщенным? 33. Какие газовые законы можно применять к ненасыщенному пару? 34. Какие газовые законы можно применять к насыщенному пару? 35. От каких параметров зависит конечная влажность материала? 36. Какую влагу обычно не удаляют при сушке и почему? 37. Почему кривая сушки характеризуется участками различной кривизны? 38. Как определяется скорость сушки? 39. В чем заключается процесс сушки топочными газами? 40. В чем заключается физическая сущность процесса адсорбции? 41. Дайте общую характеристику адсорберов и укажите, какие виды адсорберов Вам известны. 42. Равновесие при адсорбции. 43. Ионно-обменные процессы. — 310 — ÐǤ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ 44. От каких факторов и как зависит скорость процесса адсорбции? 45. Что такое адсорбционное равновесие? 46. Что называется пределом адсорбции? 47. Изобразить график изотермы адсорбции Ленгмюра и дать характеристику его участков. 48. Какие силы взаимодействия молекул адсорбата и адсорбента действуют при адсорбировании? 49. Между какими молекулами действует ориентационная сила и от чего она зависит? 50. Между какими молекулами действует индукционная сила и и как она зависит от расстояния между молекулами? 51. Как зависит от расстояния между молекулами сила отталкивания? 52. Перечислить основные положения теории адсорбции Ленгмюра. 53. В чем заключается сущность модели процесса адсорбции по Ленгмюру? 54. Каковы недостатки теории адсорбции Ленгмюра? В какой теории они устранены? 55. Какие адсорбенты чаще всего используют на практике? 56. Дать классификацию пористых тел по Дубинину и привести примеры адсорбентов и процессов, в них протекающих. ϳ͘ϴ͘ʿ̸̛̛̬̥̖̬̼̬̖̹̖̦́̌̔̌̚͘ Задача 1. Из 320 г сернистого колчедана, содержащего 45% серы, было получено 397 г 100%-ной серной кислоты. Вычислить выход кислоты (процент использования серы). Для решения задачи сначала нужно рассмотреть все процессы, которые происходят в производстве серной кислоты из сернистого колчедана, определив в каждом случае изменение степени окисляемости вещества. Исходя из общей схемы + O2 + O2 + H2O FeS2 → SO3 → SO3 → H2SO4 — 311 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Рассмотрим каждую реакцию в отдельности а) FeS2 + O2 → Fe2O3 + SO2 определим степени окисления элементов: в исходных продуктах — Fe+2, S–1, O0 в конечных продуктах — Fe+3, S–4, O–2 составим баланс перехода электронов Реакция Кол-во переходящих электронов Коэффициенты –11 4 +4 11 Fe +2 − e → Fe +3 2S −1 − 10e → 2S +4 O2 + 4e → 2O −2 Ставим соответствующие коэффициенты у исходных продуктов и определяем коэффициенты у конечных продуктов: 4FeS2 + 11O2 → 2Fe2O3 + 8SO2 Дальнейший процесс может быть выражен уравнениями следующих реакций: êàòàëèç .,t б) 2SO2 + O2 → 2SO3 в) SO3 + H2O → H2SO4 Из этих уравнений следует, что 1 MH2SO4 − MSO2 − MSO3 − MFeS2 − MS èëè MH2SO4 − MS 2 Решение. 1) Определить количество серы, содержащейся в серном колчедане. 320 кг колчедана составляют 100%, х г серы » 45% отсюда 320<45 x= = 144 (ã ) 100 — 312 — ÐǤ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ 2) Сколько грамм-атомов содержат 144 г серы? 144 : 32 = 4,5 (г-атома) 3) Сколько грамм-молекул серной кислоты получится при 100%-ном выходе? MH2SO4 − MS значит, получится 4,5 моля 100%-ной серной кислоты. 4) Сколько граммов серной кислоты получится? 98 u 4,5 = 441 (г) 5) Каков процент выхода кислоты? 441 г серной кислоты составляют 100%-ный выход 397 г » у » 397<100 = 90 (%) Отсюда у = 441 Задача 2. Для получения каких веществ используется в промышленности способность хлора растворяться в щелочах? Напишите уравнения и укажите условия проведения соответствующих реакций. а) Для получения жавелевой воды хлор растворяют в едком натре при обычной температуре: Cl2 + NaOH → NaClO + + NaCl + H2O (жавелевая вода) В этой реакции из хлора в степени окисления 0 образуется хлор в степенях окисления +1 и –1. Таким образом, один атом хлора выступает в роли восстановителя, а другой — в роли окислителя. Щелочь же является только средой и в окислительно-восстановительном процессе участия не принимает: В реакциях такого типа коэффициенты суммируются. Следовательно, для реакции требуется два атома хлора: Cl2 + 2NaOH → NaClO + NaCl + H2O б) Для получения белильной извести гашеную известь обрабатывают хлором при обычной температуре: Cl2 + Ca ( OH )2 → CaOCl2 + H2O Механизм этой реакции такой же, как и в случае растворения хлора в едком натре, но ввиду двухвалентности катиона здесь образуется смешанная соль соляной и хлорноватистой кислот. — 313 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ в) Для получения хлората калия (бертолетовой соли) хлор растворяют в горячем растворе едкого кали: Cl2 + KOH → KClO3 + + KCl + H2O В этой реакции, как и в реакции, разобранной в пункте а),. один атом хлора является восстановителем, а другой — окислителем. Но благодаря высокой температуре, окислительная способность хлора возрастает, и он уже способен перевести Сl0 в Cl+5: Cl0 − 5e → Cl +5 1 Cl0 + e → Cl −1 5 Суммируя коэффициенты, получим, что в реакции должны участвовать 6 атомов хлора, т. е. три молекулы: 3Cl2 + 6KOH → KClO3 + 5KCl + 3H2O Задача 3. Определить расход сухого воздуха и теплоты в теоретической сушилке для удаления из влажного материала 100 кг/ч влаги, если начальное состояние воздуха (до калорифера);. t0 = 15 °С, φ0 =0,8, а на выходе из сушилки: t2 = 44 °С, φ2 = 0,5. Решение. По диаграмме J-x (рис.7.7) находим: х0 = 0,009 кг/кг; х2 = 0,03 кг/кг. По уравнению определяем удельный расход сухого воздуха: 1 1 = = 47,6 кг / кг испаряемой влаги t= x2 − x0 0,03 − 0,009 Удельный расход теплоты находим по уравнению, предварительно сняв значения энтальпий по диаграмме J-x. В условиях нашего примера I2=121,5 кДж/кг; I0 =40 кДж/кг. I −I 121,5 − 40 = 3880 кг / кг испаряемой влаги q= 2 0 = x2 − x0 0,03 − 0,009 Расход сухого воздуха равен: L = WI = 100<47,6 = 1760 кг/ч Расход теплоты: Q = Wq = 100<3880 = 108 кВт 3600 — 314 — ÐƭǪƽǪǆǀÐƽǁǎÐǯǪǂǮǯǰǮǎǰǬǁǋǃǮƼǮÐ͠ǬǇǬǃǀǎ Задача 4. Рассчитайте константу Генри по изотерме адсорбции уксусной кислоты на твёрдом адсорбенте при 298 К по данным: Рис.7.12. Изотерма адсорбции. с, ммоль/л 1 2 3 5 А, ммоль г 0,04 0,07 0,12 0,19 Решение: Для расчёта константы Генри строят изотерму адсорбции в координатах A=f(c). В соответствии с уравнением Генри из графика (рис. 7.12) находят тангенс угла наклона прямой, который равен константе Генри: tgα = Ê ã = 0,038ë / ã ϳ͘ϵ͘ʯ̸̨̨̨̨̛̛̣̭̥̭̯̯̖̣̦̬̖̹̖̦̌̔̌̔́̌́̽̐́͘ Задача 1. В 300, мл воды растворено 80 г нитрата кальция. Удельный вес полученного раствора 1,2. Определите процентную, молярную и нормальную концентрации раствора, Задача 2.12,5 г пятиводного кристаллогидрата сульфата меди растворили в 87,5 мл воды. Какова процентная концентрация полученного раствора? — 315 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐǃǬ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Задача 3. По данным об адсорбции паров воды на макропористом адсорбенте определите предельную ёмкость мономолекулярного слоя. Для расчетов используйте уравнение Ленгмюра. р, Па 2,04 3,68 6,72 10,70 12,00 16,00 А, моль/кг 4,4 6,3 9,2 11,7 13,2 14,9 Задача 4. Определить по диаграмме J-x(рис.7/7) энтальпию и влагосодержание воздуха при 60°С и φ =0,3. Задача 5. Определить парциальное давление водяного пара в паро-воздушной смеси при 80°С и =150 кДж/кг сухого воздуха. — 316 — ǍưǙǚǙÍ Í Í ǓǔǒƠǎǕǕƥÍǐǋǕǕǒǓǎǔǎƚǋơƝÍ ǌÍǕƝǕǖǎǐǋǘÍǕÍǓǒƚǌƝƛǑǒ֏Í ǍǔǋǑƝƠǎ֏ÍǔǋƜƚǎƞǋÍǗǋƜÍ ǓǔƝǐǎǑƝǖǎƞƦǑǒÍǏÍǓǔǒƠǎǕǕǋǐÍ ƜǋƣƝǖƥÍǒǏǔƟƛǋƨƣǎ֏ÍǕǔǎƚƥ В результате изучения главы 8 бакалавр должен: Знать: – какие процессы, при защите окружаюшей среды от опасных и вредных факторов, являются процессами массопередачи в системах с подвижной границей раздела. – основные физико-химические закономерности процессов массопередачи в системах с подвижной границей раздела. Уметь: – обоснованно выбирать процессы для извлечения примесей из газового потока и из загрязненных сточных вод при процессе массопередачи в системах с подвижной границей раздела фаз. Владеть: – основными методами и законами физической химии для описания процессов массопередачи в системах с подвижной границей раздела. К данной группе процессов относятся процессы, протекающие в системах жидкость — газ (абсорбция, десорбция, дега— 317 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ зация и дезодорация), жидкость — пар (дистилляция и ректификация) и жидкость — жидкость (жидкостная экстракция). Абсорбция — это процесс выделения одного или нескольких компонентов газовой или парогазовой смеси путем их поглощения селективным жидким поглотителем — адсорбентом (осуществляется при массообмене между газом и жидкостью). Дистилляция и ректификация — процессы разделения жидких смесей, основанные на использовании различия составов равновесных жидкой и паровой фазы (осуществляются при массообмене между этими фазами). Жидкостная экстракция — процесс разделения жидких смесей путем поглощения из них одного или нескольких компонентов селективными растворителями (осуществляется при массообмене между двумя жидкими фазами). Цель этих процессов — разделение однородных газовых или жидких смесей и получение из них продуктов, отвечающих предъявляемым требованиям защиты окружающей среды от опасных и вредных факторов. Обычно важнейшим требованием является высокая чистота продуктов процесса, т. е. остаточные примеси в продуктах разделения должны содержать примеси в количествах, не превышающих допустимый уровень. Для достижения необходимого эффекта разделения рассматриваемые процессы чаще всего проводятся при противоточном взаимодействии фаз — непрерывном или ступенчатом. Движущая сила этих процессов определяется различием истинных составов взаимодействующих фаз и составов, отвечающих условиям фазового равновесия. Принципы расчета фазового равновесия в системах жидкость — газ, жидкость — пар и жидкость — жидкость рассматриваются на основе уравнений (2.44), а также в курсе физической химии (химическая термодинамика), а методика составления материального и энергетического баланса — в главе 1 данного учебника. Процессы абсорбции и ректификации весьма близки по условиям их проведения. Основным фактором, определяющим различие этих процессов, является большое различие в физических свойствах взаимодействующих фаз. В процессах жидкостной экстракции взаимодействующие фазы значитель— 318 — ÐǜƻǯǮ͠ƻǅǀǎÐǮƻǈǀǬÐǯǫǬƽǬǃǀǎ но меньше различаются по физическим свойствам, поскольку находятся в одинаковом (жидком) агрегатном состоянии. Основными задачами при анализе и расчете процессов массообмеиа является определение условий проведения процесса (расхода и состава фаз, температур, давлений и т.д.), а также аэро-гидродинамические характеристики процесса, которые необходимо учитывать, рассматривая процессы защиты окружающей среды от опасных и вредных веществ, как для человека, так и для живой природы. ϴ͘ϭ͘ʤ̶̨̛̭̬̍̍́;̨̛̛̺̖̭̖̖̦̍̏̔́Ϳ͘ Абсорбцией, согласно [5, 6, 9] называют процесс поглощения газов или паров из газовых или паро-газовых смесей жидкими поглотителями (абсорбентами). Физическая модель процесса абсорбции заключается в диффузии через границу раздела газ — жидкость. В месте их контакта имеются два пограничных слоя, причем каждый из них разделяется на турбулентный и вязкий подслои. В пределах турбулентного подслоя наблюдается молярный механизм переноса, а в пределах ламинарного (вязкого) — молекулярный. При физической абсорбции поглощаемый газ (абсорбтив) не взаимодействует химически с абсорбентом. Если же абсорбтив образует с абсорбентом химическое соединение, то процесс называется хемосорбция. Физическая абсорбция в большинстве случаев обратима. На этом свойстве абсорбционных процессов основано выделение поглощенного газа из раствора — десорбция. Сочетание абсорбции с десорбцией позволяет многократно применять поглотитель и выделять поглощенный компонент в чистом виде. Во многих случаях проводить десорбцию не обязательно, так как абсорбент и абсорбтив представляют собой дешевые или отбросные продукты, которые после абсорбции можно вновь не использовать (например, при очистке газов), а подвергать захоронению. В промышленности процессы абсорбции применяются главным образом для извлечения ценных компонентов из газовых смесей или для очистки этих смесей от вредных примесей. — 319 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Абсорбционные процессы широко распространены в химической технологии и являются основной технологической стадией ряда важнейших производств (например, абсорбция SO3 в производстве серной кислоты; абсорбция НСl для получения соляной кислоты; абсорбция окислов азота водой в производстве азотной кислоты; абсорбция NH3, паров С6Н6, H2S и других компонентов из коксового газа; абсорбция паров различных углеводородов из газов переработки нефти и т.п.). Кроме того, абсорбционные процессы являются основными процессами при санитарной очистке выпускаемых в атмосферу отходящих газов от вредных, примесей (например, очистка топочных газов от SO2; очистка от фтористых соединений газов, выделяющихся в производстве минеральных удобрений, и т.д.). ϴ͘ϭ͘ϭ͘ˀ̶̨̨̛̛̛̛̦̖̭̖̪̬̭̬̌̏̏̌̍̍ ;̴̨̛̛̬̦̖̭̖̥̖̙̱̥̌̏̏̔̌̌̚Ϳ͘ При абсорбции содержание газа в растворе зависит от свойств газа и жидкости, давления, температуры и состава газовой фазы (парциального давления растворяющегося газа в газовой смеси). В случае растворения в жидкости бинарной газовой смеси (распределяемый компонент А, носитель В) взаимодействуют две фазы (Ф = 2), число компонентов равно трем (К = 3) и, согласно правилу фаз, число степеней свободы системы равно трем. Для данной системы газ — жидкость переменными являются температура, давление и концентрация в обеих фазах. Следовательно, в состоянии равновесия при постоянных температуре и общем давлении зависимость между парциальным давлением газа А (или его концентрацией) и составом жидкой фазы однозначна. Эта зависимость выражается законом Генри: парциальное давление рА растворенного газа пропорционально его мольной доле xА в растворе p*A = Ex A — 320 — (8.1) ÐǜƻǯǮ͠ƻǅǀǎÐǮƻǈǀǬÐǯǫǬƽǬǃǀǎ или растворимость газа (поглощаемого компонента А) в жидкости при данной температуре пропорциональна его парциальному давлению над жидкостью 1 (8.1,а) x*A = p A E где рА — парциальное давление поглощаемого газа, находящегося в равновесии с раствором, имеющим концентрацию х, (в мол. долях); х* — концентрация газа в растворе (в мол. доА лях), равновесном с газовой фазой, в которой парциальное давление поглощаемого компонента равно рА; Е — коэффициент пропорциональности, называемый коэффициентом, или константой Генри. Числовые значения коэффициента Генри для данного газа зависят от природы поглотителя и газа и от температуры, но не зависят от общего давления в системе. Зависимость Е от температуры выражается уравнением q (8.2) +C RT где q — дифференциальная теплота растворения газа; R — газовая постоянная; С — постоянная, зависящая от природы газа и поглотителя. Как правило, процесс абсорбции экзотермический. Поэтому с повышением температуры процесса растворимость газов в жидкости уменьшается. Так, растворимость аммиака в воде при 10° С — 910 см3 в 1 см3 воды, а при 20° — 710 см3 в 1 см3, а растворимость оказывают влияние примеси в растворителе, как правило, также снижая растворимость. Повышение давления повышает растворимость газов в жидкости. Схема процесса абсорбции приведена на рис. 8.1. Газообразная примесь в газе, достигая поверхности абсорбента, растворяется в нем. Насыщенный примесью абсорбент (абсорбат) поступает на регенерацию для удаления примеси и может быть использован повторно. В качестве абсорбента часто используется вода, как наиболее доступный и дешевый материал. Если абсорбат содержит токсичные или ценные компоненты, его подвергают десорбln E = − — 321 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Рис.8.1. Схема процесса абсорбции: 1 — газ, загрязненный газообразной примесью; 2 — абсорбент; 3 — абсорбент, насыщенный газообразной примесью (абсорбат). ции, т.е. выделению из него абсорбированных компонентов. Регенерированный абсорбент может использоваться повторно. Процесс десорбции проводится при условиях уменьшающих абсорбцию: пониженное давление, высокая температура, добавка веществ, снижающих абсорбционную способность абсорбента. В природе на абсорбции кислорода водой из атмосферы основано существование растительности и живых организмов в водоемах. Поэтому, когда на море происходит авария с нефтеналивными судами и поверхность воды покрывается непроницаемым для кислорода слоем, рыбы умирают. Для идеальных растворов на диаграмме р-х (рис. 8.2) зависимость равновесных концентраций от давления изображается прямой, имеющей наклон, равный E — коэффициенту Генри. Из рис. 8.2 и уравнения (8.2) следует, что с повышением температуры (при прочих равных условиях) увеличивается значение Е и соответственно уменьшается, согласно уравнению (8.1,а), растворимость газа в жидкости. Если уА — мол. доля извлекаемого компонента А в газовой смеси и Р — общее давление в системе, то парциальное давление рА, по закону Дальтона, можно выразить зависимостью p A = Py A Подставив значение рА в уравнение (8.1), получим E y*A = x A P или закон Генри может быть представлен в форме — 322 — ÐǜƻǯǮ͠ƻǅǀǎÐǮƻǈǀǬÐǯǫǬƽǬǃǀǎ y*A = mx (8.3) где m = Е/Р — коэффициент распределения, или константа фазового равновесия. Уравнение (8.3) показывает, что зависимость между концентрациями данного компонента в газовой смеси и в равновесной с ней жидкости выражается прямой линией, проходящей через начало координат и имеющей угол наклона, тангенс которого равен т. Числовые значения величины m зависят от температуры и давления в системе: уменьшаются с увеличением давления и уменьшением температуры. Таким образом, растворимость газа в жидкости увеличивается с повышением давления и уменьшением температуры. Рис.8.2. Растворимость газа в жидкости при различных температурах (t1>t2>t3 и соответственно E1>E2>E3) Когда в равновесии с жидкостью находится смесь газов, закону Генри может следовать каждый из компонентов смеси в отдельности. Закон Генри применим к растворам газов, критические температуры которых выше температуры раствора, и справедлив только для идеальных растворов. Поэтому он с достаточной точностью применим лишь к сильно разбавленным реальным растворам, приближающимся по свойствам к идеальным, — 323 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ т.е. соблюдается при малых концентрациях растворенного газа или при его малой растворимости. Для хорошо растворимых газов, при больших концентрациях их в растворе, растворимость меньше, чем следует из закона Генри. Для систем, не подчиняющихся этому закону, коэффициент т в уравнении (8.3) является величиной переменной и линия равновесия представляет собой кривую, которую строят обычно по опытным данным. Для описания равновесия между газом и жидкостью уравнение (8.3) применимо только при умеренных давлениях, невысоких температурах и отсутствии химического взаимодействия между газом и поглотителем. При повышенных давлениях (порядка десятков атмосфер и выше) равновесие между газом и жидкостью не следует закону Генри, так как изменение объема жидкости вследствие растворения в ней газа становится соизмеримым с изменением объема данного газа. При этих условиях константу фазового равновесия можно определить следующим образом: m= E f0 (8.4) где f0 — фугитивность (летучесть) поглощаемого газа, выраженная в единицах давления. Для бинарных растворов величина f0 может быть найдена следующим образом: ln f0 A  2 = ln E − 1 − (1 − x )    x RT (8.5) где А — постоянная. При выражении состава фаз не в абсолютных, а в относительных концентрациях видоизменяется и запись закона Генри. Так, например, при использовании относительных мольных концентраций выражение (8.3) можно записать в виде Y* mX = 1 + Y ,* 1 + X откуда по правилу пропорций Y* mX = 1 + Y* − Y* 1 + X − X — 324 — ÐǜƻǯǮ͠ƻǅǀǎÐǮƻǈǀǬÐǯǫǬƽǬǃǀǎ или Y* = mX mX = 1 + X − mX 1 + (1 − m ) X (8.6) Следовательно, при выражении закона Генри в относительных концентрациях равновесие в системе газ — жидкость изображается также кривой линией. Однако для сильно разбавленных растворов (малые концентрации X газа в жидкости) можно принять (1 − m ) X ≈ 0 . Тогда знаменатель уравнения (7.6) обращается в единицу и уравнение принимает вид Y * = mX (8.7) При таком выражении закон Генри изображается прямой линией. Таким образом, уравнения (8.1), (8.1,а), (8.3), (8.4) и (8.5) являются различными выражениями закона Генри. В случае абсорбции многокомпонентных смесей равновесные зависимости значительно сложнее, чем при абсорбции одного компонента, особенно тогда, когда раствор сильно отличается от идеального. При этом парциальное давление каждого компонента в газовой смеси зависит не только от его концентрации в растворе, но также и от концентрации в растворе остальных компонентов, т. е. является функцией большого числа переменных. Поэтому, как правило, в подобных случаях равновесные зависимости основываются на опытных данных. Влияние давления паров абсорбента на равновесие. В приведенных зависимостях не учитывалось влияние давления паров поглотителя на равновесие, что допустимо, если это давление мало по сравнению с парциальным давлением абсорбируемого газа. Если же давление паров поглотителя велико, то его влияние на равновесие при абсорбции учитывают следующим образом. Согласно закону Рауля, парциальное давление компонента в растворе равно давлению пара чистого компонента, умноженному на его мольную долю в растворе, т. е. для поглотителя PÏ = PÏ (1 − X ) = PÏ XÏ — 325 — (8.8) ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Парциальное давление абсорбента в равновесной газовой фазе Pп равно Pп = Pyп (8.9) Из уравнений (8.8) и (8.9) получим: P (1 − x ) PПxП (8.10) yП = П = P P В этом, случае концентрация абсорбируемого газа в газовой фазе по отношению к концентрации инертного газа составляет y Y= (8.11) 1 − y − yП При таком выражении концентрации в качестве общего давления принимается разность P – Pп. ϴ͘ϭ͘Ϯ͘ˁ̶̡̨̨̨̬̭̯̪̬̖̭̭̽̌͘ ˁ̴̸̶̡̨̨̡̨̨̛̛̛̛̬̭̯̖̭̜̭̬̽̌̍̍̚͘ Скорость процесса абсорбции характеризуется (если движущую силу выражают в концентрациях газовой фазы) уравнением: (8.12) M = Ky F ∆yср (если движущая сила выражается в концентрациях жидкой фазы) уравнением: M = Kx F ∆xср (8.13) где ∆уср и ∆xср — средние движущие силы процесса адсорбции, зависящие от отклонения системы от равновесного состояния. В этих уравнениях коэффициенты массопередачи Ку и Кх определяются следующим образом: 1 (8.14) Ky = 1 m + βг β ж и Kx = 1 1 1 + βг βж m — 326 — (8.15) ÐǜƻǯǮ͠ƻǅǀǎÐǮƻǈǀǬÐǯǫǬƽǬǃǀǎ где βг — коэффициент массоотдачи от потока газа к поверхности контакта фаз; βж — коэффициент массоотдачи от поверхности контакта фаз к потоку жидкости. Для хорошо растворимых газов величина m незначительна, мало также диффузионное сопротивление в жидкой фазе. 1 m и можно принять, что Ky ≅ βг. Тогда βж β г Для плохо растворимых газов можно пренебречь диффузионным сопротивлением в газовой фазе (в этом случае значе1 1 ния m и βг велики). Отсюда, и можно полагать, что β ж βжm Kж ≈ βж. Рис. 8.3.Скорость абсорбции, сопровождаемой химической реакцией. Во многих практически важных процессах абсорбции поглощение газа жидкостью сопровождается химическим взаимодействием фаз. Если реакция протекает в жидкой фазе, то часть газообразного компонента переходит в связанное состояние. При этом концентрация свободного (т. е. не связанно— 327 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ го с поглощаемым газом) компонента в жидкости уменьшается что приводит к ускорению процесса абсорбции по сравнению с абсорбцией без химического взаимодействия фаз, так как увеличивается движущая сила процесса. В общем случае скорость хемосорбции зависит как от скорости реакции, так и от скорости массопередачи между фазами. В зависимости от того, какая скорость определяет общую скорость процесса переноса массы, различают кинетическую и диффузионную области протекания хемосорбционных процессов. В кинетической области скорость собственно химического взаимодействия меньше скорости массопередачи и поэтому лимитирует скорость всего процесса. В диффузионной области лимитирующей является скорость диффузии компонентов в зоне реакции, которая зависит от гидродинамики и физических свойств фаз и определяется по общему уравнению массопередачи. В тех случаях, когда скорости реакции и массопередачи соизмеримы по величине, процессы абсорбции протекают в смешанной, или диффузионно-кинетической, области. При расчете требуемой поверхности контакта фаз в условиях хемосорбции ускорение процесса можно учесть увеличением коэффициента массоотдачи рж, если считать движущую силу процесса такой же, как при физической абсорбции. Тогда коэффициент массоотдачи в жидкой фазе βж при протекании химической реакции (8.16) βж ′ = βжФ где Ф — фактор ускорения массообмена, показывающий, во сколько раз увеличивается скорость абсорбции за счет протекания химической реакции. Значение Ф может быть определено по графику (рис. 8.3) в зависимости от комплексов величин γ и N. На графике величина γ = k2xB DA приведена для реакций βж второго порядка. В этом выражении: k2 — константа скорости реакции второго порядка, м3/(к.моль-сек); хB — концентрация поглоти— 328 — ÐǜƻǯǮ͠ƻǅǀǎÐǮƻǈǀǬÐǯǫǬƽǬǃǀǎ теля, кмоль/м3; DA — коэффициент диффузии поглощаемого компонента А в растворе, м2/сек. Параметром кривых на рис. 8.3 является величина N, представляющая собой выражение D x (8.17) N= B B nDA x A где DB — коэффициент диффузии ионов реагента (абсорбента) В в растворе, м2/сек; x A — концентрация поглощаемого компонента А на границе раздела фаз, кмоль/м3; n — стехиометрический коэффициент. В кинетической и диффузионной областях выражения для расчета величины Ф упрощаются. Так, в кинетической области при условии, что 5 ≤ γ ≤ 0,5(1 + N ) , фактор ускорения Ф = γ. В диффузионной области при условии, что γ ≥ 10 (1 + N ) , величина Ф = 1 + N При хемосорбции введением в растворитель специальных веществ, образующих нерастворимые химические соединения с абсорбируемым газом, можно значительно повысить поглощение примеси из газовой смеси. Процесс протекает по реакции: A ж + B г + C → Aж + BC ↓ ж где А — адсорбент; Вг — примесь в газе; С — добавляемое вещество; ВС — нерастворимый осадок. Так в электронной промышленности при очистке отходящих газов процесса парофазной эпитаксии GaAs хлоридно-гидридным методом используют в качестве абсорбента растворы в воде щелочи Са(ОН)2 и окислителя — хлороксид кальция Са(ОС1)2. При этом протекают следующие реакции: — при очистке от НСl: 2HCl + Ca ( OH )2 ↔ CaCl2 + 2H2O Упаривая полученный адсорбат, получают товарный продукт — СаСl2. В частности, его можно использовать для регенерации соляной кислоты воздействием крепкой серной кислотой, при этом кальций выделяется в виде малорастворимого осадка сернокислого кальция CaCl2 + H2SO4 = CaSO4 ↓ +2HCl — 329 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ — при очистке от высокотоксичного гидрида мышьяка используется реакция 3 AsH3 + 4Ca ( OCl )2 + 3Ca ( OH )2 = Ca ( AsO4 )2 + 4CaCl2 + 6H2O Мышьяк выводится в виде твердого осадка; — рекуперация галлия проводится путем улавливания паров GaCl3. При этом используется реакция: 2GaCl3 + 4Ca ( OH )2 = Ca ( GaO2 )2 ↓ +3CaCl2 + 4H2O Галлий извлекают из твердого осадка. ϴ͘Ϯ͘ʪ̶̶̨̨̨̛̛̛̖̭̬̪̭̣̖̭̬͕̍́̌̍̍ ̶̶̨̨̛̛̖͕̖̬̔̐̌̌́̔̔̌́̚̚͘ ϴ͘Ϯ͘ϭ͘ʪ̶̨̛̖̭̬̍́͘ При пропускании воздуха или другого малорастворимого в воде инертного газа (азот, диоксид углерода, дымовые газы) через сточную воду летучий компонент (летучие неорганические и органические примеси, сероводород, диоксид серы, сероуглерод, аммиак, диоксид углерода и др.) из жидкой фазы диффундирует в газовую фазу. Десорбция обусловлена более высоким парциальным давлением газа над раствором, чем в окружающей среде. Процесс десорбции, в отличие от абсорбции, сопровождается поглощением теплоты, которая должна быть подведена извне. Необходимое количество теплоты рассчитывается на основании теплового баланса десорбера. Процесс десорбции (регенерации) абсорбента прямо противоположен процессу абсорбции. При десорбции из насыщенного абсорбента отпариваются целевые компоненты, т. е. из жидкой фазы переводятся в газовую. Газовая фаза в десорбере создается подачей в нижнюю часть аппарата инертного газа (газа отпарки). Компоненты, поглощенные в процессе абсорбции, должны быть выделены из насыщенного абсорбента в процессе десорбции. В результате десорбции получаются целевые компоненты в виде продукта и регенерированный абсорбент, возвращаемый в процесс абсорбции. Чем полнее отпарены целевые компонен— 330 — ÐƫǬǯǮ͠ƻǅǀǎÐ͟ǮǯǁǬÐǪƻǯǮ͠ƻǅǀǀ ÐƽǬƼǪƿǪǅǀǎ ÐƽǬƿǮƽǮ͠Ǫǅǀǎ ты из абсорбента, тем выще коэффициент извлечения их в процессе абсорбции. Чтобы целевые компоненты могли перейти в процессе десорбции из насыщенного абсорбента в газовую фазу, концентрация их в ней должна быть ниже равновесной. Для этого в десорбер подают инертный отпарной газ, не содержащий целевых компонентов и (или) подводят теплоту в нижнюю часть десорбера. Равновесное парциальное давление удаляемого газа находят по закону Генри (). Количество вещества М, перешедшего из жидкой фазы в газовую, также определяют по уравнению массопередачи : M = Ky FDñcр (8.18) где Ку — коэффициент массопередачи (в данном случае он равен коэффициенту массопередачи в газовой фазе βу); F — поверхность контакта фаз; Dcр — средняя движущая сила процесса десорбции. Степень удаления летучих веществ из сточной воды увеличи-вается с ростом температуры газожидкостной смеси, коэффициента массоотдачи и поверхности контакта фаз. Десорбируемые из воды вещества направляют на адсорбцию или каталитическое сжигание (катализатор — пиролюзит, оксид хрома и др.) при 280–350 оС. Большинство органических соединений при этом окисляется до СО2 и Н2. Математические описания процессов десорбции по существу отличается от процессов абсорбции знаками величин в уравнении балансов: в неподвижной фазе (уход вещества) знак станет отрицательным, в подвижной — положительным (приход вещества). ϴ͘Ϯ͘Ϯ͘ʪ̶̨̨̛̖̬̔̌́̚͘ Часто в сточных водах содержится аммиак, сероводород, углеводороды и другие дурнопахнущие вещества. Для удаления их из воды используют различные способы: аэрацию, хлорирование, ректификацию, дистилляцию, окисление кислородом под давлением, озонирование, экстракцию, адсорбцию. — 331 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Наиболее простым и эффективным является метод аэрации, заключающийся в продувании воздуха через слой воды. Иногда дурнопахнущие сточные воды очищают продувкой острым паром в колонне с колпачковыми или сетчатыми тарелками. От сероводорода и метилмеркаптана в этом случае степень очистки достигает 100 %, от других веществ — 90 %. В промышленности часто используют метод хлорирования дурнопахнущих сточных вод. При этом происходит окисление хлором серосодержащих соединений. Например, при хлорировании воды сероводородом или метилмеркаптаном реакции идут следующим образом: — в случае недостатка хлора образуется диметилдисульфид с неприятным запахом: H2S + Cl2 → 2HCl + S (8.19) 2CH3SH + Cl2 → 2HCl + (CH3 )2 S2 (8.20) — при избытке хлора (не менее 600 г на 1 м3) образуются диоксид серы, хлорид водорода и метансульфонилхлорид H2S + 3Cl2 + 2H2O → SO2 + 6HCl (8.21) CH3SH + 3Cl2 + 2H2O → CH3SO2Cl + 5HCl (8.22) Очистку сточных вод от сероводорода окислением кислородом воздуха при атмосферном давлении в присутствии катализатора (железная стружка, графитовые материалы и др.) проводят в аэрационном бассейне, куда подают сжатый воздух. В этом случае реакция может проходить следующим образом: — при недостатке кислорода 2H2S + O2 → 2H2O + 2S (8.23) — при избытке кислорода (8.24) 2H2S + 3O2 → 2H2O + 2SO2 Большая часть сероводорода при этом окисляется до элементарной серы, а другая часть отдувается воздухом. Вода очищается от серы, а воздух с сероводородом и окисью серы поступает на очистку в адсорбер с активным углем. После насыщения уголь регенерируют сульфатом аммония. При окислении продолжительностью 60–90 минут и расходе воздуха 10–12 м3/м3 степень очистки воды достигает 95–97%. — 332 — ÐƫǬǯǮ͠ƻǅǀǎÐ͟ǮǯǁǬÐǪƻǯǮ͠ƻǅǀǀ ÐƽǬƼǪƿǪǅǀǎ ÐƽǬƿǮƽǮ͠Ǫǅǀǎ Сероводород из воды можно удалить гидроксидом железа по реакциям: — в щелочной среде 2Fe ( OH )3 + 3H2S → Fe2S3 + 6H2O (8.25) — в нейтральной среде (8.26) Fe ( OH )2 + H2S → FeS + 2H2O Для удаления запахов из сточных вод могут быть использованы процессы озонирования и адсорбции. Однако более эффективно происходит очистка при одновременном введении в воду озона или диоксида хлора (ClО2) и фильтровании воды через слой активного угля. Наилучшие результаты очистки получены при следующих соотношениях: для сероводорода — О3/Н2S > 5; для метилмеркаптана — О3/СН3SН»10; для диметилсульфида — О3/(СН3)2S = 4–6. Степень дезодорации указанных веществ в этих условиях зависит от их концентрации в сточной воде и изменяется от 80 до 100%. Доза озона в этом случае снижается по сравнению с просто озонированием. Применение диоксида хлора вместо озона при тех же соотношениях обеспечивает степень дезодорации на 90–100%. ϴ͘Ϯ͘ϯ͘ʪ̶̛̖̐̌̌́̚͘ Присутствие в сточных водах растворенных газов затрудняет очистку и использование сточных вод, усиливает коррозию трубопроводов и аппаратуры, придает воде неприятный запах. Растворенные газы из воды удаляют дегазацией, которую осуществляют химическими, термическими и десорбционными (аэрационными) методами. Часто возникает необходимость удаления из воды диоксида углерода, аммиака, кислорода. Для удаления из воды диоксида углерода используют методы аэрации, проводимые в пленочных, насадочных, барботажных и вакуумных дегазаторах. Пленочные дегазаторы — колонны с различного вида насадками, работающие в условиях противотока дегазируемой воды и воздуха, подаваемого вентилятором. Вакуумные дегазаторы — насадочные колонны, работающие под вакуумом, в которых вода равномерно распределяется — 333 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ по поверхности насадки. Наиболее полная дегазация достигается при разбрызгивании в вакууме и одновременном подогреве воды. Воду нагревают паром в котле. Пар из змеевика попадает в теплообменник, где вода подогревается. Вакуум создают отсасыванием парогазовой среды насосом. При термической дегазации воды от растворенного диоксида углерода или кислорода пропускают пар через воду и нагревают ее до температуры кипения при внешнем давлении. В этом случае парциальное давление газа над водой снижается до нуля и растворимость его также падает до нуля. Вследствие нарушения равновесия в системе происходит выделение избыточных газов из воды (физическая десорбция). Аммиак из сточных вод удаляют продувкой водяным паром или воздухом. Ионы аммония в воде находятся в равновесном состоянии с аммиаком и ионами водорода NH4+ ↔ NH3 + H + . При рН=7 в воде могут находиться ионы аммония в истинном растворе; при рН=12 — только растворенный аммиак, который можно выделить из воды. Скорость перехода газообразного аммиака из воды в атмосферу зависит от поверхностного натяжения на границе двух фаз (воздух — вода) и от разности концентраций аммиака в воде и воздухе. Для осуществления процесса отдувки аммиака из воды повышают рН воды до значений 10,8–11,5 и создают большую поверхность контакта между воздухом или паром и водой. Химические методы дегазации применяют при низкой концентрации газов в воде или в случае нецелесообразности их использования, а также при условии, что продукты обработки не затрудняют дальнейшую очистку или использование воды. Методы связаны с проведением реакций, в результате которых происходит химическое связывание растворимых газов. Для удаления кислорода из воды ее фильтруют через легкоокисляющиеся стальные стружки. Содержание марганца в них не должно превышать 0,3%. При фильтровании воды железо окисляется (8.27) 4Fe + 3O2 → 2Fe2O3 — 334 — Ðƫǀǯǰǀǁǁǎǅǀǎ Время контактирования зависит от температуры и при 20–80оС равно 25–30 минут. Образовавшиеся оксиды железа удаляют обратной промывкой. При обработке воды сульфитом натрия образуется сульфат натрия (8.28) 2Na2SO3 + O2 → 2Na2S04 На 1 г О2 необходимо затратить 7,88 г Na2SO3. При обработке воды диоксидом серы в присутствии катализатора имеют место следующие реакции: SO2 + H2O → H2S03 ;2H2SO3 + O2 → 2H2SO4 (8.29) В качестве катализатора используют соли меди (1 мг/л Cu2+) или кобальта (0,001 мг/л Cо2+) в виде 0,01 %-ных растворов. Для удаления 1 г О2 расходуется 4 г SO2. Лучшим обескислороживающим воду реагентом является гидразин: (8.30) O2 + N2 H4 → N2 + 2H2O Реакция протекает значительно быстрее, чем при окислении сульфита натрия (Na2SO3). Катализатором служит металлическая медь, стекло, активный уголь. На 1 г О2 требуется 1 г N2H4. ϴ͘ϯ͘ʪ̶̛̛̛̭̯̣̣́́͘ Дистилляция — процесс разделения жидкой смеси путем частичного превращения ее в пар и последующей конденсации этого пара. Конденсат называется дистиллятом; а осгаток — кубовой жидкостью. Дистиллят обогащается относительно более летучими (низкокипящими) компонентами, а кубовая жидкость относительно менее летучими (высококипящими) компонентами. Самостоятельное значение как метод разделения жидких смесей дистилляция имеет, если различие составов жидкой и паровой фаз достаточно велико или если к продукту, получаемому в виде дистиллята, не предъявляются высокие ограничения по составу. Чаще всего как самостоятельный процесс дистилляция применяется для очистки продуктов от малолетучих или нелетучих примесей. — 335 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Дистилляционная установка состоит из дистилляционного аппарата — испарителя, снабженного теплообменным устройством для подвода необходимого количества теплоты к кипящему раствору, конденсатора для конденсации образующихся паров и сборников дистиллята и кубовой жидкости. Процесс дистилляции проводится периодически или непрерывно. Состав продуктов разделения, получаемых в процессе дистилляции, зависит от физико-химических свойств смесей, параметров технологического режима и от гидродинамической обстановки, которая определяется аппаратурным оформлением процесса. Расчет процессов дистилляции основывается на использовании уравнений материального и теплового балансов и фазового равновесия. Если количество или расход разделяемой смеси W, а содержание произвольного компонента в ней хi(i = 1,2, ..., n, где n — число компонентов в смеси), то условие материального баланса в дифференциальной форме выражается соотношением: d (Wxi ) + yi dG = 0 (8.31) где yi — содержание i-го компонента в паре, образующемся при дистилляции жидкости состава xi, G — количество или расход отгоняемого пара (дистиллята). Поскольку dG = –dW, то, проводя дифференцирование, получаем уравнение dxi dW = (8.32) W yi − xi связывающее состав жидкости с ее расходом или количеством (в периодическом процессе), изменяющимся в процессе дистилляции. В соответствии с уравнением (8.32) изменение состава жидкости в процессе дистилляции зависит от того, в какой связи находятся составы жидкости и образующегося из нее пара. Эта связь определяется гидродинамической обстановкой, зависящей от аппаратурного оформления процесса. По условиям проведения процесса дистилляционные аппараты делятся на емкостные и пленочные. В емкостных аппа— 336 — Ðƫǀǯǰǀǁǁǎǅǀǎ ратах находится большой объем перерабатываемой жидкости, и при кипении она интенсивно перемешивается. При этом получается пар, состав которого близок к равновесному. Поэтому величины уi и xi, входящие в уравнение (8.32), связаны условиями фазового равновесия. В пленочных аппаратах подвергаемая дистилляции жидкость распределяется по поверхности нагрева в виде пленки. Пленка создается за счет стекания жидкости под действием силы тяжести с помощью механических устройств или при восходящем движении! жидкости и пара — за счет динамического воздействия парового потока. В связи со значительно меньшим, чем в емкостных аппаратах, объемом жидкости, находящейся в пленочных дистилляционных аппаратах, для них характерно относительно большое изменение состава жидкости по высоте. ϴ͘ϯ͘ϭ͘ˀ̸̶̶̵̨̨̡̨̛̛̛̛̭̖̯̪̬̖̭̭̭̯̣̣̖̥̭̯̦̼̌̏̔́̏ ̵̪̪̬̯̌̌̌̌;̸̶̨̡̨̛̛̛̪̖̬̖̭̜̪̬̖̭̭̔Ϳ͘ В периодическом процессе в дистилляционный аппарат загружается Wн исходной смеси состава xiк, а в результате процесса получается П дистиллята состава х1д и Wк и кубового остатка — состава хiк. Количество исходной смеси и продуктов разделения, а также их составы связаны следующими условиями материального баланса: (8.33) WÍ = Ï + WÊ Wí xií = Ï xi ä + Wê xiê (8.34) На практике кроме состава и количества исходной смеси обычно бывает задано или количество кубового остатка Wк (тогда в приведенных выше уравнениях неизвестными являются П, xiд и xiк), или состав кубового остатка xiк (тогда неизвестными являются П, xiд и Wк), или состав дистиллята хiд (тогда неизвестным являются xiк, П и Wк). Поскольку во всех случаях имеются, как минимум, три неизвестные величины, необходимы дополнительна условия, связывающие параметры рассматриваемого процесса. Они получаются путем интегрирования уравнения (8.32): — 337 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Wê ∫ Wí x iê dxi dW = ∫ W x yi − xi (8.35) ií Это уравнение выражает связь между величинами Wн и Wк, xiн и xiк. Таким образом, расчет процесса периодической дистилляции сводится к решению системы уравнений (8.33), (8.34) и (8.35). Если разделяемая смесь — бинарная, то состав смеси однозначно определяется концентрацией одного компонента. Поэтому для бинарной смеси получается система из трех уравнений, содержащих три неизвестные величины. Предварительно уравнение (8.35) должно быть проинтегрировано. Для этого необходимо располагать зависимостью уi = f(xi), описывающей связь состав жидкости и образующегося из нее пара. Как было указано, при проведении процесса дистилляции в емкостном аппарате можно считать, что пар находится в равновесии с жидкостью. Для п компонентной смеси условия равновесия между жидкостью и паром описываются n–1 уравнениями. α x yi = n in i (8.36) ∑ k=1α knxk Здесь α in = pi0 γ i коэффициент относительной летучести < pn0 γ n компонентов i и n, р0i и р0n — давление их паров при температуре смеси, γi и γn — коэффициенты активности этих компонентов. Фазовое равновесие в бинарной системе описывается одним уравнением: α12x1 y1 = (8.37) 1 + ( α12 − 1) x1 Подстановка уi из (8.37) в (8.35) дает: xiê Wê x1 (1 − x1 )( α12 − 1) dW = ∫ W ∫ 1 + (α12 − 1) x1 dx1 W x í ií При α12 = const получаем: — 338 — (8.38) ÐǥǬǭǰǀǄǀǭǪǅǀǎ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐǮǯǃǮǫǊ ln Wê x α12 1 − x1ê 1 = ln 1ê − ln Wí α12 − 1 x1í α12 − 1 1 − x1í (8.39) При α12const интегрирование выполняется численными методами или графически. Из соотношения (8.38) находится связь Wк с х1к, зная которую нетрудно определить по уравнениям (8.35) количество дистиллята и его состав. Очевидно, что средний состав дистиллята xiд подчиняется условию: yipê < xi ä < yipí , где ypiк — содержание i-гo компонента в паре, наp ходящегося в равновесии с жидкостью состава xiк; уiн — состав пара, находящегося в равновесии с жидкостью состава хiн. Таким образом, средний состав дистиллята, получаемого при периодической дистилляции, является промежуточным между составами паров, находящихся в равновесии с исходной жидкостью и кубовым остатком. При расчете процесса дистилляции n-компонентной смеси обычно бывает задано распределение одного или нескольких целевых компонентов между дистиллятом и кубовым остатком или задается относительное количество отгоняемого дистиллята П/Wн. В общем случае имеется 2n–1 неизвестных: n–1 значений xiд, n–1 значений х1к и Wк (или П). Для их определения используется одно уравнение материального баланса (8.33), n–1 уравнений (8.34) и n–1 уравнений (8.35) в сочетании с n–1 уравнениями равновесия. (8.36). Методика расчета в этом случае более сложна и выходит за рамки данного пособия. Расчет дистилляции n-компонентной системы с применением компьютерных программ можно найти в специальной литературе. ϴ͘ϰ͘ˀ̴̶̡̡̛̛̛̖̯̌́͘ˇ̡̨̛̛̚Ͳ̵̸̡̨̨̛̛̛̥̖̭̖̭̦̼̏͘ Ректификация — метод разделения жидких смесей, основанный на массообмене паровой и жидкой фаз, движущихся противотоком. Массообмен происходит в результате отличия составов взаимодействующих пара и жидкости от равновесных. Чаще всего процесс протекает при условиях, близких к адиабатическим. При взаимодействии паровой и жидкой фаз из первой во вторую переходит преимущественно один или — 339 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ несколько компонентов с меньшей относительной летучестью (высококипящих), а в обратном направлении — эквивалентное количество компонентов с большей относительной летучестью (низкокипящих). В результате жидкость при ее движении вниз обогащается высококипящими, а пар, движущийся вверх, — низкокипящими компонентами. Процесс проводится в ректификационной колонне. Путем ректификации может быть достигнута достаточно высокая степень разделения однородных жидких смесей на компоненты. Сущность процессов, из которых складывается ректификация, и получаемые при этом результаты можно проследить с помощью t-х-у-диаграммы (рис. 8.4). Рис.8.4. Изображение процесса разделения бинарной смеси путем ректификации на диаграмме t-x-y. Нагрев исходную смесь состава х1 до температуры кипения получим находящийся в равновесии с жидкостью пар (точка b). Отбор и конденсация этого пара дают жидкость состава x2 обогащенную низкокипящими компонентами (х2 > x1). Нагрев эту жидкость до температуры кипения t2, получим пар (точка d) конденсация которого дает жидкость с еще большим содержанием низкокипящих компонентов, имеющую состав х3, и т.д. Проводя таким образом последовательно ряд процессов испарения жидкости и конденсации паров, можно — 340 — ÐǥǬǭǰǀǄǀǭǪǅǀǎ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐǮǯǃǮǫǊ получить в итоге жидкость (дистиллят), представляющую собой практически чистый низкокипящий компонент. Аналогично, исходя из паровой фазы, соответствующей составу жидкости x4, путем проведения ряда последовательных процессов конденсации и испарения можно получить жидкость (остаток), состоящую почти целиком из высококипящих компонентов. В простейшем виде процесс многократного испарения можно осуществить в многоступенчатой установке, в первой ступени которой испаряется исходная смесь. На вторую ступень поступает на испарение жидкость, оставшаяся после отделения паров в первой ступени, в третьей ступени испаряется жидкость, поступившая из второй ступени (после отбора из последней паров), и т. д. Аналогично может быть организован процесс многократной конденсации, при котором на каждую следующую ступень поступают для конденсации пары, оставшиеся после отделения от них жидкости (конденсата) в предыдущей ступени. При достаточно большом числе ступеней таким путем можно получить жидкую или паровую фазу с достаточно высокой концентрацией компонента, которым она обогащается. Однако, более экономично осуществлять процесс ректификации путем многократного контакта между неравновесными жидкой и паровой фазами, движущимися относительно друг друга. При взаимодействии фаз между ними происходит массо- и теплообмен, обусловленные стремлением системы к состоянию равновесия. В результате каждого контакта компоненты перераспределяются между фазами: пар несколько обогащается низкокипящими компонентами, а жидкость — высококипящими компонентами. Многократное контактирование приводит к практически полному разделению исходной смеси. Таким образом, отсутствие равновесия (и соответственно наличие разности температур фаз) при движении фаз с определенной скоростью друг относительно друга и многократное их контактирование являются необходимыми условиями проведения ректификации. — 341 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Процессы ректификации могут осуществляться периодически или непрерывно при различных давлениях: при атмосферном давлении, под вакуумом (для разделения смесей высококипящих веществ), а также под давлением больше атмосферного (для разделения смесей, являющихся газообразными при нормальных температурах). ϴ͘ϱ͘ˑ̶̡̡̛̭̯̬̌́͘ Экстракцией в широком смысле называют процессы извлечения одного или нескольких компонентов из растворов или твердых тел с помощью избирательных растворителей (экстрагентов). При взаимодействии с экстрагентом в нем хорошо растворяются только извлекаемые компоненты и значительно слабее или практически вовсе не растворяются остальные компоненты исходной смеси. В химической технологии экстракция из растворов экстрагентами более распространена, чем экстракция из твердых тел. Экстракция из твердых веществ или квазитвердых материалов (например, из тканей растительного сырья) применяется главным образом в лесохимической, пищевой и фармацевтической промышленности. В химической технологии используют в основном экстракцию из твердых пористых веществ водой или водными растворами кислот и щелочей (процесс выщелачивания), который был рассмотрен в предыдущей главе. Процесс массоотдачи в твердой фазе существенно отличается от массоотдачи в жидкостях, поэтому процессы экстракции в системах жидкость — жидкость и в системах жидкость — твердое тело должны рассматриваются раздельно. ϴ͘ϱ͘ϭ͘ʿ̶̶̵̨̡̡̛̛̛̬̖̭̭̼̭̯̬̭̭̯̖̥̾̌̏̌ ̡̨̛̙̭̯̔̽Ͳ̡̨̛̙̭̯̔̽͘ Процессы экстракции в системах жидкость — жидкость находят широкое применение в химической, нефтеперерабатывающей, нефтехимической и других отраслях промышленности. Они эффективно используются для выделения в чистом — 342 — ÐƸǭǯǰ͠Ǫǭǅǀǎ виде различных продуктов органического и нефтехимического синтеза, извлечения и разделения редких и рассеянных элементов, очистки сточных вод и т.д. Экстракция в системах жидкость — жидкость представляет собой диффузионный процесс, протекающий с участием двух взаимно нерастворимых или ограниченно растворимых жидких фаз, между которыми распределяется экстрагируемое вещество (или несколько веществ). Так, например, очистку сточных вод производят экстракцией бутилацетатом, в который предпочтительно переходят одноатомные и многоатомные фенолы. Для повышения скорости процесса исходный раствор и экстрагент приводят в тесный контакт, осуществляемый обычно многократно. В результате взаимодействия фаз получают экстракт — раствор извлеченных веществ в экстрагенте и рафинат — остаточный исходный раствор, из которого с той или иной степенью полноты удалены экстрагируемые компоненты. Полученные жидкие фазы (экстракт и рафинат) отделяются друг от друга отстаиванием, иногда центрифугированием или другими механическими способами. После этого производят извлечение целевых продуктов из экстракта и регенерацию экстрагента из рафината. Соответствующие компоненты выделяются из экстракта либо ректификцией, либо путем реэкстракции, например, перевода их в водный раствор. Основным достоинством процесса экстракции по сравнению с другими процессами разделения жидких смесей (ректификцией, выпариванием и др.) является низкая рабочая температура процесса, который проводится наиболее часто при нормальной (комнатной) температуре. При этом отпадает необходимость в затратах тепла на испарение раствора. Кроме того, при экстракции обычно возможно из многочисленных растворителей подбирать высокоизбирательный экстрагент, отличающийся по химическим свойствам от компонентов исходной смеси и часто позволяющий достичь более полного разделения, чем это осуществимо с помощью других массообменных процессов. Вместе с тем применение дополнительного компонен— 343 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ та — экстрагента и необходимость его регенерации приводит к некоторому усложнению аппаратурного оформления и удорожанию процесса экстракции. Экстракция незаменима для разделения смесей веществ, чувствительных к повышенным температурам, например антибиотиков, которые могут разлагаться при разделении их ректификацией или выпариванием. Применение экстракции часто позволяет эффективно заменять такие процессы, как разделение высококипящих веществ с использованием глубокого вакуума, например молекулярной дистилляцией, или разделение смесей методом фракционированной кристаллизации. Экстракция может служить также экономичным и эффективным методом разделения сложных смесей на классы соединений одинакового химического состава, температуры кипения которых перекрывают друг друга (разделение ароматических и предельных углеводородов, кипящих в том же интервале температур). Весьма перспективно применение экстракции для разделения смесей неорганических веществ, когда другие способы разделения неприменимы. Процессы жидкостной экстракции в настоящее время успешно используются для переработки ядерного горючего, получения циркония и гафния и многих других редких металлов. С помощью экстракции можно получать высокочистые цветные и благородные металлы. ϴ͘ϱ͘Ϯ͘ˀ̵̨̡̨̛̛̛̦̖̭̖̭̭̯̖̥̙̭̯̌̏̏̏̌̔̽Ͳ̡̨̛̙̭̯̔̽͘ Фазовое равновесие в системе жидкость — жидкость определяет предельные концентрации экстракта и рафината. Данные о равновесии необходимы при выборе экстрагента, технологической схемы процесса, конструкции и размера (высоты или длины) аппарата, для расчета оптимального соотношения потоков экстрагента и исходного раствора, а также для выяснения других условий проведения процесса. Законы распределения. Состояние равновесия в системе жидкость — жидкость определяется равенством химических потенциалов распределяемого вещества в обеих фазах. — 344 — ÐƸǭǯǰ͠Ǫǭǅǀǎ Количественно равновесие выражают двумя способами. Обычно его характеризуют отношением равновесных концентраций распределяемого вещества в фазах, или коэффициентом распределения: y* m= , (8.40) x где y* и x — равновесные концентрации распределяемого вещества в экстракте и рафинате. Для неидеальных смесей, когда величина m сильно изменяется с концентрацией раствора, более удобно пользоваться изотермой экстракции, или линией равновесия y* = f(x), вид которой обычно устанавливается опытным путем. В простейшем случае коэффициент распределения m — величина приблизительно постоянная. При этом он является функцией температуры и мало зависит от концентрации x; соответственно изотерма экстракции близка к прямой линии. Во многих случаях, несмотря на малую концентрацию распределяемого компонента, равновесная зависимость усложняется вследствие его химического взаимодействия с экстрагентом, а также из-за различия состояния компонента в обеих фазах. Количественные характеристики подобных равновесий во многих случаях могут быть установлены с помощью закона действующих масс. Рассмотрим такой подход к количественной оценке равновесий на примере наиболее типичных процессов экстракции неорганических кислот и солей металлов нейтральными органическими экстрагентами (эфирами, фосфорорганическими соединениями и т.д.). Извлекаемое вещество MeAz в этом случае в водной фазе диссоциировано, а в органической фазе образует соединения с экстрагентом (сольваты): z+ − Meâîäí + zAâîäí + qSîðã = MeAz qSîðã (8.41) где Me — извлекаемый металл; А — анион; Sорг — экстрагент; z — валентность металла; q — количество молекул экстрагента, входящих в сольват. Согласно закону действующих масс: — 345 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ [ MeAzqS]îðã z q  âîäí [ A ]âîäí [ S ]îðã =K (8.42)  Me  где выражения, стоящие в квадратных скобках, обозначают — концентраконцентрации соответствующих веществ, а K ционная константа равновесия. Пусть концентрация распределяемого компонента в органической фазе [ MeAz ]îðã = y z+ и его концентрация в водной фазе  Mez+   âîäí = x Если в растворе нет других солей с одноименным ионом, то, учитывая, что один моль соли дает z молей анионов, имеем z  A −  = zx ;  A −  = ( zx )z     Величина [S] является концентрацией свободного, т.е. не связанного в сольват, экстрагента. Один моль образовавшегося соединения связывает q молей экстрагента, а y – qy молей. Поэтому концентрация свободного экстрагента будет [S ] = S0 - qy где S0 — начальная концентрация экстрагента. С учетом сказанного получим следующее уравнение изотермы экстракции: z xz+1 (S − qy )q y = Kz (8.43) 0 и соответственно коэффициент распределения: z xz (S − qy )q m = Kz 0 (8.44) При q 3 уравнение (8.5) может быть аналитически решено относительно y. Например, для q = 1 и z = 1 (экстракция неорганических кислот): 2 Kx y= S (8.45) 2 0 1 + Kx При этом изотерма экстракции имеет вид, показанный на рис. 7.5. Коэффициент распределения в данном случае про— 346 — ÐƸǭǯǰ͠Ǫǭǅǀǎ порционален концентрации x в степени z и при x ĺ 0 обращается в нуль, а изотерма касается оси абсцисс. В результате глубокое извлечение становится невозможным. Рис. 8.5. Типичная изотерма экстракции при извлечении неорганических веществ. Эта трудность преодолевается путем введения высаливателей. Пусть концентрация высаливателя составляет xвыс, а его валентность — zвыс. Тогда концентрация анионов будет [ A ] = zx + zâûñ xâûñ и вместо уравнения (7.45) получим (zx + z x )z ( S − qy )q y = Kx (8.46) âûñ âûñ При малых концентрациях извлекаемого компонента коэффициент распределения будет конечным: (z x )z ( S − qy )q (8.47) mx→0 = Kx âûñ âûñ В этом случае вид изотермы экстракции изменяется (пунктир на рис. 8.1), и становится возможным достаточно полное извлечение веществ. В качестве экстрагентов для извлечения металлов нередко используют органические кислоты (находящиеся обычно в органической фазе в виде димеров), причем извлечение осуществляют на основе механизма катионного обмена: Mez+ + z ( HR2 )z ↔ Me ( HR2 )z + zH + По закону действующих масс — 347 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Z откуда Z  +  Me ( HR2 )   H +  Z  = m H  K=  Z Z  Mez+  ( HR2 ) ( HR )2    ( HR )  Z  H +  − Z m=K  2   (8.48) (8.49) и где lgm = C − zlg  H +  = C + z ( pH ) + lg ( HR )  Z C = lgK  2 (8.50) (8.51) Таким образом, коэффициент распределения возрастает по мере уменьшения концентрации ионов водорода. Поэтому в подобных процессах экстракцией управляют, меняя pH раствора. Для извлечения ряда благородных и редких металлов, а также других элементов эффективными экстрагентами являются органические основания — амины. Процессы экстракции аминами могут протекать по механизмам реакций присоединения и анионного обмена; в обоих случаях равновесие при экстракции аминами можно рассчитывать по уравнению (8.48). ϴ͘ϱ͘ϯ͘ˀ̵̵̨̛̛̛̦̖̭̖̦̬̦̼̭̭̯̖̥̌̏̏̏̍̌̌͘ При экстракции неорганических веществ, обычно удается подобрать экстрагенты, практически нерастворимые в водной фазе. Например, растворимость широко применяемого экстрагента — трибутилфосфата — в воде составляет около 0,02 вес.%. Это значительно упрощает регенерацию экстрагента, а при расчетах позволяет пользоваться наиболее простой прямоугольной диаграммой равновесия y-x. При экстракции органических веществ весьма часто приходится применять жидкие системы с заметной взаимной растворимостью компонентов. Простейшая (бинарная) система жидкость — жидкость с ограниченной взаимной растворимостью компонентов состоит из двух компонентов (К = 2) и двух фаз (Ф = 2) и, согласно правилу фаз, имеет две степени свободы — 348 — ÐƸǭǯǰ͠Ǫǭǅǀǎ Рис.8.6. Диаграмма t-x для бинарной смеси жидкость — жидкость с верхней КТР. (С = 2). Поэтому для такой системы состав смеси x при постоянном давлении p = const является функцией только температуры t (рис.8.6.). Часть диаграммы, ограниченная кривой и осью абсцисс, представляет собой гетерогенную область. В пределах этой области любая смесь заданного среднего состава при данной температуре (обозначенная, например, точкой М) образует два сопряженных насыщенных раствора, состав которых выражается точками Q и Р, лежащими на концах горизонтальной линии, проведенной через точку М. Такие горизонтальные линии, соединяющие точки составов взаимно насыщенных растворов, называются конодами (иногда их называют также нодами) или хордами равновесия, а кривая, соединяющая концы конод, носит название биноидальной кривой. Левая ветвь CQK биноидальной кривой соответствует насыщенным растворам В в А, а правая ее ветвь DPK — насыщенным растворам А в В. Относительные количества образующихся сопряженных растворов зависят от состава исходной смеси. С повышением температуры составы этих растворов сближаются, и при некоторой критической температуре растворения, отвечающей точке К, достигается предел взаимной растворимости компонентов и система становится однофазной. Поэтому — 349 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ для расчета процессов экстрагирования используется только область диаграммы под биноидальной кривой. Точка К называется критической точкой растворимости (КТР), причем эта точка, как правило, не совпадает с максимумом (или минимумом) на биноидальной кривой, а последняя несимметрична относительно крайних ординат диаграммы. Помимо систем с верхней КТР, имеются жидкие системы, для которых взаимная растворимость возрастает с уменьшением температуры (системы с нижней КТР), системы с верхней и нижней КТР, а также системы, не обладающие КТР. В последних системах изменением температуры может выпадать твердая фаза. ϴ͘ϱ͘ϰ͘ˀ̵̵̨̨̛̛̦̖̭̖̯̬̜̦̼̭̭̯̖̥̌̏̏̏̌͘ ˃̨̛̬̖̱̣̦̬̥̥̐̽̌́̔̌̐̌̌͘ Практически процессы экстрагирования проводятся с системами, состоящими минимально из трех компонентов (К = 3) и двух жидких фаз (Ф = 2). Для таких систем, по правилу фаз, число степеней свободы равно трем (С = 3). Следовательно, в данном случае независимыми переменными являются три параметра — температура, давление и концентрация одной из фаз. Однако влиянием давления на равновесие в системе жидкость — жидкость можно пренебречь. Зависимость состава от температуры (при p = const) для тройных систем изображается с помощью треугольной призмы, в которой температуры откладываются на оси, перпендикулярной к плоскости, на которой наносятся составы (рис.8.7 и 8.8). На диаграмме сторона АВ треугольника соответствует различным составам исходного раствора, причем вершина А представляет чистый растворитель исходного раствора, а вершина В — чистое растворенное вещество. Вершина S отвечает чистому селективному растворителю (экстрагенту). Существует предельная концентрация компонента В в исходном растворе, не превышая которую можно экстрагировать этот компонент при температуре, для которой построена диаграмма. Указанная концентрация определяет— 350 — ÐƸǭǯǰ͠Ǫǭǅǀǎ Рис. 8.7. Применение правила рычага. Рис.8.8. Треугольная диаграмма тройной системы: жидкость — жидкость с одной парой частично смешивающихся компонентов (А и В). ся отрезком АС, полученным при пересечении касательной к биноидальной кривой, проведенной из вершины S, со стороной AB треугольника в точке С. Этой предельной концентрации соответствует максимальный расход экстрагента, определяемый отрезком CE1. Из растворов, составы которых отвечают точкам, лежащим на отрезке CB, экстрагирование осуществить невозможно, при добавлении любых количеств экстрагента. — 351 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ ϴ͘ϱ͘ϱ͘ʰ̶̨̡̡̛̛̯̖̬̥̼̭̯̬̾̌̚;̡̨̛̛̬̼̖̬̦̖̭̏̌̏̏́Ϳ͘ Равновесные данные для тройных жидких систем изображают также с помощью построения зависимости между концентрациями равновесных растворов, которая, как было указано, носит название изотермы экстракции (рис. 8.9, б). Рис. 8.9. Треугольная диаграмма (а) и кривая распределения (б) для системы с одной парой частично смешивающихся компонентов. Эта кривая выражает зависимость между концентрациями компонента В (распределяемого вещества) в фазах A и S. Каждой хорде равновесия на треугольной диаграмме соответствует одна точка на кривой равновесия. Так, например, точка Q на кривой равновесия (рис.8.9, б) отвечает хорде равновесия RE на рис. 8.9, а. Кривая равновесия проходит через максимум и пересекает диагональ диаграммы в точке К, которая соответствует КТР на треугольной диаграмме. Кривые селективности. По треугольной диаграмме можно судить о селективности, или избирательности, растворителя (экстрагента). Селективность характеризует способность экстрагента предпочтительно растворять один или несколько компонентов исходного раствора. Высокая селективность обеспечивает меньший расход экстрагента и более экономичное проведение процесса экстрагирования. Селективность экстрагента (например, компонента S, рис.8.8) по отношению к экстрагируемому компоненту (В) является основным свойством — 352 — ÐƸǭǯǰ͠Ǫǭǅǀǎ экстрагента, определяющим полноту извлечения при экстрагировании. Возвращаясь к рис. 8.8, рассмотрим прямые, проведенные из вершины S через концы некоторой хорды равновесия, например хорды R1E1, до пересечения со стороны АВ, причем точка R1 соответствует фазе рафината, а точка Е1 — фазе экстракта. Точка G на стороне АВ соответствует рафинату, из которого полностью удален (регенерирован) экстрагент S, а точка С — экстракту, из которого также удален весь экстрагент. Таким образом, после регенерации экстрагента из обеих фаз получают экстракт, максимально обогащенный, а рафинат — предельно обедненный извлекаемым компонентом. Чем больше расстояние между точками G и С, тем селективнее экстрагент по отношению к компоненту В. Для количественной оценки селективности, построенной в виде зависимости концентрации распределяемого компонента (в данном случае компонента В) в фазе экстрагента (компонента S) в этих фазах. Таким образом, кривая селективности экстрагента строится в координатах yB xB (ось ординат) и (ось абсцисс). y A + yB x A + xB Аналогичным образом может быть определена селективность любого компонента смеси по отношению к другому. Величина селективности βSB, величиной которого определяется селективность экстрагента S по отношению к распределяемому компоненту В, представляет собой отношение концентраций тех же компонентов в свободной от S фазе рафината:  xB yB yA xA  = βSB  : : y A + yB y A + yB  x A + xB x A + xB  Откуда βSB = yB x A y A xB (8.52) Коэффициент селективности является аналогом относительной летучести компонентов в процессе ректификации. — 353 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ При βSB = 1 селективность равна нулю и экстракция невозможна. Чем больше βSB превышает единицу, тем при меньших габаритных размерах экстракционной установки, меньших расходах экстрагента и соответственно при более низких капитальных и эксплутационных расходах может быть проведен процесс. Сопоставляя выражение коэффициента селективности βSB и коэффициента распределения m (выражение (8.4)), можно установить зависимость между этими коэффициентами: m (8.52а) βSB = B mA Из зависимости (8.52, а) видно, что с увеличением коэффициента распределения mB селективность возрастает. Селективность зависит от тех же факторов, что и коэффициент распределения. Наиболее часто она является величиной переменной, изменяющейся в зависимости от концентрации экстракта (по распределяемому веществу) и температуры. Как уже отмечалось, коэффициенты распределения (и соответственно селективности) могут быть увеличены путем изменения pH раствора, если последний диссоциирован, или путем «высаливания» — добавления к системе неэкстрагируемых солей, изменяющих диссоциацию распределяемого компонента и растворимость многих веществ в воде. Помимо высокой селективности экстрагент должен обладать также значительной емкостью по отношению к экстрагируемому компоненту, которая характеризуется величиной xSB. Если это требование не выполняется, то возрастает количество циркулирующего в установке экстрагента и снижается экономичность процесса. ϴ͘ϱ͘ϲ͘ʺ̶̨̡̡̛̛̖̯̼̭̯̬̔̾̌͘ При экстракции неорганических веществ обычно извлекают одно или несколько веществ из водной фазы одним экстрагентом. При разделении экстракцией смесей органических веществ в зависимости от числа применяемых экстрагентов различают: — 354 — ÐƸǭǯǰ͠Ǫǭǅǀǎ 1)-экстракцию одним экстрагентом в системах, состоящих минимум из трех компонентов (двух разделяемых компонентов исходного раствора и экстрагента); 2)-экстракцию двумя экстрагентами (фракционная экстракция) в системах, состоящих минимум из четырех компонентов (двух компонентов исходного раствора, распределяющихся между несмешивающимися экстрагентами). Экстракция одним экстрагентом наиболее распространена. Рассмотрим разные варианты этого процесса на примере ступенчатой экстракции, различные способы осуществления которой приведены ниже. Рис. 8.10. Схема одноступенчатой экстракции: 1 — смеситель; 2 — сепаратор — отстойник. Одноступенчатая (однократная) экстракция. Этот простейший метод заключается в том, что исходный раствор F и экстрагент S перемешиваются в смесителе 1 (рис 7.10), после чего разделяются на два слоя: экстракт Е и рафинат R. Разделение обычно происходит в сепараторе-отстойнике 2. При таком однократном взаимодействии экстрагента и исходного раствора при достаточном времени контакта могут быть получены близкие к равновесным составы экстракта и рафината. Таким образом, количество экстрагируемого вещества фиксировано законом равновесного распределения, и степень его из— 355 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ влечения является относительно низкой. Степень извлечения можно повысить путем увеличения количества используемого экстрагента, но с увеличением объемного соотношения потоков экстрагента и исходного раствора снижается концентрация экстракта, что удорожает извлечение конечного продукта. По этим причинам одноступенчатую экстракцию применяют в промышленной практике лишь в тех случаях, когда коэффициент распределения очень высок. Процесс может проводиться как периодически, так и непрерывным способом — при непрерывном возврате экстрагента в смеситель (после его регенерации). Ниже приводится расчет одноступенчатого процесса экстракции, лежащий в основе расчета процессов многоступенчатой экстракции. Первоначально рассмотрим наиболее простой случай, когда фазы практически взаимно нерастворимы. Пусть А [кг] растворителя исходного раствора концентрацией X0 [%] смешиваются с S [кг] экстрагента, причем в результате экстракции получаются равновесные фазы: рафинат концентрацией X и экстракт концентрацией Y (в кг/кг растворителя). Весовое соотношение фаз b’ = S/A. Тогда материальный баланс по распределяемому веществу Откуда AX0 = AX + SY X0 = X + S Y = X + b,Y A Учитывая, что Y = mX , находим X0 = X + b ′ mX Следовательно, концентрация получаемого рафината X0 X= 1 + b′m и концентрация экстракта mX0 Y= . 1 + b′m — 356 — ÐƸǭǯǰ͠Ǫǭǅǀǎ Достигаемая степень извлечения распределяемого вещества ϕ= SY b′ m ε = = AX0 1 + b′ m 1 + ε где ε = b’m — экстракционный фактор. Величина ε имеет важное технико-экономическое значение при проведении процессов экстракции. Чтобы остаточное содержание экстрагируемого компонента в рафинате было низким, экстракционный фактор должен быть больше единицы. Однако при больших значениях ε лежат в пределах 1,2< ε <2. Для построения процесса на Y − X -диаграмме (рис.8.11, а) наносят равновесную линию Y * = f ( X ) и откладывают на оси абсцисс начальную точку F рабочей линии с координатами X = X0 и Y = 0 . Рис. 8.11. Изображение процесса одноступенчатой экстракции: а — на прямоугольной диаграмме Y — X; б — на треугольной диаграмме. Из точки F проводят прямую под углом tg α = –A/S, так как из материального баланса по распределяемому веществу (см. выше) уравнение рабочей линии, аналогичное общему уравнению, имеет вид: A A Y = - X + X0 . S S — 357 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Если в результате экстракции достигается равновесие фаз, то прямую из точки F продолжают до пересечения с линией равновесия в точке В. Координаты точки В выражают составы получаемых экстракта ( XK ) и рафината ( YK ) . На диаграмме Y − X экстракционный фактор ε выражается отношением наклонов линии равновесия и рабочей линии. Количество экстрагента, необходимого для получения рафината состава XK (точка R), определяют из зависимости A BR = = tgα . Количество или расход экстрагента составляет: S RF S= A RF . BR Чем больше расход экстрагента S, тем меньше tgα и, следовательно, тем меньше содержание экстрагируемого компонента в экстракте и рафинате, составы которых соответствуют, например, точке B1 на рис. 8.11, а, для которой YK1 < YK и XK1 < XK . В случае недостаточного перемешивания или слишком малого времени контакта при одноступенчатой экстракции получаемые экстракт и рафинат не равновесны друг другу. В этом случае степень извлечения экстрагируемого компонента определяется величиной φ. Более сложен расчет процесса в системах с ограниченной взаимной растворимостью компонентов. Пусть при смешении F [кг] исходного раствора с S [кг] экстрагента образуется М [кг] смеси, после расслаивания которой получают R [кг] рафината и E [кг] экстракта. Тогда материальный баланс процесса будет иметь вид: M = F+S= R+E При расчете процесса по заданному составу исходного раствора и принятому соотношению количеств экстрагента и исходного раствора находят количество экстрагента, а также количества и составы получаемых рафината и экстракта. Воспользуемся для расчета треугольной диаграммой (рис. 8.11, б), причем для упрощения рассмотрим случай, ког— 358 — ÐƸǭǯǰ͠Ǫǭǅǀǎ да исходный раствор обрабатывается чистым экстрагентом S, а получаемые экстракт и рафинад не содержат экстрагента. Для построения диаграммы процесса точку F, соответствующую составу исходного раствора, соединяют прямой с точкой S,выражающей состав экстрагента. Каждая точка прямой FS соответствует постоянному соотношению компонентов А и В исходного раствора. По правилу рычага определяют положение точки М, польF MS зуясь соотношением = . Следовательно, количество эксS FM FM . MS Зная положение хорды равновесия, проходящей через точку М, и применяя то же правило рычага, находят трагента S = F R ME R EM R ME = и = или = E + R MR + ME E MR M RE ME откуда количество рафината R = M . Тогда количество поRE лучаемого экстракта ME RE − ME RM =M =M RE RE RE Для определения состава рафината соединяют точки S и R лучом до пересечения со стороной АВ треугольника. Точка RК определяет состав конечного рафината. Аналогично, проводя луч через точки S и E, находят точку EК, выражающую состав конечного экстракта. Точки RК и EК лежат на стороне АВ треугольника, т.е. соответствуют бинарным смесям, не содержащим экстрагента. Пользуясь треугольной диаграммой, можно определить также максимальный и минимальный расходы экстрагента. При перемещении точки М по лучу SF влево (рис 8.11, б) отрезки FM уменьшаются, а отрезки MS увеличиваются. Соотве ственно, согласно уравнению (8.45) уменьшается количество S экстрагента. E= M−R = M−M — 359 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ В пределе точка M может совместиться с биноидальной кривой (точка М1 на рис. 8.11, б). При этом отрезок FM минимален, и в результате экстракции получают лишь один слой рафината. Точке М1 соответствует минимальное количество экстрагента: FM1 Smin = F M1S при котором концентрация распределяемого компонента В в рафинате является наибольшей. Аналогично при перемещении точки М вправо по лучу SF ее нижнее предельное положение выражается точкой М2. При этом получают только слой рафината. В данном случае количество необходимого экстрагента максимально и составляет: FM2 Smax = F M2S Практически количество экстрагента выбирают промежуточным между максимальным и минимальным, причем желательно, чтобы оно соответствовало экономически оптимальным условиям экстракции. При непрерывном процессе определяют расходы экстрагента, экстракта и рафината (в кг/с или в кг/ч). ϴ͘ϱ͘ϳ͘ʺ̸̶̨̨̡̡̡̨̨̡̛̛̦̭̯̱̪̖̦̯̭̯̬̪̬̪̖̬̖̬̖̭̯̦̥̯̖̐̌̌́̾̌́͘ Экстракция этим способом проводится в нескольких ступенях (рис. 8.12) через которые последовательно движется исходный раствор, причем во всех ступенях, начиная со второй, исходным раствором является рафинат предыдущей ступени. Общее количество свежего экстрагента разделяется на части и подводится в количествах R1, R2, R3,…, Rn-1 как показано на рис. 8.12, а, параллельно на все ступени. Изображение процесса в прямоугольной диаграмме приведено на рис. 8.12, б. Построение на диаграмме проведено так же, как для процесса одноступенчатой экстракции. При этом предполагалось, что экстрагент и растворитель исходного раствора нерастворимы друг в друге, экстрагент равномерно распределяется между ступенями и содержит некоторое ко— 360 — ÐƸǭǯǰ͠Ǫǭǅǀǎ личество экстрагируемого компонента, т.е. имеет начальную концентрацию xE0. При достаточно большом числе ступеней указанным способом можно получать практически в чистом виде компонент А, остающийся в рафинате, т.е. растворитель исходного раствора. Однако это связано с большими потерями данного компонента и уменьшением его выхода, так как на каждой ступени некоторая часть компонента А удаляется с экстрактом. Рис. 8.12. Схема многоступенчатой экстракции: а — при перекрестном токе; б — изображение процесса на диаграмме Y-X; 1,2,3,…,n — ступени. На каждую последующую ступень в качестве исходного раствора поступают все более обедненные экстрагируемым компонентом рафинаты R1, R2, R3,…, Rn-1 поэтому концентрации экстрактов снижаются от первой (E1) к последней (Еn) ступени. В результате для получения рафината высокой чистоты — 361 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ требуются большие объемные соотношения экстрагента и исходного раствора, т.е. большой суммарный расход свежего экстрагента, что связано со значительным удорожанием процесса его регенерации. Вследствие указанных недостатков описанный способ экстракции находит ограниченное применение в промышленности. Так, его используют в тех случаях, когда необходимо получить, не считаясь с потерями, в весьма чистом виде компонент А или когда для этой цели можно применять дешевый экстрагент (например, воду) и при этом не требуется регенерации экстрагента. ϴ͘ϲ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏͘ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Физические основы процесса абсорбции. Равновесие при абсорбции. Материальный и тепловой баланс абсорбции. Кинетика абсорбции. Физические основы процесса десорбции. Материальный и тепловой баланс десорбции. Физические основы дистилляции(перегонки) жидкостей. Характеристики двухфазной системы жидкость-пар. Простая перегонка. Материальный и тепловой баланс дистилляции. Материальный и тепловой баланс ректификации. Чем процесс дистилляции отличается от процесса ректификации? Теоретические основы процесса экстракции. Равновесие в системах жидкость-жидкость. Методы экстракции. Дайте общую характеристику процессов жидкостной экстракции. Какими свойствами должен обладать идеальный экстрагент? Дайте определение коэффициента распределения, коэффициента разделения и коэффициента извлечения при экстракции. Напишите уравнение линии рабочих концентрации при экстракции. — 362 — ÐǤ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ ϴ͘ϳ͘ʿ̸̛̛̬̥̖̬̼̬̖̹̖̦́̌̔̌̚͘ Задача 1. При температуре 25°С приведены в соприкосновение воздух атмосферного давления, содержащий 14% об. ацетилена, и вода, содержащая растворенный ацетилен в количестве: а) 0,29 10~3 кг на 1 кг воды; б) 0,153 10‘3 кг на 1 кг воды. а) Определить: 1) из какой фазы в какую будет переходить ацетилен; 2) движущую силу этого процесса перехода в начальный момент времени (в относительных мольных концентрациях). Атмосферное давление 765 мм рт.ст. Равновесные концентрации ацетилена в газовой и жидкой фазах определяются законом Генри. Коэффициент Генри равен 1,01 106 мм рт.ст. при температуре 25°С Решение. Закон Генри p* = Ex Парциальное давление ацетилена в воздухе равно p = y = 0,14<765 = 107 мм рт.ст. Мольная доля ацетилена в воде при X = 0,29 · 10–3кг ацетилена/кг воды x= X 0,29i10−3 18i0,29i10−3 = ≈ = 0,2i10−3 26 26 Mац −3 0,29i10 + X+ 18 Mв Ответы на вопросы примера могут быть получены двумя путями. 1. В условиях равновесия парциальное давление ацетилена в газовой фазе над жидкостью с х = 0,2·10–3 по закону Генри должно составлять: p* = Ex = 1,01<106 <0,2<10−3 = 202 мм рт.ст. Имеющееся в действительности над этой жидкостью парциальное давление ацетилена меньше (107 мм рт.ст.). Чтобы в процессе массопередачи система газ — жидкость приближалась к состоянию равновесия, парциальное давление ацетилена в газовой фазе должно увеличиваться, т.е. он будет переходить из воды в воздух. Движущая сила этого процесса перехода (отклонение от состояния равновесия) в начальный момент времени будет равна: в единицах парциального давления ацетилена — 363 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ ∆p = p* − p = 202 − 107 = 95 мм рт.ст. В мольных долях 202 ∆y = y* − y = − 0,14 = 0,124 765 В относительных мольных концентрациях 0,264 0,14 y* y ∆Y = Y * − Y = − = − = 1 − y* 1 − y 1 − 0,264 1 − 0,14 = 0,359 − 0,163 = 0,196 кмоль ацетилена / кмоль воздуха 2. В условиях равновесия с газовой фазой, в которой парциальное давление ацетилена равно 107 мм рт.ст., вода по закону Генри должна иметь концентрацию ацетилена (в мольных долях): 107 p = 0,106<10−3 x* = = E 1.01<10−6 Имеющаяся в действительности мольная доля ацетилена в воде больше: x = 0,2<10−3 . Для того, чтобы в процессе массоперехода система приближалась к состоянию равновесия, мольная доля ацетилена в воде должна уменьшаться, т.е. ацетилен будет переходить из воды в воздух. Движущая сила этого процесса перехода в начальный момент времени(считая ее по концентрации в жидкой фазе), в мольных долях: ∆x = x − x* = 0,2<10−3 − 0,106<10−3 = 0,094<10−3 В относительных мольных концентрациях x x* ∆X = X − X * = − 1 − x 1 − x* Так как x и x* оба много меньше единицы, то в знаменателях последнего уравнения ими можно пренебречь, и ∆X = x − x* = 0,094<10−3 кмоль ацетилена / кмоль воды Задача 2. Построить треугольную диаграмму фазового равновесия для системы вода-ацетон-хлорбензол. Необходимые данные взять из приведенной таблицы. Определить по диаграмме: а) содержание воды и хлорбензола в водном слое — 364 — ÐǤ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ с концентрацией ацетона 45% (масс.); б) состав равновесного с ним слоя хлорбензола; в) количество ацетона, при добавлении которого перестанет расслаиваться смесь 0,11 кг хлорбензола и 0,09 кг воды. Решение. Вычерчиваем равносторонний треугольник (рис. 8.12). Находим на стороне AC точки 1 и 1’, соответствующие первой строке таблицы. Внутри треугольника находим точки 2 и 2’, соответствующие второй строке таблицы, и соединяем их отрезком прямой 2–2’. При отыскании точек внутри треугольника сначала откладываем на стороне АВ содержание ацетона в растворе, а затем параллельно стороне АС — содержание хлорбензола. После нахождения всех точек соединяем их плавной кривой. Равновесные составы сосуществующих фаз, % масс. Водный слой Слой хлорбензола вода ацетон хлорбензол вода ацетон хлорбензол 99,89 0 0,11 0,18 0 99,82 89,79 10 0,21 0,49 10,79 88,72 79,69 20 0,31 0,79 22,23 76,98 69,42 30 0,58 1,72 37,48 60,80 58,64 40 1,36 3,05 49,44 47,51 46,28 50 3,72 7,24 59,19 33,57 27,41 60 12,59 22,85 61,07 15,08 25,66 60,58 13,76 25,66 60,58 13,76 a. Через точку а на стороне АВ проводим прямую ab параллельно стороне АС. Отрезок ab является геометрическим местом точек, характеризующих смеси с содержанием ацетона 45% (масс.). На пересечении отрезка ab с левой ветвью бино— 365 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ дальной кривой находим точку с, характеризующую состав водного слоя: 52,8% (масс.) воды, 2,2% (масс.) хлорбензола. b. Для определения состава сосуществующей фазы через точки 2, 2’, 3, 3’, 7, 7’ проводим прямые, параллельные боковым сторонам треугольника, и точки их пересечения 2», 3», 7» соединяем плавной кривой. Затем через точку с проводим прямую, параллельную стороне ВС, до пересечения с соединительной кривой в точке с», а из точки с»- прямую, параллельную стороне АВ, до пересечения с бинодальной кривой. Точка с является искомой. Состав слоя: 54,9% (масс.) ацетона, 4,3% (масс.) воды, 40,8% (масс.) хлорбензола. c. Находим на стороне АС точку d, характеризующую общий состав заданной смеси 0,09 d. 100 = 45%(масс.) воды и 55% (масс.) хлорбензола]. 0,09 + 0,11 e. При добавлении к этой смеси ацетона общий состав ее будет изменяться по линии dB, на пересечении которой с бинодальной кривой найдем искомую точку е. Необходимое количество ацетона найдем из соотношения отрезков Be и ed: f. Gd / GB = Be / ed ; GB = (0,09 + 0,11)53,5/33 = 0,325 êкг Рис. 8.13. К задаче 2. — 366 — ÐǤ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ Задача 3. Ацетон экстрагируется хлорбензолом из 50% водного раствора. Остаток должен содержать не более 2% (масс.) ацетона. Рис.8.14. К задаче 3. Пользуясь диаграммой, построенной в предыдущем примере, определить количество растворителя, необходимое для обработки 100 кг исходной смеси, если экстрагирование производится в одну ступень. Определить также выход рафината, выход и состав экстракта после удаления из него растворителя. Решение. Через точку R (рис. 8.14), характеризующую состав остатка, проводим хорду равновесия RE. Точку F, характеризующую состав исходной смеси, соединяем с вершиной треугольника С. Точка пересечения М линий ЕС и RE определяет состав смеси исходного раствора с растворителем, необходимый для получения рафината заданного состава. Требуемое количество растворителя находим из соотношения GS / GF = FM / MC ; GS = (100 − 81.5) /5 = 1630 кг Масса полученной смеси: GM = 1630 + 100 = 1730 êкг Количество экстракта находим из соотношения GE RM / RE ; GE = (1730 − 94,4) = = 1682 кг GM 97 — 367 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Масса рафината: GR = GM − GE = 1730 − 1682 = 48 кг Количество экстракта после удаления из него растворителя GE ≈ GE − GS = 1682 − 1630 = 52 кг так как растворимостью хлорбензола в остатке в данном случае можно пренебречь. Состав экстракта после удаления из него растворителя определяется точкой пересечения Е’ стороны AB с лучом, проведенным из вершины С через точку Е: содержание ацетона 95,5% (масс.), воды 4,5% (масс.). ϴ͘ϴ͘ʯ̸̨̨̨̨̛̛̣̭̥̭̯̯̖̣̦̬̖̹̖̦̌̔̌̔́̌́̽̐́͘ Задача 1. При температуре 25°С приведены в соприкосновение воздух атмосферного давления, содержащий 14% об. ацетилена, и вода, содержащая растворенный ацетилен в количестве 0,153 10–3 кг на 1 кг воды. Определить: 1) из какой фазы в какую будет переходить ацетилен; 2) движущую силу этого процесса перехода в начальный момент времени (в относительных мольных концентрациях). Атмосферное давление 765 мм рт.ст. Равновесные концентрации ацетилена в газовой и жидкой фазах определяются законом Генри. Коэффициент Генри равен 1,01 106 мм рт.ст. при температуре 25°С. Задача 2. В условиях предыдущей задачи 2 из раздела 8.7 определить необходимое количество растворителя, состав и выход продуктов и число ступеней экстрагирования, если па каждой ступени экстрагирование производится свежим растворителем в количестве, равном массе обрабатываемой смеси. Задача 3. В условиях задачи 3 из раздела 8.7 определить состав и выход продуктов, а также число теоретических ступеней экстрагирования, если экстракция производится противотоком при соотношении потоков 1:1. — 368 — ǍưǙǚǙÍ Í Í ƩǌƞǎǑƝǎÍǒǕǐǒǕǋÍÍ ƝÍǎǍǒÍƝǕǓǒƞƦƜǒǌǋǑƝǎÍ Í ǓǔƝÍǒơƝǕǖǏǎÍǕǖǒơǑƥǘÍǌǒƚ В результате изучения главы 9 бакалавр должен: Знать: – основные виды осмоса, его физическую природу и фундаментальные законы. Уметь: – применять явление осмоса при очистке сточных вод от примесей. Владеть: – методикой описания процесса осмоса и ее применения при очистке сточных вод . ϵ͘ϭ͘ʽ̸̨̡̨̛̛̭̥̯̖̭̖̣̖̦̖̔̌̏͘ Ряд животных и растительных тканей, например кожа, свиной пузырь, пергамент, обладает свойством свободно пропускать воду и задерживать растворенные в ней вещества. Такие полупроницаемые перегородки можно изготовлять и искусственным путем, например из коллоидных пленок, целлофана. Если раствор отделен от чистого растворителя полупроницаемой перегородкой, то растворитель просачивается через нее в раствор. Это явление называется осмосом. Гидростатическое давление, которое нужно приложить к раствору, чтобы задержать осмос, называется осмотическим — 369 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ давлением раствора. Оно наблюдается также на границе двух растворов разной концентрации, разделенных полупроницаемой перегородкой. В этом случае растворитель течет от более разбавленного раствора к более концентрированному, т.е. в направлении уравнивания их концентраций. Можно непосредственно наблюдать осмос и измерять осмотическое давление в осмометре, простейшая форма которого изображена на рис.9.1. Рис. 9.1. Принципиальная схема осмометра. Сосуд А наполнен раствором и закрыт внизу полупроницаемой перегородкой, например свиным пузырем. Если его опустить в сосуд В с чистым растворителем (или с менее концентрированным раствором), то растворитель проникает вследствие осмоса в сосуд А и уровень жидкости в нем поднимается до тех пор, пока избыточный столб жидкости высотой h не уравновесит осмотического давления. Пленки из некоторых нерастворимых солей образуют отличные полупроницаемые перегородки, особенно для водных растворов веществ с высоким молекулярным весом, как тростниковый сахар, с которым было сделано очень много измерений. Наилучшими оказались пленки из железистоцианистой меди, примененные в исследованиях Пфефера (1877). Следует подчеркнуть, что осмотическое давление возникает лишь на границе между раствором и растворителем (или — 370 — ÐǣǯǂǮǰǀǆǬǯǭǮǬÐƽǪǫǁǬǃǀǬ раствором другой концентрации), если эта граница образована полупроницаемой перегородкой. Раствор, налитый в обыкновенный сосуд, не оказывает на его стенки никакого иного давления, кроме обычного гидростатического. Поэтому правильнее всего рассматривать осмотическое давление не как свойство растворенного вещества, или растворителя, или даже самого раствора, а как свойство системы из растворителя и раствора с полупроницаемой перегородкой между ними. Величина осмотического давления раствора изменяется в зависимости от концентрации второго граничащего с ним раствора. Наибольшее значение ее, получаемое на границе с чистым растворителем, и есть то, что обычно называют осмотическим давлением данного раствора. В известной степени аналогом осмометра является прибор Рамзая (1894), примененный им в некоторых более поздних работах для измерения парциального давления водорода в газовой смеси. Основан он на том, что палладиевая жесть, нагретая выше 300°, служит отличной полупроницаемой перегородкой, свободно пропускающей водород и задерживающей остальные газы. Прибор Рамзая сделан из обогреваемой палладиевой жести и наполнен смесью водорода и азота под атмосферным давлением. Парциальное давление водорода в нем меньше 1 ат на величину парциального давления азота. Если опустить его в чистый водород с давлением 1 ат, то последний будет диффундировать в сосуд до тех пор, пока парциальное давление водорода внутри сосуда также не станет равным 1 ат. Манометр, очевидно, покажет приращение давления, равное парциальному давлению азота. Если рассматривать водород как растворитель, а азот как растворенное вещество, то мы будем иметь довольно близкое сходство с тем, что происходит в осмометре, наполненном раствором и погруженном в растворитель. Руководствуясь подобными аналогиями, Вант-Гофф и Нернст приписывали осмотическое давление односторонним ударам растворенных частиц о полупроницаемую перегородку, вызывающим ее перемещение в сторону растворителя, если она способна двигаться, или, обратно, течение растворителя в раствор, если она закреплена неподвижно. Такое объяс— 371 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ нение происхождения осмотического давления было до недавнего времени очень распространенным. В действительности это неверно. В опыте Рамзая ничего не изменится от удаления азота из сосуда и азот не играет никакой роли в перемещении водорода. Последнее объясняется просто тем, что число ударов молекул водорода о полупроницаемую стенку больше с той стороны, где его парциальное давление выше, и поэтому больше водорода переходит через эту стенку в направлении от большего давления к меньшему, чем обратно. Сходным образом осмос можно приписать тому, что концентрация молекул растворителя и число их встреч с полупроницаемой перегородкой больше в чистом растворителе, чем в растворе, и это вызывает течение первого в последний. До сих пор нет вполне достоверной и общепризнанной кинетической теории осмотического давления, что связано с отсутствием такой же теории для растворов вообще. Это не мешает тому, что осмотическое давление может быть связано точными термодинамическими зависимостями с другими измеримыми свойствами растворов, так как выводы термодинамики вообще не зависят от внутренних механизмов явлений. ϵ͘Ϯ͘ʥ̸̸̨̨̡̨̨̨̡̨̨̛̛̛̛̣̖̭̬̣̭̥̯̖̭̣̖̦̐̌́̽̐̔̌̏́͘ Живая клеточная протоплазма представляет собой хорошую полупроницаемую перегородку для водных растворов. На этом основаны простые и довольно точные биологические методы сравнения осмотического давления растворов, часто применявшиеся тогда, когда не ставилась задача измерения его абсолютной величины. Типичные клетки образованы из протоплазменных мешочков, наполненных водными растворами разных веществ (клеточный сок), осмотическое давление которых на границе с водой обыкновенно лежит в пределах 4–20 ат. Эти клетки представляют собой микроскопические осмометры. Если они погружены в воду или раствор меньшего осмотического давления, чем их содержимое, то вода проникает в протоплазменный мешочек, создавая в нем гидростатическое давление, — 372 — ÐƪǀǮǁǮƼǀǆǬǯǭǪǎÐÐ͠ǮǁǋÐǮǯǂǮǰǀǆǬǯǭǮƼǮÐÐƽǪǫǁǬǃǀǎ называемое тургором. Это давление сообщает живым растениям прочность и упругость их тканей. Если клетка отмирает, то протоплазма теряет свойство полупроницаемости, тургор исчезает и растение вянет. То же осмотическое давление играет роль механизма, подающего клеткам питательные растворы и воду. В высоких деревьях они этим путем поднимаются на десятки метров вверх от корней, что отвечает осмотическому давлению в несколько атмосфер. Если клетка погружена в раствор с более высоким осмотическим давлением, чем ее содержимое, то вода выходит из протоплазменного мешочка, который сморщивается. Это явление, называемое плазмолизом, легко наблюдать под микроскопом. Особенно пригодны для этого большие клетки эпидермиса листа традесканции (Tradescantia discolor). Таким путем де-Фриз (1884) определял концентрации разных растворов, имеющих одинаковое осмотическое давление (изотоничных) с клеточным соком этих клеток (около 4,5 ат). Вместо растительных клеток удобно также применять красные кровяные шарики, отделенные от кровяной сыворотки центрифугированием. В отличие от растительных клеток они не имеют прочной оболочки. Поэтому если они помещены в растворы с меньшим осмотическим давлением, чем их содержимое, то они увеличиваются в объеме и разрываются (гемолиз), окрашивая раствор находящимся в них гемоглобином. У высокоорганизованных животных осмотическое давление в разных органах и тканях приблизительно одинаково и устойчиво сохраняет величину около 8 ат. Изменения его быстро устраняются разными регулировочными механизмами: изменением количества и состава, выделяемых слюны, пота, мочи и количеством выдыхаемых водяных паров. Чувство жажды от соленой пищи вызывается потребностью организма восстановить введением воды нормальное осмотическое давление после того, как оно было повышено введением соли. Этим же объясняется действие больших доз солей как слабительного: в кишечнике создается повышенное осмотическое давление, что увеличивает всасывание воды, разжижающей его содержимое. Обнаженные ткани промывают не чистой водой, — 373 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ а «физиологическим» раствором (например, 0,9% NaCl), изотоничным с клеточными растворами. Это предохраняет клетки от набухания и разрушения. ϵ͘ϯ͘ʯ̸̡̨̨̨̡̨̨̛̛̦̼̭̥̯̖̭̣̖̦̌̐̔̌̏́͘ Измерения Пфефера и де-Фриза легли в основу уже упоминавшейся классической работы Вант-Гоффа (1886), в которой были найдены общие закономерности для осмотического давления и связь его с другими свойствами растворов. Осмотическое давление разбавленного раствора пропорционально его концентрации. Одним из многих примеров, подтверждающих эту закономерность, могут служить данные для водных растворов тростникового сахара, приведенные в табл. 9.1, где концентрации выражены как в моль/1000 г воды (m), так и в моль/л раствора (с). Таблица 9.1. Осмотическое давление растворов тростникового сахара в воде при 20 °C m молей на 1000 г воды С молей на 1 л раствора Р, ат P m P c 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0982 0,191 0,281 0,368 0,452 0,532 0,609 0,684 0,756 0,824 2,59 5,06 7,61 10,14 12,75 15,39 18,13 20,91 23,72 26,64 25,9 25,3 25,4 25,3 25,5 25,7 25,9 26,1 26,4 26,6 26,4 26,3 27,1 27,5 28,2 28,9 29,8 30,6 31,5 32,4 — 374 — ÐƭǪǭǮǃǊÐǮǯǂǮǰǀǆǬǯǭǮƼǮÐƽǪǫǁǬǃǀǎ В сильно разбавленных растворах осмотическое давление Р пропорционально обоим, но в более концентрированных отношение Р/m более постоянно, чем Р/c. Так как концентрация с (в моль/л) обратна молярному объему (в л/моль), то мы приходим к выводу, что в разбавленных растворах осмотическое давление подчиняется закону Бойля: оно при данной температуре обратно пропорционально молярному объему растворенного вещества. Таблица 9.2. Осмотическое давление 1%-ного водного раствора тростникового сахара (с=0,0292) t°C 6,8 13,7 14,2 15,5 22,0 32,0 36,0 P, ат 0.664 0.691 0,671 0,684 0,721 0,716 0,746 T 280,0 286,0 287,4 288,7 295,2 305,2 309,2 P, T 0,00237 0,00241 0,00234 0,00237 0,00244 0,00235 0,00241 Среднее 0,002385 Осмотическое давление разбавленных растворов подчиняется также закону Гей-Люссака: оно при данной концентрации пропорционально абсолютной температуре. Подтверждением этого может служить табл. 9.2, в которой приведены измерения с 1%-ным водным раствором тростникового сахара. Далее оказалось, что осмотическое давление разбавленного раствора подчиняется также закону Авогадро: разные вещества при одинаковой температуре и одинаковой концентрации имеют одно и то же осмотическое давление. Тем же путем, как это было сделано для газов, можно все три закона объединить одним общим уравнением состояния для осмотического давления РV=RT, совпадающим с уравнением состояния идеального газа. Вводя в него молярную концентрацию с=1/V, получаем — 375 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ P = RTc (9.1) Сходство с газами этим не ограничивается. Ван-Гофф нашел, что R численно равна газовой постоянной. Например, по данным табл. 2 P/T=0.002385 для c=0,0292 моль/л (1%-ный раствор сахара). Подставив эти числа в (9.1), получаем P 1 0,002385 = = 0,0817 ë − àò / ãðàä Tc 0,0292 тогда как для газов R=0.08206. Вант-Гофф объединил все эти закономерности в закон: растворенное вещество содержит в разбавленном растворе столько же молекул, сколько оно имело бы их в состоянии газа при той же температуре в том же объеме и при газовом давлении, равном осмотическому давлению раствора. Для ориентировки в величинах осмотического давления можно отметить, что раствор из 1 моль в 22,41 л при 0° имеет осмотическое давление 1 ат. Из аналогии законов осмотического давления с газовыми законами, однако не следует делать вывод, что растворенное вещество ведет себя в растворе подобно газу и что осмотическое давление подобно газовому вызвано ударами растворенных частиц. В частности, законы осмотического давления нельзя вывести кинетическим путем так просто, как это может быть сделано для газовых законов, основываясь лишь на статическом рассмотрении беспорядочных движений молекул, так как растворенные молекулы движутся не в пустоте, а между тесно взаимодействующими с ними молекулами растворителя. Если растворенное вещество испытывает в растворе изменения, приводящие к изменению числа его молекул (например, ассоциацию или диссоциацию), то истинная концентрация в растворе не равна аналитической, т. е. вычисленной из навески или из анализа раствора без учета этих превращений. Поэтому применение аналитической концентрации при вычислении осмотического давления приводит к результатам, не совпадающим с измеренными. Из таких кажущихся нарушений законов осмотического давления могут быть сделаны — 376 — ÐǧǬ͠ǂǮƽǀǃǪǂǀǭǪÐǮǯǂǮǰǀǆǬǯǭǮƼǮÐƽǪǫǁǬǃǀǎ важные заключения о превращениях, испытываемых молекулами в растворе. В частности, этим путем Аррениус пришел к теории электролитической диссоциации. Наконец, следует отметить, что при вычислении осмотического давления в растворах электролитов должно быть учтено взаимодействие электрических полей свободных ионов. ϵ͘ϰ͘˃̸̨̡̨̨̡̨̨̛̛̛̛̖̬̥̦̥̭̥̯̖̭̣̖̦̔̌̌̐̔̌̏́͘ Независимо от каких-либо допущений и представлений о механизме осмотического давления и о поведении частиц в растворе термодинамическим путем может быть найдено общее и точное соотношение между осмотическим давлением раствора и понижением давления пара растворителя над ним. Пусть раствор отделен от чистого растворителя полупроницаемой перегородкой, способной перемещаться, и пусть количество раствора столь велико, что прибавление к нему или отнятие от него одного моля растворителя не изменяет заметным образом его концентрации. Можно двояким путем обратимо и изотермически перевести один моль растворителя из чистого растворителя в раствор. 1. Испарим один моль растворителя из чистого растворителя под давлением его насыщенного пара р0, расширим его до давления р над раствором и под этим давлением сконденсируем пар в раствор. Работы испарения и конденсации, при постоянном давлении, равные RT и –RT, взаимно сокращаются и остается работа обратимого изотермического расширения. p0 A1 = RTln p 2. Такой же перенос можно совершить передвижением полупроницаемой перегородки в направлении от раствора к чистому растворителю до тех пор, пока через нее не пройдет раствор объемом V растворителя, отвечающий одному молю его в парообразном состоянии. Это утверждение можно принять лишь в первом приближении, т.к. из-за ассоциации или диссоциации один моль пара может быть не равен по массе одному — 377 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ молю в жидком состоянии. При этом приближенно получается работа A2 = PV за счет осмотического давления P, так как оно остается постоянным. Работа обратимого изотермического процесса не зависит от пути. Поэтому A1 = A2 или RT p0 (9.2) ln V p Это соотношение между осмотическим давлением и давлением пара растворителя верно для любых растворов, как идеальных, так и неидеальных, независимо от концентрации. Ему можно придать другую, тождественную, но более удобную для применения форму, заменив объем V одного моля растворителя его плотностью ρ. Если его молекулярный вес (в парообразном состоянии) равен M0, то M0 граммов занимают объем 1000 V см2, откуда плотность ρ=M0/1000 V, что с (8.2) дает P= P= 1000ρRT p0 ln M0 p (9.3) С помощью этого уравнения осмотическое давление может быть вычислено с большой точностью даже в очень концентрированных растворах, где оно достигает сотен атмосфер. Из (9.3) легко получить уравнение (9.2) Вант-Гоффа для сильно разбавленных растворов. Последние подчиняются закону Рауля, согласно которому ln p0 = −lnN0 = −ln (1 − N ) p где N и N0 — молярные доли растворенного вещества и растворителя. Если раствор сильно разбавлен, то достаточно точно положить — ln(1–N) равным N и последний, согласно (9.3), равным c M0/1000ρ. Делая эти замены в (9.3), получаем уравнение Вант-Гоффа P = RTc где c — концентрация в моль/л. — 378 — ÐǣǆǀǯǰǭǪÐǯǰǮǆǃǮ֬ÐǫǮƽǊÐǱǁǋǰ͠ǪǄǀǁǋǰ͠ǪǅǀǬ֬ÐǀÐǮƻ͠ǪǰǃǊǂÐǮǯǂǮǯǮǂ Более точные соотношения для идеальных растворов, справедливые и при более высоких концентрациях, получаются, если не делать указанных упрощений. Из (9.2) получаем RT (9.4а) P=− ln (1 − N ) V Заменив –ln(1–N) через N, получаем для разбавленных растворов уравнение значительно более точное, чем уравнение Вант-Гоффа: RT (9.4) P= N V Наконец, легко найти также приближенное уравнение для осмотического давления как функции от концентрации m в молях на 1000 г растворителя. В разбавленном растворе из n молей растворенного вещества и n0 молей растворителя можно n положить N = равным n/n0 (так как n мало по сравнеn + n0 нию с n0). Заметив, что n0 молей растворителя имеют объем n0V литров и массу n0V1000ρ граммов и содержат n молей раствоn ренного вещества, получаем, что 1000 г его содержат m = ρn0V молей. Окончательно: n = N = mV ρ , что с (9.4) дает (9.4б). n0 (9.4б) P = ρRTm Что объясняет постоянство отношения P/m в разбавленных растворах. Уравнение (9.4б) менее точно, чем (9.4), и еще менее, чем (9.4а), но оно точнее, чем (9.1). ϵ͘ϱ͘ʽ̸̸̴̶̡̨̨̨̛̛̛̭̯̭̯̦̜̼̱̣̯̬̣̯̬̖̜̌̏̔̽̌̽̌ ̨̨̨̨̛̬̯̦̼̥̭̥̭̥̍̌͘ Очистка воды от растворенных примесей с размером частиц 0,1–1 нм на молекулярном уровне (ультрафильтрация) проводится с использованием известного в физике явления — осмоса. — 379 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Рис.9.2. Схема процесса осмоса: а — прямой осмос; б — осмотическое равновесие; в — обратный осмос; 1 — секция чистой воды; 2 — фильтрующая перегородка; 3 — секция загрязненной воды. На рис. 9.2 показан сосуд, в котором установлена пористая перегородка (мембрана). В секции 3 находится раствор примеси в воде. Молекулы примеси окружены молекулами воды, создавая гидратный комплекс увеличенного размера. Это приводит к тому, что через пористую перегородку проникают лишь молекулы воды из секции 1 в секцию 2. При этом возникает перепад давлений между секциями 1 и 3, называемый осмотическим давлением (Н). В системе устанавливается осмотическое равновесие. Например, для растворов, содержащих 1000 мг/л воды, осмотическое давление для NaCl составляет 79 кПа, а для СаСl2 — 58 кПа. Создавая в секции 3 избыточное давление Р>Н, молекулы воды будут проходить через мембрану в секцию 1 (обратный осмос). Таким образом, в секции 1 можно получать очищенную воду. Пористая перегородка изготавливается из ацетатцеллюлозы и состоит из двух слоев: один слой толщиной 0,25 мкм служит для разделения (фильтрации), а второй, крупнозернистый толщиной 100–200 мкм обеспечивает механическую прочность перегородки. В зависимости от размера частиц примеси условно процессы очистки делятся на: • обратный осмос — улавливание частиц примеси 10- 4... –3 10 мкм; — 380 — ÐǣǆǀǯǰǭǪÐǯǰǮǆǃǮ֬ÐǫǮƽǊÐǱǁǋǰ͠ǪǄǀǁǋǰ͠ǪǅǀǬ֬ÐǀÐǮƻ͠ǪǰǃǊǂÐǮǯǂǮǯǮǂ • ультрафильтрацию — улавливание частиц 10–3... 2Â10–2 мкм; • макрофильтрацию — улавливание частиц 0,02... 10 мкм. В одном из вариантов аппаратурного оформления процесса используются трубчатые элементы. Внутри трубы устанавливают коаксиально-трубчатый фильтрующий элемент. Очищаемый раствор под давлением протекает в зазоре между стенкой трубы и фильтрующим элементом. Чистая вода собирается внутри фильтра и выводится в конце элемента. Чтобы фильтр не забивался осадком, очищаемый раствор пропускают с большой скоростью, добиваясь его турбулентного движения. Производительность фильтра составляет 0,4–1,0 м3 на 1 м2 фильтра в час при перепаде давлении 5 МПа. Хотя процесс очистки протекает медленно, но, используя батарею таких элементов, можно достичь большой производительности установки. Высокая степень очистки, проведение процесса без нагрева, несложное оборудование делают этот метод очистки дешевым и эффективным. Для очистки от органических примесей с молекулами больших размеров и неорганических примесей с молекулами меньшего размера используются фильтрующие элементы с различным размером пор. Очистку проводят последовательно сначала от органических, а затем от неорганических примесей. Метод очистки обратным осмосом нашел применение в электронной промышленности и на электростанциях для смягчения воды при производстве пара. Эффективность процесса зависит от свойств применяемых мембран. Они должны обладать следующими достоинствами: высокой разделяющей способностью (селективностью), большой удельной производительностью (проницаемостью), устойчивостью к действию среды, неизменностью характеристик в процессе эксплуатации, достаточной механической прочностью, низкой стоимостью. Селективность ϕ (в %) процесса разделения определяют по формуле: — 381 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ ( ) ( ϕ = 100 c0 − сф / c0 = 100 1 − сф/ c0 ) (9.5) где со и сф — концентрации растворенного вещества соответственно исходной сточной воде и фильтрате. Проницаемость определяется количеством фильтрата Vф полученного в единицу времени с единицы рабочей поверхности: Vф = K1 ( ∆P − ∆P0 ) (9.6) где ∆P — разность давлений воды до и после мембраны; ∆P0 — разность осмотических давлений; K1 — коэффициент пропорциональности, зависящий от проницаемости мембраны. Таким образом, скорость обратного осмоса прямо пропорциональна эффективному давлению (разности между приложенным давлением и осмотическим). Эффективное давление значительно превосходит осмотическое. Осмотическое давление для растворов некоторых солей концентрацией 1000 мг/л представлено ниже. Таблица 9.3. Осмотическое давление солей. Соль NaCl Na2SO4 Осмотическое давление, кПа 79 42 MgSO4 CaCl2 NHCO3 MgCl2 25 58 89 67 В процессе очистки некоторое количество растворенного вещества проходит через мембрану вместе с водой. Для мембран с высоким эффектом разделения этот проскок S [в кг/ (м2сут)] практически не зависит от давления и может быть определен по зависимости (К0 — константа для мембран): (9.7) S = K2 c0 − cô Из формулы следует, что чем выше концентрация загрязнений в исходной сточной воде, тем выше интенсивность проникания веществ через мембрану. Предложено несколько вариантов механизма обратного осмоса. По одному из них мембраны собирают воду, которая в поверхностном слое не обладает растворяющей способностью. ( — 382 — ) ÐǤ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ Если толщина слоя адсорбированных молекул воды составляет половину или более половины диаметра пор мембран, то под давлением через поры будет проходить только чистая пода, несмотря на то, что размер многих ионов меньше, чем размер молекул воды. Прониканию (проницанию) таких ионов через поры препятствует возникающая у них гидратная оболочка. Размер гидратных оболочек различен у разных ионов. Если толщина адсорбированного слоя молекул воды меньше половины диаметра половины диаметра пор, то вместе с водой через мембрану будут проникать и растворенные вещества. Для ультрафильтрации предложен другой механизм разделения. Растворенные вещества задерживаются на мембране потому, что размер молекул их больше, чем размер пор, или вследствие трения молекул о стенки пор мембраны. В действительности в процессе обратного осмоса и ультрафильтрации имеют место более сложные явления, рассмотрение которых выходит за рамки этого учебника. ϵ͘ϲ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏͘ 1. В чем заключается физическая сущность явления осмоса? 2. Какие существуют в настоящее время законы осмотического давления? 3. Какова биологическая роль осмотического давления? 4. Что такое обратный осмос и как он применяется при очистке сточных вод? 5. В чем сходство и различие процессов обратного осмоса и ультрафильтрации? ϵ͘ϳ͘ʿ̸̛̛̬̥̖̬̼̬̖̹̖̦́̌̔̌̚͘ Задача 1. Осмотическое давление монодисперсного гидрозоля золота с концентрацией 1 г/л равно 1,87 Па. Рассчитайте коэффициент диффузии и удельную поверхность (в м–1 и м2/г) частиц гидрозоля при 293 К, если плотность частиц золота составляет 19,3 г/см3, а вязкость дисперсионной среды равна 1 мПа с. — 383 — ǞǁǪǫǪÐ ÐǤ͠ǮǅǬǯǯǊÐǂǪǯǯǮ͟Ǭ͠ǬƽǪǆǀÐǫÐǯǀǯǰǬǂǪǲÐǯÐ͟ǮƽǫǀƾǃǮ֬ÐƼ͠ǪǃǀǅǬ֬Ð͠ǪƿƽǬǁǪÐǄǪƿ Решение: Осмотическое давление золей рассчитывается по уравнению Вант- Гоффа: c π = νkÁ T = kÁ T m где с — массовая концентрация частиц, кг/м3; m — масса одной частицы, кг. Найдём массу одной частицы: ck T 1<1,38<10−23<293 m= Á = = 2,16<10−21 êã 1,87 π Найдем объём одной частицы: m 2,16<10−21 = 1,12 • 10−25 ì 3 V= = ρ 19300 Найдем радиус частицы гидрозоля золота: r=3 3V 3 3<1,12<10−25 = = 3<10−9 ì = 3 íì 4π 4<3,14 Рассчитаем коэффициент диффузии частиц гидрозоля золота: k T 1,38<10−23 <293 D= Á = = 7,154<10−11 ì 2 / ñ 6πηr 6<3,14<10−33<10−9 Рассчитаем удельную поверхность Sуд частиц гидрозоля 6 6 = 109 ì −1 золота (в м-1) по уравнению: Sóä = = d 6<10−9 Рассчитаем удельную поверхность Sʾуд частиц гидрозоля золота (в м2/г): 6 6 = = 0,52<10−5 ì 2 / êã = 52ì 2 / ã S×óä = dρ 6<10−9 <19300 ϵ͘ϴ͘ʯ̸̨̨̨̨̛̛̣̭̥̭̯̯̖̣̦̬̖̹̖̦̌̔̌̔́̌́̽̐́͘ Задача 1. Рассчитайте осмотическое давление гидрозоля, используя данные, приведенные в таблице. Плотность дисперсионной среды примите равной 998 г/см3 при температуре 25° С. — 384 — ÐƭǪƽǪǆǀÐƽǁǎÐǯǪǂǮǯǰǮǎǰǬǁǋǃǮƼǮÐ͠ǬǇǬǃǀǎ Вариант Состав частиц Концентрация частиц, мас. % 1 YOOH 8 10 3,2 2 SiO2 5 20 2,2 3 CeO2 3 50 5,6 4 ZrO2 10 25 5,5 — 385 — Радиус Плотность частиц, нм частиц, г/см3 ǍưǙǚǙÍ Í Í ǗƞǒǖǋƠƝƩ В результате изучения главы 10 бакалавр должен: Знать: – основные физико-химические закономерности процесса флотации Уметь: – обоснованно выбирать флотореагенты для извлечения примесей из жидкостей. Владеть: – методикой проведения процесса флотации. ϭϬ͘ϭ͘ʽ̛̛̺̖̭̖̖̦̍̏̔́͘ Флотация (floatation — всплывание) — метод разделения материалов, основанный на различии физико-химических свойств поверхности материалов, их способности смачиваться жидкостью. Одни материалы в тонкоизмельченном состоянии в водной среде под действием флотационных реагентов не смачиваются водой, прилипают к пузырькам воздуха, всплывая на поверхность суспензии, и отделяются от других материалов, поверхность которых смачивается водой, и которые не прилипают к пузырькам. Все материалы обладают большей или меньшей флотационной способностью. Хорошо флотируются такие материалы, как графит, сера, уголь, сульфидные материалы — молибденит MoS2, галенит PbS, пирит FeS2, халькопирит CuFeS2 и др. В тех же условиях плохо или совсем не флотируются окисленные ма— 386 — ÐǣƻǈǀǬÐǯǫǬƽǬǃǀǎ териалы, например, церуссит РbСО3, малахит CuCО3-Cu(OH)2, хризоколла CuSiО3–2H2О, смитсонит ZnCО3, кварц и др. Флотируемость различных материалы зависит от способности поверхности материалы смачиваться водой. Эту способность можно изменять искусственно, применяя флотационные реагенты. В принципе все материалы могут быть сфлотированы, если их поверхность будет для этого подготовлена. Если поверхность материалы смачивается водой, то к ней не сможет прилипнуть пузырек воздуха, и материал не будет флотироваться. Если же поверхность минерала не смачивается водой, то к ней легко прилипает пузырек воздуха и комплекс материал — пузырек легко всплывает на поверхность суспензии. Путем подбора флотационных реагентов можно создать такие условия, при которых одни материалы будут флотироваться, а другие нет, т. е. создать условия для селективного разделения этих материалы. Например, если в полиметаллическом материале содержатся одновременно галенит PbS, халькопирит CuFeS2, сфалерит ZnS и пирит FeS2, обладающие одинаковой природной флотируемостью, то во флотационной суспензии применением различных флотационных реагентов создаются такие условия, при которых эти материалы выделяются в самостоятельные продукты. Флотация в настоящее время является основным и наиболее совершенным методом разделением различных материалов. Она применяется для разделения более 90% добываемых руд цветных металлов, большого количества руд редких, черных, благородных металлов и неметаллических материалов. Широкое применение флотационного процесса объясняется большими преимуществами его перед другими методами: возможность перерабатывать бедные руды с низким содержанием металлов, например, меди ниже 1%, олова и вольфрама до 0,1%, молибдена до 0,01% и т. п.; возможность комплексно перерабатывать сложные, например, полиметаллические руды, содержащие свинцовые, цинковые, медные и другие материалы; возможность эффективно перерабатывать тонковкрапленные руды, содержащие зерна ценных компонентов — 387 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð размерами до 0,1 и даже до 0,01 мм, тогда как гравитационное разделение на столах и отсадочных машинах эффективно лишь для смесей с крупной вкрапленностью ценных продуктов (более 0,5 мм) и лишь при значительной разнице плотностей материалов. Процесс флотации возник вначале в виде масляной флотации, основанной на избирательном смачивании сульфидных материалов маслом. Измельченный материал смешивали с минеральным маслом и водой. Сульфидные материалы при этом смачивались маслом и вместе с ним всплывали на поверхность суупензии, откуда и удалялись. При пленочной флотации материал, измельченный до 0,2–0,3 мм, подается равномерным слоем на поверхность воды. Одни материалы, хорошо смачиваемые водой, тонут, а плохо смачиваемые остаются на поверхности воды. Эти процессы флотации вскоре были вытеснены пенной флотацией. Следующим наиболее важным этапом в развитии флотации была возможность селективного разделения материалов путем применения реагентов, регулирующих этот процесс. Одновременно с развитием промышленной практики развивались и теоретические исследования флотации, которые отражены в работах А. Н. Фрумкина, П. А. Ребиндера, создавших теоретические основы физико-химии поверхностных явлений. В работах И. Н. Плаксина и других отечественных ученых, а также в работах зарубежных ученых Годена, Уорка и Таггарта разработаны теоретические основы флотационного процесса и решены задачи практического применения селективной флотации цветных и редких металлов, что явилось важнейшим шагом в развитии ресурсосберегающей технологии. ϭϬ͘Ϯ͘˃̸̶̴̶̨̡̨̨̨̨̛̛̛̛̖̬̖̯̖̭̖̭̦̼̪̬̖̭̭̣̯̏̌̌͘ Для осуществления процесса флотации в суспензию, представляющую собой смесь тонкоизмельченного материала с водой, загружают флотационные реагенты, изменяющие степень смачиваемости поверхности материалов. Под действием флотационных реагентов поверхность одних частиц смачива— 388 — ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǪÐǄǁǮǰǪǅǀǀ ется водой (гидрофильная), а поверхность удаляемых материалов — не смачивается водой (гидрофобная). Так, реагенты-собиратели закрепляются на поверхности материалов, которые становятся гидрофобными и могут прилипнуть к пузырьку воздуха. Для наилучшего контакта реагентов-собирателей с частицами материалов суспензия перемешивается определенное время, после чего в нее загружают реагенты-пенообразователи для лучшего диспергирования воздуха и создания прочных воздушных пузырьков, способных поднять на поверхность пульпы частицы материалов. Рис. 10.1. Схема взаимодействия воздушного пузырька с частицей. Гидрофобные частицы, прилипшие к пузырькам, выносятся на поверхность суспензии, где образуют слой пены, которая снимается в виде пенного продукта. На рис. 10.1. схематически показана минерализация пузырьков воздуха и образование минерализованной пены в аппарате при флотации. ϭϬ͘Ϯ͘ϭ͘ʿ̶̸̨̛̛̬̖̭̭̼̭̥̦̌̏̌́͘ Физико-химические явления, происходящие при флотации, очень сложны. Во флотационном процессе участвуют три фазы — твердая (частица материала), жидкая (вода) и га— 389 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð Рис. 10.2. Схема действий молекулярных сил. зообразная (воздух), поэтому поверхностные явления, происходящие при флотации, необходимо рассматривать на границе раздела фаз: жидкой — газообразной (Ж-Г), твердой — жидкой (Т-Ж) и твердой — газообразной (Т-Г). Всякая поверхность раздела двух фаз резко отличается по физико-химическим свойствам от объема граничных фаз. Это различие заключается в том, что на поверхности раздела фаз имеется избыток свободной энергии. На рис. 10.2. схематически показаны силы, действующие на молекулы, расположенные внутри жидкой фазы и на границе жидкой и газообразной фаз. На молекулу А, находящуюся внутри жидкости, действуют силы взаимного притяжения со стороны всех окружающих соседних молекул. В результате этого силы притяжения молекул взаимно уравновешены, сами молекулы находятся в равновесии и для их перемещения внутри жидкости не нужно затрачивать работу. Силы молекулярного сцепления действуют лишь на близких расстояниях, поэтому молекулы испытывают притяжение со стороны ближних молекул. Для молекулы Б, расположенной на поверхности жидкости, не все силы молекулярного сцепления уравновешены. Это объясняется тем, что молекулы воздуха в газообразной фазе удалены на значительные расстояния друг от друга и силы их взаимного притяжения ничтожны. Поэтому молекулы, находящиеся на поверхности, испытывают притяжение только со стороны молекул жидкости. Эти силы не уравновешены и направлены внутрь жидкой фазы, т. е. они стремятся втянуть молекулы внутрь — 390 — ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǪÐǄǁǮǰǪǅǀǀ жидкости. Чтобы создать новую поверхность раздела, необходимо затратить работу против молекулярного сцепления. Работа, затрачиваемая на образование 1 м2 поверхности раздела фаз, или эквивалентная ей свободная энергия, приходящаяся на 1 м2 поверхности, называется поверхностным натяжением. Оно обозначается буквой σ (сигма) и измеряется в дж/м2 или н/м. Поверхностное натяжение является очень важной характеристикой поверхности раздела фаз. Поверхностное натяжение воды при 20°С равно 7,275 × 10–2 н/м. Его можно изменить, растворяя в воде различные вещества. Вещества, растворимые в воде и уменьшающие поверхностное натяжение, называются поверхностно-активными (ПАВ). Обычно это органические соединения, в молекулы которых одновременно входят полярная группа (ОН, СООН, NH2) и аполярная группа (углеводородная цепь). Растворимые вещества, например неорганические соли, повышающие поверхностное натяжение, называются поверхностно-инактивными. В зависимости от химической активности и строения различают полярные, аполярные и гетерополярные вещества. Полярными веществами называют химические соединения, хорошо растворимые в воде и обладающие значительной поверхностной энергией. Молекулы полярных веществ диссоциируют на ионы. К ним относятся органические кислоты и соли, некоторые минералы др. Аполярные вещества, наоборот, химически мало активны, плохо растворяются в воде и не смачиваются ею, обладают незначительной поверхностной энергией и не распадаются в воде на ионы. К ним относятся минеральные масла, жиры и другие органические соединения. Вещества, в состав молекул которых одновременно входят полярная группа и аполярная углеводородная цепь, называются гетерополярными (рис. 10.3.). Если такое соединение растворить в воде, то его молекулы будут стремиться выйти на поверхность раздела фаз, где концентрация их больше, чем в объеме раствора. Гетерополярные молекулы ориентируются на границе раздела жидкость — газ так, что полярные группы направлены в воду, а аполярные углеводородные цепи — в воздух. Это объясняется тем, что — 391 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð Рис. 10.3. Строение гетерополярной молекулы. аполярная группа почти не имеет сродства с водой и выталкивается в воздух. Молекулы ПАВ за счет полярной группы, наоборот, имеют сродство к более полярной фазе — воде. Таким образом, в результате концентрации гетерополярных молекул на границе раздела жидкость — газ происходит снижение поверхностного натяжения. Такая самопроизвольная концентрация вещества на границе раздела двух фаз называется адсорбцией. Адсорбция сопровождается уменьшением свободной энергии (поверхностного натяжения). Адсорбцию Г (моль/см2) на поверхности раздела фаз можно вычислить, измерив поверхностное натяжение раствора концентрацией С (моль/л). Уравнение, связывающее адсорбцию с изменением поверхностного натяжения, было предложено Гиббсом dσ C (10.1) < dC RT где R — газовая постоянная, дж/(моль·градус); Т — абсолютная температура, К. Изменение поверхностного натяжения характеризуется производной dσ/dC в зависимости от концентрации вещества. Γ=− — 392 — ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǪÐǄǁǮǰǪǅǀǀ Как видно из уравнения Гиббса, адсорбция положительна, когда производная dσ/dC отрицательна. В этом случае растворимое вещество будет понижать поверхностное натяжение и концентрация его в поверхностном слое будет больше, чем в объеме раствора. При отрицательной адсорбции, когда производная dσ/dC положительна, концентрация растворенного вещества в поверхностном слое меньше, чем в объеме раствора, и поверхностное натяжение повышается. Зависимость между поверхностным натяжением и концентрацией раствора ПАВ выражается графиком (рис.9.4), который можно построить по экспериментальным данным. Используя такой график и уравнение Гиббса, можно путем расчета определить адсорбцию для ряда концентраций. Рис. 10.4.Зависимость поверхностного натяжения σ от концентрации С поверхностно-активного вещества. Зависимость адсорбции от концентрации выражается также уравнением Лангмюра bC (10.2) Γ = Γ∞ 1 + bC где Г∞ — предельное значение адсорбции, т. е. полное заполнение поверхности молекулами ПАВ, когда толщина слоя равна одной молекуле; b — константа, постоянная для данного вещества, равная той концентрации, при которой Г = 0,5 – Г∞, и увеличивающаяся при переходе к высшему гомологу в данном го— 393 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð мологическом ряду в 3–3,5 раза. На рис. 10.5. показан график зависимости адсорбции Г от концентрации С. Очень удобно для математического описания адсорбции уравнения Фрейдлиха в логарифмической форме 1 (10.3) lgÃ = lgk + lgC n где k и n — постоянные величины при Т = const. Как видно, зависимость адсорбции от концентрации имеет линейный характер, и это позволяет графически определять значение постоянных k и n. Однако уравнение Гиббса не применяется при высоких равновесных концентрациях. В этом случае применяют уравнение Лангмюра. Рис. 10.5.Зависимость величины адсорбции Г от концентрации С. Рассмотрим явление смачивания поверхности твердого тела водой. Вода является одной из взаимодействующих фаз и средой, в которой происходит разделение материалов при пенной флотации. Поэтому взаимодействие минералов с водой можно рассматривать как смачивание поверхности материалов, что в свою очередь связано с явлением гидратации. Молекула воды характеризуется несимметричным расположением атомов и поэтому в молекуле имеется два полюса — положительный и отрицательный. В целом же молекула нейтральна. Такая молекула называется полярной. За меру полярности принят дипольный момент μ, который равен произведению заряда е на расстояние между полюсами е, т. е. μ = el. Дипольный момент воды равен 1,85Д (Дебая), D = 1–1018 эл-ст. ед-см. — 394 — ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǪÐǄǁǮǰǪǅǀǀ Наличие дипольного момента у молекулы равнозначно наличию электрического поля, поэтому, если в непосредственной близости от полярной молекулы находится другая молекула, то она испытывает действие электрического поля. Так как вода обладает высоким дипольным моментом, то многие вещества под действием диполей воды диссоциируют на ионы, растворяются и гидратируются. Вокруг ионов в воде мгновенно образуется уплотненный слой диполей воды, т. е. ион гидратируется. Образование такой гидратной оболочки означает, что энергия связи между гидратированным ионом и диполями больше, чем между диполями воды. Образование гидратной оболочки вокруг молекул определяется их полярностью. Полярные молекулы гидратируются сильнее, аполярные слабее. А гетерополярные молекулы гидратируются в зависимости от своей структуры различно. В молекуле будет гидратироваться наиболее сильно полярная группа, в то время как аполярная группа гидратируется намного слабее. Явление гидратации, таким образом, тесно связано с явлением смачивания. Явление смачивания твердых минеральных поверхностей является одним из основных физико-химических явлений, определяющих поведение минералов при флотации. Рассмотрим процесс смачивания минеральной поверхности водой. Если на поверхность минерала (твердая фаза Т) в воздушной среде (газообразная фаза Г) поместить каплю воды (жидкая фаза Ж), то через некоторое время система придет в равновесие, и капля воды примет определенную форму (рис. 9.6.). Тогда на границе раздела трех фаз поверхностное натяжение будет соответственно равно на границе Ж-Т — σжт, на границе Ж-Г — σжг, на границе Г-Т — σгт. Возможность смачивания минеральной поверхности можно определить по работе адгезии. Так как под адгезией понимается взаимодействие жидкой и твердой фаз на границе раздела этих фаз, то работа адгезии есть работа, затрачиваемая на отрыв этих разнородных фаз. Когезия жидкости — это взаимодействие между молекулами в объеме жидкой фазы, а работа когезии равна работе, которую необходимо приложить, чтобы — 395 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð преодолеть взаимодействие между молекулами жидкости. Эта работа равна удвоенному значению поверхностного натяжения вновь образовавшихся при отрыве жидких фаз, т. е. (10.4) Wêîã = 2σ æã Работа адгезии связана с изменением поверхностного натяжения на границе раздела фаз Wàäã = σãò + σãæ − σ æò (10.5) В этом уравнении экспериментально можно определить лишь σгж. Поэтому Wàäã определяют косвенным путем. Составим уравнение равновесия поверхностных сил на границе раздела трех фаз (10.6) σãò − σòæ − σãæ cosθ = 0 где θ — краевой угол смачивания. Из этого уравнения определяем σãò − σòæ = σãæ cosθ (10.7) Тогда равновесное значение краевого угла смачивания можно определить из уравнения σ − σòæ cosθ = ãò (10.8) σ ãæ Подставляя это равенство в уравнение работы адгезии, получим Waäã = σãæ (1 + cosθ ) (10.9) Краевой угол измеряется всегда в жидкую фазу. Величина cosθ находится в пределах ±1. При полном смачивании поверхности материала (гидрофильная поверхность) θ=0, тогда cos θ = 1 , а работа адгезии Waдг =72,8 (1 + 1)·10–1 = = 145,6·10–1 дж/м2. На абсолютно несмачиваемых поверхностях (гидрофобная поверхность) θ = 180°, cosθ = í1, тогда работа адгезии Wадг = 0 Как видно, с гидрофобной поверхности воздух легко вытесняет воду и прилипает к этой поверхности. Абсолютно гидрофобных тел в природе нет. Даже на парафине краевой угол равен 104–107°. Примером гидрофобного материала может служить кварц. При прилипании частицы материала к пузырьку воздуха обязательно образуется краевой угол и чем он будет больше, тем — 396 — ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǪÐǄǁǮǰǪǅǀǀ Рис.10.6.Схема действия поверхностных сил при смачивании твердой поверхности водой. Рис. 10.7. Явление гистерезиса. прочнее прилипание. Величину краевого угла, а тем самым косинус его можно изменять, обрабатывая поверхность флотационными реагентами, и по его величине судить о способности материалов смачиваться водой, т. е. о флотируемости. Краевой угол, таким образом, является мерой смачиваемости поверхности. Практика флотации показывает, что частицы материала могут флотироваться не только тогда, когда краевой угол больше 90°, но и тогда, когда значение его меньше 90°. Многие материалы флотируются при θ = 10–15°. Замеряя величину краевого угла, можно качественно определять флотируемость минералов. Флотационную активность материалов методом измерения краевых углов определяют на минеральных шлифах. Практически во флотационной пульпе краевой угол замерить невозможно. — 397 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð Следует отметить, что рассмотренные зависимости будут справедливы лишь для статических условий, в то время как процесс прилипания частиц к пузырькам воздуха происходит в суспензии при непрерывном и интенсивном перемешивании. Поэтому необходимо процесс прилипания оценивать и кинетически. Прилипание, а следовательно, и флотируемость материалов зависит от большого количества факторов, к которым можно отнести физико-химические свойства поверхности флотируемых материалов и их крупность, характер и концентрацию флотационных реагентов, степень перемешивания суспензии, количество и крупность пузырьков воздуха в суспензии, вероятность столкновения частиц с пузырьками. Смачивание поверхности материала осложняется гистерезисом смачивания. Если на горизонтальную поверхность материала в воде поместить пузырек воздуха, то образуется определенный равновесный краевой угол (рис. 10.7). При наклоне пластинки периметр прикрепления пузырька или периметр смачивания остается неизменным, а величина краевого угла изменится. Причем угол θ2, называемый оттекающим, будет больше равновесного, а натекающий угол θ1 — меньше равновесного. Таким образом, изменение периметра смачивания отстает от изменения краевого угла. Это отставание в изменении периметра смачивания называется гистерезисом смачивания. Гистерезис объясняется неровностями (шероховатостью) твердой поверхности, силами трения, образованием на поверхности материалов адсорбционного слоя ориентированных молекул, аполярные концы которых могут препятствовать растеканию воды на твердой поверхности. На шероховатой, неровной поверхности минерала гистерезис смачивания всегда выше, поэтому прилипание пузырьков воздуха к такой поверхности и флотируемость частиц улучшаются. В процессе флотации пузырек воздуха обволакивается материалом благодаря прилипанию к нему большого количества частиц. Прилипание и флотация частиц происходят после столкновения их с пузырьком воздуха и разрыва водной прослойки между ними. — 398 — ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǪÐǄǁǮǰǪǅǀǀ Столкновение пузырьков с частицами чаще всего происходит при движении пузырьков снизу вверх, когда частица под действием силы тяжести падает, или при движении частицы вверх, когда поднимающийся пузырек движется с большой скоростью и сталкивается с ней. После столкновения минеральная частица огибает пузырек, толщина водной прослойки между ними постепенно уменьшается. Если поверхность материала плохо смачивается, то прослойка воды неустойчива и, достигнув малой величины (толщина в несколько молекул), разрывается самостоятельно, но не до конца. Оставшаяся тонкая устойчивая пленка не препятствует прилипанию твердой частицы к пузырьку. Работами Б. В. Дерягина и А. Н. Фрумкина показано, что, если поверхность частицы достаточно гидрофобна, то водная прослойка, достигшая минимальной толщины, при которой она становится термодинамически неустойчивой, разрывается мгновенно, скачкообразно. Этот момент и соответствует акту прилипания частиц к пузырьку, т. е. образованию краевого угла смачивания (образованию трехфазного периметра смачивания). Причем на участке прилипания частицы к пузырьку в пределах площади прилипания остается тонкая пленка воды, являющаяся новой двухмерной фазой, принципиально отличной по своим свойствам от объемной жидкости. Толщина °. водной прослойки в этом случае равна 400 A Если же поверхность частиц будет достаточно гидрофильной, то водная прослойка между частицей и пузырьком будет толстой, она останется термодинамически устойчивой, краевой угол будет небольшим и прилипания не произойдет — пузырек оттолкнется от частицы. Для осуществления флотации частиц, прилипших к пузырьку, последний должен поднять их на поверхность пульпы. Пузырек при всплывании испытывает воздействие различных механических сил (столкновение с другими частицами, пузырьками, струями суспензии, а также с движущимися частями машин и механизмов), которые могут оторвать частицы от пузырька. Чтобы частица не оторвалась, должна быть некоторая прочность прилипания ее к пузырьку, т.е. должны быть силы, — 399 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð способные удержать частицу на поверхности пузырька. Прочность прилипания частицы к пузырьку зависит от площади прилипания, радиуса пузырька и величины краевого угла смачивания, а также от массы частицы в воде. Чем больше масса частицы в воде, тем меньше должна быть смачиваемость материала, а, следовательно, тем больше должен быть краевой угол смачивания, необходимый для прилипания частицы к пузырьку. Учитывая динамические силы, действующие на частицы при их движении в суспензии, и центробежные силы инерции, развиваемые в момент огибания частицей пузырька, можно рассчитать, что сила отрыва частицы увеличивается в среднем в 4–5 раз по сравнению с силой тяжести частицы, а краевой угол возрастает при этом в 1,2–3 раза. Работами В. И. Классена установлено, что образование начальной площади прилипания на поверхности частиц материала облегчается, когда мельчайшие пузырьки воздуха (микропузырьки) образуются непосредственно на поверхности материала. Затем крупный пузырек сливается (коалесцирует) с этими мелкими пузырьками и использует имеющуюся под ним площадь прилипания. Предполагается, что образование на поверхности гидрофобных частиц микропузырьков воздуха способствует удалению гидратной пленки с поверхности материалов. Прилипание частиц к пузырьку должно рассматриваться не в равновесных, а в кинетических условиях, и с этой точки зрения важна не только прочность, но и скорость прилипания. Исследованиями М. А. Эйгелеса показано, что при минерализации пузырька продолжительность прилипания частиц к пузырьку находится в пределах 0,0001–0,015 с. Процесс флотации в целом оценивают скоростью флотации. Эта величина измеряется в минутах и характеризуется продолжительностью процесса для достижения определенного извлечения флотируемого материала при заданном качестве смеси. Для определения скорости флотации в настоящее время предложено большое количество формул. Наиболее простой из них является определение средней скорости флотации vср. по уравнению — 400 — ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǪÐǄǁǮǰǪǅǀǀ ε (10.10) t где ε — извлечение в материале, %, за время t, мин. Однако по этому уравнению нельзя определить скорость флотации в определенный промежуток времени. Скорость флотации в данный момент времени равна производной dε/dt и определяется константой скорости, численно равной тангенсу угла наклона кривой зависимости извлечения от времени. Для определения скорости флотации К. Ф. Белоглазовым предложено уравнение 1 (10.11) lg = kt 1− ε где k — константа скорости флотации. Это уравнение справедливо при флотации узких классов крупности материала из суспензии при постоянной концентрации флотационного реагента. vср = Рис. 10.8. Кривые скорости флотации. В более общем виде это уравнение имеет вид dε n (10.12) = −k (1 − ε ) dt где k и n — параметры, зависящие от свойств флотируемого материала и условий флотации. Если на основании результатов флотационных опытов построить кривую изменения скорости флотации в координатах 1 lg − t , то по форме кривой можно характеризовать скорость 1− ε — 401 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð флотации. Постоянная скорость флотации имеет прямолинейную зависимость (рис.10.8, кривая 1). При снижении скорости флотации к концу процесса кривая принимает выпуклую форму (рис. 10.8, кривая 2), а при повышении скорости к концу процесса кривая имеет вогнутую форму (рис. 10.8, кривая 3). Практически необходимое время флотации определяется требованиями к качеству получаемых продуктов флотации и извлечению флотируеимго материала, а также флотируемостыо извлекаемых материала. В основных операциях флотации время обычно составляет от 5 до 40 мин. ϭϬ͘ϯ͘ˇ̶̵̴̶̨̨̡̡̛̛̛̛̛̛̣̯̦̦̼̖̬̖̖̦̯̼̣̭̭̌̌̐̌̌́͘ Для управления флотационным процессом применяются флотационные реагенты, обеспечивающие избирательную флотацию различных материалов, т. е. отделение материалов, а также способствующие образованию прочных пузырьков воздуха и всплыванию флотируемых материалов. Применяемые в настоящее время флотационные реагенты отличаются большим разнообразием. Они представлены неорганическими и органическими соединениями различного состава — щелочами, кислотами, солями, продуктами нефтехимии, продуктами переработки древесины, угля, кокса и т. п. В зависимости от назначения флотационные реагенты делятся на три большие группы: собиратели, регуляторы (модификаторы), пенообразователи. Реагенты — собиратели (коллекторы), как правило, органические соединения, имеющие гетерополярную структуру, которые, закрепляясь на поверхности материалов, уменьшают смачиваемость их водой, т. е. гидрофобизируют и тем самым обеспечивают прилипание частиц материалов к пузырькам воздуха. Реагенты-собиратели должны быть селективными, т. е. избирательно закрепляться на тех материалах, которые необходимо в данном процессе извлечь в пенный продукт. Реагенты-регуляторы, или модификаторы, — неорганические и органические соединения, способные изменять флотируемость материалов, регулировать действие собирателей — 402 — ÐǨǁǮǰǪǅǀǮǃǃǊǬÐ͠ǬǪƼǬǃǰǊÐǀÐǀǲÐǭǁǪǯǯǀǄǀǭǪǅǀǎ на частицы материалов, т. е. улучшать флотируемость одних материалов и ухудшать флотируемость других. Действие реагентов-регуляторов при флотации весьма сложно и разнообразно. Одни регуляторы могут воздействовать на поверхность материалов, изменяя ее химический состав, ослабляя или усиливая взаимодействие собирателя с поверхностью материалов; другие могут вытеснять собиратель с поверхности материалов и закрепляться на ней, предотвращая их флотацию; третьи могут взаимодействовать с собирателем, переводя его в осадок, в результате чего действие собирателя ослабляется или прекращается. Регуляторы могут изменять свойства среды, в которой происходит взаимодействие реагентов с материалами, и, таким образом, влиять на флотацию. В зависимости от роли, которую выполняют регуляторы при флотации, их принято подразделять на активаторы, подавители (депрессоры) и регуляторы среды. Активаторы, закрепляясь на поверхности, способствуют адсорбции собирателя и гидрофобизации, улучшая флотируемость материалов. Подавители (депрессоры), наоборот, предотвращают адсорбцию собирателей, гидрофилизируют поверхность, ухудшая флотируемость материалов. Регуляторы среды создают условия в флотационной суспензии, благоприятные для одних и неблагоприятные для флотации других материалов. Они изменяют рН суспензии, химический состав применяемых реагентов-собирателей, растворимых солей в жидкой фазе пульпы, изменяют физические и химические свойства поверхности материалов. Подобная классификация флотационных реагентов является условной, так как один и тот же реагент может выполнять одновременно несколько функций, или в конкретных случаях играть различную роль. Так, некоторые собиратели обладают пенообразующими свойствами (аэрофлот и олеиновая кислота). Сернистый: натрий является активатором окисленных цветных металлов и подавителем сульфидных материалов и т. д. — 403 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð Пенообразователи (вспениватели) — поверхностно-активные вещества, добавляемые во флотационную пульпу для образования устойчивой пены. ϭϬ͘ϰ͘ʺ̵̨̛̛̛̖̦̥̖̜̭̯̭̬̯̖̣̖̜̌̔̏́̍̌̚͘ Реагенты-собиратели закрепляются на поверхности материалов путем адсорбции. Различают физическую и химическую адсорбцию или хемосорбцию. Основное различие между этими типами адсорбции заключается в характере сил, связывающих адсорбированное соединение с поверхностью материала. Если эти силы являются электростатическими, имеет место физическая адсорбция. Если же адсорбированные молекулы или ионы связаны с материалов силами обменного типа, т. е. химическими связями, то такая адсорбция называется химической. Энергия связи адсорбированной молекулы с поверхностью материала при хемосорбции значительно больше, чем при физической адсорбции. Так, при хемосорбции энергия связи достигает 1 эВ, тогда как при физической адсорбции эта величина составляет всего лишь 0,01–0,1 эВ (1 эВ = 23,053 ккал/моль). Кроме того, при физической адсорбции адсорбированную молекулу и материал можно рассматривать как две независимые системы. При хемосорбции твердая среда и прочно связанная с ней адсорбированная молекула представляют собой единую систему. Адсорбция в этом случае завершается образованием нового химического поверхностного соединения адсорбированных ионов с ионами кристаллической решетки материалов. Форма взаимодействия собирателя с материалом определяется состоянием реагента в суспензии. Если реагент диссоциирует на ионы и на поверхности материала закрепляется анион или катион, то адсорбция будет ионной, т. е. будет химическая связь. Неионо-генные собиратели адсорбируются, как правило, в молекулярной форме. Молекулярная адсорбция является физической. Изучение взаимодействия реагентов с поверхностью материалов с учетом адсорбционных явлений и химии флотацион— 404 — ÐǡǬǲǪǃǀƿǂÐƽǬ֬ǯǰǫǀǎÐǯǮƻǀ͠ǪǰǬǁǬ֬ ных реагентов имеет большое значение для развития процесса флотации. Применение новых реагентов, изучение их взаимодействия с различными материалами способствует повышению эффективности разделения материалов при флотации, повышению их извлечения и улучшению качества флотационных продуктов. В результате многочисленных исследований, проведенных российскими и зарубежными учеными, предложены различные гипотезы действия флотационных реагентов и, в частности, собирателей. Рассмотрим современные представления о механизме действия наиболее распространенного собирателя — ксантогената при флотации сульфидных материалов. Взаимодействие ксантогената с поверхностью сульфидных материалов происходит за счет химической адсорбции аниона ксантогената с образованием прочной химической связи с катионом кристаллической решетки материала, т. е. с образованием ксантогената металла. Сульфидные материалы являются соединениями с полупроводниковыми свойствами. Свежеобработанная поверхность этих материалов обладает электронной проводимостью n-типа. Поэтому, например, свежеприготовленный галенит является гидрофобным и хорошо флотируется одним вспенивателем. Так как поверхность неокисленного сульфидного материала, на которой не адсорбировался кислород, имеет свободные электроны, то на ней не может адсорбироваться отрицательно заряженный анион ксантогената. Сульфидные материалы очень быстро окисляются кислородом и на их поверхности образуются окисленные соединения, состав которых зависит от условий окисления. Например, на поверхности галенита при окислении образуется пленка окислов PbSO4, PbS2O3, PbСO3 или НРbO2. При окислении адсорбированный кислород связывает свободные электроны на поверхности материала, и поверхность приобретает дырочный тип проводимости (р-тип). В этих условиях анион ксантогената вытесняет с поверхности материала ионы SО42–, S2О32– и СO32– и адсорбируется на поверхности галенита — 405 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð с образованием более прочной химической связи с катионом материала, например: PbS + 2ROCS2− = ( ROCS2 )2 Pb + S2− При длительном действии кислорода на поверхность сульфидного материала образуется толстая окисленная пленка, которая ухудшает адсорбцию ксантогената, так как вызывает повышенные расходы собирателя при взаимодействии с этой пленкой. Однако процесс образования гидрофобной пленки на поверхности сульфидных материалов не ограничивается адсорбцией ксантогенат-иона. Как показали многочисленные исследования российских и зарубежных ученых, необходимым условием является присутствие на поверхности физически сорбированного продукта окисления ксантогената — диксантогенида. Закрепление ксантогената и диксантогенида на поверхности сульфидных материалов сопровождается одновременно протекающим процессом химической и физической сорбции. Таким образом, необходимым условием гидрофобизации, а следовательно, и флотации сульфидных материалов является одновременное присутствие на их поверхности ксантогенатов металлов и диксантогенида. Соотношение между этими двумя формами определяется концентрацией водородных ионов (рН) и концентрацией собирателя. Рассмотрим пример взаимодействия поверхности окисленных материалов с жирнокислотным собирателем — олеиновой кислотой. Анион олеиновой кислоты С17Н33—С—O– гидрофобизирует поверхность материала, закрепляясь на ней полярной группой СОOí. Углеводородный радикал С17Н33, являясь аполярной группой, ориентируется в водную фазу, обеспечивая гидрофобность поверхности. Анион олеиновой кислоты может химически взаимодействовать с катионом материала, образуя на его поверхности соответствующее труднорастворимое мыло. Например, на поверхности кальцита может образоваться олеат кальция по реакции — 406 — ÐǡǬǲǪǃǀƿǂÐƽǬ֬ǯǰǫǀǎÐǯǮƻǀ͠ǪǰǬǁǬ֬ CaCO3 + 2C17 H33COOH = (C17 H33COO )2 Ca + H2CO3 , который обеспечивает гидрофобизацию и флотацию материала. Закрепление оксигидрильных собирателей на поверхности несульфидных минералов зависит от состояния поверхности, структуры реагентов и от условий, в которых эти реагенты применяются. Состояние жирнокислотных собирателей, например олеиновой кислоты и олеата натрия, в суспензии определяется концентрацией водородных ионов. В зависимости от рН среды они могут находиться в виде молекул или в виде диссоциированных ионов и могут закрепляться на поверхности материалов в ионной форме (химическая адсорбция) или в молекулярной форме (физическая адсорбция). Обычно адсорбированный гидрофобный слой на поверхности минерала представлен этими двумя формами: химически сорбированным олеатом металла и физически сорбированным олеатом натрия или молекулами олеиновой кислоты. Закрепление аполярных реагентов на поверхности материалов происходит в виде физической адсорбции за счет сил Ван-дер-Ваальса. Капельки эмульсии аполярного собирателя при этом закрепляются на материале и если этих капелек будет много, то они, сливаясь друг с другом, могут образовать на поверхности материала сплошную гидрофобную пленку. Образование такой пленки зависит от степени гидратации самой поверхности материала, которую можно изменять, применяя поверхностно-активные вещества. Эти вещества снижают гидратированность поверхности материала и создают благоприятные условия для адсорбции аполярного собирателя. Механизм действия катионных собирателей изучен еще недостаточно. Взаимодействие их с поверхностью различных материалов определяется условиями, в которых они применяются, т. е. состоянием амина в водном растворе. Например, при рН до 10 лауриламин в растворе находится преимущественно в ионной форме и закрепляется в этих условиях на поверхности кварца химически с образованием комплексного соединения. При рН более 11 лауриламин присутствует в растворе в виде молекул, которые сорбируются на поверхности кварца — 407 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð за счет физической адсорбции. Возможно также закрепление амина на поверхности материалов путем связывания иона или молекулы амина с водородом гидроксила у силикатов или водорода амина с серой у сульфидов. Характерной особенностью катионных собирателей является непрочность закрепления их на материалах. Считается, что флотируемость различных материалов катионными собирателями зависит лишь от плотности адсорбированного слоя амина и не зависит от характера этого слоя, образованного ионами или молекулами. ϭϬ͘ϱ͘ˀ̖̖̦̯̼̌̐Ͷ̨̖̪̬̖̭̭̬̼̔͘ Реагенты-регуляторы применяются для изменения флотируемости материалов путем регулирования действия собирателей на их поверхность. Реагенты-регуляторы делят на депрессоры (подавители), активаторы и реагенты среды. Реагенты, предотвращающие адсорбцию собирателей и повышающие гидрофильность поверхности материалов, называются депрессорами. Депрессоры, активаторы и регуляторы позволяют из смеси различных компонентов, содержащих несколько материалов, выделить их в отдельные фазы. Так, например, при флотации смесей, содержащих галенит PbS, сфалерит ZnS и пирит FeS2, вначале флотируют галенит, а флотируемость сфалерита и пирита подавляют реагентами-депрессорами: известью, цианистой солью и цинковым купоросом. После свинцовой флотации восстанавливают флотационную способность сфалерита активатором — медным купоросом, а пирит депрессируется большим количеством извести. Затем восстанавливают флотационную способность пирита, например, серной кислотой и флотируют его в пиритный продукт. Почти все применяемые в настоящее время реагенты-депрессоры представлены неорганическими соединениями — кислотами, щелочами и их солями. Механизм депрессирующего действия этих соединений на поверхность может быть различным. Во-первых, депрессор может образовывать на поверхности подавляемого материала труднорастворимое химическое соеди— 408 — ÐǥǬǪƼǬǃǰǊÐèÐƽǬ͟͠ǬǯǯǮ͠Ǌ нение, в результате чего поверхность покрывается гидрофильной пленкой, которая предотвращает адсорбцию собирателя. Во-вторых, депрессия материала может произойти, если с его поверхности будут вытеснены ионы собирателя, адсорбированные ранее. В третьих, депрессоры могут связывать ионы реагента-активатора как в объеме суспензии, так и на поверхности материала, предотвращая ее активацию. В четвертых, депрессор может образовывать труднорастворимое соединение с собирателем в суспензии, которое уже не будет обладать собирательными свойствами. Депрессоры должны действовать избирательно, т. е. ухудшать флотационные свойства только тех материалов, которые в данном технологическом процессе не должны флотироваться. При взаимодействии депрессоров с материалами необходимо учитывать продолжительность их контакта и температуру суспензии, влияющих на скорость реакций в суспензии и на поверхности материалов. Если продолжительность контакта с собирателями и вспенивателями не превышает 1–5 мин, то для депрессоров она составляет более 5–10 мин. Из депрессоров, широко применяющихся при флотации смесей цветных и редких металлов, необходимо отметить цианистые соли, цинковый купорос, сернистый натрий, хромовые соли, сульфит и тиосульфат натрия, известь, жидкое стекло, щелочи, органические депрессоры и др. Цианиды — соли синильной кислоты являются депрессорами пирита, сфалерита, медных соединений, соединений серебра, ртути, кадмия и никеля. Они применяются при селективной флотации медно-цинковых, свинцово-цинковых, медно-свинцово-цинковых и медно-молибденовых продуктов. Цианиды представлены цианистым натрием или цианистым калием. Цианиды хорошо растворяются в воде. Они гидролизуются в водных растворах с выделением цианистого водорода, являющегося сильнейшим ядом NaCN + H2O → NaOH + HCN — 409 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð Поэтому применяются цианиды исключительно в щелочных средах, в которых они не подвергаются гидролизу. Использование цианидов имеет целый ряд недостатков: сильная токсичность, что требует особой осторожности при работе с ними, высокая стоимость, растворение золота, присутствующего в продуктах флотации. Однако многочисленные попытки заменить цианид другими нетоксичными депрессорами не дают такого эффекта, который достигается при использовании цианидов. В основе депрессирующего действия цианидов лежит их способность образовывать труднорастворимые комплексы с металлами. И. А. Каовский установил, что механизм депрессирующего действия цианидов при флотации сульфидов тяжелых металлов состоит в разрушении образующегося на поверхности смесей химического соединения — ксантогената металла или в предварительном образовании на поверхности смесей комплексного цианистого иона, предотвращающего адсорбцию ксантогената. На основании экспериментальных данных И. А. Каовский разделил минералы тяжелых металлов на три группы в зависимости от подавляющего действия на них цианидов. В первую группу входят материалы, металлы которых Рb, Вi, Sn, Аs и Ru не образуют с цианидом труднорастворимых цианистых комплексов, а ксантогенаты этих металлов не реагируют с цианидами, т. е. не растворяются в цианистых растворах. Во вторую группу входят материалы, содержащие ртуть, кадмий и медь, которые образуют с цианидом сложные комплексные соединения при избытке циан-ионов Нg(СN)42–, Сd(СN))42–, Сu(СN)2–. Цианиды на материалы этой группы оказывают определенное депрессирующее действие, но при повышенном расходе. Ксантогенаты этих металлов слабо растворяются в цианистых растворах. В третью группу входят материалы, содержащие цинк, платину, никель, золото, железо, которые очень чувствительны к депрессирующему действию цианидов. Ксантогенаты этих металлов хорошо растворяются в цианистых растворах, например — 410 — ÐǥǬǪƼǬǃǰǊÐèÐƽǬ͟͠ǬǯǯǮ͠Ǌ ( ROCS2 )2 Fe + 6CN − = Fe (CN )36− + 2ROCS2− Используя такую классификацию, можно определить возможность селективного разделения различных смесей цианидами. Разделение материалов, входящих в одну группу, практически невозможно. Наиболее легко и при небольших расходах цианидов разделяются материалоыпервой и третьей групп. Смеси элементов первой и второй групп разделяются только при больших расходах цианидов, а отделение элементов второй группы от материалов третьей группы очень сложная задача, которая может быть решена в каждом конкретном случае применением сочетания цианида с другими депрессорами, например с цинковым купоросом. Цинковый купорос (сульфат цинка) ZnSO4.7H2O применяется для депрессии цинковой обманки самостоятельно или в сочетании с цианидом. Цинковый купорос содержит не менее 21,8% Zn, не более 0,5% FeO, 0,5% H2SO4 и 0,05% Сu. Цинковый купорос в нейтральной и щелочной средах образует осадок Zn(OH)2, а в присутствии соды осадок ZnCO3, который, налипая на поверхность сфалерита, депрессирует его. Цинковый купорос в сочетании с цианидом широко применяется при депрессии цинковой обманки при разделении медно-цинковых и свинцово-цинковых смесей. Механизм депрессирующего действия цианида с цинковым купоросом объясняется так. В суспензии образуется цианид цинка Zn(CN)2, а также комплексные соединения Zn(CN)3ņ или Zn(CN))42–. В щелочной среде цианид цинка диссоциирует с выделением циан-иона Zn ( CN )2 ↔ 2CN − + Zn2+ Это позволяет поддерживать концентрацию циан-ионов постоянной, при которой ионы СN- адсорбируются на поверхности сфалерита, предотвращая адсорбцию ксантогената. Кроме того, цианид взаимодействует с катионами меди, являющимися активаторами, и, связывая их в комплексные соединения, снижает концентрацию ионов меди в пульпе и на поверхности — 411 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð сфалерита до такого уровня, при котором активация становится невозможной. Таким образом, происходит дезактивация поверхности сфалерита по реакции − 2CcS + 6CN − = 2 Cu ( CN )2  + 2CN + 2S2− Сернистый натрий Nа2S получают в промышленности восстановлением сульфата натрия углем при нагревании до 1200°С. Полученный сплав выщелачивают. Затем продукт выщелачивания, содержащий 28–32% Na2S, отделяют от шлама и выпаривают при 140–180°С. Полученный плавленый сернистый натрий содержит 63–68% Nа2S. Сернистый натрий широко применяется при флотации сульфидных и несульфидных минералов как активатор, сульфидизатор, подавитель, десорбент собирателей и регулятор рН суспензии. В воде сернистый натрий как соль сильного основания и слабой кислоты подвергается гидролизу и создает сильно щелочную среду Na2S + 2H2O → 2NaOH + H2S H2S → H + + HS − HS − → H + + S2− В зависимости от рН среды в суспензии могут присутствовать Н2S, НS– и S2–, которые оказывают сильное действие на флотируемые материалы. Сернистый натрий является хорошим сульфидизатором окисленных смесей тяжелых цветных металлов (карбонатов и сульфатов свинца и меди). При сульфидизации церуссита сернистым натрием образуется пленка сульфида свинца, вследствие чего материал хорошо флотируется ксантогенатами. Сульфидизация поверхности церуссита происходит по реакции PbCO3 + Na2S = Na2CO3 + PbS При избытке сернистый натрий может стать депрессором, так как в суспензии появляются свободные сернистые S2– и гидросернистые НS– ионы, которые предотвращают взаимодействие иона ксантогената с сульфидизированной поверхностью материала. — 412 — ÐǥǬǪƼǬǃǰǊÐèÐƽǬ͟͠ǬǯǯǮ͠Ǌ При флотации, например, церуссита дозировка сернистого натрия ограничивается оптимальным значением рН, не превышающим 9,5; для хризоколлы СuSiO3 × 2Н2O рН не более 8. В более щелочной среде пленка образующегося сульфида свинца РbS начинает отслаиваться с образованием коллоидного сернистого свинца. При рН выше 11 поверхность материалов покрывается слоем гидроокиси, препятствующей сульфидизации материалов и закреплению собирателя. Сернистый натрий является также сильным депрессором. Сущность депрессии заключается в предотвращении адсорбции собирателя на материалах, а также в десорбции уже закрепившегося собирателя. Способность ионов НS– и S2– вытеснять с поверхности сульфидов анионы ксантогената используется при селективной флотации коллективных сульфидных продуктов с применением сернистого натрия как десорбента собирателя. Повышенные концентрации сернистого натрия применяются также для депрессии сульфидов меди и железа при флотации молибденита, который не депрессируется сернистым натрием. При селективной флотации свинцово-цинковых, медно-цинковых и медно-свинцово-цинковых смесей в качестве депрессоров применяются соединения окислов серы, которые называются сульфоксидными. К ним относятся: сернистый газ, сернистая кислота Н2SO3, сульфиты Nа2SO3 и тиосульфаты Nа2S2О3 щелочных и щелочноземельных металлов. Сернистая кислота и ее соли применяются совместно с железным купоросом для депрессии свинцовых материалов при разделении медно-свинцовых смесей. Сульфит натрия, гипосульфит натрия совместно с сернистым натрием или цинковым купоросом являются депрессорами цинковой обманки. Действие сульфита и тиосульфата натрия как восстановителей состоит в поглощении кислорода из суспензии, что предотвращает окисление сульфидной поверхности и затрудняет адсорбцию собирателя. Кроме того, сульфоксидные соединения могут образовывать с ионами железа, меди, свинца и ионами благородных металлов довольно прочные комплексы и подобно цианиду растворять ксантогенаты металлов, но слабее. — 413 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð Жидкое стекло (растворимое стекло, силикат натрия, силикат-глыба) Nа2SiO3 представляет собой прозрачные бесцветные или светло-зеленые и светло-желтые куски, хорошо растворимые в воде. Химический состав жидкого стекла непостоянен. Общая формула его R2О×mSiO2, где R2О соответствует Na2О, а m — модуль, т. е. число молекул SiO2, приходящихся на одну молекулу R2О, равное 2–4,5. Получают жидкое стекло сплавлением кварца с содой или сульфатом натрия и углем при 1300–1500°С. Жидкое стекло, как правило, содержит 68–73% SiO2 и 26–31% Na2О. Для флотации обычно применяют 5%ные растворы жидкого стекла с модулем 2,2–3. При модуле выше 3 оно трудно растворяется в воде, образует коллоидные растворы и крупные гели кремниевой кислоты. Жидкое стекло с модулем менее 2,2 создает сильнощелочную среду, в которой снижается его депрессирующее действие. Жидкое стекло диссоциирует в водных растворах по реакциям: Na2SiO3 + 2H2O ↔ H2SiO3 + 2Na + + 2OH − H2SiO3 ↔ H + + HSiO3− HSiO3− ↔ H + + SiO32− Состав продуктов диссоциации зависит от рН раствора. Так, при рН < 8 в растворе присутствует в основном недиссоциированная кремниевая кислота Н2SiO3, при рН 9 — ионы НSiO3– и недиссоциированная Н2SiO3, при рН 10–12 — в основном ионы НSiO3–, а при рН 13 преобладают ионы SiO32–. Эти продукты диссоциации жидкого стекла, а также его коллоидная форма могут взаимодействовать с поверхностью материалов, предотвращать адсорбцию собирателя или десорбировать его. При флотации жирнокислотными собирателями жидкое стекло применяется как депрессор кварца и других силикатных материалов, а также кальцита, апатита, флюорита. Кремнефтористый натрий Na2SiF6 применяется в качестве регулятора среды и селективного депрессора при разделении смесей рутила и циркона, пирохлора и циркона и др. Депрессия материалов может быть следствием создания кислой среды, в которой затрудняется адсорбция жирных кислот; — 414 — ÐǥǬǪƼǬǃǰǊÐèÐƽǬ͟͠ǬǯǯǮ͠Ǌ следствием образования коллоидных частиц геля кремниевой кислоты H2SiO3, ионов SiF62- и мицелл, содержащих эти ионы и адсорбирующихся на поверхности материала, подвергающегося флотации. Конденсированные фосфаты натрия — пирофосфат Na4Р2O7, триполифосфат Na5Р3O10, гексаметафосфат Na6Р6O18 являются эффективными подавителями-пептизаторами шламистых частиц материалов, таких, как кварц, кальцит, апатит. Кроме того, они связывают катионы поливалентных металлов в суспензии. Их расход составляет 5–50 г/т. Положительные результаты получаются при флотации цементной меди, сульфидных медных, медно-молибденовых и молибденовых смесей. Иногда они успешно заменяют жидкое стекло, трудно растворяются в воде. Депрессирующее действие органических регуляторов связано с образованием в суспензии коллоидных частиц (мицелл), которые, закрепляясь на поверхности материалов, гидратируют ее. Для более селективного действия эти реагенты применяют в небольших количествах. Наиболее распространенными реагентами этого типа являются крахмал, декстрин, танин и карбоксиметилцеллюлоза. Крахмал применяется для депрессии ряда сульфидных и окисленных смесей. При разделении медно-молибденовых смесей его применяют для депрессии молибденита, а также для депрессии графита при флотации сульфидов ксантогенатами. Крахмал (С6Н10О5)x. является высокомолекулярным органическим веществом, плохо растворимым в воде. Применяется он обычно при рН 8–8,5 в виде 2–5%-ного раствора, который приготовляют следующим образом. Кашеобразную массу крахмала замешивают в холодной воде с едким натром (4 части крахмала на 1 часть NaОН), затем разбавляют в 95 долях объема воды затем нагревают до кипения с последующим охлаждением. Декстрин аналогичен крахмалу, но имеет более сложное строение. Он хорошо растворяется в воде, применяется в качестве депрессора окислов железа при флотации кварца, слюды и полевых шпатов катионным собирателем. Является — 415 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð хорошим депрессором серицита, талька, вторичных силикатов и барита. Танин (дубильная кислота) — органическое вещество, получаемое из различных растений. Его химический состав непостоянен и зависит от свойств растений, из которых он получается. Применяется при флотации несульфидных минералов для депрессии окислов железа, гипса, кальцита и доломита. Карбоксиметилцеллюлоза (КМЦ) — водорастворимая натриевая соль карбоксиметилового эфира целлюлозы. Применяется для депрессии материалов пустой породы, например силикатов в перечистных операциях медно-никелевых смесей при рН = 8–10. В ряде случаев может заменять жидкое стекло. Применяется в виде 1–2%-го раствора. ϭϬ͘ϲ͘ˀ̖̖̦̯̼̌̐Ͳ̡̨̛̯̯̬̼̌̏̌͘ Реагенты-активаторы применяются во флотационном процессе для активации поверхности материалов, в результате которой становится возможным закрепление на ней собирателя и селективная флотация материала. Активаторы применяются тогда, когда материал депрессирован, или когда природная флотируемость самого материала недостаточна. Активация может состоять в химической очистке поверхности материалов от пленок, которые мешают адсорбции собирателя. Например, при окислении пирита на его поверхности образуется пленка окислов железа, которая предотвращает адсорбцию собирателя. Промывка пирита кислотой, а затем водой позволяет снять эту пленку, и пирит восстанавливает свои флотационные свойства. Активация происходит также в результате ионного обмена, например активация цинковой обманки катионами меди. Катион цинка с поверхности сфалерита ZnS вытесняется ионами меди, добавляемой в виде медного купороса, и на сфалерите образуется более флотоактивная пленка сульфида меди, хорошо взаимодействующая с ксантогенатами. Такая обменная реакция имеет вид ZnS + Cu2+ ↔ CuS + Zn2+ — 416 — ÐǥǬǪƼǬǃǰǊ ǪǭǰǀǫǪǰǮ͠Ǌ Активация некоторых окисленных материалов тяжелых металлов сернистым натрием является также обменной химической реакцией, при которой с поверхности окисленных материалов ионы SO42– или СО2– вытесняются ионами S2–. По3 этому такой процесс активации называется сульфидизацией. Сульфидизация происходит при участии ионов S2– и НS–, образующихся в результате гидролиза и диссоциации сернистого натрия Na2S. При растворении в воде сернистый натрий подвергается гидролизу Na2S + H2O ↔ NaSH + NaOH А затем поверхность окисленного материала, например церуссита, взаимодействует с продуктами гидролиза PbCO3 + 3NaOH = H2O + NaHPbO2 NaSH + NaHPbO2 = 2NaOH + PbS или суммарно PbCO3 + Na2S = PbS + Na2CO3 Сернистый свинец образуется на поверхности церуссита в виде пленки, которая и взаимодействует с ксантогенатом как сульфидный материал. По такому же механизму сульфидизируются и окисленные материал меди — малахит, азурит, куприт. Активаторы представляют собой неорганические кислоты и соли. Среди них необходимо отметить серную кислоту и соли поливалентных металлов (меди, свинца, железа), плавиковую кислоту, сернистый натрий и соду. Серная кислота — типичный активатор для пирита, депрессированного большими расходами извести. Под действием серной кислоты разрушается пленка гидроокиси железа на поверхности пирита, и он восстанавливает свою флотируемость. Серная кислота применяется также при флотации слюды, рутила, ильменита, пирохлора, циркона, ильменорутила и др. Медный купорос CuSO4.5H2O — один из наиболее распространенных активаторов. Получают медный купорос действием серной кислоты на металлическую медь. Медный купорос — 417 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð активирует флотацию депрессированной цинковой обманки, т. е. восстанавливает ее способность флотировать в присутствии ксантогената. Медный купорос содержит не менее 85% CuSO4.5H2O и подается в процессе в виде 5–10%-ного водного раствора. Расход его обычно составляет 200–500 г/т. Обычно во флотационной суспензии находится большое количество различных солей вследствие содержания их в промышленных водах, а также частичного растворения в суспензии различных солей и гидроокисей. Промышленные воды, применяемые при флотации, содержат от 50 до 500 мг/л растворимых солей кальция, магния и др. Эти так называемые «неизбежные» ионы влияют на поверхностные свойства любого материала, изменяя их флотируемость. Очень часто эти ионы являются причиной нарушения селективности процесса флотации, так как, закрепляясь на поверхности ценных материалов и материалов пустой породы, уравнивают их флотационные свойства. Соли железа являются активаторами не только ценных материалов, но и материалов пустой породы, например кварца, турмалина и др. Кроме того, катионы железа связывают в объеме суспензии собиратель и образуют при флотации с олеиновой кислотой олеаты железа, которые не обладают собирательными свойствами и вызывают повышенный расход собирателя. Поэтому при флотации редких металлов очень часто стремятся удалить «неизбежные» ионы предварительной отмывкой руды или введением реагентов, способных предотвратить закрепление их на первичном материале. Для нейтрализации действия катионов поливалентных металлов применяют неорганические кислоты и щелочи. Плавиковую кислоту HF применяют при активации полевых шпатов и берилла, а также для депрессии кварца, слюды, гематита. Техническая плавиковая кислота содержит от 30 до 70% HF и 0,1–6% Na2SiFi6. Она очень токсична. Уксуснокислый свинец Рb(С2Н3O2)2 применяется для активации антимонита Sb2S3. — 418 — ÐǥǬǪƼǬǃǰǊÐèÐ͠ǬƼǱǁǎǰǮ͠ǊÐǯ͠ǬƽǊ Сода Na2CО3.10H20, взаимодействуя с катионами поливалентных металлов в суспензии, обеспечивает их осаждение. Например, катионы кальция и железа образуют труднорастворимые карбонаты и гидраты кальция и железа, которые предотвращают адсорбцию катионов на обрабатываемых материалах и улучшают процесс флотации. ϭϬ͘ϳ͘ˀ̖̖̦̯̼̌̐Ͷ̨̬̖̱̣̯̬̼̭̬̖̼̐́̔͘ Регуляторы среды применяются для изменения щелочности среды, в которой происходит флотация различных материалов. Кислотные и щелочные свойства среды характеризуются величиной рН или концентрацией ионов водорода или ионов гидроксила. Для получения оптимальных технологических показателей необходимо строго поддерживать заданное значение концентрации ионов водорода. Флотация любого материала происходит только при определенном значении рН. Сущность влияния водородных ионов на процесс флотации состоит в следующем. В суспензии обычно содержатся ионы тяжелых металлов, влияющие на процесс флотации. Эти ионы могут быть выведены из пульпы в виде гидратов окисей, так как образуют с ионами ОН- труднорастворимые осадки, например Fe3+ + 3OH − ↔ Fe ( OH )3 Ионы водорода влияют на устойчивость гидратных слоев и, следовательно, могут изменять степень гидратации поверхности материала, т. е. его флотируемость. Изменяя значение рН, можно регулировать процесс диссоциации реагентов, т. е. изменять их свойства и растворимость. Это относится не только к большинству собирателей (ксантогенаты, дитиофосфаты, олеиновая кислота, амины), но и к регуляторам. Так, депрессирующее действие цианида зависит от концентрации [Н+], так как концентрация ионов СN– в растворе определяется рН. Чем выше значение рН, тем больше ионов СN–. Следовательно, — 419 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð критическая концентрация цианида, при которой происходит депрессия, например, медных материалов, будет понижаться при повышении значения рН. От значения величины рН зависит и состояние сернистого натрия в суспензии, который диссоциирует и в зависимости от рН в растворе будет преобладать одна из трех форм Н2S, НS– или S2–. При флотации сульфидных материалов с сульфгидрильными собирателями имеется критическое значение рН, выше которого при определенной концентрации собирателя материал флотироваться уже не будет. Например, критическое значение рН для пирротина в присутствии этилового ксантогената (25 мл/л) составляет 6, для пирита 10,5, а для активированного сфалерита 13,3. Таким образом, регулируя величину рН, можно поддерживать необходимую концентрацию различных форм собирателей и регуляторов, тем самым регулируя селективность процесса флотации. При изменении величины рН изменяются свойства и растворимость не только флотационных реагентов, но и самих материалов. В качестве регуляторов щелочности суспензии применяются щелочи и кислоты (известь СаО, КОН и серная кислота), а также соединения, изменяющие концентрацию водородных ионов вследствие гидролиза (кальцинированная сода и сернистый натрий). Известь СаО наиболее дешевый и распространенный реагент. Ее применяют для создания щелочной среды и при флотации сульфидов для депрессии пирита. Во флотации обычно применяют негашеную известь СаО, которую обрабатывают водой СаО + Н2O = Са(ОН)2 и применяют в виде суспензии, называемой известковым молоком. Насыщенный раствор Са(ОН)2 имеет высокую щелочность и создает рН = 12 и выше. Серная кислота Н2SO4 применяется при флотации рутила, ильменита, пирохлора, циркона и других материалов. Кальцинированная сода К2СО3 хорошо растворяется в воде. В результате гидролиза ее растворы приобретают щелочной характер, но рН не превышает 11. Поэтому соду применяют для создания рН суспензии от 7 до 10. — 420 — ÐǥǬǪƼǬǃǰǊ ͟ǬǃǮǮƻ͠ǪƿǮǫǪǰǬǁǀ Многие депрессоры и активаторы одновременно являются и регуляторами среды. К ним в первую очередь относятся сернистый натрии, цианистый натрий, жидкое стекло, кремнефтористый натрий, железный купорос и др. Изменение щелочности суспензии может происходить и за счет состава флотируемой смеси. Окисленные смеси обычно создают кислую среду, а при наличии в смеси карбонатов щелочноземельных металлов, например СаСO3, суспензия будет иметь щелочную реакцию. ϭϬ͘ϴ͘ˀ̖̖̦̯̼̌̐Ͳ̨̨̨̛̪̖̦̬̯̖̣̍̌̏̌̚͘ Реагенты-пенообразователи (вспениватели), адсорбируясь на границе раздела газ — жидкость, повышают устойчивость воздушных пузырьков, сохраняя их в дисперсном состоянии. Это улучшает прилипание частиц флотируемых материалов к пузырькам воздуха и увеличивает устойчивость флотационной пены. От свойств и устойчивости пены зависит извлечение ценного компонента. Пенообразователь должен обеспечить большое количество мелких пузырьков, способных поднять частицы полезных материалов на поверхность пульпы. В то же время он должен создать такую пену, которая по выходе из флотационной машины быстро разрушалась бы и освобождала частицы от пузырьков воздуха. Пенообразователи не должны обладать собирательными свойствами, так как это затруднит регулирование селекции флотационного процесса. Пена представляет собой концентрированную эмульсию газа в жидкости, содержание которой в пене составляет 2–13%. Пена имеет ячеистую структуру и состоит из деформированных пузырьков, между которыми находится тонкая прослойка воды с поверхностно-активным веществом. Если в чистую воду, имеющую поверхностное натяжение 7,28 н/м2, вдувать воздух, то пузырьки воздуха, поднимаясь, сразу же лопаются, и пена не образуется. Если же в воду добавить ПАВ, то оно, адсорбируясь на границе вода — воздух, — 421 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð уменьшит поверхностное натяжение, и сопротивление пузырька разрыву увеличится. Если к двухфазной пене добавить тонко измельченный материал (третью фазу), то устойчивость такой трехфазной пены увеличится. Рис. 10.9. Схема адсорбции пенообразователя на границе раздела вода-воздух: 1 — полярная группа; 2 — аполярная группа Хрупкая пена быстро разрушается в флотационной машине, снижая извлечение. А слишком устойчивая плохо транспортируется насосами и, попадая в сгуститель, образует устойчивый слой пены, вследствие чего увеличиваются потери извлекаемого материала со сливом. С чрезвычайно устойчивой пеной приходится бороться механическим или химическим путем. Устанавливают в желобах флотационных машин брызгала, которые гасят пену, применяют ультразвук или углеводороды типа керосина, которые вытесняют ПАВ с межфазной границы и снижают пенообразование. Пенообразователи — это гетерополярные поверхностно-активные вещества, способные адсорбироваться на границе воздух — вода, таким образом, что аполярная группа направлена в воздух, а полярная — в воду (рис. 9.9.). Такая адсорбция препятствует коалесценции, т. е. слипанию воздушных пузырьков, и позволяет сохранять их длительное время в дисперсном состоянии. Пенообразующими свойствами обладает большое число гетеро-полярных веществ с самыми различными по составу полярными группами. Наиболее эффективными являются со— 422 — ÐǥǬǪƼǬǃǰǊ ͟ǬǃǮǮƻ͠ǪƿǮǫǪǰǬǁǀ единения, имеющие в своем составе одну из полярных групп: —ОН (гидроксил), —СООН (карбоксил), =С=О (карбонил), NН2 (аминогруппа) и SO2ОН (сульфогруппа). Пенообразователи должны обладать определенной растворимостью в воде, так как в противном случае они плохо распределяются и неэффективно понижают поверхностное натяжение. В зависимости от состава полярной группы пенообразователи классифицируются на кислые, нейтральные и основные. К кислым вспенивателям относятся спиртовые и крезиловые аэрофлоты, фенолы, алкиларилсульфонаты и др. Нейтральные вспениватели — терпинеол, сосновое масло, спиртовые пенообразователи с длиной углеводородного радикала от 6 до 8 атомов углерода и вспениватели с эфирными связями ОПСБ, ОПСМ, Э-1 и др. К основным вспенивателям относится тяжелый пиридин, который в настоящее время применяется в основном в зарубежных странах. Фенольные вспениватели применялись ранее довольно широко, но вследствие своей сильной токсичности и малой селективности сейчас применяются лишь в зарубежных странах. Из этих вспенивателей отметим лишь крезол или крезиловую кислоту СН3С6Н4ОН, которые получаются в коксохимическом производстве. Он обладает не только пенообразующими, но и собирательными свойствами при флотации таких материалов, как галенит и халькопирит. Алкиларилсульфонаты — поверхностно-активные вещества, представляющие собой соли алкилароматических сульфокислот. Общая формула их RSO3H, где R — алкил (углеводородный радикал). Хорошими пенообразующими свойствами эти реагенты обладают при содержании в молекуле 10–12 атомов углерода. Детергент советский (ДС) — технический продукт, состоящий из алкиларилсульфонатов с небольшими примесями смол и сернокислых солей различных катионов. Его получают при нейтрализации кислого гудрона. Он нетоксичен, хорошо растворяется в воде и дает слабощелочную реакцию. Пенообразующие свойства ДС зависят от рН среды и от применяемого регулятора. Наиболее эффективно его действие в среде Na2CО3. — 423 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð Он обладает очень слабыми собирательными свойствами при больших расходах по отношению к халькопириту, сфалериту, галениту и пирротину, может применяться при флотации полиметаллических смесей. Нейтральные вспениватели представлены соединениями, содержащими терпинеол, алифатические спирты, циклогексанол и соединения с эфирными связями. Терпинеол С10Н17ОН получается из скипидаров. В практике применяют флотационное масло, содержащее от 40 до 90% терпинеола. Сосновое масло — продукт сухой перегонки древесины сосновых пород. В СССР его получают из пневого осмола, т.е. из пней деревьев сосновых пород, которые измельчают и обрабатывают паром. Полученный скипидар — сырец подвергают фракционной возгонке при температуре 170°С с получением в кубовом остатке соснового масла. В таком сосновом масле содержится не менее 50% терпеновых спиртов. Масло должно быть прозрачным, желтого цвета с запахом скипидара. Недостатком его является некоторое непостоянство состава. Расход соснового масла при флотации обычно составляет 25–100 г/т смеси. Спиртовые пенообразователи — это алифатические спирты с общей формулой R—ОН, где R — углеводородный радикал с 6–8 атомами углерода. Среди них необходимо отметить реагент ИМ-68 и циклогексанол. Циклогексанол (циклогексиловый спирт) получают гидрированием фенола в присутствии медно-никелевого катализатора. Он относится к спиртовым пенообразователям, которые имеют постоянный состав, обладают сильными пенообразующими и слабыми собирательными свойствами и высокой селективностью. Применяется циклогексанол при селективной флотации полиметаллических смесей. Расход его в 2 раза меньше расхода крезола. Недостаток — высокая температура кристаллизации (+15–17°С), поэтому в зимнее время растворы его подогревают. Он токсичен, представляет собой прозрачную, бесцветную маслянистую жидкость с запахом камфары и амилового спирта. — 424 — ÐǥǬǪƼǬǃǰǊ ͟ǬǃǮǮƻ͠ǪƿǮǫǪǰǬǁǀ Особую группу составляют пенообразователи, содержащие эфирные связи. К ним относятся ОПСБ, ОПСМ, Э-1, Д-3 и Т-66. ОПСБ (окись пропилена спирт бутиловый) — смесь монобутиловых эфиров полипропиленгликолей. Очень сильный пенообразователь, превосходящий крезол, терпинеол и сосновое масло, наиболее эффективен при флотации крупноизмельченных материалов, а также в присутствии реагентов, гасящих пену, хорошие показатели дает при флотации медных, свинцовых и молибденовых смесей, селективен, нетоксичен. ОПСБ применяется также в тех случаях, когда в качестве собирателя используют углеводородные масла. Расход ОПСБ в 2–4 раза меньше расхода крезола, соснового масла и составляет 10–30 г/т смеси. ОПСМ (окись пропилена спирт метиловый) — светло-коричневая жидкость со слабым запахом эфира, хорошо растворяется в воде, не затвердевает при низких температурах, эффективно заменяет крезол при флотации полиметаллических смесей. Расход его в 1,5í2 раза меньше расхода крезола. Э-1 аналогичен ОПСБ и состоит из смеси монобутиловых эфиров. Для его производства вместо окиси пропилена используют окись этилена. Э-1 хорошо растворяется в воде, может заменять ОПСБ, но уступает ему по флотационным свойствам и требует большого расхода, применяется при флотации цинковых и сурьмяных смесей. Д-3 (диметилфталат) — сложный эфир метилового спирта и ортофталевой кислоты. Хорошо растворяется в органических жидкостях (спиртах, углеводородах), плохо — в воде, может применяться при флотации цветных металлов и некоторых несульфидных материалов. Пенообразователь Т-66 является побочным продуктом производства диметилдиоксана, который получают из изо-бутилена и формалина. В его состав входят различные вещества, преимущественно одноатомные спирты пиранового и диоксанового ряда, а также гликоли. Он является эффективным вспенивателем при флотации полиметаллических смесей, нетоксичен. — 425 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð ϭϬ͘ϵ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏͘ 1. В чем заключается физическая сущность процесса флотации? 2. Какие фундаментальные теоретические законы лежат в основе процесса флотации? 3. Процессы адсорбции и смачивания. 4. С какими явлениями тесно связано явление смачивания поверхности материала? Как влияет явление гидратации на процесс смачивания? 5. Что такое гистерезис смачивания? 6. Как определить скорость флотации? 7. Какие флотационные реагенты Вы знаете и их классификация? 8. Какие реагенты собиратели Вы знаете и каков механизм их действия? 9. Какие реагенты пенообразователи Вы знаете и каков механизм их действия? 10. Зачем нужны реагенты-депрессоры? 11. Зачем нужны реагенты-активаторы? 12. Зачем нужны реагенты регуляторы среды? ϭϬ͘ϭϬ͘ʿ̸̛̛̬̥̖̬̼̬̖̹̖̦́̌̔̌̚͘ Задача 1. Рассчитайте работу адгезии ртути к стеклу при 293 К, если угол смачивания равен 130°. Поверхностное натяжение ртути составляет 475 мДж/м2 . Найдите коэффициент растекания ртути по поверхности стекла. Решение: Работа адгезии рассчитывается по уравнению Дюпре-Юнга: Wà = σ æ −ã (1 + cos θ) = 475(1 + cos130°) = = 475(1 + cos0,64) = 171ìÄæ / ì 2 Коэффициент растекания по Гаркинсу рассчитывают по соотношению: f = Wà − Wë = Wà − 2σ æ −ã = 171 − 2<475 = −779 ìÄæ / ì 2 — 426 — ÐƭǪƽǪǆǀÐƽǁǎÐǯǪǂǮǯǰǮǎǰǬǁǋǃǮƼǮÐ͠ǬǇǬǃǀǎ где Wк — работа когезии смачивающей (растекающейся) жидкости. Отрицательное значение коэффициента растекания означает отсутствие растекания жидкости. Задача 2. Две вертикальные параллельные пластинки частично погружены в жидкость на расстоянии d = 1 мм друг от друга. Угол смачивания θ пластинок жидкостью составляет 30°. Поверхностное натяжение жидкости равно 65 мДж/м2, разность плотностей жидкости и воздуха составляет 1 г/см3. Рассчитайте избыточное давление в жидкости и высоту, на которую поднимется жидкость между пластинами. Решение: Капиллярное (избыточное) давление в жидкости между параллельными пластинками рассчитывается по уравнению Лапласа для цилиндрического вогнутого мениска жидкости: 2σ cos θ 2<65<10−3 <0,87 ∆p = = = −113,1Ïà d 1<10−3 Высота поднятия жидкости рассчитывается по уравнению Жюрена для цилиндрического мениска жидкости: 2σ cos θ 2<65<10−3 <0,87 = = 0,0115 ì = 1,15ñì h= ∆ð gd 1<103 <9,81<1<10−3 ϭϬ͘ϭϭ͘ʯ̸̨̨̨̨̛̛̣̭̥̭̯̯̖̣̦̬̖̹̖̦̌̔̌̔́̌́̽̐́͘ Задача 1. Оцените размер частиц диоксида церия СеО2, зная, что их растворимость в воде на 5 мас. % больше растворимости крупных кристаллов. Межфазное натяжение при 298 К примите равным 730 мДж/м2 , плотность СеО2 7,13 г/см3. Задача 2. Рассчитайте межфазное натяжение в системе СеО2 — вода, зная, что растворимость частиц СеО2 диаметром 0,1 мкм (при 298 К) превышает растворимость крупных кристаллов на 7 мас. %. Плотность СеО2 примите равной 7,13 г/см3. — 427 — ǞǁǪǫǪÐ ÐǨǁǮǰǪǅǀǎ Ð Задача 3. Оцените размер частиц оксида цинка ZnO, зная, что их растворимость на мас. 7% больше растворимости крупных кристаллов. Межфазное натяжение при 298 К примите равным 960 мДж/м2 , плотность 7иО 5,60 г/см3. Задача 4. Рассчитайте межфазное натяжение в системе ZnO — вода, зная, что растворимость частиц ZnO диаметром 0,7 мкм (при 298 К) превышает растворимость крупных кристаллов на 3,26 мас. %. Плотность ZnO примите равной 5,60 г/см3 . — 428 — ǍưǙǚǙÍ Í Í ǘƝǐƝơǎǕǏƝǎÍƝÍƙƝǒƞǒǍƝơǎǕǏƝǎÍ ǐǎǖǒƚƥÍǒơƝǕǖǏƝÍǕǖǒơǑƥǘÍǌǒƚ В результате изучения главы 11 бакалавр должен: Знать: – основные химические и биологические методы очистки сточных вод от растворимых примесей. Уметь: – обоснованно выбирать реагенты для очистки сточных вод химическими методами, а также биологические среды при очистке сточных вод биологическими методами. Владеть: – основами теоретической химии для описания механизмов очистки сточных вод химическими и биологическими методами. К химическим методам очистки сточных вод относят следующие: нейтрализацию, окисление, восстановление, реагентные методы выделения загрязняющих веществ в виде малорастворимых и нерастворимых соединений, ионный обмен. Химическая очистка сточных вод производится перед их подачей систему оборотного водоснабжения, а также перед спуском их в водоем или городскую канализационную сеть. Кроме того, указанный метод применяется для предварительной очистки сточных вод перед биологической или физико-химической очисткой, а также в системах локальной очистки производственных сточных вод. Химическая обработка нахо— 429 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð дит применение и как метод глубокой очистки сточных вод с целью их дезинфекции или обесцвечивания. ϭϭ͘ϭ͘ʻ̶̛̛̖̜̯̬̣̌̌́̚͘ Производственные сточные воды, содержащие кислоты и щелочи, должны быть нейтрализованы перед сбросом их в водоемы или перед дальнейшим использованием в технологических процессах. Практически нейтральными следует считать смеси с pH = 6,5–8,5. Реакция нейтрализации в водных растворах происходит между гидратированными ионами водорода и ионами гидроксила, содержащимися, соответственно, в сильных кислотах и основаниях: H + + OH − → H2 O Чаще всего сточные воды загрязнены следующими минеральными кислотами: серной H2SO4, соляной НСl, азотной HNО3, а также их смесями. Кроме того, сточные воды могут содержать в своем составе такие кислоты, как азотистую HNО2, фосфорную Н3РО4, сернистую H2SO3, сероводородную H2S, плавиковую HF, хромовую Н2СlO4, уксусную СН3СООН, пикриновую НОС6Н2(NО2)3, угольную Н2СО3, салициловую С6Н4(ОН)2 и др. Обычно концентрация кислот в сточных водах не превышает 3%, но встречаются и более концентрированные смеси. Различают следующие способы нейтрализации сточных вод: 1. Взаимная нейтрализация кислых и щелочных сточных вод. 2. Реагентная нейтрализация, при которой используются такие вещества, как растворы кислот, негашеная известь СаО, гашеная известь Са(ОН)2, аммиачная вода NH4OH, кальцинированная (Na2СО3) и каустическая (NaOH) сода. В последнее время для нейтрализации щелочных сточных вод предложено использовать дымовые газы, содержащие в своем составе СО2, SO2, NO2, N2O3 и др. При этом одновременно нейтрализуют сточные воды и происходит достаточно эффективная очистка отходящих газов от вредных компонентов. — 430 — ÐǢǬ֬ǰ͠ǪǁǀƿǪǅǀǎ ϭϭ͘ϭ͘ϭ͘ʻ̶̛̛̛̖̜̯̬̣̭̥̖̹̖̦̖̥̌̌́̚͘ Взаимную нейтрализацию кислых и щелочных сточных вод осуществляют путем их смешения в стехиометрическом соотношении, которое производят в устройстве, называемом нейтрализатор смешения. Нейтрализатор представляет собой емкость, снабженную мешалкой для перемешивания кислых и щелочных стоков. Перемешивание указанных стоков в нейтрализаторе возможно путем барботирования воздуха. Нейтрализованную воду используют в оборотных системах водоснабжения, а полученные осадки обезвоживают ϭϭ͘ϭ͘Ϯ͘ˀ̶̛̛̖̖̦̯̦̦̖̜̯̬̣̌̐̌́̌̌́̚͘ Реагенты для нейтрализации кислых сточных вод выбирают в зависимости от вида кислот и их концентрации. Кроме того, учитывают, образуется ли в процессе реакции нейтрализации осадок. Для нейтрализации минеральных кислот применяют любой щелочной реагент, но чаще всего известь в виде пушонки или известкового молока и карбонаты кальция или магния в виде суспензии. В практике очистки сточных вод доза нейтрализующего реагента обычно принимается на 10% больше стехиометрического соотношения. Указанные данные представлены в табл. 11.1 Таблица 11.1 Расход реагентов, кг/кг, для нейтрализации 100%-ных кислот и щелочей. Щелочь серная Известь: гашеная негашеная Сода: кальцинированная каустическая аммиак Кислота соляная азотная 0,56/1,79 0,77/1,3 0,76/1,32 1,01/0,99 уксусная 0,46/2,2 0,59/1,7 0,47/2,15 0,62/1,62 1,08/0,93 1,45/0,69 0,84/1,19 0,82/1,22 1,1/0,91 0,64/1,57 0,35/2,88 0,47/2,12 0,27/3,71 0,88/1,4 0,67/1,5 – — 431 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð Примечание: над чертой указан расход щелочи, под чертой — расход кислоты. Количество реагентов для нейтрализации сточных вод может быть рассчитано по следующей формуле: 100 (11.1) G=k QaA B где G — количество реагентов, кг; k — коэффициент запаса расхода реагента по сравнению с теоретическим (для известкового молока k=1,1, для известкового теста и сухой извести k= 1,5); B — количество активной части в товарном продукте,%; Q — количество сточных вод, подлежащих нейтрализации, м3 ; а — расход реагента для нейтрализации, кг/кг (данные представлены в табл. 10.1); А — концентрация кислоты или щелочи, кг/м3. Следует указать, что наиболее дешевым реагентом является гидроксид кальция (известковое молоко) с содержанием активной извести Са(ОН)2 5–10%. При нейтрализации сточных вод, содержащих серную кислоту кальциевыми реагентами, образуется гипс CaSO4‫ޣ‬2Н2O, растворимость которого в температурном интервале 0–40°С лежит в пределах 1,76–2,11 г/л. При более высокой концентрации CaSO4‫ޣ‬2Н2O выпадает в осадок, забивая трубопроводы и аппаратуру. Для устранения этого явления рекомендуется промывать трубопроводы чистой водой и увеличивать скорость движения нейтрализованных вод в них. Кроме того, хороший эффект дает введение в сточные воды специальных умягчителей (гексаметафосфат) — (NаРО3)6 а также замена металлических трубопроводов на пластмассовые. ϭϭ͘ϭ͘ϯ͘ʻ̶̵̸̵̡̨̨̛̛̛̖̜̯̬̣̭̣̼̭̯̦̼̪̱̯̖̥̌̌́̏̔̚ ̵̴̸̨̛̛̛̛̛̛̣̯̬̦̖̬̖̦̖̜̯̬̣̱̺̖̥̯̖̬̣̼̽̏̌́̌̀̌̌̚̚͘ Данный процесс ведут в горизонтальных или вертикальных фильтрах — нейтрализаторах. При нейтрализации сточных вод, содержащих серную кислоту, ее концентрация не должна превышать 1,5 г/л, так как при большей концентрации поверхность нейтрализующих материалов покрывается сдоем гипса, и процесс нейтрализации прекращается. — 432 — ÐǣǭǀǯǁǀǰǬǁǋǃǊ֬ÐǂǬǰǮƽÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ При нейтрализации сточной воды, содержащей серную кислоту, на вертикальном фильтре его высоту определяют по следующей формуле: (11.2) H = Kdn (3 + lgb) V где Н — высота слоя загрузочного материала, см; К и п — эмпирические константы; b — концентрация кислоты, г-экв/л; d — диаметр зерен загрузочного материала, мм; V — скорость фильтрования, равная 4–8 м/ч. Величина n = 1,47; величина К зависит от сорта доломита и лежит в пределах 0,62–1,31. У горизонтальных фильтров скорость течения сточных вод составляет 1–3 м/с. ϭϭ͘ϭ͘ϰ͘ʻ̶̸̵̸̵̨̨̨̛̛̖̜̯̬̣̺̖̣̦̼̭̯̦̼̌̌́̏̔̚ ̡̛̛̛̭̣̼̥̥̐̌̌̚͘ В процессе нейтрализации щелочных сточных вод используют отходящие газы, содержащие СО2, SO2, N2O3, NO2 и др. При этом происходит нейтрализация сточных вод и одновременная высокоэффективная очистка газов от вредных компонентов, что характерно для ресурсосберегающей (малоотходной) технологии. Преимуществами этой технологии также является исключение использования кислот для нейтрализации, а также возможность создания бессточной схемы водопотребления. Процесс нейтрализации может быть проведен в реакторах с мешалкой, в распылительных, пленочных и тарельчатых колоннах. Нейтрализация щелочных вод дымовыми газами использована в ряде производств, в т. ч. и в асбоцементом производстве. ϭϭ͘Ϯ͘ʽ̸̸̵̡̨̨̡̨̨̛̛̛̛̭̣̯̖̣̦̼̜̥̖̯̭̯̭̯̦̼̽̔̏̔͘ Этот метод очистки используют для обезвреживания производственных сточных вод от цианидов, сероводорода, сульфидов и других веществ. Сточные воды, включающие перечисленные соединения, встречаются в машиностроительной (цехи гальванических покрытий), горно-добывающей (обогатительные фабрики свинцово-цинковых и медных руд), нефтехими— 433 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð ческой (нефтеперерабатывающие и нефтехимические заводы), целлюлозо-бумажной (цехи варки целлюлозы) и в других отраслях промышленности. Наиболее часто в практике очистки сточных вод используют следующие окислители: хлор, гипохлорит кальция, хлорную известь, диоксид хлора, озон, технический кислород и кислород воздуха. Реже используются пероксид водорода, оксиды марганца, перманганат и бихромат калия. Для очистки производственных сточных вод возможно также использование процесса радиационного окисления, при котором загрязняющие вещества (обычно органического происхождения) разрушаются под действием излучений высоких энергий. ϭϭ͘Ϯ͘ϭ͘ʽ̡̛̛̛̭̣̖̦̖̬̖̖̦̯̥͕̌̐̌ ̵̨̡̨̛̛̛̭̖̬̙̺̥̯̦̼̜̣̬̔̌̌̏͘ Указанный метод используется для обезвреживания циансодержащих стоков различных объемов и концентраций, а также от таких органических и неорганических соединений, как сероводород, гидросульфид, сульфид, метилмеркаптан и т. д. Следует указать, что сточные воды, содержащие цианиды, образуются при нанесении медных, цинковых и кадмиевых покрытий из цианистых электролитов. Кроме того, циансодержащие стоки образуются при термической закалке стальных изделий в расплавах цианистых солей, а на металлургических предприятиях цианиды попадают в сточные воды из доменных газов (при их промывке и охлаждении). Концентрация простых цианидов (KCN, NaCN) в промывных водах обычно не превышает 200 мг/л. В этих водах также содержатся в небольших количествах комплексные цианиды меди, цинка, кадмия, железа и других веществ. При введении хлора в воду образуются хлорноватистая и соляная кислоты по реакции: Cl2 + H2 O = HOCl + HCl Далее НОСl диссоциирует, причем степень ее диссоциации зависит от pH. В сильнокислой среде равновесие этой реакции — 434 — ÐǣǭǀǯǁǀǰǬǁǋǃǊ֬ÐǂǬǰǮƽÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ сдвинуто влево, и в воде присутствует Cl2. При pH > 4 молекулярный хлор в воде практически отсутствует: HOCl ↔ H + + OCl − Сумма Cl2 + HOCl + OCl − называется свободным «активным» хлором. Очистка сточных вод от цианидов основана на их окислении в менее токсичные (приблизительно в 1000 раз) цианат-ионы с их поcледующим гидролизом в нейтральной среде до NH4+ и СО32– по следующим реакциям: при pH ≥ 9 − 10 CN − + 2OH − + Cl2 → CNO − + H2 O + 2Cl − при pH ≈ 7 CNO − + 2H2 O → NH4+ + CO32 − Образующиеся цианаты можно окислить до элементарного азота и диоксида углерода: 2CNO − + 4OH − + 3Cl2 → 2CO2 ↑ +6Cl − + N2 ↑ +2H2 O При снижении pH возможно протекание реакции прямого хлорирования цианида с образованием токсичного хлорциана: CN − + Cl2 → CNCl + Cl − В кислой среде ( pH ≤ 6,5 ) эта реакция протекает с достаточно высокой скоростью и может быть описана следующим уравнением: 2CNO − + 3ClO − + 2H + → 2CO2 ↑ +3Cl − + N2 ↑ + H2 O При использовании в качестве окислителей гипохлоритов реакцию проводят при pH =10–11 CN − + OCl − → CNO − + Cl − Активный хлор окисляет находящиеся в сточных водах соединения аммония, аммиак и органические вещества, содержащие аминогруппы до моно- и дихлораминов, а также до треххлористого азота по следующим реакциям: NH3 + HOCl → NH2 Cl + H2 O NH2 Cl + HOCl → NHCl2 + H2 O NHCl2 + HOCl → NCl3 + H2 O — 435 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð Возможна обработка циансодержащих сточных веществ диоксидом хлора СlO2, который обладает высокой окислительной способностью. Следует отметить, что при обработке сточных вод диоксидом хлора не образуется высокотоксичных хлорциана, хлорфенола и других продуктов прямого хлорирования при любых значениях pH среды. Хлорирование применяется и для дезодорации сточных вод целлюлозно-бумажных комбинатов. Указанные сточные воды содержат водород, сульфиды, метилмеркаптан и др. В щелочной среде хлор окисляет сульфиды до сульфатов. Процесс может быть описан следующим уравнением: Na2 S + 4Cl2 + 8NaOH → Na2 SO4 + 8NaCl + 4 H2 O В кислой и нейтральной среде образуются сульфиты: H2 S + 3Cl2 + 3H2 O → H2 SO3 + 6HCl NaHS + 3Cl2 + 3H2 O → NaHSO3 + 6 HCl Хлораторные установки для очистки сточных вод включают складское хозяйство и устройства для дозирования хлора, в качестве которых чаще всего применяются вакуумные хлораторы ЛОНИИ-100, дающие производительность по хлору 0,08–20 кг/ч. ϭϭ͘Ϯ͘Ϯ͘ʽ̡̨̡̨̨̨̨̛̛̛̭̣̖̦̖̪̖̬̭̥̬̔̏̔̔̌͘ Пероксид водорода используют для окисления нитритов, альдегидов, фенолов, серосодержащих отходов, активных красителей, а также цианидов. Основная химическая реакция, протекающая при окислении цианидов H2O2, следующая: CN − + H2 O2 → CNO − + H2 O Например, цианид натрия окисляется пероксидом водорода по схеме: NaCN + 2H2 O2 → NaCNO + H2 O Оптимальное значение pH для этих реакций — 10–11. Комплексные цианиды окисляются пероксидом водорода быстрее и легче простых цианидов. Окисление цианидов каталитически ускоряется в присутствии соединений меди. — 436 — ÐǣǭǀǯǁǀǰǬǁǋǃǊ֬ÐǂǬǰǮƽÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Используя катализаторы (Fe2+, Cu2+, Мп2+, Co2+, Cr2+, Ag+), можно также ускорить процессы окисления вышеперечисленных органических веществ пероксидом водорода. ϭϭ͘Ϯ͘ϯ͘ʽ̵̡̡̨̨̨̨̛̛̛̭̣̖̦̖̭̣̬̥̱̔̏̔̌̚͘ Кислород используется для очистки сточных вод целлюлозных, нефтеперерабатывающих и нефтехимических заводов. Окисление гидросульфидной и сульфидной серы протекает через ряд последовательных стадий: S2 − → S → Sn O6 → S2 O32 − → SO32 − → SO42 − Метилмеркаптан в водных растворах под действием кислорода воздуха также окисляется постадийно: CH3 SH → CH3 SSCH3 → CH3 SO2 H → CH3 SO3 H Окисление кислородом воздуха может быть использовано для очистки от железа как природных, так и производственных сточных вод. При аэрировании происходит окисление двухвалентного железа в трехвалентное по следующей суммарной реакции: 4Fe2+ + O2 + 10H2 O → 4Fe ( OH )3 ↓ +8H + Вместо кислорода воздуха для перевода Fe2+ в Fe3+ можно использовать и другие окислители, например, хлор и перманганат калия. ϭϭ͘Ϯ͘ϰ͘ʽ̨̨̛̛̦̬̦̖̏̌̚͘ Процессы озонирования применяют для очистки сточных вод от фенолов, нефтепродуктов, сероводорода, соединений мышьяка, ПАВ, цианидов, красителей, ароматических углеводородов, пестицидов и др. Одновременно с очисткой обеспечивается обесцвечивание воды, устранение привкусов и запахов и обеззараживание. Озон подают в сточную воду в виде озоно-воздушной или озоно-кислородной смеси, концентрация озона в смеси приблизительно составляет 3%. Рассмотрим типичные реакции, протекающие при очистке сточных вод озо— 437 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð нированием. Окисление сероводорода протекает следующим образом: H2 S + O3 → H2 O + SO2 3H2 S + 4O3 → 3H2 SO4 Аммиак при взаимодействии с озоном в щелочной среде окисляется до азотной кислоты и воды по реакции: NH3 + 4O3 → NO3− + 4O2 + H2 O + H + Цианиды в слабощелочной среде, реагируя с озоном, образуют первоначально менее токсичные цианаты, которые затем гидролизуются в воде или окисляются озоном в соответствии со следующими уравнениями: CN − + O3 → CNO − + O2 ↑ CNO − + 2H + + 2H2 O → CO2 ↑ + H2 O + NH4+ CNO − + 2H2 O → HCO3− + NH3 2CNO − + H2 O + 3O3 → 2HCO3− + 3O2 ↑ + N2 ↑ Озон получают в промышленных озонаторах-генераторах из кислорода воздуха под действием электрического разряда. Электроды озонаторов могут быть трубчатой или пластинчатой формы и обычно изготавливаются из металлизированного стекла. ϭϭ͘Ϯ͘ϱ͘ʽ̡̨̡̛̛̛̭̣̖̦̖̪̖̬̥̦̦̯̥̣̌̐̌̌̌́͘ Перманганат калия может быть использован для очистки сточных вод от катионов двухвалентного железа и марганца. Окисление двухвалентного железа протекает в соответствии со следующим уравнением: 3Fe ( HCO3 )2 + KMnO4 + 2H2 O → → 3Fe ( OH )3 ↓ + MnO2 ↓ +5CO2 ↑ + KHCO3 В случае двухвалентного марганца схема окисления следующая: — 438 — ÐǣǆǀǯǰǭǪÐǫǮǯǯǰǪǃǮǫǁǬǃǀǬǂ 3Mn2+ + 2MnO4− + 2H2 O → 5MnO2 ↓ +4H + При этом ионы железа и марганца выделяются из сточных вод в виде труднорастворимых соединений Fe(OH)3 и МnО2. ϭϭ͘Ϯ͘ϲ͘ˀ̶̨̨̨̡̛̛̛̛̦̦̖̭̣̖̦̖̌̔̌͘ Метод радиационного окисления может быть использован для очистки сточных вод от фенолов, цианидов, красителей, инсектицидов, лигнина, а также ПАВ. Очистка сточных вод осуществляется при воздействии на них излучения высоких энергий, в качестве которых используются: радиоактивный кобальт и цезий, ТВЭЛы, радиационные контуры, ускорители электронов. Загрязняющие воду вещества вступают в реакцию с продуктами радиолиза воды: ОН–, НО2– (в присутствии кислорода), H2O2– перечисленные вещества являются окислителями, а также Н+ и е–гидр (гидратированный электрон). Метод радиационного окисления в ряде случаев может быть использован для нейтрализации сточных вод. ϭϭ͘ϯ͘ʽ̸̡̨̨̛̛̭̯̭̭̯̦̣̖̦̖̥̌̏̌̏͘ При содержании в сточных водах легко восстанавливаемых соединений меди, хрома, мышьяка, ртути применяют методы восстановительной очистки. Катионы меди, содержащиеся в кислых сточных водах, могут быть выделены цементацией на железном скрапе или никелевом песке. При этом протекают следующие реакции восстановления: Cu2+ + Fe → Cu ↓ + Fe2+ Cu2+ + Ni → Cu ↓ + Ni2+ Медь выделяется на железе ИЛИ никеле в виде металла, и вместо нее в раствор переходят катионы железа или никеля. Метод цементации применяют для грубой, предварительной очистки достаточно концентрированных по меди сточных вод. Очищенная цементацией вода затем нейтрализуется до pH = 8–9 — 439 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð при одновременной доочистке ее от оставшихся катионов меди и перешедших в раствор катионов железа или никеля. Высокотоксичные соединения шестивалентного хрома содержатся в промывных сточных водах и отработанных технологических растворах, образовавшихся в процессе хромирования, при химической обработке поверхностей стальных изделий (травление, пассирование), при анодировании изделий из алюминия и при проведении других технологических процессов. Обработка сточных вод осуществляется в две ступени: 1) перевод (восстановление) шестивалентного хрома в трехвалентную форму; 2) осаждение трехвалентного хрома в виде гидроксида. В качестве реагентов-восстановителей наибольшее распространение получили натриевые соли сернистой кислоты — сульфит (Na2SO3), бисульфит (NaHSO3) и гидросульфит (Na2SO5). Кроме того, используют следующие восстановители: сульфит железа (FeSO4), диоксид серы (SO2), гидразин (N2H4) и др. При обработке хромсодержащих сточных вод солями сернистой кислоты, протекают следующие химические реакции: Cr2 O72 − + 3HSO3− + 5H + → 2Cr 3+ + 3SO42 − + 4H2 O Cr2 O72 − + 3SO32 − + 8H + → 2Cr 3+ + 3SO42 − + 4H2 O Скорость и полнота восстановления Сr6+ до Сr3+ указанными солями в значительной степени зависит от величины pH, причем наибольшая скорость наблюдается при pH = 2–2,5, что требует дополнительно подкисления сточных вод. Для этих целей обычно используют 10–15%-ные растворы серной кислоты. Для очистки сточных вод от шестивалентного хрома используют установки непрерывного или периодического действия. После восстановления в кислой среде шестивалентного хрома до трехвалентного состояния сточные воды подвергают нейтрализации, при которой хром осаждается в виде гидроксида. В качестве реагентов-нейтрализаторов используют Са(ОН)2, Nа2СОз, NaOH. Во всех случаях осуществляется следующая химическая реакция: — 440 — ÐǣǆǀǯǰǭǪÐǫǮǯǯǰǪǃǮǫǁǬǃǀǬǂ Cr 3+ + 3OH − → Cr ( OH )3 ↓ Оптимальное значение pH этой реакции — 8,0–9,5. Сr(ОН)3 обладает амфотерными свойствами и при pH ≥ 12 растворяется в избытке едкой щелочи. При этом протекает следующая химическая реакция: Cr ( OH )3 + NaOH → NaCrO2 + 2H2 O При использовании в качестве восстановителя сульфата двухвалентного железа (FeS04) процесс можно проводить в кислой, нейтральной и щелочной среде: 2CrO3 + 6FeSO4 + 6H2 SO4 → 2Fe2 ( SO4 )3 + Cr2 ( SO4 )3 + 6H2 O 2CrO3 + 6FeSO4 + 6Ca2 ( OH )2 + 6H2 O → 2Cr ( OH )3 + 6Fe ( OH )3 + 6CaSO4 Восстановление диоксидом серы происходит по схеме: SO2 + H2 O → H2 SO3 2CrO3 + 3H2 SO3 → Cr2 ( SO4 )3 + 3H2 O В присутствии в сточных водах соды протекает следующая химическая реакция 6Na2 CrO4 + SO2 + Na2 CO3 + nH2 O → Cr2 O3 <nH2 O + 3Na2 CO3 + CO2 ↑ В результате протекания этой реакции происходит практически полное удаление шестивалентного хрома из раствора. Реакция восстановления шестивалентного хрома гидразином протекает в нейтральной или слабощелочной среде: 4K2 Cr 04 + 3N2 H4 → 4Cr ( OH )3 ↓ +3N2 ↑ +8KOH Метод восстановления также применяют для очистки сточных вод от соединений ртути. Их восстанавливают до металлического состояния, а образовавшуюся ртуть отделяют от воды (отстаиванием, фильтрованием или флотацией). В качестве реагента-восстановителя используют алюминиевую пудру, железный порошок, гидросульфид натрия, гидразин, сульфид железа и др. При выделении мышьяка из концентрированных растворов (до 110 г/л) используют диоксид серы, который восстанав— 441 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð ливает мышьяковую кислоту до мышьяковистой. Последняя имеет малую растворимость в кислой и нейтральной среде и осаждается в виде триоксида мышьяка. ϭϭ͘ϰ͘ˀ̵̨̛̛̖̖̦̯̦̼̖̥̖̯̼̼̖̣̖̦̬̦̺̖̺̖̭̯̌̐̔̏̔́̌̐́́̀̏̏̚̚ ̵̵̨̨̨̨̛̛̛̛̛̛̖̥̣̬̭̯̬̥̼̦̖̬̭̯̬̥̼̭̖̦̖̦̜̏̏̔̌̌̏̌̏̔͘ Известно, что вещества условно можно разделить на растворимые, малорастворимые и практически нерастворимые. Растворимость первых составляет примерно 1 г вещества в 100 мл растворителя (воды) и приблизительно 0,1 М по катиону, а последних — менее 0,1 г вещества в 100 мл растворителя или примерно 0,01 М по катиону. Вещества, занимающие промежуточное положение между ними, называют малорастворимыми. (В химической и экологической литературе нередко используют термин «труднорастворимые соединения», включая в него как практически нерастворимые, так и малорастворимые вещества.). Рассмотрим, следуя Л. Полингу, основные классы нерастворимых веществ. К ним в первую очередь относятся все гидроксиды, за исключением гидроксидов щелочных металлов, аммония и бария, причем Са(ОН)2 и Sr(OH)2 — малорастворимы. Все средние карбонаты и сульфаты нерастворимы, за исключением соответствующих соединений щелочных металлов и аммония. Все сульфиды, за исключением сульфидов щелочных и щелочноземельных металлов, нерастворимы. Для очистки производственных сточных вод от соединений тяжелых цветных металлов и в первую очередь от соединений Сu, Ni, Со, Pb, Cd, Hg их осаждают в виде соответствующих гидроксидов, сульфатов либо карбонатов. Растворимость вышеуказанных соединений может быть охарактеризована также произведением растворимости. Для выделения из кислых сточных вод тяжелых цветных металлов и железа используются те же реагенты, что и при нейтрализации. При этом протекают следующие реакции: Me2+ + 2OH − → Me ( OH )2 ↓ — 442 — ÐǥǬǪƼǬǃǰǃǊǬÐǂǬǰǮƽǊÐǫǊƽǬǁǬǃǀǎÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǫǀƽǬÐǂǪǁǮ͠ǪǯǰǫǮ͠ǀǂǊǲ ÐǯǮǬƽǀǃǬǃǀ֬ Me3+ + 3OH − → Me ( OH )3 ↓ Количество реагентов (G, кг), необходимых для нейтрализации кислых сточных вод, содержащих тяжелые цветные металлы, рассчитывают по следующей формуле: 100 G=k Q (aA + b1C1 + b2 C2 + …+ bn Cn ) (11.3) B где k — коэффициент запаса расхода реагента по сравнению с теоретическим (для известкового молока k = 1,1, для известкового теста и сухой извести k = 1,5); В — количество активной части в товарном продукте,%; Q — количество сточных вод, подлежащих нейтрализации, м3; а — расход реагента для нейтрализации, кг/кг; А — концентрация щелочи, кг/м3; С1 С2,..., Сn — концентрации металлов в сточных водах, кг/м3; b1, b2,..., bп — расход реагентов, требуемых для перевода металлов из растворенного состояния в осадок (данные представлены в табл. 11.2), кг/кг. Значения pH, соответствующие началу и окончанию осаждения гидроксидов цветных металлов и железа, представлены в табл. 11.3. В многокомпонентных сточных водах значения pH, соответствующие началу и окончанию осаждения гидроксидов, существенно сдвинуты в сторону больших величин. Следует указать, что ионы тяжелых цветных металлов могут осаждаться не только в виде гидроксидов, но и гидроксид-карбонатов (в случае использования для осаждения реагентов, содержащих в своем составе карбонатные ионы). Гидроксиды цинка, свинца, меди, алюминия и некоторых других металлов растворяются в избытке едкой щелочи с образованием компдексных анионов. Цинк, алюминий и некоторые другие металлы, обладающие амфотерными свойствами, могут содержаться в виде анионов в щелочных сточных водах. Для их удаления используют растворы кислот. При этом образуются осадки гидроксидов этих металлов согласно следующим уравнениям: AlO2− + H + + H2 O → Al ( OH )3 ↓ — 443 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð Таблица 11.2. Расход реагентов, требуемых для удаления металлов. Металл CaO 0,85 0,95 0,88 1 0,27 Цинк Никель Медь Железо свинец Реагент Na2CO3 Ca(OH)2 1,13 1,6 1,26 1,8 1,16 1,66 1,32 1,9 0,36 0,51 NaOH 1,22 1,36 1,26 1,43 0,38 Таблица 11.3. Величины рН осаждения гидроксидов металлов. Вид катиона Fe2+ Fe3+ Zn2+ Cr3+ Ni2+ Al3+ Cd2+ Начало осаждения при исходной концентрации осаждаемого иона 0,01М 7,5 2,3 6,4 4,9 7,7 4,0 8,2 Полное осаждение 9,7 4,1 8,0 6,8 9,5 5,2 9,7 ZnO2− + 2H + → Zn ( OH )2 ↓ Необходимо указать, что эффективнее совместное осаждение ионов двух или нескольких металлов при одной и той же величине pH, чем при осаждении каждого металла в отдельности. Это связано с образованием смешанных кристаллов и адсорбционными процессами на их поверхности. — 444 — ÐǥǬǪƼǬǃǰǃǊǬÐǂǬǰǮƽǊÐǫǊƽǬǁǬǃǀǎÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǫǀƽǬÐǂǪǁǮ͠ǪǯǰǫǮ͠ǀǂǊǲ ÐǯǮǬƽǀǃǬǃǀ֬ При обработке щелочными реагентами сточных вод, содержащих ионы тяжелых цветных металлов, достигается снижение их концентраций до величин, позволяющих осуществлять сброс очищенной воды в городскую канализацию или водоемы санитарно-бытового пользования. В том случае, когда требуется более глубокая степень очистки, тяжелые металлы рекомендуется выделять в виде сульфидов. Обычно в виде сульфидов выделяют Сu, Со, Ni, Fe, Sn, Mo, As, Sb, Hg, Ag, Zn, Cd, Pb. Для двухвалентного катиона металла реакция образования сульфида может быть записана в следующем виде: Me2+ + S2 − → MeS ↓ В качестве осадителя обычно используют Na2S (реже — (NH4)2S). Растворимость сульфидов зависит от pH раствора. В отечественной практике для выделения из сточных вод сурьмы и мышьяка в виде малорастворимых сульфидов в качестве реагента-осадителя используют сульфат железа. Sb3+ в зависимости от величины pH содержится в сточных водах в виде анионов тиосолей (SbS2–), либо в виде кислородсодержащихх анионов, что практически встречается редко. Указанные анионы тио-солей диссоциируют в растворе с образованием сульфид-ионов. При выделении из раствора сульфид-ионов эта реакция практически целиком сдвигается вправо. При этом образуется нерастворимый сульфид сурьмы, и вода оказывается очищенной. Данный метод позволяет очистить сточную воду от сурьмы практически полностью. Рассмотренный метод может быть использован и для очистки сточных вод от мышьяка, если он присутствует в растворах в виде тио-солей. Существуют методы осаждения катионов тяжелых цветных металлов в виде труднорастворимых соединений, в основе которых лежат окислительно-восстановительные реакции. Примером этого является способ выделения из растворов и промышленных сточных вод двухвалентного кобальта с использованием органического реагента — этилксантогената калия KSCSOC2H5. — 445 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð Гидроксиды и сульфиды тяжелых металлов образуют устойчивые коллоидные системы, поэтому для интенсификации процесса их осаждения в сточные воды добавляют коагулянты и флокулянты. В качестве коагулянтов чаще всего используют сульфаты алюминия (Al2(SO4)3‫ޣ‬18Н2O) ИЛИ трехвалентного железа (Fe2(SO4)3‫ޣ‬9H2O). Расширению оптимальных режимов коагуляции (по pH и температуре) способствуют флокулянты. Они также в несколько раз увеличивают скорость выпадения осадков тяжелых металлов. Чаще всего в качестве флокулянта применяют полиакриламид, который обычно вводят в количестве 0,1–10 г/м3 очищаемой воды. К преимуществам реагентного метода следует отнести высокую степень очистки от тяжелых металлов (до ПДК), а также простоту эксплуатации оборудования. Основные недостатки метода — это образование значительного количества трудно перерабатываемого шлама, а такжe существенный расход реагентов и связанная с этим необходимость организации реагентного хозяйства, что естественно удорожает их стоимость. Кроме того, очищенная этим методом вода содержит значительное количество солей и может быть использована в оборотных системах водоснабжения лишь после дополнительной очистки. ϭϭ͘ϱ͘ʰ̨̨̦̦Ͳ̸̸̵̨̨̡̨̨̛̥̖̦̦̭̯̭̯̦̼̍̌́̌̏̔͘ При очистке сточных вод ионообменом используются специальные вещества иониты, способные обмениваться с раствором ионами растворенных примесей. Этим методом можно производить глубокую очистку от вредных примесей или извлекать с большой эффективностью ценные элементы. Иониты — синтетические смолы, имеющие углеводородный каркас (R), фиксированные (анкерные) ионы и противоионы, которые и участвуют в обмене. Существует два типа ионитов: катиониты, у которых противоионами являются катионы, и аниониты, у которых противоионами являются анионы. Реакции ионообмена — обратимые и записываются в виде: при обмене катионами RSO3 H + NaCl → RSO3 Na + HCl — 446 — ÐƮǮǃǃǮ ǮƻǂǬǃǃǪǎÐǮǆǀǯǰǭǪÐǯǰǮǆǃǊǲÐǫǮƽ при обмене анионами ROH + NaCl → RCl + NaOH Обратимость процесса позволяет при определенных условиях проводить процесс регенерации ионитов для повторного их использования. При регенерации вымывание уловленных ионов можно производить, используя меньший объем реагента, чем достигается при получении более концентрированных растворов уловленной примеси. Ионит представляет собой пористый материал, в котором имеются макропоры размером ~ 100 нм и микропоры размером ~ 1 нм. Обычная поверхность пор ионитов составляет ~ 60...80 м2/г ионита. Эффективность ионита оценивается по его объемной емкости. Различают полную емкость, когда все ионы замещены ионами примеси; статическую емкость, когда в системе установилось равновесие, и динамическую емкость, когда при протекании раствора через слой ионита не обнаруживатся неуловленная примесь (до так называемого явления проскока). Ионит используется в виде зерен размером 0,3–2 мм. Перед употреблением иониты выдерживают в воде. При этом они набухают, увеличивая свой объем и размер пор в 1,5–3 раза. В набухшем состоянии ионит представляет собой гель. Кинетика процесса. Процесс ионообмена — гетерогенный и включает три стадии: диффузию улавливаемого иона в растворе к поверхности зерна ионита и обратную диффузию нового иона от поверхности зерна в раствор — внешняя кинетика; диффузию иона по макро- и микропорам ионита и обратную диффузию нового иона по порам — внутренняя, или гелиевая, кинетика, и сам процесс ионообмена. Последний процесс протекает быстро и не лимитирует общую скорость. Обычно лимитирующими являются внешняя или внутренняя кинетика. Внешняя кинетика является лимитирующей при малых концентрациях примеси в растворе (< 10“3 моль/л). Для интенсификации процесса увеличивают скорость движения жидкости (перенос за счет конвективной диффузии). — 447 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð Внутренняя (гелиевая) кинетика является лимитирующей при большом диаметре зерна и (или) при большой концентрации примеси в растворе. Процесс проводится обычно в колонном аппарате, где раствор для очистки подается снизу, а ионит может находиться в колонне неподвижно (периодический процесс) или загружаться свежий сверху, а отработанный выводиться снизу. В слое ионита можно наблюдать три зоны (рис. 11.1). В нижней зоне 1 процесс ионообмена закончился, ионит насыщен улавливаемой примесью, и раствор проходит ее не меняя своей первоначальной концентрации. В зоне 2 протекает процесс ионообмена. В нижнем слое ионита достигнуто его насыщение, и раствор имеет начальную концентрацию, а в верхнем раствор полностью очищен. Зона 3 является защитной, в ней ионообмен не происходит. Здесь находится свежий ионит, а раствор по всей высоте имеет конечную концентрацию примеси. В колоннах периодического действия следят, когда вверху колонны появится раствор с повышенной концентрацией примеси (проскок). При этом защитный слой будет полностью выработан, и процесс следует прекращать. Ионит подвергается регенерации и только после этого можно проводить процесс вновь. Рис. 11.1. Изменения концентрации примеси по высоте ионита. Ионообмен нашел применение в различных целях: – получение чистой воды в электронной промышленности; — 448 — ÐƪǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ – улавливание токсичных веществ из сточных вод (тяжелых металлов, мышьяка, фосфора, цианистых соединений, радиоактивных веществ); – извлечение ценных компонентов из сточных вод, в том числе шахтных вод (Си, Zn, Cd, Сг, Ni, Pb, Hg, V, Mn и др.) – отпреснение морской воды. ϭϭ͘ϲ͘ʥ̸̸̸̵̨̨̡̨̨̡̨̨̛̛̛̛̛̣̖̭̖̥̖̯̼̭̯̭̯̦̼̐̔̏̔͘ Биологический (или биохимический) метод очистки сточных вод применяется для очистки производственных и бытовых сточных вод от органических и неорганических загрязнителей. Данный процесс основан на способности некоторых микроорганизмов использовать загрязняющие сточные воды вещества для питания в процессе своей жизнедеятельности. Основной процесс, протекающий при биологической очистке сточных вод, — это биологическое окисление. Данный процесс осуществляется сообществом микроорганизмов (биоценозом), состоящим из множества различных бактерий, простейших водорослей, грибов и др., связанных между собой в единый комплекс сложными взаимоотношениями (метабиоза, симбиоза и антагонизма). Главенствующая роль в этом сообществе принадлежит бактериям. Очистку сточных вод рассматриваемым методом проводят в аэробных (т. е. в присутствии растворенного в воде кислорода) и в анаэробных (в отсутствие растворенного в воде кислорода) условиях. ϭϭ͘ϲ͘ϭ͘ʽ̨̨̡̛̭̦̦̼̖̪̯̖̣̏̌̌̚͘ Сточные воды, направляемые на биохимическую очистку; характеризуются величиной БПК и ХПК. БПК — это биохимическая потребность в кислороде или количество кислорода, использованного при биохимических процессах окисления органических веществ (не включая процессы нитрификации) за определенный промежуток времени (2, 5, 8, 10, 20 сут.), в 1 мг кислорода, на 1 мг вещества. Например: БПК5 — биохимическая потребность в кислороде за 5 сут, БПКполн — полная — 449 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð биохимическая потребность в кислороде до начала процессов нитрификации. ХПК — химическая потребность в кислороде, т.е. количество кислорода, эквивалентное количеству расходуемого окислителя, необходимого для окисления всех восстановителей, содержащихся в воде. ХПК также выражают в1 мг кислорода на 1 мг вещества. Контактируя с органическими веществами, микроорганизмы частично разрушают их, превращая в воду, диоксид углерода, нитрит- и сульфат-ионы и др. Другая часть вещества идет на образование биомассы. Разрушение органических веществ называют биохимическим окислением. Некоторые органические вещества способны легко окисляться, а некоторые не окисляются совсем или очень медленно. Для установления возможности подачи промышленных сточных вод на биохимические очистные сооружения устанавливают максимальные концентрации токсичных веществ, которые не влияют на процессы биохимического окисления (MKб) и на работу очистных сооружений (МКб.о.с). При отсутствии таких данных возможность биохимического окисления устанавливают по отношению БПКполн и ХПК. При отношении (БПК/ХПК)* 100 = 50% вещества поддаются биохимическому окислению. ϭϭ͘ϲ͘Ϯ͘ʯ̸̵̡̨̨̨̨̡̛̛̛̦̥̖̬̦̭̯̬̭̪̬̦̖̭̖̺̖̭̯̌̌̌̔̌̐̌̏̏͘ Для того чтобы происходил процесс биохимического окисления органических веществ, находящихся в сточных водах, они должны попасть внутрь клеток микроорганизмов. К поверхности клеток вещества поступают за счет конвективной и молекулярной диффузии, а внутрь клеток — диффузией через полупроницаемые цитоплазматические мембраны, возникающей вследствие разности концентраций веществ в клетке и вне ее. Однако большая часть вещества попадает внутрь клеток при помощи специфического белка-переносчика. Образующийся растворимый комплекс вещество-переносчик диффундирует через мембрану в клетку, где он распадается, и белок-переносчик включается в новый цикл переноса. — 450 — ÐƪǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Основную роль в процессе очистки сточных вод играют процессы превращения вещества, протекающие внутри клеток микроорганизмов. Эти процессы заканчиваются окислением вещества с выделением энергии и синтезом новых веществ с затратой этой энергии. Внутри клеток микроорганизмов происходит непрерывный и очень сложный процесс химических превращений. В строгой последовательности с большой скоростью протекает большое число реакций. Скорость реакций и их последовательность зависят от вида и содержания ферментов, которые выполняют роль катализаторов. Ферменты ускоряют только те реакции, которые протекают самопроизвольно, но с очень малой скоростью. Ферменты (или энзимы) представляют собой сложные белковые соединения с молекулярной массой, достигающей сотен тысяч и миллионов. По строению молекулы ферменты подразделяются на одно — и двух компонентные. Первые из них являются простыми белками — протеинами, вторые — сложными белками — протеидами, молекула которых состоит из двух частей: первая часть, белковая, называется носителем, или апоферментом, вторая — небелковая, называется коферментом. Каталитической активностью обладает кофермент, а белковый носитель увеличивает его активность. Каталитические реакции протекают на поверхности молекул ферментов, на которой возникают активные центры. По сравнению с химическими катализаторами ферменты способны действовать в более «мягких условиях», т. е. при невысоких температурах, нормальном давлении и реакции среды, близкой к нейтральной. Другой особенностью ферментов является то, что каждый из них взаимодействует только с определенным химическим соединением и катализирует одно из многих превращений, которым подвергается данное химическое соединение. При изменении состава и концентрации веществ требуются ферменты иного состава. Таким образом, каждую реакцию катализирует один соответствующий фермент. При этом продукт одной реакции служит субстратом для следующей. Все это является существенным отличием ферментного катализа. — 451 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð Скорость биохимических реакций определяется активностью ферментов, которая зависит от температуры, pH и присутствия в сточной воде различных веществ. С повышением температуры скорость ферментативных процессов повышается, но до определенного предела. Для каждого фермента имеется оптимальная температура, выше которой скорость реакции падает. Для разрушения сложной смеси органических веществ необходимо 80–100 различных ферментов. К числу веществ (активаторов), которые повышают активность ферментов, относятся многие витамины и катионы Са2+ Mg2+, Мn+. В то же время соль тяжелых металлов, синильная кислота, антибиотики являются ингибиторами. Они блокируют активные центры фермента, препятствуя его реакции с субстратом, т. е. резко снижают активность. Скорость образования и распада ферментов зависит от условий роста микроорганизмов и определяется скоростью поступления в клетку веществ, ингибирующих и активирующих биохимические процессы. Клетки каждого вида микробов имеют определенный набор ферментов. Некоторые из них независимо от субстрата постоянно присутствуют в клетках микроорганизмов. Такие ферменты называются конститутивными. Другие ферменты синтезируются в клетках вследствие изменений в окружающей среде, например, изменения состава или концентрации загрязнений сточных вод. Эти ферменты появляются в период приспособления организмов к изменению среды, поэтому называются адаптивными. Сроки адаптации (приспособления) различны и продолжаются от нескольких часов до десятков и сотен дней. Если в сточных водах находится несколько веществ, то процесс окисления будет зависеть от содержания и структуры всех растворенных органических веществ. В первую очередь будут окисляться те вещества, которые необходимы для создания клеточного материала и для получения энергии. Другие вещества потребляются микроорганизмами в зависимости от набора ферментов с равными или разными скоростями окисления одновременно или последовательно. Порядок окисления вещества сказывается на продолжительности очистки сточных — 452 — ÐƪǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ вод. При последовательном окислении вещества продолжительность очистки определяется суммой длительности окисления каждого вещества в отдельности. Внутри клетки химические соединения подвергаются различным анаболическим и катаболическим превращениям. Анаболические превращения приводят к синтезу новых клеточных компонентов, а катаболические являются источниками необходимой для клетки энергии. Очистка сточных вод подразумевает практически полное биологическое разложение органических соединений в воде. По существующим нормам, содержание органических веществ в очищенной воде не должно превышать 10 мг/л. Разрушение органических веществ микроорганизмами в аэробных и в анаэробных условиях осуществляется с разными энергетическими балансами суммарных реакций. Так, например, при аэробном биоокислении глюкозы 59% энергии, содержащейся в ней, расходуется на прирост биомассы и 41% составляют тепловые потери. Этим обусловлен активный рост аэробных микроорганизмов. Чем выше концентрация органических веществ в обрабатываемых стоках, тем сильнее разогрев, выше скорость роста микробной биомассы. При анаэробной деградации глюкозы с образованием метана лишь 8% энергии расходуется на прирост биомассы, 3% составляют тепловые потери и 89% переходит в метан. Анаэробные микроорганизмы растут медленно и нуждаются в высокой концентрации субстрата. Аэробный процесс C6 H12 O6 + 6O2 → 6CO2 + 6H2 O + микробная биомасса + тепло Анаэробный процесс C6 H12 O6 → 3CH4 + 3CO2 + микробная биомасса + тепло Аэробное микробное сообщество представлено разнообразными микроорганизмами, в основном бактериями, окисляющими различные органические вещества в большинстве случаев независимо друг от друга, хотя окисление некоторых веществ осуществляется путем соокисления (кометаболизм). Аэробное микробное сообщество в системах аэробной очистки воды представлено исключительным биоразнообразием. В последние годы с помощью новых мокулярно-биологических — 453 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð методов, в частности специфических рРНК проб, в активном иле показано присутствие бактерий родов Paracoccus, Caulobacter, Hyphomicrobium, Nitrobacter, Acinetobacter, Sphaerotilus, Aeromonas, Pseudomonas, Cytophaga, Flavobacterium, Flexibacter, Halisomenobacter, Artrobacter, Corynebacterium, Microtrix, Nocardia, Rhodococcus, Bacillus, Clostridium, Lactobacillus, Staphylococcus. Считается, однако, что к настоящему времени идентифицировано не более 5% видов микроорганизмов, участвующих в аэробной очистке воды. Следует отметить, что многие аэробные бактерии являются факультативными анаэробами. Они могут расти в отсутствии кислорода за счет других акцепторов электронов (анаэробное дыхание) или брожения (субстратное фосфорилирование). Продуктами их жизнедеятельности являются углекислота, водород, органические кислоты и спирты. Анаэробная деградация (разложение) органических веществ, при метаногенезе осуществляется как многоступенчатый процесс, в котором необходимо участие по меньшей мере четырех групп микроорганизмов: гидролитиков, бродильщиков, ацетогенов и метаногенов. В анаэробном сообществе между микроорганизмами существуют тесные и сложные взаимосвязи, имеющие аналогии в многоклеточных организмах, поскольку ввиду субстратной специфичности метаногенов, их развитие невозможно без трофической связи с бактериями предыдущих стадий. В свою очередь, метановые археи, используя вещества, продуцируемые первичными анаэробами, определяют скорость реакций, осуществляемых этими бактериями. Ключевую роль в анаэробной деградации органических веществ до метана играют метановые археи родов Methanosarcina, Methanosaeta (Methanothrix), Мethanomicrobium и другие. При их отсутствии или недостатке анаэробное разложение заканчивается на стадии кислотогенного и ацетогенного брожений, что приводит к накоплению летучих жирных кислот, в основном масляной, пропионовой и уксусной, снижению рН и остановке процесса. Преимуществом аэробной очистки является высокая скорость и использование веществ в низких концентрациях. Существенными недостатками, особенно при обработке концентрированных — 454 — ÐƪǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ сточных вод, являются высокие энергозатраты на аэрацию и проблемы, связанные с обработкой и утилизацией больших количеств избыточной биомассы. Аэробный процесс используется при очистке бытовых, некоторых промышленных и свиноводческих сточных вод с ХПК не выше 2000. Исключить указанные недостатки аэробных технологий может предварительная анаэробная обработка концентрированных сточных вод методом метанового сбраживания, которая не требует затрат энергии на аэрацию и более того сопряжена с образованием ценного энергоносителя — метана. Преимуществом анаэробного процесса является также относительно незначительное образование микробной биомассы. К недостаткам следует отнести невозможность удаления органических загрязнений в низких концентрациях. Для глубокой очистки концентрированных сточных вод анаэробную обработку следует использовать в комбинации с последующей аэробной стадией. Выбор технологии обработки сточных вод определяются содержанием органических загрязнений в них. Разложение органических веществ в анаэробных условиях происходит с образованием СО2, Н2O, нитрат- и сульфат-ионов. Вместе с органическими соединениями разлагаются некоторые неорганические соединения, такие как H2S, MeS, NH3, нитраты. За счет восстановления тяжелых металлов снижается токсичность сточных вод. При очистке сточных вод под действием нитрифицирующих бактерий протекают процессы нитрификации и денитрификации. Нитрифицирующие бактерии окисляют азот аммонийных соединений сначала до нитритов, а потом до нитратов. Этот процесс называется нитрификацией. Под действием денитрифицирующих бактерий связанный кислород отщепляется от нитритов и нитратов и вновь расходуется на окисление органических веществ. Этот процесс называется денитрификацией. Условиями осуществления процесса денитрификации являются: наличие органических веществ, небольшой доступ кислорода, нейтральная или слабощелочная реакции. Денитрификация — процесс многостадийный и может протекать с образованием аммиака, молекулярного азота либо оксидов азота. При очистке сточных вод денитри— 455 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð фикация протекает, главным образом, с образованием азота (редко образуется NH3). Сухая масса образуемой бактериями биомассы, на 70–90% состоит из органических веществ и 10–30% неорганических веществ. Органическая часть биомассы представляет собой амфотерную коллоидную систему, при pH = 4–9 имеющую отрицательный заряд. Несмотря на существенные различия состава сточных вод, химический состав биомассы достаточно близок. Состав биомассы при очистке городских сточных вод — CН21О82N8S7. Качество биомассы определяется ее способностью к осаждению. Очищенная таким способом вода пригодна для повторного использования. По современным представлениям биомасса при биохимической очистке сточных вод существует в виде активного ила и биопленки. Активный ил представляет собой совокупность сообщества микроорганизмов и субстрата (твердая отмершая часть остатков водорослей и других остатков); к субстрату прикрепляются организмы активного ила (количество субстрата в активном иле — до 40%). Масса активного ила поддерживается во взвешенном состоянии за счет перемешивания или аэрации. Активный ил рассматривают как коллоидную систему. Элементный химический состав активных илов в различных сточных водах достаточно близок. Биопленка представляет собой плотный слой, состоящий из клеток бактерий, способных прикрепляться к твердой поверхности (так называемой загрузке фильтра) и образовывать фиксированную полимерную пленку, которая препятствует их удалению. В биопленке концентрация бактерий гораздо выше, чем в активном иле. Каждая отдельная бактерия, находящаяся внутри биопленки, ведет себя так же, как в суспензии активного ила. Толщина биопленки порядка 1 мм. В процессе очистки сточных вод (СВ) происходит процесс прироста биомассы бактерий (масса ила, покидающего реактор в единицу времени). Получаемая биомасса имеет состав C5H7NO2. Коэффициент прироста ила (биомассы) Y при аэробном разложении органических веществ определяется как отноше— 456 — ÐƪǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ ние концентрации взвешенных веществ X к концентрации растворенных веществ S: (11.4) Y = ∆X / ∆S т.е. коэффициент прироста ила определяется как прирост биомассы в результате потребления определений массы субстрата. Прирост биомассы, при прочих равных условиях (состав загрязнений, вид микроорганизмов, БПК и ХПК, температура), зависит от скорости размножения микроорганизмов. Основные фазы роста микроорганизмов — приспособление к условиям (клетки увеличиваются в размерах, но их число не возрастает), рост микроорганизмов (клетки делятся с максимальной скоростью), замедление роста (истощение питательных веществ), отмирание микроорганизмов. Для приближенных расчетов прирост биомассы Пр.б. рекомендуют определять по формуле: Пр.б. = К { ХПК — БПК} (11.5) где К — коэффициент (изменяется от 0,1 до 0,9), характеризующий качество ила (качество ила во многом определяется скоростью его осаждения). При аэробном росте микробной биомассы максимальное количество органического вещества, превращаемого в новую биомассу (состав C H NO ), составляет, по расчетам датских ученых, около 50% по ХПК. Для роста микроорганизмов необходимы макроэлементы. Коммунальные СВ, в отличие от промышленных, обычно содержат достаточное количество макроэлементов. Промышленные СВ часто обеднены азотом и фосфором, что приводит к замедлению процесса очистки и полноты окисления загрязнителей. При низких концентрациях азота и фосфора микробный рост замедляется. Для поддержания высокой скорости размножения микроорганизмов необходимо поддерживать на определенном и стабильном уровне как концентрацию питательных веществ, так и продуктов распада (т. е. необходимо обеспечить непрерывное поступление свежего субстрата и удаление продуктов разложения). 5 7 2 — 457 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð При неизменной температуре и pH главными влияющими факторами на аэробный процесс очистки СВ являются концентрации субстрата и кислорода. Кинетика роста биомассы и зависимость скорости аэробного процесса от концентрации кислорода описываются уравнениями Моно. Кинетика роста биомассы:  S  (11.6) μнабл = μмакс    S + KS  μнабл — наблюдаемая удельная скорость роста, ч–1 или сут–1; μмакс — максимальная удельная скорость роста, ч–1 или сут–1; S — концентрация субстрата в реакторе (концентрация растворенного вещества), кг/м3 или кг XПK(S)/м3; KS — константа насыщения по субстрату, г/м3 или г XПK(S)/м3, где ХПК(S) — растворимый субстрат в единицах ХПК. Зависимость скорости аэробного процесса от концентрации кислорода:   SO2 (11.7) μнабл = μмакс    SO2 + KS,O2  где SO2 — концентрация кислорода в реакторе, г O2/м3 ; Ks,o2 — константа насыщения по кислороду (зависит от температуры и размера флокул), г О2/м3. Объединяя эти два выражения, получают двойное уравнение Моно, подчеркивающее наиболее важные для описания процесса моменты    SO2 μнабл = μмакс  S  <  (11.8)  + + S K S K  O2  S  S,O 2   Реальный процесс, естественно, намного сложнее (на рост биомассы оказывают влияние расход субстрата, возраст ила, макроэлементы и другие факторы). ϭϭ͘ϲ͘ϯ͘ʽ̸̸̵̵̵̡̨̨̨̨̛̛̛̭̯̭̯̦̼̪̬̬̦̼̱̭̣̌̏̔̏̔̏́͘ Аэробные процессы биохимической очистки могут протекать в природных условиях и в искусственных сооружениях. В естественных условиях очистка происходит на полях орошения, полях фильтрации и биологических прудах. Искус— 458 — ÐƪǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ ственными сооружениями являются аэротенки и биофильтры разной конструкции. Тип сооружений выбирают с учетом местоположения завода, климатических условий, источника водоснабжения, объема промышленных и бытовых сточных вод, состава и концентрации загрязнений. В искусственных сооружениях процессы очистки протекают с большей скоростью, чем в естественных условиях. ϭϭ͘ϲ͘ϰ͘ʤ̵̸̸̨̨̨̡̨̨̡̛̛̛̛̛̦̬̦̼̖̥̖̯̼̥̖̭̜̭̯̌̾̍̔̍͘ Анаэробные методы обезвреживания используют для сбраживания осадков, образующихся при биохимической очистке производственных сточных вод, а также как первую ступень очистки очень концентрированных промышленных сточных вод (БПКполн 4–5 г/л), содержащих органические вещества, которые разрушаются анаэробными бактериями в процессах брожения. В зависимости от конечного вида продукта различают следующие виды брожения: спиртовое, пропионовокислое, молочнокислое, метановое и др. Конечными продуктами брожения являются: спирты, кислоты, ацетон, газы брожения (СО2, Н2, СН4). Для очистки сточных вод используют метановое брожение. Этот процесс очень сложный и многостадийный. Механизм его окончательно не установлен. Считают, что процесс метанового брожения состоит из двух фаз: кислой и щелочной (или метановой). В кислой фазе из сложных органических веществ образуются низшие жирные кислоты, спирты, аминокислоты, аммиак, глицерин, ацетон, сероводород, диоксид углерода и водород. Из этих промежуточных продуктов в щелочной фазе образуются метан и диоксид углерода. Предполагается, что скорости превращений веществ в кислой и щелочной фазах одинаковы. Основными параметрами аэробного сбраживания являются температура, регулирующая интенсивность процесса, доза загрузки осадка и степень его перемешивания. Процессы сбраживания ведут в мезофильных (30–35°С) и термофильных (50– 55°С) условиях в метантенках. Метантенки применяются для минерализации осадков бытовых и производственных сточных — 459 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð вод, содержащих доступные для микроорганизмов органические вещества. Полного сбраживания органических веществ в метантенках достичь нельзя. Все вещества имеют свой предел сбраживания, зависящий от их химической, природы. В среднем степень распада органических веществ составляет около 40%. Для достижения высокой степени анаэробного сбраживания необходимо соблюдать по возможности высокую температуру процесса, концентрацию беззольного вещества более 15 г/л, интенсивную степень перемешивания, рН среды 6,8– 7,2. Снижают эффективность сбраживания присутствие катионов тяжелых металлов (меди, никеля, цинка); избыток ионов NH4+, сульфидов, некоторых органических соединений и в том числе детергентов. Процесс брожения сточных вод ведут в две ступени. При этом часть осадка из второго метантенка возвращают в первый, В первой ступени обеспечивают хорошее перемешивание. Возбудителями метанового брожения в метантенке являются те же группы микробов, которые участвуют в минерализации органического вещества в двухярусном отстойнике. Широкое использование биохимического метода обусловлено: 1. Возможностью удалять из сточных вод разнообразные органические и некоторые неорганические соединения, находящиеся в воде в растворенном, коллоидном и нерастворенном состоянии, в том числе и токсичные. 2. Простотой аппаратурного оформления. 3. Относительно невысокими эксплуатационными затратами. 4. Глубиной очистки. К недостаткам метода относятся: 1. Высокие капитальные затраты. 2. Необходимость строгого соблюдения технологического режима очистки. 3. Токсичное действие на микроорганизмы ряда органических и неорганических соединений. 4. Необходимостью разбавления сточных вод в случае высокой концентрации примесей. — 460 — ÐǠǮǃǰ͠ǮǁǋǃǊǬÐǫǮ͟͠ǮǯǊ Для определения возможности подачи промышленных сточных вод на биохимические очистные сооружения устанавливают максимальную концентрацию токсических веществ, которые не влияют на процессы биохимического окисления и на работу очистных сооружений. При отсутствии таких данных возможность биохимического окисления устанавливается по биохимическому показателю: при отношении БПКп /ХПК > 50 % вещества поддаются биохимическому окислению. При этом необходимо, чтобы сточные воды не содержали ядовитых веществ и примесей солей тяжелых металлов. Биохимическую очистку считают полной, если БПКп сточной воды < 20 мг /л и неполной, если БПКп > 20 мг /л. ϭϭ͘ϳ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏͘ 1. Рассмотрите использования процесса нейтрализации для очистки сточных вод, а также области его применении, достоинства, недостатки и эффективность. 2. Объясните суть процессов очистки сточных вод окислением хлором, Назовите область применения и эффективность. 3. Объясните суть процессов очистки сточных вод окислением кислородом. Назовите область применения и эффективность. 4. Объясните суть процессов очистки сточных вод окислением озоном. Назовите область применения и эффективность. 5. Рассмотрите основы расчетных методов удаления из сточных вод ионов тяжелых металлов. Достоинства и недостатки методов и эффективность. 6. По современным представлениям, на какие виды можно разделить образующуюся при очистке сточных вод биомассу? 7. Чем отличается состав активного ила от состава биопленки? 8. Какие общие закономерности распада органического вещества в процессе биологического окисления? — 461 — ǞǁǪǫǪÐ ÐǩǀǂǀǆǬǯǭǀǬÐǀÐƻǀǮǁǮƼǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ Ð 9. Как производится очистка сточных вод в природных условиях? 10. Какие аппараты или сооружения для очистки сточных вод в природных условиях вы знаете? 11. Чем отличается очистка сточных вод в анаэробных условиях от очистки в аэробных условиях. 12. Как устроен биофильтр? 13. Опишите процесс очистки сточных вод в биофильтре. 14. Опишите процесс очистки сточных вод в окситенке. 15. Можно ли проводить биохимическими методами проводить совместную очистку бытовых и промышленных сточных вод? 16. В чем заключаются особенности очистки сточных вод в метантенках? 17. Какие методы обработки осадков сточных вод вы знаете? Чем руководствуются при выборе того или иного метода при обработке осадков? — 462 — ǍưǙǚǙ Í Í ǗƝƜƝơǎǕǏƝǎÍǒǕǑǒǌƥÍƧƞǎǏǖǔǒƚǑƥǘÍ ǓǔǒƠǎǕǕǒǌÍǓǔƝÍǒơƝǕǖǏǎÍǕǖǒơǑƥǘÍ ǌǒƚÍǒǖÍǓǔƝǐǎǕǎ֏ В результате изучения главы 12 бакалавр должен: Знать: – основные физико-химические закономерности электродных процессов при очистке сточных вод от примесей. Уметь: – применять электродные процессы при очистке сточных вод от примесей. Владеть: – основами теоретической электрохимии для описания механизмов очистки сточных вод электродными процессами. ϭϮ͘ϭ͘˔̶̡̨̨̛̛̛̛̛̣̖̦̣̖̯̬̣͕̪̣̬̏́̾̌́̌̚̚ ̛̛̪̖̬̖̦̪̬̙̖̦̌́́͘ ϭϮ͘ϭ͘ϭ͘ˑ̡̨̛̣̖̯̬̣̚͘ Пропускание постоянного тока через раствор электролита сопровождается химическими процессами на электродах — это явление называется электролизом. Явления электролиза обратны процессам, происходящим в замкнутом элементе, где, наоборот, электрический ток возникает за счет химических ре— 463 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð акций. В электролитической ячейке будем называть катодом электрод, соединенный с отрицательным электродом источника тока, а анодом тот электрод, который соединен с положительным электродом источника. Соединим гальванический элемент, например элемент Даниеля, с внешним источником тока так, чтобы его отрицательный цинковый электрод был соединен с отрицательным электродом источника тока, т.е. был бы катодом, а положительный медный — с положительным электродом источника так, чтобы он был анодом. Тогда, если приложенная электродвижущая сила достаточна, через элемент будет проходить ток в направлении, обратном направлению его собственного тока, и на электродах будет происходить процессы, обратные процессам, идущим в замкнутом элементе. На цинковом катоде будет идти осаждение цинка, а на медном аноде — растворение меди Zn2+ + 2e − → Zn и Cu → Cu2+ + 2e − Обобщая это, можно установить, что при электролизе на катоде идут процессы восстановления, а на аноде идут процессы окисления. Для того чтобы через элемент Даниеля проходил обратный ток, достаточно, чтобы приложенная внешняя электродвижущая сила E была немного больше собственной электродвижущей силы Ep самого элемента. Тогда между электродами установится разность потенциалов E – Ep, позволяющая преодолеть омическое сопротивление w элемента, и возникает ток, сила i которого определяется законом Ома: (12.1) E − Ep = iw Эта сила тока растет с увеличением приложенной электродвижущей силы E. В тех случаях, когда оба электрода элемента имеют одинаковый потенциал, имеем Ep=0, и электролиз начинается при как угодно малой приложенной электродвижущей силе. Так будет идти, например, электролиз раствора CuSO4 между двумя медными электродами с выделением меди на катоде Cu2+ + 2e − → Cu (восстановление). И растворением ее на аноде Cu → Cu2+ + 2e − (окисление). — 464 — ÐƺǫǁǬǃǀǎÐǌǁǬǭǰ͠ǮǁǀƿǪ Ð͟Ǯǁǎ͠ǀƿǪǅǀǀÐǀÐ͟Ǭ͠ǬǃǪ͟͠ǎƾǬǃǀǎ Далеко не всегда явления электролиза точно повторяют в обратном направлении процессы, происходящие в работающем гальваническом элементе. Это возможно лишь тогда, когда обе электродные реакции и все остальные процессы, происходящие в элементе, термодинамически обратимы. В противном случае процессы при электролизе могут быть иными, чем в замкнутом элементе, и тогда величина Ep в (10.1) не равна электродвижущей силе элемента. Разные случаи и причины необратимости будут рассмотрены ниже. Необратимость увеличивается с увеличением скорости электролиза, т.е. силы тока, проходящего через ячейку. Она поэтому особенно существенна в технических электрохимических процессах, где применяют токи большой силы и где, в частности, она вызывает увеличение расхода необходимой для электролиза энергии. ϭϮ͘ϭ͘Ϯ͘ʶ̛̛̬̦̪̬̙̖̦̏̌́̌́́͘ Соединим с внешним источником тока два платиновых электрода, опущенных в раствор серной кислоты, включив в цепь гальванометр. Приложим сначала небольшую электродвижущую силу, например 1 вольт. После короткого отброса стрелка гальванометра вернется почти к нулю, т.е. через цепь почти не будет проходить тока, и не будет наблюдаться электролиза. То же будет происходить при последовательном увеличении приложенной электродвижущей силы E до тех пор, пока она не превзойдет некоторую величину Ep (в данном примере 1,7 вольта), называемую электродвижущей силой разложения. При этой электродвижущей силе начинается разложение воды с выделением водорода на катоде и кислорода на аноде и появляется длительный ток, сила которого растет с увеличением приложенной электродвижущей силы E. Кривая силы тока в функции от электродвижущей силы называется кривой напряжения. В простых случаях, не осложненных побочными факторами, она имеет вид, показанный на рис. 12.1. Электродвижущую силу разложения можно найти как из положения точки изгиба этой кривой, так и по началу элек— 465 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð тролиза (появление пузырьков газов на электродах). Оба способа не очень точны. Рис.12.1. Кривая напряжения. Эти явления объясняются так. После включения внешней электродвижущей силы на электродах начинается выделение водорода и кислорода, что превращает катод в водородный электрод, а анод — в кислородный. При этом ячейка превращается в водородно-кислородный гальванический элемент, дающий собственную обратную электродвижущую силу, растущую по мере насыщения электродов газами до тех пор, пока она не станет равной приложенной электродвижущей силе E, после чего ток прекратится. Если увеличить E, то снова через короткое время наступит стационарное состояние с более высокой степенью насыщения электродов газами. Последнее не может, однако, расти безгранично. Когда достигнуто равновесие с внешним давлением, газы начинают покидать электроды в виде пузырьков, и дальнейший рост приложенной электродвижущей силы не будет сопровождаться ростом обратной электродвижущей силы, которая достигла наибольшей возможной величины Ep. Дальнейшее увеличение E сверх Ep будет давать длительный ток, растущий согласно (12.1), т.е. линейно, как это показано на рис.12.1. Наклон прямой определяется величиной сопротивления w ячейки. Из рисунка видно, что при E<Ep также имеется небольшой длительно сохраняющийся остаточный ток, вызванный — 466 — ÐƺǫǁǬǃǀǎÐǌǁǬǭǰ͠ǮǁǀƿǪ Ð͟Ǯǁǎ͠ǀƿǪǅǀǀÐǀÐ͟Ǭ͠ǬǃǪ͟͠ǎƾǬǃǀǎ утечкой некоторых количеств водорода и кислорода из электродов путем диффузии, так что обратная электродвижущая сила всегда несколько отстает от приложенной. Ускорение диффузии путем нагревания или размешивания электролита увеличивает остаточный ток. Рассмотрим теперь более простой случай, когда электролиз не изменяет природы электролитов, например ячейку из двух серебряных электродов в растворе AgNO3. Если пренебрегать концентрационными изменениями у электродов, сопровождающими электролиз, то обратная электродвижущая сила равна нулю и (12.1) превращается в E = iw Тогда кривая напряжения имеет форму прямой, выходящей из начала координатных осей, как изображено пунктиром на рис.12.1. Если электролиз сопровождается необратимыми процессами, из которых наиболее часто встречаются рассматриваемые ниже перенапряжение и концентрационная поляризация, то кривая напряжения имеет более сложный вид. Изменения, происходящие в гальванической цепи при прохождении через нее тока, называют поляризацией (не смешивать с диэлектрической поляризацией молекул в электрическом поле.), а вызываемую ими обратную электродвижущую силу называют электродвижущей силой поляризации. Эти изменения, большей частью термодинамически необратимые, могут быть как химическими, так и концентрационными. ϭϮ͘ϭ͘ϯ͘ˑ̡̨̨̛̛̛̛̣̖̯̬̙̱̺̖̭̣̼̬̣̙̖̦̔̏̌́̚͘ Как было выше объяснено, электродвижущая сила разложения Ep должна быть равной по величине и обратной по закону электродвижущей силе того гальванического элемента, который образуется при электролизе. Следует, однако, отметить, что из-за побочных осложнений обе электродвижущие силы редко вполне совпадают. Электродвижущая сила разложения водных растворов всех неорганических оснований и кислородных кислот между гладкими платиновыми электродами одна и та же, около — 467 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð 1,7 вольта при 20 °C с колебаниями не больше 0,05 вольта в обе стороны. Объясняется это тем, что все они при электролизе дают одни и те же электродные реакции: выделение водорода на катоде и кислорода на аноде. Электродвижущая сила разложения в этих случаях равна электродвижущей силе водородно-кислородного элемента, которая действительно не зависит от рода и концентрации электролита. Соли щелочных или щелочноземельных металлов дают при электролизе одни и те же продукты на электродах. Например, суммарная схема электродных реакций при электролизе раствора Na2SO4 может быть представлена в следующем виде: 1 1 Na + + H2O = NaOH + H2 и SO42− + H2O = H2SO4 + O2 + 2e − 2 2 Их электродвижущая сила разложения, однако, выше, чем для кислот и щелочей, а именно 2,1–2,2 вольта, так как образование щелочи на катоде повышает положительный потенциал водородного электрода, а образование кислоты на аноде повышает отрицательный потенциал кислородного электрода. В кислотах и щелочах этого осложнения нет, так как избыток их поддерживает равенство pH около обоих электродов. Если металл находится ниже водорода в ряду напряжений, то величина Ep другая и зависит от рода металла. Она, например, равна 0,8 и 0,7 вольта для растворов AgNO3 и Ag2SO4 и 1,5 вольта для раствора CuSO4. Объясняется это тем, что здесь электродный процесс на катоде иной, чем в рассмотренных выше примерах: выделяется не водород, а серебро или медь. При сравнении величин Ep с электродвижущими силами соответствующих обратимых элементов следовало бы брать последние для тех же активностей, какие имеет электролизуемый раствор, однако и тогда не следует ожидать полного согласия из-за уже упоминавшейся ниже и более подробно рассматриваемой необратимости многих электродных процессов. ϭϮ͘ϭ͘ϰ͘ʿ̶̨̨̛̛̯̖̦̣̼̬̣̙̖̦̌̌́̚͘ Вместо измерения электродвижущих сил разложения лучше находить потенциал разложения каждого электрода от— 468 — ÐƺǫǁǬǃǀǎÐǌǁǬǭǰ͠ǮǁǀƿǪ Ð͟Ǯǁǎ͠ǀƿǪǅǀǀÐǀÐ͟Ǭ͠ǬǃǪ͟͠ǎƾǬǃǀǎ дельно. Для этого обыкновенно применяют схему, изображенную на рис. 12.2, и ее варианты. Рис. 12.2. Измерение кривой напряжения Ток, отбираемый от потенциометра, поляризует ячейку AB; потенциал электрода A измеряют обычным методом против вспомогательного неполяризующего электрода K, например каломельного. Дополнительную электродвижущую силу, равную iw, необходимую для преодоления омического сопротивления, по возможности уменьшают, подводя носик сифона вспомогательного электрода вплотную к измеряемому электроду, или же ее вычитают из измеренных E. Измерение силы тока производят или во время прохождения поляризующего тока, или непосредственно после его выключения. Второй, так называемый коммутаторный метод, при котором чередуют включение поляризующего тока и цепи, измеряющей ток поляризации, раньше считали более точным, что оказалось неверным. Им, однако, пользуются для изучения скорости возникновения и падения поляризации после включения или выключения поляризующего тока. Зависимость силы тока от поляризующего потенциала дает такие же кривые напряжения, как изображенная на рис.12.1. Разность потенциалов разложения обоих электродов равна, очевидно, электродвижущей силе разложения данного раство— 469 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð ра; если один из электродов не поляризующийся, то она совпадает с потенциалом разложения второго электрода. Большей частью, по крайней мере при не слишком больших силах поляризующего тока, потенциалы разложения металлов на платине равны по величине и обратны по знаку электродным потенциалам этих металлов с соответствующими поправками на активности раствора. Например, для меди в 1 н. растворе Cu++(точнее, при активности Cu++, равной единице) получим −0,34 вольта. Почти ту же величину, немного увеличенную из-за концентрационной поляризации, имеет потенциал разложения медного раствора той же концентрации на платине. Когда он достигается, платина начинает покрываться мелью и превращаться в медный электрод. При выделении газов на электродах, а также в некоторых других случаях нарушается из-за перенапряжения. ϭϮ͘ϭ͘ϱ͘ʶ̶̶̶̨̨̨̛̛̛̦̖̦̯̬̦̦̪̣̬̌̌́́̌́̚͘ Электролиз сопровождается изменением концентрации электролита около электродов, что ведет к появлению обратной электродвижущей силы. Это явление называется концентрационной поляризацией. Сущность его можно пояснить на уже упоминавшемся примере электролиза раствора азотнокислого серебра между двумя серебряными электродами. Выделение серебра на катоде уменьшает около него концентрацию растворенного AgNO3, а растворение серебра на аноде увеличивает ее около последнего. В результате получается концентрационный элемент с обратной электродвижущей силой концентрационной поляризации. Возникающая разность концентраций выравнивается путем диффузии, но лишь частично; даже при перемешивании раствора, значительно уменьшающем концентрационную поляризацию, около электродов всегда остаются так называемые диффузионные слои, не участвующие в общем движении жидкости при размешивании. После того как приложенная электродвижущая сила достигла потенциала разложения, дальнейший ее рост увели— 470 — ÐƺǫǁǬǃǀǎÐǌǁǬǭǰ͠ǮǁǀƿǪ Ð͟Ǯǁǎ͠ǀƿǪǅǀǀÐǀÐ͟Ǭ͠ǬǃǪ͟͠ǎƾǬǃǀǎ чивает силу тока, однако не безгранично. Скорость диффузии растет пропорционально разности концентраций электролита в общем объеме раствора и около электрода. Первая остается практически постоянной, вторая же падает с увеличением скорости разряда. Когда они доходит до малой величины, то разность концентраций достигает наибольшей величины, практически равной концентрации в объеме, и скорость диффузии достигает предела, пропорционального ей. Дальнейшее увеличение приложенной электродвижущей силы уже не вызывает увеличения силы тока, так как скорость подвода ионов к электроду достигла предела. Эта максимальная сила тока, называемая током насыщения, дает на кривой напряжения горизонтальный участок BC. В точке C достигается потенциал разложения какого-нибудь другого иона (например, H+ из воды), и ток снова растет за счет разряда этого иона до тез пор, пока не будет достигнут его ток насыщения DF, и т. д. ϭϮ͘ϭ͘ϲ͘ʪ̶̨̛̛̖̪̣̬́̌́̚͘ Деполяризацией называют уменьшение обратной электродвижущей силы поляризации путем более или менее полного устранения ее причин. В случае концентрационной поляризации деполяризация частично достигается размешиванием жидкости или вращением электродов. Полностью она не может быть устранена из-за упоминавшегося ранее диффузионного слоя жидкости, окружающего электроды. Концентрационная поляризация сильно уменьшается при применении насыщенного раствора с избытком твердой соли. Это использовано в некоторых технических элементах и в стандартном элементе Вестона; для этой цели в последний вводят кристаллы твердого сернокислого кадмия. Для катодной реакции восстановления деполяризаторами могут служить разнообразные окислители. Например, водородный электрод деполяризуется кислородом воздуха или такими окислителями, как MnO2 в элементе Лекланше, H2CrO4 в элементе Грене и HNO3 в элементе Бунзена. В качестве катодных деполяризаторов часто применяют разнообразные органи— 471 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð ческие окислители, продукты восстановления которых и служат целью электролиза. Таким путем, например, получают на катоде анилин и другие промежуточные продукты восстановления из нитробензола. Анодными деполяризаторами, наоборот, служат разные восстановители, например этиловый спирт, окисляющийся до ацетальдегида и уксусной кислоты. Деполяризаторы снижают потенциалы разложения и уменьшают этим расход энергии при электролизе. ϭϮ͘ϭ͘ϳ͘ʿ̛̖̬̖̦̪̬̙̖̦̖̌́͘ Если потенциал выделения отличается от термодинамического обратимого электродного потенциала, то мы имеем перенапряжение. Поясним это явление несколькими примерами. Черненая платина, насыщенная водородом под атмосферным давлением, дает в растворе с активностью H+, равной единице, водородный электрод, потенциал которого в водородной шкале равен нулю. Этот электрод почти совершенно обратим. Выделение водорода на катоде из черненой платины, если сила тока не очень велика, начинается при том же потенциале. С точки зрения термодинамики равновесных процессов замена платины другим нерастворимым металлом не должна влиять на величину потенциала разложения, так как такой металл не участвует в электродном процессе и служит лишь проводником электронов. На самом же деле уже замена черненой платины гладкой платиной вызывает повышение потенциала разложения водорода на 0,2 вольта, а на ртути он растет еще значительно больше. Этот избыточный потенциал, повышающий положение водорода в ряду напряжений, и называется перенапряжением. Перенапряжение водорода можно найти в виде электродвижущей силы разложения в цепи, составленной из данного водородного электрода и другого обратимого водородного электрода. Осуществить обратимые кислородные электроды вообще невозможно. На любом металле кислород дает перенапряжение, которое увеличивает его потенциал разложения, т.е. по— 472 — ÐƸǁǬǭǰ͠ǮǭǪ͟ǀǁǁǎ͠ǃǊǬÐǎǫǁǬǃǀǎ нижает его в ряду напряжений. На гладкой платине перенапряжение кислорода равно примерно 0,5 вольта. Обратимая электродвижущая сила кислородно-водородного элемента при атмосферном давлении равна 1,23 вольта. Если при электродах из гладкой платины опыт дает для электродвижущей силы разложения 1,7 вольта, то это объясняется тем, что к ней прибавляются перенапряжение кислорода, а также небольшое перенапряжение водорода. Измерять перенапряжение можно разными способами. Чаще всего применяют методы, описанные в (Потенциалы разложения). Такие измерения производились многократно и не всегда с согласными результатами, так как перенапряжение сильно зависит от чистоты металла и состояния его поверхности. Иногда различают перенапряжение, отвечающее началу выделения пузырьков газа (или другого продукта электролиза) на электроде, от перенапряжения, которое отвечает изгибу на кривой напряжения. Обе величины могут не совпадать из-за пересыщения или других осложняющих причин. Так как перенапряжение, особенно водородное, имеет большое теоретическое и прикладное значение, то ему было посвящено много экспериментальных и теоретических исследований. Несмотря на это, многие стороны вопроса продолжают и сейчас оставаться неясными. ϭϮ͘Ϯ͘ˑ̡̨̡̛̛̣̖̯̬̪̣̣̬̦̼̖̣̖̦̌́́̏́͘ ϭϮ͘Ϯ͘ϭ͘ʯ̵̨̨̨̨̨̨̛̛̛̭̥̭̯̪̖̬̦̭̯̦̦̯̙̖̦̯̬̌̏̽̏̐̌́́̌́̔̌̚͘ Ртуть на границе с водой образует выпуклый мениск из-за поверхностного натяжения. Сообщая ртути заряд, можно изменить ее поверхностное натяжение и кривизну мениска. Это явление легко наблюдать в простом приборе, называемом капиллярным электрометром (рис. 12.3). В U-образную трубку и в шарик прибора наливают ртуть и вводят в них электроды. Поверх ртути наливают раствор электролита, лучше всего 2н серную кислоту. При соединении обоих электродов с источником тока ртуть получает заряд, — 473 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð ее поверхностное натяжение изменяется, и мениск в капилляре U-образной трубки перемещается. Этим прибором раньше часто пользовались при измерении электродвижущих сил в качестве нулевого инструмента, но для точных измерений он не годится, так как его чувствительность не превосходит 0,5–1 милливольта. Рис. 12.3. Капиллярный электрометр Изменение поверхностного натяжения ртути с величиной заряда связано с образованием двойного электрического слоя на ее границе с раствором. Поверхность ртути на границе с ним заряжается положительно. Этот заряд ей сообщают ионы ртути, переходящие на нее из раствора, даже если их концентрация в растворе ничтожна, так как электролитическая упругость растворения ртути очень мала. Положительные заряды на поверхности ртути друг от друга отталкиваются, что уменьшает ее поверхностное натяжение по сравнению с тем, которое она имела бы в отсутствие заряда. Если сообщить ртути извне отрицательный потенциал (катодная поляризация), то число положительных зарядов на ее поверхности уменьшается, и поверхностное натяжение растет до тех пор, пока потенциал не дойдет до величины, отвечающей снятию всего заряда с поверхности. В этой точке поверх— 474 — ÐƸǁǬǭǰ͠ǮǭǪ͟ǀǁǁǎ͠ǃǊǬÐǎǫǁǬǃǀǎ ностное натяжение ртути достигает максимума. Дальнейшее повышение отрицательного потенциала сообщает ртути отрицательный заряд, и поверхностное натяжение ее снова начинает падать из-за взаимного отталкивания перешедших на ее поверхность отрицательных зарядов. Описанные явления, называемые электрокапиллярными, были впервые изучены Липманом (1873). Приведенное выше их объяснение было дано Нернстом (1894), подтвердившим его прибавлением к раствору возрастающих количеств CN−, связывающих Hg2++ в прочный комплекс. Уменьшение концентрации последних в растворе сдвигало потенциал ртути в отрицательную сторону и вызывало те же изменения в поверхностном натяжении, как и катодная поляризация внешним током. ϭϮ͘Ϯ͘Ϯ͘ˑ̡̨̡̡̛̛̣̖̯̬̪̣̣̬̦̬̌́̌́̏̌́͘ Описанная зависимость поверхностного натяжения ртути или другого материала от приложенного поляризующего потенциала E изображается электрокапиллярной кривой, близкой к параболе. Типичный пример ее дан на рис. 12.4 (ртуть на границе с чистой водой). Рис. 12.4. Электрокапиллярная кривая Максимум ее отвечает максимальной величине поверхностного натяжения, когда заряд поверхности ртути равен нулю. Он наступает при некотором потенциале Emax. — 475 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð Изучение электрокапиллярных кривых в разных растворах велось Гюи (1903–1906) и рядом других авторов. Для получения электрокапиллярных кривых обычно пользуются капиллярным электрометром Липмана, изображенным на рис. 12.5. Рис. 12.5. Капиллярный электрометр Липмана Он сделан из наполненного ртутью суженного внизу капилляра, опущенного в раствор. Его соединяют с отрицательным электродом поляризующего источника тока, положительный электрод которого соединяют с неполяризующимся вспомогательным электродом, например каломельным, опущенным в тот же раствор. Смещенный при поляризации мениск в конце капилляра возвращают в прежнее положение поднятием или опусканием резервуара с ртутью. Поверхностное натяжение измеряют высотой столба ртути, поддерживаемого мениском. Электрокапиллярная кривая выражается уравнением ∂σ (12.2) = −ε ∂E где ε — заряд, преходящий (в виде ионов) из раствора на ртуть при увеличении ее поверхности на 1 см2 при постоянном потенциале E. Оно может быть выведено из уравнения адсорбции Гиббса и уравнения для зависимости электродного потенциала — 476 — ÐƸǁǬǭǰ͠ǮǭǪ͟ǀǁǁǎ͠ǃǊǬÐǎǫǁǬǃǀǎ от концентрации ионов. В более общем виде уравнение электрокапиллярной кривой было получено А. Н. Фрумкиным (1922). Им же (1919) была выполнена проверка уравнения (11.2). ∂σ находилась из наклона электрокапиллярных Величина ∂E кривых, а ε — путем измерения заряда, переносимого каплями ртути, вытекающими из капилляра. Этот заряд перечислялся затем на 1см2 поверхности капель. Результаты проверки представлены в табл.12.1. Таблица 12.1. Проверка уравнения электрокапиллярной кривой (величины в кулон/см2 ) Раствор ε 106 – ∂σ ·106 ∂E 1н. NaCl+Hg2Cl2 47 50 1н. KOH+HgO 17 21 1н .H2SO4+Hg2SO4 39 39 1н.KNO3+0.01н.KJ+Hg2J2 90 86 –1.3 –1.5 1н. KOH+C4H9OH+HgO ϭϮ͘Ϯ͘ϯ͘ʦ̶̨̛̛̛̛̣̦̖̭̬́̌̔̍ ̡̨̡̡̛̛̦̣̖̯̬̪̣̣̬̦̱̬̱̌̾̌́̀̏̀͘ Прибавление к воде поверхностно-активных веществ, склонных адсорбироваться на границе с ртутью, понижает электрокапиллярную кривую и смещает ее максимум. Примером таких измерений может служить рис. 12.6, воспроизводящий данные для ртути в 1н. NaCl с добавкой разных количеств третичного амилового спирта. Такие изменения вызываются не только нейтральными молекулами, но и некоторыми склонными к адсорбции ионами. При этом анионы, например Cl−, Br−, I−, HS−, понижают левую ветвь электрокапиллярной кривой, где ртутная поверх— 477 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð ность заряжена положительно, и смещают Emax в сторону более отрицательных потенциалов, а некоторые катионы, как Tl+, N(C3H7)4+, понижают правую ветвь, где ртуть заряжена отрицательно, и смещают Emax в обратную сторону. В 0,5н. KI смещение Emax достигает 0,32 вольта в отрицательную сторону. Рис. 12.6. Электрокапиллярные кривые ртути в присутствии поверхностно-активных веществ Все эти изменения, как показал А. Н. Фрумкин, вызываются специфической адсорбцией молекул или ионов под действием адсорбционных сил. На ионы эти силы действуют одновременно с электростатическими силами их зарядов, так что, например, положительный заряд ртутной поверхности содействует адсорбции анионов, но она возможна также на незаряженной поверхности и даже при небольшом отрицательном ее заряде. Адсорбируемые молекулы и ионы внедряются в двойной слой и изменяют его строение, что вызывает смешение Emax. Вместе с тем их адсорбция уменьшает поверхностное натяжение и понижает электрокапиллярную кривую. Адсорбируются специфически также и молекулы растворителя, что объясняет влияние его природы на электрокапиллярные кривые. — 478 — ÐƸǁǬǭǰ͠ǮǭǪ͟ǀǁǁǎ͠ǃǊǬÐǎǫǁǬǃǀǎ Поверхностно-неактивные ионы, например Na+, K+, SO4–, H2PO4−, участвуют в образовании двойных слоев лишь своими зарядами и потому мало влияют на форму и положение электрокапиллярной кривой. В растворах Na2SO4, KH2PO4 и др. Emax остается таким же, как в чистой воде: на 0,48 вольта более отрицательным, чем потенциал нормального каломельного электрода. Природа металла сильно влияет на электрокапиллярную кривую. Например, для 33%-ной амальгамы таллия смещение Emax равно 0,45 вольта, а для жидкого галлия в щелочном растворе оно равно 0,4 вольта в отрицательную сторону по сравнению со ртутью. Значительные разницы Emax были также найдены для жидких Pb, Sn, Cd, Tl и др. в расплавленных электролитах (Карпачев, 1936–1940). Определение изменений поверхностного натяжения жидких металлов с зарядом можно производить не только с помощью капиллярного электрометра, но также по величине или форме вытекающих капель. Для этой же цели может служить измерение краевого угла пузырька газа или капли органической жидкости, сидящих в растворе на поверхности металла. Последний способ был применен и для получения электрокапиллярных кривых твердых тел. В точке Emax, где поверхностное натяжение максимально, вода плохо смачивает металл, но смачиваемость растет с удалением от этой точки как в сторону положительных, так и в сторону отрицательных потенциалов. Поэтому, если металлу, опущенному в щелочной раствор, сообщить сильный отрицательный заряд, то вода вытесняет жир с его поверхности. Этим можно объяснить процесс катодного обезжиривания металлов. По этой же причине в щелочном растворе, где потенциал водорода высок, а кислорода невелик, первый выделяется в виде мелких легко отрывающихся пузырьков, а второй в виде крупных и сильно прилипающих к электроду пузырьков. Из влияния заряда на смачиваемость можно сделать ряд других практических выводов. Для определения точки Emax твердых поверхностей может служить также адсорбционный метод: при достижении это— 479 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð го потенциала электрод, заряд которого становится равным нулю, перестает адсорбировать неспецифические адсорбируемые ионы данного знака заряда, что может быть обнаружено аналитическим путем. Принципиально новый способ получения электрокапиллярных кривых твердых тел был дан в работе П. А. Ребиндера и Е. Венстрем (1944), показавших, что твердость поверхности пирита и пластическая деформация олова на границе с растворами изменяются при катодной поляризации по кривой, точно повторяющей электрокапиллярную кривую. Объясняется это тем, что адсорбция одинаково влияет на поверхностное натяжение и на твердость. Эти же авторы нашли, что шлифование пирита карборундом в растворе NaCl идет на 17% быстрее при катодной поляризации до 1,6 вольта, отвечающей точке Emax. ϭϮ͘Ϯ͘ϰ͘ʿ̵̶̨̨̨̨̛̬̣̖̥̭̣̯̦̼̪̯̖̦̣̍̌̌̍̀̌̏͘ Уже указывалось, что современная наука не дает ни экспериментальных, ни теоретических путей для определения абсолютных величин потенциалов отдельных электродов. С этим связана неразрешимость важного вопроса о распределении электродвижещей силы гальванического элемента на границах раздела фаз, в частности на границах металл-металл и металл-раствор. Вернемся к рассмотрению этих вопросов в свете новых данных об электрокапиллярных явлениях. Если бы можно было построить электрод, потенциал которого заведомо равен нулю, и можно было бы пренебрегать скачками потенциала на границах металлическими проводниками, то задача определения абсолютных потенциалов была бы решена, так как измеренная электродвижущая сила такого электрода в комбинации с любым другим электродом была бы просто равна потенциалу последнего. Долгое время считали это возможным. В точке максимума электрокапиллярной кривой заряд ртути равен нулю. По классическим представлениям теории гальванических элементов Нернста отсутствию зарядов на поверхности металлов отвечают отсутствие двойного слоя — 480 — ÐƸǁǬǭǰ͠ǮǭǪ͟ǀǁǁǎ͠ǃǊǬÐǎǫǁǬǃǀǎ и нулевая разность потенциалов между металлом и раствором. Поэтому ртуть в максимуме электрокапиллярной кривой считали нулевым электродом, и потенциал нормального каломельного электрода относительно нее (–0,48 вольта) считали его абсолютным потенциалом. Тот же результат давали капельные электроды в виде тонкой струйки ртути, вытекающей из капилляра в раствор; образующиеся капли уносят ионы ртути из раствора до тех пор, пока их концентрация не достигнет величины, при которой они перестают переходить на постоянно возобновляющуюся у отверстия капилляра поверхность ртути, заряд которой таким образом автоматически падает до нуля. А. Н. Фрумкин в ряде работ доказал ошибочность всех этих предположений. Отсутствие заряда на поверхности металла вовсе не означает отсутствия двойного слоя и разности потенциала между металлом и раствором. Адсорбированные из раствора молекулы и ионы или разрядившиеся атомы образуют около поверхности металла двойные слои адсорбированного происхождения, целиком лежащие в жидкости и дающие свои собственные скачки потенциала даже тогда, когда заряд на поверхности металла отсутствует. Для образования таких двойных слоев уже достаточно наличия молекул самого растворителя. По всем этим причинам максимуму электрокапиллярной кривой, так же как и другим случаям, где металл не заряжен, вовсе не отвечает отсутствие разности потенциала между металлом и раствором. Эти положения экспериментально доказываются данными, изложенными в предыдущем параграфе. Положение максимума электрокапиллярной кривой зависит от состава раствора и природы металла, а не остается постоянным. Ясно, что это было бы невозможным, если бы в Emax потенциал равнялся нулю. Один и тот же каломельный электрод имеет –0,48 вольта против ртути и –0,9 вольта против жидкого галлия, если оба металла поляризованы до максимума. Оба эти потенциала не имеют ничего общего с абсолютным потенциалом каломельного электрода, и все литературные данные относительно абсолютных потенциалов электродов лишены смысла. — 481 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð ϭϮ͘ϯ͘ˑ̸̡̨̡̡̛̛̛̛̣̖̯̬̦̖̯̖̭̖̣̖̦́̏́͘ ϭϮ͘ϯ͘ϭ͘ʪ̴̴̨̨̨̨̛̛̱̦̦̼̜̜̦̜̭̣̜̔̏̚ ̸̶̡̨̡̡̨̛̛̛̛̛̣̖̯̬̦̖̯̖̭̜̪̯̖̦̣̾̌͘ При движении раствора электролита относительно граничащей с ней твердой поверхности и, обратно, при движении этой поверхности относительно раствора возникают рассматриваемые ниже электрокинетические явления. Они зависят от особенностей строения двойного электрического слоя на границах раздела фаз. По первоначальным представлениям Гельмгольца двойной электрический слой имеет плоское строение. Он образован, подобно очень тонкому плоскому конденсатору, из двух прилегающих друг к другу слоев противоположных зарядов, разделенных расстоянием порядка атомных диаметров, т.е. 10–8 см (рис. 12.7а). Рис. 12.7. Плоский (а) и диффузионный (б) двойные слои На самом же деле, как показал Гюи (1906), двойной слой имеет диффузное строение, так как тепловые движения растворенных ионов нарушают их плоское расположение в об— 482 — ÐƸǁǬǭǰ͠ǮǭǀǃǬǰǀǆǬǯǭǀǬÐǎǫǁǬǃǀǎ кладке двойного слоя, обращенной к раствору, вследствие чего она размывается и проникает в раствор на некоторую глубину, причем плотность ее заряда быстро убывает с расстоянием от границы раздела (рис. 12.7б). Это диффузное распределение зарядов было уже рассмотрено в виде ионных атмосфер теории электролитов Дебая и Гюккеля. В диффузном двойном слое согласно современным представлениям часть зарядов плоско прилегает к твердой поверхности, прочно с ней связана и не размывается тепловыми движениями. Это плоская часть двойного слоя, отвечающая представлениям Гельмгольца. Скачок потенциала в ней обозначим через ψ. Вторая, диффузная часть двойного слоя, отвечающая представлениям Гюи, более или менее далеко проникает в глубь жидкости и увлекается с нею при ее движении. Скачок потенциала в ней обозначим через ξ. Его называют электрокинетическим или ξ (дзета)-потенциалом. Сумма обоих E= ψ+ξ есть обыкновенный «нернстовский» потенциал, измеряемый в гальваническом элементе или вычисляемый из термодинамических данных уже известными нам способами. До тех пор, пока речь шла о таких измерениях при вычислениях, строение двойного слоя и распределение его потенциала между обоими слагаемыми не было существенным, но при движении жидкости относительно твердой поверхности и в некоторых других явлениях это распределение играет решающую роль. Три типичных случая распределения скачка потенциала в двойном слое изображены на рис. 12.8. Общий скачок потенциала E во всех этих случаях один и тот же, но он различно распределен между обоими слагаемыми. Кривая в левой части рисунка отвечает плоскому двойному слою, когда ξ =0 и E=ψ; верхняя кривая в правой части рисунка относится к случаю, когда E и ξ одного знака, а нижняя — когда они различны. Потенциал ψ плоской части двойного слоя быстро падает по линейному закону плоского конденсатора, а электрокинетический потенциал диффузной части двойного — 483 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð Рис. 12.8. Распределение скачка потенциалов в двойных слоях слоя падает гораздо медленнее, по показательному закону, как в ионной атмосфере. Строение двойного слоя сильно изменяется при добавлении электролитов к раствору, в особенности если ион, знак заряда которого противоположен знаку заряда твердой поверхности, имеет высокую валентность. Еще сильнее влияние поверхностно-активных веществ, адсорбирующихся на твердой поверхности. Они располагаются на ней тонким слоем толщиной в одну или несколько молекул. Поэтому очень небольшие количества адсорбируемых веществ достаточны для того, чтобы строение двойного слоя и величина ξ-потенциала сильно изменились. Адсорбция вызывается специфическими адсорбционными силами. Адсорбированные вещества сосредоточиваются в плоской части двойного слоя. Роль адсорбции в строении двойного слоя была детально изучена в ряде новых работ А. Н. Фрумкина с сотрудниками, применивших для этого разные методы. Эти работы легли в основу современных представлений о двойном слое и о природе электрических явлений на границах фаз. При движении жидкости относительно твердой поверхности плоская часть AB двойного слоя остается с ней связанной, — 484 — ÐƸǁǬǭǰ͠ǮǭǀǃǬǰǀǆǬǯǭǀǬÐǎǫǁǬǃǀǎ тогда как диффузная часть BC увлекается жидкостью. Поэтому электрокинетические явления определяются не общим скачком потенциала E, а электрокинетическим потенциалом ξ. Это объясняет сильное влияние на них электролитов и особенно адсорбируемых веществ. В работе Фрейндлиха и Рона (1920), изменявших одновременно E и ξ, было впервые показано, что обе величины не тождественны и даже могут иметь разные знаки. Согласно теории плотности заряда в плоской части двойного слоя пропорциональна концентрация электролита, если последняя не очень велика. В диффузной части двойного слоя, как следует из теории Дебая и Гюккеля, плотность заряда пропорциональна корню квадратному из концентрации. Из этих соотношений следует, что в сильно разбавленных растворах большая часть заряда двойного слоя сосредоточена в его диффузной части, а в более концентрированных — в плоской. Иначе говоря, с увеличением концентрации ионов ни все ближе подтягиваются к твердой поверхности, диффузная часть двойного слоя становится меньше, и ξ-потенциал падает. В достаточно концентрированных растворах он близок к нулю, и электрокинетические явления становятся мало заметными. ϭϮ͘ϯ͘Ϯ͘ʫ̡̨̨̨̨̨̥̭̯̜̦̭̣̽̔̏̐́͘ Подобно конденсатору двойной слой имеет электрическую емкость, зависящую от его строения. Ее можно в принципе, измерять теми же методами, как у обыкновенного конденсатора: по количеству электричества, необходимому для увеличения потенциала на единицу. Другой способ основан на получении электрокапиллярной кривой, из кривизны которой может быть найдена емкость ∂2 σ ∂ε =− = емкость ∂E ∂E2 Изучение емкости двойных слоев, особенно в комбинации с адсорбционными измерениями, дает детальные сведения об их строении. При уменьшении степени диффузности емкость растет, так как заряды сближаются. В согласии с этим — 485 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð А. Н. Фрумкин, М.Н. Проскурин и М.И. Ворсина (1939) нашли, что увеличение концентрации раствора KCl и других электролитов (вызывающее, как было указано, уменьшение диффузии) увеличивает емкость двойного слоя ртути. При данной концентрации кривая зависимости емкости от поляризующего потенциала имеет минимум точно при том потенциале, который отвечает максимуму электрокапиллярной кривой. В этой точке поверхность ртути не заряжена и поэтому двойной слой наиболее диффузен, а емкость наименьшая. Минимум исчезает в 0,1н. и более концентрированных растворах KCl, где двойной слой становится плоским. Эти исследования впервые дали наглядные экспериментальные доказательства диффузного строения двойных слоев. Из измеренных емкостей были вычислены ξ-потенциалы в удовлетворительном согласии с тем, что дает теория. Другой, не зависящий от часто противоречивых электрокинетических измерений способ вычисления ξ-потенциала основан на измерении перенапряжения η в функции от концентрации электролитов. При постоянной плотности тока и постоянной концентрации теория дает η = const–ξ. Величины ξ, вычисленные из измеренных η, находятся в хорошем согласии с результатами предыдущего метода и с теорией. Величину const можно найти из предельного η при больших добавках электролитов, когда ξĺ0. ϭϮ͘ϯ͘ϯ͘ˑ̡̨̨̨̣̖̯̬̭̥̭͘ В электрическом поле возникает движение жидкости относительно твердой поверхности. Это явление, называемое электроосмосом, можно наблюдать в приборе, изображенном на рис. 12.9. Капилляр К соединяет два сосуда, наполненные жидкостью, с введенными в них электродами Е, соединенными с источниками тока. Скорость течения жидкости через капилляр может быть измерена по перемещению ее мениска в трубке М. Капилляр может быть заменен пористой перегородкой. Направление течения зависит от материала твердой поверхности и от состава жидкости. Например, вода в стеклянном капилля— 486 — ÐƸǁǬǭǰ͠ǮǭǀǃǬǰǀǆǬǯǭǀǬÐǎǫǁǬǃǀǎ Рис. 12.9. Схема измерения электроосмоса ре заряжается относительно его стенок положительно потому и течет в направлении к отрицательному электроду. Электроосмос, так же как и рассматриваемый ниже электрофорез, был открыт в России Ф.Ф. Рейсом (1809). Теория его была дана Гельмгольцом (1879) и дополнена Смолуховским (1903), Перреном (1904) и др. Это явление возникает вследствие образования двойного электрического слоя на границе твердого тела с жидкостью. В случае диэлектрика он возникает из-за неодинаковой адсорбции ионов обоих знаков. Благодаря этому двойному слою твердая поверхность и прилегающая к ней тонкая пленка жидкости с плоской частью двойного слоя заряжаются одним знаком, а остальной объем жидкости, содержащий диффузную часть двойного слоя, — другим знаком, что вызывает его движение в электрическом поле. Таки образом, это явление существенно зависит от знака и величины электрокинетического потенциала ξ. Если приложенная электродвижущая сила равна Е, сечение капилляра (или сумма сечений пор) равно q, расстояние между электродами равно l, диэлектрическая постоянная жидкости равна D и ее вязкость равна η, то для скорости и течения жидкости теория дает ξDE (12.3) u=q 4πηl Это уравнение получается из условия равенства силы трения и приложенной электродвижущей силы. Оно не совсем точно из-за изменения электропроводности жидкости в капилляре вследствие адсорбции ионов его стенкам и переноса их движущейся жидкостью. — 487 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð Так как в (12.3) все величины, кроме ξ, известны или могут быть изменены, то из наблюдений электроосмоса можно найти величину электрокинетического потенциала большей частью в удовлетворительном согласии с величиной, получаемой из других рассматриваемых ниже электрокинетических явлений. Она обычно не превышает 0,05–0,1 вольта. Поэтому для получения заметных скоростей электроосмоса приложенное поле Е должно иметь большое напряжение порядка десятков и сотен вольт. Например, при градиенте потенциала в 1 вольт/см и ξ=0,05 вольта скорость u равна лишь 1·10–3см/ сек при q=0,01см2. Электроосмос получил ряд технических применений. Например, помещая водные Гали (глину, силикагель, клей и др.) между сетчатыми электродами, можно их обезвоживать. Дубление кожи сильно ускоряется электроосмотическим прониканием дубящего раствора в ее поры, если ее поместить в этом растворе между двумя электродами. Электроосмосом воды через ряд пористых диафрагм можно ее очистить от большинства взвешенных и растворенных примесей; этот способ очистки мало уступает дистилляции. Большинство твердых поверхностей (стекло, глина, асбест, благородные металлы, шерсть и др.) заряжается отрицательно относительно воды. Неблагородные металлы, ряд окислов, сульфидов и других неорганических соединений, наоборот, заряжаются положительно. Прибавление электролитов, особенно поливалентных, сильно влияет на величину ξ-потенциала, вплоть до перемены его знака, что сопровождается переменой направления электроосмоса. Примером довольно сложных соотношений между ξ-потенциалом, концентрацией и валентностью ионов может служить рис.12.10, относящийся к границе воды со стеклом. Прибавление 0,2 мг/л изменяют его направление на обратное. Как уже указывалось, в более концентрированных растворах ξ-потенциал приближается к нулю, и электроосмос прекращается. Еще большее влияние, чем электролиты, оказывают сильно поверхностно-активные вещества, хорошо адсорбируемые — 488 — ÐƸǁǬǭǰ͠ǮǭǀǃǬǰǀǆǬǯǭǀǬÐǎǫǁǬǃǀǎ Рис. 12.10. Зависимость ξ -потенциала от концентрации электролита стенкой Часто ничтожные их количества оказывают огромное влияние на величину ξ-потенциала и на скорость электроосмоса, а также на другие электрокинетические явления. ϭϮ͘ϯ͘ϰ͘ʿ̶̸̨̛̛̯̖̦̣̯̖̖̦̌́͘ Явление это обратно электроосмосу: при продавливании жидкости через капилляр или пористую перегородку прибора, изображенную на рис.10.9, между электродами возникает разность потенциалов, для которой теория дает ξD P < E= (12.4) 4πη χ где P — гидростатическое давление, χ — удельная электропроводность жидкости, а остальные значения те же, что в (12.1). Потенциалы течения чаще всего применяют для нахождения величин электрокинетического потенциала ξ. В частности, этим путем было выполнено уже упоминавшееся исследование Фрейндлиха и Рона, в котором было экспериментально доказано, что ξ-потенциал не тождествен с общим скачком потенциала во всем двойном слое. ϭϮ͘ϯ͘ϱ͘ˑ̴̡̨̨̣̖̯̬̬̖̚͘ Если твердая фаза образована частицами, взвешенными в жидкости, то в электрическом поле возникает явление, об— 489 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð ратное электроосмосу: взвешенные твердые частицы вместе с прилегающими к ним тонкими пленками жидкости движутся от одного электрода к другому в жидкости неподвижной или же движущейся в обратном направлении, но гораздо медленнее. Такое движение называют электрофорезом или катафорезом. Его можно наблюдать в приборах, похожих на те, которые применяют для измерения чисел переноса ионов по Гитторфу, например, в U-образной трубке с электродами на обоих ее концах. Скорость электрофореза подсчитывается по тому же уравнению, что и скорость электроосмоса: ξDE u= (12.5) 4πηl Примечательно, что в это уравнение не входят ни заряд, ни величина частиц. Действительно опыт подтверждает, что частицы разных размеров и зарядов движутся почти одинаково быстро. Скорость электрофореза так же зависит от концентрации электролита, валентности его ионов и присутствия поверхностно-активных веществ, как скорость электроосмоса. Электрофоретические измерения широко применяют при изучении коллоидов, так как они дат сведения о величинах ξ-потенциалов на поверхности коллоидных частиц, от которых зависит стабильность коллоидных растворов. Заряд коллоидной частицы в диспергирующей среде зависит как от ее строения, так и от присутствия электролитов и поверхностно-активных веществ в растворе. Они могут изменить величину ξ-потенциала, а следовательно, скорость и направление электрофореза. При ξ=0 последний прекращается. Это изоэлектрическая точка, около которой легче всего происходит коагуляция коллоидных частиц в более крупные агрегаты и выпадение коллоида из раствора. Чем выше валентность иона, вводимого в раствор, тем меньшая его концентрация нужна для достижения изоэлектрической точки и коагуляции коллоида (правило Гарди-Шульца, 1882). Дальнейшее увеличение концентрации электролита может изменить знак ξ-потенциала на обратный. — 490 — ÐƸǁǬǭǰ͠ǮǭǀǃǬǰǀǆǬǯǭǀǬÐǎǫǁǬǃǀǎ Электрофорез получил ряд технических применений, например для выделения торфа, каучука из суспензии или эмульсии. Недавно Тизелиус (1938) предложил получивший быстрое распространение метод электрофоретического анализа сложных, главным образом, белковых смесей. Он основан на том, что при электрофорезе каждый компонент коллоидного раствора образует свою независимо движущуюся границу раздела. С помощью специальных оптических приспособлений можно фотографировать эти границы и находить количественные соотношения между составными частями смеси. Можно легко показать связь между уравнением (12.5) для скорости электрофореза крупных коллоидных частиц и уравнением для скорости движения ионов, полученным из закона Стокса. Различие между ионом и более крупной коллоидной частицей заключается в том, что вокруг первого отсутствует плоская часть двойного слоя: ионная атмосфера вокруг иона целиком диффузна. По тому скачок потенциала между ионом и раствором отвечает величине ξ. Если ион имеет заряд ze и радиус r, то по формуле для потенциала шара ze ξ= Dr что с (12.5) дает zeE u= 4πηrl Так как, очевидно, действующая на заряд иона электричеzeE (произведение из заряда на градиент потенская сила K = l циала приложенного поля), то это выражение совпадает с для скорости движения ионов за исключением коэффициента 1/4 вместо 1/6; эта разница может быть теоретически обоснована. ϭϮ͘ϯ͘ϲ͘ʿ̶̨̨̛̛̯̖̦̣̼̭̙̖̦̌̌̔́͘ Если заряженные частицы движутся в жидкости, то в последней возникает электрическое поле в направлении этого — 491 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð движения. Его можно, например, наблюдать при оседании взвешенного осадка в жидкости, наполняющей вертикальную трубку, если вверх и низ ее ввести электроды. Возникающая между последними разность потенциалов называется потенциалом осаждения. Это явление, открытое Дорном (1878), обратно электрофорезу и подчиняется тем же законам. Оно не нашло еще интересных применений. ϭϮ͘ϰ͘ˑ̵̸̸̸̵̡̨̡̨̨̡̨̨̛̛̛̛̛̣̖̯̬̥̖̭̖̥̖̯̼̭̯̭̯̦̼̔̏̔͘ Для очистки сточных вод от различных растворимых и диспергированных примесей применяют процессы анодного окисления, катодного восстановления, электрокоагуляции, электрофлотации и электродиализа. Все эти процессы протекают на электродах при пропускании через воду постоянного электрического тока. Электрохимические методы позволяют извлекать из сточных вод ценные продукты по относительно простой автоматизированной технологической схеме очистки без использования химических реагентов. Эффективность электрохимических методов оценивается рядом факторов: плотностью тока, напряжением, коэффициентом полезного использования напряжения, выходом по току, выходом по энергии. Напряжение в электролизе складывается из разности электродных потенциалов и падением напряжения в растворе: (12.6) u = ϕa − ϕ k + ∆ϕa + ∆Uýë + ∆ϕ k + ∆Uäèô ∆ϕa и ∆ϕ k — величина анодной и катодной поляризации; ϕa и ϕ k — равновесные потенциалы анода и катода; ∆Uýë и ∆Uäèô — падение напряжения в электролите и диафрагме. Падение напряжения в электролите (сточной воде) при отсутствии пузырьков определяется по закону Ома. (12.7) ∆Uýë = ipδ i — плотность тока в сточной воде (а/см2); р — удельное сопротивление (ом*см); δ — расстояние между электродами (см). — 492 — ÐƸǁǬǭǰ͠ǮǲǀǂǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ При выделении газовых пузырьков, вследствие удлинения потока между электродами ∆Uýë возрастает. Отношение (12.8) η = ( Ia − Ik )U Выход по току — это отношение теоретически необходимого количества ( Закон Фарадея) к практически затраченному, которое выражают в долях единицы или в процентах. ϭϮ͘ϰ͘ϭ͘ʤ̨̨̨̡̡̨̨̨̨̛̛̛̛̦̦̖̭̣̖̦̖̯̦̖̭̭̯̦̣̖̦̖̔̌̔̏̌̏͘ На первый взгляд этот процесс тривиален. На положительном электроде-аноде ионы отдают электроны, т.е. протекает реакция электрохимического окисления, на отрицательном электроде катода происходит присоединение электронов, т.е. протекают реакции восстановления. Эти процессы разработаны для очистки сточных вод от растворимых примесей — роданидов, цианидов, аминов, спиртов, альдегидов, нитросоединений, азокрасителей, сульфидов, меркаптанов и др. В результате в процессе электрохимического окисления вещества находящиеся в сточных водах полностью распадаются с образованием СО2, NH3 и воды, и образуются более простые нетоксичные вещества, которые удаляются более простыми методами. В качестве анода используют различные нерастворимые электролитические материалы — графит, магнетит, диоксиды свинца, марганца, рутения, которые наносят на катоды, которые изготавливают из молибдена, сплава вольфрама с железом, никелем, из графита нержавеющей стали и др. материалов покрытых молибденом, вольфрамом или их сплавами. Процесс, как правило, проводят в электролизерах с диафрагмой или без нее. Кроме основных процессов электроокисления и восстановления одновременно может протекать электрофлотация, электрофорез, электрокоагуляция. Сточные воды, содержащие цианиды — это продукты черной, цветной металлургии и химической промышленности. В состав вод простых цианидов (KCN, NaCN) входят комплексные цианиды (Zn, Cu, Fe). рH таких растворов равен 8–12. — 493 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð Анодное окисление протекает по схеме: CN − + 2OH − − 2e → CNO − + H2O CNO − + 2H2O → NH4 + CO3− Окисление может быть проведено и с образованием азота: 2CNO − + 4OH − − 6e → 2CO2 + N2 + 2H2O Обычно дня повышения электропроводности сточных вод и снижения энергии к водам добавляют NaCl . Получаем 2Cl − − 2e → Cl2 CN − + 2OH − + Cl2 → CNO − + H2O + 2Cl − 2CNO − + 4OH − + 3Cl2 → 2CO2 ↑ +6Cl − + N2 ↑ +2H2O Роданиды разрушаются по схеме. CNS − + 10OH − + 8e → CNO + SO42− + 5H2O Сульфид-ионы при рН = 7 окисляются до сульфатов. Если РН<7 то может образоваться элементарная сера. Окисление фенолов в присутствии хлоридов в сточной воде протекает по реакции 4OH − − 4e → 2H2O + O2 ;2H + + 2e → H2 2Cl − − 2e → Cl2 ; Cl2 + H2O → HClO + HCl HCl + OH − → H2O + ClO − 12ClO − + 6H2O − 12e → 4HClO3 + 8HCl + 3O2 C6 H5OH + 14O → 6CO2 + 3H2O Катодное восстановление применяют для удаления из сточных вод ионов металлов с получением осадков для перевода загрязняющего компонента в менее токсичные соединения или в легко выводимую из воды форму (осадок). Его можно использовать для очистки сточных вод от ионов тяжелых металлов Pb2+, Sn2+, Ng2+, Cu2+, As3+, Cr6+. Катодное восстановление металлов происходит по схеме: Men+ + ne → Me0 — 494 — ÐƸǁǬǭǰ͠ǮǲǀǂǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ При этом металлы, осаждающиеся на катоде, могут быть рекупированы. Например, при восстановлении соединений Сr была достигнуты высокая степень очистки — концентрация снижалась с 1000 до 1 мг/л. При электролизе сточных вод, содержащих Н2СrO7 оптимальное значение pН = 2, а плотность тока 0,2–2 а/дм2. Реакция восстановления протекает следующим образом: Cr2O72− + 14H + + 12e → 2Cr + 7 H2O Очистку сточных вод от ионов Hg2+, Pb2+, Cd2+, Cu2+ проводят на катодах, состоящих из смеси угольного и сернистого порошков в соотношении C:S от 80:20 до 20:80 при pН < 7. Примером реакции, обеспечивающей удаление загрязнения в газовую фазу, является очистка от нитратов аммония. При восстановлении нитрата аммония на графитовом электроде, он превращается в нитрат аммония, который разлагается при нагревании до элементарного азота: NH4 NO3 + 2H + + 2e → NH4 NO2 + H2O NH4 NO2 → N2 + 2H2O Повышенная токсичность органических веществ, как правило, связана с наличием в молекуле атомов галогенов, альдегидной, аминной, нитратной, нитритной групп. Таким образом, продукты восстановления, например, альдегидов и кетонов — спирты и углеводороды будут менее токсичны. Потеря атома галогена приводит к тому же результату: RCl + 2e + H + → R − H + Cl − Рассмотрим процесс анодного растворения, на примере железа. В щелочной среде реакция идет в две стадии: Fe − e + OH − → Fe ( OH )àäñ Fe ( OH )àäñ + OH − − e → HFeO2− + H + или Fe ( OH )àäñ + OH − − 2e → FeO ( OH ) + H + На первой стадии, включающей адсорбцию гидроксида на железном электроде и потерю первого электрона, образует— 495 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð ся промежуточное кислородосодержащее соединение одновалентного железа. На второй стадии реакция протекает по двум возможным направлениям и завершается образованием двух или трехвалентного железа. Отмечу, что общая скорость процесса анодного растворения лимитируется второй стадией. В кислой среде протекает следующая реакция: Fe − e + OH − → Fe ( OH )àäñ Fe ( OH )àäñ + Fe → Fe ( FeOH )àäñ ( Fe ( FeOH )àäñ + OH − − 2e → Fe ( OH )àäñ + Fe OH + ( ) ) Fe OH + + H + → Fe2+ + H2O Рис. 12.11. Схема установки. Лимитирующей стадией является предпоследняя реакция. Скорость электрохимического растворения металла определяется величиной тока, которая зависит от приложенного напряжения (потенциала анода) — ψ . Процессы анодного окисления используются для очистки сточных вод целлюлозно-бумажных, нефтеперерабатывающих, нефтехимических и других заводов. ϭϮ͘ϰ͘Ϯ͘ˑ̶̡̨̡̨̛̣̖̯̬̱̣̌̐́́͘ При прохождении сточной воды через межэлектродное пространство электролизера происходит электролиз воды, поляризация частиц, электрофорез, окислительно-восстано— 496 — ÐƸǁǬǭǰ͠ǮǲǀǂǀǆǬǯǭǀǬÐǂǬǰǮƽǊÐǮǆǀǯǰǭǀÐǯǰǮǆǃǊǲÐǫǮƽ вительные процессы, взаимодействие продуктов электролиза друг с другом. При использовании нерастворимых электродов коагуляция может происходить в результате электрофоретических явлений и разряда заряженных частиц на электродах, образованных в растворах веществ (Сl, О2), которые разрушают сольватные соли на поверхности частиц. Такой способ применяется для очистки сточных вод при невысоком содержании коллоидных частиц и низкой устойчивости загрязнений. Для очистки промышленных сточных вод содержащих высокоустойчивые загрязнения проводят электролиз с использованием растворимых стальных или алюминиевых анодов. Под действием тока происходит растворение металла в результате чего в воду переходят катионы железа или алюминия, которые встречаясь с гидроксидными группами, образуют гидроксиды металлов в виде хлопьев наступает интенсивная коагуляция. На процесс электрокоагуляции оказывает влияние материал электродов, расстояние между ними, скорость движения сточной воды между электродами, ее температура и состав, плотность тока. Достоинство метода коагуляции — компактность установок, простота управления, отсутствие потребности в реагентах, малая чувствительность к изменениям условий проведения процесса очистки. (температура pН-среды, присутствие токсичных веществ) — получение материалов с хорошими структурно-механическими свойствами. Недостаток — повышенный расход металла и электроэнергии. Элекрокоагуляция находит применение в пищевой, химической, целлюлозно-бумажной промышленности. ϭϮ͘ϰ͘ϯ͘ˑ̴̶̡̨̨̛̣̖̯̬̣̯̌́͘ В этом процессе очистка сточных вод происходит при помощи пузырьков газа, образующихся при электролизе воды. На аноде возникают пузырьки кислорода, а на катоде водорода. Поднимаясь в сточной воде эти пузырьки флотируют взвешенные частицы. При использовании растворимых электро— 497 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð дов происходит образование хлопьев коагулянтов и пузырьков газа, что способствует более эффективной флотации. Основную роль при электрофлотации играют пузырьки, образующиеся на катоде. Размер пузырьков значительно меньше, чем при других методах флотации. Он зависит от краевого угла смачивания и кривизны поверхности электрода. Диаметр пузырьков меняется от 20 до 100 мкм. Мелкие пузырьки водорода обладают большой растворимостью, чем крупные. Как правило, из пересыщенных растворов мельчайшие пузырьки выделяются на поверхности частичек загрязнений и тем самым способствуют эффекту флотации. Для получения пузырьков требуемого размера необходим правильный подбор материала, диаметр проволоки катода и плотности тока. Оптимальное значение плотности тока 200–260 а/м2, газосодержание около 0,1%. ϭϮ͘ϰ͘ϱ͘ˑ̡̨̛̛̣̖̯̬̣̔̌̚͘ Процесс очистки сточных вод электродиализом основан на разделении ионизированных веществ под воздействием электродвижущей силы, создаваемой в растворе по обе стороны мембран. Процесс проводят в электродиализаторах. В среднюю камеру заливают раствор, а в боковые, где расположены электроды чистую воду. Анионы током переносятся в анодное пространство, на аноде выделяется кислород и образуется кислота. Одновременно катионы переносятся в катодное пространство, на катоде выделяется водород и образуется щелочь. ϭϮ͘ϱ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏͘ 1. 2. 3. 4. 5. 6. 7. Что понимается под процессом электролиза? Какие химические процессы протекают на катоде? Какие химические процессы протекают на аноде? Всегда ли обратимы процессы электролиза? Что понимается под электродвижущей силой разложения? Что такое явления поляризации в гальванической цепи? Что понимают под электродвижущей силой разложения? Совпадает ли электродвижущая сила разложения — 498 — ÐǠǮǃǰ͠ǮǁǋǃǊǬÐǫǮ͟͠ǮǯǊ 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. по величине с электродвижущей силой элемента? Если нет, то почему? Если да, то почему? Что понимает под потенциалом разложения? В каких случаях разность потенциалов равна электродвижущей силе разложения? Что такое концентрационная поляризация? Какие явления называется деполяризацией гальванического элемента? Что понимается под термином перенапряжения? Как зависит поверхностное натяжение от заряда на границе между двумя средами? Что такое электрокапиллярная кривая? Как абсорбция влияет на электрокапиллярную кривую? Как на границе раздела двух фаз возникает двойной электрический слой, какое он имеет строение и как связан с электрокинетическим потенциалом? Как можно определить емкость двойного электрического слоя? Что такое электрокапиллярная кривая? Как абсорбция влияет на электрокапиллярную кривую? Как на границе раздела двух фаз возникает двойной электрический слой, какое он имеет строение и как связан с электрокинетическим потенциалом? Как можно определить емкость двойного электрического слоя? Какое явление называется электроосмосом? Что такое потенциал течения? Что понимают под явлением электрофореза? Что понимают под потенциалом осаждения и может ли это явление найти применение технологии очистки сточных вод? Перечислите, какие электрохимические процессы широко используются в промышленности для очистки сточных вод? Приведите пример процессов анодного окисления и катодного восстановления при очистке сточных вод. Можно ли в качестве источника питания для проведения этих — 499 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð 27. 28. 29. 30. 31. 32. 33. процессов использовать источник питания переменного тока? В чем заключается процесс электрокоагуляции? В чем достоинство и недостатки процесса электрокоагуляции при очистке сточных вод? Какой процесс более выгоден коагуляции или электрокоагуляции? Изложите свои соображения. Что такое процесс электрофлотации и как это процесс используется при очистке сточных вод? Почему процесс электрофлотации используется для очистки сточных вод? Почему этот процесс позволяет удалять самые мелкие частицы? Что понимается под процессом диализа? В каких аппаратах проводиться процесс электролиза? Как этот аппарат устроен? ϭϮ͘ϲ͘ʿ̸̛̛̬̥̖̬̼̬̖̹̖̦́̌̔̌̚͘ Задача 1. В процессе электролиза под действием тока плотностью 300 А/м2 на электроде выделился слой меди толщиной 0,03 мм. В течение какого времени протекал этот электролиз? Эта задача прежде всего на первый закон Фарадея ∆m = kIt Отсюда выразим время, необходимое для такого электро∆m лиза: t = kI Данное выражение не содержит величин из условия задачи, поэтому мы не можем его пока что использовать. Распишем неизвестные величины через известные. Начнем с массы: ∆m = ρV . Плотность меди — табличная величина, которая равна 9 103 кг/м3. Объем слоя меди можно выразить через его толщину и площадь: ∆m = ρSd . Силу тока также свяжем с его плотностью. Плотность тока I определяется как: j = . S Отсюда: I = jS . — 500 — ÐǤ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ Подставим все выражения в первый закон Фарадея: ρSd ρd t= = kjS kj Электрохимический эквивалент также является табличной величиной, и для меди он равен 0,3 10–6 кг/Кл. Подставим численные значения: t= 9<103 <0,03<10−3 = 3<103ñ = 50 ìèí 0,3<10−6 <300 Задача 2. Рассчитайте электрокинетический потенциал частиц гидрозоля Fе2О3 по данным электрофореза: частицы за 50 мин сместились на 15 мм к катоду, разность потенциалов 100 В, расстояние между электродами 40 см. Диэлектрическая проницаемость среды 80, вязкость дисперсионной среды 1·10–3 Па с. Решение: По данным электрофореза электрокинетический потенциал рассчитывается по уравнению: ζ= η 1<10−3 0,015<0,40 < = 0,0279 Â = 27,9 ìÂ uýô = εε 0 80<8,85<10−12 3000a100 Задача 3. Рассчитайте электрокинетический потенциал поверхности Al2O3 по данным электроосмоса: сила тока 3·10–3 А, объёмная скорость переноса раствора хлорида калия 0,035 мл/с, удельная электропроводность раствора 1,4·10–2 см м-1 , вязкость 1·10–3 Па с, относительная диэлектрическая проницаемость 80. Решение: По данным электроосмоса электрокинетический потенциал рассчитывается по формуле: ζ= η 1<10−3 1,4<10−20,035<10−6 < = 0,228 Â = 228 ìÂ uýô = −12 εε 0 80<8,85<10 3<10−3 — 501 — ǞǁǪǫǪ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐǌǁǬǭǰ͠ǮƽǃǊǲÐ͟͠ǮǅǬǯǯǮǫÐ͟͠ǀÐǮǆǀǯǰǭǬÐǯǰǮǆǃǊǲÐǫǮƽÐǮǰÐ͟͠ǀǂǬǯǬ֬ Ð ϭϮ͘ϳ͘ʯ̸̨̨̨̨̛̛̣̭̥̭̯̯̖̣̦̬̖̹̖̦̌̔̌̔́̌́̽̐́͘ Задача 1. Определите массу серебра, которое выделилось на катоде при электролизе азотнокислого серебра за 2 часа, если к раствору приложено напряжение 2 В, а его сопротивление — 5 Ом. Задача 2. Электролиз проходил в течение 5 минут при силе тока 1,5 А. При этом на катоде выделилось 137 мг некоторого вещества. Что это за вещество? Задача 3. Рассчитайте электрокинетический потенциал частиц гидрозоля SiО2 в зависимости от рН дисперсионной среды по данным электрофореза при следующих условиях: напряжение 125 В, расстояние между электродами 45 см, вязкость дисперсионной (водной) среды 1·10–3 Пас, относительная диэлектрическая проницаемость 78,2, температура 298 К. Время проведения опыта 30 мин. рН 0,5 1,5 3,5 6 7,5 Смещение границы к катоду, мм 4 2 –10 –18 –25 Постройте полученную зависимость ζ = f(pH). Объясните полученные результаты. Задача 4. Рассчитайте скорость электроосмоса раствора хлорида натрия через корундовую диафрагму, если известно, что её электрокинетический потенциал равен 35 мВ, вязкость дисперсионной среды 1·10 -3 Пас, диэлектрическая проницаемость среды 80, электропроводность раствора 2·10–2 См/м, сила тока 2·10–2 А. — 502 — ǍưǙǚǙÍ Í Í ǗƝƜƝǏǒ̤ǘƝǐƝơǎǕǏƝǎÍÍǒǕǑǒǌƥÍ ǓǔǒƠǎǕǕǒǌÍǓǎǔǎǔǋƙǒǖǏƝÍǖǌǎǔƚƥǘÍ ǒǖǘǒƚǒǌ В результате изучения главы 13 бакалавр должен: Знать: – основные виды процессов переработки твердых отходов. – физические закономерности процессов дезинтеграции, сепарации, специальных методов обогащения, термического обезвреживания. Уметь: – обоснованно выбирать технологическую схему переработки твердых отходов. Владеть: – теоретическими основами механохимии и теории горения и взрыва для описания процессов переработки твердых отходов. Для сохранения литосферы необходимо разрабатывать мало- или безотходные технологии, проводить захоронение твердых отходов с рекультивацией земли. Отходы одного производства могут служить сырьем для другого. При этом сокращается объем отходов и уменьшается потребность в добыче рудного сырья. Часто твердые отходы могут использоваться в производстве стройматериалов. — 503 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð ϭϯ͘ϭ͘ʶ̴̶̵̵̡̨̨̨̛̛̛̣̭̭̯̖̬̼̯̌̌́̏̔̔̏͘ В настоящее, время отсутствует общая научная классификация твердых отходов, что объясняется многообразием их видов. На одном предприятии число разнообразных отходов может быть больше сотни. С позиции ликвидации твердых отходов их можно разделить на три типа: • отходы, содержащие ценные компоненты; • отходы, содержащие токсичные компоненты; • отходы, не содержащие вредных и ценных компонентов. Отходы первого типа нуждаются в переработке с извлечением ценных составляющих. Для этого часто приходится использовать сложные технологические схемы, как правило, осуществляемые на химических или металлургических предприятиях. Например, германий в небольших количествах содержится в некоторых месторождениях каменных углей. При сжигании угля он концентрируется в пыли отходящих газов. Уловленная пыль подвергается переработке для извлечения германия. Отходы второго типа либо подвергаются захоронению в специальных контейнерах на большой глубине в отработанных шахтах, либо переработке с переводом токсичных соединений в нетоксичные. Отходы третьего типа либо используются для производства стройматериалов, либо размещают на специально отведенном полигоне. Наибольшие технологические трудности возникают при переработке отходов первой и второй групп. Рассмотрим, какие технологические процессы наиболее часто используются при их переработке. ϭϯ͘Ϯ͘ʿ̵̵̨̨̨̡̨̨̨̯̯̖̬̼̯̔̐̏̌̏̔̔̏ ̡̨̨̡̪̭̣̖̱̺̖̜̪̖̬̖̬̯̖̔̀̌̍͘ Процессы переработки твердых отходов часто бывают дорогими, поэтому вопросы экономики при их переработке явля— 504 — Ðƫ͠ǮƻǁǬǃǀǬÐǀÐǀƿǂǬǁǋǆǬǃǀǬÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ ются первостепенными. С этой точки зрения первостепенное значение имеют способы сбора отходов и их хранения. Смешивание отходов различного состава приводит к значительному удорожанию их последующей переработки. Наглядно это можно наблюдать при сборе бытовых отходов в населенных пунктах. Смешанные отходы столь сложно перерабатывать, что до сих пор переработке подвергается лишь небольшая их часть. Вместе с тем раздельный сбор различных отходов позволял бы легко их перерабатывать. Бумажные отходы могли бы пойти на производство бумаги, уменьшая при этом расход лесоматериала. Отходы стекла позволяют экономить сырье при производстве стеклянных изделий. Металлические отходы и пластмассовые проще перерабатывать раздельно. Однако, к сожалению, мы наблюдаем, как загрязняются большие площади земли смешанными бытовыми отходами без всякой переработки. ϭϯ͘ϯ͘ʪ̸̵̵̨̨̨̨̛̛̛̛̬̣̖̦̖̥̖̣̖̦̖̯̖̬̼̯̍̽̏̔̔̏̚͘ Твердые отходы могут быть как крупнокусковыми, так и в виде тонкой пыли. Крупнокусковые отходы подвергаются дроблению или измельчению в зависимости от требований последующей переработки. ϭϯ͘ϯ͘ϭ͘ʻ̸̶̸̨̨̛̛̛̛̛̛̦̖̦̖̪̖̬̜̬̣̖̦̥̖̣̖̦̌̌̌̔̍́̽́̚̚͘ Согласно [1, 4, 10, 16–19, 28] дробление и измельчение — процессы уменьшения размеров материалов путем разрушения их действием внешних сил, преодолевающих внутренние силы сцепления, связывающие между собой частицы твердого вещества. Принципиально процессы дробления и измельчения не различаются между собой. Условно считают, что при дроблении получают продукты преимущественно крупнее, а при измельчении мельче 5 мм. Для дробления применяют дробилки, а для измельчения — мельницы. Дробление и измельчение в промышленности являются подготовительными операциями или перед обогащением при— 505 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð родных твердых тел или в технологическом процессе для получения материала заданной крупности и имеют своим назначением разъединение (раскрытие) частичек материала, тесно переплетенных и сросшихся между собой. Чем полнее раскрываются (освобождаются одна от другой) частички материала при дроблении и измельчении, тем успешнее последующие технологические процессы. Иногда частички природных материалов, слагающие куски твердого тела, обладают различными физико-механическими свойствами. После дробления или измельчения таких материалов в специально подобранных условиях одни, более твердые и прочные материалы, будут представлены крупными кусками, другие, хрупкие и менее твердые — кусками значительно меньшего размера. Последующий рассев дробленого продукта позволяет отделить одни материалы от других, т. е. произвести более или менее совершенное разделение. Дробление или измельчение в этом случае имеет значение обогатительной операции и называется избирательным дроблением. Крупность частиц, до которой надо дробить или измельчать исходный материал в частности перед обогащением, определяется размером вкрапленности полезного продукта и процессом, принятым для обогащения данного компонента. Эта крупность устанавливается опытным путем при исследованиях обогатимости каждого продукта. Дробление применяется не только на обогатительных фабриках. Дроблению и измельчению подвергают различные материалы, используемые в технологических процессах порошковой металлургии: уголь или сланец па электростанциях, сжигающих топливо в пылевидном состоянии; уголь на коксохимических заводах перед коксованием; известняки и доломиты, используемые в качестве флюсов на металлургических заводах; камень с целью приготовления щебня для промышленного и дорожного строительства и т. д. В этих случаях продукты дробления и измельчения используются непосредственно, и процесс дробления имеет самостоятельное значение. Крупность получаемых при этом продуктов устанавливается исходя из требований технологии потребляющих производств. — 506 — Ðƫ͠ǮƻǁǬǃǀǬÐǀÐǀƿǂǬǁǋǆǬǃǀǬÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ ϭϯ͘ϯ͘Ϯ͘ˁ̸̨̛̛̛̛̯̖̪̖̦̬̣̖̦̥̖̣̖̦̽̔̍́̽́̚͘ Отношение размеров кусков или частиц исходного материала перед дроблением и измельчением к размеру кусков или частиц дробленого или измельченного продукта называется степенью дробления или степенью измельчения (по отношению к процессам дробления применяют степень дробления, а по отношению к измельчению — степень измельчения). Степень дробления — количественная характеристика процесса, показывающая, во сколько раз уменьшился размер кусков или частиц материала при дроблении или измельчении. Со степенью дробления связаны расход энергии и производительность дробилок и мельниц. Для определения степени дробления предложено несколько расчетных формул. Чаще всего степень дробления определяется как отношение размеров максимальных по крупности кусков материала до и после дробления Dmax (13.1) dmax где Dmax и dmax — диаметр максимального куска материала соответственно до дробления и после. В практике диспергирования диаметром кусков сыпучих материалов считают наименьший размер отверстия сит, через которые при грохочении куски еще проходят. Поэтому степень дробления по формуле (13.1) вычисляется как отношение диаметров предельных отверстий сит грохочения дробимого материала и дробленого продукта. Форма отверстий сита при этом должна быть одинаковой, так как она влияет на результаты грохочения. Для характеристики дробилок машиностроительные заводы применяют так называемую конструктивную степень дробления, вычисляемую по формуле B B или i = 0,85 (13.2) i= b b i= где В — ширина загрузочного отверстия дробилки, мм; b — ширина выпускной щели, мм; для дробилок крупного дробле— 507 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð ния она максимальная при отходе дробящих элементов одного от другого, для дробилок среднего и мелкого дробления — при их сближении. Формула (13.2) позволяет вычислить наибольшую достижимую степень дробления, когда в продукте дробления нет кусков размером более разгрузочной щели, а поступающий в дробилку кусок меньше загрузочного отверстия на 15% . Степень дробления, подсчитанная по рассмотренным выше формулам, характеризует процессы дробления и измельчения недостаточно полно. Правильнее вычислять ее как отношение средних диаметров, которые находятся с учетом характеристик крупности исходного материала и продукта дробления: Dñð (13.3) i= dñð где Dср и dср — средний диаметр кусков соответственно исходного материала и дробленого продукта. Средние диаметры Dср и dср надо подсчитывать по формулам, выбираемым особо в каждом конкретном случае, исходя из физической сущности вопроса, для разрешения которого надо найти степень дробления. Иногда для вычисления степени дробления применяют формулу i= D1 d1 (13.4) где D1 и d1 — размер квадратных отверстий сита, через которое проходит t (%) дробленного или измельчаемого материала; dt — размер квадратных отверстий сита, через которое проходит t (%) продукта дробления или измельчения. Для дробления принимают t = 80%, а для измельчения t = 95%. Размеры отверстий сит, через которые проходит 80 или 95% материала, выбраны не случайно. Опыт показал, что размеры наиболее крупных кусков, составляющих небольшую часть материала (не более 20% для продуктов дробления и не более 5% для продуктов измельчения), не характеризуют его крупность. Величины D и d, зависят от вида суммарных ха— 508 — Ðƫ͠ǮƻǁǬǃǀǬÐǀÐǀƿǂǬǁǋǆǬǃǀǬÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ рактеристик крупности материала до и после дробления или измельчения и определяются по соответствующим кривым. В формуле (13.4), так же как и формуле (13.3) степень дробления вычисляется с учетом соответствующих характеристик крупности, и поэтому она будет достаточно полно характеризовать процессы дробления или измельчения материала. ϭϯ͘ϯ͘ϯ͘ˁ̵̸̨̨̛̛̛̛̛̛̯̜̦̭̯̭̖̥̼̬̣̖̦̥̖̣̖̦̌̔̽̔̍́̽́̚͘ На обогатительных фабриках дробление и измельчение различных материалов перед обогащением производятся с высокой степенью сокращения крупности. Например, перед флотационным обогащением некоторые материалы иногда измельчают до крупности менее 0,1 мм. Если при этом материал поступает с карьеров, то размер максимальных кусков в исходном продукте может доходить до 1500 мм. Тогда степень из1500 мельчения i = = 15000 . 0,1 Перед гравитационным обогащением материалы часто дробят до 10 мм. При крупности максимальных кусков в исходном материале около 300 мм степень дробления 300 i= 10 − 30 Получение таких высоких степеней дробления в одной дробильной машине практически невозможно. Вследствие своих конструктивных особенностей машины для дробления и измельчения эффективно работают только при ограниченных степенях измельчения, а поэтому рациональнее дробить и измельчать материал от исходной крупности до требуемого размера в нескольких последовательно работающих дробильных и измельчающих машинах. В каждой из таких машин будет осуществлена лишь часть общего процесса дробления или измельчения, называемая стадией дробления или измельчения. В зависимости от крупности дробимого материала и дробленого продукта стадии дробления имеют особые названия: первая стадия — крупное дробление от 1500–300 до 350– — 509 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð 100 мм; вторая стадия — среднее дробление от 350–300 до 100–40 мм; третья стадия — мелкое дробление от 100–40 до 30–5 мм. Необходимо понимать, что пределы крупности исходного материала и дробленого продукта, ограничивающие стадии, условны и приблизительны. Известны случаи, когда дробление осуществляется в четыре стадии. Например, четырехстадиальные схемы дробления применены на некоторых обогатительных фабриках для железных руд, содержащих значительную долю крупных плоских кусков. При четырехстадиальных схемах можно считать, что две первые стадии — это крупное дробление, а третья и четвертая стадии — среднее и мелкое дробление; либо первая стадия — крупное, вторая — среднее и две стадии мелкого дробления. Последующая операция, в которую поступает материал после среднего или мелкого дробления (куски размером менее 50 мм), называется измельчением. В зависимости от требуемой крупности материал перед сепарацией или обогащением можно измельчать в одну, две или даже в три последовательные стадии, которые соответственно называются первой, второй и третьей стадиями измельчения. Степень дробления, достигаемая в каждой отдельной стадии, называется частной, а во всех стадиях — общей степенью дробления. Общая степень дробления i равна произведению частных D d d степеней дробления ri r1r2r3 <<<rj <<<rn = max 1 <<< n −1 d1 d2 dmax или i = r1r2 <<<rj <<<rn = Dmax dmax где rj — частная степень дробления в j-й стадии; j= 1, ..., n. Если во всех n стадиях частные степени дробления одинаковы, то общая степень дробления (13.5) i = rn Дробление и особенно измельчение — весьма энергоемкие операции, на которые расходуется более половины энергии, потребляемой предприятием. Поэтому стремятся в возможно — 510 — Ðƫ͠ǮƻǁǬǃǀǬÐǀÐǀƿǂǬǁǋǆǬǃǀǬÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ большей степени сократить объем материала, направляемого в эти операции, руководствуясь принципом — «Не дробить ничего лишнего». В материалах, подлежащих дроблению или измельчению, всегда имеются куски (частички) мельче того размера, до которого идет дробление или измельчение в данной стадии. Такие куски целесообразно выделить из исходного материала перед дробильными или измельчительными машинами на грохотах или в классификаторах. В материалах, подлежащих измельчению, всегда содержится некоторая доля частиц, уже не являющихся сростками полезных продуктов с другими материалами, а поэтому не нуждающихся в дальнейшем измельчении. Если содержание таких частиц большое или если они представляют собой весьма ценные продукты, которые при последующем измельчении могут быть потеряны вследствие переизмельчения, то для их выделения иногда вводят промежуточные операции сепарации. Дробилки и мельницы могут работать в открытом и замкнутом циклах (рис. 13.1). При открытом цикле материал проходит через дробилку или мельницу один раз и в дробленом продукте всегда присутствует некоторая доля кусков избыточного размера. Кусок избыточного размера, или «избыточное зерно», имеет размер больше ширины разгрузочной щели. При замкнутом цикле материал неоднократно проходит через дробилку или мельницу. Дробленый продукт поступает на классифицирующий аппарат, выделяющий из него куски избыточного размера, которые возвращаются для додрабливания (доизмельчения) в ту же дробилку или мельницу. Для классификации продуктов дробления применяют грохоты, а для классификации продуктов измельчения механические классификаторы, гидроциклоны и также грохоты. Последовательность операций при дроблении называется схемой дробления. Такие схемы поясняются чертежом, на котором кроме наименования стадий указываются масса, выход и крупность продуктов дробления, а также размеры выпускных щелей дробилок в каждой стадии. — 511 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð Рис. 13.1. Схема открытого и замкнутого циклоп дробления и измельчения: а — открытый цикл; б — открытый цикл с предварительным грохочением или классификацией; в — замкнутый цикл с совмещенными предварительной и поверочной классификациями; г — замкнутый цикл с раздельными операциями грохочения или классификации; д — замкнутый цикл. ϭϯ͘ϯ͘ϰ͘˄̵̨̨̖̣̦̪̖̬̦̭̯̔̽̌́̏̽ ̨̨̨̛̛̛̭̪̖̬̬̦̦̥̯̖̬̣̔̐̏̌̐̌̌̌͘ Площадь поверхности диспергированного материала, состоящего из отдельных кусков, зависит от их крупности. Найдем связь между удельной поверхностью материала — поверхностью одной массовой единицы материала — и средней крупностью его кусков. Заменим действительный материал идеальным, в котором все куски имеют одинаковый средний размер и одинаковую правильную, например кубическую, форму. Тогда масса одного куска 3 Góä = δdñð — 512 — Ðƫ͠ǮƻǁǬǃǀǬÐǀÐǀƿǂǬǁǋǆǬǃǀǬÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ где δ — плотность материала; dcp — средний диаметр кусков. Число кусков в Q тоннах материала N= Q 3 δdñð Поверхность одного куска 3 s = 6dñð Поверхность Q тонн материала 2 6dñð Q 6Q S = sN = 3 = δdñð Q δdñð Удельная поверхность материала S 6 Sóä = = Q δdñð (13.6) Удельная поверхность материала обратно пропорциональна размеру кусков и может служить мерой крупности материала. Формулу (13.6) можно применить для исчисления удельной поверхности действительного материала, состоящего из кусков разного размера и различной формы, если, как это, средний диаметр куска вычислять по формуле ∑ω (13.7) dñð = ω ∑d где ω — массовый выход узкого класса крупности; d — средний диаметр узкого класса, выделенного при ситовом анализе (среднее арифметическое из крайних диаметров, ограничивающих данный класс). ϭϯ͘ϯ͘ϱ͘ˁ̨̛̬̖̥̖̦̦̼̖̪̬̖̭̯̣̖̦̏̔̌̏́ ̨̨̨̛̛̛̬̬̱̹̖̦̯̖̬̥̯̖̬̣̌̏̔̐̌̌̌̚͘ Под прочностью твердого тела понимают его способность оказывать сопротивление разрушению под действием внешним воздействием. — 513 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð При разрушении рвутся связи между частицами кристаллической структуры без изменения агрегатного состояния вещества. Теоретическую прочность можно рассчитать по силам взаимодействия частиц в кристалле. Реальная прочность тела на несколько порядков меньше теоретической. Это расхождение между теоретической и реальной прочностью объясняется тем, что в теле имеются дефекты кристаллической структуры, микропоры и микротрещины. ϭϯ͘ϯ͘ϲ͘ʪ̴̸̡̡̡̨̡̛̛̖̖̯̼̬̭̯̣̣̖̭̜̭̯̬̱̯̱̬̼̌͘ Дефекты кристаллической структуры подразделяют на точечные и линейные. Точечные — это вакансии, т. е. незанятые узлы кристаллической решетки или внедрения чужеродных атомов или ионов в решетку. Линейные — это дислокации или смещения одной части кристалла относительно другой. На прочность кристаллов наибольшее влияние оказывают дислокации. Под влиянием внешней нагрузки дислокации легко перемещаются, взаимодействуют между собой и с другими дефектами, объединяются и выходят на поверхность кристалла. Уже само смещение структуры хотя бы на один ряд атомов ослабляет кристалл. Дислокации способствуют образованию зародышевых трещин, развивающихся далее в трещины разрушения. Поскольку задача операций дробления и измельчения в производственном процессе — раскрытие частиц поликристаллического материала при ограниченном переизмельчении, т. е. при минимальном разрушении самих частиц (монокристалликов), так как желательно концентрировать и умножить дефекты структуры измельчаемого материала в межчастичных слоях, чтобы при последующем механическом воздействии вызвать разрушение в первую очередь по этим слоям на поверхности частиц. В зависимости от свойств разрушаемого материала можно воздействовать на межчастичные слои разными способами, приводящими к его разупрочнению. Если вещество состоит из различных материалов, заметно отличающихся по термическим объемным коэффициентам — 514 — Ðƫ͠ǮƻǁǬǃǀǬÐǀÐǀƿǂǬǁǋǆǬǃǀǬÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ расширения, или обладает другими свойствами, зависящими от температуры, то можно применить нагрев (или охлаждение) вещества перед механическим разрушением, т. е. термический способ. Если межчастичные слои измельчаемых материалов характеризуются повышенной электрической проводимостью по сравнению с самими материалами, то можно применить электрический способ, формируя электрический разряд таким образом, чтобы он проходил по межчастичным слоям. Могут быть и другие способы воздействия — акустический, магнитный и др. Проведение операций измельчения с предварительной специальной подготовкой материалов к разрушению, т.е. с разупрочнением, и выбор самого способа разрушения могут дать в перспективе лучшее, более полное раскрытие частичек материала без переизмельчения и экономию в суммарном расходе энергии. Перспективное направление в современной теории и практике диспергирования — идея предварительного разупрочнения материала в ходе технологического процесса, как результат управление кусковатостью и прочностью материала благодаря использованию энергии взрыва. Это достигается некоторым увеличением расхода взрывчатых веществ (ВВ), изменения схем расположения и конструкции зарядов, схем их взрывания и в целом кинетики взрыва. В результате заметно снижаются энергетические затраты на разрушение. Взрывные работы — это механическое дробление — измельчение, так как часть энергии взрыва расходуется не только на образование новой поверхности и перемещение взрываемого материала, а на создание также сети зародышевых трещин, разупрочняющих материал. Как следствие, разупрочнение материала приводит к резкому увеличению эффективности в последующих процессах дробления и измельчения. Опытно-промышленная проверка ведения буровзрывных работ дифференцированными параметрами при повышенном (до 30–50%) удельном расходе ВВ показала, что реализация идеи сквозной подготовки материала по схеме: взрывное дро— 515 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð бление — механическое дробление — измельчение позволяет увеличивать производительность дробилок на 30–80%, мельниц на 10% при снижении расхода электроэнергии в цикле дробления на 30 % и в цикле измельчения на 10%. Одновременно повышаются качество получаемого продукта на 0,2–0,5% и производительности на 0,8–2%. Например, на процессы дробления и измельчения минерального сырья в мире расходуется более 10% всей потребляемой энергии. В то же время затраты энергии на буровзрывные работы составляют всего лишь 3–8% общих ее затрат на дробление и измельчение. В кусках различных материалов действуют несколько групп сил сцепления. Одна группа сил действует внутри кристаллов, другая — между отдельными кристаллами. Обе группы сил имеют одинаковую физическую природу и различаются между собой по значению. Силы взаимодействия между кристаллами во много раз меньше сил внутри кристалла, так как расстояния между взаимодействующими частицами при сцеплении кристаллов во много раз больше расстояний между частицами внутри кристаллов. Кроме того, как правило, продукты подвергаемые диспергированию состоят из нескольких веществ и контакты между зернами этих веществ имеют свои силы сцепления и могут рассматриваться как места, в которых в первую очередь могут зарождаться дефекты и микротрещины. Процесс разрушения твердого тела внешней нагрузкой начинается с изменений на микроскопическом и субмикроскопическом уровнях. В телах разных типов эти изменения имеют различный характер. В металлах и полупроводниках разрушению предшествует заметная пластическая деформация, т. е. необратимые взаимные сдвиги слоев материала. В дальнейшем это приводит к появлению сети микропор и микротрещин, которые затем увеличиваются в размерах, объединяются в одну или несколько больших трещин, разделяющих тело на части. В горных породах, стеклах и других хрупких телах система микроскопических трещин и пор уже имеется в начальном состоянии и даже при относительно небольшом увеличении — 516 — Ðƫ͠ǮƻǁǬǃǀǬÐǀÐǀƿǂǬǁǋǆǬǃǀǬÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ внешних воздействий, размеры и плотность микроповреждений быстро растут, и наступает разрушение. При периодических нагружениях образца при каждом цикле в образце происходят необратимые изменения микроструктуры, накапливающиеся с увеличением числа циклов. Этим объясняется явление, известное как усталость материала. Некоторые из микротрещин можно представить себе в форме сплющенного эллипсоида. При расширении трещины под действием растягивающих напряжений в устьях, т.е. в местах наибольшей кривизны поверхности происходит концентрация напряжений. Эта концентрация может быть очень большой, в сотни раз превышающей среднее напряжение по сечению. В результате кусок разрушится при относительно малом среднем напряжении. Энергия, подводимая к телу при нагружении, превращается в энергию деформации, накапливаемую в материале, и в поверхностную энергию трещины. По достижении некоторой критической длины при определенном напряжении трещина будет распространяться далее самопроизвольно, так как при этом суммарная энергия системы (кусок под напряжением и с трещиной) будет уменьшаться, а по законам термодинамики процессы в направлении уменьшения энергии системы могут протекать самопроизвольно. Критическое напряжение δкр обратно пропорционально квадратному корню из длины трещины l: const (13.8) δêð = l Константа зависит от модуля упругости материала Е и удельной поверхностной энергии трещины. Эта трещина критической длины называется трещиной Гриффитса. Энергия, затрачиваемая на измельчение, во много раз превышает прирост свободной поверхностной энергии твердого тела, полученной в результате уменьшения размеров зерен. Энергетический кпд измельчения, подсчитанный по поверхностной энергии, составляет около 0,1–0,6%. Энергия, подводимая к рабочим поверхностям дробилки или мельницы, расходуется на: — 517 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð – упругую и пластическую деформации частиц дробимого материала и рабочих поверхностей машины, изменение структуры материала (нарушение и смещение в кристаллической решетке), механохимические реакции; – сообщение кинетической энергии обломкам частиц; – трение частиц между собой и на поверхностях разрушения; – износ рабочих поверхностей машины; – безрезультатные (т. е. без распада частиц на обломки) напряжения и нагружения частиц; – звуковые колебания и пр. Все эти потери энергии, подведенной к рабочим поверхностям машины, в конечном счете превращаются в тепло. Общие потери подтверждаются простыми опытами, например помещением работающей мельницы в калориметр. В реальных условиях дробление и измельчение проходят непрерывно и одновременно машина воздействует не на одну частицу, а на их массу. При этом одна часть частиц получает недостаточные нагрузки и не разрушается, другая — избыточные нагрузки и часть энергии теряется; некоторая часть частиц проходит через машину, не получив нагрузки (например, при малом времени пребывания в мельнице). В целом условия массового дробления и измельчения резко отличаются от разрушения одиночной частицы и перенос закономерностей, установленных для одной частицы, на массовое разрушение едва ли возможен. При массовом разрушении должны выявляться статистические закономерности. ϭϯ͘ϯ͘ϳ͘ʺ̵̸̵̡̨̛̛̖̦̖̭̖̭̜̭̯̯̖̬̼̯̖̣̌̏̏̌̏̔ ̵̵̴̶̨̨̛̛̛̛̪̬̪̬̭̯̼̖̬̥̏̔̌̔̌͘ Испытание твердых тел на одноосное сжатие или растяжение является основным для характеристики их прочности. Образцы цилиндрической формы или прямоугольного сечения нагружаются на испытательном прессе до разрушения. В табл. 13.1 приведен ряд механических параметров твердых тел. — 518 — Таблица 13.1 Механические параметры твердых тел. Наименование Обознапараметров чение Предел прочности при сжатии Pmax F Pmax F Модуль продольной упругости (модуль Юнга) E Коэффициент Пуассона ν ∆Pl lF l∆d d∆l Пределы Единица Определение изменения измерения Па Критическое значение 107–3·108 одноосного сжимающего напряжения, при котором происходит разрушение породы Па Критическое значение 0–2·107 одноосного сжимающего напряжения, при котором происходит разрушение породы Па Коэффициент пропорцио- 109–3·1011 нальности между соответствующим нормальным напряжением и соответствующей ему продольной упругой деформацией Коэффициент пропорцио0,1–0,45 нальности между упругими продольными и поперечными деформациями при одноосной нормальной нагрузке Ðƫ͠ǮƻǁǬǃǀǬÐǀÐǀƿǂǬǁǋǆǬǃǀǬÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ — 519 — Предел прочности при растяжении Расчетная формула ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð Примечание. F — площадь поперечного сечения образца, м2; l, d — длина и диаметр образца, м; ∆d и ∆l — изменение диаметра и длины образца, соответствующие изменению нагрузки на величину ∆Р, м; Pmax — максимальная нагрузка, Н. Испытания показали, что при одноосном сжатии большинства твердых тел наблюдается течение материала (т.е. пластическая деформация) перед началом разрушения. Показатели механических свойств твердых тел зависят от их состава и строения. Силы сцепления между кристаллитами, цементирующим веществом и обломками, кристаллитами цементирующего вещества колеблются в широких пределах, что обусловливает большие колебания в механических свойствах твердых тел. На показатели влияет способ испытаний, пористость, влажность, слоистость, крупность слагающих твердое вещество частиц и др. Этими причинами объясняется широкий разброс показателей при испытаниях образцов одного и того же материала, не отличающихся один от другого по петрографическому описанию. Например, специальные исследования образцов одинаковых природных материалов на одноосное сжатие показал, что временное сопротивление сжатию изменилось в 8,45 раза (от 530 до 1830 кПа) и средний коэффициент вариации (отношение среднеквадратичного отклонения к среднему значению) был равен 21,3%. Были проведены на микроаппаратуре опыты по разрушению сжатием малых по размерам частиц (шаров) стекол и природных материалов. При этом было установлено, что чем меньше размер разрушаемой частицы, тем больше пластическая деформация, предшествующая разрушению. Для очень мелких частиц имеется предел размера, ниже которого возникает только пластическая деформация. Для кварца он составляет около 1 мкм, для полевого шпата — 3–5 мкм (практический предел механического разрушения частиц). Испытание природных материалов на растяжение производится редко, главным образом из-за трудности изготовления — 520 — Ðƫ͠ǮƻǁǬǃǀǬÐǀÐǀƿǂǬǁǋǆǬǃǀǬÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ образцов. Испытание на разрыв весьма чувствительно к неоднородности материала и мелким дефектам его строения (микротрещины). Сопротивление разрыву природных материалов в несколько раз меньше по сравнению с временным сопротивлением сжатию. Отношение σсж/σр по опытам колеблется в широких пределах (от 1 до 102). Испытания природных твердых материалов на сдвиг и изгиб проводятся только при специальных исследованиях. Прочность на сдвиг выше, чем прочность на изгиб и растяжение (разрыв): σсж ≥ τс ≥ σи ≥ σр где σсж, τс, σи, σр, — временное сопротивление соответственно на сжатие, изгиб, растяжение и сдвиг. Наиболее выгодным видом деформации для разрушения материала является растяжение. Это необходимо иметь в виду при конструировании дробильно-измельчительного оборудования. ϭϯ͘ϯ͘ϴ͘ʤ̨̨̨̛̦̯̬̪̦̼̖̭̜̭̯̏̏̌̚ ̵̨̨̛̛̪̬̬̦̼̥̯̖̬̣̔̌̌̏͘ Анизотропными называют тела, обладающие различными свойствами в разных направлениях. Анизотропия природных материалов связана с их слоистостью, сланце- и трещиноватостью. С увеличением трещиноватости степень анизотропии понижается. Практически об анизотропии прочности природных материалов судят по показателям прочности, определенным поперек (перпендикулярно) и вдоль слоистости. Коэффициентом относительной анизотропии свойств называют отношение показателя свойства поперек слоистости к показателю того же свойства вдоль слоистости. Коэффициент анизотропии на сжатие для многих природных материалов в среднем равен 1,34. Для показателей временного сопротивления растяжению (отрыву) коэффициент анизотропии бывает в среднем 0,59, т.е. сопротивление перпендикулярно к слоистости меньше. — 521 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð ϭϯ͘ϯ͘ϴ͘ϭ͘ʺ̴̡̨̭̹̯̦̼̜̯̬̌̌̍̌͘ Согласно статистической теории прочности, дефекты в строении твердого тела распространены в объеме стохастически. Чем больше объем нагружаемого куска, тем выше вероятность встречи в нем с крупным дефектом, достаточным для разрушения куска по всему сечению при данной нагрузке. С уменьшением размера кусков в них уменьшается число больших дефектов, они были уже реализованы при разрушении до данного размера. Удельная прочность кусков повышается. Зависимость прочности твердых тел от их линейных размеров называют масштабным эффектом или масштабным фактором. Большая часть экспериментов подтверждает положение, что образцы (куски) материала меньших размеров, при прочих равных условиях, обладают большей удельной прочностью по сравнению с кусками больших размеров. Для природных материалов наблюдается заметное увеличение прочности частиц размером 0,1–0,5 мм. Особенное значение масштабный фактор имеет для природных материалов, в которых частицы одного твердого материала связаны (сцементированы) более мягким связующим материалом. В этом случае разрушение до необходимого размера частиц измельчаемого материала проходит относительно легче, чем разрушение самих твердых частиц. Природные материалы настолько разнообразны по своему составу и свойствам, что в некоторых случаях наблюдается обратное влияние масштабного фактора, т. е. удельная прочность кусков возрастает с увеличением их размеров. Поэтому влияние масштабного фактора должно изучаться применительно к конкретному природному материалу и к интересующему диапазону крупностей кусков. ϭϯ͘ϯ͘ϴ͘Ϯ͘˃̨̨̨̨̛̛̖̬̭̯̪̬̬̦̥̯̖̬̣̏̔̽̔̐̌̌̌͘ Твердость природного материала определяет ее сопротивляемость к внедрению инструмента. Простой способ определения твердости, так называемой контактной прочности, разработан в Институте горного дела. В нешлифованную по— 522 — Ðƫ͠ǮƻǁǬǃǀǬÐǀÐǀƿǂǬǁǋǆǬǃǀǬÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ верхность куска природного материала вдавливают стальной цилиндрический штамп с плоским основанием диаметром 2–3 мм. Контактная прочность определяется в момент выкола лунки по нагрузке, отнесенной к площади штампа, т. е. она измеряется в ньютонах на 1 мм2. К самым твердым относят материалы, имеющие контактную прочность более 5,66 Н/мм2, к материалам средней твердости — 0,65–1,25 кН/мм и к слабым — менее 0,3 кН/мм2. ϭϯ͘ϯ͘ϴ͘ϯ͘ʽ̴̴̶̡̨̡̨̛̛̛̛̛̺̜̖̦̯̬̖̪̭̯̥̯̖̬̣̍̾̌̌̌͘ Вследствие большой изменчивости показателей свойств материала и зависимости их от технологических процессов, для которых они определяются, в практике нашли применение частные показатели свойств, характерные для определенных процессов. Так, выработаны показатели буримости, взрываемости, дробимости, абразивности, измельчаемости природного материала и др. Общая методика разработки частных показателей, характерных для данного технологического процесса, следующая. Процесс моделируют (воспроизводят) в малом масштабе, изготовляют специальную аппаратуру и приборы, на которых определяют показатели на отдельных пробах. Эти показатели сопоставляются с показателями промышленных установок и выявляются корреляционные зависимости между ними. После этого показатель, полученный при испытаниях пробы, можно использовать для расчета промышленных установок и проектирования технологического процесса. Для характеристики прочностных свойств природных материалов существует общий показатель (коэффициент) крепости, разработанный проф. М. М. Протодьяконовым. Этот коэффициент крепости обоснован многолетней практикой и специальными испытаниями и хотя по точности он не может заменить частных показателей, применяемых к конкретным процессам, его можно использовать для общего сравнения прочности природных материалов в разных отраслях промышленности и для разных процессов при ориентировочных расчетах. — 523 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð По шкале проф. М. М. Протодьяконова все материалы делятся на 10 категорий, характеризуемых коэффициентами крепости от 0,3 для самых слабых, плывучих грунтов до 20 для наиболее прочных и вязких кварцитов и базальтов. Коэффициент крепости f, как показали исследования, можно приближенно определить по временному сопротивлению раздавливанию σсж цилиндрического образца (d = h = = 32÷42 мм) по формуле σñæ σ f = ñæ + 300 30 ϭϯ͘ϯ͘ϵ͘ʯ̡̨̨̛̦̼̬̣̖̦̌̔̍́͘ Под законами дробления понимается зависимость между затраченной на дробление энергией (работой) и крупностью продукта, получаемого в результате дробления (измельчения). Общее выражение эмпирической зависимости, характеризующей энергетические затраты на сокращение крупности, может быть представлено в виде dx (13.9) dE = k f (x) x где Е — удельная энергия, сообщаемая единице объема разрушенного тела, необходимая для прироста энергии вновь образованной поверхности; k — коэффициент пропорциональности; х — средний диаметр зерен; f(x) — показатель степени, зависящий от крупности частиц. Дифференциальное уравнение (13.9) может быть представлено в более простой форме: dx (13.10) dE = −k x x где k — коэффициент, который зависит от диапазона крупности и способа дробления (измельчения). На рис. 13.2 показана геометрическая интерпретация выражения (13.10). Эта зависимость есть обобщенная форма теоретических и эмпирических уравнений Риттингера, Кика, Кирпичева, Бонда, Свенссона, Холмса и других авторов. — 524 — Ðƫ͠ǮƻǁǬǃǀǬÐǀÐǀƿǂǬǁǋǆǬǃǀǬÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Наиболее известными являются уравнения Риттингера, Кика-Кирпичева, Бонда, которые принято называть «законами». Первые два «закона» (Риттингера и Кика-Кирпичева) имеют теоретическую основу, но они не применимы для всего диапазона крупностей. Третий «закон» (Бонда) является чисто эмпирической зависимостью, выведенной из анализа результатов периодического измельчения большого числа руд. Рис. 13.2. Зависимость удельного расхода энергии Е от крупности разрушаемых частиц. П. Риттингер (1867) установил, что энергия разрушения пропорциональна вновь образованной поверхности (13.11) E = k1 (Sk − Sn ) = k1 ∆S где Sk, Sn — поверхность материала до и после разрушения, м2; k1 — коэффициент пропорциональности, Дж/м2. Это уравнение может быть получено путем интегрирования уравнения (13.10) при п = 2:  1 1 − E = k1   dñð Dñð    (13.12) где Dср и dср — средняя крупность частиц соответственно исходного и дробленого продукта. — 525 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð Закон дробления Кика–Кирпичева (1874, 1875) гласит: подобным деформациям геометрически подобных и физически одинаковых тел соответствуют работы, пропорциональные объемам тел, т. е. (13.13) E = kv V = k3 D3 где kv — коэффициент пропорциональности, Дж/м3; V — объем кубического куска с ребром D, м. Уравнение (13.13) может быть получено также из (13.10) интегрированием его в тех же пределах при т = 1 Dñð E = k3 ln = k3 ln i (13.14) dñð где i — степень сокращения. В результате обработки данных многочисленных серий опытов, охватывающих широкий диапазон природных материалов, Бонд (1951) нашел, что  1 1  − E = k4   (13.15)  dñð Dñð  Общий вид уравнения, используемого Бондом,  1 1  (13.16) E = k4  −  D80   d80 где D80 и d80 — размер отверстий сита, через которые проходит 80% материала соответственно до и после дробления. Уравнения (13.15) и (13.16) могут быть получены из (13.10) при интегрировании для n= 1,5. Выражение (13.16) широко используется в зарубежной практике для выбора дробилок. В работах Бонда и каталогах фирмы «Аллис-Чалмерс» подобная формула также рекомендуется для определения производительности (кВтч/т) дробилок: ( N1 10W1 D80 − d80 = Q1 0,907 D80d80 ) (13.17) где N1 — мощность приводного двигателя рассчитываемой дробилки, кВт; Q1 — производительность рассчитываемой дро— 526 — Ðƫ͠ǮƻǁǬǃǀǬÐǀÐǀƿǂǬǁǋǆǬǃǀǬÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ билки, т/ч; W1, — индекс работы по Бонду; D80, d80 — размер отверстий сит, через которые проходит 80% исходного для дробления материала и 80% дробленого продукта, мкм. Индексом работы W1 Бонд называет удельный расход энергии в киловатт-часах на одну короткую тонну (короткая тонна — единица измерения массы, принятая в США, равна 0,907 метрической тонны), необходимый для дробления от бесконечного массива до продукта крупностью 80% — 100 мкм. Из формулы (13.17) работу дробления 1 т материала от бесконечного массива Dср = ∞ до продукта 80% — 100 мкм (dср = 100 мкм2) можно представить в виде E 1   1 = k −   100 Q ∞ и индекс работы êâò − ÷ 0,907  1 1  = − Wi =  = 0,907kS  100 Q êîð <ò <ìêì 0,5 ∞ Для определения производительности дробилки необходимо мощность приводного электродвигателя дробилки разделить на удельный расход энергии, вычисленный по формуле (13.17). ϭϯ͘ϯ͘ϭϬ͘ˁ̴̶̨̨̨̡̡̛̛̛̛̪̭̼̬̣̖̦͕̣̭̭̍̔̍́̌̌́ ̸̨̛̛̛̛̛̥̹̦̣̬̣̖̦̥̖̣̖̦̌̔́̔̍́̽́̚͘ Под способом дробления понимается вид воздействия разрушающей силы па куски дробимого материала. Известны четыре основных способа дробления: раздавливание, раскалывание, истирание и удар (рис. 13.3). Необходимые для разрушения кусков материала усилия развиваются в дробильных машинах, конструкции которых обеспечивают осуществление определенного способа дробления. В условиях непрерывного процесса, вследствие неупорядоченности размещения кусков в рабочем пространстве дробильной машины, наблюдаются все способы дробления, но всегда главную роль играет тот способ, для осуществления которого сконструирована данная машина. — 527 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð Рис. 13.3. Основные способы дробления: а — раздавливание; б — раскалывание; в — истирание, г — удар Способ дробления выбирается в зависимости от физико-механических свойств дробимого материала и крупности его кусков. Различают природные материалы прочные, или твердые, и менее прочные, или мягкие, вязкие и хрупкие. Способность горных пород противостоять разрушению зависит также от наличия трещин в кусках и способа воздействия на них разрушающего усилия. Трещиноватость уменьшает сопротивление кусков разрушению. Наибольшее сопротивление оказывают природные материалы раздавливанию, меньшее — изгибу и наименьшее — растяжению. Из соображений конструктивного характера, а также вследствие нежелательности переизмельчения в современной практике применяются дробилки, работающие главным образом раздавливанием и ударом при добавочных истирающих и изгибающих воздействиях на дробимый материал. В схемах дробления выделяют стадии крупного, среднего и мелкого дробления со следующими номинальными диаметрами кусков исходного материала (ориентировочно): Таблица 13.2. Стадии дробления. Стадия дробления Dн.исх., мм Крупное 1200–460 Среднее 500–150 Мелкое 180–40 — 528 — Ðƫ͠ǮƻǁǬǃǀǬÐǀÐǀƿǂǬǁǋǆǬǃǀǬÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Крупное, среднее и мелкое дробление твердых (прочных) и хрупких природных материалов целесообразно производить раздавливанием, а твердых и вязких материалов — раздавливанием с участием истирания. Крупное дробление мягких и хрупких природных материалов целесообразно выполнять раскалыванием, а среднее и мелкое — ударом. Все природные материалы измельчают ударом с участием истирания. Крупное, среднее и мелкое дробление обычно сухое. Мокрое дробление применяют только в тех случаях, если дробимый материал содержит глину, которую и стараются отмыть одновременно с дроблением. Промывка, например, производится при дроблении глинистых железных и марганцевых руд. Вода для промывки подается в рабочее пространство дробилок. В некоторых случаях вода подается в небольшом количестве из брызгал в завалочную воронку дробилки крупного дробления. Назначение этой воды — увлажнить дробимый материал и тем самым уменьшить пылеобразование. Некоторые природные материалы измельчаются с водой. Мокрое измельчение более производительно, оно осуществляется без пылеобразования и позволяет легко транспортировать измельченные продукты. Сухое измельчение применяется только в тех редких случаях, когда нельзя допускать контакта дробимого материала с водой или если измельчаемый материал обрабатывается в сухом состоянии. Машины для дробления и измельчения по механико-конструктивным признакам и основному методу дробления, осуществляемому в них, разделяются на пять основных классов: дробилки щековые; конусные; валковые; ударные (молотковые, роторные дробилки и дезинтеграторы); барабанные мельницы. Для крупного дробления применяют конусные дробилки и щековые дробилки. Для среднего дробления используют в основном конусные дробилки, а для мелкого молотковые и роторные дробилки. Валковые, молотковые, роторные дробилки и дезинтеграторы применяют для дробления углей, солей, бокситов, марганцевых руд, известняков. — 529 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð Существенным отличием дробилок от мельниц является то, что у дробилок нет непосредственного соприкосновения между рабочими (дробящими) деталями. Между ними всегда имеется зазор, заполняемый при работе дробимым материалом. Дробящие детали мельниц имеют непосредственное соприкосновение между собой при холостом ходе. При работе в режиме измельчения они разделяются слоем материала или частично могут соприкасаться друг с другом. Эффективность работы дробильных машин Э оценивается расходом энергии на дробление и выражается в тоннах дробленого продукта на 1 кВт*ч израсходованной энергии. Обратная величина — киловатт-часы на 1 т дробленого продукта — удельный расход энергии Eуд: Q Ý= E E Eóä = Q где Q — массовая производительность дробильной машины, т/ч; Е — энергия, затраченная на дробление, кВт*ч. ϭϯ͘ϰ͘ʿ̶̵̸̨̨̨̛̬̖̭̭̬̖̦̐́͘ ϭϯ͘ϰ͘ϭ͘ʽ̸̵̸̨̨̨̨̛̛̛̛̭̦̦̼̖̪̦̯̦̦̖̦̖̬̖̦̏́́̌̌̐́̚͘ Грохочение — процесс разделения сыпучих материалов по крупности на просеивающих поверхностях с калиброванными отверстиями. Частицы (куски) материала, размер которых больше размера отверстий сита, остаются при просеивании на сите, а частицы меньших размеров проваливаются через отверстия. Помимо грохочения, представляющего из себя непрерывный процесс, использующийся главным образом в промышленном масштабе, разделение частиц (кусков) по крупности происходит при просеивании, представляющем периодический процесс, используемый для лабораторных и полупромышленных установок. — 530 — ÐǤ͠ǮǅǬǯǯÐƼ͠ǮǲǮǆǬǃǀǎ Материал, поступающий на грохочение или просеивание, называется исходным, остающийся на сите — надрешетным (верхним) продуктом, проваливающийся через отверстия сита — подрешетным (нижним) продуктом. При последовательном просеивании материала на п ситах получают n + 1 продуктов. В этом случае один из продуктов предыдущего просеивания служит исходным материалом для последующего просеивания. Последовательный ряд значений размеров отверстий сит (от больших к меньшим), применяемых при грохочении, называется шкалой грохочения или классификации. Модуль шкалы классификации — постоянное отношение размера отверстий предыдущих сит к размеру отверстий последующих. Например, для шкалы классификации 100; 50, 25; 12,5; 6,25 мм модуль равен 2. Размер d наибольших частиц (кусков) подрешетного продукта так же, как и размер наименьших кусков надрешетного продукта, условно принимают равным величине отверстий сита l, через которое просеивается материал, т. е. d=l. Соответственно обозначают: подрешетный продукт −l (минус l) или −d (минус d); надрешетный продукт +l (плюс l) или +d (плюс d). Материал, прошедший через сито с отверстиями l1 и оставшийся на сите с отверстиями l2, причем l2 < l1, называется классом крупности. Крупность класса обозначают следующими тремя способами: –l1 + l2 (минус l1 плюс l2) или –d1 + d2 ; l1 – l2 или d1 – d2 ; l2 – l1 или d2 – d1. Например, классы –25 + 10; 25 – 10 и 10 – 25 мм. Из приведенных способов обозначения крупности классов наиболее широко применяют первый и третий, обязательный для использования при грохочении углей (ГОСТ 2093-82) и щебня. В получаемых при грохочении классах размер наибольших кусков материала d1 всегда меньше величины отверстий сита l1 и размер наименьших кусков d2 больше отверстий l2. Обозначения крупности классов −d1 + d2 или d1 − d2 указывают лишь на то, что данный класс был получен последовательным — 531 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð просеиванием материала на двух ситах с отверстиями размером d1 = l1 и d2 = l2. Машины и устройства для грохочения называют грохотами. Всякий грохот имеет одну или несколько рабочих (просеивающих) поверхностей — сит, установленных в одном или нескольких коробах, совершающих возвратно-поступательные качательные или встряхивающие движения. В некоторых конструкциях грохотов просеивающую поверхность образуют вращающиеся диски (валки), располагаемые параллельно в несколько рядов. Для грохочения крупного материала иногда используют неподвижные решетки, собранные из колосников различной формы или стержней, которые устанавливают с наклоном, достаточным для свободного скольжения по ним материала. Операции грохочения широко применяют на обогатительных и брикетных фабриках и сортировках, в промышленности строительных материалов, химической и многих других отраслях промышленности. В технологической схеме обогащения или при подготовке природных материалов к переработке выделяют следующие виды операций грохочения: самостоятельное, подготовительное и вспомогательное. Самостоятельное грохочение применяют на сортировках для выделения классов — готовых продуктов, направляемых непосредственно потребителям. Сортировке подвергают угли, железные руды, каменные строительные и дорожные материалы, абразивы и т. д. Подготовительное грохочение применяют на обогатительных фабриках с целью разделения перерабатываемого материала на классы, поступающие далее в операции обогащения. Такое грохочение часто необходимо перед гравитационными процессами, электромагнитной сепарацией и др. Вспомогательное грохочение применяют в сочетании с операциями дробления, для выделения готового по крупности продукта перед дробилками и контроля крупности дробленого продукта. Первый вид грохочения часто называют предварительным, а второй — контрольным или поверочным. Типичные схемы грохочения при дроблений изображены на рис. 13.4. — 532 — ÐǤ͠ǮǅǬǯǯÐƼ͠ǮǲǮǆǬǃǀǎ В ряде случаев при грохочении происходит выделение полезного продукта; такое грохочение называется избирательным. В результате получают продукты, отличающиеся не только по крупности, но и содержанию в них того или иного компонента. При избирательном грохочении используют различия в физических свойствах отдельных компонентов, входящих в состав сырья, например, различие в твердости и крепости или в форме кусков выделяемого компонента и сопутствующего материала. При получении, транспортировании и дроблении такого сырья в продуктах разной крупности будет неодинаковое содержание выделяемого материала. Рис. 13.4. Схема грохочения при дроблении: а — предварительное грохочение; б — предварительное и поверочное грохочение. Грохочение применяется также для отделения воды из пульпы, например, для обезвоживания обогащенных углей, промытых материалов и отделения суспензии от продуктов разделения в тяжелых средах. — 533 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð ϭϯ͘ϰ͘Ϯ͘ʿ̵̨̨̨̛̬̭̖̺̪̖̬̦̭̯̏̌̀̌́̏̽͘ В качестве просеивающей (рабочей) поверхности грохотов используют проволочные сетки, листовые сита (решета, т.е. перфорированные листы) и колосниковые решетки. ϭϯ͘ϰ͘ϯ͘ˁ̨̨̨̛̪̭̼̪̬̖̖̣̖̦̍̔́ ̸̨̡̨̨̨̛̬̦̱̣̥̖̯̬̖̭̭̭̯̐̌̐̌̏̌͘ При дроблении, измельчении и грохочении приходится иметь дело с рыхлыми смесями частиц материалов различного размера — от максимальных кусков, измеряемых сотнями миллиметров, до мельчайших частиц величиной в несколько микронов. Куски обычно имеют неправильную форму и их крупность может быть охарактеризована лишь несколькими размерами. Для практических целей желательно характеризовать величину отдельного куска одним размером. Этот размер обычно называют диаметром куска. Диаметром кусков сферической формы будет диаметр шара. Для кусков кубической формы за диаметр принимают длину ребра куба; для кусков неправильной формы диаметр определяют по главным измерениям — длине l, ширине b и толщине t параллелепипеда, в который вписывается измеряемый кусок. При этом за диаметр куска принимают ширину параллелепипеда d = b, либо среднее из двух или трех измерений. Номинальным диаметром диспергированного материала называют размер квадратной ячейки контрольного сита, через которое проходит 95% пробы материала. Для оценки номинального диаметра помимо прямых измерений используется поведение частицы в некоторых специфических условиях, например, осаждение в воде. Крупность всей массы сыпучего материала оценивают по содержанию в ней классов определенной крупности, т. е. по ее гранулометрическому составу. Наиболее часто для контроля процессов грохочения, дробления и измельчения применяют ситовый анализ. — 534 — ÐǤ͠ǮǅǬǯǯÐƼ͠ǮǲǮǆǬǃǀǎ ϭϯ͘ϰ͘ϰ͘ˁ̨̨̛̛̯̜̦̣̏̌̌̚͘ Рассев сыпучего материала с целью определения его гранулометрического состава называют ситовым анализом. Методы проведения ситовых анализов унифицированы. Пробы рассеивают сухим или мокрым способом в зависимости от крупности материала и необходимой точности ситового анализа. Если не требуется особой точности и материал не слипается, то применяют сухой способ рассева. При наличии в пробе значительной доли мелкого материала и необходимости повышенной точности анализа пробу рассевают мокрым способом. Гранулометрический состав измельченных материалов определяется методами, установленными ГОСТ 2093-82, 17495-80 и 24236-80 (последние два относятся к отбору и подготовке проб). ϭϯ͘ϰ͘ϱ͘ˈ̡̡̡̨̛̛̛̬̯̖̬̭̯̬̱̪̦̭̯̌̌̌͘ Характеристикой крупности называют графическое изображение гранулометрического состава сыпучего материала. Характеристики крупности строят в прямоугольной системе координат: частные — по выходам отдельных классов и суммарные (кумулятивные) — по суммарным выходам классов. При построении частной характеристики по оси абсцисс откладывают размер отверстий сит, применявшихся при ситовом анализе, а по оси ординат — выхода соответствующих классов в процентах. Ординаты, определяющие выхода отдельных классов, строят на меньшем или большем из диаметров, ограничивающих данный класс, или на диаметре, равном среднему арифметическому значению двух крайних диаметров. Полученные точки соединяют. По выходам отдельных классов можно построить график, называемый в статистике столбиковой диаграммой. Последняя составляется из прямоугольников, высота которых пропорциональна выходам классов, а основанием служит интервал крупности классов. Пример построения частной характеристики — 535 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð крупности по выходам отдельных классов и столбиковая диаграмма показаны на рис. 13.5а. Суммарную характеристику крупности Y = f(x) строят по точкам, положение которых находят по абсциссам х — диаметрам кусков и ординатам Y — суммарным выходам классов мельче или крупнее x (х = l, где l — размер отверстий сита, через которые просеивается материал). Если по оси ординат отложены выходы материала, крупнее данного диаметра, то характеристика построена «по плюс х», если мельче данного диаметра, то — «по минус х». Обе характеристики зеркально отражают одна другую и, будучи построены на одном графике, пересекаются в точке, соответствующей выходу материала, равному 50%. Пример построения суммарных характеристик показан на рис. 13.5б. Выход какого-либо класса ( −x1 + x2 ) по суммарной характеристике определяется разностью ординат, построенных на диаметрах х1 и х2. Суммарные характеристики «по плюс х» бывают выпуклыми, вогнутыми и прямолинейными. Выпуклая кривая получается при преобладании в материале крупных зерен, вогнутая — при преобладании мелких зерен. Прямолинейная кривая свидетельствует о равномерном распределении в материале зерен по крупности, т. е. на любом участке характеристики на единицу изменения диаметра приходится одинаковое изменение суммарного выхода материала. По виду частной характеристики заключения о распределении в материале крупных кусков и мелких зерен сделать нельзя, так как ее вид зависит от набора сит, применявшихся при ситовом анализе. Изменение шкалы сит изменяет и вид частной характеристики. По кривой суммарной характеристики можно определить выход любого класса крупности. При построении суммарных характеристик в широком диапазоне крупностей зерен материала отрезки на оси абсцисс в области мелких классов получаются весьма малого размера, что затрудняет построение и использование характеристик. Приходится строить непомерно большие графики. Чтобы избежать этого недостатка, суммарные характеристики строят в системе координат с по— 536 — ÐǤ͠ǮǅǬǯǯÐƼ͠ǮǲǮǆǬǃǀǎ Рис. 13.5. Графическое представление данных ситового анализа: а — частная характеристика крупности по выходам отдельных классов; б — суммарные характеристики крупности; в — полулогарифмическая характеристика крупности; г — логарифмическая характеристика крупности; д — характеристика крупности по Розину-Раммлеру; е — дифференциальная функция распределения по крупности — 537 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð лулогарифмическими или логарифмическими шкалами. Полулогарифмическую суммарную характеристику крупности строят в системе координат lgx,Y где х = l — размер отверстий сита, Y — суммарный выход классов. Преимущество полулогарифмической кривой по сравнению с обыкновенной кривой Y = f(x) состоит в том, что расстояния между соседними значениями отверстий сит на оси абсцисс в области мелких зерен увеличиваются, а в области крупных — сокращаются, что позволяет более точно отсчитывать выхода мелких классов при обычном размере графика. Если набор сит, применяемых для ситового анализа, имеет постоянный модуль, то построение полулогарифмической характеристики значительно упрощается, так как отрезки на оси абсцисс будут одинаковой величины. Например, для ряда сит с постоянным модулем М разница между логарифмами размеров смежных сит представлена в табл. 13.3. Таблица 13.3. Характеристики сит с постоянным модулем. Размеры отверстий сит Логарифмы размеров отверстий сит Разность между логарифмами размеров отверстий сит l1 lgl1 — lgl1+lgM lgl1+lgM–lgl1=lgM lgl1+2lgM (lgl1+lgM) — (lgl + 2lgM)1=lgM l1M 2 l1M Каждый отрезок на оси абсцисс между соседними ситами равен lgM. При построении характеристики за lgM можно принять произвольный отрезок. Полулогарифмическая суммарная характеристика крупности показана на рис. 13.5в. В отличие от обыкновенных кривых суммарной характеристики левая ветвь полулогарифмической кривой не доходит до ординаты, соответствующей — 538 — ÐǤ͠ǮǅǬǯǯÐƼ͠ǮǲǮǆǬǃǀǎ выходу 0%, так как этому выходу по оси абсцисс соответствует . Логарифмическая суммарная характеристика крупности строится в системе координат lgx, lgy, где x = l размер отверстий сита, Y — суммарный выход классов. Логарифмическая характеристика позволяет в некоторых случаях установить закономерность распределения в материале зерен по крупности. Для дробленого и измельченного материала логарифмическая характеристика, построенная «по минус l», большей частью получается прямолинейной. Пример построения логарифмической суммарной характеристики крупности показан на рис. 13.5г. ϭϯ͘ϰ͘ϲ͘ʤ̸̵̡̨̡̡̡̨̛̛̛̛̛̛̦̣̯̖̭̖̪̬̖̭̯̣̖̦̖̬̯̖̬̭̯̬̱̪̦̭̯̌̔̌̏̌̌͘ Гранулометрические характеристики крупности могут быть представлены в аналитической, табличной форме или графически. Интегральная характеристика f(x) представляет интегральную функцию распределения частиц крупности x; она связана с частной (дифференциальной характеристикой) F(x) соотношением dF ( x ) (13.18) y = f (x) = d Все уравнения являются эмпирическими зависимостями, которые более или менее точно описывают реальные свойства гранулометрических характеристик продуктов сокращения крупности. Наиболее общее выражение интегральной гранулометрической характеристики (функция распределения по крупности) имеет вид  x (13.19) Y− = F *  x  где Y − — суммарный выход зерен крупности меньше размера отверстий х; х* — крупность, принятая для сравнения. Поскольку х* есть оценка некоторой средней крупности частиц, то часто ее определяют как модуль крупности. Когда — 539 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð уравнение включает верхний предел крупности (например, уравнение Годэна-Андреева), х* фактически представляет максимальную крупность частиц в распределении. Если уравнение не включает верхнего предела (например, уравнение Розина-Раммлера), х* обычно ближе к истинному среднему. Уравнение типа (13.19) также включает второй параметр, который может быть назван модулем распределения, поскольку он является мерой формы характеристики крупности. В некоторые уравнения включают третий параметр, связанный с асимметрией гранулометрической характеристики, но это вводит дополнительную сложность, которая редко оправдывается. Некоторые наиболее общие случаи подобных (13.19) уравнений даны в табл. 13.4. Если логарифмическая суммарная характеристика «по минусу» прямолинейна, то для того материала гранулометрический состав можно представить уравнением lg Y − = k lg x + lg A где Y − — суммарный выход класса мельче отверстий сита (по минусу); k — коэффициент, равный тангенсу угла наклона прямой; х — размер отверстий сита; lg A — отрезок, отсекаемый прямой на оси ординат. Следовательно, получаем Y − = F ( x ) = Axk (13.20) Уравнение (13.20) суммарной характеристики, построенной «по минус х», известно под названием уравнения Годэна-Андреева. Значение показателя k определяет направление и степень изгиба кривой характеристики. Если характеристику построить «по плюс х», то она будет: при k < 1 выпуклой, при k = 1 прямой, при k < 1 вогнутой. Следовательно, по значению показателя k можно судить о преобладании в материале крупных или мелких зерен. Из уравнения (13.20) при х = хтах; Y − = 100% имеем A= 100 k xmax — 540 — Таблица 13.4. Уравнения гранулометрических характеристик крупности частиц. Аналитическая функция Нормальное распределение Математическое уравнение −   x − x  dF ( x )   1 = exp − dx 2σ2 σ 2π Параметры уравнения 2 — 541 — dF ( x ) lg e (lg x − a) = exp − d (lg x ) σ 2π 2σ2 Уравнение Розина-Раммлера   n x F ( x ) = exp  −      xp     дартное отклонение 1 a = ∑ lg xi n 2 1 σ2 = ∑ (lg xi − a ) n xp — крупность, при которой Y–=0,632; п — константа, характеризующая исследуемый материал Действительные смеси частиц редко могут быть описаны этой функцией, поскольку большинство распределений асимметричны В некоторых случаях этому распределению подчиняются продукты дробления Хорошо согласуется с экспериментальными данными по смесям измельченых материалов ÐǤ͠ǮǅǬǯǯÐƼ͠ǮǲǮǆǬǃǀǎ Логарифмически-нормальное распределение − x — среднее арифметическое; σ — стан- Примечание Математическое уравнение Уравнение Годэна-Андреева  x  F (x) =   xmax  — 542 — Уравнение Харриса k   x S  F ( x ) = 1 −    xm   R Параметры уравнения Примечание xmax — модуль крупности, отрезок отсекаемый на оси крупности при F(x) = 1; k — константа, модуль наклона распределения логарифмической характеристики Делает возможным использование стандартной логарифмической координатной бумаги хт — максимальная крупность в пробе; S — параметр, связанный с наклоном логарифмического графика в тонком диапазоне крупностей; R — параметр, связанный с наклоном логарифмического графика в грубом диапазоне крупностей Наиболее применим для описания полимодальных распределений ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð Аналитическая функция ÐǤ͠ǮǅǬǯǯÐƼ͠ǮǲǮǆǬǃǀǎ Значение параметра А при данном показателе k зависит от диаметра максимального зерна материала xmax. Уравнение характеристики позволяет решать ряд задач, например, определять число зерен в любом классе, поверхность зерен, удельную поверхность и т. п. Параметры уравнения находят следующим образом. На логарифмической характеристике выбирают две точки, соответствующие двум наиболее удаленным диаметрам, и определяют показатель k как тангенс угла наклона прямой: k= lg Y2− − lg Y1− lg x2 − lg x1 Параметр А находят подстановкой значения k в уравнение (13.20) для одной из точек: Y2− = Ax2k ; A = Y2− x2k Если диаметры зерен брать по отношению к диаметру максимального куска в материале, то уравнение Годэна-Андреева преобразуется в «приведенное» уравнение с одним постоянным параметром Y− =  100  100 − k ;Y = 100  k  = 100xîòí k xmax  xmax  k или, если Y − выражено в долях единицы, Y − = xîòí . Показатель k находят описанным выше вычислением или, если принять за исходные для расчета x2 и x1 = x2/2, то k= lg Y2− − lg Y1− lg2 (13.21) Для продуктов шаровых мельниц значение показателя k в уравнениях характеристик крупности находится в пределах 0,7–1. Обработка большого числа гранулометрических анализов продуктов дробления и измельчения показала, что во многих случаях лучшее соответствие опытным данным по сравнению — 543 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð с уравнением Годэна-Андреева дает уравнение, предложенное Розиным и Раммлером: n (13.22) R = 100e − bx где R — суммарный выход класса, крупнее х, по плюсу, %; х — размер отверстий сита; b и п — параметры, зависящие от свойств материала и размерности х. Соответствие опытных данных уравнению (13.22) можно проверить графически путем нанесения опытных точек на функциональную координатную систему. При двойном последовательном логарифмировании уравнение (13.22) приобретает вид 100 100 lg = bxn lg e lglg = n lg x + lg (b lg e ) R R В координатах уравнение Розина-Раммлера изображается прямой линией с угловым коэффициентом п. Пример построения такого графика показан на рис. 13.5д. На осях против соответствующих логарифмических величин приведены выхода классов и диаметры зерен материала. Параметры b и п уравнения (13.22) находят по двум известным точкам, решая систему уравнений: R1 = 100e R2 = 100e − bx1n n − bx2 При совместном решении этих уравнений получим 100 100 − lglg lglg R1 x2 n= (13.23) lg x1 − lg x2 Зная n, определяем b: 100 100 R1 = ;bx1n lg e = lg bx1n R1 e 100 lg R b= n 1 x1 lg e — 544 — (13.24) ÐǤ͠ǮǅǬǯǯÐƼ͠ǮǲǮǆǬǃǀǎ Уравнение Розина-Раммлера охватывает опытные точки в широком диапазоне крупностей, но оно не удовлетворяет одному конечному условию — нулевой выход классов достигается только при бесконечно большой крупности материала: n R = 100e − bx = 100 и R = 0 при х = ∞. n ebx При использовании уравнения Розина-Раммлера приходится считаться с этим обстоятельством и принимать конечную крупность материала, соответствующую какому-то определенному значению выхода класса. Сливы классификаторов шаровых мельниц, работающих в замкнутом цикле, большей частью удовлетворяют уравнению Розина-Раммлера при n = 1. ϭϯ͘ϰ͘ϳ͘ʪ̴̴̶̴̶̡̛̛̛̛̖̬̖̦̣̦̼̖̱̦̌̽ ̨̡̨̛̛̬̭̪̬̖̖̣̖̦̪̬̱̪̦̭̯̌̔́͘ Дифференциальные функции распределения по крупности показывают число зерен или массовые выхода каждого класса крупности в данном материале. Материал, состоящий из смеси зерен разных размеров, разделенный на классы крупности, можно рассматривать как статистический коллектив. Размер зерен будет аргументом коллектива, а общее число зерен в пробе материала или ее общая масса составят числовой или массовый объем статистического коллектива. Число зерен в каждом классе или их массу называют численностью класса, частотой или абсолютной частостью, а частоты классов, отнесенные к объему коллектива, — относительными частостями классов. Если в прямоугольных координатах по оси абсцисс отложить крупность классов и на соответствующих интервалах крупности построить прямоугольники, площади которых будут пропорциональны частоте класса, то получим гистограмму распределения зерен материала. Это равнозначно построению прямоугольников высотой, равной частости на единицу длины интервала, на интервале как основании прямоугольника. При уменьшающемся интервале ступенчатая линия, сверху — 545 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð ограничивающая прямоугольники, приближается к плавной кривой; в пределе она дает дифференциальную функцию распределения (рис. 12.5е). Ординаты функции распределения γ(х) выражают частость на единицу длины бесконечно узкого интервала по оси абсцисс, а площадь под кривой определяет число объектов (число зерен, массовый выход их) в соответствующих промежутках. Зерна, диаметры которых меньше хn и больше хn−1, образуют n-й класс — xn + хn-1 с интервалом крупности ∆хn = хп – хп−1. Если число зерен в этом классе Nn, а масса их Wn, то относительная частость по числу зерен будет Nn / n и по массе Wn / W, где N — общее число зерен в пробе материала, a W — их общая масса. Таким образом, для построения функции распределения по числу зерен следует по оси абсцисс на интервале хп – хп–1 построить прямоугольник высотой Nn / N ∆хп, а затем — прямоугольники для всех других классов и соединить кривой точки на серединах верхних сторон прямоугольников. Относительное число зерен в бесконечно малом интервале dх Nn dN = dx N ∆xn и в классе хп – хп–1 Nxn −xn−1 = lim ∑ dx→0 dN = x 1 n Nn dx N x ∫ ∆xn n −1 Аналогично имеем следующее выражение для массовых выходов зерен класса хn – хп−1; x Wxn −xn−1 = 1 n Wn dx W x ∫ ∆xn (13.25) n −1 Последнее выражение соответствует уравнению (12.18) dF ( x ) y = f (x) в следующей записи dx ∞ F ( x ) = ∫ f ( x )dx 0 — 546 — (13.26) ÐǤ͠ǮǅǬǯǯÐƼ͠ǮǲǮǆǬǃǀǎ В этом уравнении пределы интегрирования определяют границы класса крупности, массовый выход которого определяется, а подынтегральная функция f(x) есть дифференциальное распределение по крупности. Кривые распределения дают более наглядное представление о гранулометрическом составе сыпучих материалов в сравнении с суммарными характеристиками крупности. В классах с наибольшим выходом кривая показывает максимум, а при отсутствии в материале зерен какого-либо размера — падает до нуля. Выхода класса на кривой распределения пропорциональны площадям, ограниченным кривой и двумя ординатами, проведенными на диаметрах, ограничивающих данный класс. Дифференциальные функции распределения и суммарные характеристики крупности полностью характеризуют гранулометрический состав материала с точки зрения математической статистики. Возможен аналитический переход от одной кривой к другой, если известно уравнение какой-либо из них (см. формулу 12.18). ϭϯ͘ϰ͘ϴ͘ʦ̸̵̸̸̶̨̨̛̛̛̛̛̛̼̭̣̖̦̖̪̖̬̦̭̯̭̣̭̯̏̌̌ ̵̨̨̡̡̡̨̛̛̛̛̛̪̱̬̦̖̦̥̭̱̥̥̬̦̜̬̯̖̬̭̯̬̱̪̦̭̯̌̏́̌̌̌͘ Если известно уравнение суммарной характеристики крупности, то общий ход вычисления поверхности и числа зерен может быть принят следующий. Пусть уравнение характеристики «по минусу» будет Y − = f ( x ) где Y − — выход зерен (г) меньше диаметра х, см. Тогда Y − = f ( x ) — выход элементарного класса крупностью от х до х + dх. В 1 г материала плотностью σ (г/см3) объем элементарного класса (см3) dY − f ( x ) dx = δ δ Для одного зерна кубической формы объем равен х3, а поверхность 6х2. Число зерен в элементарном классе а поверхность зерен (см ) 2 — 547 — , ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð 6x2 DY − 6DY − = δx δ x3 Число зерен и их поверхность в классе мельче х2 и крупнее х1 находят интегрированием из выражений в пределах от х1 до х2: dS = x2 N− x 2 + x1 = dY ∫ δx 3 x2 S− x2 + x1 = x1 ∫ x1 6dY − δx При вычислении поверхности безразлично, будет ли принят формой зерен куб или шар. В самом деле, если принять все зерна шарообразной формы, то получим dY 6 dY − πx2 = dS = 3 δ dx πx δ 6 Конкретные выражения для числа и поверхности зерен в заданном классе крупности — х2+ х1 в предположении, что распределение соответствует уравнению Розина-Раммлера. ϭϯ͘ϰ͘ϵ͘ˑ̴̴̶̵̸̡̨̨̨̨̛̛̖̯̦̭̯̪̬̖̭̭̬̖̦̏̽̌̐́͘ Для количественной оценки полноты отделения мелкого материала от крупного при грохочении введено понятие эффективности (точности) грохочения. Эффективностью грохочения называют выраженное в процентах или в долях единицы отношение массы подрешетного продукта к массе нижнего класса в исходном материале. Нижним классом называют материал, крупность которого меньше размера отверстия сита грохота. Содержание нижнего класса в любом продукте можно определить тщательным рассевом пробы на сите с отверстиями размерами, равными размерам отверстий сита грохота. Эффективность грохочения можно также определить как извлечение нижнего класса в подрешетный продукт. Рассмотрим баланс материала при грохочении: Q = C +T — 548 — (13.27) ÐǤ͠ǮǅǬǯǯÐƼ͠ǮǲǮǆǬǃǀǎ где Q — масса исходного материала; С — масса подрешетного продукта; Т — масса надрешетного продукта. Также имеем: Q α /100 — масса нижнего класса в исходном материале; Tϑ /100 — масса нижнего класса в надрешетном продукте, α — содержание нижнего класса в исходном материале, %; ϑ — содержание нижнего класса в надрешетном продукте, %. Эффективность грохочения (%), согласно определению, C C (13.28) E= 100 = 104 Qα Qα 100 Для определения эффективности грохочения по формуле (12.28) необходимо знать массу исходного материала Q и подрешетного продукта С, непосредственное определение которых при непрерывном процессе на производств представляет известные трудности. Поэтому отношение масс C/Q (выход подрешетного продукта) определяют по содержанию нижнего класса в исходном материале и надрешетном продукте. Баланс нижнего класса Qα Tϑ = C+ 100 100 Заменив Т, воспользовавшись формулой (12.27), получим Qα = 100C + ( Q − C ) ϑ Откуда α−ϑ C = Q 100 − ϑ (13.29) Подставив отношение C/Q в формулу (13.28), получим в окончательном виде формулу для определения эффективности грохочения (%) по нижнему классу α −β (13.30) E= 104 α (100 − ϑ ) Содержание нижнего класса α и ϑ определяют тщательным рассевом проб исходного материала и надрешетного продукта на ситах с отверстиями той же величины и формы, что и в сите грохота, эффективность грохочения которого определяют. — 549 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð Подобным же образом можно определить эффективность грохочения по любому суммарному или узкому классу крупности, который мельче размера отверстий сита грохота, считая эффективностью грохочения по данному классу отношение массы этого класса в подрешетном продукте к массе того же класса в исходном материале. К ранее принятым обозначениям добавим α1, β1, ϑ1 — соответственно содержания заданного класса крупности в исходном материале, подрешетном и надрешетном продуктах в процентах. Эффективность (%) по любому заданному классу крупности Cβ1 Cβ1 100 100 = 100 E= Qα1 Qα1 100 Выход (%) подрешетного продукта C/Q находят из баланса данного класса при грохочении: C α − ϑ1 Qα1 − Cβ1 + ( Q − C ) ϑ1; = 1 Q β1 − ϑ1 α1 − ϑ1 β1 (13.31) 100 β1 − ϑ1 α1 Формула (13.30) для эффективности по нижнему классу получится из формулы (13.31), если подставить в нее значение β1 = 100 %, так как в этом случае весь подрешетный продукт будет состоять из зерен нижнего класса. В некоторых случаях результаты грохочения оценивают упрощенно по содержанию ϑ нижнего класса в надрешетном продукте, т. е. по так называемому «замельчению». Если этим способом пользуются для целей текущего контроля операции грохочения при относительно постоянном или мало изменяющемся содержании α1 нижнего класса в исходном материале, то результаты контроля будут достаточно хорошо характеризовать работу грохотов, так как каждому «замельчению» надрешетного продукта соответствует определенное извлечение данного класса в подрешетный продукт [см. формулу (13.30)]. При колеблющемся в значительных пределах содержании нижнего класса в исходном материале оценка по «замельчению» дает E= — 550 — ÐǤ͠ǮǅǬǯǯÐƼ͠ǮǲǮǆǬǃǀǎ только качественную характеристику операции грохочения и не позволяет судить о полноте выделения в подрешетный продукт нижнего класса. ϭϯ͘ϰ͘ϭϬͨ͘ʸ̸̶̡̛̛̛̛̖̖͕̯̬̱̦̼̖̯̬̱̦̺̖̭̯̼̐ͩͨ̔ͩͨ̌̔́̀ͩ̌̚͘ Просеивание зерен нижнего класса сыпучего материала сквозь сито можно рассматривать как операцию, состоящую из двух стадий: зерна нижнего класса должны пройти сквозь слой зерен верхнего класса, чтобы достигнуть поверхности сита; зерна нижнего класса должны пройти через отверстия сита. Осуществлению обеих стадий помогает соответствующий характер движения короба грохота, приводящий слой зерен на сите в разрыхленное состояние и освобождающий сито от зерен, застрявших в его отверстиях. При встряхивании короба в слое зерен, лежащем на сите, происходит их сегрегация (расслоение по крупности), причем наиболее крупные зерна оказываются в верхнем слое, а наиболее мелкие — на поверхности сита. Последние легко достигают поверхности сита и проходят через его отверстия. Но зерна, близкие по величине к размеру отверстий сита, с трудом проходят в промежутках между более крупными зернами слоя материала, лежащего на сите, а также и через отверстия сита. Практика грохочения показала, что зерна, диаметр которых меньше чем три четверти отверстия сита, легко проходят в промежутках между крупными зернами материала на сите и по достижении ими поверхности сита немедленно проваливаются через отверстия. Такие зерна в отношении их проходимости называют «легкими». Зерна крупнее трех четвертей отверстия сита с трудом проходят в промежутках между крупными зернами и через отверстия сита. Эта трудность прохождения прогрессивно возрастает по мере приближения диаметра зерен к размеру отверстий сита. Такие зерна называют «трудными». Зерна, диаметр которых более полуторного размера отверстия сита, существенно не влияют на перемещение «легких» и «трудных» зерен к поверхности сита. На сите нижний слой материала, состоящий из зерен диаметром меньше полутор— 551 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð ного размера отверстия сита, затрудняет проникновение к его поверхности близких к ним по крупности «трудных» зерен. Кроме того, зерна, близкие по диаметру к размеру отверстия сита, но больше их, легко застревают в отверстиях и забивают сито. Зерна, размер которых больше отверстий сита, но меньше полуторной величины их, называют «затрудняющими». Чем меньше в исходном материале «трудных» и «затрудняющих» зерен, тем легче его грохочение и тем выше, при прочих равных условиях, эффективность грохочения. Характеристики крупности легко- и трудногрохотимого материала на ситах с размером отверстий l показаны на рис. 13.6. Рис. 13.6. Суммарные характеристики крупности: а — легкогрохотимого материала; б — трудногрохотимого материала: 1 — выход «трудных» зерен; 2 — выход «затрудняющих» зерен Эффективность грохочения по «трудным» зернам определяют по общей формуле (12.31), в которой — содержания «трудных» зерен соответственно в исходном материале, подрешетном и надрешетном продуктах. ϭϯ͘ϰ͘ϭϭ͘ˇ̶̵̸̡̨̨̨̨̛̛̛̯̬̼͕̣̺̖̦̪̬̖̭̭̬̖̦̌̏́̀̌̐́͘ Ряд факторов, определяющих скорость, с которой частицы проходят через сито грохота, можно разделить на две группы: – зависящие от исходного материала: насыпная плотность; форма кривой гранулометрической характеристики; форма частиц; поверхностная влажность; — 552 — ÐƸǁǬǭǰ͠ǮǂǪƼǃǀǰǃǪǎÐǯǬ͟Ǫ͠Ǫǅǀǎ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǪ – зависящие от оборудования: поверхность грохочения (площадь, доля живого сечения, размер, форма и толщина отверстий); характеристика вибраций (амплитуда, частота, направление); угол наклона грохота; способ подачи материала. ϭϯ͘ϰ͘ϭϮ͘ʶ̶̵̸̡̨̨̨̛̛̛̦̖̯̪̬̖̭̭̬̖̦̌̌̐́͘ Во всех случаях грохочения сыпучего материала наблюдается закономерная связь эффективности грохочения от его продолжительности. Эффективность в первые моменты грохочения быстро растет, а затем нарастание ее замедляется (рис. 13.7). Это объясняется тем, что масса зерен, проходящих сквозь сито в каждый данный момент, зависит от массы находящихся на сите к данному моменту зерен крупностью мельче размера отверстий. Кроме того, некоторое влияние на замедление прохождения зерен сквозь сито оказывает и то обстоятельство, что в первые моменты времени проходят «легкие» зерна, а с каждым следующим промежутком времени их становится все меньше и на сите остаются «трудные» зерна, требующие длительного времени для прохождения через его отверстия. Рис. 13.7. Зависимость эффективности грохочения E от продолжительности рассева t. ϭϯ͘ϱ͘ˑ̶̡̨̛̛̣̖̯̬̥̦̯̦̭̖̪̬̌̐̌́̌̌́͘ ˇ̸̶̡̨̨̨̛̛̛̖̭̖̭̦̼̪̬̖̭̭̏̌̚͘ При переработке твердых промышленных отходов (особенно минеральных, содержащих черные и цветные металлы; вышедшей из строя радиоэлектронной аппаратуры и других изделий — 553 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð на основе металлов и сплавов; некоторых топливных зол; смесей пластмасс; шлаков цветной и черной металлургии и др.) используют различные магнитные методы сепарации. Магнитные методы тесно переплетаются с гравитационными, а также используются в некоторых видах флотации. Они позволяют создать мощные силы воздействия на материалы, которые превышают силу гравитации в 100 и более раз, что облегчает процессы разделения. Эти методы обладают высокой избирательной способностью, экологической чистотой, простотой обслуживания и низкой себестоимостью. Магнитные методы используют для отделения парамагнитных (слабомагнитных) и ферромагнитных (сильномагнитных) компонентов смесей твердых материалов от их диамагнитных (немагнитных) составляющих. Магнитной сепарацией можно выделить вещества с удельной магнитной восприимчивостью выше 1×10–5 м3 /кг. Сильномагнитными свойствами обладают железо и его сплавы, слабомагнитные оксиды железа после их обжига и некоторые другие вещества. Ряд оксидов, гидроксидов и карбонатов железа, марганца, хрома и редких металлов относится к материалам со слабомагнитными свойствами. Различные породообразующие минералы (кварц, полевые шпаты, кальцит и т.п.) относятся к немагнитным материалам. Слабомагнитные материалы разделяют в сильных магнитных полях (напряженностью Н = 800–1600 кА/м), сильномагнитные — в слабых полях (Н = 70–160 кА/м). Магнитные поля промышленных сепараторов бывают в основном постоянными или переменными; комбинированные магнитные поля применяют редко. В магнитных сепараторах неоднородность магнитного поля создаются полюсными наконечниками различной формы. Для получения магнитных полей с малой величиной gradН применяют естественные или искусственные магниты из специальных сплавов с постоянным магнитным полем. Сильные магнитные поля с высоким градиентом напряженности создаются катушками, питаемыми постоянным током и снабженными стальными сердечниками. При этом, чем больше величина намагничивающего тока и количество витков в катушке, тем выше напряженность магнитного поля в рабочем зазоре сепаратора. — 554 — ÐƸǁǬǭǰ͠ǮǂǪƼǃǀǰǃǪǎÐǯǬ͟Ǫ͠Ǫǅǀǎ ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǪ Магнитная сила Fпонд, действующая на частицу материала в магнитном поле, определяется по формуле: Fïîíä = V χHgradH (13.32) где V — объем частицы; χ — объемная магнитная восприимчивость; Н — напряженность магнитного поля. Удельное значение магнитной силы fпонд определяется по формуле. F VcHgradH fпонд = понд = = cуд HgradH (13.33) m Vd где m — масса частицы. Принцип работы магнитного сепаратора схематически показан на рис. 13.8. Кроме магнитной силы, на частицу, находящуюся в рабочей зоне сепаратора, действуют силы тяжести Р, трения Fт, центробежная Fц и сопротивления среды Fс. Для успешного разделения магнитных и немагнитных частиц в магнитном поле сепаратора магнитная сила, действующая на магнитные частицы, должна превышать равнодействующую всех механических сил. Взаимодействие между всеми силами зависит от способа подачи сырья в рабочую зону сепаратора, конструктивных особенностей аппарата, режима его работы. Подлежащие магнитной сепарации материалы, как правило, подвергают предварительной обработке (дроблению, измельчению, грохочению, гомогенизирующему обжигу и др.). Магнитное обогащение материалов крупностью 3–50 мм проводят сухим способом, материалов мельче 3 мм — мокрым. Технология магнитной сепарации зависит, прежде всего, от состава подлежащего переработке материала и определяется типом используемых сепараторов. Последние обычно снабжены многополюсными открытыми или закрытыми магнитными системами, создающими различные типы магнитных полей. Сепараторы отличаются способами питания (верхняя или нижняя подача материала) и перемещения продуктов обогащения (барабанные, валковые, дисковые, ленточные, роликовые, шкивные сепараторы) и другими характеристиками. — 555 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð Рис. 13.8. Принцип работы магнитного сепаратора. а — верхняя зона; б — нижняя зона; в — вертикальная зона; I-исходное сырье; II — магнитный продукт; III — немагнитный продукт Оценить производительность магнитных сепараторов весьма сложно вследствие влияния на нее многих факторов. Опыт эксплуатации этих аппаратов позволяет в ряде случаев рассчитывать их производительность с использованием выражения: Q = qnLp (13.34) где Q — производительность сепаратора по сухому исходному питанию, т/ч; q — удельная производительность, т/(м-ч); n — число головных барабанов, валков или роликов в сепараторе; Lp — рабочая длина барабана, валка или ролика, м. Эвакуируемые из магнитного поля зерна сильномагнитных материалов вследствие остаточной намагниченности могут агломерироваться в агрегаты разного вида. С целью устранения последствий этого явления, называемого магнитной флокуляцией, используют многократное перемагничивание таких материалов в переменном магнитном поле размагничивающих аппаратов. — 556 — ÐƸǁǬǭǰ͠ǮǯǬ͟Ǫ͠Ǫǅǀǎ ϭϯ͘ϲ͘ˑ̸̶̡̨̡̛̛̛̣̖̯̬̦̥̖̭̭̖̪̬̔̌̌́̌̌́͘ Это комбинированный процесс магнитного обогащения, основанный на использовании различий в магнитной восприимчивости обогащаемых материалов. Извлечение обогащаемых материалов происходит в переменном магнитном поле. В постоянном магнитном поле магнитный момент диамагнетика направлен против поля, а у парамагнетика наоборот магнитный момент ориентируется по полю. Поэтому согласно выражению (13.32) при определенном направлении магнитного поля диамагнетик будет выталкиваться из зазора постоянного магнита, а парамагнетик наоборот втягиваться. Следовательно, для разделения, как ферромагнитных материалов, так и слабомагнитных материалов необходимо применять переменное магнитное поле. Основная область применения электродинамической сепарации — извлечение из потока твердых отходов цветных металлов, а также разделение цветных металлов по видам. Преимущественная крупность извлекаемых компонентов +40 (+50) мм. Содержащиеся в ТБО цветные металлы являются одним из основных ценных компонентов. Цветной металлолом в ТБО в основном представлен различными видами отслужившей упаковки и посуды из алюминия (банки из-под напитков, баллончики, тюбики, тарелки, ложки, вилки, кастрюли), значительно реже — сантехническими изделиями из сплавов не медной основе (бронзы, латуни). Содержание цветных металла в ТБО — на уровне 0,7%. ϭϯ͘ϳ͘ˑ̶̡̨̛̣̖̯̬̭̖̪̬̌̌́͘ Электросепарация — это процесс обогащения (разделения) материалов основанный на разнице в величине и знаке заряда частиц разделяемых материалов. Зарядка частиц разделяемых материалов может быть достигнута различными способами. При соприкосновении с заряженным электродом частица материала в зависимости от ее электропроводности может приобрести заряд определенной величины и знака или — 557 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð остаться незаряженной. Частицы материалов с высокой электропроводностью при соприкосновении с электродом мгновенно получают заряд, частицы же с низкой электропроводностью за это время не успевают зарядиться. Различные материалы различаются своей электропроводностью. Так, например, бумага, макулатура уже при влажности в 20% хорошо проводят электричество, приближаясь по проводимости к металлам, тогда как полимерная пленка является плохим проводником. Но электропроводность одних и тех же материалов может в значительной степени изменяться в зависимости от содержания в них примесей и состояния поверхности. Наличие на поверхности материалов окислов, тончайших пленок солей, шламов и влаги сильно влияет на их электропроводность. Частица материала может приобрести электрический заряд в результате трения о другое тело (о лоток, о частицы других материалов и т. д.). Одна и та же частица при трении о различные тела может приобрести заряды, отличающиеся по величине и по знаку. Электрический заряд может возникнуть на частице при воздействии на нее электрического поля на расстоянии. Например, зарядка частиц в поле коронного разряда происходит за счет различной способности частиц адсорбировать на себе ионы воздуха, создаваемые в поле разряда при напряжении 20–50 тыс. вольт. Трибоадгезионная сепарация основана на различной адгезии наэлектризованных за счет трения о поверхность электрода частиц. При перемещении частиц материала в электрическом поле, между ними возникают силы притяжения или отталкивания, различно изменяющие траекторию их движения в зависимости от электропроводности. Сила взаимодействия двух заряженных частиц в первом приближении определяется законом Кулона: 1e e F = 1 22 ε r (13.35) где H — диэлектрическая постоянная среды; e1, е2 — заряды частиц; r — расстояние между частицами. — 558 — ÐƸǁǬǭǰ͠ǮǯǬ͟Ǫ͠Ǫǅǀǎ Напряженность поля в данной точке характеризуется силой, с которой поле действует на единицу положительного электричества, помещенного в какой- либо точке. Электрическая сила, действующая на помещенную в электрическом поле частицу с зарядом е, будет равна: (13.36) F1 = eE где Е — напряженность электрического поля. Эффективность электрического разделения, как мы уже упоминали, в значительной степени зависит от состояния поверхности материалов. Естественное состояние поверхности материалов в ряде случаев может быть изменено в желаемом направлении искусственно вследствие образования на частицах поверхностных пленок. Это достигается обработкой разделяемого материала реагентами, обладающими избирательным действием на различные материалы. Электрическому обогащению подвергается обычно материал крупностью от 2 до 0,1 мм. При этом лучшие результаты получаются на материале, классифицированном в узких пределах. Разделяемый материал должен быть сухим. Этот метод в обогащении применяется, главным образом, для доводки гравитационных или флотационных концентратов, полученных при обогащении оловянных, вольфрамовых, фосфоритных и других руд. Для электрического обогащения чаще всего применяют специальные аппараты — электросепараторы, которые бывают различных конструкций. В настоящее время широкое распространение получили коронные сепараторы барабанного и ленточного типа. В общем случае результирующая сила F, определяющая траекторию движения частицы, является векторной суммой основных взаимодействующих сил: F = ± Fk + Fçî − Fö ± FT (13.37) где Fк — сила Кулона; Fзо — сила зеркального отображения, обусловленная искажением электрического поля поверхностью электрода и равная Fзо = q/(4r2) (r — расстояние от заземленного электрода); Fц — центробежная сила; Fт — сила тяжести. Если на барабане находится компонент-проводник, знак его заряда совпадает со знаком заряда барабана, а направление — 559 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð силы электрического поля меняется на противоположное. После выхода из зоны действия коронирующего электрода проводник отрывается от поверхности барабана, причем в момент отрыва он движется по линии, касательной к поверхности барабана в точке отрыва. Разность потенциалов между электродами колеблется в пределах от 20000 до 40000 в: Производительность сепаратора в зависимости от крупности обогащаемого материала, удельного веса и разности в электропроводности минералов колеблется от 1,5 до 2 т/час. Работа сепаратора регулируется изменением разности потенциалов, скорости вращения барабана и положения делительных перегородок. Электросепарация применяется при обогащении техногенного сырья (ТБО, отработанные демеркуризированные ртутные лампы, металлосодержащие пластмассовые отходы, электронный лом, электрокабельный лом, вольфрамовые спирали, стеклобой, металлы и пластмассы), а также, как мы уже упоминали, полимерная пленка и бумага. Преимущественная крупность разделяемого техногенного сырья — от 100 до 1 мм. Желательна классификация материала в узких пределах крупности. ϭϯ͘ϴ͘ʤ̶̨̛̬̭̖̪̬̾̌̌́͘ Аэросепарация — это процесс обогащения в движущейся газовой (воздушной) среде, основанный на использовании различий в плотности компонентов и их скорости витания. Аэросепарацию (пневмосепарацию) применяют при обогащении полезных ископаемых (угля, асбеста) и техногенного сырья (ТБО, дробленого электрокабельного лома — удаление неметалических компонентов, дробленого демеркуризованного стеклобоя, отработанных ртутных ламп, других отходов). Аэросепарация эффективна для обеспыливания материалов, выделения тонких классов крупности при сухом измельчении строительных материалов (воздушный сепаратор работает в замкнутом цикле с аппаратом измельчения). При обогащении ТБО аэросепарацию применяют для разделения потока отходов на легкую и тяжелую фракции (это — 560 — Ðǜǌ͠ǮǯǬ͟Ǫ͠Ǫǅǀǎ необходимо прежде всего по условиям технологии извлечения металлов), а также для выделения горючих компонентов с целью последующей термической переработки (в принципе возможна не только энергетическая утилизация легких компонентов) и для очистки от примесей компоста, полученного из ТБО. При аэросепарации ТБО в легкую фракцию переходят макулатура, полимерная пленка, некоторые текстильные компоненты (в основном синтетические), уличный смет и т.п. Рекомендуемая крупность аэросепарации ТБО — 250 мм. ϭϯ͘ϴ͘ϭ͘˃̸̶̨̡̨̨̨̛̛̖̬̖̯̖̭̖̭̦̼̪̬̖̭̭̏̌͘ На поведение легких компонентов ТБО в процессе аэросепарации решающее влияние оказывает подъемная аэродинамическая сила — равнодействующая всех сил (нормальных и тангенциальных), распределенных по поверхности частицы, находящейся в воздушном потоке. Аэродинамическая сила зависит от параметров как частиц (форма, размеры, состояние поверхности, положение в потоке), так и воздушного потока и пневмосепарирующей системы в целом (скорость воздуха и ее направление, турбулентность, равномерность скоростного потока, ширина струи). Расчет скорости воздуха, обеспечивающей разделение ТБО на две фракции — легкую и тяжелую, можно производить приближенно по скорости витания компонентов легкой фракции, определяемой графоаналитическим методом. На одиночную частицу, падающую в воздушной среде, действуют: сила тяжести, направленная вниз и определяемая объемом V и плотностью ρт твердой частицы: FT = mg = V ρT g (13.38) сила аэродинамического сопротивления среды Fc , направленная вверх, которая выражается квадратичным законом сопротивления Ньютона: Fc = Wâ2ñ à ρâ lT2 (13.39) где V — объем частицы (компонента), м3; ρт и ρв — плотности соответственно компонента и воздуха, кг/м3; cа — коэффици— 561 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð ент лобового сопротивления (аэродинамический коэффициент сопротивления воздуха движению частицы); Wв — скорость витания компонента, м/с; lT — характерный линейный размер компонента, м. Под скоростью витания понимают конечную скорость, которую приобретает частица (компонент) при свободном падении, когда силы тяжести и сопротивления среды уравновешиваются. Из условия равновесия сил FT и Fc V ρT g = Wâ2ñ à ρâ lT2 (13.40) δ ρ g V ρT g ;Wâ = T T Wâ2 = 2 caρâ caρâ LT (13.41) где δт — толщина пленочного материала (например, макулатуры, полимерной пленки), м. Для определения скорости витания необходимо вычислить коэффициент лобового сопротивления cа, характеризующий способность частицы сопротивляться воздушному потоку и в общем случае зависящий от критерия режима движения Re, от фактора К, учитывающего влияние формы частицы (σт, lт), концентрации частиц β и геометрических характеристик аппарата L и частиц L/ σт и L/lт. (13.42) c = f ( Re, K,β, L σ , L l ,Γ ) a T T l а также от положения компонента в потоке воздуха (от его ориентации по отношению к направлению движения). Однако в основном значение cа определяется критерием режима движения и является функцией числа Рейнольдса Re, которое характеризует режим движения тел в жидкой среде (турбулентный или ламинарный) и, соответственно, преобладание того или иного вида сопротивления (динамического сопротивления среды или сопротивления вязкости среды). Исходя из подобия физических явлений в движущейся жидкости и газе и их воздействия на обтекаемые ими тела, коэффициент сопротивления cа можно выразить в виде критериальной зависимости от числа Рейнольдса: — 562 — Ðǜǌ͠ǮǯǬ͟Ǫ͠Ǫǅǀǎ Wâ ρâ lò Fc ;c = a µâ Wâ2ρâ lò2 (13.43) где μв — коэффициент вязкости воздуха. Для определения скорости витания Wв с использованием числа Рейнольдса Re можно применить графический метод П.В. Лященко, который для практических расчетов ввел параметр Re2ca и построил диаграмму зависимости Re2ca от Re (рис. 12.9). Пользуясь графиком, по найденному значению Re2ca определяют Re и по нему вычисляют скорость Wв. Пользуясь установленными зависимостями, определяем параметр Re2ca = f(Re) и по диаграмме Лященко находим число Рейнольдса, с помощью которого вычисляем скорость витания: Reµâ (13.44) Wâ = ρâ lò При аэросепарации используются два основных способа разделения компонентов: в горизонтальном потоке воздуха, когда направление воздуха перпендикулярно действующей на компоненты силе тяжести, и в вертикальном, когда направление воздуха противоположно направлению действующей на компоненты силе тяжести. В аэросепараторе компоненты легкой фракции транспортируются воздухом соответственно в горизонтальном направлении или вертикальном. Re = Рис.13.9. Диаграмма Лященко. — 563 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð Выражения для определения теоретической рабочей скорости воздуха в процессе аэросепарации имеют вид: в вертикальном потоке воздуха Wðâ ≥ (1,2 − 1,5) Wâ Wl в горизонтальном потоке воздуха Wðã ≥ â h где l — смещение частиц в горизонтальном потоке воздуха, равное примерно 20lт, м; lт — линейные размеры частицы; h — высота рабочей зоны сепарации, м. Расчетом по двум последним выражениям получены значения теоретической рабочей скорости воздуха для сепарации ТБО в вертикальном потоке 5 м/с, в горизонтальном — 2,5 м/с. Практически для обеспечения эффективности процесса разделения ТБО на две фракции — легкую и тяжелую — скорость воздуха должна быть увеличена в 1,5–2 раза. ϭϯ͘ϵ͘ˁ̶̵̨̛̛̖̪̬̯̖̬̼̥̯̖̬̣̌̌́̏̔̌̌̏ ̴̴̶̨̡̨̛̛̛̪̖̦̯̱̯̬̖̦̾́͘ Обогащение по трению основано на различии в величине коэффициентов трения. Различают коэффициент трения скольжения и качения, причем коэффициент трения скольжения больше, чем качения. Куски кубической и округленной многогранной формы стремятся быстро сталкиваться по наклонной плоскости, тогда как плоские куски в этих же условиях будут скользить медленнее. Обогащение по трению применяется для тех полезных ископаемых, у которых разница в коэффициентах трения значительна. Наглядным примером может служить разделение асбеста и змеевиковой породы или отделение угля от сланца. При движении по наклонной плоскости змеевик или уголь значительно опережают асбест или сланец и эффективно отделяются. Движение рудных кусков происходит под действием силы тяжести. Если (рис. 13.10) на плоскости, наклоненной под углом α, находятся две частицы a и b с различным коэффициентом трения, то для каждой из них можно определить соотношение сил при весе зерна P и коэффициенте трения f. — 564 — ÐǦǬ͟Ǫ͠ǪǅǀǎÐǰǫǬ͠ƽǊǲÐǂǪǰǬ͠ǀǪǁǮǫÐ͟ǮÐǭǮǌǄǄǀǅǀǬǃǰǱÐǰ͠Ǭǃǀǎ Сила, движущая частицу по наклонной плоскости P·sinα, равна силе трения F, направленной противоположно: F = fCosα следовательно: P dν = Psinα − fPcosα g dt или при установившемся движении dν = g ( sinα − fcosα ) = g0 = const (13.45) dt При начальной скорости движения u, т. е. если частица при начале движения имела некоторую скорость, то в конце пути скорость её движения выразится: v = u + g0t. Обозначая длину пути по наклонной плоскости через l, получим: g t2 l = ut + 0 2 Или 2u 2l =0 t2 + t− g0 g0 откуда: 2 t=− u  u 2l +   g0  g0  g0 (13.46) и, подставляя в уравнение скорости, получим:  u u2 2l  ν = u + g0  − + −  = u2 + 2glsinα − fcosα 2 g g0  g  0 0 (13.47) Если начальная скорость равна 0, то скорость движения частицы в конце пути на плоскости составит: ν = 2lgsinα − fcosα Эта скорость будет меньше для зерна, обладающего большим коэффициентом трения, и, наоборот, скорость v будет большей для частицы, обладающей меньшим коэффициентом — 565 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð трения. Следовательно, в момент достижения конца наклонной плоскости обе частицы с разными коэффициентами трения будут иметь разные скорости движения (рис. 13.10). Благодаря этой разнице после схода с плоскости на некотором уровне А–А (рис. 13.11) произойдет отделение одной частицы от другой. Рис. 13.10. Схема движения зерен по наклонной плоскости. Рис. 13.11. Схема падения зерен с наклонной плоскости После схода с наклонной плоскости каждая частица будет двигаться дальше по наклону к горизонту. При падении по параболе с временем t, необходимым для достижения плоскости А–А, расстояние Н определится: gt2 H = νsinα t + 2 — 566 — ÐǦǬ͟Ǫ͠ǪǅǀǎÐǃǪÐǮǯǃǮǫǬÐǎǫǁǬǃǀǎÐǯǂǪǆǀǫǪǬǂǮǯǰǀ тогда: t= 1 g ( ν2sinα + 2Hg − νsinα ) (13.48) и за это время в горизонтальном направлении частица пройдет путь 1 L = νcosα t = νcosα ν2sin2α + 2Hg − νsinα (13.49) g Путь L для каждой частицы будет различным, так как скорости v различны. Следовательно, уголь отделится от сланца и змеевик от асбеста. Угол трения скольжения для крупного каменного угля колеблется в пределах от 20Û до 60Û. В зависимости от крупности частиц угол наклона изменяется. Для частиц от 16 до 9,5 мм угол будет от 21 до 27Û37ƍ. Для угля крупностью 4,8–3,2 мм — угол наклона 28Û. Содержание влаги в материале оказывает влияние на изменение угла наклона, так как влага изменяет коэффициент трения. При движении частиц винтообразно по наклонной плоскости развивается, помимо указанных выше сил, также центробежная сила. ( ) ϭϯ͘ϭϬ͘ˁ̶̸̨̨̨̛̛̛̛̖̪̬̦̭̦̖̣̖̦̭̥̖̥̭̯̌̌́̌̏́̏́̌̏̌͘ Физико-химическое свойство селективного смачивания минералов некоторыми жирами, так же как и свойство смачивания самородного золота ртутью, очень давно используется в практике обогащения с целью извлечения из руд или россыпей ценных компонентов, например извлечения алмазов жировыми поверхностями. Как известно, минералы пустой породы — кварц, известняк, полевые шпаты и пр. — не смачиваются маслами и не прилипают к поверхностям, покрытым слоем жира. В то время как металлы, металлоиды, сплавы металлов. Сульфиды, арсениды и некоторые другие смачиваются жирами и прилипают к жирам и жирным поверхностям. Аналогичное явление наблюдается в процессе амальгамации. — 567 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð На рис. 13.12 показано поведение капли ртути на поверхности золота в водной среде. Краевой угол смачивания золота ртутью в первый момент растекания капли близок к 20Û. Пустая порода смывается водой, а золото задерживается, образуя с ртутью амальгаму. Амальгама в полужидком виде представляет гетерогенную систему с весьма малой растворимостью металлов в жидкой ртути при обыкновенной температуре. Отжатая амальгама является твердой фазой дисперсной системы. Рис. 13.12. Схема смачивания золота ртутью. Для повышения эффективности прилипания золотинок к поверхности, покрытой слоем ртути, применяются методы так называемой активной амальгации. С этой целью для активизации поверхности металла в пульпу добавляют некоторые реагенты, повышающие смачиваемость золота ртутью, или применяют цинковую амальгаму в слабом растворе серной кислоты. В этом случае амальгамируется не только золото, но даже и платина. Отрицательная поляризация поверхности ртути также представляет собой весьма эффективный способ активной электроамальгамации. При обработке золотых руд применяются специальные амальгамационные шлюзы, представляющие наклонные деревянные столы, аналогичные обычным шлюзам, но с поверхностью, покрытой чистым медным листом, который с одной рабочей стороны натерт тонким ровным слоем ртути. Медные листы бывают толщиной 2–3 мм и перед натиранием ртутью тщательно очищаются сначала механически, а затем химически (раствором хлористого аммония или цианидами). На процесс амальгации оказывает влияние состав рудного золота. Лучше всего извлекается чистое золото. Сплавы золота с другими металлами ухудшают смачивание ртутью, а следовательно, уменьшается и извлечение. Особенно неблагоприятно для — 568 — ÐǤǬ͠Ǭ͠ǪƻǮǰǭǪÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫÐǂǬǰǮƽǮǂÐǮǭǀǯǁǬǃǀǎÐǫÐ͟͠ǮǂǊǇǁǬǃǃǮǬÐǯǊ͠ǋǬ процесса амальгации покрытие золотинок пленками шламов или окислов (золото «в рубашке»). Снимают золотую амальгаму с листов резиновыми скребками так, чтобы не обнажать медных листов. Амальгаму помещают в эмалированные ендовы, отжимают и затем подвергают выпариванию в ретортах. Ртуть регенерируется. ϭϯ͘ϭϭ͘ʿ̵̵̨̡̨̨̨̨̨̨̡̛̛̖̬̖̬̯̯̖̬̼̯̥̖̯̥̭̣̖̦̌̍̌̏̔̔̏̔́ ̨̨̪̬̥̼̹̣̖̦̦̖̭̼̬̖̏̽͘ Одним из процессов уничтожения и переработки отходов в промышленное сырье является их окисление (сжигание или пиролиз). ϭϯ͘ϭϭ͘ϭ͘ˁ̵̨̨̨̛̛̙̦̖̯̐̌̔̏͘ Сжигание отходов — это метод очистки, основанный на сжигании отходов жизнедеятельности. Стоки и возникающие при сжигании пары могут быть вредными (содержать тяжелые металлы, диоксины, пыль, CO, HCl, HF, SO2, NO, NO2 …), и поэтому должны быть проверены и очищены, прежде чем выбросить их в атмосферу. Для этого применяют очистку дымовых газов. Другие твердые отходы состоят из шлака (который может служить сырьем в строительстве, например). Тепло, получаемое при сжигании, можно использовать для обогрева и получения электричества. ϭϯ͘ϭϭ͘Ϯ͘ʿ̴̶̨̡̛̛̛̛̛̛̬̣̐̌̌́̚̚͘ Также перевод отходов в сырье возможен в процессе пиролиза. Пиролиз является эндотермическим разложением отходов в восстановительной атмосфере (менее 2% O2) под действием тепла. Этот процесс позволяет разложить твердые органические вещества на три вида: твердые (пиролизный кокс), жидкие (состоящие из тяжелых конденсатов -пиролизные масла или смолы) и газообразные (CO, H2, CO2, CH4, C2 H4, C2 H6). — 569 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð Скорость пиролитического разложения вещества зависит от типа отходов, распределения продуктов этой реакции, температуры, скорости нагрева (° C / с), подводимого внешним нагревом, времени пребывания материала в реакторе. Методом пиролиза можно проводить переработку отходов в сырье и получать биотопливо. На практике, часть газообразных и жидких продуктов пиролиза используются в самом процессе, чтобы обеспечить энергию, необходимую для его поддержания. Пиролиз — достаточно интересный процесс с целью получения сырья для промышленности из отходов, таких как, например, отходы сельского хозяйства (солома и початки кукурузы, жмых, кора, древесные отходы, скорлупа кокосовых орехов, кешью, арахиса и т.д.). Еще одним способом получения сырья из отходов является газификация, представляющая собой эндотермические реакции, при которых из твердого топлива (биомасса, отходы) может быть получен горючий газ (синтез-газ). Она включает в себя процессы термохимической обработки (сушка, удаление летучих веществ, крекинг, реформинг газа), в том числе реакции газификации полукокса. Данный процесс проводят в два этапа (пиролиза и газификации). Газификация — реальная альтернатива сжиганию, потому что общая эффективность преобразования в цепи газификация — газовая турбина для получения электрической энергии все равно гораздо лучше (45%–55%), чем в цепи сжигание — котел — паровая турбина. Учитывая преимущества пиролиза и газификации по сравнению со сжиганием, можно констатировать, что эти два способа позволяют проводить переработку отходов в энергию с более высоким коэффициентом, чем по сравнению с обычными мусоросжигательными заводами. По сравнению с другими биологическими или биохимическими путями получения энергии и промышленного сырья из отходов, термохимические процессы обладают преимуществом очистки не биоразлагаемых отходов. Тех, отходов, которые не могут быть превращены в компост или метан, например, изношенные шины, пластмассы, отходы дерева, некоторые сельскохозяйственные отходы и т.д. Термохимические процессы полностью разрушают твердые отходы, — 570 — ÐǠǮǃǰ͠ǮǁǋǃǊǬÐǫǮ͟͠ǮǯǊ превращая их в газ (единственно остающиеся остатки: потенциально извлекаемые золы, которые в некоторых случаях могут использоваться, как удобрение). ϭϯ͘ϭϮ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏͘ 1. 2. 3. 4. 5. Что такое сепарация отходов? Что такое дробление? Чем дробление отличается от измельчения? Что называется степенью дробления или измельчения? Почему существуют стадийные схемы процесса дробления(измельчения)? 6. Что такое удельная поверхность диспергированного материала? 7. Опишите современные представления о разрушении твердого материала. 8. Что такое прочность материла? 9. Что такое крепость материала? 10. Как влияют дефекты кристаллической структуры на прочность материала? 11. Что такое анизотропия? 12. Какие способы разрушения материала Вы знаете? 13. Что такое грохочение и какие его основные понятия? 14. Что такое просеивающая поверхность? 15. Как определить гранулометрический состав измельченного материала? 16. Что такое ситовой анализ? 17. Что такое характеристика крупности измельченного материала? 18. Что такое «легкие», «трудные» и «затрудняющие» частицы? 19. Какие факторы влияют на эффективность грохочения? 20. Что такое электромагнитная сепарация и какие физические основы этого процесса? 21. Что такое электродинамическая сепарация и какие физические основы этого процесса? 22. Какое электрическое поле необходимо создать в образ— 571 — ǞǁǪǫǪÐ ÐǨǀƿǀǭǮ ǲǀǂǀǆǬǯǭǀǬÐÐǮǯǃǮǫǊÐ͟͠ǮǅǬǯǯǮǫÐ͟Ǭ͠Ǭ͠ǪƻǮǰǭǀÐǰǫǬ͠ƽǊǲÐǮǰǲǮƽǮǫ Ð це цветного металла для извлечения его из отходов при электродинамической сепарации? 23. Что такое электро сепарация и какие физические основы этого процесса? 24. В каком поле осуществляется электросепарация? 25. Что такое аэросепарация и какие физические основы этого процесса? 26. В чем заключается сепарация материалов по коэффициенту трения? 27. В чем заключается сепарация материалов на основе явления смачивания? 28. С какой целью проводится термическая переработка отходов? 29. Что такое сжигание отходов? 30. Что такое газификация отходов? 31. Что такое пиролиз отходов? 32. Как изменяется масса после сжигания ТБО? 33. Какая технология сжигания ТБО чаще всего применяется в практике? — 572 — ǍưǙǚǙÍ Í Í ǖǎǒǔǎǖƝơǎǕǏƝǎÍǒǕǑǒǌƥÍ ƜǋƣƝǖƥÍǒǏǔƟƛǋƨƣǎ֏ÍǕǔǎƚƥÍ ǒǖÍƧǑǎǔǍǎǖƝơǎǕǏƝǘÍǌǒƜƚǎ֏ǕǖǌƝ֏ В результате изучения главы 14 бакалавр должен: Знать: – основные методы защиты окружающей среды от энергетических воздействий. Уметь; – классифицировать энергетические воздействия и выбирать соответствующие методы защиты окружающей среды. Владеть: – теоретическими методами расчета средств защиты окружающей среды от энергетических воздействий. Энергетические воздействия на окружающую среду есть следствие параметрических загрязнений, вызывающих изменение ее физических параметров. По своей природе энергетические загрязнения условно можно разделить на загрязнения, представляющие собой колебательно-волновое движение частиц упругой среды газовой, жидкой, твердой фаз (шум, ультразвук, инфразвук, вибрации) и загрязнения электромагнитного происхождения, представляющие собой постоянные и переменные электрические и магнитные поля различных частот от промышленной вплоть до рентгеновского и γ-диапазонов. — 573 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð ϭϰ͘ϭ͘ʽ̵̸̵̡̡̡̨̛̛̛̛̛̺̬̯̖̬̭̯̦̖̬̖̯̖̭̖̜̭̯̜̍̌́̌̌̌̾̐̏̔̏̚͘ ϭϰ͘ϭ͘ϭ͘ˌ̶̛̛̛̛̱̥̬̏̍̌͘ Шум определяют как совокупность апериодических звуков различной интенсивности и частоты. Источниками этого явления в окружающей среде являются транспортные средства, промышленные и бытовые предприятий, пневмо — и гидроустановки различного назначения и многое другое. Присутствие шума на улицах, в жилых домах, школах, больницах, местах отдыха населения и т. д. приводит к акустическому дискомфорту человека, способствует развитию заболеваний. Шумовое загрязнение способно вызывать также нарушение естественного баланса в экосистемах и приводить к нарушению ориентирования в пространстве, общения, поиска пищи и т. д. В то же время значительная часть информации об окружающем мире поступает человеку в виде звуковых сигналов, передающих информацию и концентрирующих внимание человека на возможных опасностях. С физической точки зрения звук представляют собой механические колебательные движения, которые характеризуются амплитудой и частотой. Амплитуда колебаний определяет значение интенсивности звука, J, (Вт/м 2) или звукового давления P, (Па). Диапазон слухового восприятия человека составляет: по интенсивности и 102–10–12 Вт/м2, звуковому давлению 2·10–5–2·102 Па, по частоте 20 Гц — 20 кГц. Звуки с частотой менее 20 Гц (инфразвук) и выше 20 кГц (ультразвук) слуховым анализатором человека не воспринимаются. Для физиологической характеристики звука существенными являются не столько абсолютные значения интенсивности звука и звукового давления, сколько их отношение к абсолютному порогу слышимости. В качестве таких относительных единиц измерения используют уровни интенсивности звука и звукового давления L, децибелы (дБ): L = 10lg(J/J0) = = 20lg(P / P0), где J и Р — текущее значение интенсивности — 574 — ÐǣƻǈǪǎÐǲǪ͠ǪǭǰǬ͠ǀǯǰǀǭǪÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ звука и звукового давления; J0 и Р0 — их значения на пороге слышимости. Тогда почти весь диапазон слышимых звуков укладывается менее чем в 140 дБ, что удобно как для акустических расчетов, так и для нормирования шума. Распространяясь в пространстве, звуковые колебания создают акустическое поле, в котором шумы, как правило, имеют разный уровень интенсивности, дБА: разговорная речь — 50– 60, автосирена — 100, шум двигателя легкового автомобиля — 80, громкая музыка — 70, шум от движения трамвая — 70–80, шум в обычной квартире — 30–40. По спектральному составу в зависимости от преобладания звуковой энергии в соответствующем диапазоне частот различают низко- средне- и высокочастотные шумы, по временным характеристикам — постоянные и непостоянные (колеблющиеся, прерывистые и импульсные), по длительности действия — продолжительные и кратковременные. С гигиенических позиций придается большое значение амплитудно-временным, спектральным и вероятностным параметрам непостоянных шумов, наиболее характерных для современной техносферы. В биологическом отношении шум является заметным стрессовым фактором, оказывающим влияние на весь организм человека: угнетает ЦНС, вызывает изменение ритма дыхания и пульса, способствует нарушению обмена веществ, возникновению сердечно-сосудистых заболеваний, гипертонической болезни, может приводить к профессиональной тугоухости. Интенсивный шум способствует снижению внимания, замедлению скорости реакции и увеличению числа ошибок в процессе деятельности, затрудняет своевременное восприятие сигналов, что способствует возникновению несчастных случаев. Специфическое шумовое воздействие, сопровождающееся повреждением слухового анализатора, проявляется медленно прогрессирующим снижением слуха. Снижение слуха на 10 дБ практически неощутимо, на 20 дБ — начинает серьезно мешать человеку, так как нарушается способность слышать важные звуковые сигналы, наступает ослабление разборчивости речи. — 575 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð Степень шумовой патологии зависит от интенсивности и продолжительности воздействия, функционального состояния ЦНС и, что очень важно, от индивидуальной чувствительности организма к акустическому раздражителю. Женский и детский организмы особенно чувствительны к шуму. Высокая индивидуальная чувствительность может быть одной из причин повышенной утомляемости и развития различных неврозов. Помимо патологии органа слуха при воздействии шума наблюдаются отклонения в состоянии вестибулярной функции, а также общие неспецифические изменения в организме; Нормируемые параметры шума в местах пребывания людей определены Санитарными нормами СН 2.2.4/2.1.8.562-96 «Шум на рабочих местах, в помещениях жилых, общественных зданий и на территории жилой застройки». При оценке шума допускается использовать дозу шума, т. к. установлена линейная зависимость доза — эффект по временному смещению порога слуха, что свидетельствует об адекватности оценки шума по энергии. Дозный подход позволяет также оценить кумуляцию шумового воздействия с течением времени. Ультразвук как упругие волны не отличается от слышимого звука, однако частота колебательного процесса способствует большему затуханию колебаний вследствие трансформации энергии в теплоту. По частотному спектру ультразвук классифицируют на: низкочастотный — колебания 1,12·104…1,0·105 Гц; высокочастотный — 1,0·105…1,0·109 Гц; по способу распространения — на воздушный и контактный ультразвук. Низкочастотные ультразвуковые колебания хорошо распространяются в воздухе. Биологический эффект воздействия их на организм зависит от интенсивности, длительности воздействия и размеров поверхности тела, подвергаемой действию ультразвука. Длительное систематическое влияние ультразвука, распространяющегося в воздухе, вызывает функциональные нарушения нервной, сердечно — сосудистой и эндокринной систем, слухового и вестибулярного анализаторов. У работающих на ультразвуковых установках отмечают выраженную астению, со— 576 — ÐǣƻǈǪǎÐǲǪ͠ǪǭǰǬ͠ǀǯǰǀǭǪÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ судистую гипотонию, снижение электрической активности сердца и мозга. Изменения ЦНС в начальной фазе проявляются нарушением рефлекторных функций мозга (чувство страха в темноте, в ограниченном пространстве, резкие приступы с учащением пульса, чрезмерной потливостью, спазмы в желудке, кишечнике, желчном пузыре). Наиболее характерны вегетососудистая дистония с жалобами на резкое утомление, головные боли и чувство давления в голове, затруднения при концентрации внимания, торможение мыслительного процесса, на бессонницу. Контактное воздействие высокочастотного ультразвука на руки приводит к нарушению капиллярного кровообращения в кистях рук, снижению болевой чувствительности, т.е. развиваются периферические нарушения. Установлено, что ультразвуковые колебания могут вызвать изменения костной структуры с разрежением плотности костной ткани. Профессиональные заболевания зарегистрированы лишь при контактной передаче ультразвука на руки — вегетосенсорная или сенсомоторная полиневропатия рук. Гигиенические нормативы ультразвука определены СанПиН 2.2.4/2.1.8.582-96, где в качестве гигиенической характеристики воздушного ультразвука служат уровни звукового давления (дБ) в третьоктавных полосах со среднегеометрическими частотами 12,5…100 кГц. Инфразвук — область акустических колебаний с частотой, ниже 16…20 Гц. Источниками инфразвука естественного происхождения могут быть землетрясения, извержения вулканов, значительные водные поверхности, а источниками, связанными с человеческой деятельностью, являются крупногабаритные конструкции, здания, взрывы, орудийные выстрелы, ударные волны от сверхзвуковых самолётов, акустическое излучение реактивных двигателей и др. Всякий очень громкий звук несёт с собой, как правило, и инфразвуковую энергию. Основная особенность инфразвука, обусловленная его низкой частотой, — это малое поглощение, вследствие чего он может распространяться на очень большие расстояния. При распространении в глубоком море и в атмосфере на уровне земли — 577 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð инфразвуковые волны частоты 10–20 Гц затухают на расстоянии 1000 км не более чем на несколько дБ. Из-за большой длины волны на инфразвуковых частотах мало и рассеяние звука в естественных средах; заметное рассеяние создают лишь очень крупные объекты — холмы, горы, крупные здания и др.. Известно, что звуки извержения вулканов, атомных взрывов могут многократно обходить вокруг земного шара, сейсмические волны могут пересекать всю толщу Земли. По этим же причинам инфразвук почти невозможно изолировать, и все звукопоглощающие материалы теряют свою эффективность на инфразвуковых частотах. При воздействии инфразвука на организм уровнем 110…150 дБ могут возникать неприятные субъективные ощущения и многочисленные реактивные изменения: нарушения в ЦНС, сердечно-сосудистой и дыхательной системах, вестибулярном анализаторе. Отмечают жалобы на головные боли головокружение, осязаемые движения барабанных перепонок, звон в ушах и голове, снижение внимания и работоспособности; может появиться чувство страха, сонливость, затруднение речи; специфическая для действия инфразвука реакция — нарушение равновесия. При воздействии инфразвука с уровнем 105 дБ отмечены психофизиологические реакции в форме повышения тревожности и неуверенности, эмоциональной неустойчивости. Гигиеническая регламентация инфразвука производится по Санитарным нормам СН 2.2.4/2.1.8.583-96, которые задают для постоянного инфразвука предельно допустимые уровни звукового давления (УЗД) для различных видов деятельности, а также в жилых и общественных помещениях и на территории жилой застройки. Вибрация представляет собой упругие механические колебания в технике (машинах, механизмах, конструкциях и др.). Это весьма сложный колебательный процесс в широком диапазоне частот, возникающий в результате передачи колебательной энергии от какого-то источника в твердом теле. Источниками вибрации являются компрессорные, насосные станции, вентиляторы, виброплощадки, кондиционеры, градирни, — 578 — ÐǣƻǈǪǎÐǲǪ͠ǪǭǰǬ͠ǀǯǰǀǭǪÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ турбины дизельных электростанций. Вибрации распространяются по металлическим конструкциям оборудования и через их основания достигают фундаментов общественных и жилых зданий, передаются на ограждающие конструкции отдельных помещений. При передаче вибраций происходит неравномерная осадка фундаментов и оснований, что может привести к деформации и разрушению инженерных сооружений. Негативный эффект вибраций состоит в значительном воздействии на организм человека, нарушении работы и ускоренном износе технических систем, снижении точности показаний приборов, вызывает знакопеременные напряжения, приводящие к усталостному разрушению в конструкции, и т.д. Вибрации могут быть полезными, когда они специально закладываются в принципы действия машин и технологий для повышения их эффективности виброинструмент, специальное оборудование для ускорения химических реакций и т.п.). В общем случае вибрации могут осуществляться как возвратно- поступательно вдоль трех осей координат, так и возвратно — вращательно вокруг них и характеризуются частотой, амплитудой смещения, скоростью и ускорением. По способу передачи на человека (в зависимости от характера контакта с источниками вибрации) вибрации условно подразделяют на общие (воздействие на все тело человека) и локальные (воздействие на отдельные части тела — руки и ноги). Особенно вредны вибрации с резонансной частотой, т.е. вынужденной частотой, совпадающей с частотой собственных колебаний тела человека или его отдельных органов (для тела человека — 6–9 Гц, головы — 6 Гц, желудка — 8 Гц, других органов — в пределах 25 Гц). Частотный диапазон расстройств зрительных восприятий лежит между 60 и 90 Гц, что соответствует резонансу глазных яблок. Длительное воздействие вибрации ведет к развитию профессиональной вибрационной болезни. Общую вибрацию по источнику ее возникновения и возможности регулирования ее интенсивности оператором подразделяют на следующие категории (ГОСТ 12.1.012-90 «Вибрационная безопасность. Общие требования»). — 579 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð Категория 1 — транспортная вибрация, характерная для движущихся транспортных средств, оператор может в известных пределах регулировать воздействие вибрации. Категория 2 — транспортно-технологическая вибрация на рабочих местах машин с ограниченной подвижностью, когда оператор может лишь иногда регулировать воздействие вибрации. Категория 3а — технологическая вибрация, воздействующая на оператора на рабочих местах стационарных машин или передающаяся на рабочие места, не имеющие источников вибрации. Категория 3б — вибрация на рабочих местах работников умственного труда и персонала, не занимающегося физическим трудом. Локальная вибрация вызывает спазмы сосудов, которые начинаются с концевых фаланг пальцев рук и распространяются на всю кисть, предплечье, захватывают сосуды сердца. Диапазон частот между 35 и 250 Гц является наиболее критическим для развития вибрационной болезни. Благодаря наличию мягких тканей, костей, суставов, внутренних органов и особенностей конфигурации тело человека представляет собой сложную колебательную систему, первичная механическая реакция которой на вибрационное воздействие зависит от диапазона частот, предопределяя последующие физиологические эффекты. Для гигиенического нормирования и контроля вибраций используются среднеквадратичные значения виброускорения и виброскорости, а также их логарифмические уровни в децибелах СН 2.2.4/2.1.8.566-96 «Производственная вибрация, вибрация в помещениях жилых и производственных зданий». ϭϰ͘ϭ͘Ϯ͘ˑ̸̡̨̨̛̛̛̛̣̖̯̬̥̦̯̦̼̖̪̣̣̱̖̦̌̐́́̚͘ Электромагнитные поля занимают весьма широкий частотный спектр и включает в себя неионизирующие и ионизирующие излучения. Электромагнитные поля разной частоты несут разную энергию и по-разному действуют на вещество — 580 — ÐǣƻǈǪǎÐǲǪ͠ǪǭǰǬ͠ǀǯǰǀǭǪÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ биологические ткани. В гигиенической практике к неионизирующим излучениям относят электромагнитные поля (ЭМП), энергия которых недостаточна для ионизации материи. К источникам ЭМП промышленной частоты (50 Гц) относят линии электропередачи (ЛЭП) с напряжением до 1150 кВ, открытые распределительные устройства, включающие коммутационные аппараты, устройства защиты и автоматики, измерительные приборы. Длительное действие таких полей на человека напряжением выше даже 400 кВ уже приводит к функциональным нарушениям центральной нервной и сердечно-сосудистой систем, к изменениям состава крови, которые субъективно выражаются в головной боли, вялости, расстройстве сна, снижении памяти, повышенной раздражительности, апатии. Нормирование ЭМП промышленной частоты осуществляется по предельно допустимым уровням напряженности электрического E, В/м и магнитного H, А/м полей частотой 50 Гц в зависимости от времени пребывания в нем и регламентируется СанПиН 2.2.4.1191-03 «Электромагнитные поля в производственных условиях». Основные требования к обеспечению безопасности населения от электрического поля промышленной частоты, создаваемого системами передачи и распределения электроэнергии, изложены в Санитарных нормах и правилах «Защита населения от воздействия электрического поля, создаваемого воздушными линиями электропередачи переменного тока промышленной частоты» № 2971-84. В качестве предельно допустимых уровней приняты следующие значения напряженности электрического поля: – внутри жилых зданий — 0,5 кВ/м; – на территории жилой застройки — 1 кВ/м; – в населенной местности, вне зоны жилой застройки (земли городов в пределах городской черты в границах их перспективного развития на 10 лет, пригородные и зеленые зоны, курорты, земли поселков городского типа, в пределах поселковой черты этих пунктов), а также на территории огородов и садов — 5 кВ/м; — 581 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð – на участках пересечения воздушных линий (ВЛ) с автомобильными дорогами I-IV категорий — 10 кВ/м; – в ненаселенной местности (незастроенные местности, хотя бы и частично посещаемые людьми, доступные для транспорта, и сельскохозяйственные угодья) — 15 кВ/м; – в труднодоступной местности (не доступной для транспорта и сельскохозяйственных машин) и на участках, специально выгороженных для исключения доступа населения — 20 кВ/м. Кроме электрических полей промышленной частоты, на работающих воздействуют переменные магнитные поля (МП) промышленной частоты 50 Гц, которые образуются вблизи выводов генераторов, токопроводов, силовых трансформаторов и т.д., в электроустановках, работающих на токе любого напряжения. Согласно современным представлениям основным механизмом биологического действия МП являются вихревые токи, которые индуцируются им в теле человека. При этом реакции организма имеют неспецифический характер, проявляющийся в возникновении изменений функционального состояния нервной, сердечно-сосудистой, иммунной систем. Интенсивность воздействия МП определяется напряженностью Н, А/м или магнитной индукцией В, Тл. Регламентацию МП на человека, согласно СанПиН 2.2.4.1191-03 «Электромагнитные поля в производственных условиях», производят на основании интенсивности и продолжительности воздействия. Предельно допустимые уровни МП устанавливают в зависимости от длительности пребывания персонала в зоне МП для условий общего (на все тело) и локального (на конечности) воздействия. При необходимости пребывания персонала в зонах с различной напряженностью МП общее время выполнения работ не должно превышать предельно допустимое для зоны с максимальной напряженностью может быть реализовано за один раз или дробно в течение рабочего дня. Требования по защите персонала от воздействия импульсных электромагнитных полей даны в СанПиН 2.2.4.1329–03. — 582 — ÐǣƻǈǪǎÐǲǪ͠ǪǭǰǬ͠ǀǯǰǀǭǪÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Воздействие электростатического поля (ЭСП) — статического электричества — на человека связано с протеканием через него слабого тока (несколько микроампер), что практически исключает электротравмы. Однако вследствие рефлекторной реакции на ток возможна механическая травма при ударе о рядом расположенные элементы конструкций, падении с высоты и т.д. Исследование биологических эффектов показало, что наиболее чувствительны к электростатическому полю центральная нервная и сердечно-сосудистая системы и анализаторы, что выражается в раздражительности, головной боли, нарушении сна, появлении своеобразных фобий, обусловленных страхом ожидаемого разряда, и др. Уровни напряженности ЭСП нормируются по СанПиН 2.2.4.1191-03 в зависимости от времени пребывания персонала на рабочих местах. При напряженности менее 20 кВ/м время пребывания в ЭСП не регламентируется. В диапазоне 20–60 кВ/м допустимое время пребывания tдоп (ч) персонала в ЭСП без средств защиты определяется как tдоп = Ефакт/Епред, где Ефакт — фактическое значение напряженности, кВ/м, Епред — предельно допустимый уровень напряженности, равный 60 кВ/м при действии в течение 1 ч. Источниками постоянных магнитных полей (ПМП) являются постоянные магниты, электромагниты, сильноточные системы постоянного тока (линии передачи постоянного тока, электролитные ванны и др. электротехнические устройства), широко используемые в приборостроении и медицинской практике. Воздействие МП на человека зависит от его напряженности и при постоянной работе в условиях превышения норматива ведет к нарушениям функции нервной, сердечно-сосудистой, кроветворной и других систем организма, а также к локальным вегетативным и трофическим нарушениям (зуд, отечность и уплотнением кожи). В соответствии с СанПиН 2.2.4.1191-03 напряженность МП на рабочем месте не должна превышать 8 кА/м. Напряженность МП линии электропередачи напряжением до 750 кВ обычно не превышает 20–25 А/м, что не представляет опасности для человека. — 583 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð Большую часть спектра неионизирующих электромагнитных излучений (ЭМИ) составляют радиоволны (3 Гц — 3000 ГГц), в зависимости от частоты которых ткани живых организмов проявляют различные электрические свойства и ведут себя как проводники или как диэлектрики. Многообразный характер воздействия ЭМИ на организм определяются плотностью потока энергии, частотой излучения, продолжительностью воздействия, режимом облучения (непрерывный, прерывистый, импульсный), размером облучаемой поверхности, индивидуальными особенностями организма, наличием сопутствующих факторов (повышенная температура окружающего воздуха (свыше 28°C), наличие рентгеновского излучения). Биологические эффекты от воздействия ЭМИ могут проявляться как в форме незначительных функциональных сдвигов, так и в виде явной патологии. Следствием поглощения энергии ЭМИ является тепловой эффект, когда избыточная теплота воздействует прежде всего на ткани со слаборазвитой сосудистой системой или недостаточным кровообращением (глаза, мозг, почки, желудок, желчный и мочевой пузырь). Облучение глаз может привести к помутнению хрусталика (катаракте), причем это является одним из немногих специфических поражений, вызываемых ЭМИ радиочастот в диапазоне 300 МГц — 300 ГГц при плотности потока энергии (ППЭ) свыше 10 мВт/см 2. Для длительного воздействия ЭМИ различных диапазонов длин волн при умеренной интенсивности (выше ПДУ) характерным считают развитие функциональных расстройств ЦНС с слабо выраженными сдвигами эндокринно-обменных процессов и состава крови, что выражается в головных болях, колебаниях давления, замедлении пульса, изменении возбудимости анализаторов, быстром развитии утомления и возможных трофических нарушениях (выпадение волос, ломкость ногтей, снижение массы тела). В пределах радиоволнового диапазона доказана наибольшая биологическая активность микроволнового СВЧ — поля в сравнении с ВЧ и УВЧ. Определенное беспокойство у специалистов в области электромагнитной безопасности человека вызывают сотовые теле— 584 — ÐǣƻǈǪǎÐǲǪ͠ǪǭǰǬ͠ǀǯǰǀǭǪÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ фоны и компьютеры, а также разнообразные радиоэлектронные и электрические бытовые приборы. В настоящее время имеются данные, свидетельствующие о том, что ЭМИ следует рассматривать как один из факторов риска в развитии атеросклероза, гипертонии болезней сердца депрессии, мышечной атрофии и др. Нормирование ЭМИ радиочастотного диапазона для проводится по СанПиН 2.2.4.1191-03, а для окружающей среды — по СанПиН 2.1.8/2.2.4.1383-03 «Гигиенические требования к размещению и эксплуатации передающих радиотехнических объектов». В диапазоне частот 0,03–300 МГц интенсивность магнитного поля выражается предельно допустимой напряженностью Епду электрического и Нпду магнитного полей. В диапазоне частот 300 МГц–300 ГГц интенсивность ЭМИ характеризуется плотностью потока энергии (ППЭ); энергетическая нагрузка представляет собой произведение плотности потока энергии поля на время воздействия ЭНппэ = ППЭ · Т. Предельно допустимые значения ППЭ электромагнитного поля ППЭпду = k ЭНппэпду/T, где k = 10 — коэффициент ослабления биологической эффективности вращающихся сканирующих антенн; k = 1 — коэффициент ослабления биологической эффективности для всех остальных случаев. ЭНппэпду — предельно допустимая энергетическая нагрузка, равная 2 Вт/м2 · ч; Т — время пребывания в зоне облучения за рабочую смену, ч. Во всех случаях максимальное значение ППЭпду не должно превышать 10 Вт/м2, а при локальном облучении кистей рук — 50 Вт/м2. Инфракрасное излучение (ИК) — часть электромагнитного спектра с длиной волны λ = 0,78–1000 мкм, энергия которого при поглощении в веществе вызывает тепловой эффект. С учетом особенностей биологического действия ИК-диапазон спектра подразделяют на три области: ИК-А (0,78–1,4 мкм), ИК-В (1,4–3,0 мкм) и ИК-С (3,0–1000 мкм). Наиболее активно коротковолновое ИК-излучение, способное глубоко проникать в ткани организма и интенсивно поглощаться жидкостями тканей организма. Наиболее поражаемые у человека органы — кожный покров (ожоги, пигментации кожи) и органы зрения (конъюк— 585 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð тивы, помутнение и ожог тканей глаза, катаракта). ИК-излучение способно воздействовать и на обменные процессы в миокарде, водно-электролитный баланс в организме, на состояние верхних дыхательных путей (развитие хронического ларингита, ринита, синуситов); возможен также мутагенный эффект облучения. Нормирование ИК — излучения осуществляется по интенсивности допустимых интегральных потоков излучения с учетом спектрального состава, размера облучаемой площади, защитных свойств спецодежды для продолжительности действия более 50% смены. Видимое (световое) излучение — диапазон электромагнитных колебаний с длиной волны 0,4–0,78 мкм при достаточных уровнях энергии также может представлять опасность для кожных покровов и органа зрения, механизмов регуляции обменных процессов, сердечной мышцы с развитием дистрофии миокарда и атеросклероза. Ультрафиолетовое излучение (УФИ) — спектр электромагнитных колебаний с длиной волны 0,39–0,315 мкм. По биологическому эффекту выделяют три области УФИ: УФ-А — с длиной волны 0,39–0,315 мкм, и сравнительно слабым биологическим действием; УФ-В — с длиной волны 0,315– 0,28 мкм, обладающим выраженным загарным и антирахитическим действием; УФ-С — с длиной волны 0,28–0,2 мкм с выраженным бактерицидным действием. Естественное УФИ, составляющее приблизительно 5% потока солнечного излучения, — жизненно необходимый фактор, оказывающий благотворное стимулирующее действие на организм (активизирует деятельность сердца, обмен веществ, повышает активность дыхания, улучшают кроветворение) и понижающий его чувствительность к некоторым вредным воздействиям за счет интенсификации окисления и выведения вредных веществ (марганца, ртути, свинца) из организма. К сожалению, загрязнение атмосферы больших городов понижает ее прозрачность для УФИ, ограничивая его благотворное влияние на население. УФИ искусственных источников (электросварочных дуг, плазмотронов) может стать причиной острых и хронических — 586 — ÐǣƻǈǪǎÐǲǪ͠ǪǭǰǬ͠ǀǯǰǀǭǪÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ профессиональных поражений (электроофтальмия, катаракта, эритема кожи лица и век) с кумуляцией биологических эффектов при повторном воздействии. В комбинации УФИ с химическими веществами наблюдается явление фотосенсибилизации — повышенной чувствительности организма к свету с развитием фототоксических и фотоаллергических реакций; возможен также канцерогенный эффект УФИ для кожи, что зависит от дозы регулярного УФ — облучения и некоторых других сопутствующих факторов (диеты, приема лекарственных препаратов, температуры кожи). Гигиеническое нормирование УФИ в производственных помещениях осуществляется по СН 2.2.4-13-45-2005 «Санитарные нормы ультрафиолетового излучения производственных источников», устанавливающим допустимые плотности потока излучения в зависимости от длины волн при условии защиты органов зрения и кожи. Допустимая интенсивность УФ — облучения работающих при незащищенных участках кожи не более 0,2 м 2 (лицо, шея, кисти рук и др.) общей продолжительностью воздействия излучения 50%рабочей смены и длительности однократного облучения свыше 5 мин и более не должно превышать 10 Вт/м2 для области УФ-А и 0,01 Вт/м2 — для области УФ-В. Излучение в области УФ-С при указанной продолжительности не допускается. При использовании специальной одежды и средств защиты лица и рук, не пропускающих излучение (кожа, ткани с плен очным покрытием и т.п.), допустимая интенсивность облучения в областях УФ-В и УФ-С не должна превышать 1 Вт/м 2. Лазерное излучение (ЛИ) представляет собой особый вид излучения, охватывающий с длиной волны генерируемого в почти весь оптический диапазон электромагнитных волн — от ультрафиолетового до дальней инфракрасной области спектра. Световой пучок излучения лазера монохроматичен, когерентен и высокой степени направленности, что позволяет получить большую плотность потока мощности на облучаемой поверхности (1011–1014 Вт/см2), в связи с чем опасность в той — 587 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð или иной степени) характерна как для прямого, так и отраженного и рассеянного ЛИ. Взаимодействие ЛИ с тканями в зависимости от его режима сопровождается различными эффектами (тепловой, фотохимический, ударно — акустический и др.), зависящими от длины волны, длительности и частоты импульса, площади облучаемого участка, а также от биологических и физико-химических особенностей облучаемых тканей и органов. Повреждение кожи может быть вызвано лазерным излучением любой длины волны с преобладанием тепловых эффектов, следствием которых может стать широкий спектр последствий — от покраснения кожи до испарения биологической ткани. Прямое лазерное излучение дальней инфракрасной области в импульсном режиме способно проникать через ткани тела на значительную глубину, поражая внутренние органы. Это связано с преобразованием энергии излучения в энергию механических колебаний с образованием ударной волны, вызывающей повреждения глубоких тканей (брюшной полости, внутричерепного пространства и др.). Наибольшую опасность лазерное излучение представляет для глаза из-за его способности его оптической системы увеличивать плотность энергии на глазном дне более 6·104 раз по отношению к роговице. Степень повреждения глаза может изменяться от слабых ожогов сетчатки до полной потери зрения. Длительное хроническое действие диффузно отраженного лазерного излучения вызывает неспецифические, преимущественно вегетативно-сосудистые нарушения. При нормировании ЛИ в соответствии с СанПиН 5804-91 «Санитарные нормы и правила устройства и эксплуатации лазеров» устанавливают предельно допустимые уровни ЛИ для двух условий облучения — однократного и хронического, для трех диапазонов длин волн: 180–300 нм, 380–1400 нм, 1400–100 000 нм. Нормируемыми параметрами являются энергетическая экспозиция H и облученность E. Ионизирующее излучение — это потоки элементарных частиц и квантов электромагнитного поля, которые при движении через вещество ионизируют его атомы и молекулы, что вызывает в организме цепочку обратимых и необратимых из— 588 — ÐǣƻǈǪǎÐǲǪ͠ǪǭǰǬ͠ǀǯǰǀǭǪÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ менений, состоящую в нарушении биохимических процессов в организме, замедлении и прекращении роста тканей, возникновении новых химических соединений, не свойственных организму, и приводит к нарушению деятельности отдельных функций и систем организма. Специфика действия ионизирующего излучения на биологические объекты состоит в том, что эффекты развиваются в течение разных промежутков времени: от нескольких секунд до многих часов, дней, лет. Ионизирующая радиация при воздействии на организм человека может вызвать целый ряд заболеваний (лучевая болезнь, лучевой ожог, лучевая катаракта, лучевое бесплодие, злокачественные опухоли, лейкозы, наследственные болезни). Основной физической величиной, определяющей степень радиационного воздействия, является поглощенная доза ионизирующего излучения, единицей измерения которой в системе СИ является грей (Гр). Острые поражения развиваются при однократном равномерном гамма- облучении всего тела и поглощенной дозе при поглощенной дозе 0,25–0,5 Гр в виде временных, быстро проходящих изменений в крови. В интервале дозы 0,5–1,5 Гр возникает чувство усталости, и умеренные изменения в крови, при 1,5–2,0 Гр наблюдается легкая форма острой лучевой болезни, которая проявляется продолжительной лимфопенией, при 2,5–4,0 Гр возникает лучевая болезнь средней тяжести (тошнота, резко снижение лейкоцитов в крови, подкожные кровоизлияния, возможен смертельный исход через 2–6 недель после облучения), при 4,0–6,0 Гр развивается тяжелая форма лучевой болезни, приводящая в 50% случаев к смерти в течение первого месяца, при превышении 6,0 Гр, развивается крайне тяжелая форма лучевой болезни, которая почти в 100% случаев заканчивается смертью вследствие кровоизлияния или инфекционных заболеваний. Хроническая лучевая болезнь в виде изменений в крови, локальных поражений кожи, поражения хрусталика, пневмосклероза, снижения иммунореактивности организма может развиться при непрерывном или повторяющемся облучении в дозах, существенно ниже, вызывающих острую форму. — 589 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð Степень воздействия радиации зависит от того, является ли облучение внутренним (при попадании радиоактивного изотопа внутрь организма) или внешним. Внутреннее облучение возможно при вдыхании, заглатывании радиоизотопов и проникновении их в организм через кожу. Некоторые радиоактивные вещества поглощаются и накапливаются в конкретных органах, что приводит к высоким локальным дозам радиации. Кальций, радий, стронций и др. накапливаются в костях, изотопы йода вызывают повреждение щитовидной железы, редкоземельные элементы вызывают преимущественно опухоли печени. Равномерно распределяются изотопы цезия, рубидия, вызывая угнетение кроветворения, атрофию семенников, опухоли мягких тканей. При внутреннем облучении наиболее опасны альфа-излучающие изотопы полония и плутония. Способность вызывать отдаленные последствия: лейкозы, злокачественные новообразования, раннее старение — одно из коварных свойств ионизирующего излучения. Основные дозовые пределы облучения и допустимые уровни устанавливаются нормативным документом «Нормы радиационной безопасности (НРБ-99). Санитарные правила СП 2.6.1.758- 99» для следующих категорий облучаемых лиц: – персонал — лица, работающие с техногенными источниками (группа А) или находящиеся по условиям работы в сфере их воздействия (группа Б); – все население, включая лиц из персонала, вне сферы и условий их производственной деятельности. Для категорий облучаемых лиц устанавливают три класса нормативов: основные пределы доз (ПД), допустимые уровни, соответствующие основным пределам доз, и контрольные уровни. ϭϰ͘Ϯ͘ʽ̨̨̨̨̨̛̺̖̦̦̖̺̯̦̖̱̭̯̬̜̭̯̍̍̌̏̚͘ В общем виде воздействие материально — энергетического потока на объект защиты в любой точке пространства определяется интенсивностью потока I и длительностью экспозиции τ, т.е. E (x, y, z) = f(I, τ), где Е — степень воздействия — 590 — ÐǣƻǮƻǈǬǃǃǮǬÐƿǪǈǀǰǃǮǬÐǱǯǰ͠Ǯ֬ǯǰǫǮ в точке пространства с координатами х, у, z /1/. Минимизация интенсивности потока обеспечивается за счет технических решений, а уменьшение времени воздействия за счет организационных мероприятий. При техническом решении задачи защиты от энергетических воздействий выделяют источник, приемник энергии и защитное устройство, которое уменьшает до допустимых уровней поток энергии к приемнику. Рис. 14.1. Энергетический баланс защитного устройства. В общем случае защитное устройство (ЗУ) может отражать, поглощать, быть прозрачным по отношению к потоку энергии W+ (рис.14.1). При условии, что из этого потока часть Wα поглощается, часть W– отражается и часть W~ проходит сквозь преграду, ЗУ можно охарактеризовать следующими энергетическими коэффициентами: коэффициентом поглощения σ = Wá / W + , коэффициентом отражения ñ = W − / W + , коэффициентом передачи φ= W ~ / W + . Исходя из равенства ρ + α + τ = =1 при α = 1 ЗУ поглощает всю поступающую энергию, при ρ = 1 ЗУ полностью отражает ее, а при τ = 1 энергия проходит через устройство без потерь. В соответствии с изложенным можно выделить следующие принципы защиты: 1) принцип, при котором ρ ĺ 1; защита осуществляется за счет отражательной способности ЗУ; 2) принцип, при котором α ĺ 1; защита осуществляется за счет поглощательной способности ЗУ; 3) принцип, при котором τ ĺ 1; защита осуществляется с учетом свойств прозрачности ЗУ. — 591 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð На практике принципы обычно комбинируют, получая различные методы защиты, из которых наибольшее распространение получили методы изоляции и поглощения. Методы изоляции используют тогда, когда источник и приемник энергии являющийся одновременно объектом защиты, располагаются с разных сторон от ЗУ (рис.14.2). В основе этих методов лежит уменьшение прозрачности среды между источником и приемником, т.е. выполнение условия τ ĺ 0. При этом можно выделить два основных метода изоляции: метод, при котором уменьшается прозрачность среды за счет поглощения энергии ЗУ (условие τ ĺ 0 обеспечивается условием α ĺ 1) (рис.15.2, а), и метод, при котором уменьшение прозрачности среды достигается за счет высокой отражательной способности ЗУ (условие τ ĺ 0 обеспечивается условием ρ ĺ 1 (рис.14.2, б). Рис. 14.2. Методы изоляции при расположении источника и приемника с разных сторон от ЗУ: а – энергия поглощается; б – энергия отражается В основе методов поглощения лежит принцип увеличения потока энергии, прошедшего в ЗУ, т.е. достижение условия τĺ 1. Принципиально можно различать как бы два вида поглощения энергии ЗУ: поглощение энергии самим ЗУ за счет ее отбора от источника в той или иной форме, в том числе в виде необратимых потерь (характеризуется коэффициентом α, рис.14.3, а), и поглощение энергии в связи с большой прозрачностью ЗУ (характеризуется коэффициентом τ, рис.14.3, б). Так как при τĺ 1 коэффициент ρ ĺ 0, то методы поглощения используют для уменьшения отраженного потока энергии; при этом источник и приемник энергии обычно находятся с одной стороны от ЗУ. — 592 — ÐǡǬǰǮƽǊÐǀÐǯ͠ǬƽǯǰǫǪÐƿǪǈǀǰǊÐǮǰÐǇǱǂǪÐǀÐǫǀƻ͠Ǫǅǀǀ Рис. 14.3. Методы поглощения при расположении источника и приемника с одной стороны от ЗУ: а – энергия отбирается; б – энергия пропускается В большинстве случаев качественная оценка степени реализации целей защиты может осуществляться двумя способами. 1. При изоляции определяют коэффициент защиты kw в виде отношения kw = ПЭ / ПЭзу, где ПЭ и ПЭзу — потоки энергии в данной точке при отсутствии ЗУ и при его наличии. 2. При поглощении определяют коэффициент защиты kw в виде отношения kw = ПЭвх / ПЭвых, где ПЭвх и ПЭвых — потоки энергии на входе и выходе ЗУ. ϭϰ͘ϯ͘ʺ̶̨̨̛̛̛̛̛̛̖̯̼̭̬̖̭̯̺̯̼̯̹̱̥̬̔̔̏̌̌̌̏̍̌̚͘ Мероприятия по снижению шума определяется на основании акустического расчета, включающего: 1. выявления источников шума и определение их шумовых характеристик; 2. выбор расчетных точек акустического расчета и определение для них допустимых уровней звукового давления (УЗД); 3. определение ожидаемых УЗД в расчетных точках до проведения мероприятий по снижению шума; 4. определение требуемого снижения УЗД в расчетных точках; 5. выбор мероприятий для обеспечения требуемого снижения УЗД; 6. расчет и проектирование шумоглушащих, звукопоглощающих и звукоизолирующих конструкций (глушители, экраны, звукопоглощающие облицовки и т.п.). — 593 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð Акустический расчет базируется на шумовых характеристиках машин: уровне звуковой мощности (УЗМ) LP на стандартных среднегеометрических частотах октавных полос (LP = 10lg P / P0, где P — звуковая мощность источника, Вт; P0 — пороговое значение мощности, P0 = 10–12 Вт) и факторе направленности шума Ф, которые, как правило, приводятся в технической документации на оборудование. При отсутствии таких данных шумовые характеристики определяются расчетным путем. Суммарный уровень шума от n одинаковых по интенсивности источников в равноудаленной от них точке определяется по формуле L∑ = Li + 10 lgn, где Li — уровень звукового давления i-го источника шума, дБ; n — количество источников шума. Например, суммарный уровень шума от 10 одинаковых по интенсивности источников со звуковым давлением 70 дБ составит по этой формуле L∑ = 70 + 10 lg10 = 80 дБ. При одновременном действии двух источников с различными уровнями суммарный уровень определяется по формуле L∑ = Li + ΔL (14.1) где Li — наибольший из двух уровней шума, дБ; ΔL — добавка к функции разности уровней источников шума (табл. 14.1). Таблица 14.1. Добавка для определения суммарного уровня шума. Разность уровней двух источников 0 1 2,5 4 6 10 Величина добавки, ΔL 3 2,5 2 1,5 1 0,5 При наличии двух источников шума при разности их уровней в 2,5 дБ и уровне звукового давления более мощного источника 70 дБ суммарный уровень по приведенной формуле и на основании табл. 14.1 составит L∑ = 70 + 2 = 72 дБ. При большом числе источников шума суммирование интенсивности производится последовательно от большого — 594 — ÐǡǬǰǮƽǊÐǀÐǯ͠ǬƽǯǰǫǪÐƿǪǈǀǰǊÐǮǰÐǇǱǂǪÐǀÐǫǀƻ͠Ǫǅǀǀ к меньшему. Из табл. 14.1 следует, что при разности уровней более 6–8 дБ уровнем интенсивности менее мощного источника можно пренебречь. При расположении расчетной точки в помещении и в открытом пространстве акустический расчет проводится по формулам 4⎞ ⎛ Φ (14.2) + ⎟ L = Lp + 10lg ⎜ 2 ⎝ 4πr B⎠ L = Lp + 10lgΦ − 10lgS − ΔLp (14.3) где Lp — уровень звуковой мощности источника, дБ; L — искомый уровень звукового давления, дБ; B — постоянная помеA ; A = Lср S ; Lср — средний коэффициент щения, м2, B = 1 − α cp звукопоглощения внутренних поверхностей помещения; S — площадь поверхности, принимающей излучение; ΔLp — снижение уровня звуковой мощности на пути распространения (до 50 м и ΔLp = 0). Из анализа приведенных формул вытекают основные методы борьбы с шумом: уменьшение шума в источнике; изменение направленности излучения; рациональная планировка предприятий и цехов, акустическая обработка помещений; уменьшение шума на пути его распространения; использование средств индивидуальной защиты (СИЗ). Борьба с шумом посредством уменьшения его в источнике (снижение LP) является предпочтительной и обеспечивается с помощью целого ряда конструкторско-технологических решений. Для механического шума это замена ударных процессов безударными, возвратно-поступательных движений равномерными вращательными, прямозубых шестерен косозубами, зубчатых и цепных передач клиноременными и зубчатоременными, подшипников качения подшипниками скольжения, использование материалов с большим внутренним трением; и др. Аэрогидродинамический шум можно уменьшить снижением скорости обтекания, улучшением аэродинамики тел, выбором оптимальных режимов работы оборудования. Однако — 595 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð в большинстве случаев эти меры оказываются недостаточными, и требуется дополнительное, а часто и основное снижение шума за счет звукоизоляции источника и установки глушителей. Причиной электромагнитного шума является главным образом взаимодействие ферромагнитных масс под влиянием переменных во времени и пространстве магнитных полей, поэтому его снижение осуществляется путем конструктивных изменений в электрических машинах, более плотной компоновки пакетов магнитопроводов, использования демпфирующих материалов. Изменение направленности излучения достигается соответствующей ориентацией источника по отношению к рабочим местам. Рациональная планировка предприятий и цехов, акустическая обработка помещений обеспечиваются соответствующим расположением шумных помещений, соблюдением требуемых расстояний между помещениями, увеличением эквивалентной площади поглощения путем размещения звукопоглощающих облицовок и штучных звукопоглощателей. Уменьшение шума на пути его распространения заключается в установке звукоизолирующих преград в виде стен, перегородок, кожухов, кабин и т.д. Звукоизолирующая способность однородной перегородки R может быть определена по формуле 20lg(Gf) — 60, где G — масса 1 м2 ограждения, кг; f — частота звуковой волны, Гц. При невозможности изолировать шумные машины изолируют рабочее место с пультом управления (экраны). Основными направлениями борьбы с вибрацией являются снижение вибраций в источнике возникновения посредством снижения или ликвидации действующих переменных сил; отстройка от режимов резонанса путем рационального выбора приведенной массы или жесткости системы; вибродемпфирование — увеличение механического импеданса колеблющихся элементов путем увеличения активных потерь (трения) при колебаниях вблизи резонансных режимов; динамическое гашение колебаний, увеличение механического импеданса узла, — 596 — ÐǡǬǰǮƽǊÐǀÐǯ͠ǬƽǯǰǫǪÐƿǪǈǀǰǊÐǮǰÐǇǱǂǪÐǀÐǫǀƻ͠Ǫǅǀǀ механизма, агрегата путем внесения в систему дополнительных реактивных импедансов; виброизоляция; использование СИЗ. Снижение вибраций в источнике возникновения состоит в конструктивно-технологических мероприятиях, аналогичным при борьбе с шумом (замена ударных процессов безударными, повышение точности изготовления деталей, использование специальных видов зацеплений, балансировка вращающихся масс и др.). Отстройка от режимов резонанса заключается в расчетном или экспериментальном определении собственных частот колебаний отдельных элементов и устранении резонансных режимов либо изменением массы и жесткости системы, либо установлением нового рабочего режима. Вибродемпфирование состоит в уменьшении уровня вибраций путем превращения энергии механических колебаний в другие виды энергии за счет использования материалов с большим внутренним трением (сплавы на основе Cu–Ni, Ni–Ti, марганцевые и магниевые сплавы, пластмассы, дерево, резина вместо чугуна и стали); нанесения слоя упруго-вязких материалов, обладающих большими потерями на внутреннее трение (твердые пластмассы, рубероид, пенопласт, резина, различные мастики); снижения сил поверхностного трения и др. Виброгашение — это уменьшение уровня вибраций путем введения дополнительных реактивных импедансов. Оно реализуется за счет устройства самостоятельных фундаментов, использования виброгасителей, ребер жесткости. Виброизоляция — уменьшение уровня вибраций объекта путем уменьшения передачи колебаний этому объекту от источника колебаний. Реализуется виброизоляция посредством введения в систему дополнительной упругой связи в виде пружин, резиновых прокладок или комбинированных амортизаторов. К средствам индивидуальной защиты от шума относятся вкладыши (снижение шума до 5–20 дБ), наушники (35–47 дБ), шлемы для уровня шума более 120 дБ. Для защиты от общей вибрации применяют обувь с амортизирующим подошвами (сапоги, полусапоги, полуботинки — — 597 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð для защиты от вертикальной вибрации свыше 11 Гц, а также от ударов и нетоксичной пыли). Для защиты рук используют рукавицы с упругодемпфирующими вкладышами; рукавицы и перчатки с мягкими наладонниками; упругодемпфирующие прокладки и пластины для обхвата вибрирующих рукояток и деталей и т.п. Борьба с инфразвуком состоит в основном в его подавлении в источнике: повышение быстроходности машин, что обеспечивает перевод максимума излучений в область слышимых частот, повышение жесткости конструкций больших размеров, устранение низкочастотных вибраций, установке глушителей реактивного типа. Такие методы борьбы с шумом, как звукоизоляция и звукопоглощение, при инфразвуке малоэффективны. Борьба с ультразвуком включает изоляцию ультразвуковых установок в специальных помещениях, использование звукоизолирующих кожухов или экранов, располагающихся на пути распространения ультразвука. ϭϰ͘ϰ͘ʺ̨̛̛̖̯̼̭̬̖̭̯̺̯̼̔̔̏̌̌̚ ̵̨̡̨̨̛̯̣̖̯̬̥̦̯̦̼̪̣̖̜̾̌̐͘ Защита от воздействия электромагнитных излучений радиочастот (ЭМИ РЧ) осуществляется путем проведения организационных и инженерно-технических, лечебно-профилактических мероприятий, а также использования СИЗ. К организационным мероприятиям относятся выбор рациональных режимов работы оборудования, ограничение места и времени нахождения персонала в зоне воздействия ЭМИ РЧ (защита расстоянием и временем) и т.п. Инженерно-технические мероприятия включают рациональное размещение оборудования, ограничение поступления ЭМИ на рабочие места персонала (поглотители мощности, экранирование, использование минимальной мощности генератора), обозначение и ограждение зон с повышенным уровнем ЭМИ РЧ. Лечебно-профилактические мероприятия осуществляются в целях предупреждения, ранней диагностики и лечения — 598 — ÐǡǬǰǮƽǊÐǀÐǯ͠ǬƽǯǰǫǪÐƿǪǈǀǰǊÐǮǰÐǌǁǬǭǰ͠ǮǂǪƼǃǀǰǃǊǲÐ͟ǮǁǬ֬ нарушений в состоянии здоровья работника, связанные с воздействием ЭМИ РЧ, и включают предварительные при поступлении на работу и периодические медицинские осмотры. К средствам индивидуальной защиты относятся защитные очки, щитки, шлемы, защитная одежда (комбинезоны, халаты и т.д.). Защита временем предусматривает ограничение времени пребывания объекта защиты в электромагнитном поле и применяется, когда нет возможности снизить интенсивность излучения до допустимых значений. Значения предельно допустимых уровней напряженности электрической (Eпду) и магнитной (Hпду) составляющих в зависимости от продолжительности воздействия приведены в табл. 14.2, а предельно допустимые уровни плотности потока энергии (ППЭПДУ) в зависимости от продолжительности воздействия ЭМИ РЧ — в табл.14.3. Защита расстоянием заключается в увеличении расстояния между излучателем и объектом защиты и применяется в том случае, если невозможно ослабить интенсивность облучения другими мерами. Уменьшение мощности излучения в его источнике достигается за счет применения специальных устройств (поглотителей мощности, аттенюаторов). Экранирование источников излучения используется для снижения интенсивности электромагнитного поля на рабочем месте или устранении опасных зон излучения. Основной характеристикой экрана является степень ослабления Э электромагнитного поля, называемая эффективностью экранирования, которая представляет собой отношение E, H, ППЭ в данной точке при отсутствии экрана соответственно к Eэ, Hэ, ППЭэ в той же точке при наличии экрана: Э = E/Eэ; Э = H/Hэ; Э = ППЭ/ ППЭэ. Экранирование источников ЭМИ РЧ или рабочих мест осуществляется с помощью отражающих или поглощающих экранов (стационарных или переносных). Экранирование источников ЭМИ РЧ или рабочих мест осуществляется с помощью отражающих или поглощающих экранов (стационарных или переносных), выполняемых в виде замкнутых камер, шкафов — 599 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð Таблица 14.2. Предельно допустимые уровни напряженности электрической Eпду и магнитной Hпду составляющих в диапазоне частот 30 кГц-300 МГц в зависимости от продолжительности воздействия. Eпду, В/м Hпду, А/м Продолжительность воздействия, t, ч 0,03…3 МГц 3…30 МГц 30…300 МГц 0,03…3 МГц 30…50 Мгц 8,0 и более 7,5 7,0 6,5 6,0 5,5 5,0 50 52 53 55 58 60 63 30 31 32 33 34 36 37 10 10 11 11 12 12 13 5,0 5,0 5,3 5,5 5,8 6,0 6,3 0,30 0,31 0,32 0,33 0,34 0,36 0,38 4,5 4,0 3,5 3,0 2,5 2,0 1,5 1,0 0,5 0,25 0,125 0,08 и менее 67 71 76 82 89 100 115 141 200 283 400 500 39 42 45 48 52 59 68 84 118 168 236 296 13 14 15 16 18 20 23 28 40 57 80 80 6,7 7,1 7,6 8,2 8,9 10,0 11,5 14,2 20,0 28,3 40,0 50,0 0,40 0,42 0,45 0,49 0,54 0,60 0,69 0,85 1,20 1,70 2,40 3,00 Примечание. При продолжительности воздействия менее 0,08 ч дальнейшее повышение интенсивности воздействия не допускается. — 600 — ÐǡǬǰǮƽǊÐǀÐǯ͠ǬƽǯǰǫǪÐƿǪǈǀǰǊÐǮǰÐǌǁǬǭǰ͠ǮǂǪƼǃǀǰǃǊǲÐ͟ǮǁǬ֬ Таблица 14.3. Предельно допустимые уровни плотности потока энергии (ППЭПДУ) в диапазоне частот 300 МГц…300 ГГц в зависимости от продолжительности воздействия. Продолжительность воздействия, t, ч ППЭПДУ, мкВт/см2 8,0 и более 7,5 7,0 6,5 6,0 5,5 5,0 4,5 4,0 3,5 3,0 2,5 2,0 1,5 1,0 0,5 0,25 0,20 и менее 25 27 29 31 33 36 40 44 50 57 67 80 100 133 200 400 800 1000 Примечание. При продолжительности воздействия менее 0,2 часа дальнейшее повышение интенсивности воздействия не допускается. — 601 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð и кожухов из металлических листов, сетки, металлизированной ткани и др. ϭϰ͘ϱ͘ˁ̴̴̨̡̨̨̨̨̨̨̛̛̛̬̖̭̯̺̯̼̯̦̬̬̭̦͕̱̣̯̬̣̖̯͕̔̏̌̌̌̌̐̽̌̏̐̚ ̸̨̨̨̨̛̛̛̛̛̛̣̖̬̦̦̬̱̺̖̣̱̖̦̜̌̐̀̐̚̚̚͘ Наиболее распространенный и эффективный способ защиты от ИК- излучения — экранирование как источников излучения, так и рабочих мест конструкциями из алюминия, стали, меди, асбеста и других материалов. Основной мерой защиты от УФ-излучений являются конструкторско-технологические решения, исключающие генерацию или обеспечивающие снижение интенсивности излучения. Предупреждают распространение и уменьшают интенсивность этих излучений такие меры защиты, как окраска ограждающих поверхностей в светлые тона в помещениях. В качестве СИЗ рекомендуются для глаз очки или щитки со стеклами-светофильтрами, для кожи — мази с веществами-светофильтрами (салолом, салициловометиловым эфиром и др.) и спецодежда из льняных и хлопчатобумажных тканей (с искростойкой пропиткой) и грубошерстного сукна, рукавицы. Средства защиты от лазерного излучения подразделяются на коллективные и индивидуальные. Коллективные средства защиты от лазерного излучения включают: – защитные экраны (или кожухи), препятствующие попаданию лазерного излучения на рабочие места (экраны по возможности должны поглощать излучения основной длины волны и оставаться прозрачными на остальном участке спектра); – размещение пульта управления лазерной установкой в отдельном помещении с телевизионной или другой системой наблюдения за ходом процесса; – экранирование света импульсных ламп накаливания и ультрафиолетового излучения газового разряда; системы блокировок и сигнализации, предотвращающие доступ персонала во время работы лазера в опасную зону; — 602 — ÐǦ͠ǬƽǯǰǫǪÐƿǪǈǀǰǊÐǮǰÐǀǃǄ͠Ǫǭ͠ǪǯǃǮƼǮ ÐǱǁǋǰ͠ǪǄǀǮǁǬǰǮǫǮƼǮ ÐǁǪƿǬ͠ǃǮƼǮÐǀÐǀǮǃǀƿǀ͠ǱǍǈǬƼǮÐǀƿǁǱǆǬǃǀ֬ – окраска внутренних поверхностей помещений, а также находящихся в них предметов (за исключением специальной аппаратуры) в матовый цвет с минимальным коэффициентом отражения, обеспечивающим максимальное рассеяние света на длине волны излучения (стены рекомендуется окрашивать до потолка; двери окрашивают под цвет стен; перегородки делают из непроницаемого для лазерного излучения материала). При использовании лазеров открытого типа (в том числе в цеховых, полевых и других условиях) для предотвращения облучения персонала и других лиц применяют следующие средства коллективной защиты: ограждение (маркировку) лазерноопасной зоны; экранирование открытого луча лазера; вынесение пульта управления из лазерноопасной зоны. К СИЗ от лазерного излучения относятся: специальные противолазерные очки, щитки, маски, технологические халаты из хлопчатобумажного или бязевого материала светло-зеленого или голубого цвета и перчатки (применяются в тех случаях, когда существует опасность воздействия лазерного излучения на кожу). Основные принципы обеспечения радиационной безопасности включают: уменьшение мощности источников до минимальных величин (защита количеством); защита временем; защита расстоянием и экранирование источников излучения материалами, поглощающими ионизирующие излучения. Защита количеством подразумевает проведение работы с минимальными количествами радиоактивных веществ, т.е. пропорционально сокращает мощность излучения. Однако требования технологического процесса часто не позволяют сократить количество радиоактивного вещества в источнике, что ограничивает на практике применение этого метода защиты. Защита временем основана на сокращении времени работы с источником, что позволяет уменьшить дозы облучения персонала. Этот принцип особенно часто применяется при непосредственной работе персонала с малыми активностями. Защита расстоянием — достаточно простой и надежный способ защиты. Это связано со способностью излучения терять свою энергию при взаимодействиях с веществом: чем больше — 603 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð расстояние от источника, тем больше процессов взаимодействия излучения с атомами и молекулами, что в конечном итоге приводит к снижению дозы облучения персонала. Экранирование — наиболее эффективный способ защиты от излучений. В зависимости от вида ионизирующих излучений для изготовления экранов применяют различные материалы, а их толщина определяется мощностью излучения. Лучшими экранами для защиты от рентгеновского и гамма-излучений являются материалы с большим коэффициентом поглощения, например свинец, позволяющий добиться нужного эффекта по кратности ослабления при наименьшей толщине экрана. Более дешевые экраны делаются из просвинцованного стекла, железа, бетона, баррибетона, железобетона и воды. ϭϰ͘ϲ͘ʶ̨̨̨̨̦̯̬̣̦̼̖̪̬̭̼̽̏͘ 1. Какие виды энергетических загрязнений Вам известны? 2. Каковы источники шума, ультра- и инфразвука в окружающей среде? 3. Каково воздействие шума, ультра- и инфразвука на окружающую среду? 4. Каковы источники вибраций и их воздействие на окружающую среду? 5. Каковы источники ЭМП в окружающей среде? 6. Каково воздействие ЭМП на окружающую среду? 7. Каковы источники ИК и УФ излучения в окружающей среде? 8. Каково воздействие ионизирующих излучений на окружающую среду? 9. Каково воздействие ЭМП на окружающую среду? 10. Какие принципы и методы защиты можно сформулировать на базе обобщенного защитного устройства и как оценить ее эффективность? 11. Назовите методы защиты от вибраций и шума. 12. Назовите методы защиты от электромагнитных полей, как определяется при этом эффективность защиты? — 604 — ÐǤ͠ǀǂǬ͠ǊÐ͠ǬǇǬǃǀǎÐƿǪƽǪǆ 13. Какие методы защиты от ионизирующих излучений существуют, и как определяется при этом эффективность защиты? ϭϰ͘ϳ͘ʿ̸̛̛̬̥̖̬̼̬̖̹̖̦́̌̔̌̚͘ Задача 1. Определить уровень звукового давления L на расстоянии r=17 м от источника шума при следующих значениях исходных данных: Lp=110 дБ, Ф=1,75, S=180 м2 αср=0,65. αñð S . ВыРешение. Расчет выполняем по формуле B = 1 − αñð 0,65<180 2 = 334,3ì числяем B = 1 − 0,65 4 ⎞ ⎛ 1,75 + = 90,9 äÁ L = 110 + 10lg ⎜ ⎝ 4π172 334,3 ⎟⎠ Задача 2. Определить площадь оконных проемов, обеспечивающих естественное освещение для КБ размерами 30х20х5 м. Окна выходят на юг. Работа высокой точности. Решение. Площадь светопроема при боковом освещении определяется по формуле: S e K K S0 = ï í 0 ç çä 100τ 0r1 где Sп – площадь пола, равная 60 × 20=600 м2, ен — нормируемое значение КЕО при боковом освещении равно 2,0 (точные работы); Кз — коэффициент запаса, для помещений с малыми выделениями пыли равен 1,3; Кзд — коэффициент, учитывающий затенение окон противостоящими зданиями, принимаем за 1, так как про затенение в условиях задачи не упоминается; τ0 — общий коэффициент светопропускания, равный 0,34 и учитывающий потери света в материале, в переплетах светопроема, а также в слое загрязнения остекления, т.е. τ 0 = τ1τ2 τ3 = 0,8<0,6<0,7 = 0,34 ;r1 = 4,1 и учитывающий влияние отраженного света. — 605 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð Поскольку отношение длины помещения к его глубине составляет 1,5, а высота от уровня условной рабочей поверхности до верха окна равна 5 м, при этих условиях η0=19. Подставив численные значения в формулу, получим 600<2<19<1,3<1 ≈ 213 ì 2 S0 = 100<0,34<4,1 Задача 3. Рассчитать общее равномерное искусственное освещение сборочного цеха с размерами 20 × 15 × 5 м, работа точная, К=0,3. Для расчета рабочей поверхности основным является метод светового потока, учитывающий световой поток, отраженный от потолка и стен. Световой поток лампы рассчитывается по формуле: E SKç z Ôë = â Nn где Фл — световой поток лампы (лм); Ев — нормируемая минимальная освещенность при тонкой работе Ев =150 л для ламп накаливания; n — число ламп в светильнике, z -коэффициент, учитывающий отношение средней освещенности к минимальной (для ламп накаливания равен 1,15). Общая площадь помещения S=20 × 15=300 м2. Индекс помещения рассчитывается по формуле: 20<15 S = = 1,714 i= H p ( A = B) 5(20 + 15) что соответствует коэффициенту использования η=0,54. Принимаем z=1,15, коэффициент запаса Кз=1,5 для лампы накаливания, а световой поток Фл=2100 лм. Отсюда число ламп, необходимых для освещения, будет равно E SKç z 150<300<1,5<1,15 N= â = ≈ 20 øò . 2100<0,54<2 Ôï Задача 4. Определить толщину металлического экрана δ, обеспечивающего заданное ослабление электромагнитного поля при следующих значениях исходных данных: заданное ослабление ЭМП Э = 50 дБ; частота поля f = 2·109 Гц; абсолют— 606 — ÐƭǪƽǪǆǀÐƽǁǎÐǯǪǂǮǯǰǮǎǰǬǁǋǃǮƼǮÐ͠ǬǇǬǃǀǎ ная магнитная проницаемость μ=0,3 10–6 Гц/м; удельная проницаемость материала σ= 30 106 Ом/м. Решение. Расчет выполняется по формуле Ý 50 δ= = = 0,24<10−4 = 24 ìêì . 15,4 f μσ 15,4 2<109 <0,3<10−6 <30<106 Задача 5. Рассчитать величину Ir при прикосновении к одной из фаз нормально работающей трехфазной сети с заземленной нейтралью с фазным напряжением Uф=220 В при следующих значениях исходных данных: сопротивление тела человека Rт=1 кОм; сопротивление пола, на котором находится человек Rп=10 кОм; сопротивление обуви человека Rоб=100 кОм; сопротивление заземлений нейтрали r=10 кОм. Оценить опасность поражения током человека. Решение. Расчет выполняем по формуле: Uô 220 = = 5,7<10−3 À Ir = 3 3 Rò + Rï + Rîá + r0 1,5<10 + 2<10 + 25<103 + 10<103 ϭϰ͘ϴ͘ʯ̸̨̨̨̨̛̛̣̭̥̭̯̯̖̣̦̬̖̹̖̦̌̔̌̔́̌́̽̐́͘ Задача 1 Определить уровень звукового давления и требуемое снижение шума в расчетной точке производственного помещения объемом 1·103 м3 , в котором находятся 8 однотипных источников шума, имеющих максимальный линейный размер. РТ находятся на расстоянии 5 м от ближайших четырех источников шума и на расстоянии 8 м от остальных источников шума. Задача 2. Определить необходимую площадь фонарей для освещения производственного помещения размером 20 × 10 × 3 м естественным верхним светом при следующих значениях исходных данных: ен=10; Кз=1,5; Кзд=1; ηф=2; τ1=0,9; τ2=0,75; τ3=0,65. — 607 — ǞǁǪǫǪÐ ÐǧǬǮ͠ǬǰǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐƿǪǈǀǰǊÐǮǭ͠ǱƾǪǍǈǬ֬Ðǯ͠ǬƽǊÐǮǰÐǌǃǬ͠ƼǬǰǀǆǬǯǭǀǲÐǫǮƿƽǬ֬ǯǰǫǀ֬ Ð Задача 3. Рассчитать равномерное искусственное освещение в помещении при следующих исходных данных: размеры помещения 20 × 10 × 3 м; Ев =150; Фл =101 лм; n=1; η=58%; z =1,15; Кз =1,7. Задача 4. Определить толщину металлического экрана δ, обеспечивающего заданное ослабление электромагнитного поля при следующих значениях исходных данных: заданное ослабление ЭМП Э = 30 дБ; частота поля f= 3,0 ГГц; абсолютная магнитная проницаемость μ = 0,4 мкГц/м; удельная проницаемость материала σ = 35,4 Мом/м. Задача 5. Оценить опасность поражения током человека при прикосновении к одной из фаз нормально работающей трехфазной сети с заземленной нейтралью с фазным напряжением Uф=220 В при следующих значениях исходных данных: сопротивление тела человека Rт=1 кОм; сопротивление пола, на котором находится человек Rп=10 кОм; сопротивление обуви человека Rоб=100 кОм; сопротивление заземлений нейтрали r = 10 кОм. — 608 — ǍưǙǚǙÍ Í Í ƚƝǗǗƟƜƝǒǑǑƥǎÍǓǔǒƠǎǕǕƥÍ ǌÍǋǖǐǒǕǗǎǔǎÍƝÍǍƝƚǔǒǕǗǎǔǎ Í ǔǋǕǕǎƝǌǋǑƝǎÍƝÍǔǋƜƙǋǌƞǎǑƝǎÍ ǓǔƝǐǎǕǎ֏ В результате изучения главы 15 бакалавр должен: Знать: – основные виды процессов рассеивания и разбавления примесей в атмосфере и гидросфере. Уметь: – рассчитывать необходимую степень рассеивания примеси в атмосфере, а также необходимую степень разбавления в гидросфере (до величин ниже ПДК) в зависимости от химического и гранулометрического состава примеси. Владеть: – математическим аппаратом для описания физических закономерностей диффузионных процессов в атмосфере и гидросфере. ϭϱ͘ϭ͘ˇ̸̡̨̨̨̨̛̛̛̛̛̖̭̖̭̦̼̬̭̭̖̦̼̬̭̏̌̏̌́̏̍̏̚ ̵̴̨̛̬̦̺̖̺̖̭̯̯̥̭̖̬̖̌̐́́̀̏̏̏̌̚̚͘ ϭϱ͘ϭ͘ϭ͘ˁ̴̡̨̨̛̯̬̱̯̱̬̭̭̯̯̥̭̖̬̼̌̌̏̌͘ Атмосфера — газовая оболочка Земли. Ее масса около 5,9 × 1015 т, она имеет слоистое строение и состоит из несколь— 609 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ ких сфер, между которыми располагаются переход слои — паузы. В сферах изменяются количество воздуха и температура. Наиболее плотный слой воздуха, прилегающий к земной поверхности, носит название тропосферы. Толщина ее в средних широтах составляет 10–12 км над уровнем моря, на полюсах 7–10, над экватором 16–18 км. В тропосфере сосредоточено более 4/5 массы земной атмосферы. Из-за неравномерности нагрева земной поверхности в ней образуются мощные вертикальные токи воздуха, отмечаются неустойчивость температуры, относительной влажности, давления и т.д. Температура воздуха в тропосфере по высоте уменьшается на 0,6 град на каждые 100 м и колеблется от +40 до –50°С. Выше тропосферы находится стратосфера, а между ними расположена тропопауза. В разных широтных зонах имеются два и иногда три уровня тропопаузы с разрывом по высоте между ними. Различают тропическую с высотой от 15 до 18 км и полярную тропопаузу высотой примерно 10 км. Граница разрыва между тропической и полярной тропопаузами постоянно меняется, но чаще всего она лежит между 35 и 50° широты в северном и южном полушариях. Третья тропопауза иногда появляется на промежуточных широтах и называется межширотной. Место разрыва ее с тропической тропопаузой приходится примерно на 30° широты, а с полярной — на 45°. Стратосфера имеет протяженность около 40 км. Воздух в ней разрежен, влажность невысокая. Температура воздуха от границы тропосферы до высоты 30 км постоянная (около –50°С), а затем начинает повышаться и на высоте 50 км достигает 10°С. В стратосфере под воздействием космического излучения и коротковолновой части ультрафиолетового излучения Солнца молекулы воздуха ионизируются, в результате чего образуется озон. Озоновый слой находится на высоте 25–40 км. Стратопауза отделяет стратосферу от лежащей выше мезосферы. Высокая температура стратосферы, вероятно, является результатом полного поглощения солнечной ультрафиолетовой и инфракрасной радиации озоновым слоем. В мезосфере количество озона уменьшается, поэтому средняя температура там значительно ниже. На высоте примерно 80 км она равна — 610 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ –70°С. В слое мезосферы наблюдаются серебристые облака. Выше мезосферы расположена термосфера (или ионосфера), между ними имеется мезопауза. Для термосферы характерно непрерывное повышение температуры с увеличением высоты. На высоте 150 км температура достигает 200–240°С, на уровне 200 км — 500°С, а на высоте 500–600 км превышает 1500°С. В термосфере газы очень разрежены, молекулы их движутся с большой скоростью, но редко сталкиваются между собой и поэтому не могут вызвать даже небольшого нагревания находящегося здесь тела. Под действием солнечной радиации протекает множество реакций, в которых участвуют кислород, озон, азот, оксид азота, пары воды, диоксид углерода. Ионизация в основном происходит на высоте 70–80 км; при этом образуются отрицательные (N–, O–, О2–, СО3v, NО2–, NO3– и положительные N+, Н+, О+, О2+ и др.) ионы. Эти ионы образуют различные комплексы: NO+. N2; NО+.CО2; NO+.H2; О2+.(Н2О). Наиболее удалена от Земли экзосфера (от 800 и до 1600 км). В ней еще обнаруживаются газы атмосферы и происходит утечка атомов (в основном водорода и гелия) в мировое пространство. Состав воздуха в нижних слоях атмосферы приведен в табл. 15.1. До высоты 100 км химический состав воздуха существенно меняется. Выше атмосфера состоит в основном из кислорода и азота. На высоте 110–120 км почти весь кислород становится атомарным. Предполагается, что выше 400–500 км и другие газы, составляющие атмосферу, находятся в атомарном состоянии. Кислородно-азотный состав сохраняется примерно до высоты 400–600 км. Выше 600 км в атмосфере начинает преобладать гелий. «Гелиевая корона» Земли простирается примерно до высоты 1600 км, а выше 200–3000 км преобладает водород. ϭϱ͘ϭ͘Ϯ͘ʶ̴̶̵̴̡̨̛̛̛̛̣̭̭̬̦̺̯̥̭̖̬̱̖̺̖̭̯̌̌́̌̐́́̀̌̏̏̚̚͘ По агрегатному состоянию все загрязняющие атмосферу вещества делят на четыре группы: твердые, жидкие, газо— 611 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ Таблица 15.1. Состав воздуха в нижних слоях атмосферы. Содержание Компоненты Азот Кислород Аргон Диоксид углерода Неон Гелий Криптон Ксенон Содержание % масс. % объем. 75,52 23,15 1,28 0,046 78,09 20,94 0,93 0,033 1,2·10–3 7,2·10–5 3,3·10–4 3,9·10–5 1,8·10–5 5,2·10–4 1·10–4 8·10–6 Компоненты Оксид азота Водород Метан Диоксид азота Озон Диоксид серы Оксид углерода Аммиак % масс. % объем. 2,5·10–3 2,5·10–4 3,5·10–6 0,8·10–5 8·10–5 5·10–5 1,5·10–4 1,5·10–4 10–6–10–5 – 2·10–8 2·10–5 – 1·10–5 – 1·10–5 образные и смешанные. Кроме того, промышленные выбросы в атмосферу могут классифицироваться: – по организации отвода и контроля (организованные и неорганизованные); – по режиму отвода (непрерывные и периодические); – по температуре (нагретые, у которых температура газопылевой смеси выше температуры воздуха, и холодные); – по локализации (в основном, вспомогательном и подсобном производствах); – по признакам очистки: на выбрасываемые без очистки (организованные и неорганизованные) и после очистки (организованные). При этом под очисткой газа понимается отделение от газа или превращение в безвредное состояние загрязняющего вещества, поступающего от промышленного источника. Организованный промышленный выброс — это выброс, поступающий в атмосферу через специально сооруженные газоходы, воздуховоды, трубы. — 612 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ Неорганизованным называется промышленный выброс, поступающий в атмосферу в виде ненаправленных потоков газа в результате нарушения герметичности оборудования, отсутствия или неудовлетворительной работы оборудования по отсосу газа в местах загрузки, выгрузки и хранения продуктов. Промышленные выбросы в атмосферу подразделяют также на первичные и вторичные. Первичные — это выбросы, непосредственно поступающие в атмосферу от тех или иных источников, а вторичные, будучи продуктами образования первичных, могут быть более токсичными и опасными, чем первичные. Типичное превращение некоторых веществ — их фотохимическое окисление. Космическая пыль образуется из остатков сгоревших метеоритов при их прохождении через атмосферу. Ежегодно ее выпадает на Землю 2–5 млн т. Природная пыль является постоянной составной частью земной атмосферы и представляет собой мельчайшие твердые взвешенные в воздухе частицы радиусом 10–4 –10–3 см и ядра конденсации со средним радиусом 5.10–6 см. Частицы природной пыли имеют органическое и неорганическое происхождение и образуются в результате разрушения и выветривания горных пород и почвы, вулканических извержений, лесных, степных и торфяных пожаров, испарения с поверхности морей. Одним из источников пыли в нижних слоях атмосферы являются безводные пустыни и степи. Кроме того, она образуется аэропланктоном — бактериями, спорами растений, плесневыми и другими грибами, продуктами гниения, брожения и разложения растений и животных. Атмосферный воздух над океаном включает мельчайшие кристаллы солей магния, натрия, калия, кальция, образующиеся в результате высыхания в воздухе брызг воды. Как правило, естественное загрязнение не угрожает отрицательными последствиями биогеоценозам и обитающим в них живым организмам, хотя кратковременные последствия возможны. Атмосферная пыль имеет большое значение для процессов, происходящих на Земле. Она способствует конденсации водяных паров, а, следовательно, и образованию осадков. Кроме того, она поглощает прямую солнечную радиацию и защи— 613 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ щает организмы от солнечного излучения. Академик В.И. Вернадский отмечал, что атмосферная пыль играет огромную роль в жизни планеты. Биологическое разложение веществ на Земле, в том числе жизнедеятельность почвенных бактерий, ведет к образованию больших количеств сероводорода, аммиака, углеводородов, оксидов азота (N2O, NO, NО2), оксида и диоксида углерода. Все они попадают в атмосферу. Источниками антропогенного загрязнения атмосферы примесями служат теплоэнергетика, промышленность, нефте- и газопереработка, транспорт, испытания термоядерного оружия. Каждый из этих источников (и каждая отрасль производства) связан с выделением специфических примесей, состав которых насчитывает десятки тысяч веществ, иногда сразу не поддающихся идентификации. Однако наиболее обычные загрязняющие вещества, поступающие в атмосферу в массе и называемые поэтому многотоннажными, сравнительно немногочисленны. Наиболее распространенные выбросы промышленности — зола, пыль, оксид цинка, силикаты, хлорид свинца, оксиды серы, сероводород, меркаптан, альдегиды, углеводороды, смолы, оксид и диоксид азота, аммиак, озон, оксид и диоксид углерода, фтористый и хлористый водород, кремнефтористый натрий, радиоактивные газы, аэрозоли. Источники загрязнения воздушного пространства промышленными выбросами могут быть классифицированы последующим признакам: 1. По назначению: 1) технологические, содержащие хвостовые газы после улавливания на установках (рекуперации, абсорбции, адсорбции и т. п.), продувки аппаратов, воздушников и др. (для этих выбросов характерны высокие концентрации вредных веществ и сравнительно малые объемы удаляемого воздуха); 2) вентиляционные выбросы — местные отсосы от оборудования и общеобменная вытяжка. 2. По месту расположения: 1) незатененные, или высокие, находящиеся в зоне недеформированного ветрового потока (к этим источникам от— 614 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ носятся высокие трубы, а также точечные источники, удаляющие загрязнения на высоту, превышающую высоту здания в 2,5 раза); 2) затененные, или низкие, расположенные на высоте в 2,5 раза меньше высоты здания; 3) наземные — находящиеся вблизи земной поверхности (к этим источникам относятся открыто расположенное технологическое оборудование, колодцы производственной канализации, пролитые токсичные вещества, сбросы отходов производства). 3. По геометрической форме: 1) точечные (трубы, шахты, крышные вентиляторы); 2) линейные (аэрационные фонари, открытые окна, близко расположенные вытяжные шахты и факелы). 4. По режиму работы: 1) непрерывного и периодического действия 2) залповые и мгновенные. В случае залповых выбросов за короткий промежуток времени в воздух поступает большое количество вредных веществ. Залповые выбросы возможны при авариях, при сжигании быстрогорящих отходов производства на специальных площадках уничтожения. При мгновенных выбросах загрязнения выбрасываются в доли секунды иногда на значительную высоту. Они происходят при взрывных работах и аварийных ситуациях. 5. По дальности распространения: 1) внутриплощадочные, когда выбрасываемыми в атмосферу загрязнениями создаются высокие концентрации только на территории промышленной площадки, а в жилых районах ощутимых загрязнений не наблюдается (для таких выбросов предусмотрена достаточных размеров санитарно-защитная зона); 2) внеплощадочные, когда выбрасываемые в атмосферу загрязнения потенциально способны создавать высокие концентрации (порядка ПДК для воздуха населенных пунктов) на территории жилого района. — 615 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ ϭϱ͘ϭ͘ϯ͘ʯ̴̨̨̨̛̬̦̖̦̖̯̥̭̖̬̼̯̬̦̭̪̬̯̥̌̐́̌̌̚ ̨̨̛̪̬̥̼̹̣̖̦̦̭̯̽̀͘ Наибольшее количество загрязняющих атмосферу веществ выбрасывается выхлопными газами автомобилей (табл. 15.2). Таблица 15.2 Состав выхлопных газов бензиновых и дизельных двигателей, % об. Компоненты выхлопных газов Азот Кислород Пары воды Диоксид углерода Оксид углерода Оксиды азота Углеводороды Альдегиды Сажа (г/м3) Бензиновые двигатели Дизельные двигатели 74–77 0,3–8,0 3,0–5,5 5,0–12,0 5,0–10,0 0,0–0,8 0,2–3,0 0,0–0,2 0,0–0,04 74–78 2–18 0,5–4,0 1,0–10,0 0,01–0,5 0,0002–0,5 0,009–0,5 0,001–0,009 0,1–1,1 В настоящее время в мире насчитывается свыше 200 млн автомобилей, выхлопные газы которых содержат примерно 200 веществ, в том числе канцерогенные углеводороды и тетраэтилсвинец. Однако количество основных компонентов значительно меньше. Как видно из табл. 15.2, бензиновые двигатели выбрасывают больше несгоревших углеводородов и продуктов их неполного окисления (оксида углерода и альдегидов), чем дизели. Каждая машина с бензиновым двигателем, прошедшая 15 тыс. км, потребляет 4350 кг кислорода, а выбрасывает 3250 кг диоксида углерода, 530 кг оксида углерода, 93 кг углеводородов, 27 кг оксидов азота. Тепловые электростанции выделяют в атмосферу газы, содержащие оксиды серы и азота, золу, металлы; предприятия черной металлургии — газы, включающие пыль, окси— 616 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ ды серы и металлов. На 1 т передельного чугуна приходится 4,5 кг пыли, 2,7 кг SО2, 0,1–0,5 кг марганца, а также соединения мышьяка, фосфора, сурьмы, свинца, ртути, редких металлов, смолистые вещества. Агломерационные фабрики выбрасывают пыль и диоксид серы (190 кг SO2 на 1 т руды). Мартеновские и конвертерные цехи выделяют пыль. На 1 т мартеновской стали выделяется 300–4000 м3 газов (с концентрацией пыли в среднем 0,5 г/м3), 60 кг СО и 3 кг SO2. Коксохимические цехи загрязняют атмосферу пылью и смесью летучих соединений. Предприятия цветной металлургии выбрасывают запыленные газы, содержащие диоксид серы, фтористые газы и металлы. Из 1 т пыли, выделяемой в атмосферу при плавке медных руд, можно извлечь до 100 кг меди и немного меньше свинца и цинка. Выбросы нефтедобывающей и нефтеперерабатывающей промышленности в атмосферу содержат углеводороды, сероводород и дурнопахнущие газы (стирол, дивинил, толуол, ацетон, изопрен). Заводы промышленности строительных материалов выбрасывают в атмосферу пыль, фториды, диоксиды серы и азота. Предприятия химической промышленности загрязняют атмосферу пылью, содержащей неорганические и органические вещества, и различными газами. Наиболее характерные газовые выбросы некоторых производств приведены в табл. 15.3. ϭϱ͘ϭ͘ϰ͘ʿ̴̨̨̛̛̭̣̖̭̯̬̦̖̦̯̥̭̖̬̼̔̏́̌̐́́̌̚̚͘ Наибольшее загрязнение атмосферного воздуха приходится на долю оксидов углерода, соединений серы и азота, углеводородов промышленной пыли. За год в атмосферу Земли выбрасывается 200 млн. т оксида углерода, более 20 млрд. т диоксида углерода, 150 млн. т диоксида серы, 53 млн. т оксидов азота, свыше 250 млн. т пыли, 120 млн. т золы, более 50 млн. т различных углеводородов. Постоянно увеличивающееся насыщение биосферы тяжелыми металлами — одно из наиболее существенных глобаль— 617 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ Таблица 15.3. Наиболее характерные выбросы в атмосферу некоторых производств химической промышленности (по И.Е. Кузнецову и Т.М. Троицкой, 1979 г.) Производство Азотной кислоты Серной кислоты (нитрозной и контактной) Соляной кислоты Щавелевой кислоты Сульфаминовой кислоты Фосфора и фосфорной кислоты Уксусной кислоты Сложных удобрений Карбамида Аммиачной селитры Суперфосфата Аммиачной воды и жидких углеаммиаков Жидкого хлора Хлорной извести Полихлорвиниловой смолы Тетрахлорэтилена Ацетона Компоненты выбросов в атмосферу NO, NO2, NH3 NO, NO2, SO2, SO3, H2SO4 HCl, Cl2 NO, NO2, C2H2O4 (пыль) NH3, NH(SO3NH4)2, H2SO4 P2O5, H3PO4, HF, Ca5F(PO4) (пыль) CH3CHO, CH3CO2H NO, NO2, NH3, HF, H2SO4, P2O5, HNO3 NH3, CO, (NH2)2CO (пыль) CO, NH3, HNO3, NH4NO3 (пыль) H2SO4, HF, (пыль суперфосфата) NH3 HCl, Cl2, Hg Cl2, CaCl2 (пыль) Hg, HgCl2, NH3 HCl, Cl2 CH3CHO, (CH3)2CO ных последствий научно-технической революции. Подсчитано, что за всю историю человеческого общества выплавлено около 20 млрд. т железа. Его количество, находящееся в сооружениях, машинах, оборудовании и т. д., состав приблизительно 6 млрд. т, следовательно, примерно 14 млрд. т рассеяно в окружающей среде. Другие металлы рассеиваются еще больше. Например, рассеивание ртути и свинца составляет 80–90% их годового производства. При сжигании угля с золой — 618 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ и отходяшими газами некоторых элементов в окружающую среду поступает больше, чем добывается из недр: магния — в 1,5 раза, молибдена — в 3, мышьяка — в 7, урана, титана — в 10, алюминия, йода, кобальта — в 15, ртути — в 50, лития, ванадия, стронция, бериллия, циркония — в сотни раз, галлия, германия — в тысячи раз, иттрия — в десятки тысяч раз. В связи с загрязнением атмосферы возникают проблемы плохой видимости, неприятных запахов и запыленности. Загрязнение воздуха создает угрозу здоровью человека и нормальному функционированию экосистем, выбрасываемые газы действуют на многие организмы. Энергетический баланс планеты меняется вследствие изменения альбедо (отражательная способность) земной поверхности, прозрачности атмосферы и выделения в нее большого количества тепла. Альбедо изменяется при культивировании растительности определенного характера, а также при орошении или осушении поверхности Земли. Запыленность атмосферы оказывает влияние на отражательную способность Земли. Гигиенический стандарт атмосферы допускает суммарную запыленность 1,5 т/га, а в отдельных промышленных районах она достигает 60 т/га. Частицы пыли какое-то время остаются в атмосфере, сокращая доступ ультрафиолетовой радиации и образуя ядра конденсации. Запыленность атмосферы способствует увеличению количества отраженной солнечной радиации и уменьшению количества радиации, достигающей Земли, что приводит к похолоданию климата. В то же время пыль, попадающая на поверхность ледников, поглощает солнечную энергию, способствуя их таянию. Основную роль в изменении прозрачности воздуха играет накопление в атмосфере диоксида углерода. Ежегодно количество СО2 в атмосфере возрастает на 0,4 % и в настоящее время составляет 0,032 %. Считается, что содержание СО2 в атмосфере будет удваиваться каждые 23 года. Диоксид углерода поглощает инфракрасное тепловое излучение, что при определенной концентрации может привести к глобальному повышению температуры. При сжигании топлива выделяется в год 14,2–1016 кДж тепла, которое рассеивается в окружающей среде, изменяя — 619 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ температурный режим планеты. По расчетам, при ежегодном росте производства энергии на 6% в середине XXI в. начнется повышение средней планетарной температуры. Количество озона в атмосфере невелико (2–10–6 % об.), но он играет важную роль в предохранении земной поверхности от солнечной радиации. Разрушение озонового слоя происходит в результате окисления озоном различных веществ, в том числе продуктов сгорания сверхзвуковых самолетов и ракет, и грозит увеличением дозы ультрафиолетовой радиации, облучающей земную поверхность. По некоторым данным разрушение озонового слоя на 50% повлечет за собой увеличение дозы ультрафиолетовой радиации в 10 раз. Под действием солнечной радиации в атмосфере протекают различные реакции, в которых участвуют кислород, азот, озон, оксид азота, пары воды, диоксид углерода. Диоксид азота, поступающий с выхлопными газами в атмосферу, под воздействием ультрафиолетовых лучей преобразуется в оксид азота и атомарный кислород. Затем атомарный кислород вступает в реакцию с кислородом воздуха, образуя озон. При соединении озона с оксидом азота получаются диоксид азота и кислород. Кислород может вступать в реакцию с рядом углеводородов и образует ряд вторичных загрязняющих веществ (формальдегид, альдегиды и пероксиацетиловые нитраты). Все они содействуют формированию фотохимического смога. Количество кислорода ежегодно уменьшается более чем на 10 млрд т. За последние 50 лет его было использовано столько же, сколько за последний миллион лет, т. е. примерно 0,02% от всего его атмосферного запаса. Уменьшение количества кислорода в атмосфере происходит в результате увеличения сжигания ископаемого топлива и уменьшения фотосинтетической активности растений, что связано с загрязнением окружающей среды. Однако если сжечь все запасы ископаемого топлива, то будет использовано лишь ~3 % запасов кислорода. Таким образом, значительного уменьшения кислорода в ближайшее время не предвидится. Однако при развитии экономики для сохранения стабильности состава атмосферы необходимо это учитывать. — 620 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ Наиболее острой является проблема загрязнения атмосферы серосодержащими веществами. Наиболее сильно загрязнено северное полушарие Земли, в атмосфере которого находится до 90% серы антропогенного происхождения. При соответствующих климатических и географических условиях в отдельных районах Земли возможно резкое повышение уровня загрязнения атмосферы серой. Диоксид серы оказывает вредное действие на растения. Поступая внутрь листа при дыхании, SO2 угнетает жизнедеятельность клеток. При этом листья растений сначала покрываются бурыми пятнами, а потом засыхают. В атмосфере SО2 окисляется до SО3. Окисление происходит каталитически под воздействием следов металлов, главным образом марганца. Кроме того, газообразный и растворенный в воде SO2 может окисляться озоном или пероксидом водорода. Соединяясь с водой, SО3 образует серную кислоту, которая с металлами, имеющимися в атмосфере, образует сульфаты. Кислые сульфаты по сравнению с SО2 обладают более выраженным вредным биологическим эффектом при равенстве концентраций. Диоксид серы существует в атмосфере от нескольких часов до нескольких дней в зависимости от влажности и других условий. Количество SО2 и SO42– на разной высоте неодинаково. На небольших высотах SO2 превалирует над SO42–, отношение SО2/SO42– уменьшается с высотой. Переносу SО2 на дальние расстояния и его рассеиванию в верхних слоях тропосферы способствует строительство высоких дымовых труб, что снижает локальное загрязнение атмосферы. В результате такого процесса, рассчитанного на естественное самоочищение воздуха, увеличивается время пребывания серосодержащих соединений в воздушной среде и, следовательно, увеличивается степень их превращения в серную кислоту и сульфаты. Причиной ухудшения качества водных ресурсов служит не только сброс в водоемы бытовых и промышленных отходов, но и выпадение кислых атмосферных осадков. За последние 35 лет кислотность дождевой воды увеличилась в 40 раз — 621 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ (pH снизился с 5,6 до 4,1). Отмечены случаи выпадения осадков с pH ниже 2,1, что соответствует повышению кислотности по сравнению с нормой в 4000 раз. Такая дождевая вода способна реагировать с некоторыми материалами, например мрамором, и наносит вред городским строениям. Соединения, содержащие серу, не только вымываются из атмосферы при выпадении осадков, но и удаляются из нее под действием гравитационных сил в сухом виде. Среднегодовое количество серосодержащих соединений, вымываемых из атмосферы над территорией Европы, равно 1,1 г/м2 и составляет ~ 12.106 т/год. Для сохранения водоемов предложено нейтрализовать пресные воды с повышенной кислотностью путем внесения извести в водоемы. Однако процесс дорог, так как для этого необходимо известковать водоемы каждые 2–3 года. Другая серьезная проблема, связанная с присутствием сульфатов в атмосфере, — образование туманов и снижение прозрачности воздуха за счет взвешенных пылевидных частиц размером 0,1–1 мкм. Атмосферные частицы сульфатов таких размеров наиболее сильно рассеивают свет, ухудшают видимость и оказывают отрицательное воздействие на организм человека. На интенсивность рассеивания света влияет и влажность воздуха. Сульфат и бисульфат аммония — гигроскопичные вещества, поэтому повышение относительной влажности воздуха способствует поглощению влаги этими веществами и усилению рассеивания света, а следовательно, ухудшению прозрачности атмосферы. Выбросы диоксида серы с отходящими газами промышленности наносят большой экономический ущерб, так как безвозвратно теряется огромное количество ценных для народного хозяйства веществ. Учитывая то, что мировые разведанные запасы серы близки к истощению, необходима разработка эффективных методов улавливания и переработки газов, содержащих SО2, на серу, серную кислоту и сульфаты. Наибольшее количество диоксида серы выбрасывается с отходящими газами предприятий теплоэнергетики, черной и цветной металлургии, химической и нефтехимиче— 622 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ ской промышленности, промышленности стройматериалов, транспорта и др. ϭϱ͘ϭ͘ϱ͘ˈ̸̴̡̨̛̛̛̛̥̖̭̖̪̬̖̬̺̖̦̖̺̖̭̯̯̥̭̖̬̖̏̌́̏̏̏̌͘ Химические вещества, попавшие в атмосферу, подвергаются различным превращениям, которые зависят от времени пребывания веществ в атмосфере. Под временем пребывания понимают промежуток между поступлением компонента в атмосферу и удалением (стоком) из нее. Превращения происходят под действием солнечной радиации. Фотоны, излучаемые Солнцем, имеют энергию hv (где ν — частота, связанная с определенным фотоном; h — постоянная Планка, равная 6,62.10–34 Дж-с). В общем случае при поглощении кванта света с частотой ν могут происходить следующие процессы: • образование электронно-возбужденных молекул: A + hν → A * • дезактивация за счет флуоресценции: A * → A + hν • дезактивация (тушение) за счет соударения с другими молекулами A * + Q → A + Q ′ • диссоциация: A * → B + C Для атмосферной фотохимии наибольший интерес представляют явления фотохимической диссоциации электронно-возбужденных молекул А*. Возбужденное состояние весьма нестабильно, так что вслед за появлением А* быстро следует реакция образования продуктов В и С. Один или оба из них могут быть очень активны и приводят к началу цепи реакций, в результате которых возникают нежелательные соединения, в том числе фотохимический смог. Химические превращения в тропосфере и стратосфере инициируются главным образом продуктами фотохимии таких молекул, как O3, О2, Н2О, N2О и NО2. Важнейшим компонентом, определяющим химию стратосферы, является озон. Образование атомарного кислорода в атмосфере (выше 80 км) происходит по следующей реакции: O2 + hν → 2O — 623 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ Атомарный кислород участвует в реакциях возникновения О2 и О3. Озон получается по уравнению: O + O2 + M → O3 + M где М — третье вещество, принимающее избыток энергии. Озон подвергается фотохимической диссоциации O3 + hν → O2 + O В атмосфере присутствуют пять основных азотсодержащих газов: N2, NH3, NO, NО2, N2O. В конденсированной фазе азот присутствует в форме иона аммония (NH4+) и нитратного иона (NОз–). Оксиды азота антропогенного происхождения в большинстве случаев попадают в атмосферу в виде NO. Затем происходят следующие реакции: 2NO + O2 → 2NO2 O + O2 + M → O3 + M NO2 + hν → NO + O O3 + NO → NO2 + O2 Возможны и другие многочисленные реакции в атмосфере с участием различных веществ. Прогнозировать химические реакции, протекающие в атмосфере возможно, применяя методы классической термодинамики — известный метод минимизации энергии Гиббса или стандартный метод констант равновесия. Например, для веществ, содержащих азот и кислород можно записать следующие реакции: O + NO2 → NO + O2 O + NO2 + M → NO3 + M O + NO + M → NO2 + M NO3 + NO → 2NO2 NO2 + O3 → NO3 + O2 NO3 + NO2 + M → N2O5 + M — 624 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ Цикл соединений азота в тропосфере дополняется образованием азотной кислоты: 4NO2 + 2H2O + O2 → 4HNO3 . Диоксид азота может гидролизоваться также в газовой фазе: 3NO2 + H2O ↔ 2HNO3 + NO Выделяющаяся по этим реакциям азотная кислота далее может реагировать с ионами металлов, образуя нитраты. Атомарный кислород и озон способны вступать в соединения с различными органическими веществами, в результате чего получаются органические и неорганические свободные радикалы. Для олефиновых углеводородов возможна следующая подобная реакция: O3 + RCH = CHR → RCHO + RO* + HCO* где RO* и НСО* — свободные радикалы. Полученный альдегид RCHO может подвергаться фотодиссоциации по реакции: RCHO + hν → R * + HCO* Кроме альдегидов, фотохимически активны также кетоны, пероксиды и ацилнитраты, которые при поглощении солнечной радиации также образуют свободные радикалы. Свободные радикалы с молекулярным кислородом образуют пероксидные радикалы (ROO*), т.е. R * + O2 → ROO* ϭϱ͘ϭ͘ϲ͘ʿ̴̨̨̛̖̬̖̦̭̬̦̖̦̜̯̥̭̖̬̖̌̐́̏̌̚̚͘ Количество солнечной энергии, поступающей на Землю и отражаемой от нее в атмосферу, в различных широтах неодинаково. В результате этого атмосфера в разных районах земного шара нагревается неравномерно. Особенно большие различия температуры у поверхности наблюдаются между полярными и экваториальными областями. Эта неравномерность служит главной причиной общей циркуляции атмосферы, представляющей собой сложную систему воздушных течений над Землей. Благодаря такой циркуляции усредняется состав основных компонентов воздуха, а воздушные течения переносят водяной — 625 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ пар океанов в континентальные районы, а также загрязнения. Кроме крупномасштабных воздушных течений в нижних слоях атмосферы возникают многочисленные местные циркуляции, связанные с особенностями нагревания атмосферы в отдельных районах. Вследствие образования различных течений в атмосфере перемешиваются большие массы воздуха и на значительные расстояния перемешиваются соединения, выделяемые теми или иными источниками на поверхности земли. Движение воздушных масс в атмосфере имеет турбулентный характер. Наряду со скоростью ветра, которую можно принять в первом приближении горизонтальной, возникают турбулентные пульсации в направлении осей х, у, z (соответственно и, v, w). Эти пульсации вместе с молекулярной диффузией перемешивают токсичные примеси с атмосферным воздухом. Принимается, что ось х совпадает с направлением ветра, ось у — перпендикулярна к направлению ветра и параллельна плоскости Земли, а ось z — перпендикулярна поверхности Земли. Изменение концентраций загрязнений в разных направлениях определяется уравнением турбулентной диффузии: dc dc dy dc d dc d dc d dc +U +V +W = + + − α c (15.1) K K K dz dy dx dz dx x dx dy y dy dz z dz где с — концентрация загрязнений; τ — время; αс — коэффициент изменения концентрации за счет превращений; Кх, Kv, Кz — коэффициенты турбулентной диффузии в направлении соответствующих осей. При равенстве коэффициентов Кх = Кy = Кz наблюдается изотропная турбулентная диффузия. Для решения уравнения турбулентной диффузии и расчета концентрации загрязнений на разном расстоянии от источников выбросов определяют коэффициенты К и вводят ряд ограничений. Например, загрязнители выбрасываются из непрерывного точечного источника; процесс квазистационарен, т. е. dc/dW = 0; направление основного переноса, обусловленного ветром, совпадает с осью х; скорость ветра U предполагается постоянной в любой точке в системе координат X, Y, Z; перенос загрязнителей по ветру — 626 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ в направлении оси x преобладает над диффузией вдоль направления ветра. ϭϱ͘ϭ͘ϳ͘ʺ̸̨̨̨̡̛̛̖̯̖̬̣̖̭̖̪̬̥̖̯̬̼̐̌̌ ̵̸̨̛̛̛̪̖̬̖̦̭̪̬̥̖̭̖̜̱̖̯̌͘ Климат нашей планеты определяет солнечная энергия. В атмосфере солнечные лучи рассеиваются, но поглощаются слабо (около 10%). Еще 30–35% лучей отражаются облаками. Оставшиеся 55–60% солнечной радиации, попадая на воду и сушу, частично отражаются и частично расходуются на нагрев поверхности, испарение влаги, таяние снега и льда. Свойства атмосферы способствуют тому, что она почти непрозрачна для длинноволновой радиации, излучаемой Землей, благодаря водяному пару и облачности, в меньшей степени изза углекислого газа, метана и озона. В то же время атмосфера сама испускает длинноволновую радиацию. Однако поток излучения, уходящий в космос, существенно меньше потока, берущего начало от Земли. В связи с этим атмосфера обладает своеобразной «мембранной» способностью пропускать больше теплоты вниз, чем обратно вверх, и удерживать теплоту — так называемый парниковый эффект. При отсутствии этого эффекта температура у поверхности планеты в среднем равнялась бы –20 °С, что сделало бы жизнь на Земле невозможной. В результате парникового эффекта атмосфера нагревается снизу. В тропиках Земля получает теплоту, а в высоких широтах в основном теряет. Перенос энергии из низких широт в высокие осуществляют течения в атмосфере и океане. Нагретый воздух расширяется. Возникает различие в весе и, соответственно, давлении. Воздух начинает двигаться от теплых областей к холодным. В умеренных широтах в атмосфере появляются вихри с областью низкого давления в центре (циклоны) и с областью высокого давления (антициклоны) и достигают размеров от нескольких сот до нескольких тысяч километров в поперечнике. В северном полушарии циклоны закручены против часовой стрелки и движутся с запада на восток. В антициклоне воздушная спираль раскручивается по часовой стрелке, воздух не под— 627 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ нимается, а опускается; облаков мало» осадков почти нет, ветер слабый или умеренный, а иногда стоит полный штиль. Только нижняя часть атмосферы высотой 10–12 км (тропосфера) оказывает влияние на погоду. В тропосфере часто образуются вертикальные течения, скорость которых невелика и редко превышает 0,07 м/с (0,01–1,0 м/с). В тропосфере температура падает при увеличении высоты. Изменение температуры на каждые 100 м высоты называется температурным градиентом, который в среднем составляет 0,5–0,6 °С. С метеорологических позиций состояние атмосферы при неизменной температуре по высоте называется изотермией. Такое изменение состояния (температуры, давления и плотности), происходящее без теплообмена с окружающей средой, называется адиабатическим, а, следовательно, связанный с этим изменением градиент температуры — адиабатическим градиентом, который численно равен уменьшению температуры на 1°С на 100 м высоты. Если температура уменьшается с высотой на большую величину, то градиент температуры будет сверхадиабатическим. Примеси могут распространяться в атмосфере посредством конвекции. Конвективный перенос загрязняющих веществ в атмосфере происходит вместе с движением воздушных масс и вызывается в первую очередь ветром. Общеизвестно, что движущей силой ветра является градиент давления. Свой вклад вносит и вращение Земли. При этом возникает «ускорение Кориолиса», или отклоняющая сила вращения Земли. Ветры подразделяются на виды: геострофический, агеострофический, антитриптический, градиентный, изаллобарический, термический. Различные виды ветра взаимодействуют между собой. В отдельных слоях возникает напряжение сдвига, что способствует перемешиванию их между собой. При выбросе загрязняющих веществ из горячих источников (например, из дымовой трубы котельной, факел выброса которой бывает хорошо виден в холодный период года), когда температура газовоздушной смеси существенно выше температуры окружающего воздуха, происходит естественная конвек— 628 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ ция. В связи с тем, что плотность выбрасываемой смеси меньше плотности окружающего воздуха, возникает сила Архимеда и факел выброса «всплывает». Атмосферную конвекцию, которую также относят к естественной, вызывает прогрев воздушных масс и поверхности земли в дневное время и охлаждение их в ночное. Из-за того что процесс перемешивания происходит неодинаково и неравномерно, возникают восходящие и нисходящие воздушные потоки. При атмосферной конвекции температура воздуха вблизи поверхности земли меняется в зависимости от свойств подстилающей поверхности. Так, над сухой дорогой температура может быть выше на 5°С и более, чем у близлежащего луга. Комплексный учет скорости ветра, степени инсоляции и времени суток в жизнедеятельном слое атмосферы (Н< 100 м) характеризуется его устойчивостью. Согласно классификации Пэсквилла, выделяют шесть классов устойчивости. • класс 1 — сильная неустойчивость; • класс 2 — умеренная неустойчивость; • класс 3 — слабая неустойчивость; • класс 4 — равновесное (безразличное) состояние; • класс 5 — слабая устойчивость; • класс 6 — умеренная устойчивость. Данная классификация может быть продолжена, при этом уточнение будет происходить с учетом высоты солнца, облачности, наличия снежного покрова и т. д. Так, можно выделить класс 7 — очень сильная устойчивость. Классификация устойчивости приземного слоя в зависимости от скорости ветра, степени инсоляции и времени суток приведена в табл. 15.4. Существует диффузионный механизм переноса примесей. Факел выброса перемещается ветром, который в большинстве случаев имеет турбулентный характер. Поэтому говорят о турбулентной диффузии. Турбулентность также порождает различного размера вихри, которые и приводят к рассеиванию примесей. Для свободной атмосферы, когда нет ограничивающих поверхностей, например, как в трубе, феноменоло— 629 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ Таблица 15.4. Классы устойчивости по Пэсквиллу Скорость ветра на высоте 10 м, м/с <2 2–3 3–5 <5–6 >6 Степень инсоляции днем сильная умеренная слабая 1 1–2 2 3 3 1–2 2 2–3 3–4 4 2 3 3 4 4 Облачность ночью, баллы 10 (об<4 щая) или >5 (ниж- (нижняя) няя) – – 5 6 4 5 4 4 4 4 гический и статистический подходы малоприменимы. В этом смысле теория диффузии подвергается критике. Итак, различные виды распространения примесей в атмосфере можно условно соотнести с помощью следующей упрощенной модели. Если бы ветер представлял собой ламинарный поток, параллельный поверхности земли, устье источника было ориентировано не вверх, а вбок, по направлению ветра, то (в отсутствии диффузии при изотермии и равенстве температур выброса и окружающей атмосферы) факел выброса являлся бы струей с диаметром устья, равным устью источника загрязнения атмосферы. Концентрация примесей в струе зависела бы от соотношения скоростей ветра и выброса в устье источника загрязнения атмосферы. Диффузия обеспечивает расширение факела выброса, а турбулентная диффузия усиливает этот процесс. Разность между температурами выброса и окружающего воздуха, а также атмосферная конвекция придают факелу выброса вертикальное перемещение. Большое влияние на рассеивание оказывает инверсия температуры в атмосфере, представляющая собой метеорологическое состояние, при котором происходит повышение температуры воздуха с высотой, вместо обычного для тропосферы понижения. Нормальное понижение температуры воздуха с высотой составляет 0,5–0,6°С на 100 м. Инверсию темпе— 630 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ ратуры можно периодически наблюдать на протяжении всего года. Приземные инверсии температуры связаны с излучением земной поверхности. В теплое время года их можно наблюдать лишь в ясные тихие ночи в отсутствие облачности. Мощность таких инверсий невелика, всего несколько десятков метров, а величина составляет несколько градусов. В холодное время года приземные инверсии температуры видны как ночью, так и днем. Их мощность может достигать нескольких сот метров, а величина составлять 10–15°С и более. Особенно интенсивны инверсии зимой при наличии снежного покрова. В этом случае они могут продолжаться 5–7 сут. Хорошо развитая инверсия действует как преграда для восходящих течений, т. к. они задерживаются устойчивым слоем более теплого воздуха. Особенно ухудшает рассеивание такое аномальное состояние, как приподнятая инверсия непосредственно над источником с холодным выбросом. В этом случае концентрации примесей могут во много раз превышать концентрации при обычных условиях рассеивания. Аномальными метеоусловиями также являются туманы, при которых значительно возрастает опасность загрязнения воздуха. Их сопровождают штили и инверсии. Примеси частично поглощаются водяными парами, что иногда приводит к образованию новых более вредных веществ. Осаждение влаги на аэрозольных частицах увеличивает их размеры и скорость гравитационного смещения к земной поверхности. Туманы провоцируют образование смогов. метеорологических аспектов загрязнения атмосферы, закономерностей распространения атмосферных примесей и особенностей их пространственновременного распределения проводит головная организация в этой области — Главная геофизическая обсерватория им. А. И. Воейкова в Санкт-Петербурге (ГГО). Данные исследования являются основой для объективной оценки состояния и тенденции изменений загрязнения воздушного бассейна, а также разработки мероприятий по обеспечению чистоты атмосферы. Без них невозможно определение репрезентативных мест и времени наблюдений в целях создания системы контроля чистоты воздуха. Характеристики загрязнения атмосферы — 631 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ в настоящее время все в большей степени рассматривают как метеорологические величины. Задача рассеивания выбросов загрязняющих веществ в атмосфере связана с краткосрочным прогнозом условий (большей частью в пределах суток), при которых могут достигаться высокие концентрации примесей в приземном слое атмосферы. Для прогнозирования используют численные, статистические и синоптические методы. Результаты теоретического и экспериментального изучения закономерностей распространения примесей от источников загрязнения атмосферы являются основой для развития методов прогноза загрязнения воздуха. Первое направление включает разработку теории атмосферной диффузии на основе математического описания распространения примесей с помощью решения уравнения турбулентной диффузии. Другое направление связано в основном с эмпирико-статистическим анализом распространения загрязняющих веществ в атмосфере и использованием для этой цели интерполяционных моделей большей частью гауссовского типа. Из уравнения атмосферной диффузии следует, что при фиксированных параметрах источника при α = 0 турбулентным обменом и скоростью ветра определяется изменение концентрации примеси в атмосфере. При прогнозе загрязнения воздуха основной интерес представляет жизнедеятельный слой атмосферы толщиной 50–100 м. Многочисленными исследованиями установлено, что данный слой имеет в качестве одной из главных характеристик сохранение в нем по высоте вертикальных потоков теплоты и количества движения. Изменение касательного напряжения в слое происходит не более чем на 10–20%. Вместе с тем для него свойственно значительное изменение с высотой скорости ветра, температуры и турбулентности. При этом весьма четко проявляется влияние устойчивости атмосферы, непосредственно связанное с температурной стратификацией. Различают равновесную (безразличную) стратификацию, когда вертикальный поток теплоты равен нулю, а изменение температуры воздуха с высотой происходит по адиабатическому закону. Такая стратификация ха— 632 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ рактерна и при изотермии, когда температура мало меняется с высотой. Неравновесная стратификация характеризуется температурными градиентами, отличными от нуля. В настоящее время определяют коэффициенты обмена kг и kу в зависимости от скорости ветра и распределения температуры по высоте. При этом стало возможным использование данных наблюдений на метеостанциях за температурой воздуха на двух уровнях в жизнедеятельном слое атмосферы. Для использования данных наблюдений на метеорологической сети и установления их качественной оценки применяют также классификацию устойчивости приземного слоя в зависимости от скорости ветра, степени инсоляции и времени суток (см. табл.14.4). Используя зависимости k7 и kу от скорости ветра и принимая граничные условия для точечного источника с координатами x = 0, y = 0, z = Н: (15.2) uc = Mδ ( y ) δ ( z − H ) ∂c = 0 ïðè z = 0 , ∂z уравнение атмосферной диффузии решают аналитическим путем. Последнее условие показывает, что примесь уносит снова в атмосферу с турбулентными вихрями и она не скапливается у поверхности земли. Большое значение имеет вопрос о влиянии продолжительности интервала времени с относящимися к нему концентрациями, полученными в результате решения уравнения диффузии, и времени отбора проб при экспериментальном определении концентрации. Это существенно и потому, что на результаты воздействия загрязнения атмосферы на окружающую среду и живые организмы оказывают влияние не только концентрации примесей, но и продолжительность воздействия. На сегодняшний день были даны решения уравнения атмосферной диффузии, где учтены следующие факторы, влияющие на рассеивание выбросов: • начальный подъем примеси. Выбросы газовоздушной смеси от дымовых и вентиляционных труб могут иметь зна- при х = 0; c→0 при y → ∞ ; c→0 при z → ∞ ; kz — 633 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ чительную скорость в устье. В сочетании со слабым ветром источник как будто приподнят над трубой. Для решения вводят условный источник с эффективной высотой и сводят задачу к определению высоты подъема струи в зависимости от скорости ветра, перегрева примеси и т. д. В системах вентиляции устраивают факельные выбросы; • аномальное распределение скорости ветра с высотой; • диффузия примеси при штиле; • приподнятая инверсия температуры; • влияние стратификации на начальный подъем примеси; • туманы и смоги; • рельеф. Решения уравнения атмосферной диффузии, в том числе с учетом перечисленных выше факторов, носят оценочный характер, т.к. полученные «формулы позволяют только как бы предвычислить уровень загрязнения». На практике обычно используют методику ОНД-86, которая создана на основе фундаментального закона сохранения массы, применяя численные и статистические методы расчета. ϭϱ͘ϭ͘ϴ͘ʺ̨̡̛̖̯̔̌ʽʻʪͲϴϲ͘ Основным нормативным документом по расчету выбросов в атмосферу, при проектировании предприятий, а также при установлении допустимого уровня выбросов. реконструируемых и действующих предприятий является ОНД-86[13]. Данная методика предназначена для расчета приземных концентраций на высоте 2м над поверхностью земли, а также расчета вертикального распределения концентраций. Степень опасности загрязнения атмосферного воздуха характеризуется максимальным рассчитанным значением концентрации, соответствующим неблагоприятным метеорологическим условиям, в том числе опасной скорости ветра. Данные нормы не учитывают в расчете концентраций на дальних (более 100 км) расстояниях от источника выброса. В случае одновременного и совместного присутствия в атмосферном воздухе n веществ, обладающих в соответствии с пе— 634 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ речнем и кодов веществ, загрязняющих атмосферный воздух, суммацией вредного действия, для каждой группы указанных веществ однонаправленного вредного действия рассчитывают безразмерную суммарную концентрацию q по формуле cn c1 c2 (15.3) q= + +"+ ÏÄÊ 1 ÏÄÊ 2 ÏÄÊ n где c1 , c2 ,…, cn - расчетные концентрации вредных веществ в атмосферном воздухе в одной и той же точке местности, мг/м3; ПДК1, ПДК2,…, ПДКn — соответствующие максимально разовые предельно допустимые концентрации вредных веществ, претерпевающих полностью или частично химические превращения (трансформацию) в более вредные вещества, производят по каждому исходному и образующемуся веществу отдельно. При этом мощность источников для каждого вещества устанавливают с учетом максимально возможной трансформации исходных веществ в более токсичные. Методика ОНД-86 позволяет проводить расчет загрязнения приземного слоя атмосферы выбросами одиночного точечного источника и группы источников при опасной скорости ветра и скорости ветра, отличающейся от опасной, расчет максимальной приземной концентрации, расчет приземной концентрации по оси и перпендикуляру к оси факела выброса, расчет загрязнения атмосферы на различных высотах над уровнем земли, расчет загрязнения атмосферы выбросами от группы источников. Методика также нормирует учет фоновых концентрация при расчетах загрязнения атмосферы и учет фонового загрязнения при нормировании выбросов. Методика ОНД-86 позволяет также проводить учет трансформации вредных веществ в атмосфере и нормирование предельно допустимых выбросов от различных источников. Основным документом по установлению предельно допустимых выбросов (ПДВ) также является ОНД — 86. При установлении ПДВ концентрация c каждого вредного вещества в приземном слое атмосферы не должна превышать максимально разовой ПДК данного вещества в атмосферном воздухе, утвержденной Минздравом России: c ≤ ÏÄÊ — 635 — (15.4) ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ При наличии в атмосфере n веществ с эффектом суммации вредного воздействия их безразмерная суммарная концентрация q, определенная по формуле (15.3), не должна превышать единицы: q ≤1 (15.5) Для веществ со среднесуточными предельно допустимыми концентрациями ПДК, мг/м3, для которых используют приближенное соотношение между максимальными значениями разовых и среднегодовых концентраций, должно быть установлено условие 0,1c ≤ ÏÄÊ (15.6) При отсутствии нормативов ПДК вместо них используют ориентировочно безопасные уровни загрязнения воздуха (ОБУВ). Нормы концентрации вредных веществ в атмосферном воздухе для растительности и животного мира, утвержденные в установленном порядке, принимают при расчетах только в случаях, когда они более жесткие, чем у ПДК, утвержденных Минздравом России. При наличии фонового загрязнения атмосферы в формулах (15.4), (15.6) вместо с принимают c + cô (где ñô — фоновая концентрация вредного вещества). Для веществ с эффектом суммации вредного воздействия учет фоновых концентраций в формуле (15.4) производят согласно п.п. 2.6 и 2.7.1 ОНД — 86. ( ) ϭϱ͘ϭ͘ϵ͘ʤ̵̶̨̛̛̛̛̛̦̣̭̱̺̖̭̯̱̺̭̬̖̭̯̯̥̯̌̏̀̔̏̌̏̌̌̚̚ ̴̡̨̨̨̨̛̛̛̛̭̖̬̖̣̺̯̼̱̹̦̜̭̬̖̼̏̾̐̌̏̔̔̚̚͘ На отечественном рынке программного обеспечения присутствует ряд готовых решений для автоматизации деятельности специалистов в сфере экологии, природопользования и охраны окружающей среды. Программные продукты, предназначенные для целей мониторинга состояния атмосферного воздуха, как правило, реализуют функции расчета загрязнения атмосферы в соответствии с «Методикой расчета концентраций в атмосферном воздухе вредных веществ, содержащихся в выбросах промышленных предприятий (ОНД-86)», — 636 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠ǪǯǯǬǀǫǪǃǀǎÐǫǊƻ͠ǮǯǮǫÐƿǪƼ͠ǎƿǃǎǍǈǀǲÐǫǬǈǬǯǰǫÐǫÐǪǰǂǮǯǄǬ͠Ǭ построение санитарно-защитных зон предприятий и определение нормативов предельно допустимых выбросов (ПДВ). Это: • Унифицированный программный комплекс расчета загрязнения атмосферы «ПРИЗМА». Разработчик — НПП «Логус». • Программа «ПРИЗМА» — унифицированная программа расчета загрязнения атмосферы; реализует методику ОНД86; обеспечивает расчет полей концентрации загрязняющих веществ для отдельного предприятия и для города (региона) в целом; • Унифицированная программа расчета загрязнения атмосферы УПРЗА «Эколог». Разработчик — фирма «Интеграл». • УПРЗА «Эколог» предназначена для расчета приземных концентраций загрязняющих веществ в атмосфере в соответствии с методикой ОНД-86. • Система «ЭКОЛОГ-ГОРОД». Разработчик — научно-производственная фирма «ЛОГОС». • Система предназначена для автоматизации деятельности экологических служб и администраций городов (регионов) и проведения сводных расчетов загрязнения атмосферы. Следует отметить, что существуют и другие готовые решения в рассматриваемой области, например, автоматизированная система «ЭКОЛОГ-ГОРОД» (компания Проект Мастер); «АЗС-Эколог», «Котельные», «Котельные-ТЭС», «Магистраль-город», «Сжигание ТБО» (компания АСКОН); экологический программный комплекс (ЭПК) РОСА (ЛиДа инжиниринг); «АЗС-Эколог», «Факел 2.0», «РВУ-Эколог 3.2», «2-ТП (ОБЗОР)-Воздух 2.1», «Лаборатории 1.0» («Интеграл») и др. Программные продукты для автоматизации деятельности специалистов-экологов обычно предназначены для расчета загрязнения атмосферы по методике ОНД-86, построения СЗЗ предприятий, определения нормативов ПДВ; некоторые из них позволяют строить карты распределения концентраций загрязняющих веществ на рассматриваемой территории и определять вклады отдельных источников в общий уровень загрязнения, Эти программы предназначены для обработки — 637 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ данных о состоянии воздуха и принятия решений на основе получаемых результатов. ϭϱ͘Ϯ͘ˇ̸̡̨̨̨̛̛̛̛̖̭̖̭̦̼̬̭̪̬̭̯̬̦̖̦̏̌̌́̚ ̨̨̛̪̬̥̖̭̖̜̦̜̭̬̖̖̏̏̔̔͘ В последнее время загрязнение природных вод приобрело глобальный характер, что в значительной степени объясняется чрезвычайным многообразием источников загрязнения. Еще относительно недавно считалось, что основным источником загрязнения вод является промышленность. Это обусловливало основной поток информации по оценке воздействия промышленных сточных вод на водные ресурсы, распространению струй в водоемах и водотоках, вопросам разбавления и т.п. При этом в качестве основных мер борьбы рассматривались вопросы перевода промышленности на оборотное водоснабжение и безводную технологию. В целом ряде случаев это было осуществлено, но угроза загрязнения природных вод не уменьшилась. Зачастую ни промышленные, ни коммунально-бытовые хозяйства не представляют реальную картину распространения вредных примесей в воде. Прогнозирование массового переноса загрязняющих веществ — важная и актуальная задача, решение которой позволит принимать адекватные решения о мерах и силах, требуемых для реабилитации водной среды и прилегающих территорий. Для того, чтобы разобраться каким образом можно смоделировать поведение примеси в воде необходимо понимать, какие источники загрязнения существуют, какие методики позволяют определить качественный и количественный состав воды в различных точках водоема. ϭϱ͘Ϯ͘ϭ͘ʰ̸̵̨̡̨̨̛̛̛̛̭̯̦̬̦̖̦̪̬̬̦̼̌̐́́̔̏̔̚̚͘ Хозяйственные и бытовые стоки наибольшее воздействие оказывают на водные ресурсы рек. Это влияние необходимо рассматривать в совокупности с воздействием других источни— 638 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠Ǫǯ͟͠Ǯǯǰ͠ǪǃǬǃǀǎÐ͟͠ǀǂǬǯǬ֬ÐǫÐǫǮƽǃǮ֬Ðǯ͠ǬƽǬ ков поступления загрязняющих веществ, например, склонового стока, атмосферных осадков и пр. Загрязнение природных вод начинается с момента поступления соответствующих веществ в водный объект, т.е. начальный этап процесса загрязнения в значительной степени зависит не только от свойств загрязняющих веществ, но и от пространственно-временных характеристик источника загрязнения. При этом важная роль принадлежит не только самому веществу, но и типу первоначального воздействия на водоем, т.е. от способа поступления стоков. Вопросы контроля, охраны и управления качеством воды также в значительной мере зависят от пространственно- временных типов источников, так как борьба с одним и тем же видом загрязняющих веществ зависит от путей его поступления и изменчивости во времени. По временному признаку поступление загрязняющих веществ может быть мгновенным, которое возникает в результате залпового сброса, например при авариях танкеров и других судов, авариях на очистных сооружениях, а также во время сильных ливней, резко увеличивающих количество загрязненных вод склонового стока, и непрерывным, под которым подразумевается постоянное (или изменяющееся во времени) поступление веществ, нежелательных с точки зрения водопотребителей или отрицательно воздействующих на экологию водоемов. Сочетания класса загрязняющих веществ с временным характером поступления могут вызывать кратковременное или долговременное загрязнение, обладающее специфическими свойствами, определяющими его дальнейшую судьбу. Это относится прежде всего к способам борьбы, так как опасность загрязнения тесно связана со степенью консервативности и временем поступления вещества. По пространственному признаку источники загрязнения подразделяются на: • Точечные — различные виды промышленных и бытовых стоков, а также некоторые сельскохозяйственные загрязнения (в основном связанные с животноводством и обслуживанием сельского хозяйства), поступающие через коллекторы — 639 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ сточных вод и проходящие, как правило, предварительную очистку. • Неточечные (как правило, линейные), иногда называемые распределенными, склоновый сток с сельскохозяйственных угодий, урбанизированных территорий (ливневый сток) и другие, главной особенностью которых является практически полное отсутствие очистки (за исключением собственных процессов разложения или комплексообразования веществ перед поступлением в водоемы или водотоки). • Площадные (пространственные) — главным образом выпадения с атмосферными осадками вследствие загрязнения атмосферы промышленными выбросами. Чрезвычайно важным типом источников загрязнения, который требует самостоятельного выделения, являются вторичные источники загрязнения — донные отложения, фильтрации из подземных горизонтов, а также косвенные причины (химические реакции между компонентами естественной водной среды и антропогенным поступлением вещества). Кроме перечисленных типов источников загрязнения вод антропогенного происхождения, можно также выделить и естественные источники загрязнения (вулканические породы, засоленные почвы и т.д.). Выделенные типы источников загрязнения обладают определенными специфическими особенностями воздействия на водную среду. Одно и то же вещество, поступающее из источников разных типов, по-разному взаимодействует с окружающей средой. Указанные типы источников (с учетом их пространственных и временных сочетаний) охватывают все виды стоков, определяемых хозяйственным фактором. Такой подход к вопросу об источниках загрязнения позволяет наиболее точно охарактеризовать тип воздействия на водный объект, а также более полно определить возможные последствия поступления вещества. Нетрудно убедиться, что распространение одного и того же вещества, поступившего в водоем из точечного и неточечного источников, будет в значительной мере различаться. С точки зрения потенциальной опасности загрязнения водоема или водотока и поведения загрязняющего вещества — 640 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠Ǫǯ͟͠Ǯǯǰ͠ǪǃǬǃǀǎÐ͟͠ǀǂǬǯǬ֬ÐǫÐǫǮƽǃǮ֬Ðǯ͠ǬƽǬ в зависимости от типа источника необходимо принимать во внимание характеристику зоны водного объекта по отношению к источнику. К таким характеристикам относятся гидродинамические, гидрохимические и гидробиологические особенности ближней водной акватории, которые, определяя начальный этап разбавления и трансформации вещества, можно в некотором смысле рассматривать как самостоятельные «источники» поступления загрязняющих веществ в водный объект в целом. С гидродинамической точки зрения эта область для точечных источников загрязнения определяется в первую очередь гидравлическими характеристиками струи сточных вод в сочетании с динамической активностью водной массы. Для остальных типов источников загрязнения эта начальная зона полностью определяется параметрами течений и интенсивностью перемешивания. Особое значение этот фактор имеет для вторичного загрязнения, связанного с поступлением вещества из донных отложений вследствие вертикального турбулентного обмена. Уровневый режим водотока определит интенсивность поступления подземного стока, а с ним и загрязняющих веществ. Динамика состояния природных вод обусловливает процессы переноса, перемешивания и концентрирования загрязняющих веществ, поступающих от различных источников. Специфической особенностью точечных источников загрязнения является локализованное поступление промышленных или коммунально-бытовых сточных вод через подводные или поверхностные коллекторы. К точечным источникам можно также отнести устья ручьев, рек и каналов по отношению к рекам, озерам или морям, принимающим сток загрязненных водотоков. Отличительной чертой поступления загрязняющих веществ через коллекторы сточных вод является потенциальная возможность выбора положения сбросных устройств, определяемого путем анализа гидрофизических, гидрохимических и гидробиологических закономерностей водного объекта. Обычно используются подводные сбросы сточных вод. Первые глубинные подводные сбросы сточных вод в море осуществля— 641 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ лись на побережье Калифорнии (США), затем в Великобритании, Нидерландах и Дании. Для определения возможности выпуска сточных вод и выбора места расположения глубинных подводных водосборов необходимо учитывать особенности морского дна (глубины, геологические и морфологические характеристики, условия осадконакопления), метеорологические условия прибрежной зоны, гидрологические особенности (температуру воды, прозрачность, соленость, мутность, плотность), динамику моря (течения, перемешивание), химические, биологические и бактериологические характеристики моря. Основными процессами, определяющими выбор положения сбросных коллекторов, являются: разбавление и смешение сточных вод, распространение под действием течений, отмирание бактерий, седиментация взвешенных веществ и биохимическое окисление загрязняющих веществ под воздействием микроорганизмов. Для точечных источников наиболее характерными проблемами следует считать: технические, экономические, санитарные и экологические аспекты, развитие технологий производства и очистки сточных вод, а также отмеченные физические, химические и биологические процессы, протекающие в водных массах принимающего стоки водоема или водотока. Фундаментальной проблемой загрязнения от точечных источников является вопрос о положении сбросных устройств и интенсивности разбавления стоков под действием процессов переноса и турбулентной диффузии с учетом плотности сточных вод, расхода воды в водотоке, объема стоков и т.п. Исследования в этой области связаны с изучением гидродинамических характеристик потока реки или водоема. Влияние точки сброса сточных вод на дисперсию загрязняющих веществ в мелководных реках или эстуариях (пойма реки) сказывается на концентрации вещества вниз по течению от места его поступления в водоток и непосредственно зависит от «облака» загрязнения, размеры которого в основном определяются продольной турбулентной диффузией. В непо— 642 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠Ǫǯ͟͠Ǯǯǰ͠ǪǃǬǃǀǎÐ͟͠ǀǂǬǯǬ֬ÐǫÐǫǮƽǃǮ֬Ðǯ͠ǬƽǬ средственной близости от места сброса сточных вод дисперсия и скорость перемещения облака загрязнения в значительной мере зависят от положения сбросного устройства в поперечном сечении потока. Так как сдвиговая дисперсия максимальна при больших градиентах скорости, что наблюдается на удалении от стержня реки. Сегодня важное значение имеют степень очистки сбрасываемых вод, условия их разбавления, эффективность совместного сочетания очистки и разбавления, оценка стоимости с целью достижения требуемых норм с меньшими экономическими затратами и достаточной степенью надежности. При рассмотрении механизмов разбавления сбрасываемых вод основные факторы, способствующие изменению начальной концентрации в точке сброса, следующие: условия окружающей среды (течение, температура, соленость, ветер, приливы и отливы и т.д.); случайные дополнительные загрязняющие вещества; химические и биологические процессы в среде. Наиболее важными механизмами разбавления являются начальное разбавление и горизонтальная дисперсия. Сегодня важное значение имеют степень очистки сбрасываемых вод, условия их разбавления, эффективность совместного сочетания очистки и разбавления, оценка стоимости с целью достижения требуемых норм с меньшими экономическими затратами и достаточной степенью надежности. При рассмотрении механизмов разбавления сбрасываемых вод основные факторы, способствующие изменению начальной концентрации в точке сброса, следующие: условия окружающей среды (течение, температура, соленость, ветер, приливы и отливы и т.д.); случайные дополнительные загрязняющие вещества; химические и биологические процессы в среде. Наиболее важными механизмами разбавления являются начальное разбавление и горизонтальная дисперсия. Основные типы загрязняющих веществ, поступающих от различных отраслей промышленности представлены в табл.15.5. — 643 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ Таблица 15.5. Основные типы загрязняющих вещеста, поступающих от различных отраслей промышленности. Промышленность Загрязняющее вещество Лесная Растворенные органические вещества (углеводороды, органические кислоты, спирты, лигнин), органические и неорганические частицы, биогенные вещества Добывающая Тяжелые металлы (Fe,Zn, Cu), нефть, «хвосты» Металлургическая (железо, сталь) Тяжелые металлы (Zn, Pb, As, Ni, Cr), взвешенные вещества, нефть, цианидыб фенолы Фармакологическая Различные химикаты в зависимости от процессов и выпускаемой продукции Удобрений Фосфор, азот, тяжелые металлы, фтор Нефтехимическая Нефть, нефтепродукты, различные токсичные вещества (винилхлориды, поливинилхлориды) Текстильная Различные химикалии, органические вещества Кожевенная Сульфиды, известь, хром, красители, органические вещества Электрохимическая Тяжелые металлы (Zn, Ni, Cu, Pb, Sn, Cd, Hg), хроматы, цианиды, фосфаты, органика Пищевая Большое количество органических веществ, взвешенного материала — 644 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠Ǫǯ͟͠Ǯǯǰ͠ǪǃǬǃǀǎÐ͟͠ǀǂǬǯǬ֬ÐǫÐǫǮƽǃǮ֬Ðǯ͠ǬƽǬ ϭϱ͘Ϯ͘Ϯ͘ʦ̸̨̨̛̛̯̬̦̖̬̦̖̦̖̌̐́̚̚͘ Загрязняющие вещества, поступающие в водоемы из различных источников, приводят к загрязнению не только вод, но и донных отложений в результате процессов сорбции на взвешенных частицах, которые в дальнейшем осаждаются на дне. Это явление ведет к очищению воды, но приводит к образованию загрязненных донных отложений. В этом случае вертикальное перемешивание, воздействие придонных течений, волнения на мелководных участках могут вызвать вторичное загрязнение вод. ϭϱ͘Ϯ͘ϯ͘ʺ̨̨̛̖̯̼̦̣̼̔̌̌̌̏̔̚͘ 1) Потенциометрические методы анализа воды Потенциометрические методы количественного химического анализа предназначены для определения различных ионов в воде, например, измерение концентрации Н+, pH, Сl–, F–, Са2+, Na+, К+ и др. Этот метод основан на измерении потенциала электрода, погруженного в раствор. Значение потенциала зависит от концентрации соответствующих ионов в растворе. 2) Анализ воды с помощью ионоселективных электродов. В настоящее время число ионоселективных электродов с четко выраженной селективностью к определенному иону (Na+, К+, Са2+, Н+, NО3–, Сl–, Вr–, I–, F–, Fe и др.) составляет более сотни. Их селективность определяется типом или видом чувствительной мембраны. В зависимости от типа мембраны электроды подразделяют на: • твердые (гомогенные и гетерогенные на основе ионообменных смол, стекол, осадков, поли- и монокристаллов); • жидкостные (на основе жидких ионитов — нейтральных переносчиков, биологически активных веществ); • пленочные или матричные (на основе активных веществ, полимерной матрицы и пластификатора). Преимущество работы с рассматриваемыми электродами — это возможность без нарушения целостности объекта — 645 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ определять активности соответствующих ионов. Чем более селективен электрод к данному иону, тем шире область его применения в различных средах. Способность ионоселективных электродов измерять не концентрацию, а активность ионов является в большинстве случаев их важным преимуществом по сравнению с другими методами физико-химического анализа. Именно это обусловило их использование для изучения процессов ассоциации ионов, комплексообразования и др. При этом применяется прямая потенциометрия, с помощью которой определяется активность данного иона в растворах в отсутствие и в присутствии комплексообразующего реагента. 3) Вольтамперометрические методы анализа воды. Вольтамперометрия — это электрохимический метод количественного анализа, основанный на определении зависимости между силой тока и напряжением поляризации при электролизе раствора или расплава изучаемого вещества. В оснащенных современным оборудованием аналитических лабораториях, в задачу которых входит контроль объектов окружающей среды, пищевых продуктов, продовольственного сырья на содержание токсичных примесей, электрохимические методы оказались конкурентноспособными по отношению к известным физическим методам анализа. Вольтамперометрия позволяет с высокой избирательной способностью и точностью измерять ионный состав воды. Основан метод на анализе вольтамперных характеристик (зависимости тока от напряжения) электрохимической ячейки с твердыми электродами. При использовании жидких (ртутных) электродов этот метод называют полярографией. /В основу этого метода положены законы электролиза. ϭϱ͘Ϯ͘ϰ͘ʽ̶̸̡̡̨̖̦̖̭̯̼̌̌̏̌̏̔͘ В соответствии с Санитарными правилами и нормами СанПиН 2.1.4.559-96 питьевая вода должна быть безопасна в эпидемическом и радиационном отношении, безвредна по хи— 646 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠Ǫǯ͟͠Ǯǯǰ͠ǪǃǬǃǀǎÐ͟͠ǀǂǬǯǬ֬ÐǫÐǫǮƽǃǮ֬Ðǯ͠ǬƽǬ мическому составу и должна иметь благоприятные органолептические свойства. Под качеством воды в целом понимается характеристика ее состава и свойств, определяющая ее пригодность для конкретных видов водопользования; при этом показатели качества представляют собой признаки, по которым производится оценка качества воды. По санитарному признаку устанавливаются микробиологические и паразитологические показатели качества воды (число микроорганизмов и число бактерий группы кишечных палочек в единице объема). Токсикологические показатели качества воды, характеризующие безвредность ее химического состава, определяются содержанием химических веществ, которое не должно превышать установленных нормативов. Наконец, при определении качества воды учитываются органолептические (воспринимаемые органами чувств) свойства: температура, прозрачность, цвет, запах, вкус, жесткость. Требования к качеству воды нецентрализованного водоснабжения определены Санитарными правилами и нормами СанПиН 2.1.4.1175-02 «Гигиенические требования к качеству воды нецентрализованного водоснабжения. Санитарная охрана источников», причем нормируются запах, вкус, цветность, мутность, коли-индекс (количество бактерий в 1 мл исследуемой воды), а также указывается, что содержание химических веществ не должно превышать значений соответствующих предельно допустимых концентраций (ПДК). Предельно допустимая концентрация в воде водоема хозяйственно-питьевого и культурно-бытового водопользования (ПДКв) — это концентрация вредного вещества в воде, которая не должна оказывать прямого или косвенного влияния на организм человека в течение всей его жизни и на здоровье последующих поколений, а также не должна ухудшать гигиенические условия водопользования. Предельно допустимая концентрация в воде водоема, используемого для рыбохозяйственных целей (ПДКвр) — это концентрация вредного вещества в воде, которая не должна оказывать вредного влияния на популяцию рыб, в первую очередь промысловых: — 647 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ При интерпретации результатов мониторинга состояния водной среды важно знать, к какому типу водных объектов отнесены река, озеро, водохранилище, и использовать для оценки ситуации соответствующие нормативы. В гидрохимической практике используется метод интегральной оценки качества воды по совокупности находящихся в ней загрязняющих веществ и частоты их обнаружения. В этом методе для каждого ингредиента на основе фактических концентраций рассчитывают баллы кратности превышения ПДКвр — Ki, повторяемости случаев превышения ПДК Hi, а также общий оценочный балл — Bi,: Ki = N ci ; Hi = ÏÄÊ i ; Bi = Ki Hi Ni ÏÄÊ i (14.7) где сi — концентрация в воде i-го ингредиента; ПДК — предельно допустимая концентрация i-го ингредиента для водоемов рыбохозяйственного назначения; NÏÄÊ i — число случаев превышения ПДК по i-му ингредиенту; Ni — общее число измерений i-го ингредиента. Ингредиенты, для которых величина общего оценочного балла Вi: 11, выделяются как лимитирующие показатели загрязненности (ЛПЗ). Комбинаторный индекс загрязненности рассчитывается как сумма общих оценочных баллов всех учитываемых ингредиентов. По величине комбинаторного индекса загрязненности устанавливается класс загрязненности воды. Также оценка качества воды и сравнение современного состояния водного объекта с установленными в прошлые годы характеристиками проводятся на основании индекса загрязнения воды по гидрохимическим показателям (ИЗВ). Этот индекс представляет собой формальную характеристику и рассчитывается усреднением как минимум пяти индивидуальных показателей качества воды. Обязательны для учета следующие показатели: концентрация растворенного кислорода, водородный показатель pH и биологическое потребление кислорода БПК5. — 648 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠Ǫǯ͟͠Ǯǯǰ͠ǪǃǬǃǀǎÐ͟͠ǀǂǬǯǬ֬ÐǫÐǫǮƽǃǮ֬Ðǯ͠ǬƽǬ ϭϱ͘Ϯ͘ϱ͘ˁ̸̨̡̨̛̭̯̬̭̖̯̼̪̱̭̌̏̌̏̏;̨̨̭̬̭̍̏Ϳ̸̵̨̨̭̯̦̼̏̔͘ Основными источниками загрязнений водоемов являются производственные, бытовые и поверхностные сточные воды. Производственные сточные воды образуются в результате использования воды в технологических процессах. Типовой состав примесей таких сточных вод включает взвешенные вещества, маслопродукты, кислоты, щелочи и т.д. Бытовые сточные воды содержат крупные примеси (остатки пищи, ветошь, песок и т.п.); примеси органического и минерального происхождения в нерастворенном, коллоидном и растворенном состояниях; различные, в том числе болезнетворные, бактерии. Концентрация указанных примесей в бытовых сточных водах зависит от степени их разбавления водопроводной водой. Поверхностные сточные воды образуются в результате смывания дождевыми, снеговыми и поливочными водами загрязнений, имеющихся на поверхности грунтов, на крышах и стенах зданий и т.п. Основными примесями поверхностных сточных вод являются механические частицы (земля, песок, камень, древесные и металлические стружки, пыль, сажа) и нефтепродукты (масла, бензин, керосин, используемые в двигателях транспортных средств). При выборе схемы станции очистки и технологического оборудования необходимо знать расход сточных вод и концентрацию содержащихся в них примесей, а также допустимый состав сточных вод, сбрасываемых в водоемы. Допустимый состав сточных вод рассчитывают с учетом Правил охраны поверхностных вод, которые устанавливают нормы на ПДК веществ, состав и свойства воды водоемов. Расчет допустимой концентрации примесей в сточных водах, сбрасываемых в водоемы, проводят в зависимости от преобладающего вида примесей сточных вод и характеристик водоема. При преобладающем содержании взвешенных веществ их допустимая концентрация в очищенных сточных водах c0 ≤ câ + nÏÄÊ (15.8) где св — концентрация взвешенных веществ в воде водоема до сброса в него сточных вод, кг/м3; n — кратность разбавления — 649 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ сточных вод в воде водоема, характеризующая часть расхода воды водоема, участвующую в процессе перемешивания и разбавления сточных вод; ПДК — предельно допустимая концентрация взвешенных веществ в воде водоема, кг/м3. При преобладающем содержании растворенных веществ допустимая концентрация каждого из них в очищенных сточных водах c0i ≤ n (cmaxi − câ i ) + câ i (15.9) где свi — концентрация i-го вещества в воде водоема до сброса в него сточных вод, кг/м3; сmахi — максимально допустимая концентрация того же вещества в воде водоема с учетом максимальных концентраций и ПДК всех веществ, относящихся к одной группе лимитирующих показателей вредности, кг/м3. Кратность разбавления сточных вод в воде водоема c0 − câ (15.10) c − câ где с0 — концентрация загрязняющих веществ в сбрасываемых сточных водах, кг/м3; св и с — концентрации тех же веществ в воде водоема, соответственно, до и после сброса в них сточных вод, кг/м3. Для водоемов с направленным течением кратность разбавления (15.11) n = Qâ + mQð Qâ n= ( ) где Qв — объемный расход сточных вод, сбрасываемых в водоем с объемным расходом Qp, м3/ч; т — коэффициент смешения, показывающий долю расхода воды водоема, участвующей в процессе смешения. Условия смешения сточных вод с водой озер и водохранилищ существенно отличаются от условий их смешения в реках и каналах. Концентрация примесей сточных вод в начальной зоне смешения уменьшается более существенно, однако полное их перемешивание происходит на значительно больших расстояниях от места выпуска, чем в реках и каналах. — 650 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠Ǫǯ͟͠Ǯǯǰ͠ǪǃǬǃǀǎÐ͟͠ǀǂǬǯǬ֬ÐǫÐǫǮƽǃǮ֬Ðǯ͠ǬƽǬ ϭϱ͘Ϯ͘ϲ͘ʺ̨̨̨̛̛̛̖̣̬̭̪̬̭̯̬̦̖̦̬̦̖̦̜̖̔̌̌́̌̐́̏̏̔̚̚͘ 1) Классификация моделей распространения примесей в сплошной среде. Основное уравнение модели, описывающее явления переноса и диффузии веществ в сплошной среде, имеет вид: dc (15.12) = ∇ ( k∇c ) − ∇ (uc ) + Qc + R c dt где с — концентрация примесей, биогенных веществ, микроорганизмов, планктона и т.д., и = (и, v, w) — вектор осредненного поля скоростей среды (воды, воздуха), элементы которого совпадают с осями координат х, у k; к — тензор коэффициентов турбулентной диффузии, сочетающий в себе возможные механизмы смешения; Qc, Rc — источники образования (распада) веществ. На практике весьма часто используется уравнение типа (15.12), в котором k является диагональной матрицей. Ее элементы могут быть представлены в виде: (15.13) k = E+ D+ε где Е — коэффициент турбулентной диффузии; D — коэффициент молекулярной диффузии. Зависит от градиента концентраций и доминирует при малых скоростях движения среды; ε — коэффициент термодиффузии. Зависит от градиента температуры и приемлем для водных сред. Нужно отметить, что уравнение (15.12) описывающее явления переноса и диффузии веществ в сплошной среде, является более общим, чем уравнение турбулентной диффузии (15.1) и применимо, для описания распространения примесей, как в атмосфере, гидросфере и литосфере. Интенсивность источника образования веществ Qc, входящая в правую часть уравнения (15.12), в общем случае зависит от вектора координат r=(х, у, z) и времени t. Так для мгновенно действующего точечного источника (15.14) Qc = Qδ (r − r0 ) δ (t − t0 ) где Q — интенсивность источника; r0 — вектор координат его размещения; t0 — момент времени действия. Для L фиксированных источников имеем — 651 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ L Qc = ∑Ql (t ) δ (r − rl ) (15.15) l =1 где Ql(t) — переменная во времени интенсивность l -го источника; rl — вектор координат его размещения. Для случая М мобильных источников Qc запишется следующим образом: Qc = M ∑ Qm (t) δ ⎣⎡r − rm (t)⎦⎤ (15.16) m =1 где rт() — вектор координат траектории движения т-го мобильного источника. Наконец, для источника поверхностного типа Qc = Q (r,t ) В частном случае вещество, выделяемое источником, можно считать инертным материалом, плотность которого совпадает с плотностью среды. Во всех других случаях оно является химически или биологически активным, отличающимся по плотности внешней среды. Для химически активных веществ можно записать: S N j =1 i =1 Qc = ∑α j kj ∏ciVij (15.17) Где N — количество веществ в химической системе, k — константа скорости реакции; Vij — порядок j-ой реакции по i-му веществу; αj — значение стехиометрических коэффициентов. Если в результате химического или биологического взаимодействия вещество поглощается, тогда такие взаимодействия рассматриваются как механизмы стока вещества и в уравнении (15.12) обозначаются символом Rc. В общем случае в (15.12) одновременно присутствуют Qc и Rc. Действие стокового механизма зависит от многих переменных: (15.18) R c = R c (c,T,ϕ, I ) Где с — концентрация вещества; T, ϕ — температура и влажность среды; I — интенсивность солнечного излучения. Зная параметры среды (и, k) источников Qc, стоков Rc, граничных и начальных условий, в принципе можно построить решение уравнения (15.12) в виде пространственно-временного поля, концентраций с(х, у, z, t). Однако на практике чаще — 652 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠Ǫǯ͟͠Ǯǯǰ͠ǪǃǬǃǀǎÐ͟͠ǀǂǬǯǬ֬ÐǫÐǫǮƽǃǮ֬Ðǯ͠ǬƽǬ всего применяют различные виды его аппроксимации. Это объясняется следующими причинами. Во-первых, постановка природоохранных задач может ориентировать исследователя на поиск более простых, «оперативных» и менее трудоемких операций. Во-вторых, не все компоненты векторов и и k могут быть известны точно, а значит упрощается интегрирование уравнения (15.12). В-третьих, процесс получения численного решения многомерного нелинейного уравнения всегда сложен и требует от программистов исключительно высокой квалификации. В связи с этим используют два подхода к упрощению уравнения (15.12). Первый из них основан на выявлении наиболее значимых (в смысле переноса или диффузии) членов уравнения. Незначимые члены из рассмотрения исключаются. Второй подход предполагает возможность осреднения поля концентраций по одной или нескольким пространственным координатам, а затем оперирует понятием средней (по координате, площади или объему) концентрации вещества. Поскольку предпосылки использования подходов различны, модели одного и того же вида могут давать различные значения концентраций. В результате упрощений уравнение (15.12) из четырехмерного преобразуется в одно-двух или трехмерное, и может быть линейным или нелинейным. Для линейных уравнений удается получить аналитические решения, для нелинейных уравнений — численные. На основе уравнения (15.12) можно провести классификацию современных моделей распространения примесей в водной среде. Классификация эта достаточно проста: это – Камерные модели, в которых рассматриваемая область делится на подобласти — камеры, внутри которых изучаемые характеристики считаются постоянными. Связь между камерами осуществляется введением фундаментальных балансовых соотношений. – Непрерывные модели. Большинство используемых непрерывных моделей распространения примеси в водоемах, построены на основе уравнения Навье-Стокса («гидродинами— 653 — ǞǁǪǫǪÐ ÐƫǀǄǄǱƿǀǮǃǃǊǬÐ͟͠ǮǅǬǯǯǊÐǫÐǪǰǂǮǯǄǬ͠ǬÐǀÐƼǀƽ͠ǮǯǄǬ͠Ǭ ческая составляющая») и уравнений, описывающих распространение примеси либо конвекционным, либо диффузионным или смешенным механизмом. При этом пользуются некоторыми допущения, упрощающие решение этих уравнений. При схематизации процесса конвективно-диффузионного переноса примесей следует учитывать: – Мерность исследуемой области и процесса; модель одномерная или двухмерная в вертикальном сечении или в плане, трехмерная и т.п.; – Тип режима конвективно-диффузионного переноса: стационарный или нестационарный; – Граничные условия (1, II, III рода); – Описание конвективно-диффузионного процесса; – Связь с направлением диффузии: изотропная, анизотропная или смешанная; – По степени неоднородности: однородная или неоднородная; – По типу загрязняющих веществ. Такая схематизация позволяет, с одной стороны, учесть все основные определяющие процесс факторы, характер водного режима, его гидравлические, морфологические и гидрохимические характеристики, условия выпуска сточных вод и самоочищения для различных фаз водного состояния и так далее, а с другой стороны, использовать современные методы и средства математического моделирования. Рассмотрим несколько моделей в общем виде, для того, чтобы иметь представление о том, каким образом происходит процесс моделирования. 1) Камерные модели. Камерные модели — достаточно удобный инструмент для прогнозирования распространения примеси в водоемах типа озеро или водохранилище. Как правило, это достаточно сложные объекты с самой разной конфигурацией, глубиной, наличием сточных вод, притоков, впадающих рек и т.п. В этих случаях математическое описание водохранилища сводится к разработке достаточно громоздкой и в общем слу— 654 — ÐǨǀƿǀǆǬǯǭǀǬÐǮǯǃǮǫǊÐ͠Ǫǯ͟͠Ǯǯǰ͠ǪǃǬǃǀǎÐ͟͠ǀǂǬǯǬ֬ÐǫÐǫǮƽǃǮ֬Ðǯ͠ǬƽǬ чае нелинейной модели. Решение и использование такой модели — задача чрезвычайно сложная, требующая значительных вычислительных ресурсов и временных затрат. В практике необходимо использовать более простые способы описания водных объектов, что сведет к минимуму случайные ошибки, возникающи

Кольцов В.Б. Кондратьева О.В. - Теоретические основы защиты окружающей среды - 2018

Похожие документы

Разделы

Поддержка

Кольцов В.Б. Кондратьева О.В. - Теоретические основы защиты окружающей среды - 2018

Похожие документы

Добавить этот документ в коллекции

Добавить этот документ в сохраненные

Предложите, как улучшить StudyLib