геом_эл 1 - Камышинский технологический институт

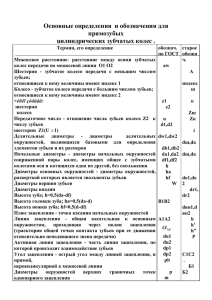
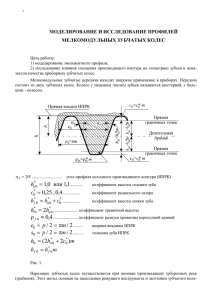
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
ВОЛГОГРАДСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО
УНИВЕРСИТЕТА
КАФЕДРА ОБЩЕТЕХНИЧЕСКИЕ ДИСЦИПЛИНЫ
ГЕОМЕТРИЧЕСКИЕ ЭЛЕМЕНТЫ
ЗУБЧАТЫХ КОЛЕС
Методические указания к лабораторной работе
по дисциплине «Теория механизмов и машин»
РПК «Политехник»
Волгоград
2002
УДК 621. 831/. 833
Г 35
ГЕОМЕТРИЧЕСКИЕ ЭЛЕМЕНТЫ ЗУБЧАТЫХ КОЛЕС: Методические указания к лабораторной работе по дисциплине «Теория механизмов
и машин» / Сост. Е. А. Малявин, А. В. Белов; Волгоград. гос. техн. ун-т. –
Волгоград, 2002. – 10 с.
Излагаются краткие сведения теории эвольвентного зацепления.
Рассматривается порядок определения основных параметров зубчатых колес.
Предназначены в помощь студентам, обучающимся по направлениям
551200, 552900.
Ил. 4. Табл. 2. Библиогр.: 2 назв.
Рецензент Н. Г. Неумоина
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета
Составители: Евгений Александрович Малявин
Александр Владимирович Белов
ГЕОМЕТРИЧЕСКИЕ ЭЛЕМЕНТЫ ЗУБЧАТЫХ КОЛЕС
Методические указания к лабораторной работе по дисциплине
«Теория механизмов и машин»
Редакторы: Попова Л. В., Просондеев М. И.
Темплан 2002г., поз. № 135
Подписано в печать 03. 07. 2002 г. Формат 1/16.
Бумага потребительская. Усл. печ. л. 0,5.
Уч.-изд. л. 0,63. Тираж 100 экз. Заказ
.
Волгоградский государственный технический университет.
400131 Волгоград, просп. им. В. И. Ленина, 28.
РПК «Политехник» Волгоградского государственного технического университета
400131 Волгоград, ул. Советская, 35.
ООО «Камипринт» 403850 г. Камышин, Волгоградской обл., ул. Ленина, 20.
 Волгоградский
государственный
технический
университет, 2002
2
Цель работы – изучить основные параметры зубчатых колес, соотношения между параметрами. Научиться определять их практически.
1. КРАТКИЕ СВЕДЕНИЯ
ИЗ ТЕОРИИ ЭВОЛЬВЕНТНОГО ЗАЦЕПЛЕНИЯ
Весьма распространенным видом передач вращательного движения
являются плоские зубчатые передачи. Передача вращательного движения
с заданным кинематическим законом при помощи зубчатых колес должна
иметь такую очерчивающую кривую профиля зубьев, которая обеспечивала бы заданный закон движения и была бы геометрически простой.
Кроме того, зубья принятого профиля должны обладать наибольшей
прочностью при минимальном износе, а давление на валы и опоры валов
оставаться постоянным по величине и направлению в соответствии с передаваемой мощностью. Важным требованием является и взаимозаменяемость зубчатых колес.
Профиль зуба теоретически может очерчиваться любой кривой, но
лишь некоторые из них наиболее полно удовлетворяют поставленным
требованиям и приняты в машиностроении. Чаще всего это эвольвента.
Эвольвентой называется линия, описываемая любой точкой прямой, перекатывающейся без скольжения по окружности.
Окружность, по которой перекатывается прямая, называется основной окружностью, а прямая – производящей прямой (рис. 1).
Рис. 1.
3
Важным свойством эвольвенты является то, что нормаль N-N, проведенная к эвольвенте в любой ее точке (например, в точке 7), обязательно будет касательной к основной окружности. Точка касания (например, точка 7) будет центром кривизны, а расстояние между точкой эвольвенты и точкой касания (например, отрезок 7-7) будет радиусом кривизны эвольвенты в соответствующей точке. На этом свойстве эвольвенты
основано практическое определение основных параметров зубчатых колес с эвольвентным профилем зуба.
На рис. 2 изображена часть зубчатого колеса с эвольвентным профилем зуба, где обозначены основные геометрические параметры колеса.
Рис. 2.
Различают следующие окружности и соответствующие им диаметры
зубчатого колеса: основная окружность dв – окружность по которой пере4
катывается производящая прямая, образующая профиль зуба; делительная окружность d – окружность, шаг по которой равен стандартному
шагу; начальная окружность dw – окружность, по которой как бы перекатывается колесо, находящееся в зацеплении с другим (для нулевых колес
dw = d); окружность вершин зубьев dа и окружность впадин зубьев df. Шаг
зубьев Р – длина дуги по делительной, начальной, основной или другой
соосной окружности зубчатого колеса между одноименными точками
профиля соседних зубьев. Шаг зацепления в общем случае выражается
через диаметр окружности следующим образом:
P
d
,
Z
(1)
где: d – диаметр той окружности, по которой определяется шаг;
Z – число зубьев колеса.
Основным параметром, определяющим размеры зубчатого колеса и
его элементов, является окружной модуль m, мм:
m
P
,

(2)
где Р – шаг по делительной окружности, мм.
ЗНАЧЕНИЯ МОДУЛЕЙ ГОСТ 9563-60
(стандартизованы в диапазоне от 0,05…100 мм)
Таблица 1
Ряды
Модуль, мм
1-й
1
2-й
1,125
1,25
1,375
1,5
2
1,75
2,5
2,25
3
4
2,75
5
3,5
6
8
4,5
5,5
10
5,7
12
9
16
11
20
14
25
18
22
Примечание. Следует предпочитать 1 ряд.
Зубчатое колесо называется нулевым, если оно изготовлено без смещения инструмента при нарезании колеса, при этом толщина зуба S и ширина
впадины S, измеренные по делительной окружности, равны друг другу:
S  S 
P m
.

2
2
(3)
Для колеса, выполненного без смещения, диаметры начальной и делительной окружности совпадают и определяются по формуле:
d  d w  mZ .
5
(4)
Расстояние между окружностью вершин зубьев dа и начальной
окружностью dw называется высотой головки зуба и обозначается hа.
Расстояние между начальной окружностью dw и окружностью впадин
df называется высотой ножки зуба и обозначается hf.
Расстояние между окружностью вершин da и окружностью впадин df
называется высотой зуба и обозначается h.
Высота зуба h, высота hа головки и высота hf ножки зуба нулевого прямозубого колеса, предусмотренные ГОСТ 13755-81, соответственно равны.
h = 2,25 m; ha = m; hf = 1,25 m.
Для нулевого колеса диаметр окружности вершин зубьев выражается
равенством:
диаметр окружности впадин:
d a  m( Z  2) ,
(5)
d f  m( Z  2,5) .
(6)
Угол зацепления w – острый угол между линией зацепления NN и
прямой, перпендикулярной к межосевой линии О1О2, проходящей через
полюс зацепления Р (см. рис. 2).
Для нулевого колеса: w =  = 20, где:  – угол профиля делительный, по ГОСТ 13755-81,  = 20.
Применение нормальных (нулевых) зубчатых колес с постоянной
высотой головки зуба и постоянным углом зацепления ограничивает конструктора в смысле выбора наилучших для работы передачи параметров.
Помимо этого, многие передачи не могут быть вообще построены с нормальными зубчатыми колесами. В таких случаях можно отказаться от
нормальных соотношений и параметры могут быть выбраны из условия
наибольшего благоприятствования работы передачи.
Зубчатые передачи с геометрическими параметрами, отличающимися от нормальных (с углом зацепления w  20, высотой головки зуба
hа  m), называются передачами со смещением. Такие передачи применяются для улучшения условий работы зубьев (увеличения их прочности,
уменьшения наибольших значений удельного скольжения и т. д.).
Коэффициент смещения Х равен отношению величины смещения
инструментальной рейки при нарезании зубьев к модулю. Коэффициент
смещения положительный, если смещение рейки от центра колеса, и отрицательный – при смещении к центру. Для нулевого колеса коэффициент смещения равен нулю.
Если охватить несколько зубьев колеса губками штангенциркуля таким образом, чтобы они были касательны к профилям зубьев (размер АВ,
6
рис. 3), то линия АВ будет касательной к основной окружности, т. е. прямая АВ является производящей прямой.
Таким образом, если измерить вначале размер Сn, соответствующий
n зубьям, а затем измерить размер Сn+1, то по свойству эвольвенты шаг по
основной окружности определяется как разность этих измерений:
Pв  С n 1  C n .
(7)
Это выражение справедливо, если при измерении губки штангенциркуля касаются эвольвентной части профиля зуба. Поэтому при выборе
числа зубьев n для измерения необходимо исходить из общего числа
зубьев Z колеса и руководствоваться таблицей 2.
Таблица 2
Z 12 …18
n
2
19…27
3
28 … 36
37 …45
46 …54
55 …63
64 … 72
73 … 81
5
6
7
8
9
4
Рис. 3.
Зная Рв, можно приближенно определить значение модуля зацепления по формуле:
m
P


Pв
C  Cn
.
 n1
  сos   сos
(8)
За истинный модуль следует принять ближайший по величине из
стандартного ряда (см. табл. 1).
Путем измерений и дополнительных вычислений можно определить
тип зубчатого колеса – нулевое или со смещением.
Действительная толщина зуба по основной окружности:
Sв  C n 1  n  Pв .
7
(9)
Расчетная толщина зуба по основной окружности определяется по
формуле:
S

Sв  d в   inv   ,
d

(10)
где: S – толщина зуба по делительной окружности;
d – диаметр делительной окружности:
d  m  Z;
(11)
inv  – эвольвентная функция (инволюта): inv 20 = 0,0149.
Толщина зуба по делительной окружности для нулевого колеса определяется по формуле:
S  0,5m ,
(12)
для колеса со смещением:
S  0,5  m  2Xm  tg
(13)
Разность толщин зубьев по основной окружности колеса со смещением Sв и нулевого Sв определяется выражением:
 S

S
 d
Sв  Sв  d в   inv    d в   inv    в S  S .
d

d
 d
(14)
Подставив значение:
S, S
и
d в  d  сos ,
(15)
получим:
S в  S в  сos 0,5m  2mX  tg  0,5m  2mX  sin  ,
(16)
откуда:
X 
S в  S в
.
2m  sin 
(17)
Диаметры окружностей вершин и впадин зубьев определяются непосредственным измерением, если число зубьев колеса четное. При нечетном числе зубьев, когда непосредственное измерение невозможно, измерения проводятся по следующей схеме (рис. 4).
8
Рис. 4.
d a  d отв  21
d f  d отв  2 2
.
(18)
2. ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ
1. Сосчитайте число зубьев колеса.
2. Выберите по табл. 2 число охватываемых зубьев «n» и проведите измерение значений Cn и Cn+1. Измерение производится в трех разных местах по
периметру колеса, в расчет принимается среднее арифметическое число.
3. Определите модуль зацепления по формуле 8, принимая  = 20.
4. По полученному приближенному значению модуля выберите в
табл. 1 ближайшее стандартное значение.
5. Используя стандартное значение модуля, по формуле 8 определите шаг зацепления по делительной Р и основной окружности Рв, а также
диаметры d, da, df, dв по формулам 4, 5, 6, 15.
6. Определите действительную толщину зуба по основной окружности Sв по формуле 9.
7. Определите расчетную толщину зуба по основной окружности Sв
нулевого колеса согласно формуле 10.
8. Вычислите коэффициент смещения Х по формуле 17. Определите тип колеса (нулевое, с положительным смещением, с отрицательным
смещением).
9. Определите диаметры окружностей вершин зубьев da и впадин df
путем непосредственных измерений либо согласно рисунку 5 и формуле 18.
9
10. Проведите все измерения и расчеты для второго зубчатого колеса по аналогии с первым.
11. По результатам обмера и расчетов оформите отчет.
12. Выполните рабочий чертеж одного из колес.
3. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Требования к профилю зуба зубчатого колеса.
2. Какая кривая называется эвольвентой?
3. Что такое основная окружность?
3. Основные свойства эвольвенты.
4. Понятие основных геометрических характеристик зубчатого колеса:
делительная окружность; основная окружность; окружность вершин зубьев; окружность впадин зубьев; шаг зацепления; модуль зацепления; ширина впадин; высота зуба; угол зацепления.
5. Как проводится и на чем основано измерение шага по основной
окружности?
6. Что такое коэффициент смещения зубчатого колеса?
7. Как производится измерение диаметров вершин и впадин зубьев при
четном и нечетном числах зубьев?
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Артоболевский И. И. Теория механизмов и машин: Учебник для
втузов. – 4-е изд., доп. и перераб. – М.: Наука, 1988. – 640 с.
2. Иванов М. И. Детали машин: Учебник для студентов высш. учеб.
заведений. – 6-е изд., перераб. – М.: Высш. шк., 1998. – 383 с.
10