2. Сходимость. Открытые и замкнутые множества

§ 2. Сходимость. Открытые и замкнутые множества
1. Предельные точки. Замыкание
2. Сходимость
3. Плотные подмножества
4. Открытые и замкнутые множества
5. Открытые и замкнутые множества на прямой
1. Предельные точки. Замыкание
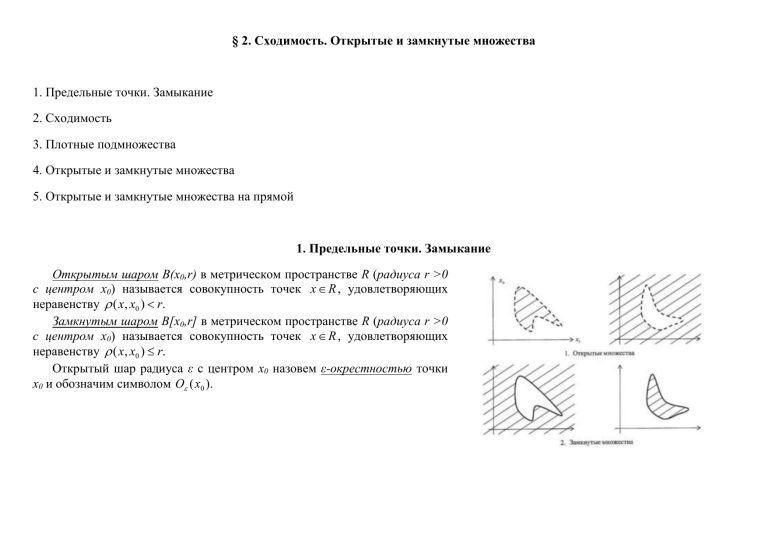
Открытым шаром В(х0,r) в метрическом пространстве R (радиуса r >0
с центром х0) называется совокупность точек х  R , удовлетворяющих
неравенству  ( х, x0 )  r.
Замкнутым шаром В[х0,r] в метрическом пространстве R (радиуса r >0
с центром х0) называется совокупность точек х  R , удовлетворяющих
неравенству  ( х, x0 )  r.
Открытый шар радиуса ε с центром х0 назовем ε-окрестностью точки
х0 и обозначим символом O ( x0 ).
Классификация точек множества
1. точка x называется предельной точкой множества В, если любая
окрестность точки x содержит точки множества В, отличные от x;
2. точка x называется граничной точкой множества В, если любая
окрестность точки x содержит как точки множества В, так и точки его
дополнения;
3. точка x называется внутренней точкой множества В, если некоторая
окрестность точки x целиком содержится в множестве В;
4. точка x называется внешней(изолированной) точкой множества В, если
x ∈ В, но некоторая окрестность не содержит точек множества В (можно
сказать и так: некоторая окрестность точки x не содержит точек из В, кроме
самой точки x).
Упражнение
Привести пример метрического пространства и таких двух шаров B( x, 1 ), B( y,  2 ) в нем, что 1   2 , и тем не
менее B( x, 1 )  B( y,  2 ) .
Решение:
Возьмём:
1.
пространство с дискретной метрикой.
2.
два шара в этом пространстве с радиусами, например, 3 и 2 (чтобы было выполнено условие 1   2 ).
Оба эти шара будут совпадать со всем пространством, так как между любыми двумя точками при дискретной
метрике расстояние меньше либо равно единице (= 0 или =1)
Так как оба шара включают все элементы пространства, то они взаимно вложены друг в друга (взаимно содержат друг друга)
=> B( x, 1 )  B( y,  2 ) .
Любой шар радиуса >1 в пространстве с дискретной метрикой совпадает с этим пространством.
Таким образом, условие задачи выполнено.
Множество M  R называется ограниченным, если оно содержится целиком в некотором шаре.
Точка называется точкой прикосновения множества M  R , если любая ее окрестность содержит хотя бы одну точку из М.
[М] замыкание множества М – совокупность всех точек прикосновения множества М.
Операция замыкания – переход от множества М к его замыканию [М].
Теорема 1. Операция замыкания обладает следующими свойствами:
1. M  [ M ],
2. [[ M ]]  [ M ],
3. если M 1  M 2 , то [ M 1 ]  [ M 2 ],
4. [ M 1
M 2 ]  [ M 1 ] [ M 2 ].
Доказательство.
1. Первое утверждение очевидно, так как всякая точка, принадлежащая М, является для М точкой прикосновения.
2. Докажем второе.
Пусть x [[ M ]]. Тогда в любой окрестности O ( x ) этой точки найдется точка x1  [ M ]. Положим    ( x, x1 )  1 и
рассмотрим шар O1 ( x1 ). Этот шар целиком лежит внутри шара O ( x ) . Действительно, если z  O1 ( x1 ),  ( z, x1 )  1 , и так как
 ( x, x1 )    1 , то по аксиоме треугольника
 ( z, x )  1  (  1 )   ,
т.е. z  O ( x ). Так как x1  [ M ], то в O1 ( x1 ) найдется точка x2  M . Но тогда x2  O ( x ). Так как O ( x ) - произвольная
окрестность точки х, то x [ M ]. Второе утверждение доказано.
3. Третье свойство очевидно.
4. Докажем четвертое.
Если x  [ M 1 M 2 ], х содержится по крайней мере в одном из множеств [ M 1 ] или [ M 2 ], т.е.
[M1
Так как M 1  M 1
M 2 и M 2  M1
M 2 ]  [ M 1 ] [ M 2 ].
M 2 , то обратное включение следует из свойства 3. Теорема доказана полностью.
Точка х  R называется предельной точкой множества M  R , если любая ее окрестность содержит бесконечно много точек
из М.
Предельная точка может принадлежать, а может и не принадлежать М. Например, если М – множество рациональных чисел
отрезка [0,1], то каждая точка этого отрезка – предельная для М.
Точка х, принадлежащая М, называется изолированной точкой этого множества, если в достаточно малой ее окрестности
O ( x ) нет точек из М, отличных от х.
Докажем следующее утверждение:
Всякая точка прикосновения множества М есть либо предельная, либо изолированная точка этого множества.
Доказательство.
Пусть х – точка прикосновения множества М. Это означает, что всякая ее окрестность O ( x ) содержит хотя бы одну точку,
принадлежащую М. Возможны два варианта:
1. Всякая окрестность точки х содержит бесконечно много точек множества М. В этом случае х является предельной точкой
для М.
2. У точки х найдется окрестность O ( x ) содержащая лишь конечное число точек из М. В этом случае х будет
изолированной точкой множества М. Действительно, пусть x1 , x2 ,..., xi - отличные от х точки множества М, содержащиеся в
O ( x ) . Пусть, далее,  0 есть наименьшее из положительных чисел  ( x, xi ), i  1,2,..., k . Тогда окрестность O 0 ( x ) , очевидно, не
содержит ни одной отличной от х точки множества М. Сама точка х при этом обязательно должна принадлежать М, так как
иначе O 0 ( x ) , вообще не содержала бы ни одной точки из М, т.е. х не была бы точкой прикосновения множества М. Теорема
доказана.
Отсюда можно заключить, что замыкание [М] состоит из точек трех типов:
1. изолированные точки множества М;
2. предельные точки множества М, принадлежащие М;
3. предельные точки множества М, не принадлежащие М.
Таким образом, замыкание [М] получается присоединением к М всех его предельных точек.
Множество М называется замкнутым, если [М] = М.
Из теоремы 1 вытекает, что замыкание любого множества – замкнутое множество.
Множество, все точки которого внутренние, называется открытым.
Между открытым и замкнутым множеством имеется следующая связь.
Для того чтобы множество М было замкнуто, необходимо и достаточно, чтобы его дополнение R\M до всего
пространства R было открыто.
Открытые и замкнутые множества обладают следующими свойствами:
1. Объединение любого числа (конечного или бесконечного) открытых множеств является открытым множеством.
2. Пересечение любого конечного числа открытых множеств является открытым множеством.
3. Объединение любого числа замкнутых множеств является замкнутым множеством.
4. Пересечение любого числа (конечного или бесконечного) замкнутых множеств является замкнутым множеством.
2. Сходимость
Пусть x1, x2, . . . — последовательность точек (элементов) в метрическом пространстве R.
Говорят, что последовательность {xn }n1 сходится к точке х, если
lim  ( xn , x )  0 ,
n
т. е. если для всякого ε > 0 найдется такое число N = N(ε), что для всех n > N имеет место  ( xn , x )   . Точка x называется
пределом последовательности {xn}. Из определения предела вытекает, что если предел существует, то он единственен.
Действительно, пусть x и y — два предела последовательности {xn}. Тогда, используя неравенство треугольника, получаем
0   ( x, y )   ( x, xn )   ( xn , y )  0 при n  .
Таким образом, ρ(x, y) = 0 и, следовательно, x = y.
Из определения предела вытекает, что
1. никакая последовательность не может иметь двух различных пределов.
2. если последовательность {xn} сходится к точке х, то и всякая ее подпоследовательность сходится к той же самой точке.
Следующая теорема устанавливает тесную связь между понятиями точки прикосновения и предела.
Теорема 2. Для того чтобы точка х была точкой прикосновения множества М, необходимо и достаточно, чтобы
существовала последовательность {xn} точек из М, сходящаяся к х.
Доказательство.
Если х – точка прикосновения множества М, то в каждой ее окрестности O1/ n ( x) содержится хотя бы одна точка xn  M . Эти
точки образуют последовательность, сходящуюся к х. Достаточность очевидна.
Если х – предельная точка множества М, то точки xn  O1/ n ( x) M , отвечающие разным n, можно выбрать попарно
различными. Таким образом, для того чтобы точка х была предельной для М, необходимо и достаточно, чтобы в М
существовала последовательность попарно различных точек, сходящаяся к х.
Отображение y  f ( x) непрерывно в точке х0, если для всякой последовательности {xn}, сходящейся к х0,
последовательность { y  f ( x)} сходится к y0  f ( x0 ).
3. Плотные подмножества
Пусть А и В – два множества в метрическом пространстве R. Множество А называется плотным в В, если [ A]  B. В
частности множество А называется всюду плотным (в пространстве В), если его замыкание [ A] совпадает со всем пространством
R.
Множество рациональных чисел всюду плотно на числовой прямой. Множество А называется нигде не плотным, если оно
не плотно ни в одном шаре, т.е. если в каждом шаре B  R содержится другой шар B’, не имеющий с А ни одной общей точки.
Сепарабельные пространства – это пространства, в которых имеется счетное всюду плотное множество.
Сепарабельность пространства указывает на некоторую простоту его устройства, служит основой для различных
приближённых методов, позволяет использовать множество базисных элементов небольшой мощности и т. д.
Примеры пространств, имеющих всюду плотное счетное множество:
0, x  y ,
1.  ( x, y )  
1, x  y.
2.  ( x, y )  x  y
Данное «Дискретное» пространство содержит счетное всюду плотное в нем множество
тогда и только тогда, когда оно само состоит лишь из счетного числа точек. Замыкание [М]
любого множества М в этом пространстве совпадает с М.
В пространстве R1, то есть в множестве действительных чисел, совокупность Q всех
рациональных чисел образует счётное, всюду плотное подмножество. Для произвольного m
эту роль выполняет множество Y = Qm = Q×Q× . . .×Q.
Рациональные точки.
3.  ( x, y ) 
n
( y
k 1
k
В пространствах R n , R1n , Rn содержаться совокупности векторов с рациональными
координатами.
Пусть А – некоторое множество в нормированном пространстве В. Это множество
называется плотным в пространстве В, если любой шар содержит хотя бы одну точку этого
множества. Отсюда следует, что А плотно в В тогда и только тогда, когда для любого
элемента х  B и любого   0 существует вектор y  A такой, что || x  y ||  .
Пусть в пространстве В задана последовательность векторов x1 , x2 , x3 ,... Эта
последовательность называется полной в В, если ее линейная оболочка плотна в
пространстве В. Последовательность x1 , x2 , x3 ,... является полной тогда и только тогда,
 xk ) 2
n
4. 1 ( x, y )   | xk  yk |
k 1
5.   ( x, y )  max yk  xk
n
когда для любого элемента х  B и любого   0 найдется линейная комбинация y   ai xi
1k  n
i 1
векторов x1 , x2 , x3 ,... такая, что || x  y ||  .
Нормированное пространство, в котором существуют полные последовательности,
называется сепарабельным.
6.  ( f , g )  max | g (t )  f (t ) |
a t b
8.
1/2
b

 ( x, y )    ( x(t )  y (t )) 2 dt 
a

7.  ( x, y ) 

( y
k 1
k
 xk ) 2
В пространствах С[a,b], С2[a,b] содержится совокупность всех многочленов с
рациональными коэффициентами.
Множество всех многочленов Рn(x)=a0xn+a1xn–1+...+an с рациональными коэффициентами,
является счетным.
Теоремы: Множество Q всех рациональных чисел является счетным и Любое бесконечное
подмножество счетного множества является счетным.
Согласно теореме, что любое бесконечное подмножество счетного множество является
счетным, мы получаем, что совокупность всех многочленов с рациональными
коэффициентами будет счетным, а следовательно и сепарабельным.
В пространство l2 содержится совокупность последовательностей, в каждой из которых все
члены рациональны и лишь конечное (свое для каждой последовательности) число этих
членов отлично от нуля.
Рассмотрим множество L всех последовательностей с рациональными членами, у которых
только конечное, для каждого своё, число членов не равно нулю. Это множество счётно, как
объединение счётного числа счётных множеств. Покажем, что множество L образует счётный
скелет ( множество точек с рациональными координатами ) в l2. Пусть последовательность
{xn}∈l2. Так как
Так как множество
то есть ряд сходится, то
рациональных чисел Q
всюду
плотно
на
числовой
оси,
то
Нормировочный множитель выбран для удобства и в
силу произвольности ε.
Рассмотрим последовательность {qn}∈L, члены которой при n>n+1 равны нулю. Тогда
расстояние между x∈l2 и q∈Q
Это значит, что
ρ(x,q)<ε и замыкание L совпадает с l2, то есть множество L образует счётный скелет в l2.
Следовательно пространство l2 сепарабельно.
9.  ( x, y )  sup yk  xk
k
Пространство ограниченных последовательностей m несепарабельно.
Рассмотрим всевозможные последовательности, состоящие из 0 и 1. Они образуют
множество мощности континуума. Расстояние между двумя такими точками определяемое
формулой  ( x, y )  sup yk  xk равно 1. Окружим каждую из этих точек открытым шаром
k
радиуса 1/2. Эти шары не пересекаются. Если некоторое множество всюду плотно в m, то
каждый из построенных шаров должен содержать хотя бы по одной точке из этого
множества, и, следовательно, оно не может быть счетным.
4. Открытые и замкнутые множества
1. Открытое множество — это множество, каждый элемент которого
входит в него вместе с некоторой окрестностью.
2. Замкнутое множество – множество, которое содержит все свои
предельные точки.
Замкнутое множество
Напомним определение предельной точки.
Точка х называется предельной точкой множества М, если в любой окрестности точки х имеется, по крайней мере, ещё одна
точка множества М, кроме точки х.
В метрическом пространстве R замыкание любого множества есть замкнутое множество. Кроме того, замыкание [М]
любого множества М  R есть наименьшее замкнутое множество, содержащее M.
Мы определили операцию замыкания множества в метрическом пространстве как совокупность его точек прикосновений.
Сейчас дано определение замкнутого множества как такого множества, которое совпадает со своим замыканием. Речь идет о
том, чтобы выявить связь между этими понятиями.
Доказательство. Поскольку в метрическом пространстве [[ M ]]  [ M ], то отсюда автоматически следует, что [М] –
замкнутое множество. Кроме того, так как из M  N следует, что [M]  [N]. Отсюда следует, что замыкание [М] есть
наименьшее замкнутое множество, содержащее M. Действительно, если M  N и N замкнуто, то [M]  [N] = N, т.е. [M]  N. В
силу произвольности N получаем, что [М] – наименьшее замкнутое множество, содержащее M.
Примеры.
1. Всякий отрезок [a,b] числовой прямой есть замкнутое множество.
2. Замкнутый шар представляет собой замкнутое множество. В частности, в пространстве С [a,b] множество функций f ,
удовлетворяющих условию | f (t ) | K , замкнуто.
3. Множество функций в С [a,b], удовлетворяющих условию | f (t ) | K (открытый шар), не замкнуто; его замыкание есть
совокупность функций, удовлетворяющих условию | f (t ) | K .
4. Каково бы ни было метрическое пространство R, пустое множество Ø и все R замкнуты.
5. Всякое множество, состоящее из конечного числа точек, замкнуто.
Основные свойства замкнутых множеств можно сформулировать в виде следующей теоремы.
Теорема 3. Пересечение любого числа и сумма любого конечного числа замкнутых множеств есть замкнутые множества.
Доказательство. Пусть F  Fa - пересечение замкнутых множеств Fa и пусть х – предельная точка для F. Это означает, что
любая её окрестность O ( x ) содержит бесконечно много точек из F. Но тогда тем более O ( x ) содержит бесконечно много
точек из каждого Fa и, следовательно, так как все Fa замкнуты, точка х принадлежит каждому Fa; таким образом x  F  Fa ,
т.е. Fa замкнуто.
Пусть теперь F – сумма конечного числа замкнутых множеств: F 
n
Fi , и пусть точка х не принадлежит F. Покажем, что х
i 1
не может быть предельной для F. Действительно х не принадлежит ни одному из замкнутых множеств Fi, следовательно не
является предельной ни для одного из них. Поэтому для каждого i можно найти такую окрестность O i ( x) точки х, которая
содержит не более чем конечное число точек из Fi. Взяв из окрестностей O1 ( x ),..., O n ( x ) наименьшую, мы получим
окрестности O ( x ) точки х, содержащую не более чем конечное число точек из F.
Итак, если точка х не принадлежит F, то она не может быть предельной для F, т.е. F замкнуто. Теорема доказана.
Открытое множество
Напомним определение внутренней точки.
Точка х называется внутренней точкой множества М, если существует окрестность O ( x ) этой точки х, целиком
содержащаяся в М.
Множество, все точки которого внутренние, называется открытым.
Примеры.
1. Интервал (a,b) числовой прямой R1 есть открытое множество; действительно, если a    b, то O ( ), где
  min(  a, b   ), целиком содержится в интервале (a,b).
2. Открытый шар В(a,r) в любом метрическом пространстве R есть открытое множество. Действительно, если х  B(a, r ),
то  (a, х)  r. Положим   r   (a, x). Тогда B( x,  )  B(a, r ).
3. Множество непрерывных функций на [a,b], удовлетворяющих условию f (t )  g (t ), где g (t ) - некоторая фиксированная
непрерывная функция, представляет собой открытое подмножество пространства С[a,b].
Теорема 4. Для того чтобы множество М было открыто, необходимо и достаточно, чтобы его дополнение R\M до всего
пространства R было замкнуто.
Доказательство. Если М открыто, то каждая точка х из М имеет окрестность, целиком принадлежащую М, т.е. не имеющую
ни одной общей точки с R\M. Таким образом, ни одна из точек, не принадлежащих R\M, не может быть точкой прикосновения
для R\M, т.е. R\M замкнуто. Обратно, если R\M замкнуто, то любая точка из М имеет окрестность, целиком лежащую в М, т.е. М
открыто.
Так как пустое множество и все R замкнуты и в то же время служат дополнениями друг друга, то пустое множество и все R
открыты.
Из теоремы 3 и из принципа двойственности* вытекает следующая важная теорема, двойственная теореме 3.
*Принцип двойственности:
Aa 
1. S \
a
( S \ Aa ) - дополнение суммы равно пересечению дополнений.
a
Aa 
2. S \
a
( S \ Aa ) - дополнение пересечения равно сумме дополнений.
a
Теорема 3’. Сумма любого (конечного или бесконечного) числа и пересечение любого конечного числа открытых множеств
есть открытые множества.
Борелевское множество - это любое множество в топологическом пространстве, которое может быть сформировано из
открытых множеств (или, что эквивалентно, из замкнутых множеств) посредством операций счетного объединения, счетного
пересечения и относительного дополнения.
5. Открытые и замкнутые множества на прямой
Теорема 5. Всякое открытое множество на числовой прямой представляет собой сумму конечного или счетного числа
попарно непересекающихся интервалов*.
* Множества вида (, ), ( , ), (,  )
мы при этом также включаем в число интервалов.
Доказательство. Пусть G – открытое множество на прямой. Введем для точек из G отношение эквивалентности, считая,
что x y , если существует такой интервал ( ,  ), что x, y  ( ,  )  G. Очевидно, это отношение рефлексивно и симметрично,
оно и транзитивно, так как если x y и y z , то существуют такие интервалы ( ,  ) и ( ,  ), что
x, y  ( ,  )  G и y, z  ( ,  )  G.
Но тогда    и интервал ( ,  ) лежит целиком в G и содержит точки x и z. Следовательно, G распадается на
непересекающиеся классы I эквивалентных между собой точек:
G  I .
Докажем, что I есть интервал (a,b), где a  inf I , b  sup I , то по самому определению I интервал (x,y) содержится в I . В
любой близости от b слева есть точки из I . Поэтому I содержит любой интервал (a’,b’), откуда I  (a, b). Система таких
непересекающихся интервалов I не более чем счетна; действительно, выбрав в каждом из этих интервалов произвольным
образом рациональную точку, мы установим взаимно однозначное соответствие между этими интервалами и некоторым
подмножеством множества рациональных чисел. Теорема доказана.
Так как замкнутые множества – это дополнения открытых, то отсюда следует, что всякое замкнутое множество на прямой
получается выбрасыванием из прямой конечного или счетного числа интервалов.
Рассмотрим пример замкнутого множества на прямой – так называемое канторово множество.
Пусть F0 – отрезок [0,1]. Выбросим из него интервал (1/3, 2/3), а оставшееся
замкнутое множество обозначим F1 = [0,1/3]  [2/3,1] Затем выбросим из F1
интервалы (1/9, 2/9) и (7/9, 8,9), а оставшееся замкнутое множество (состоящее
из четырех отрезков) обозначим F2. В каждом из этих четырех отрезков
выбросим средний интервал длины (1/3)3 и т.д. Продолжая этот процесс,
получим убывающую последовательность замкнутых множеств Fn.
Канторово множество представляет собой один из простейших фракталов, который обозначает геометрическую фигуру,
обладающую свойством самоподобия, т.е. составленную из нескольких частей, каждая из которых подобна всей фигуре
целиком.
Положим F 

Fn .
n 0
F – замкнутое множество (как пересечение замкнутых). Оно получается из отрезка [0,1] выбрасыванием счетного числа
интервалов.
Рассмотрим структуру множества F. Ему принадлежат, очевидно, точки: 0,1,1/3,2/3,1/9,2/9,7/9,8/9,...
(1)
– концы выбрасываемых интервалов. Однако множество F не исчерпывается этими точками. Действительно, те точки
отрезка [0,1], которые входят в множество F, можно охарактеризовать следующим образом. Запишем каждое из чисел х,
0  x  1 в троичной системе:
a
a a
x  1  22  ...  nn  ...,
3 3
3
где числа аn могут принимать значения 0,1 и 2. Как в случае десятичных дробей, некоторые числа допускают двоякую запись.
Легко проверить, что множеству F принадлежат те и только те числа х, 0  x  1 , которые могут быть записаны хотя бы
одним способом, в виде троичной дроби так, чтобы в последовательности а1, а2,...,аn,... ни разу не встретилась единица. Таким
образом, каждой точке х  F можно поставить в соответствие последовательность
а1, а2,...,аn,...
(2)
где an равно 0 или 2. Совокупность таких последовательностей образует множество мощности континуума. В этом можно
убедиться, поставив в соответствие каждой последовательности (2) последовательность
b1,b2,…,bn,…,
(2’)
где bn=0, если an=0, bn=1, если an=2. Последовательность (2’) можно рассматривать как запись некоторого действительного
числа y, 0  y  1 , в виде двоичной дроби. Таким образом, мы получаем отображение множества F на весь отрезок [0,1]. Отсюда
вытекает, что F имеет мощность континуума*. Так как множество точек (1) счетно, то эти точки не могут исчерпывать все F.
*Установленное соответствие между F и отрезком [0,1] однозначно, но не взаимно однозначно (из-за того, что одно и то же число иногда может изображаться
различными дробями). Отсюда следует, что F имеет мощность не меньше, чем мощность континуума. Но F – часть отрезка [0,1], следовательно, его мощность не
может быть больше, чем мощность континуума.
Упражнения
1. Доказать непосредственно, что точка ¼ принадлежит множеству F, не являясь концом ни одного из выбрасываемых
интервалов.
Указание. Точка ¼ делит отрезок [0,1] в отношении 1:3. Отрезок [0,1/3], оставшийся после первого выбрасывания, она делит
также 1:3 и т.д.
F0  [0,1]
1
2
F1  [0, ]  [ ,1]
3
3
1
2 1
2 7
8
F2  [0, ]  [ , ]  [ , ]  [ ,1]
9
9 3
3 9
9
...
Для
решения
данного
упражнения
мы
воспользуемся
свойством
Канторова
множества:
если
точка Канторова множества не является концом ни одного из смежных интервалов, то она является точкой второго рода
Канторова множества. По условию задачи, точка 1/4, не является концом ни одного выбрасываемого интервала, поэтому она
точка второго рода. А множество всех точек второго рода является множеством мощности континуума, т.е. содержит столько
же точек, сколько и весь отрезок [0,1]. Следовательно, точка 1/4 принадлежит F.
2. Доказать, что точки первого рода образуют в F всюду плотное множество.
Концы выбрасываемых интервалов являются точка первого рода множества F. Рассмотрим всевозможные последовательности.
Они образуют множество мощности континуума. Расстояние между двумя такими точками определяемое формулой
 ( x, y )  sup yk  xk равно 1. Окружим каждую из этих точек открытым шаром одинакового радиуса. Эти шары не
k
пересекаются, и содержат хотя бы по одной точке из этого множества. Точки первого рода образуют всюду плотное множество
А в множестве F, т.к. выполняется условие F  [ A] .
Дополнительные замечания
1. Пусть М – некоторое множество в метрическом пространстве R и х – точка этого же пространства. Расстоянием от
точки х до множества М называется число
 ( x, M )  inf  ( x, a).
aM
Если x  M , то  ( x, M )  0, однако из того, что  ( x, M )  0, не следует, что x  M . Из определения точки
прикосновения непосредственно получаем, что  ( x, M )  0 в том и только том случае, когда х – точка прикосновения
множества М. Таким образом, операцию замыкания можно определить как присоединение к множеству всех тех точек,
расстояние которых до множества равно нулю.
2. Аналогично определяется расстояние между двумя множествами. Если А,В – два множества в метрическом
пространстве R, то
 ( A, B)  inf  (a, b).
aA
bB
Если
A B  , то  ( A, B)  0; обратное, вообще говоря, неверно.
3. Пусть M K - множество всех функций f из С [a,b], удовлетворяющих условию Липшица: для всех t1 , t2  [a, b]
| f (t1 )  f (t2 ) | K | t2  t1 |,
где К – некоторое фиксированное число. Множество M K замкнуто. Оно совпадает с замыканием множества всех
дифференцируемых на [a,b] функций таких, что | f '(t ) | K.
4. Множество M 
M K всех функций, каждая из которых удовлетворяет условию Липшица при каком-либо K, не
K
замкнуто. Его замыкание есть все С [a,b].
5. Открытое множество G в n-мерном евклидовом пространстве называется связным, если любые две точки x, y  G
2
2
могут быть соединены ломаной, целиком лежащей в G. Например, внутренность круга x  y  1 - связанное
множество. Наоборот, сумма двух кругов
x 2  y 2  1 и ( x  2)2  y 2  1
- не связанное множество (хотя у этих кругов есть общая точка прикосновения!). Открытое подмножество Н открытого
множества G называется компонентой множества G, если оно связано и не содержится ни в каком большем связном
открытом подмножестве G.
Введем в G отношение эквивалентности: x y, если существует открытое связанное подмножество Н из G,
накрывающее x и y:
x , y  H  G.
Как и в случае прямой, легко проверяется транзитивность и поэтому G распадается на непересекающиеся классы:
G  I . Эти классы – открытые компоненты G. Число их не более чем счетно.
В случае n=1, т.е. на прямой, всякое связное открытое множество есть интервал. Таким образом, теорема 5 о
строении открытых множеств на прямой состоит из двух утверждений:
 всякое открытое множество на прямой есть сумма конечного или счетного числа компонентов;
 связное открытое множество на прямой есть интервал.