Лекция 1 ИП

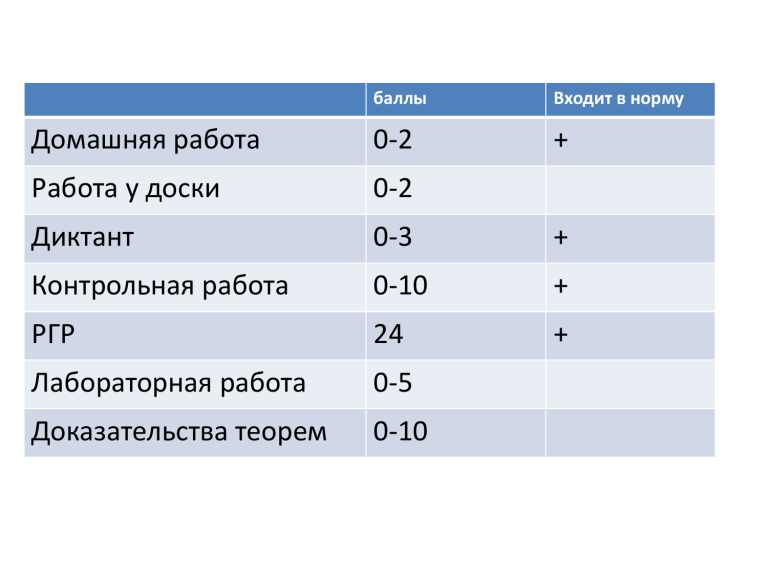
баллы
Входит в норму
Домашняя работа
0-2
+
Работа у доски
0-2
Диктант
0-3
+
Контрольная работа
0-10
+
РГР
24
+
Лабораторная работа
0-5
Доказательства теорем
0-10
Отлично:
1)Посещение не менее 75%
2)Балл не менее 85% от нормы
3) Контрольные работы не менее 7 баллов за каждую
4)Сумма баллов за контрольные сроки не менее 3
Хорошо:
1)Посещение не менее 70%
2)Балл не менее 70% от нормы
3) Контрольные работы не менее 6 баллов за каждую
4) За контрольные сроки нет нулей
Остальные сдают экзамен в виде теста. Для
получения оценки удовлетворительно требуется
набрать
(1-СуммаБаллов/Норма) *100% правильных
ответов
Глава 1. Элементы теории множеств
1.1 Множества и их спецификация
1.1.1 Элементы и множества
А, В, С x, y, z {a, b, c} x  A x  A
Множество, элементами которого являются другие
множества, обычно называется семейством, или
классом множеств. B
 U
|M|
N – множество натуральных чисел,
Z – множество целых чисел, Z +
R – множество действительных чисел,
P – множество простых чисел,
Q – множество рациональных чисел.
1.1.2 Способы задания множеств
I. Перечислением элементов множества
1) А = {2, 4, 6}; 2) B = {1, 3, 5}; 3) C = {A, B};
II. Указанием свойств элементов множества,
или заданием т.н. характеристического
предиката: D = {x | P(x)}
4) D = {x R | x>0};
III. Порождающей процедурой: E = {y | y:=f(x)}.
5) E = {2·y | y=1, 2, …, n,…};
E={2,4,6,8,…}
6) F = {x | x=1 или x=2·y, yF }
F={1, 2, 22, 23, 24, …}
1.2 Операции над множествами.
1.2.1 Сравнение множеств.
B⊆C ⇔ ꓯx ∈ B ⇒ x ∈ C ⊈
B⊂C ⇔ B⊆C и B≠ C
  А ꓯА
А=В АВ
Множества A и B равны ⇔ B⊆A и A⊆B
Примеры
1) Для числовых множеств: P ⊂ N ⊂ Z ⊂ R
2) А = {2, 4, 6}; B = {1, 3, 5}; C = {A, B}; верно ли
a) A ∈ C
b)A ⊆ C
Совокупность всех подмножеств множества M
называется булеаном и обозначается P (M)
Пример: B = {1, 3, 5}
P (B)= {,{1},{3},{5},{1,3},{1,5},{3,5},{1,3,5}}
1.2.2 Операции над множествами. Диаграммы
Венна
-Объединение (или сумма)
-Пересечение (или произведение)
-Разность
-Симметрическая разность
-Дополнение
1) Объединение (сумма)
A  B = {x | x  A или x  B}.
2) Пересечение (произведением)
множеств A  B = {x | x  A и
x  B}.
Если A  B = , то А и В
непересекающимися.
3) Разность
A \ B = {x | x  A и x  B}
4) Симметрическая разность
A Δ B = (A  B) \ (A  B) =
{x | (x  A и x  B) или (x  B и
x  A)}.
5) Дополнение
A = U \ A = {x | x  A}.
Пример: А = {1, 2, 3, 4}; B = {1, 3, 5, 7}
A  B = {1, 2, 3, 4, 5, 7};
A  B = {1, 3};
A \ B = {2, 4}
B \ A = {5, 7};
A Δ B = {2, 4, 5, 7}.
Операции объединения и пересечения допускают
обобщение для большего количества множеств (в
том числе и бесконечного)
k
A
i
i 1
 A1  A2  ...  Ak
1.2.3 Разбиения и покрытия
• Пусть E ={Ei} для i I – некоторое семейство
непустых подмножеств множества M, Ei  M.
Тогда семейство E называется покрытием
множества M, если каждый элемент множества M
принадлежит хотя бы одному из Ei:
M  ∪Ei  x M  i I | x Ei.
• Семейство E называется дизъюнктным, если
элементы этого семейства попарно не
пересекаются, т.е. каждый элемент множества M
принадлежит не более чем одному из множеств
Ei: i,j I, ij  Ei  Ej=.
• Дизъюнктное покрытие E называется разбиением
множества M.
Пример:
M={1,2,3}
{{1,2}, {2,3}, {3,1}}
– покрытие, но не разбиение
{{1},{2},{3}}
– покрытие и разбиение
{{1},{2}}
является дизъюнктным, но не является ни
покрытием, ни разбиением
1.2.4 Свойства операций над множествами
Пусть задан универсум U. Тогда A, B, C  U
выполняются свойства:
Идемпотентность A  A = A, A  A = A
Коммутативность A  B = B  A, A  B = B  A
Ассоциативность
• A  (B  C) = (A  B)  C
• A  (B  C) = (A  B)  C
Дистрибутивность
• A  (B  C) = (A  B)  (A  C)
• A  (B  C) = (A  B)  (A  C)
Операции с пустым множеством
• A=A
• A=
Операции с универсальным множеством
• AU=U
• AU=A
Свойства дополнения
A A = U
A A=
Поглощение
• (A  B)  A = A
• (A  B)  A = A
Двойственность (законы де Моргана)
Выражение для разности
A \ B = A B
Пример:
Доказать (A\B) (B\A) = (A  B)\(A  B)
(A  B)\(A  B) = (A  B)  (A͞ ͞͞ ͞B̅)̅ =
(A  B)  (A̅  B̅)=
((A  B)  A̅ )  ((A  B)  B̅)=
((A  A̅ )  (B  A̅ ))  ((A  B̅)  (B  B̅))=
(  (B  A̅ ))  ((A  B̅)   )=
(B  A̅ )  (A  B̅) =
(B\A)  (A\B)=
(A\B)  (B\A)
Принцип двойственности.
Принцип двойственности состоит в том, что из
любого равенства, относящегося к системе
подмножеств фиксированного множества U,
автоматически может быть получено другое,
двойственное, равенство, путем замены всех
рассматриваемых множеств их дополнениями,
объединений множеств – пересечениями,
пересечений множеств – объединениями.
1.3 Отношения на множествах
1.3.1 Прямое произведение множеств
{1,2}={2,1}
(1,2)≠(2,1)
A⨯B ={(x,y)| x  A, y  B}
(1,2,1)≠(2,1,1)
A⨯B⨯C ={(x,y,z)| x  A, y  B, z  C}
Прямым (или декартовым) произведением
множеств А1, А2, …, Аn называется
множество всех упорядоченных наборов
(x1 ,x2, … xn) таких, что xi  Ai при  i = 1, 2, …, n.
А1⨯ А2⨯…⨯ Аn ={(x1 ,x2, … xn)| xi  Ai  i = 1, 2, …, n}
Пример:
A={1,2,3}, B={a,b}
A⨯B=
{(1,a),(2,a),(3,a),(1,b),(2,b),(3,b)}
B⨯A=
{(a,1),(a,2),(a,3),(b,1),(b,2),(b,3)}
A⨯B≠B⨯A
B ⨯ B=
{(a,a),(a,b),(b,a),(b,b)} = B2
А1⨯ А2⨯…⨯ Аn ⨯ = 