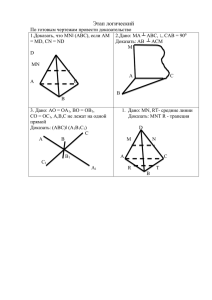
Запиши решение, заполняя пропуски. №1. Катет AC прямоугольного треугольника ABC с прямым углом C лежит в плоскости α, а угол между плоскостями α и ABC равен 60°. Найди расстояние от точки B до плоскости α, если AC=5 см, AB=13см. Решение. Проведём перпендикуляр BO к плоскости α. Отрезок BC — наклонная к _____, отрезок OC — проекция наклонной _____ на _____, а прямая AC, лежащая в плоскости α, перпендикулярна к наклонной BC. Следовательно, согласно __________, AC⊥OC. Таким образом, ∠BCO — линейный угол двугранного угла между плоскостями α и ABC, и, значит, ∠BCO= _____. △ABC прямоугольный: ∠C= _____, AC= _____, AB= _____, поэтому BC= _____. △BCO прямоугольный: ∠O= _____, ∠BCO= _____, BC= _____, следовательно, BO= _____ см = _____ см = _____ см. Ответ: №2. Сторона ромба ABCD равна 12 см, ∠A=30°, AM⊥ABC, AM=6 см. Найди расстояние от точки M до прямой CD. Решение. Из вершины A ромба ABCD проведём отрезок AH⊥DC. Так как ∠ADC= _____ — тупой, то основание H перпендикуляра AH лежит на продолжении луча _____. Таким образом, из точки M к плоскости ABC проведены перпендикуляр MA и наклонная MH, при этом прямая CD плоскости _____ перпендикулярна к проекции _____ наклонной _____. Поэтому, согласно __________, CD⊥ _____. Итак, длина перпендикуляра MH и есть расстояние от точки _____ до прямой _____. △AHD __________, ∠ADH= _____, AD= _____, поэтому AH= _____ см. △MAH __________, так как __________ и AM= _____, AH= _____ см, поэтому MH= _____ см. Ответ: №3. В прямоугольном треугольнике ABC С∠С=90°, AB=43 см. Точка P не лежит в плоскости ABC и удалена от каждой вершины треугольника на расстояние 43 см. Найди угол между прямой PC и плоскостью ABC. Решение. Пусть PO — перпендикуляр к плоскости ABC. Поскольку отрезки PA, PB и PC — равные наклонные, проведённые из _____ к _____, то их проекции тоже _____, т. е. OA= _____ = _____, а потому точка O — центр окружности, __________. Следовательно, точка O — середина _____. Так как AB= _____, то CO = 21 _____ = _____ см. Искомый угол φ между прямой _____ и плоскостью _____ есть угол между __________, т. е. φ = ∠ _____. △POC прямоугольный, так как __________, PC = _____, CO = _____ см, поэтому cosφ = _____ = _____ = _____. Отсюда получаем, что φ= _____. Ответ: