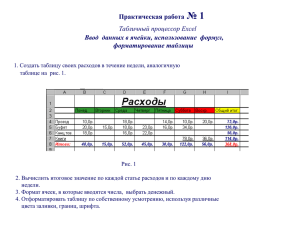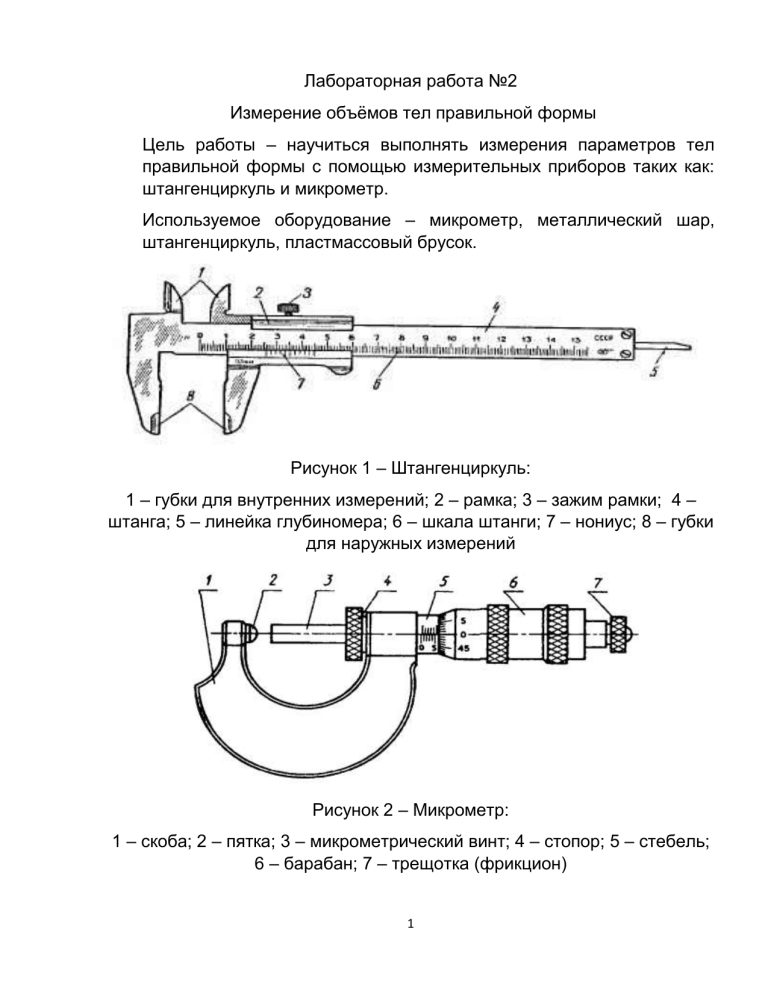
Лабораторная работа №2 Измерение объёмов тел правильной формы Цель работы – научиться выполнять измерения параметров тел правильной формы с помощью измерительных приборов таких как: штангенциркуль и микрометр. Используемое оборудование – микрометр, металлический шар, штангенциркуль, пластмассовый брусок. Рисунок 1 – Штангенциркуль: 1 – губки для внутренних измерений; 2 – рамка; 3 – зажим рамки; 4 – штанга; 5 – линейка глубиномера; 6 – шкала штанги; 7 – нониус; 8 – губки для наружных измерений Рисунок 2 – Микрометр: 1 – скоба; 2 – пятка; 3 – микрометрический винт; 4 – стопор; 5 – стебель; 6 – барабан; 7 – трещотка (фрикцион) 1 Расчётные формулы: 𝑐 ∆𝑥окр = 𝑃 , (1) 2 где ∆𝑥окр – погрешность округления, 𝑃 – доверительная вероятность , 𝑐 – цена деления измерительного прибора ∆𝑥пр = 2,0 3,0 𝛿, (2) где ∆𝑥пр – абсолютная приборная погрешность, 𝛿 – предельная погрешность ⟨𝑥⟩ = ∑𝑛 𝑖=1 𝑥𝑖 𝑛 , (3) где ⟨𝑥⟩ - среднее значение, n – число измерений ∆𝑥сл = 𝑡𝑛,𝑃 √ 2 ∑𝑛 𝑖=1(𝑥𝑖 −⟨𝑥⟩) 𝑛(𝑛−1) , (4) где ∆𝑥сл – случайная погрешность, 𝑡𝑛,𝑝 – коэффициент Стьюдента ∆𝑥 = √(∆𝑥пр )2 + (∆𝑥окр )2 + (∆𝑥сл )2 , (5) где ∆𝑥 – полная погрешность Δ𝑥 𝜀 = ⟨𝑥⟩ , (6) где 𝜀 – относительная погрешность ∆𝑦 = √∑𝑘𝑖=1( 𝜕𝑓(𝑥𝑖) 𝜕𝑥𝑖 где ∆𝑦 − погрешность косвенных измерений, функции 2 ∆𝑥𝑖 )2 , 𝜕𝑓(𝑥𝑖) 𝜕𝑥𝑖 (7) – частная производная ⟨𝑉ш ⟩ = 𝜋⟨𝐷⟩3 6 , (8) где ⟨𝐷⟩ – среднее значение диаметра шара ⟨ 𝑉п ⟩ = ⟨𝑎⟩⟨𝑏⟩⟨ℎ⟩, (9) где 𝑉п – объём параллелепипеда, ⟨𝑎⟩ – среднее значение длины, ⟨𝑏⟩ – среднее значение ширины, ⟨ℎ⟩ – среднее значение высоты Δ𝑎пр 𝜀𝑚𝑖𝑛 = √( ⟨𝑎⟩ + Δ𝑏пр ⟨𝑏⟩ + Δℎпр 2 ⟨ℎ⟩ Δ𝑎окр 2 ) +( ⟨𝑎⟩ 𝑛 𝜀сл Δ𝑏окр 2 ) +( ⟨𝑏⟩ Δℎокр 2 ) +( ⟨ℎ⟩ ) , (10) 2 Δ𝑥сл 𝑖 = √∑ ( ) ⟨𝑥⟩𝑖 𝑖=1 Выполнение работы: Задание 1 Определение объёма шара Таблица 1 N D, мм 1 15,00 2 15,00 3 15,00 Расчёты: По формуле (1) 𝛥𝐷окр = 0,004750 мм По формуле (2) 𝛥𝐷пр = 0,0026666 мм По формуле (3) ⟨𝐷⟩ = 15,004 мм По формуле (4) 𝛥𝐷сл = 0,0068095 мм По формуле (5) 𝛥𝐷 = 0,008720 мм 3 4 15,01 5 15,01 По формуле (6) 𝜀𝐷 = 0,06 % По формуле (7) 𝛥𝑉ш = 3,8746 мм3 По формуле (8) ⟨𝑉ш ⟩ = 1768 мм3 По формуле (6) 𝜀𝑣 = 0,2 % Окончательный результат: 𝑉ш = (1,768 ± 0,003875)*103, мм3, 𝜀𝑣 = 0,2 %, 𝑃 = 0,95 Задание 2 Определение объёма параллелепипеда Таблица 2 N 1 2 3 a 27,25 27,15 27,55 b 18,30 18,55 18,50 h 38,15 38,20 38,30 4 5 27,35 27,55 18,55 18,50 38,15 38,10 Расчёты: По формуле (1) 𝛥𝑎окр = 0,02375 мм По формуле (1) 𝛥𝑏окр = 0,02375 мм По формуле (1) 𝛥ℎокр = 0,02375 мм По формуле (2) 𝛥𝑎пр = 0,03333 мм По формуле (2) 𝛥𝑏пр = 0,03333 мм По формуле (2) 𝛥ℎпр = 0,03333 мм По формуле (3) ⟨𝑎⟩ = 27,37 мм 4 По формуле (3) ⟨𝑏⟩ = 18,48 мм По формуле (3) ⟨ℎ⟩ = 38,18 мм По формуле (4) 𝛥𝑎сл = 0,2224 мм По формуле (4) 𝛥𝑏сл = 0,1289 мм По формуле (4) 𝛥ℎсл = 0,09427 мм По формуле (5) Δ𝑎 = 0,2261 мм По формуле (5) Δ𝑏 = 0,1352 мм По формуле (5) Δℎ = 0,10277 мм По формуле (6) 𝜀𝑎 = 0,89 % По формуле (6) 𝜀𝑏 = 0,78 % По формуле (6) 𝜀ℎ = 0,27 % По формуле (7) 𝛥𝑉п = 219,3445 мм3 По формуле (9) ⟨𝑉п ⟩ = 19311 мм3 По формуле (6) 𝜀𝑣 = 1,14 % По формуле (10) 𝜀𝑚𝑖𝑛 = 0,42 % Окончательный результат: 𝑉ш = (1,9311 ± 0,02194) ∗ 104 , мм3, 𝜀𝑣 = 1,14 %, 𝑃 = 0,95 Вывод: В этой лабораторной работе я провела измерения длины, ширины и высоты параллелепипеда с помощью штангенциркуля, а также диаметра шара с помощью микрометра. Рассчитала приборную погрешность, случайную погрешность, погрешность округления, полную погрешность и относительную погрешность для прямых измерений, погрешность косвенных измерений и полную погрешность косвенных измерений. Для повышения точности результатов я провела по 5 измерений для каждого параметра в каждом задании. 5 Нашла объёмы параллелепипеда и шара. Рассчитала погрешности косвенных измерений объёмов параллелепипеда и шара. Небольшие значения относительной погрешности измерений объёмов свидетельствуют о высокой точности измерительных приборов. Точность измерений диаметра шара выше, чем точность измерений длины, ширины и высоты параллелепипеда, из-за этого относительная погрешность измерения объёма шара меньше относительной погрешности объёма параллелепипеда. 6