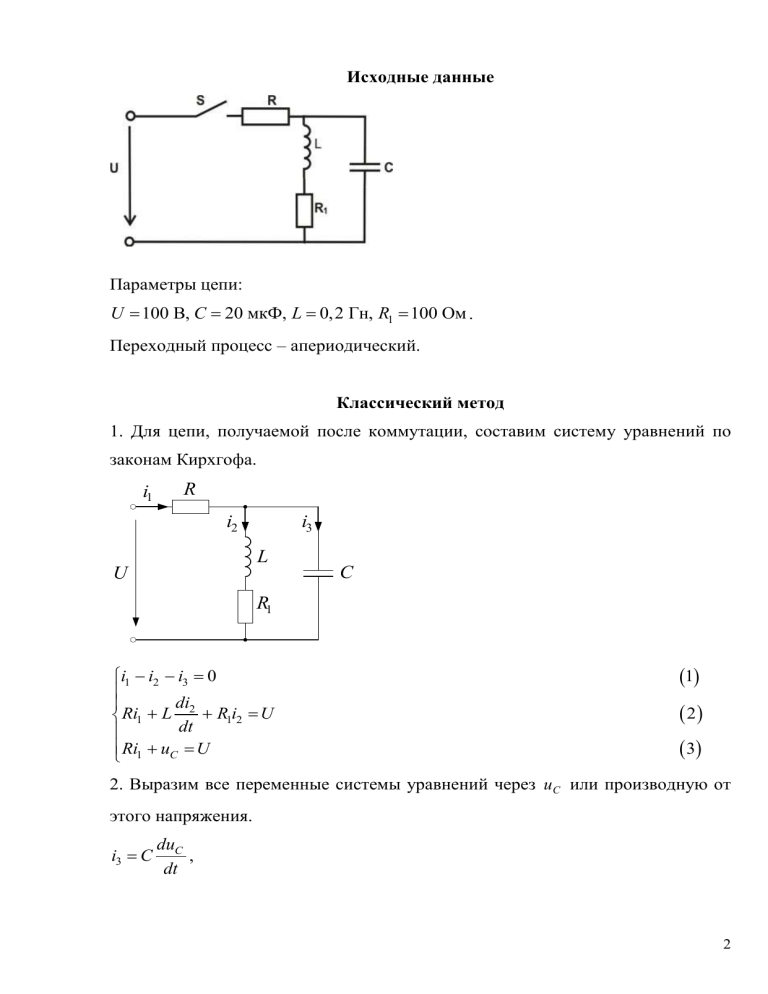
Исходные данные Параметры цепи: U 100 B, C 20 мкФ, L 0,2 Гн, R1 100 Ом . Переходный процесс – апериодический. Классический метод 1. Для цепи, получаемой после коммутации, составим систему уравнений по законам Кирхгофа. i1 R i2 i3 L U C R1 i1 i2 i3 0 di2 R1i2 U Ri1 L dt Ri1 uC U 1 2 3 2. Выразим все переменные системы уравнений через uC или производную от этого напряжения. i3 C duC , dt 2 из уравнения (3) выразим i1 U uС , R подставим в (1) U uС du i2 C С 0, R dt откуда i2 U uС du C С . R dt Подставим полученные выражения для токов в (2) du U uС d C С duС dt U uС U uС R R L R C 1 R dt dt R U, d 2uC L R1 R1 duС LC CR 1 U 1 U, 1 R R dt 2 R dt получаем ЛНДУ второго порядка d 2uC du LCR 2 L CRR1 С R R1 U R1. dt dt Поделив на коэффициент при старшей производной, получим d 2uC 1 R1 duС R R1 UR1 CR L dt LCR LCR . dt 2 Для проверки решения получим ЛНДУ относительно тока i2 и его производных. i3 C duC . dt из уравнения (3) выразим i1 U uС , R подставим в (2) U uС L di2 R1i2 U , dt 3 откуда uC L di2 R1i2 , dt тогда duC d 2i2 di d di2 i3 C C L R1i2 LC 2 R1C 2 . dt dt dt dt dt Из (2) i1 U L di2 R1i2 dt . R Подставим полученные выражения для токов в (1) U L di2 R1i2 d 2i2 di dt i2 LC 2 R1C 2 0, R dt dt d 2i2 L R U di LC 2 CR1 2 1 1 0, R R dt R dt получаем ЛНДУ второго порядка d 2i2 L R U di LC 2 CR1 2 1 1 , R R dt R dt d 2i2 1 R1 di2 R R1 U CR L dt LCR LCR . 2 dt 3. Характеристическое уравнение полученных ЛНДУ одинаково: R R R1 1 p2 1 p 0. LCR CR L Дискриминант полученного квадратного уравнения 2 2 R R R1 L CRR1 R R1 1 D 1 4 4 CR L LCR LCR LCR 2 L CRR1 4 LCR R R1 , 2 LCR для определения Rкр приравняем D 0 : L CRR1 2 4 LCR R R1 0, 4 L2 2 LCRR1 C 2 R 2 R12 4 LCR 2 4 LCRR1 0, R 2 C 2 R12 4 LC 2 LCR1 R L2 0, подставим численные значения 1,2 105 R 2 8 104 R 0,04 0, корни этого уравнения R1 33,3, R 2 100. Т.к. R 0 , то принимаем Rкр 33,3 Ом . Исследуем зависимость D от R , т.к. коэффициент при R 2 отрицательный, то график зависимости D R имеет вид. При R Rкр D 0 , что соответствует апериодическому переходному процессу. Примем R 10 Ом , тогда значение дискриминанта 2 2 R R R1 1 100 10 100 1 D 1 4 4 LCR 20 106 10 0,2 0,2 20 106 10 CR L 1,925 107 0. 3. Решение ЛНДУ ищем в виде uС uCсв uCпр , причем свободная составляющая uCсв A1e p1t A2 e p2t , где A1 , A2 - постоянные интегрирования. 5 Характеристическое уравнение R R R1 1 p2 1 p 0, LCR CR L p 2 5500 p 2,75 106 0, дискриминант D 1,925 107 , корни уравнения p1 5500 1,925 107 4944 с 1 , 2 5500 1,925 107 p2 556 с 1. 2 Итак, свободная составляющая напряжения uCсв A1e 4944t A2 e 556t . 4. Найдем принужденную составляющую напряжения uCпр (напряжение на конденсаторе в новом установившемся режиме) i1пр R i3пр i2пр L C U uCпр R1 uCпр i2 пр R1 U 100 R1 100 90,9 B . R R1 10 100 uС uCсв uCпр A1e4944t A2e556t 90,9 . 5. Для определения двух постоянных интегрирования A1 и A2 необходимо использовать второе уравнение, найдем производную uC duС A1 p1e p1t A2 p2 e p2t . dt 6 При t 0 uС 0 A1 A2 uCпр , uС 0 p1 A1 p2 A2 . Найдем начальные условия uC 0 и uC 0 . i3 C duС du i , следовательно, С 3 . dt dt C До коммутации цепь разомкнута, поэтому uC 0 0, i3 0 0 , uC 0 i3 0 C 0. Таким образом, имеем систему уравнений 0 A1 A2 90,9, 0 4944 A1 556 A2 . Отсюда A1 11,5 A2 102,4 . Искомое напряжение uC 11,5e4944t 102,4e556t 90,9, B . 6. Вычислим токи в цепи duC d 20 106 11,5e4944t 102,4e556t 90,9 dt dt 1,14e4944t 1,14e556t , A. i3 C 4944t 102,4e556t 90,9 U uС 100 11,5e i1 R 10 1,15e4944t 10,24e556t 0,91, A, i2 i1 i3 1,15e4944t 10,24e556t 0,91 1,14e4944t 1,14e556t 0,01e4944t 9,1e556t 0,91, A. 7 7. Найдем значения полученных величин в моменты времени t 0 (начальные значения после коммутации) и t (принужденные значения): t 0 t i1 , A 10 0,91 i2 , A 10 0,91 i3 , A 0 0 uC , B 0 90,9 8. Построение графиков изменения напряжения uC t и токов i1 t , i2 t , i3 t . Построим графики изменения на интервале от t 0 до t 3 pmin , где pmin - меньший по модулю корень характеристического уравнения. 3 pmin 3 0,0054 c . 556 8 9 Операторный метод К моменту коммутации в цепи установились начальные условия: i1 0 i2 0 i3 0 0 , uC 0 0 . После коммутации уравнения Кирхгофа в операторной форме имеют вид: I1 p I 2 p I 3 p 0 R I1 p R1 pL I 2 p U p Li2 0 uC 0 1 R I p I p U p 1 3 pC p Учитывая, что U p U , а также i2 0 0, uC 0 0 , совместно решим p уравнения относительно тока I1 p . U R I1 p p I2 p , R1 pL U R I1 p p I3 p , 1 pC тогда U U R I1 p R I1 p p p I1 p 0, 1 R1 pL pC U R I1 p 1 pCR R1 pL p 1 pC , R1 pL откуда 10 1 U pC 1 pC R1 pL R pL p 1 I1 p R R pL R pCR R pL 1 1 1 pCR R1 pL U p p 2 LCU pCR1U U p p 2 LCR p L CRR1 R R1 F1 p pF3 p . Подставив числовые значения, получим F1 p p 2 0,2 20 106 100 p 20 106 100 100 100 0,0004 p 2 0,2 p 100, F3 p p 2 0,2 20 106 10 p 0,2 20 106 10 100 10 100 0,00004 p 2 0,22 p 110. По изображению тока найдем его оригинал при помощи теоремы разложения с использованием формулы i1 t F1 0 F3 0 2 k 1 F1 pk e pk t . pk F3 pk При p 0 F1 p 100, F3 p 110. Найдем корни уравнения F3 p 0 : 0,00004 p 2 0,22 p 110 0, 0,22 0,222 4 0,00004 110 p1,2 , 2 0,00004 p1 4944, p2 556. Вычислим значения F1 p1 0,0004 4944 0,2 4944 100 8887,5, 2 F1 p2 0,0004 556 0,2 556 100 112,5, 2 F3 p 0,00008 p 0,22 , 11 F3 p1 0,00008 4944 0,22 0,175, F3 p2 0,00008 556 0,22 0,175. После подстановки функций в формулу теоремы разложения, получим значение искомого тока i1 t 100 8887,5 112,5 e4944t e556t 110 4944 0,175 556 0,175 0,91 1,15e4944t 10,24e556t 1,15e4944t 10,24e 556t 0,91, A. Полученное выражение тока совпадает с выражением, найденным классическим методом. 12






![К употреблению указательных местоимений в шугнанском языке[1]](http://s1.studylib.ru/store/data/003711712_1-25a98130f71ee74a801780f3cd9f8c66-300x300.png)

