РГР1 Рахматуллеав

Некоммерческое акционерное общество
«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»
Кафедра “ЭТ ”
Расчетно-графическая работа № 1
По дисциплине ТОЭ1_______________________________________________
___________________________________________________________________
На тему: Расчёт разветвлённых линейных цепей постоянного тока
___________________________________________________________________
___________________________________________________________________
Специальность 5В071800 – Электроэнергетика______________
__________________________________
___________________________________________________________________
Выполнил: Рахматуллаев Ташмухаммад
Группа: ЭиЭИО-19-27
№ зачетной книжки: 154137
Приняла: Смагулова Г
(ученая степень, звание, Ф.И.О.)
_______ ________________ «____» ________________ 2022 г.
(оценка) (подпись)
Алматы 2022
1 Задание № 1. Расчёт разветвлённых линейных цепей постоянного тока
Для электрической цепи, заданной в соответствии с вариантом таблицами
2.1-2.3 и рисунками 2.1-2.20, выполнить следующее:
а) составить систему уравнений по законам Кирхгофа;
б) рассчитать токи во всех ветвях методами контурных токов и узловых
потенциалов, сопоставить результаты расчётов двумя методами, определить
погрешность расчётов;
в) составить уравнение баланса мощностей и проверить точность, с которой
он выполняется.
г) рассчитать один из токов (таблица 2.3) методом активного
двухполюсника (эквивалентного генератора) и сопоставить полученный результат
со значениями этого тока, полученными при расчете методами контурных токов и
узловых потенциалов.
2 Расчетная часть
Выпишем значения ЭДС, сопротивлений и тока источника тока:
Е1, В
Е2, В
Е3, В
Е4, В
Е5, В
Е6, В
0
0
100
150
200
220
R1, Ом
R2, Ом
R3, Ом
R4, Ом
R5, Ом
30
80
40
90
60
J, A
6
2
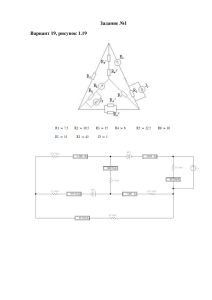
Рисунок 1 – Заданная схема цепи
Для начала необходимо выполнить эквивалентное преобразование схемы.
Преобразуем 3 ветвь цепи содержащую источник тока и ЭДС, в одну ветвь
содержащую ЭДС,тогда:
Направления J и E5 не совпадают, значит справедлива формула:
Eэкв5=E5-R5J
Eэкв5= 200-60*6= -160 В
Перерисуем схему с преобразованной ветвью и удалим ЭДС равные нулю:
3
Рисунок 2 – Перерисованная схема цепи
Расставим номера узлов, токи в ветвях, а также обозначим направление
обхода контуров:
4
Рисунок 3 – Перерисованная схема цепи
Составим на основании законов Кирхгофа систему уравнений для расчёта
токов в ветвях схемы классическим методом. Поскольку схема имеет 4 узла, то по
1-му закону Кирхгофа составим 4-1=3 уравнения. Так как всего 6 ветвей, то по 2му закону Кирхгофа составим 6-4+1=3 уравнения. Всего составим 6 уравнений для
6 неизвестных токов:
𝐼2 − 𝐼1 − 𝐼5 = 0
- для узла 1
𝐼4 − 𝐼3 − 𝐼2 = 0
- для узла 2
𝐼1 + 𝐼3 − 𝐼6 = 0
- для узла 3
−𝐼2 𝑅2 − 𝐼4 𝑅4 − 𝐼5 𝑅5 = −𝐸4 − 𝐸5- контур 1241
𝐼1 𝑅1 − 𝐼3 𝑅3 + 𝐼2 𝑅2 = −𝐸3 - контур 1321
{ 𝐼3 𝑅3 + 𝐼4 𝑅4 = 𝐸3 + 𝐸6 + 𝐸4 - контур 2342
1 Метод контурных токов
Определим токи в ветвях схемы методом контурных токов, предварительно
выбрав все независимые контуры и произвольно задав направления контурных
токов. Данная схема имеет 3 независимых контура, следовательно, составим
систему из 3 уравнений для расчета контурных токов:
5
𝐼11 (𝑅1 + 𝑅4 + 𝑅5 ) − 𝐼22 𝑅2 − 𝐼33 𝑅4 = −𝐸4 − 𝐸5
{ −𝐼11 𝑅2 + 𝐼22 (𝑅1 + 𝑅2 + 𝑅3 ) − 𝐼33 𝑅3 = −𝐸3
−𝐼11 𝑅4 − 𝐼22 𝑅3 + 𝐼33 (𝑅4 + 𝑅3 ) = 𝐸3 + 𝐸6 + 𝐸4
Определяем собственные сопротивления контуров. Для этого складываем
сопротивления в каждом контуре:
𝑅11 = 𝑅1 + 𝑅4 + 𝑅5 = 30 + 90 + 60 = 180 Ом
𝑅22 = 𝑅1 + 𝑅2 + 𝑅3 = 30 + 80 + 40 = 150 Ом
𝑅33 = 𝑅4 + 𝑅3 = 90 + 40 = 130 Ом
Затем определяем общие сопротивления:
𝑅12 = 𝑅21 = −𝑅2 = −80 Ом
𝑅13 = 𝑅31 = −𝑅4 = −90 Ом
𝑅23 = 𝑅32 = −𝑅3 = −40 Ом
Определим контурные ЭДС:
𝐸11 = −𝐸4 − 𝐸5 = −150 − 200 = −350 В
𝐸22 = −𝐸3 = −100 В
𝐸33 = 𝐸3 + 𝐸6 + 𝐸4 = 100 + 220 + 150 = 470 В
Система уравнений для расчета токов по методу контурных токов имеет вид:
180𝐼11 − 𝐼22 ∙ (−80) − 90𝐼33 = −350
{−𝐼11 ∙ (−80) + 150𝐼22 − 40𝐼33 = −100
−90𝐼11 − 40𝐼22 + 130𝐼33 = 470
Решая систему при помощи определителей, определим токи I11, I22, I33.
Рассчитаем определитель системы  :
𝑅11
𝛥 = |𝑅21
𝑅31
𝑅12
𝑅22
𝑅32
𝑅13
180 −80 −90
𝑅23 | = |−80 150 −40| = 599000
𝑅33
−90 −40 130
Рассчитаем определители 11, 22, 33 :
6
𝛥11
𝐸11
= |𝐸22
𝐸33
𝑅12
𝑅22
𝑅32
𝑅13
−350 −80 −90
𝑅23 | = |−100 150 −40| = 184000
𝑅33
470 −40 130
𝛥22
𝑅11
= |𝑅21
𝑅31
𝐸11
𝐸22
𝐸33
𝑅13
180 −350 −90
𝑅23 | = |−80 −100 −40| = 338000
𝑅33
−90 470 130
𝑅11 𝑅12 𝐸11
180 −80 −350
𝛥33 = |𝑅21 𝑅22 𝐸22 | = |−80 150 −100| = 2397000
𝑅31 𝑅32 𝐸33
−90 −40 470
Определим контурные токи по формулам:
𝐼11 =
𝛥11 184000
=
= 0,3071 𝐴;
𝛥
599000
𝐼22 =
𝛥22 338000
=
= 0,5642 𝐴;
𝛥
599000
𝐼33 =
𝛥33 2397000
=
= 4,5025 𝐴.
𝛥
599000
Рассчитаем токи в ветвях электрической цепи.
Токи в ветвях 𝐼1 ,
𝐼5 ,
𝐼6 равны контурным токам:
𝐼1 = 𝐼22 = 0,5642 𝐴;
𝐼5 = −𝐼11 = −0,3071 𝐴;
Токи в ветвях 𝐼2 , 𝐼3 , 𝐼4 , общих для нескольких контуров равны
алгебраической сумме контурных токов, протекающих по этим ветвям:
𝐼2 = 𝐼22 − 𝐼11 = 0,5642 − 0,3071 = 0,2571 А;
𝐼3 = 𝐼33 − 𝐼22 = 4,5025 − 0,5642 = 3,9383 А;
𝐼4 = 𝐼33 − 𝐼11 = 4,5025 − 0,3071 = 4,1954 А.
Ток I₆ определим по первому закону Кирхгофа:
𝐼6 = 𝐼1 + 𝐼3 = 0,5642 + 3,9383 = 4,5025 А.
7
2 Метод узловых потенциалов
Определим узловые потенциалы для электрической цепи.
Рассчитаем проводимости каждой ветви:
1
= 0,0333 См;
𝑅1
1
𝑔2 =
= 0,0125 См;
𝑅2
𝑔1 =
1
= 0,025 См;
𝑅3
1
𝑔4 =
= 0,0111 См;
𝑅4
1
𝑔5 =
= 0,0166 См;
𝑅5
𝑔3 =
Приравниваем к нулю потенциал любого узла, пусть φ3=0, тогда φ4=E6
Запишем уравнения для определения узловых потенциалов:
𝜙1 (𝑔1 + 𝑔2 + 𝑔5) − 𝑔2 𝜙2 = ∑ 𝐸𝑔 + 𝜑4𝑔2
1
−𝑔2𝜙1 + 𝜙2 (𝑔2 + 𝑔3 + 𝑔4) = ∑ 𝐸𝑔 + 𝜑4𝑔4
2
}
g11, g22 - cобственная узловая проводимость, равна сумме проводимостей
ветвей, присоединенных к данному узлу.
𝑔22
𝑔11 = 𝑔1 + 𝑔2 + 𝑔5 = 0,0333 + 0,0125 + 0,0166 = 0,0624 𝐶м;
= 𝑔2 + 𝑔3 + 𝑔4 = 0,0125 + 0,025 + 0,0111 = 0,0486 𝐶м.
𝑔12 = 𝑔21 −общая узловая проводимость, равна сумме проводимостей
ветвей, соединяющих между собой рассматриваемые узлы.
g12 = g 21 = −g 2 = −0,0125 Cм.
 Eg - алгебраическая сумма произведений э.д.с. на соответствующие
проводимости для всех ветвей, присоединенных к рассматриваемому узлу. Если
8
э.д.с направлена к рассматриваемому узлу, записывается знак «+», если э.д.с
направлена от узла - « -».
∑1 𝐸𝑔 + 𝜑4𝑔2 = −𝐸5 𝑔5 + 𝜑4𝑔2 = −0,57 В;
∑2 𝐸𝑔 + 𝜑4𝑔4 = 𝐸4 𝑔4 − 𝐸3 𝑔3 + 𝜑4𝑔4 = 1,607 В.
Уравнение для расчета узловых потенциалов запишется в виде:
0,0624𝜙2 − 0,0125𝜙3 = −0,57 В }
−0,0125𝜙2 + 0,0486𝜙3 = 1,607 В
Рассчитаем потенциалы φ2, φ3 при помощи определителей. Определители
для системы уравнений равны:
𝑔22 𝑔23
0,0624 −0,0125
𝛥=|
|=|
| = 0.00287639
𝑔32 𝑔33
−0,0125
0,0486
𝛥11
∑ 𝐸𝑔
= || 2
∑ 𝐸𝑔
𝑔23
𝑔33
| = |−0,57 −0,0125| = −0.0076145
|
1,607
0,0486
3
Δ22=|
𝑔22 ∑2 𝐸𝑔
0,0624
|=|
𝑔32 ∑3 𝐸𝑔 −0,0125
−0,57
|= 0.0931518
1,607
Потенциалы 1, 2 определим по формулам:
𝜙1 =
𝛥11 −0.0076145
=
= −2,647 В;
𝛥
0.00287639
𝜙2 =
𝛥22
0.0931518
=
= 32,385 𝐵.
𝛥
0.00287639
Токи в ветвях электрической цепи определим по закону Ома:
𝜙1 − 𝜙3 −2,647 − 0
=
= 0,5641 𝐴;
𝑅1
30
𝜙2 − 𝜙1 32,385 − (−2,647)
𝐼2 =
=
= 0,2572 А;
𝑅2
80
𝐼1 =
9
𝜙2 − 𝜙3 + 𝐸3 32,385 − 0 + 100
=
= 3,9384 𝐴;
𝑅3
40
𝜙2 − 𝜙4 − 𝐸4 32,385 − 220 − 150
𝐼4 =
=
= 4,1953 𝐴;
𝑅4
90
𝜙1 − 𝜙4 −2,647 − 220
𝐼5 =
=
= −0,3071 𝐴;
𝑅5
60
𝐼3 =
Ток I₆ определим по первому закону Кирхгофа:
𝐼6 = 𝐼1 + 𝐼3 = 0,5641 + 3,9384 = 4,5025 А.
Сравним расчетные токи по МКТ и МУП:
I, А
𝐼1
𝐼2
𝐼3
𝐼4
𝐼5
𝐼6
МКТ
0,5642
0,2571
3,9383
4,1954
−0,3071
4,5025
МУП
0,5641
0,2572
3,9384
4,1953
−0,3073
4,5025
Составим баланс мощностей для данной схемы:
5
𝑃пот = ∑ 𝐼𝑘2 ∙ 𝑅𝑘
𝑘=1
Суммарная мощность потребителей электроэнергии:
𝑃пот = 𝐼12 𝑅1 + 𝐼22 𝑅2 + 𝐼32 𝑅3 + 𝐼42 𝑅4 + 𝐼52 𝑅5
𝑃пот = (0,56422 ∙ 30) + (0,25712 ∙ 80) + (3,93832 ∙ 40) + (−0,30712 ∙
90)+(4,50252 ∙ 60)=1843,10 Вт
Суммарная мощность источников электроэнергии:
4
𝑃ист = ∑ 𝐸𝑘 ∙ 𝐼𝑘
𝑘=1
10
𝑃ист = 𝐸3 𝐼3 + 𝐸4 𝐼4 − 𝐸5 𝐼5 + 𝐸6 𝐼6
𝑃ист = (3,9383 ∙ 100) − (4,1954 ∙ 260) − (0,3071 ∙ 200) + (4,5025 ∙ 220)
= 1843,124 Вт
Баланс мощностей сошёлся: Pпот=Рист - токи определены верно.
Вывод: Я научился составлять уравнения 1 и 2 законов Кирхгофа, а также
применять методы контурных токов и узловых потенциалов для расчета
электрических цепей постоянного тока. Также научился составлять баланс
мощностей.
11
Список литературы
1 Атабеков Г.И. ТОЭ. Линейные электрические цепи.-СПб.: «Лань», 2010.
2 ТОЭ т.1/под ред. Демирчян К.С. и др.-СПб., 2006.
3 Сборник задач по теоретическим основам электротехники/
Л.Д.Бессонов, И.Г.Демидова, М.Е.Заруди и др.-М.: Высшая школа, 2003.-52с.
4 Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические
основы электротехники. Т.1. - СПб.: Питер, 2003.-463с.
Прянишников В.А. ТОЭ: Курс лекций: Учебное пособие – 3-е изд., перераб.
и доп. – СПб., 2000 – 368 с.
5 Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы
теории цепей.- М.: Энергоатомиздат, 1989. -528с.
6 Денисенко В.И., Креслина С.Ю. Теоретические основы электротехники 2.
Конспект лекции (для студентов всех форм обучения специальности 050718 –
Электроэнергетика). - Алматы: АИЭС, 2007. - 62 с.
7 Денисенко В.И., Креслина С.Ю. Теоретические основы электротехники 1.
Конспект лекции (для студентов всех форм обучения специальности 050718 –
Электроэнергетика). - Алматы: АИЭС, 2006. - 63 с.
8 Денисенко В.И., Зуслина Е.Х. ТОЭ. Учебное пособие.- Алматы:
АИЭС, 2000. 83 с.
12