Метод сил. Каноничекое уравнение

Расчет статически неопределимых
систем методом сил
Степень статической неопределимости (ССН)
плоской стержневой системы
Статически неопределимыми называются системы, имеющие лишние (с точки зрения
обеспечения их геометрической неизменяемости) связи. ССН связана с числом степеней свободы
ССН  W . Для плоских рам, имеющих замкнутые бесшарнирные
контуры, ССН увеличивается на 3К, где К - число таких контуров: ССН  W  3K .
системы соотношением:
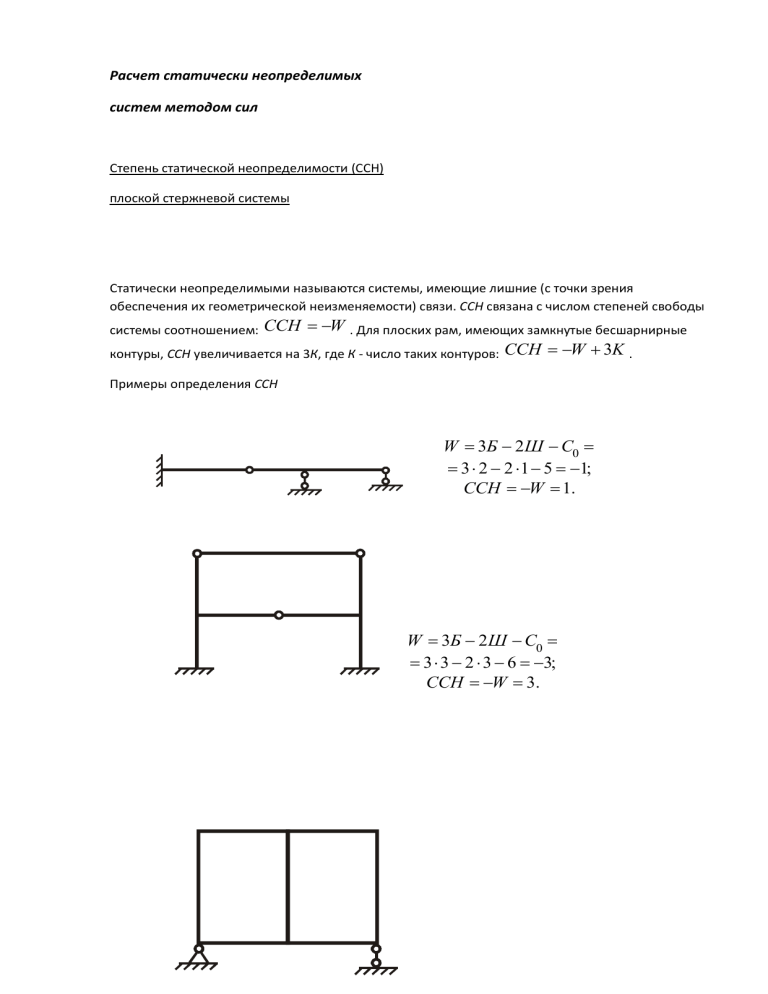
Примеры определения ССН
W  3Б  2 Ш  С0 
 3  2  2 1  5  1;
ССН  W  1.
W  3Б  2 Ш  С0 
 3  3  2  3  6  3;
ССН  W  3.
W  3Б  2Ш  С0  3 1  2  0  3  0;
K  2;
ССН  W  3K  6.
Основная система метода сил
В методе сил любая статически неопределимая система рассчитывается с помощью
соответствующей статически определимой системы, полученной из заданной путем отбрасывания
X , X , , X (n  ССН )
2
n
лишних связей и замены их неизвестными силами (реакциями) 1
.
Полученная таким образом статически определимая система называется основной системой (ОС)
метода сил.
Из заданной статически неопределимой системы можно получить множество вариантов ОС,
отбрасывая различным образом лишние связи (рис. 2.1).
q
q
X2
а
B
X1
Исходная
система:
ССН=2
B
ОС
A
A
q
б
X1
B
q
в
ОС
C
X2
A
A
X2
B
X2
ОС
Рис. 2.1.
X1
Канонические уравнения метода сил
X , X , , X
2
n определяются из условия отсутствия перемещений
Неизвестные силы 1
(абсолютных или относительных) в ОС в направлениях данных сил. Эти условия записываются в
форме канонических уравнений метода сил. Получим такие уравнения на примере системы,
имеющей ССН  2 (рис. 2.2а). Считается, что ОС является линейно-деформируемой системой. В
такой системе справедлив принцип независимости действия сил (принцип суперпозиции).
Согласно данному принципу исходное состояние ОС (рис. 2.2б) можно разложить на три
независимых состояния (рис. 2.2в, 2.2г, 2.2д).
X1 в направлениях X1 и X 2
От силы
в ОС возникают перемещения
этих же направлениях получаются перемещения
X1 и X 2
возникают перемещения
1X ,  2 X
2
2
1X ,  2 X
1
1 . От силы
X2
в
. От нагрузки в направлениях сил
1P ,  2P .
Чтобы ОС была эквивалентной заданной системе, в ней должны выполняться следующие условия:
1X  1X  1P  0;
1
2
 2 X   2 X   2P  0.
1
а)
2
q
P
в)
2X1
1X1
X1
б)
q
P
X1
ОС
г)
X2
X2
д)
Рис. 2.2.
 2X2
1X2
P
1P
q
 2P
Т.к. ОС считается линейно-деформируемой системой, то перемещения в ней от сил
пропорциональны данным силам:
X1 и X 2
1X  11X1; 1X  12 X 2;
1
2
2 X  21 X1;  2 X  22 X 2.
1
2
 (i; j  1; 2)
X 1 
X
j
Здесь i j
- перемещение в ОС в направлении силы i от силы
( ij коэффициенты податливости). Подставляя данные выражения в предыдущие равенства, получаем
канонические уравнения метода сил:
11 X1  12 X 2  1P  0;
21 X1  22 X 2   2P  0.
При
ССН  n
должно быть
n
таких уравнений, которые можно записать в матричном виде:
[]{X }  { P}  0 .
Здесь
11 12


[]   21 22
 
n1 n2
1n 
 X1 
 1P 
 X 
 
1n 
, {X }   2 , { P}   2P 



 


nn 
 X n 
 nP 




,
[] - матрица податливости основной системы.

Свойства матрицы [] : матрица [] всегда является симметричной ( ij

определенной ( i i
0
  ji
) и положительно
).
Определение коэффициентов при неизвестных
и свободных членов канонических уравнений

Так как коэффициенты i j и свободные члены
в направлениях неизвестных сил
рам):
i j   
l
M,M ,M
MiM j
EI
Xi
iP
канонических уравнений - перемещения в ОС
, то их можно определить по формуле Мора (для балок и
ds; iP   
l
MiM P
ds
EI
.
i
j
P
Здесь
- изгибающие моменты в ОС соответственно от сил
заданной нагрузки.
Xi  1 X j  1
,
и
Для ферм:
i j  
k
N k(i) , N k( j) , N k( P)
N k(i) N k( j )lk
N k(i) N k( P)lk
; iP  
EFk
EFk
k
.
- продольные силы в стержнях ОС соответственно от сил
заданной нагрузки;
k
- номер стержня;
EFk , lk
Xi  1 X j  1
,
и
- продольные жесткости и длины стержней.
Определение внутренних сил N, Q, M в заданной системе
Для определения внутренних сил
N , Q, M
(построения эпюр
N , Q, M ) в заданной системе
X
используется ОС при совместном действии
известных сил i и заданной нагрузки по
методике, принятой для расчета статически определимых систем.
Правильность расчета проверяется выполнением условий равновесия узлов конструкции, а также
с помощью кинематической проверки
i   
l
M iM
ds  0 (i  1, 2, ..., n)
EI
,
смысл которой состоит в отсутствии перемещений в ОС направлениях сил
X1, X 2, , X n
.
Пример: дана статически неопределимая рама указанными размерами и нагрузкой (рис. 2.3а).
Построить эпюры N, Q, M.
а
б
q
P
q
P
EI
C
ОС
B
А
D
C
q 16 кН м ;
EI
P  30 кН.
EI
2м
D
X1
А
B
3м
Рис. 2.3.
1. Определение ССН и выбор ОС
ССН  W  (3Б  2 Ш  С0 )  (3  1  2  0  4)  1.
Выбираем ОС, отбрасывая одну лишнюю связь и заменяя ее неизвестной силой
определяемой из канонического уравнения
X1 (рис. 2.3б),
11X1  1P  0.
2. Построение эпюр M1 и MP в ОС
Эпюры
M1 и M P
строятся в ОС соответственно от силы
X1  1 и нагрузки. Для построения
данных эпюр в выбранной ОС в обоих состояниях достаточно определить только реакцию
(рис. 2.4). Эпюры
M1 и M P
приведены на рис. 2.5.
XA
q
А
P
D
C
XA  1
X1  1 B
YA
D
C
А
RB
X A  P  30
B
YA
RB
Рис. 2.4.
2
2
2
2
C
D
C
60
48
D
60
ql 2
 18
8
M1
А
А
B
MP
B
Рис. 2.5.
3. Определение δ11, Δ1P и силы X1
 ,
Значения 11 1P определяются по формуле Мора. Интегралы Мора на каждом участке
находятся по справочным формулам или по правилу Верещагина:
11  
l
M1M1
1 1
1
 17,333
ds    2  2  2   2  2  2  2  3 2 
EI
EI  3
3
EI

;
q
Δ1P  
P
l
D
C
А
X1
XA
YA
Рис. 2.6.

M1MP
ds 
EI
1  1
3





2

60

2

2

60

4

2

48

2

0
 
EI  3
6
Δ
332
332

; X1   1P 
 19,154кН.
EI
11 17,333
B
RB
4. Построение эпюр N, Q, M
Определяем реакции опор в ОС при совместном действии нагрузки и силы
 M A   P  2  q  3 1,5  RB  3  0;
X1 (рис. 2.6):
RB  44 кН.
 X  P  X A  X1  0; X A  10,846 кН;
 Y  YA  q  3  RB  0; YA  4 кН.
Определяем
N , Q, M
на участках рамы.
Участок АС:
N  YA  4 кН; Q  X A  10,846 кН; M A  0; M C  X A  2  21,692 кН  м.
Участок CD:
N  X A  P  19,154 кН; QC  YA  4 кН;
QD  YA  q  3  44 кН; M C  X A  2  21,692 кН  м;
M D  X A  2  YA  3  q  3 1,5  38,308 кН  м.
Участок BD:
N   RB  44 кН; Q  X1  19,154 кН; M B  0; M D  X1  2  38,308 кН  м.
По полученным результатам строятся эпюры
раме (рис. 2.7).
N , Q, M
4
D
C
в заданной статически неопределимой
D
C
-
-
19,154
- 4
-
N, кН
А
C
44
Q, кН
19,154
44
B
21,692
10,846 +
+
А
B
38,308
9,692
2
ql
 18
8
D
M, кН м
А
B
Рис. 2.7.
5. Проверка равновесия узлов
Равновесие изгибающих моментов в узлах C и D рамы следует из эпюры M. Проверим равновесие
горизонтальных и вертикальных сил в данных узлах (рис. 2.8). Направления
действительными.
N
и
Q
указаны
P
30 C
4
19,154
44
19,154
10,846
D
19,154
4
44
Рис. 2.8.
Узел С:
 X  30  10,846  19,154  0;  Y  4  4  0.
Узел D:
 X  19,154  19,154  0;  Y  44  44  0.
6. Кинематическая проверка
M1M
1  1
1
ds 
  2  21,692  2   2  38,308  2 

EI  3
3
l EI
3
 2,7 103
 (2  21,692  4  2  9,692  2  38,308) 
 0.
6
EI

1   
Особенности расчета методом сил статически
неопределимых неразрезных балок
Наиболее рациональная основная система (ОС) для расчета неразрезной балки методом сил
получается путем врезания шарниров над всеми опорами балки кроме крайних. Если крайняя
опора – заделка, то она заменяется шарнирной неподвижной опорой. Неизвестными
X ,X ,  , X
n,
обобщенными силами в этом случае являются опорные моменты 1 2
определяемые из канонических уравнений метода сил. Коэффициенты податливости и свободные
члены канонических
уравнений определяются по известным формулам:
i j   
l
M iM j
EI
ds; iP   
l
MiM P
ds
EI
.
Для построения окончательной эпюры изгибающих моментов целесообразно использовать
принцип суперпозиции
n
M   Mi Xi  M P
i 1
.
Первое слагаемое дает эпюру изгибающих моментов от действия опорных моментов
Xi
,
X
которую можно построить откладывая ординаты i в точках приложения этих моментов и
соединяя их на каждом пролете балки прямыми линиями.
Поперечные силы на концах участков балки определяются по формулам
Qлев. 
где
l
М прав.  М лев.
- длина участка;
l
М прав., М лев.

ql
;
2
Qправ. 
М прав.  М лев.
l
ql
,
2
- изгибающие моменты соответственно на левом и правом
концах участка, подставляемые в эти формулы с учетом их знаков;
нагрузка на участке. Если на участке балки
данного участка поперечную силу
Q

q - постоянная погонная
q  0 , то данные формулы дают постоянную для
М прав.  М лев.
l
.
Правильность расчета проверяется выполнением условий равновесия балки:
Y  0 ;  M 0  0 .
Необходимые для этого реакции опор определяются по формуле
Ri  Qправ.  Qлев.
Q
,
,Q
лев.
где прав.
- поперечные силы в сечениях непосредственно справа и слева от
рассматриваемой опоры.
Пример: дана статически неопределимая неразрезная балка с указанными размерами и
нагрузкой (рис. 2.9а). Построить эпюры Q, M.
q1  18 кН м
а)
B
A
q1
X1
C
2,5 м
5м
q2  12 кН м
P 60 кН
X2 X2
6м
P
D
3м
q2
ОС
б)
Рис. 2.9.
1. Определение ССН и выбор ОС
ССН  W  (3Б  2 Ш  С0 )  (3  1  2  0  5)  2.
Выбираем ОС, заменяя заделку неподвижной шарнирной опорой и врезая шарнир над опорой B
(рис. 2.9б). Составляем канонические уравнения для определения опорных моментов
X1 и X 2 :
11 X1  12 X 2  1P  0;
21 X1  22 X 2   2P  0.
2. Построение эпюр M1, M2 и MP в ОС
Эпюры
M1, M 2
строятся в ОС соответственно от моментов
X1  1, X 2  1 (рис. 2.10а, 2.10б).
X1  1
а)
M1
1
0,5
X2  1 X2  1
M2
б)
0,5
0,583
1
Рис. 2.10.
Для построения эпюры
MP
от нагрузки рассмотрим участки AB и BCD основной системы как
отдельные балки на двух опорах (рис. 2.11). На балке AB:
M P,max  q1  52 8  56,25кН  м
M A  M B  0;
.
q1
B
A
q2
P
C
K
B
RB
D
RC
Для балки BCD предварительно определим реакции опор:
 M B  P  2,5  q2  3  7,5  RC  6  0;
 Y  RB  P  RC  q2  3  0;
Находим значения
MP
RC  70 кН;
RB  26 кН
в характерных сечениях балки BCD:
M P, B  0; M P, K  RB  2,5  65 кН  м; M P, D  0;
.
Рис. 2.11.
M P,C  q2  3 1,5  54 кН  м
MP
Строим эпюру
.
(рис. 2.12).
54
2,5 м
B
A
56,25
MP
K
65
C
D
Рис. 2.12.
3. Определение δ11, δ12, δ21, δ22, Δ1P, Δ2P, X1, X2
11   
l
M1  M1
1 1
1,667
dx 
 1 1  5 
;
EI
EI 3
EI
12  21   
l
M1  M 2
1 1
0,833
dx 
  1 1  5 
;
EI
EI 6
EI
22   
M2  M2
1 1
1
 3,667
dx 
;
  1 1  5  1 1  6  
EI
EI  3
3
EI

1P   
M1  M P
1 5
93,75
dx 
  4  56,25  0,5 
;
EI
EI 6
EI
 2P   
M2 MP
1 5
2,5
dx 
 4  56,25  0,5 
(2  65  0,583  65  1) 

EI
EI  6
6
l
l
l

3,5
2  65  0,583  54  0,583  178,259
6
EI .

Подставляя полученные значения в канонические уравнения, из них находим опорные моменты
X1, X 2 : X1  36,038 кН  м; X 2  40,425 кН  м .
4. Построение эпюр М и Q
Строим в ОС эпюру
M
M1X1  M 2 X 2 (рис. 2.13а). Складывая ее с эпюрой M P , получаем эпюру
в заданной неразрезной балке (рис. 2.13б).
40,425
36,038
а)
B
A
56,25
B
A
44,123
A
C
D
54
40,425
C
K
D
36
32,738
B +
+
M
41,419
18,018
в)
M1 X 1  M 2 X 2
K
36,038
б)
23,581
45,877
K
27,262
C +
Q
D
Рис. 2.13.
По известным изгибающим моментам определяем поперечные силы на участках балки:
Участок AB:
QA   40,425  36,038 5  18  5 2  44,123 кН ;
QB   40,425  36,038 5  18  5 2  45,877 кН .
Участок BK:
Q  41,419  40,425 2,5  32,738 кН .
Участок KC:
Q   54  41,419 3,5  27,262 кН .
Участок CD:
QC  0  54 3  12  3 2  36 кН;
QD  0  54 3  12  3 2  0 .
Строим эпюру
Q
(рис. 2.13в).
5. Определение реакций опор и проверка равновесия балки
RA  44,123  0  44,123 кН; RB  32,738 
 45,877  78,615 кН; RC  36  27,262  63,262 кН
Реактивный момент
эпюре
MA
.
и его действительное направление определяется непосредственно по
M : M A  36,038 кН  м .
Проверяем равновесие балки (рис. 2.14):
q1
MA
B
A
RA
5м
RB
q2
P
2,5 м
C
6 м RC
D
3м
Рис. 2.14.
 Y  RA  q1  5  RB  P  RC  q2  3  0;
 M A  M A  q1  5  2,5  RB  5  P  7,5  RC 11  q2  3 12,5  0,005.