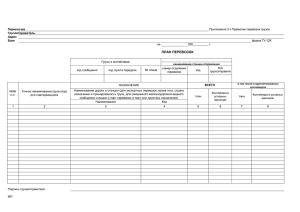
1. ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ Процесс принятия решений может быть неформализованным и формализованным. Принятие неформализованных решений — это творчество, если угодно, искусство. Чтобы принять неформализованное решение, человеку зачастую ничего не надо. Есть вопрос. Пусть даже не совсем четкий. Сел, подумал, решил. Правда, никакой гарантии правильности решения при этом нет. Достаточно часто человек принимает решение вообще без всяких обоснований, руководствуясь так называемым здравым смыслом, опытом, интуицией и другими аналогичными понятиями, которые никому совершенно ничего не объясняют. А потом для убедительности и убеждения самого себя и других придумывают достаточно веские и обоснованные причины, доказывающие правильность интуитивно принятого решения. Что же касается формализованных решений, то они принимаются по четким рекомендациям. При этом различные люди, руководствуясь этими рекомендациями, будут принимать одни и те же решения. Принятие формализованных решений — наука. Этому можно научить. Принятие формализованных решений базируется на двух основных методах: логическом моделировании и оптимизации. Правила определяют, что надо делать в тех или иных случаях. Для этого служат логические функции: И, ИЛИ, ЕСЛИ, НЕ. Самое простое правило выглядит примерно так: ЕСЛИ идет дождь, ТО возьми зонт. Это правило можно уточнить: ЕСЛИ идет дождь И надо выйти из дома, ТО возьми зонт ИЛИ одень плащ. Очевидно, что с помощью подобных уточнений можно давать достаточно конкретные рекомендации по принятию решений в весьма сложных ситуациях. Чтобы моделирование было успешным, надо выполнить три правила. Эти правила, применительно к задачам математического моделирования, формулируются так: учитывать главные свойства моделируемого объекта; пренебрегать его второстепенными свойствами; уметь отделить главные свойства от второстепенных. Составление математической модели начинается с содержательной постановки задачи. Если модель описывает зависимость между исходными данными и искомыми величинами, то алгоритм представляет собой последовательность действий, которые надо выполнить, чтобы от исходных данных перейти к искомым величинам. 2. ПРИМЕР МАТЕМАТИЧЕСКОЙ МОДЕЛИ a b h Cпроектируем, например, бак, имеющий форму прямоугольного параллелепипеда, объем которого 𝑉 = 𝑎 ∙ 𝑏 ∙ ℎ, (1) где a, b, h – стороны бака/ Постановка задачи: требуется определить размеры бака, объемом 𝑉 = 2000, чтобы на его изготовление ушло как можно меньше материала, площадь которого 𝑆 = 2 ∙ [𝑎 ∙ 𝑏 + (𝑎 + 𝑏) ∙ ℎ]. (2) Это же можно записать следующим образом: 𝐹 = 𝑆 → 𝑚𝑖𝑛 𝑉 = 2000 (3) Эта запись читается так: минимизировать величину S при условии, что V = 2000. Подставим в (3) значения V (1) и S (2), тогда получим: 𝐹 = 2 ∙ [𝑎 ∙ 𝑏 + (𝑎 + 𝑏) ∙ ℎ] → 𝑚𝑖𝑛 𝑎 ∙ 𝑏 ∙ ℎ = 2000 Ограничения: a, b, h > 0 , тогда математическая модель решения примет вид: задачи (4) поиска оптимального ЦФ ОГР ГРУ 𝐹 = 2 ∙ [𝑎 ∙ 𝑏 + (𝑎 + 𝑏) ∙ ℎ] → 𝑚𝑖𝑛 𝑎 ∙ 𝑏 ∙ ℎ = 2000 𝑎, 𝑑, ℎ > 0 (6) Эта модель состоит из трех составляющих: целевой функции (ЦФ), ограничения (ОГР), граничных условий (ГРУ). ЦФ — целевая функция или критерий оптимизации, показывает, в каком смысле решение должно быть оптимальным, т. е. наилучшим. Целевая функция зависит от много числа переменных. Можно записать: 𝐹 = 𝑓(𝑥1 , 𝑥2 , 𝑥3 , … 𝑥𝑛 ) (7) ЦФ может принимать одно из трех значений: max; min; Const. ОГР — ограничения переменными. устанавливают зависимости между ГРУ — граничные условия показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении. 3. КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ Рисунок 1 — Классификация по виду математических моделей Исходными данными для математической модели являются: целевая функция, левые части ограничений и их правые части. Как видно из рис. 1, исходные данные могут быть детерминированными и случайными. Детерминированными называются такие исходные данные, когда при составлении модели их точные значения известны. В достаточно распространенных задачах распределения ресурсов точное значение имеющегося ресурса, а также других элементов, входящих в модель, может быть заранее неизвестно. В таких случаях эти элементы модели являются случайными величинами Искомые переменные могут быть непрерывными и дискретными. Непрерывными называются такие величины, которые в заданных граничных условиях могут принимать любые значения. Дискретными называются такие переменные которые могут принимать только заданные значения. Целочисленными называются такие дискретные переменные, которые могут принимать только целые значения. Зависимости между переменными (как целевые функции, так и ограничения) могут быть линейными и нелинейными. Напомним, что линейными называются такие зависимости, в которые переменные входят в первой степени и с ними выполняются только действия сложения или вычитания. Если же переменные входят не в первой степени или с ними выполняются другие действия, то зависимости являются нелинейными. При этом следует иметь в виду, что если в задаче хотя бы одна зависимость нелинейная, то и вся задача является нелинейной. 4. ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ Составить математическую модель объекта оптимизации Выбрать критерий оптимальности и составить целевую функцию Установить возможные ограничения, которые должны накладываться на переменные Выбрать метод оптимизации, который позволит найти экстремальные значения искомых величин ПРОЦЕСС ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ 1.Для определения каких величин строится модель (т.е. каковы переменные модели)? 2.В чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные? 3.Каким ограничениям должны удовлетворять неизвестные? Методы решения Методы исследования функций классического анализа Методы, основанные на использовании неопределенных множителей Лагранжа Вариационное исчисление Принцип максимума Линейное программирование Нелинейное программирование Динамическое программирование Геометрическое программирование . 5. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ОПТИМИЗАЦИИ Задача Небольшая фабрика выпускает два типа красок: для внутренних работ – І, наружных работ − Е. Продукция обоих видов поступает в оптовую продажу. Для производства красок используют два исходных продукта А и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 тонн соответственно. Расходы продуктов А и В на 1 т соответствующих красок приведены в таблице 1. Таблица 1. Исходные данные задачи Исходный продукт Расход исходных продуктов на 1 т краски, т Максимально возможный запас, т Краска Е Краска І А 1 2 6 В 2 1 8 Изучение рынка сбыта показало, что суточный спрос на краску І никогда не превышает спроса на краску Е более, чем на 1 т. Кроме того, установлено, что спрос на краску І никогда не превышает 2 т в сутки. Оптовые цены одной тон-ны красок равны: 3000 руб. − для краски Е, 2000 руб. − для краски І. Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным? ОПРЕДЕЛЕНИЕ СОСТАВА СПЛАВОВ Условие Для получения сплавов А и В используются четыре металла I, II, III и IV, требования к содержанию которых в сплавах А и В приведены в таблице 2. Таблица 2 Требования к содержанию металлов в задаче определения состава сплавов Сплав А В Требования к содержанию металла Не более 80 % металла І Не более 30 % металла ІІ От 40 до 60 % металла ІІ Не менее 30 % металла ІІІ Не более 70 % металла IV Характеристики и запасы руд, используемых для производства металлов I, II, III и IV, указаны в таблице 3. Таблица 3 Характеристики и запасы руд в задаче об определении состава сплавов Руда 1 2 3 Максима льный запас, т 1000 2000 3000 Состав, % I II III IV 20 10 5 10 20 5 30 30 70 30 30 20 Другие Цена компоненты 10 30 10 40 0 50 Пусть цена 1 т сплава А равна 200 долларов, а 1 т сплава В — 210 долларов. Необходимо максимизировать прибыль от продажи сплавов A и В. . Решение Обозначим через х1A, х2A, х3A, х4A и х1B, х2B, х3B, х4B количество I, II, III и IV металлов, используемых для получения сплавов А и В, соответственно. і Количество использованной -й руды обозначим yi , i 1, 3 . Математическая модель: Необходимо максимизировать: z 200( x1 A x 2 A x3 A x 4 A ) 210( x1B x 2 B x3 B x 4 B ) 30 y1 40 y 2 50 y 3 Накладываются ограничения: на состав сплавов (на основании данных из таблицы 2): x1A 0,8( x1A x2 A x3 A x4 A ), x2 A 0,3( x1A x2 A x3 A x4 A ), x2 B 0,6( x1B x2 B x3B x4 B ), x2 B 0,4( x1B x2 B x3B x4 B ), x3B 0,3( x1B x2 B x3B x4 B ), x4 B 0,7( x1B x2 B x3B x4 B ), на характеристики и состав руды (на основании данных из таблицы 3): x1A x1B 0,2 y1 0,1y 2 0,05 y3 , x2 A x2 B 0,1y1 0,2 y 2 0,05 y3 , x3 A x3B 0,3 y1 0,3 y 2 0,7 y3 , x4 A x4 B 0,3 y1 0,3 y 2 0,2 y3 , диапазоны использования переменных: xiA 0, xiB 0, i [1,4], 0 y1 1000, 0 y2 2000, 0 y3 3000 Создадим таблицу в Excel следующего вида: Введем функцию цели в ячейку G9 =200*СУММ(C3:C6)+210*СУММ(D3:D6)30*F3-40*F4-50*F5 Введем левые части ограничений С8:С17 Ячейка С8 С9 С10 С11 Формула =СЗ-0.8*СУММ(СЗ:С6) =С4-0.3*СУММ(СЗ:С6) =D4-0.6*СУММ(D3:D6) =0.4*CУMM(D3:D6)-D4 Ячейка С12 С13 С14 С15 С16 С17 Формула =0.3*CУMM(D3:D6)-D5 =D6-0.7*CУMM(D3:D6) =CУMM(C3:D3)-0.2*$F$3-0.1*$F$40.05*$F$5 =CУMM(C4:D4)-0.1*$F$3-0.2*$F$40.05*$F$5 =CУMM(C5:D5)-0.3*$F$3-0.3*$F$40.7*$F$5 =CУMM(C6:D6)-0.3*$F$3-0.3*$F$40.2*$F$5 Используя средство «Поиск решения» получим следующий результат: ТРАНСПОРТНАЯ ЗАДАЧА Условие Рассмотрим пример, где используется средство поиска решений. Предположим, что фирма имеет 4 фабрики и 5 центров распределения её товаров. Фабрики фирмы располагаются в Гродно, Бресте, Витебске и Гомеле с производственными возможностями 200, 150, 225, и 175 единиц продукции ежедневно, соответственно. Центры распределения товаров фирмы располагаются в Минске, Могилеве, Киеве, Москве и СанктПетербурге с потребностями в 100, 200, 50, 250 и 150 единиц продукции ежедневно, соответственно. Хранение на фабрике единицы продукции, не поставленной в центр распределения, обходится в 0,75 $ в день, а штраф за просроченную поставку единицы продукции заказанной потребителем в центре распределения, но там не находящейся, равен 2,5 $ в день. Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в таблице 4. Таблица 4 Транспортные расходы 1 2 3 4 5 Минск Могилев Киев Москва Санкт-Петербург 1 Гродно 1,5 2 1,75 2,25 2,25 2 Брест 2,5 2 1,75 1 1,5 3 Витебск 2 1,5 1,5 1,75 1,75 4 Гомель 2 0,5 1,75 1,75 1,75 Необходимо так спланировать перевозки таким образом, чтобы минимизировать суммарные транспортные расходы. Поскольку данная модель сбалансирована (суммарный объём произведённой продукции равен суммарному объему потребностей в ней), то в этой модели не надо учитывать издержки, связанные с недопоставками продукции. В противном случае в модель нужно было бы ввести: ●В случае перепроизводства – фиктивный пункт распределения, стоимость перевозок единицы продукции, в который предполагается равной стоимости складирования, а объём перевозок – объёмом складирования излишков продукции на фабриках. ●В случае дефицита – фиктивную фабрику, стоимость перевозок единицы продукции, с которой полагается равной стоимости штрафов за недопоставку продукции, а объём перевозок – объёмам недопоставок продукции в пункты распределения. Построим математическую модель. Неизвестными в данной задаче являются объёмы перевозок. Пусть xij – объём перевозок с i-й фабрики в j-й центр распределения. Функция цели – это суммарные транспортные расходы, т.е. 4 5 z Ci j X i j i 1 j 1 где cij – стоимость перевозки единицы продукции с i-й фабрики в распределения. j -й центр Неизвестные в данной задаче должны удовлетворять следующим ограничениям: − объёмы перевозок не могут быть отрицательными; − так как модель сбалансирована, то вся продукция должна быть вывезена с фабрик, а потребности всех центров распределения должны быть полностью удовлетворены. В результате имеем следующую модель: Необходимо минимизировать: 4 5 z Ci j X i j i 1 j 1 при ограничениях: 4 X i 1 ij 5 X i 1 ij bj , j 1, 5 ai , i 1, 4 X i j 0, i 1, 4, j 1, 5 где – объём производства на i-й фабрике, спрос в j-м центре распределения. Создадим таблицу следующего вида: Данная задача является сбалансированной. В ячейки B2:F5 введены стоимости перевозок. Ячейки B7:F10 отведены под значения неизвестных (объёмы перевозок). В ячейки H7:H10 введены объёмы производства на фабриках, а в ячейки B12:F12 введена потребность в продукции в пунктах распределения. В ячейку G12 введена целевая функция Целевая функция Ячейка G12 Формула =СУММПРОИЗВ (B2:F5;B7:F10) В ячейки B11:F11 введены формулы, определяющие объём продукции, ввозимой в центры распределения. Ячейка B11 C11 D11 E11 F11 Формула =СУММ(B7:B10) =СУММ(С7:С10) =СУММ(D7:D10) =СУММ(Е7:Е10) =СУММ(F7:F10) В ячейки G7:G10 введены формулы, вычисляющие объём продукции, вывозимой с фабрик. Ячейка G7 G8 G9 G10 Формула =СУММ(B7:F7) =СУММ(B8:F8) =СУММ(B9:F9) =СУММ(B10:F10) Промежуточные результаты решения транспортной задачи Фрагмент диалогового окна Поиск решения для транспортной задачи Для линейных задач используется симплекс-метод Фрагмент диалогового окна Параметры Оптимальное решение транспортной задачи