Блудова И.В., Белянова Э.Н. - Начала топологии в примерах и задачах - 2016

Московский государственный технический университет имени Н.Э. Баумана И.В.Блудова,Э.Н.Белянова Начала топологии в примерах и задачах Рекомендовано УМО по математике педвузов и университетов Волго-Вятского региона в качестве учебного пособия для студентов высших учебных заведений Москва ИЗДАТЕЛЬСТВО МГТУ им. Н. Э. Баумана 2 О 1 б УДК 515.1(075.8) ББК 22.152 Б70 Издание доступно в электронном виде на портале ebooks.bmstu.ru по адресу: http://ebooks.bmstu.ru/catalog/291/Ьookl 494.html Специализированный учебно-научный центр Кафедра «Основы математики и информатики» Рецензенты: д-р физ.-мат. наук, профессор Ю. В. Садовничий, д-р техн. наук, профессор С. С Граськин Блудова, И. В. Б70 Начала топологии в примерах и задачах: учебное пособие/ И. В . Блудова, Э. Н. Белянова. МГТУ им. Н. Э. Баумана, 2016. - - Москва : 126, [4] с.: ил. Издательство ISBN 978-5-7038-4230-0 В учебном пособии рассмотрены различные классические приме ры топологических и метрических пространств и непрерывных отоб ражений, сформулированы все необходимые топологические опреде ления и утверждения. Читателям предлагается самостоятельно доказать некоторые свойства указанных вьШiе топологических и метрических пространств, а в случае недостаточной успешности попыток получить эти доказательства - узнать подробные решения предложенных задач. Для студентов технических вузов. Может использоваться как пре подавателями в качестве иллюстрации топологических понятий, так и студентами для самостоятельной работы. Отдельные разделы пособия могут быть полезны при проведении элективных курсов для средней школы, а также для занятий с учащимися в классах с углубленным изу чением математики. УДК ББК ISBN 978-5-7038-4230-О 515.1(075.8) 22.152 © МГТУ им. Н. Э. Баумана, 2016 © Оформление. Издательство МГТУ им. Н. Э. Баумана, 2016 ПРЕДИСЛОВИЕ Вся математика строится на базе теории множеств, а на теоре тико-множественную топологию опираются все разделы матема тики, в которых используется понятие непрерывного отображения . Таким образом, теоретико-множественная топология является вто рой по общности (после теории множеств) фундаментальной частью математики. Она тесно связана со многими разделами ма тематики, в первую очередь с классическим математическим ана лизом, теориями функций действительного и комплексного пере менного, обыкновенными дифференциальными уравнениями, функциональным анализом, геометрией, алгеброй, теорией дина мических систем, теорией вероятностей. Студенты сталкиваются с топологией уже на первом курсе при изучении математического анализа. Например, наличие у последо вательности вложенных отрезков числовой прямой общей точки является топологическим свойством этой прямой, называемым ло кальной бикомпактностью. Теорема Вейерштрасса об ограничен ности непрерывной на отрезке функции и достижении ею точной верхней грани выражает топологическое свойство отрезка, называ емое бикомпактностью, а теорема о промежуточных значениях непрерывной на отрезке функции - другое топологическое свой ство отрезка, называемое связностью. Часто теоремы о существо вании и единственности решения обыкновенного дифференциаль ного уравнения или системы таких уравнений выводятся из теоремы Банаха о неподвижной точке сжимающего отображения полного метрического пространства в себя. (Теория метрических пространств - часть теоретико-множественной топологии.) В настольной книге всех теоретико-множественных топологов Р . Энгелькинга «Общая топология» [1] говорится : «Весьма важ- 3 ную роль в приложениях в настоящее время начали играть специ альные примеры из общей топологии: канторово совершенное множество, прямая Александрова, ковер Серпинского, пример Кнастера, возникшие ранее из чисто внутренних, логических по требностей топологии. Они легли в основу новых методов распо знавания образов и теории динамических систем». Более подробные сведения о топологии пространств приведе ны в учебных изданиях [2- 5]. Пособие состоит из трех глав, первая из которых имеет вспомогательный характер. В ней сформулированы все необхо димые топологические главу можно определения и утверждения. рекомендовать студентам технических Первую вузов как краткий справочник по теоретико-множественной топологии. Многие задачи, связанные с классическими примерами тополо гических пространств найти в литературе и непрерывных отображений, можно [1, 6-10]. Вторая глава посвящена рассмотрению нескольких классических примеров топологических и метрических пространств и непрерыв ных отображений канторова множества, канторовой лестницы, - пространства иррациональных чисел, ковра Серпинского, универ сальной кривой Менгера, метризуемых и неметризуемых «ежей», стрелки Зоргенфрея, двух стрелок Александрова, лексикографически упорядоченного квадрата. В ней также подробно рассмотрены неко торые простейшие топологические свойства подмножеств Rп, в частности, дана топологическая классификация вещественных ал гебраических линий и поверхностей второго порядка. Свойства указанных выше топологических и метрических про странств представлены в виде задач, которые предлагаются уча щимся для самостоятельного решения. В случае недостаточной успешности попыток читателя получить доказательства свойств в третьей главе приведены подробные решения предложенных во второй главе задач. Пособие может использоваться в процессе обучения на мате матических факультетах университетов, а также в технических вузах, так как в учебной литературе для технических вузов нет си стематического изложения основных топологических и метриче ских понятий и утверждений, и особенно примеров, позволяющих 4 студентам разобраться в этих понятиях и утверждениях. Предлага емое учебное пособие является, в частности, попыткой в какой-то степени заполнить этот пробел . Кроме того, отдельные разделы пособия, например, простейшие типологические свойства под множеств Rп, могут оказаться полезными для исследовательской деятельности и при проведении элективных курсов в школах и классах с углубленным изучением математики (в частности, в СУНЦ МГТУ им. Н.Э. Баумана) . Выражаем искреннюю благодарность профессору Борису Алексеевичу Пасынкову за помощь при написании книги. Мы по стоянно польз овались его советами и рекомендациями. Глава 1 НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ ОБЩЕЙ ТОПОЛОГИИ Приведем некоторые определения и теоремы, лежащие в осно ве теоретико-множественной топологии. Определение 1. Метрическим пространством называют пару (Х, р), состоящую из некоторого множества (пространства) Х эле ментов (точек) и расстояния (= метрики) р, т. е. однозначной не отрицательной действительной функции р(х,у), определенной для любых х и у из Х и удовлетворяющей следующим аксиомам: 1) р( х, у) = О тогда и только тогда, когда х = у; 2) р(х,у) = р(у,х) (аксиома симметрии); 3) p(x,z) ~ р(х,у) + p(y,z) (аксиома треугольника). Пример. Положив для элементов произвольного множества р(х,у) = о если х {1, ' если х =у =1=- у, ' получим метрическое пространство. Его называют дискретным метрическим пространством . Определение 2. Если р есть расстояние на множестве Х, то сужение р на каждое множество ЕсХ(т. е. расстояние между точ ками в Е равно расстоянию между ними в Х) также есть расстоя ние. Метрическое пространство Е называют подпространством метрического пространства Х Определение 3. Отображение «на» : f: (Х, р) • (У, р') - отоб- ражение метрического пространства Х с метрикой р на метрическое пространство У с метрикой р' называют изометрическим (или изо- 6 метрией), если для любых х 1 , х2 ЕХ имеем р(х1 , х2 ) Если f = p'(.fx1,.fx2). есть отображение «в», то его называют изометрическим вложением . Определение Сферической окрестностью ОЕ х точки х ради- 4. уса Е в метрическом пространстве Х ( = (Х, р)) называют множество {у ЕХ: р(х,у)<Е}. Определение Точку 5. хЕХ называют внутренней точкой множества А с Х, если :3Е >О : ОЕх с А. Определение 6. Подмножество О метрического пространства Х называют открытым, если в О нет невнутренних точек, т. е. лю бая его точка является внутренней. Теорема 1. Любая сферическая окрестность любой точки мет рического пространства является открытым множеством . Определение 7. Систему всех открытых подмножеств метриче~ ского пространства называют его ~ топологиеи, или топологиеи , ( = порожденной) метрикой. индуцированной Теорема 2 (свойства топологии метрического пространства). Для любого метрического пространства Х выполнены следую щие условия : 1) Х, 0 открыты; 2) пересечение любой конечной системы открытых множеств открыто; 3) объединение любой системы открытых множеств открыто. Определение 8. Отображение f: Х • У метрического про- странства Х в метрическое пространство У называют непрерывным в точке х0 ЕХ, если VE > 0:38>0: (р(х,х0 )<8 ~ ( х Е OЕ х0 • .fx Е OE.fxo) ~ \f OE.fxo :3O8 х0 : Определение 9. • p(.fx,.fx0)<E) ~ f(O8 x 0 ) с OE.fx0. Окрестностью точки в метрическом про странстве называют любое открытое множество в этом простран стве , содержащее данную точку. Теорема 3. Отображение f :Х • У метрических пространств непрерывно в точке х0 Е Х тогда и только тогда, когда для любой окрестности V точки fxo в пространстве окрестность И точки х0 в пространстве Х, что У существует такая f (И) с V. 7 Определение странств 1 О. называют f: Х • Отображение непрерывным, если У оно метрических про непрерывно во всех точках пространства Х. Теорема 4. Отображение f: Х • У метрических пространств непрерывно тогда и только тогда, когда прообраз любого открыто го в пространстве У множества Определение 11. V открыт в пространстве Х Последовательность { хп} ;= 1 точек метриче ского пространства называют фундаментальной, или последова тельностью Коши, если для любого Е для любых k, п: k ~ п и т ~ п, имеем: > О найдется п, такое, что p(xk,xm) < Е (другими сло вами, p(xk,xm) • O при k,m • oo). Определение 12. Метрическое пространство (Х, р) и метрику р называют полными, если любая фундаментальная последователь ность в х сходится. Определение 13. Множество Х называют топологическим про странством, если среди всех его подмножеств выделены некото рые, называемые открытыми, причем выполнены следующие ак сиомы топологического пространства: 1) Х, 0 открыты; 2) пересечение любой конечной совокупности открытых мно жеств является открытым множеством; 3) объединение любой совокупности открытых множеств явля ется открытым множеством. Совокупность Т всех открытых подмножеств данного тополоm ческого пространства называют его топологией. Элементы тополоm ческого пространства, как и метрического, называют точками. Пример. Если Х- топологическое пространство, У - жество множества Х, то множество Ту = { V = И п У: подмно И открыто в Х} является топологией на множестве У. Топологию Ту называют ин дуцированной, а топологическое пространство ( У,Ту) - подпро странством пространства Х Из теоремы 2 следует, что каждое метрическое пространство является топологическим. Определение 14. Отображение /: Х • У топологических про- странств называют непрерывным (на пространстве Х'), если у лю- 8 бого множества V, открытого в пространстве У, прообраз f - v 1 открыт в пространстве Х Определение Окрестностью точки в топологическом про 15. странстве Х называют любое открытое в этом пространстве мно жество, содержащее эту точку. Определение Отображение 16. f: Х • У топологических про- странств называют непрерывным в точке х0 е Х, если для любой окрестности V образа fxo в пространстве У существует такая окрестность И точки х0 в пространствеХ, что /(И) с V. Теорема Отображение 5. f: Х • У топологических про странств непрерывно на всем пространстве Х (в смысле определе ния 14) тогда и только тогда, когда оно непрерывно в каждой точ ке этого пространства. Определение 17. Топологическое пространство, топология ко торого может быть порождена какой-нибудь метрикой, называют метризуемым. Определение Отображение 18. /: Х • У топологических про- странств называют гомеоморфизмом (или топологическим отоб ражением), если оно взаимно однозначно, непрерывно и обратное к нему отображение также непрерывно. Определение 19. Топологические пространстваХи У называют гомеоморфными (или топологически эквивалентными), если су ществует гомеоморфизм одного пространства на другое. 20. Определение Топологическими инвариантами называют свойства топологических пространств, сохраняющиеся при гомео морфизмах. Определение 21. Подмножество F топологического простран ства Х называют замкнутым, если множество Х\ F открыто. Замечание. Пусть Х - топологическое пространство, А с Х; множество В с А замкнуто в А тогда и только тогда, когда существует такое замкнутое в Х множество Определение 22. F, что В = А п F. Множество, которое является одновременно и открытым, и замкнутым, называют открыто-замкнутым . Теорема 6 (свойства замкнутых множеств топологического пространства Х): 1) Х, 0 замкнуты; 9 2) пересечение любой системы замкнутых множеств есть замк нутое множество (в пространстве Х); 3) объединение любой конечной системы замкнутых множеств есть замкнутое множество (в пространстве Х). Теорема Отображение 7. /: Х • У топологических про- странств непрерывно тогда и только тогда, когда прообраз любого замкнутого в У множества замкнут в Х 23. Определение Пусть Х топологическое пространство, - А с Х. Точку х Е Х называют точкой прикосновения множества А, если любая окрестность точки х пересекается со множеством А. 24. Определение Замыканием [ У] множества У, содержащегося в топологическом пространстве Х, называют множество всех его точек прикосновения. Теорема Отображение 8. /: Х • У топологических про- странств непрерывно тогда и только тогда, когда для любого мно жества А с Х и для любой точки х Е [А] выполняется следующее соотношение:ft Е [/А] (или Определение 25. f[A] с [fA]). Совокупность открытых подмножеств I: называют базой топологического пространства Х, если каждое не пустое открытое в Х множество может быть представлено в виде суммы некоторой системы множеств из I:. Теорема множеств 9. Пусть во множестве Х выделена система I: Ga, обладающая следующими свойствами: 1) каждая Ga, Е I:; 2) если х EG'Y с Ga, точка х Е Х хЕ п Ga. и под содержится по крайней мере в одном х Е G~, то существует такое Gr Е I:, что G~. Если объявить в Х открытыми пустое множество и все множе ства, представимые в виде суммы каких-либо топологическим пространством, а система Теорема 10. I: Ga Е I: , то Х будет будет в нем базой. Для того чтобы система открытых множеств {Ga} была базой топологического пространства Х, необходимо и достаточ но, чтобы для каждого открытого множества нашлось бы такое множество 10 G и каждой точки х Е G Ga из этой системы, что х Е Ga с G. Определение 26. Множество А называют всюду плотным в то пологическом пространстве Х, если его замыкание [А] есть все Х Определение 2 7. Топологическое пространство называют се парабельным, если в нем имеется счетное всюду плотное множе ство. Топологическое пространство называют наследственно се парабельным, если любое его подпространство сепарабельно. Теорема 11. Метрическое пространство Химеет счетную базу в том и только в том случае, если оно сепарабельно. Определение 28. Подмножество А топологического простран ства Х называют нигде не плотным в Х, если для любого непустого открытого множества И можно указать непустое открытое множе ство V сИ: V n Определение А=0. 29. Определяющей системой окрестностей точ ки х топологического пространства Х называют такую систему ее окрестностей, что каково бы ни было открытое множество содержащее точку х, найдется окрестность из системы лежащая в I., I. G, целиком G. Если точка х топологического пространства Х имеет счетную определяющую систему окрестностей, то говорят, что в этой точке выполнена первая аксиома счетности. Если это верно для каждой точки пространства Х, то пространство Х называют пространством с первой аксиомой счетности . Определение 30. Непустое топологическое пространство Х называется индуктивно нульмерным (или нульмерным), если каж дая из двух произвольных точек пространства Х имеет окрест ность, не содержащую вторую точку (=Х есть Т1 -пространство), и Х имеет базу из открыто-замкнутых множеств. Определение 31. Систему странстве Х множеств Оа I. открытых в топологическом про называют предбазой пространства Х, если множества, являющиеся пересечениями Оа 1 n ... n возможных конечных подсистем системы I., Оа, все образуют базу про странства Х. Теорема ние f 12. Для того чтобы взаимно однозначное отображе пространства Х на пространство У было гомеоморфным, необходимо и достаточно, чтобы при этом отображении некоторая база пространства Х отображалась на базу пространства У. 11 Теорема 13. Отображение f: Х • У топологических пространств 1 непрерывно, если прообразы /- оа элементов некоторой предбазы L = { Оа } , а, е А , пространства У открыты в пространстве Х Определение 32. Минимальное кардинальное число, являюще еся мощностью какой-либо базы пространства Х, обозначают через wX и называют весом этого пространства. Теорема 14 (Александрова - Урысона). Если вес простран ства Х равен 't, то всякая база В пространства содержит подмноже ство В' мощности 't, также являющееся базой пространства Х Аксиома отделимости Т 0 • Из любых двух точек пространства Х по крайней мере одна имеет окрестность, не содержащую вто рую точку. Аксиома отделимости Т1• Каждая из двух произвольных то чек пространства Х имеет окрестность, не содержащую вторую точку. Аксиома отделимости Т1. Все одноточечные множества в про странстве Х замкнуты. Аксиомы Т1 и Т{ эквивалентны. Аксиома отделимости Т 2 (аксиома Хаусдорфа). Любые две точки пространства Х имеют непересекающиеся окрестности. Аксиома отделимости Т3 • Если х странства Х и F F- произвольная точка про не содержащее эту точку замкнутое множество, с Х\{х}, то х и Fимеют непересекающиеся окрестности. Аксиома отделимости Т3 . Каковы бы ни были точка х е Х и ее окрестность Ох, существует окрестность O1 х точки х, удовлетво ряющая условию [0 1х] с Ох. Аксиомы Т3 и т; эквивалентны. Аксиома отделимости Т 4 • Любые два дизъюнктных замкну тых множества пространства Х имеют дизъюнктные окрестности. Пространства, удовлетворяющие аксиомам Ti, i = О, 1, 2, 3, 4, называют соответственно Т г пространствами. Т2 -пространства называют также хаусдорфовыми простран ствами . Т 1 -пространства, удовлетворяющие аксиомам Т3 , называют ре гулярными. 12 Т1-пространства, удовлетворяющие аксиомам Т4, называют нормальными. Теорема 15 (малая лемма Урысона). Пространство Х тогда и только тогда нормально, когда для любого замкнутого множе ства F с Х и любой его окрестности 0 1F, для которой Определение OF можно найти окрестность [01F] с OF. Пространство Х называют наследственно 33. нормальным, если любое его подпространство ХO с Х нормально. Определение 34. Множеством типа вают любое множество Мс Х, Fcr пространства Х назы являющееся суммой счетного числа замкнутых (вХ) множеств . Множеством типа G0 пространства Х называют любое мно- жество Мс Х, являющееся пересечением счетного числа откры тых множеств пространства Х. Определение 35. Нормальное пространство, в котором любое открытое множество есть множество типа Fcr , называют совер- шенно нормальным . Замечание. Поскольку в любом пространстве Х множества типа Fcr и G0 являются взаимно дополнительными, можно опреде лить совершенно нормальные пространства как нормальные про странства, в которых все замкнутые множества являются G0- множествами . Определение 36. Два множества Р и Q, лежащие в топологиче ском пространстве Х, назьmают функционально отделимыми, если существует определенная на всем Х действительная непрерьmная функция f: Х • [а,~], принимающая во всех точках одного множе- ства значение а, а во всех точках другого множества значение ~ так, что а::; fx::; ~ Теорема для всех точек х е Х (например, 16. Если два множества Р и Q fP =а, fQ = ~). функционально отде лимы, то они имеют дизъюнктные окрестности . Теорема 17 (большая лемма Урысона). Пусть F0 и F1- два з амкнутых непересекающихся множества нормального простран ства Х Для любых двух действительных чисел а, Ь, а ствует действительная непрерывная функция f, < Ь, суще определенная во всем пространстве Х, принимающая значение а во всех точках 13 множества Fo, значение Ь - во всех точках множества влетворяющая всюду в Х неравенству а Теорема 18. ::;; .fx ::;; F1 и удо Ь. Каждая непрерывная функция, заданная на замк нутом подпространстве нормального пространства Х со значения ми в R, непрерывно продолжается на Х Определение Топологическое 37. пространство называется вполне регулярным, если всякая его точка функционально отдели ма от всякого не содержащего эту точку замкнутого множества. Определение 38. Систему cr = {М} подмножеств множества Х называют покрытием множества Х0 с Х, если Х0 с б, где б объединение всех М Е - cr. Покрытие топологического пространства Х открытыми (замк нутыми) в нем множествами называют открытым (замкнутым) покрытием. Определение компактным 39. Топологическое пространство Х называют би ( соответственно, финально компактным), если каж дое открытое покрытие пространства Х содержит конечное (соот ветственно, счетное) подпокрытие этого пространства. З а м е ч а в и е. Подмножество топологического пространства Х назьшают бикомпактным (финально компактным), если оно биком пактно (финально компактно) как подпространство пространства Х Определение Топологическое пространство Х называется 40. топологически однородным, если для любых двух различных то чек Xi,X 2 Е Х f(x1) существует гомеоморфизм f:X • Х, такой, что = Х2. Теорема 19. Любое взаимно однозначное непрерывное отоб ражение бикомпактного топологического пространства на хау сдорфово пространство является гомеоморфизмом. Определение 41. Непрерывное отображение f:X • А тополо- гического пространства Х в свое подпространство А называют ре тракцией, если для любого х Е А имеем Определение 42. f(x) = х. Пусть М- подпространство пространствах Отображение iм: М • Х, заданное формулой iм(х) = х, называ ют вложением подпространства Мв пространство Х. Вложение iм называют замкнутым (открытым), если подпространство М замк нуто (открыто) в Х 14 Отображение f: Х • У называют гомеоморфным вложением, если оно является композицией гомеоморфизма и вложения, т. е. если существуют подпространство L пространства У и гомеомор физм /': Х • L, такие, что f = ir O f'. Г омеоморфное вложение f : Х • У называют замкнутым ( от крытым), если.f{Х) замкнуто (открыто) в У. Определение 43. Топологическое пространство Х называют не связным, если Х можно представить в виде суммы двух непустых непересекающихся открытых (замкнутых) множеств . Замечание. Пространство Х несвязно тогда и только тогда, когда в Х существует нетривиальное (т. е. не совпадающее с 0 и с Х) открыто-замкнутое множество. Определение 44. Пространство, не являющееся несвязным, называют связным. Определение 45. Подмножество топологического пространства называют связным (несвязным), если оно связно (несвязно) как подпространство этого пространства. Теорема 20. Замыкание связного множества связно. Определение 46. Квазикомпонентой точки (в пространстве) называют пересечение всех открыто-замкнутых (в этом простран стве) множеств, содержащих рассматриваемую точку. Пространство называют вполне несвязным, если квазикомпо нента каждой точки содержит только ее. З а м е ч а н и е. Пространство Х вполне несвязно тогда и только тогда, когда оно не имеет никаких связных подмножеств, кроме одноточечных. Определение 47. Пространство Х называют локально связ ным, если для любой точки хЕХ и любой ее окрестности существует меньшая окрестность, являющаяся связным множе ством. Определение 48. Пространство Х называют линейно связным, если для любых двух различных точек непрерывное отображение странство Х), что.f{а) = х1, f: [а, Ь] • Xi, х2 Е Х существует такое 1 Х (отрезка [а, Ь] с R в про j{b) = х2. Пример (топологическое произведение). Пусть дано множе ство А любой мощности 't, элементы которого будем называть ин- 15 дексами и обозначать греческими буквами а. Пусть каждому ин дексу а соответствует некоторое определенное множество Ха. Произведение Х = П Ха полученной системы обозначенных аЕА множеств, по определению, есть множество Х, элементами х = = {ха} которого являются наборы точек ха , получающиеся, если каждому индексу а Е А отнести по одному элементу ха Е Ха. Если дано х ={ха} Е Х, то ха Е х называют а-й координатой точки х Е Х или проекцией этой точки в множество Ха . Отобра жение, ставящее в соответствие произвольной точке х Е Х ее а-ю координату ха, назовем проектированием произведения Х на сомножитель Ха и будем обозначать (обычно) через па . Пусть теперь дано некоторое подмножество А' с А множества индексов и для каждого а Е А' рас Ха; положим для а Е А\ А ' дано некоторое подмножество ра = ха. Тогда множество Р = П Ра с Х называют цилиндром над основанием Р' = П Ра, аЕА аеА' или просто цилиндром над множествами Ра, а Е А'. Легко прове- рить, что р = n 1 7t~ ра. Пусть теперь множества Ха - топологические пространства. Следуя А.Н. Тихонову, введем в произведение Х = П Ха тополоаеА гию следующим образом. Выберем произвольное конечное число индексов ai, ... , as и в каждом Ха, а= а1' ... , a s, возьмем откры- тое множество Иа. Обозначим через о( Иа1 , •• • , Uas) цилиндр над множествами Иа1 сХа1 , •• • , Иа" с Ха., ' т. е. o(ua 1 s , ••• ,uaJ=Пn~~Ua;· Эти i=l множества назовем элементарными открытыми множествами про странства Х = П Ха (с его тихоновской топологией). Открытые аеА множества в этом пространстве 16 определяются как всевозможные суммы элементарных открытых множеств. Условия 1, 2 теоремы 9 при этом, как легко увидеть, выполняются. Теорема 21. Топологическое произведение Х = П Ха любого as4 числа индуктивно нульмерных пространств индуктивно нульмерно. Теорема 22. Топологическое произведение счетного числа метризуемых пространств метризуемо. Теорема 23 (первая теорема Тихонова). Топологическое про изведение Х любой системы {Ха} бикомпактных топологических пространств Ха бикомпактно. Теорема Топологическое произведение любого числа хау 24. сдорфовых пространств есть хаусдорфово пространство. Определение а Е А, 49. Пусть дана система отображений fa: Х • ~' топологического пространства Х в топологические про странства Уа. Тогда отображение f: Х ➔ У= П Уа, ставящее в аЕА соответствие каждой точке х Е Х точку fx = {fax} Е У, называют диагональным произведением отображений Теорема ражений Диагональное 25. fa. произведение f непрерывных непрерывно. fa Определение 50. топологических Пусть дана система отображений пространств Уа, а Е А. Отображение Ха = П Ха в топологические f: П Ха • а54 ведения Х отоб fa: Ха • ¾. пространства П Уа топологического произas4 в топологическое произведение as4 У= П Уа, as4 ставящее в соответствие точке х fx = {fa ха} Е У, и обозначают f = П fa . = {ха} Е Х назьmают произведением отображений fa точку as4 Теорема 26. Произведение f = П fa непрерывных отображе а54 ний fa: ха • уа непрерывно. Определение fi, / 2 , ••• , h, ... 51. Последовательность какого-либо множества Х в отображений метрическое про странство У называют равномерно сходящейся к отображению 17 / :Х • У, если VЕ > О :J k 0 Е N: Vk 2::: k0 и Vх Е Х имеем p(fx,hx) < f,. Теорема 27. Отображение f: Х • У, являющееся пределом равномерно сходящейся последовательности непрерывных отоб ражений топологического пространства Х в метрическое про странство У, есть непрерывное отображение. Определение называют 52. Подмножество метрического пространства ограниченным в этом пространстве, если расстояние между любыми двумя его точками не превосходит некоторого фиксированного числа. Теорема 28 (критерий компактности подмножеств в ев клидовом пространстве). Подмножество евклидова пространства Е п компактно тогда и только тогда, когда оно замкнуто и ограни чено в Е п. Глава 11. КЛАССИЧЕСКИЕ ПРИМЕРЫ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ § 1. Некоторые простейшие подмножества Rn Множество действительных чисел с расстоянием р(х,у) = = (у - х) образует метрическое пространство R 1 . Множество упорядоченных наборов п действительных чисел х п (х~,···,хп ) с расстоянием р(х,у) = называют L(Yk -xk)2 k =I п-мерным арифметическим евклидовым пространством Rп. Предлагаем читателю самостоятельно решить следующие за дачи, доказав топологические свойства подмножеств № 1. Доказать, R n. что любое непустое открытое множество на чис 1 ловой прямой R представляет собой объединение конечной или счетной совокупности попарно непересекающихся интервалов (ограниченных и неограниченных). Пр им е чаи и е. Такое представление открытого множества в виде объединения интервалов единственно (эти интервалы назы вают составляющими интервалами открытого множества на пря мой, а также смежными интервалами замкнутого множества, яв ляющегося дополнением к этому открытому множеству). № 2. Доказать эквивалентность связности и выпуклости под- множеств числовой прямой R 1 . (Напомним, что подмножество R n называют выпуклым, если вместе с любыми двумя своими точ ками оно содержит и весь отрезок, соединяющий эти точки.) 19 № 3. Доказать, что на числовой прямой R нет никаких других 1 связных подмножеств, кроме [а, Ь] , (а, Ь), (а, + оо), (-оо,а] , (-оо,а), (-оо, + оо), {а} , (а, Ь] , [а, Ь), [а, + оо), 0. № 4. Доказать связность п-мерной сферы № 5. sn, п ~ 1. Привести пример связного, но не локально связного и не линейно связного пространства. № 6. Дать топологическую классификацию вещественных ал гебраических линий и поверхностей второго порядка. 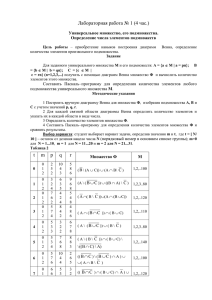§ 2. Канторово Пусть [О, 1] - множество отрезок числовой прямой R два отрезка Л 0 = [О, 1/3] и Л1 = [2/3, 1] 1 Рассмотрим на нем . (будем называть их отрезками первого ранга). Между ними находится интервал (ин 8 = (1/3, 2/3) тервал первого ранга). На каждом отрезке первого ранга выберем по два отрезка второго ранга Л 00 = [О, = [2/3, 7/9], Л 11 = второго ранга • о Лоо [8/9, 1]. Между 80 = (1/9, 2/9) и 81 = (7/9, 8/9) и т. д. &о и Л 10 = (рис. 1). ... ...... Ло1 2/9 [2/9, 1/3] этими отрезками лежат интервалы ... ... ... 1/9 Л 01 = 1/9], 1/3 2/3 Рис. 7/9 • 8/9 1 2n отрезков п-го рангаЛ 1 ½ ... iп (индексы ik принимают значения О или 1). Разделим каждый отрезок Л 1, ½• •·iп на Пусть построены три равные ЧаСТИ . Два КраЙНИХ Отрезка Лit½ ··· iп O И Лit½ ··· iп l Назовем отрезками (п + 1)-го ранга. Лежащий между ними интервал8 11 i назовем интервалом (п 2 •• • iп + 1)-го ранга. Пусть П п есть объединение отрезков ранга п: с= п {Пп: п EN} . Множество С называют канторовым множеством . 20 Множество Пп замкнуто для любого п Е нением является лов (-оо, О) и объединение (1, +оо) двух f\i2 ... iп, так как его допол бесконечных интерва и всех интервалов ранга меньше или равного п , т. е. открытое множество (см. задачу № С= п {Пп: п Е N} N, есть замкнутое а также интервалы 1). Поэтому пересечение множество. •, (-оо, О), (1, +оо) Все интервалы называют смежными интервалами к множеству С. Длина каждого отрезка п-го ранга равна 1/З п. Расстояние между двумя различными отрезками п-го ранга больше или равно 1/Зп. Поэтому каждая точках Е С принадлежит единственному отрезку п-го ранга Лiii 2 ...in, т. е. каждой точке х Е С однозначно соответ- ствует последовательность отрезков (*) а значит, и последовательность индексов (**) При этом каждая последовательность индексов поставлена в соот ветствие одной-единственной точке х Е С, а именно точке, при надлежащей всем отрезкам(*) . Последовательность (**) можно рассматривать как запись не которого действительного числа у, О =:;; у =:;; 1, в виде двоичной дро- би. Таким образом, установлено взаимно однозначное отображе ние множества С на весь отрезок [О, 1]. Следовательно, множество С имеет мощность континуума. Точки множества С, являющиеся концами смежных интерва лов, называют односторонними точками (их, очевидно, лишь счет ное множество), все остальные точки множества С называют дву сторонними точками . Из построения множества С видно, что никакая точка из С не может быть концом двух смежных к С интервалов. Сделаем теперь следующее обобщение классического построе ния канторова множества. 21 Пусть имеем отрезок [а, Ь] Е R 1 . Исключим из него интервал ro, длина которого меньше длины отрезка [а, Ь] и концы которого не совпадают с концами отрезка [а, Ь]. Такое «выбрасывание» интер вала из отрезка назовем стандартным. Оставшиеся отрезки обозна чим cr 0 cr 1 и cr 1 и и назовем отрезками первого ранга. Из отрезков стандартным образом исключим Оставшиеся отрезки обозначим cr 00 , cr 01 , cr 10 , cr11 .. ..... m0 интервалы и и назовем отрез .. ками второго ранга. Продолжим этот процесс бесконечно (рис. ... 800 а • ... 801 Рис. cr 0 m1 • 2). ь 2 Пусть построены 2n отрезков п-го ранга cri1 i,_ ... in (индексы ik принимают значения О или 1). Из каждого отрезка cr ii i 2 ... in стандарт ным образом исключим интервалы roiii2 •..in, два крайних отрезка cr 11 i2 ••• 1n O и назовем отрезками (п cr ii i,, ... i,, 1 + 1)-го ранга. Обозначим через Кп объединение отрезков ранга п. Пусть К= п{Кп: п Е N}. Предлагаем читателю самостоятельно решить следующие за дачи, доказав свойства канторова множества. No 7. Доказать, что множество К = п {Кп: п Е N} и классиче ское канторово множество С (как подпространства числовой пря мой) гомеоморфны. No 8. Построить канторово множество любой меры, заключен ной между О и No 9. 1. Доказать, что канторово множество можно вложить в про странство иррациональных ~ ~ странство числовои прямои No 1О. чисел, рассматриваемое как подпро- Rl . Доказать, что у канторова множества нет изолированных точек. Каждая его точка является точкой конденсации (т. е. в лю бой окрестности любой точки канторова множества содержится континуум его точек). 22 № 11. Доказать, что канторово множество нигде не плотно на прямой. № 12. Доказать, мерно и, что канторово множество индуктивно нуль следовательно, несвязно, вполне несвязно. Привести примеры открытых, но не замкнутых, и наоборот, замкнутых, но не открытых подмножеств пространства С. № 13. Доказать, что канторово множество гомеоморфно счет ной степени простого двоеточия. № 14. Доказать, ства в что при любом вложении канторова множе пространство иррациональных чисел оно является ретрак том этого пространства. № 15. Доказать топологическую однородность канторова мно жества. № 16 (дальнейшее обобщение построения канторова мно жества). Представление пространства в виде объединения k не пустых попарно не пересекающихся замкнутых множеств будем называть разбиением этого пространства на k множеств . Пусть для бикомпактного пространства К для любого п п 2 множеств: EN имеется следующее разбиение на где К00 u u п= 1 К = К0 п= 2 К = К0 0 К01 = К0 , К10 u К1 ; u К0 1 u К1 0 u К11 = К1 и т. д. Если имеем разбиение пространства К на (индексы принимают значения О или = Ki1 •••in_ 1 , то, разбивая каждое множество K i1... in O К11 , 1), 2п множеств где К ii .. .in-i O u К ii ...i,,_11 = K ~... in на два множества и Ki1· ··iп l ' получим разбиение пространства к на жеств К 1. Ki1 ... in 2n+l мно .. . 1 • •• 1п 1п+I Доказать, что если при этом каждая последовательность мно- жеств Ki ::, K i ½ 1 1 ::, ••• ::, Ki .. .in 1 :::, • • . имеет единственную общую точку х Е К, то пространство К и классическое канторово множе ство С гомеоморфны. № 17. Доказать, что канторово множество гомеоморфно своей счетной степени. 23 № 18. Доказать, что любое компактное метрическое простран ство является непрерывным образом канторова множества. № 19 (внутренняя характеризация канторова множества). Доказать, что любое компактное метрическое нульмерное про странство без изолированных точек гомеоморфно канторову мно жеству. № 20. Доказать, что тихоновское произведение любой счетной системы конечных дискретных неодноточечных пространств го меоморфно канторову множеству. № 21. Доказать, что неодноточечных произведение любой нульмерных метризуемых счетной системы компактов гомео морфно канторову множеству. № 22. Доказать, что гильбертов кирпич является непрерывным образом канторова множества. № 23. Доказать, что канторово множество является универсаль ным пространством в смысле гомеоморфного вложения для индук тивно нульмерных метризуемых пространств со счетной базой. № 24. Доказать, что канторово множество можно вложить в лю бое полное метрическое пространство без изолированных точек. § 3. Канторова лестница С канторовым множеством связана обладающая некоторыми весьма интересными свойствами непрерывная функция с(х), назы ваемая канторовой лестницей. Построим на отрезке [О, функцию тервала 't 1] канторово множество С. Зададим (х) следующим образом: 't(O) = О, 't(l) = 1; в точках ин 't(x) = 1/2; в точках интервала 80 первого 2 ранга и в его концах 't(x) = 1/4 = 1/2 ; в точках интервала 81 первого 2 ранга и в его концах 't(x) = 3/4 = 3/2 ; вообще на смежных интерва лах k-го ранга и в их концах полагаем 't(x) = l /2k на самом первом 8 и в его концах интервале k-го ранга (если двигаться слева направо) и в его концах 't(x) = 112\ на втором интервале k-го ранга и в его концах 't(x) = = 312\ на третьем интервале k-го ранга и в его концах 't(x) = 512k и т. д.; на последнем интервале k-го ранга и в его концах 't(x) = = 2k - l /2k (чем правее интервал, тем больше на нем значение функции 't(x)) и т. д. 24 В результате получим график, часть которого изображена на рис. 3. Функция 811 ... in, ik 't(x) определена на множестве G точек интервалов 8, = О, 1, k = 1, ... , п, п = 1, 2, ... и множестве концов этих ин- тервалов. Это определение корректно в силу свойства канторова множества: между любыми двумя смежными к С интервалами ле жит смежный к С интервал. у 1 ----------------------------~ 7/8 п 1 1 1 1 1 1 1 3/4 5/8 п 1/2 3/8 п 1 1 1 1 1 1 1 1 1 1/4 1/8 r-, 1 1 1 1 о 1/9 2/9 1 1 1 1 1 1 1 1 1 1/3 2/3 Рис. 7/9 8/9 't(x) на множестве тонно (хотя и не строго) возрастает. Значениями G х 3 Из построения видно, что функция множестве 1 G моно функции 't(x) на являются все двоично-рациональные числа, заклю 1. Это множество всюду плотно на [О, 1]. Доопределим функцию 't(x), считая ее значение в произвольной двусторонней точке х Е С равным sup 't(~) (т. е. в качестве зна ченные между О и ~<х, ~EG чений в двусторонней точке х Е С принимаем верхнюю грань зна- 25 чений этой функции на той части множества слева от х) . Таким образом, функция резке [О, 't(x) которая лежит G, определена на всем от 1]. Из построения видно, что функция на всем отрезке [О, 't(x) монотонно возрастает 1]. Докажем, что функция 't(x) непрерывна на [О, была разрывна в какой-то точке х0 Е [О, 1], то 1]. Если бы она (в силу монотонно- сти функции) существовал бы интервал ('t(x0 Е), 't(x0)) - или ('t (х0 ), 't (х0 + Е)) , который не содержал бы ни одного значения функции. Но это невозможно, так как значениями функции явля ются, в частности, все двоично-рациональные числа отрезка [О, 1], а они расположены всюду плотно на этом отрезке . Из непрерывности ет, что 't([O, 1]) = [О, 't(x) и соотношений 't(O) = О, 't(l) = 1 следу 1]. Так как для любого смежного к С интервала значения функции 't на нем и в его концах одинаковы, Таким образом, функция 't(C) = [О, 1]. 't(x) осуществляет отображение канторова множества на отрезок [О, Функция 't(x) непрерывное 1]. во всех точках смежных к С интервалов имеет ну левую производную, т. е. ее производная почти всюду существует и равна нулю, но сама функция не постоянная, а растет от нуля до единицы (напомним, что какое-либо свойство имеет место почти всюду на множестве Е, если оно выполняется во всех точках этого множества, кроме точек некоторого подмножества меры нуль). Канторова лестница - непрерывное отображение отрезка на отрезок, в качестве подотображения содержит отображение канторова множества на отрезок (двукратное отображение). § 4. Обозначим через Q Ковер Серпинского 2 единичный квадрат {(х, у)е R 2 : О ::; х, 2 у ::; 1} плоскости R и назовем его квадратом нулевого ранга. Гори зонталями и вертикалями ось ординат - (считая ось абсцисс горизонтальной, а вертикальной) разделим Q 2 на 9 одинаковых квад ратов 1-го ранга (с длиной стороны 26 1/3). Открытый центральный квадрат 1-го ранга выбросим, оставив 8 нецентральных замкнутых квадра тов 1-го ранга. Сумму этих квадратов обозначим через S 1. Затем каждый оставшийся квадрат 1-го ранга, как и ранее, разделим вертикалями на горизонталями 9 и равных квадратов 2-го ранга и центральный открытый квадрат опять оставшихся 64 выбросим. Сумму квадратов 2-го ранга обозначим через S2 (рис. 4). Продолжая описанный процесс деления горизонталями и Рис. 4 вертикалями оставшихся квадратов п-го ранга на 9 равных квадратов (п + 1)-го ранга, выбрасывания центральных квадратов и получения сумм Sn+I всех оставшихся квадратов (п + 1)-го концов получим ковер Серпинского ранга, п 1, 2, ..., в конце S = п {Sn: п = 1, 2, ...} (впервые = О, это множество построил польский математик В . Серпинский). Плоские линии (т. е. линии, лежащие на плоскости) можно оха рактеризовать (Кантор первоначально принимал эту характеристику в качестве определения плоских линий) как замкнутые, ограниченные (т. е . компактные) и связные подмножества плоскости, не содержа щие внутренних (относительно плоскости) точек. Оказывается, что S является плоской линией и любая плоская линия вкладьmается (т. е . топологически отображается) в ковер Серпинского S. Предлагаем читателю самостоятельно решить следующие за дачи, доказав свойство ковра Серпинского. No 25. Доказать, что ковер Серпинского плотное множество на плоскости, 6) S есть: а) нигде не совершенное множество (т. е. замкнутое множество без изолированных точек), в) компактное подмножество плоскости. § 5. Универсальная кривая Менгера Универсальная кривая Менгера М была впервые построена од ним из двух (наряду с П.С. Урысоном) основателей теории раз мерности, австрийским математиком К. Менгером. Она является 27 пространственным аналогом канторова множества и ковра Сер пинского и называется универсальной потому, что сама является линией и топологически содержит все вообще линии и даже все одномерные подмножества пространства. Линией (по принадле жащему П . С. Урысону наиболее общему определению) называют одномерное связное и компактное метрическое пространство. Построим кривую М Для этого возьмем в пространстве R единичный куб Q 3 = {(х,у, z)E R 3 : О~х,у, z~ 1}, назовем его кубом 3 нулевого ранга и поделим плоскостями, параллельными коорди натным плоскостям, на 27 равных кубов 1-го ранга. В кубе оставим 20 Q3 замкнутых кубов 1-го ранга, не имеющих с централь ным кубом общих двумерных граней, удалив из куба Q 3 все остальные. Эти остальные грани образуют нечто похоже на проти вотанковый еж (т. е. три сваренных посередине ных и взаимно перпендикуляр имеющих одинаковую длину рельса). Каждый из оставшихся ку бов 1-го ранга опять поделим плос костями, параллельными координат ным плоскостям, на 27 равных кубов 2-го ранга и оставим, как и ранее, в каждом оставшемся кубе 1-го ранга 20 кубов 2-го ранга, не имеющих с центральным (из этих 27 кубов) ку бом общей двумерной грани. Про должая описанный процесс выбрасывания Рис. 5 получим «ежей», в конце универсальную Менгера М (рис. концов кривую 5). Предлагаем читателю самостоятельно решить задачу, доказав свойство универсальной кривой Менгера. № 26. Доказать, что универсальная кривая Менгера М есть : а) нигде не плотное множество в пространстве R , 6) совершенное множество в R 3 , в) компактное подмножество пространства R 3 . 3 § 6. Задачи № Пространство иррациональных чисел 27-34 связаны со свойствами пространства/ ирраци ональных чисел, рассматриваемого как подпространство числовой прямойR 1 • № 27. Доказать, ляется всюду что пространство I иррациональных чисел яв плотным незамкнутым подмножеством типа G0 на прямой. № 28. Доказать, что пространство I иррациональных чисел ин дуктивно нульмерно и, следовательно, несвязно, вполне несвязно. № 29. Доказать, что стандартная метрика на пространстве ир рациональных чисел не полна, но на нем можно ввести полную метрику. № 30. Доказать, что пространство меоморфно счетной степени: сел; 1) I иррациональных чисел го пространства натуральных чи N Z целых чисел (/, N, Z рассматриваются как 1 подпространства числовой прямой R ). № 31. Доказать, что пространство I иррациональных чисел: 2) пространства 1) топологически однородно; 2) ни в одной точке не является ло кально бикомпактным . № 32. Доказать, что все метризуемые, со счетной базой и ин дуктивно нульмерные пространства вкладываются в пространство иррациональных чисел . № 33. Доказать, что канторово множество топологически вкла дывается в пространство иррациональных чисел и наоборот. № 34. Доказать, что любое индуктивно нульмерное полное сепа рабельное метрическое пространство (У, р) без точек локальной бикомпактности гомеоморфно пространству иррациональных чисел. § 7. Метризуемые «ежи» (конечной, счетной и континуальной «колючести») Пусть К есть множество всех точек замкнутого единичного круга с центром в начале координат на плоскости R 2 . Введем на множестве К метрику р' следующим образом : если точки х и у из круга К расположены на одном радиусе, то р'(х, у)= р(х, у), где р есть обычная евклидова метрика на плоскости R 2 ; если же точки х 29 и у расположены на разных радиусах, то р'(х, у)= р(х, О)+ р(у, О), т. е . р'(х, у) есть сумма расстояний от точек х и у до точки О - центра круга. Легко заметить, что аксиомы метрического про странства при этом выполняются. Пространство (К, р') назовем метризуемым «ежом» континуальной «колючести». Заметим, что каждый радиус («иголка») изометричен обычному единичному отрезку, любые два радиуса (две «иголки») изометричны отрезку длиной 2. Подпространство (К, р')п пространства К, состоящее из точек, лежащих на п радиусах, п Е N, будем называть метризуемым «ежом» «колючести» п. Если множество радиусов счетное, то (К, р')~ («иголок») будем называть метризуемым «ежом» счет- 0 ной «колючести». Предлагаем читателю самостоятельно решить следующие за дачи, доказав свойства метризуемых «ежей». № 35. Доказать, и счетной что метризуемый «колючести» можно «еж» любой конечной изометрически вложить в про странство непрерывных действительных функций, определенных на отрезке [а, Ь] (т. е. в пространство С [а, Ь] (см. № 36. Доказать, что [8])). метризуемый «еж» «колючести» 3 (и выше) изометрически не вкладывается ни в какое евклидово пространство. № 37. Доказать, что метризуемый «еж» любой «колючести» является полным метрическим пространством. § 8. Бикомпактные «ежи» (счетной и континуальной «колючести») Пусть К есть множество всех точек замкнутого единичного круга на плоскости R 2 . Обозначим через ro окружность, ограничи вающую круг К. Возьмем на множестве К топологию, порожден ную базой В, состоящей из множеств следующего вида (рис. 1 - 6): открытый интервал произвольной длины, лежащий на произвольном радиусе («иголке») круга К; 2 - полуинтервал произвольной длины, лежащий на произ вольном радиусе («иголке») круга К и удовлетворяющий условию, что принадлежащий полуинтервалу конец лежит на окружности 30 ro; 3отрезках множество всех точек круга К, кроме точек, лежащих на произвольной длины, удовлетворяющих условиям: а) каждый отрезок лежит на радиусе; каждого отрезка лежит на окружности ro; 6) следующим один из концов в) множество отрезков конечно; г) отрезки попарно не пересекаются; д) ни один из отрез ков не содержит центр круга. о 2 3 Рис.6 Обозначим через 't топологию, порожденную базой В. Про странство (К, -r) будем называть бикомпактным «ежом» контину альной «колючести». Подпространство (К, -r)~ 0 пространства (К, -r), состоящее из точек, лежащих лишь на счетном числе радиусов («иголок»), бу дем называть бикомпактным «ежом» счетной «колючести». Предлагаем читателю самостоятельно решить следующие за дачи, доказав свойства бикомпактных «ежей». No 38. Доказать, что на любом радиусе пространство (К, -r) индуцирует обычную евклидову топологию. No 39. Доказать бикомпактность пространства (К, -r). No 40. Доказать хаусдорфовость пространства (К, -r). No 41. Доказать нормальность пространства (К, -r). No 42. Доказать, что в центре круга К для бикомпактного «ежа» континуальной «колючести» (К, -r) не выполняется первая аксиома счетности, а в остальных точках выполняется. No 43. Доказать, что метризуемый «еж» континуальной «колю чести» (К, р') уплотняется на бикомпактный «еж» континуальной «колючести» (К, -r). 31 № 44. Доказать, что бикомпактный «еж» счетной «колючести» (К, 't)~ метризуем и гомеоморфен подпространству гильбертова 0 кирпича, состоящему из всех точек, у которых имеется не более одной отличной от нуля координаты. § 9. (счетной Неметризуемые «ежи» и континуальной «колючести») Пусть К- множество всех точек замкнутого единичного круга на плоскости R 2 . Возьмем на множестве К топологию, порож денную базой L, состоящей из множеств следую щего вида: элементы базы как и элементы вида вида базы 3 L 1и2 L вида 1 и базы В в§ 2 такие же, 8. Элементы являются объединениями полуин тервалов произвольной длины, начинающихся в Рис. точке О (центре круга К) и идущих по всевозмож 7 ным направлениям из этой точки (рис. 7). Обозначим через Т топологию, порожденную базой L. Про странство (К, Т) будем называть неметризуемым «ежом» континуальной «колючести». Подпространство (К, Т)~ 0 пространства (К, Т), состоящее из точек, лежащих лишь на счетном числе радиусов («иголок»), будем называть неметризуемым «ежом» счетной «колючести». Предлагаем читателю самостоятельно решить следующие за дачи, доказав свойства неметризуемых «ежей». № 45. Доказать, что на любом радиусе пространство (К, Т) индуцирует обычную евклидову топологию. № Доказать, что в центре круга К для пространств (К, Т) 46. и (К, Т)~ 0 не выполняется первая аксиома счетности, а в осталь ных точках круга К- выполняется. № 47. Доказать, что неметризуемый «еж» (К, Т) ( соответ- ственно, (К, Т)~ ) уплотняется на метризуемый «еж» (К, р) (со- 0 ответственно, (К, р)~ 32 ). 0 № Доказать хаусдорфовость и регулярность пространств 48. (К, Т) и (К, Т)'к • 0 № 49. Доказать финальную компактность неметризуемого 0 «ежа» счетной «колючести» (К, Т)'к • § 10. Стрелка Зоргенфрея Пространство состоит из всех точек полуинтервала [О, смотрим О :s;; а семейство < р < 1. В всех полуинтервалов Очевидно, что условия 1 и 2 вида теоремы 9 [а, 1). Рас Р), где выполнены. Следовательно, В есть база некоторой топологии. Построенное про странство называют стрелкой. Будем обозначать его буквой S. Предлагаем читателю самостоятельно решить следующие за дачи, доказав свойства стрелки. № 50. Доказать, что все элементы базы В стрелки открыто замкнуты . № 51. Какими подмножествами стрелки будут отрезки, интер валы и полуинтервалы? № № 52. 53. Доказать, что стрелка несвязна, вполне несвязна. Доказать, что для стрелки справедлива первая аксиома счетности. № 54. Доказать, что стрелка: а) не бикомпактна, б) хаусдорфо ва, в) нормальна, г) вполне регулярна. № 55. Доказать, что стрелка: а) финально компактна, б) наследст венно финально компактна, в) совершенно нормальна, г) наслед ственно нормальна. № 56. Доказать сепарабельность и наследственную сепара бельность стрелки. № № 57. 58. Доказать, что стрелка не имеет счетной базы. 59. Уплотнить Доказать, что топологический квадрат стрелки не нор мален. № стрелку на: а) полуинтервал, б) отрезок, в) интервал (т. е. построить взаимно однозначное непрерывное отображение стрелки на полуинтервал, отрезок, интервал). № № 60. 61. Доказать топологическую однородность стрелки. Доказать, что подпространство стрелки метризуемо в том и только в том случае, когда оно не более чем счетно. 33 № 62. Доказать, что любое бикомпактное подпространство стрелки не более чем счетно. № 63. Доказать, что топологический квадрат стрелки сепарабе лен, но не наследственно сепарабелен. § 11. Две стрелки Александрова Пусть Х = С0 u С1 с R2, где Со = {(х, О): О < х ::; 1} и С1 = = {(х, 1): о::; х < 1} (рис. 8). Возьмем на Х топологию, порож денную базой у С1 L, состоящей из мно- жеств вида Г 1 = [а, В) 1------- =(a,B)u(a',B'], u (а', В'), Г 2 = где [а,В) интервал на С1, а (а', В') интервала (а, В) - на Со; проекция (а', В'] полуинтервал на Со, а (а, В) о х Рис. Легко Г2 некоторой топологии - - про- екция интервала (а', В') на С1. ность 8 полу- - заметить, совокуп всех множеств вида Г 1 L действительно (топологии, что образует и базу индуцированной линейным порядком). Предлагаем читателю самостоятельно решить следующие за дачи, доказав свойства двух стрелок. № 64. Построить все интервалы, отрезки и полуинтервалы в про странстве Х и указать их отношение к открытости и замкнутости. 65. Почему пространство Х = С0 u С1 называют «две стрелки»? № 66. Доказать индуктивную нульмерность, несвязность, пол № ную несвязность двух стрелок. № 67. Доказать бикомпактность двух стрелок. № 68. Доказать, что пространство «две стрелки» наследственно финально компактно. № 69. Доказать, что две стрелки ственно сепарабельное пространство. 34 - сепарабельное и наслед № 70. Доказать, что две стрелки - пространство с первой ак сиомой счетности. № 71. Доказать, что пространство «две стрелки» не имеет счетной базы. № 72. Доказать: а) хаусдорфовость, б) регулярность, в) нор мальность, г) наследственную нормальность, д) совершенную нормальность двух стрелок. № 73. Построить непрерывное и: а) двукратное отображение двух стрелок на отрезок числовой прямой, 6) строго двукратное отображение двух стрелок на окружность. № № 74. 75. Доказать топологическую однородность двух стрелок. Доказать, что топологический квадрат двух 1) не наследственно нормален, 2) не № 76. стрелок: совершенно нормален. Доказать, что подпространство «две стрелки» метризуе мо тогда и только тогда, когда оно не более чем счетно. № 77. Доказать, что пространство «две стрелки» - недиадиче ский бикомпакт. (диадическим бикомпактом называют биком пактные хаусдорфовы пространства, являющиеся непрерывными образами пространства D 1 при различных кардинальных числах 't: D - простое двоеточие.) § 12. Лексикографически упорядоченный квадрат Рассмотрим линейное упорядочение по возрастанию на единич ном квадрате 1 х1 ~ х2 и у1 2 < у2 Для а, Ь Е 1 2 , определенное правилом (х1 ,у1 ) < (х2 ,у 2 ), если (это упорядочение является лексикографическим). , удовлетворяющих отношению а < Ь, положим (а, Ь) = {х Е 1 : а < х < Ь} ; 2 (-оо, а)= {х е 1 2 : х < а}; (а,+оо)={х е1 2 :а<х}. Такие множества будем называть интервалами в 1 2 • Предлагаем читателю самостоятельно решить следующие задачи, доказав свойства лексикографически упорядоченного квадрата. 35 № 78. Доказать, что семейство В всех интервалов в лексико графически упорядоченном квадрате 1 2 является базой некоторой топологии (топологии, индуцированной лексикографическим по рядком). № 79. Построить все интервалы, отрезки и полуинтервалы в 1 2 и указать их отношение к открытости и замкнутости. № 80. Доказать хаусдорфовость пространства 1 № 81. Доказать, что 1 2 - 2 • пространство с первой аксиомой счетности. № 82. Доказать, что пространство 1 2 не сепарабельно. № 83. Доказать, что пространство 1 2 не наследственно фи нально компактно. № 84. Доказать бикомпактность и нормальность лексикогра- фически упорядоченного квадрата 1 2 . № 85. Доказать, что пространство 1 2 не совершенно нормально. № 86. Доказать, что две стрелки и стрелка являются подпространствами лексикографически упорядоченного квадрата 1 2 • № 87. Доказать, что пространство 1 2 допускает такое непре рывное отображение на отрезок числовой прямой, при котором прообраз каждой точки также гомеоморфен отрезку. № 88. Доказать, что пространство 1 связно, но 3) не линейно связно. 2 : 1) связно, 2) локально Глава № 111. РЕШЕНИЯ ЗАДАЧ 1. Пусть Е - непустое открытое множество на прямой R 1 , х0 ЕЕ. Обозначим через а нижнюю грань левых концов интервалов, со держащих х0 и включающихся в Е, а через f3 - правых концов таких интервалов (возможно, f3 = +оо ). Тогда ( а, f3) с Е, а ~ Е, f3 ~ Е. верхнюю грань что = -оо а Если бы, например, или f3 ЕЕ, то, в силу открытости множества Е, существовал бы некоторый ин- тервал (f3- Е, f3 + Е) с Е (Е > ( а, f3 + Е) О). Но тогда интервал же включался бы в Е, что противоречит выбору точки Аналогично, (а - Е, а + Е) с Е. если бы а ЕЕ, так- f3. то существовал бы интервал Тогда интервал (а - Е, f3) также включался бы в Е, что противоречит выбору точки а. Таким образом, каждая точка х0 Е Е содержится в некотором интервале, включающемся в Е, концы которого не принадлежат Е. Докажем, что такой интервал (для данной точки х0) единственный. Действительно, пусть существуют два таких интервала и (a 2 ,f32 ). Если х0 < f3 1 < f3 2 , то f31 E(a 2 ,f32 ) • f31 EE, ( а 1 , f31 ) что проти воречит условию. Аналогично, а2 < а1 • не может выполняться условие а1 < а2 или Единственность доказана. Интервал, входящий в Е, концы которого не принадлежат Е, и будет составляющим интервалом для Е. Множество составля ющих интервалов не более чем счетно. Действительно, фиксируя в каждом составляющем интервале по одной рациональной точке, мы получим взаимно однозначное соответствие между множе- 37 ством всех составляющих интервалов и некоторым подмноже ством множества рациональных чисел (а это подмножество конеч но или счетно). №2. 1. Пусть Х с R 1 связно. Докажем, что Х выпукло. Предполо жим, что концы отрезка [а, Ь] принадлежат множеству Х, но на [а, Ь] имеется такая точка с, что с ~Х. Положим: ½ =Xn (с, ЬЕ +оо), а<с<Ь. Так как aEYi, J; , то J; * 0 . Докажем, что Х = Yi u J;. Yi u-½ = ( (-оо,с) п Х) u то Yi = Х п (-оо, с), Yi -::f:-0, и так как Действительно, ( (с,+оо) пХ) = ( (-оо,с) u (с,+оо)) п Х = =((-oo,c)u{c}u(c, +oo))nX =R1 nX=X. Кроме того, fi nJ; =0 (так как (-00,с)п(с,+00)=0). Получили, что Х несвязно, что противоречит условию. Следо вательно, Х выпукло. 2. Пусть Х с R 1 выпукло. Докажем, что Х связно. Сначала до кажем следующую лемму. Лемма . Если для любых двух точек множества Е существует связное множество Q, содержащее эти точки и включающееся в Е, то Е связно. Доказательство. Пусть Е несвязно. А, В* 0, АпВ =А u В, где Q с Е, у ЕВ. По условию существует связное множе такое, открыты в = 0 ). что хЕ Q и уЕ Q. Следовательно, xEQnA,yEQnB, множества QnA, Q. Кроме того, (Q п А) п (Q п В)= 0 (так как Q=(QnA)u(QnB), QпВ Е А п В= 0, А, В открыты в Е. Пусть х Е А, ство Тогда где Таким образом, мы получили, что Q несвязно, а это противоречит условию . Следовательно, Е связно. Лемма дока зана. Итак, Х с R 1 выпукло, т. е. для любых двух точек х, у ЕХ отре зок [х, у] с Х Но отрезок связен множество Х связно. 38 [3, гл. 1, § 4]. Следовательно, №3. Пусть Е есть непустое и неодноточечное связное подмножество прямой, а = infЕ, Ь = sup Е. Рассмотрим сначала тот случай, когда а и Ь - конечные числа (а < Ь). Тогда любое число с: а < с < Ь вхо дит в Е. Действительно, так как Ь = sup Е, то 3 Ь 1 ЕЕ: с< Ь 1 ::; Ь . Аналогично, так как а = inf Е, то 3а1 ЕЕ: а::; а1 < с. Тогда (так как Е связно на прямой, а следовательно, и выпукло) • [а1 , Ь1 ] с Е • с ЕЕ. Таким образом, интервал (а,Ь) принадлежит Е, а точки, лежащие за пределами отрезка [а, Ь ], не принадлежат Е. Следова тельно, Е является одним из следующих множеств: (а, Ь), (а, Ь], [а, Ь), [а, Ь] . Аналогично доказывается, что если а= -оо, Ь конечно, то Е имеет вид ( -оо, Ь] или ( -оо, Ь); ( а, + оо) или [а, + оо ); если если а конечно, Ь вид а = -оо, Ь = +оо, = +оо, то Е №4. Сфера sп состоит из двух замкнутых полусфер ресекающихся по экваториальной сфере sn-l, то Е имеет = ( -оо, + оо ). s: и S~, пе- а каждая полусфера связна как непрерывный образ диска. Следовательно, сфера [3, гл. I, § 4]. Покажем это подробнее. Пусть имеем Rп, п ~ 2. Пусть sn связна sn- 1 , сфера и открытый п-диск единичного радиуса с центром в Dn - s;-1 часть сфе- точке (О, О, ... , О) соответственно. Обозначим через ры, где~п > О (северное полушарие). Докажем, что диск Dn-I го меоморфен полусфере R n-I s;- 1 • Можно считать, что пространство совпадает с подпространством точек (~i, ~2 , странства (~ 1, ~2 , ••• , R n, если отождествить ~п- 1 , О). ТогдаD п-l и точки Dn-l ={(~1 , .. · ,~п): (~ 1 , s;-1 лежат в R п s:-l ={(~1, ... , ~п) : ~f + ... + ~~ •• • , ~п-1' О) про ~ 2 , ... , ~ п-l) и и задаются так: =1,~п >0}; ~f + ... +~ ~ < 1,~п =О} . 39 ~3 В случае R 3 имеем следую si щую ситуацию: s; ,,, .; .,,.,,....---7--- . . . 1 1 / без экватора, .... 1 2 D - внутренность единично2 го круга в R (рис. 9); .... ' 1 ,,,,,,,, / ,,,,::,ко---- верхняя половина сферы ---- -- x=(~1,~2,~3)ES;, ~3 >0; ~2 ~, Рис. у= (~1, ~2, О) Е D2. 9 Проекция (~1, ~2, ~3) • (~1, ~2, О) S; и D является гомеоморфизмом в Rn пространстве f ( ~ i , . . . , ~ п-1' ~ п) • ное отображение поступим • Проекция ( ~ i , .. . , ~ п-1' О) задает биективное непрерыв- s;- 1 на пп- 1 • Обратное отображение имеет вид • ( ~Р аналогично. 2 f -1 : (~ 1 , ... , ~n- l' О) • ... ,~п-1' ,J1- ~~ -... - ~~-l) и непрерывно. Замкнутый диск jjn-l является выпуклым подмножеством К, следовательно, связен. Тогда и s:- связно. Аналогично, s::- связно: 1 1 s;-1 п s::-1 = sn-2 -:t=0. Таким образом, сфера sn-1 = s;-1 us::--1 связна. No 5. Пусть п есть плоскость с фиксированной декартовой системой координат хОу (рис. 1О) . Положим А= {(х,у) Е п: О< х 1= {(х, у) Е п: х :s; 1, у = sin 1/х}; = 0,-1::; у :s; 1}; Ф = Множество Ф компактно (в А u J. силу замкнутости и ограниченно сти на плоскости п). Покажем, что пространство Ф связно. Действительно, пространство А связно, так как является непре- рывным образом (при отображении х • 40 ( х, sin 1/ х) полуинтервала (О, т. е. связного множества. Но 1], Ф = [А], следовательно, Ф связно как замыкание связного множества. Докажем, что пространство Ф не локально связно в точке М0 (0,-1). у м о 1 х -1 Рис. 10 Рассмотрим такую окрестность И точки М0 : И= V = {(х, у) Е 7t: у < О} . МO, являющейся связным множе ством. Покажем это. Так как последовательность = sin 1/ х что для любого п Wс Пусть два = = sin 1/ х, •••} ми W точки МO найдется такой номер все точки Мп попадут в окрестность W. И есть некоторая окрестность точки М0 • Рассмотрим «соседних» sin 1/ х, >N {Mi,M2 , сходится к точке М0 в пространстве Ф, то для любой окрестности N, пФ, где В этой окрестности не найдется никакой меньшей окрестности точки нимумов функции у V минимума лежащих в W. Мni и Мп 2 функции у Обозначим через К максимум функции у = 1 лежащий на «гребне» между точками Мп точку К проведем прямую !, и М1½ • Через параллельную оси Оу. Эта прямая разобьет плоскость 7t на две открытые полуплоскости 7t 1 и 7t 2 • Множества как ство 01 = п1 п W и 02 = п2 п W открыты в W, непусты (так Mnl Е 01' мп2 Е 02 ), и 01 п 02 = 0. Таким образом, множе W несвязно и, следовательно, пространство Ф не локально связно. 41 Докажем, что пространство Ф не линейно связно. Рассмотрим точки М0 (О; такое, что -1) и М Пусть отображение (1; sin 1). /(О)= М0 , /(1) = М1 , [О, f непрерывно. 1] • Ф, Множество F= Г\I) с [О, 1] замкнуто (как прообраз замкнутого множества при непрерывном отображении). Пусть грань множества F. Пусть С0 Так как t0 Е = .f{_ t0 ). та: (а) С0 Тогда t0 Е С0 El \ {(0,1)}; (6) Е [О, есть верхняя 1] (в силу замкнутости F F, t0 то С0 Е El\{M0 } . F) и t0 < 1. Возможны два вариан 1. Рассмотрим вариант (а). Пусть И есть такая окрестность точки С0 , которая не содержит точек множества Ф с ординатами, равными сти отображения f существует такое Е = JП t0 , t 0 + Е )) с И. Полуинтервал > 1. В силу непрерывно О, что множество Н [ t0 , t 0 + Е) = связен, следователь но, его образ Н связен. Так как одна точка множества Н, а именно точка С0 , лежит на вертикальном отрезке 1, то в силу связности множества Ни включения Нс И все множество Н лежит на отрез ке 1, что невозможно. Вариант (6) аналогичен, только в качестве И нужно взять такую окрестность точки С0 , которая не содержит то чек множества Ф с ординатами -1 . №6. Чтобы доказать, что два топологических пространства гомео морфны, между ними устанавливают гомеоморфизм. Негомео морфность двух топологических пространств обычно доказывают указанием топологического инварианта, которым одно из про странств обладает, а другое нет. Нам потребуются: Лемма 1. Любое аффинное преобразование плоскости (про странства) является гомеоморфизмом. Лемма 2. Если пространства Х' f: Х • У гомеоморфизм, то для любого под- - пространства Х отображение f': Х' • fX с У также является гомеоморфизмом. Доказательство. Очевидно, что отображение нозначно. Докажем, что /' крыто в пространстве JX', 42 f' взаимно од- непрерывно. Пусть множество И' от следовательно, И '= И п JX', где И открыто в У. В силу непрерывности f прообраз / - И открыт в Х 1 1 и, кроме того, (/')- И'= f -1 И п Х', 1 т. е. (/')- И' открыто в Х'. 1 Следовательно, f' непрерывно. Аналогично, и (/')- непрерывно. Лемма 3. График непрерывной функции гомеоморфен ее обла сти определения [3, гл. I, § 8]. А. Классификация линий 1. Любые два интервала гомеоморфны между собой и любой интервал гомеоморфен прямой (рис. ь а Пусть х Е (а, Ь ), у Е (с, функция у d). = tg х, 11 Тогда = (х - физмом интервалов (а, Ь) и Функция у d с Рис. Линейная 11 ). х-а у-с Ь-а d-c - - =- - . d-c а) - Ь- а +с является гомеомор (c, d). определенная на интервале (- п/2, п/2 ), яв ляется гомеоморфизмом этого интервала на всю числовую прямую 1 R (рис. 12). Следовательно, любой интервал гомеоморфен прямой. у у 71: 2 - - -- - - - - - - -- - - -- 71: 11: 2 2 х х 71: 2 y=arctgx y=tgx Рис . 12 43 Аналогично можно доказать следующие утверждения. 2. Любые два отрезка гомеоморфны. 3. Любые два полуинтервала гомеоморфны. 4. Все эллипсы гомеоморфны между собой и гомеоморфны окружности. Это следует из лемм 1 и 2 и из того факта, что любые два эл липса аффинно-эквивалентны. 5. Любые две параболы гомеоморфны, и любая парабола го меоморфна прямой. Любые две параболы подобны, следовательно, аффинно эквивалентны и (по леммам 1 и 2) гомеоморфны. 2 По лемме 3 парабола у = 2рх гомеоморфна своей области опредления - оси Оу. 6. Любые две гиперболы гомеоморф ны между собой, и любая гипербола го меоморфна двум параллельным прямым (или «проколотой» прямой, или двум ин тервалам) . Любые х две эквивалентны, ~1 лемм гиперболы следовательно , 1 и 2, гомеоморфны. 2 Рис. любая гипербола х2 13 а - {О} = (-оо, О) u (О, учетом Таким образом, у2 = 1 гомеоморф Ь Областью определения непрерывной функции R \ с 2 на гиперболе у= 1/х (рис. «проколотая» прямая аффинно + оо ). 13). у = 1/х является Следовательно, любая гипербола гомеоморфна или двум параллельным прямым, или двум интервалам (п. 1 и лемма 3). Таким образом, мы получили четыре класса гомеоморфных между собой вещественных алгебраических линий второго по рядка : 1) прямая, парабола, интервал; 2) пара параллельных прямых, гипербола, два интервала, «про- колотая» прямая; 3) эллипс, окружность; 4) пара пересекающихся прямых. 44 Любые две линии из разных классов негомеоморфны. Укажем различающие топологические инварианты. Эллипс компактен, все остальные линии некомпактны, т. е. 3) +1), 2), 4). Линии класса 2) несвязны, все остальные линии связны, т.е. 2) +1), 3), 4). Осталось показать, что прямая негомео морфна паре пересекающихся прямых (рис. 14). Рис. 14 Удалив точку М пересечения двух прямых, получим про странство, состоящее из четырех непересекающихся открытых связных множеств. На прямой такой точки нет. Следовательно, по лемме 2, 1) +4). Б. Классификация поверхностей 1. Любые два эллипсоида гомеоморфны, и любой эллипсоид гомеоморфен сфере (это следствие аффинной эквивалентности любых двух эллипсоидов и лемм 2. Любые 1 и 2). два эллиптических параболоида гомеоморфны, и лю бой эллиптический параболоид гомеоморфен плоскости. Гомеоморфность любых двух эллиптических параболоидов следует из их аффинной эквивалентности. 2 2 Эллиптический параболоид х 2 + у2 = 2z является графиком а 2 Ь 2 непрерывной функции z = ~ + у 2 , область определения кото2а 2Ь рой есть плоскость хОу. По лемме 3, эллиптический параболоид 45 гомеоморфен плоскости. (Гомеоморфизмом является проектиро вание п, такое, что п: (х, у, 2ах\ + 2ЬУ 2 J • (х, у, О)). 2 3. Любые два гиперболических параболоида гомеоморфны, и любой гиперболический параболоид гомеоморфен плоскости. Аналогично п. 2. Гомеоморфизмом является проектирование п: ( х, у, х\ + У 2 J • (х, у, О), следовательно, любой эллиптический 2 2а 2Ь параболоид гомеоморфен любому гиперболическому параболоиду. 4. Двуполостный гиперболоид гомеоморфен паре параллель ных плоскостей, и любые два двуполостных гиперболоида гомео морфны: Одна (вторая) «чаша» гиперболоида является графиком непре- 2 + ;-2 [ х = -а 1+ у 2 + z 2J , область рывной функции х = а 1 + у2 2 2 ь с ь определения которой есть плоскость с (yOz). Следовательно, двуполостный гиперболоид гомеоморфен паре параллельных плоскостей, например, х = аих = -а. 5. Плоскость гомеоморфна открытому кругу. Полусфера без граничной окружности гомеоморфна открыто му кругу. Гомеоморфизмом служит ортогональное проектирова ние на касательную плоскость, параллельную плоскости, чивающей сферу (рис. 15). ,,. ..... - - --о- - ...... ' ,,. ... - - ~ - - 'N ' ..... --"Т""--.~ lo' ' - - ~--' ~N / ____ i' Рис. 46 15 ограни Полусфера без граничной окружности гомеоморфна плоскости. Гомеоморфизм На рис. центральное проектирование из центра сферы. 16 видно, что центральное проектирование из точки О и обратное к нему отображение непрерывны. Рис. 6. Однополостный 16 гиперболоид гомеоморфен открытому коль цу на плоскости, «проколотой» плоскости или плоскости без замк нутого круга. 2 2 Однополостный гиперболоид \ + У2 а х2 липтическому цилиндру Ь 2 z2 - с =1 гомеоморфен эл у2 2 + 2 = 1. а Ь z Гомеоморфизмом является проектиро вание одной поверхности на другую, ставящее в соответствие точке М(х, у, z) на гиперболоиде точку пересечения с цилиндром (О, О, луча, идущего из точки z) в точку М (рис. 17). Гомеоморфизмом является тирование из точек оси Oz проек 1 1 перпендику .,,,,,,.--- - г--~ --.,,---------- , о--- --- лярно этой оси. V Неограниченныи цилиндр х2 у2 d + Ь2 = 1 гомеоморфен ограниченному цилиндру х2 у2 7t 7t =1 - -<z<a2 Ь2 ' 2 2 Отображение h: (х, у, z) • arctg z)-гомеоморфизм. - +- .,,,,,....- ' 1 х 1 1 1 1 1 у 1 ----- f-------- 1 1 ,,f1 ------1--. ,,,- 1 ----- -- -г----1 '- ( l '- '\1 / т ---- (х, у, 1 1 1 1 1 1 1 1 -----т---Рис. / 17 47 Ограниченный на плоскости (рис. цилиндр гомеоморфен открытому кольцу 18). Гомеоморфизмом является центральное проектирование из не которой точки М на оси цилиндра (рис. 19). м / 1t Рис. 18 м 1t Рис. 19 Если М является точкой пересечения оси цилин дра с одним из оснований цилиндра, то центральное проектирование из этой точки на плоскость, в кото /11 \\ I 111 \ I 111\ I 1 1 1\ I 1 1 1\ I 1 1 1\ I 1 1 1\ / 1 1 1\ -j -::,1 ..... / рой лежит второе основание цилиндра, является го меоморфизмом ограниченного кость без круга (рис . цилиндра на плос 20). Ограниченный цилиндр гомеоморфен ограничен ному конусу без основания и без вершины. Гомеомор физмом является проектирование из общей оси цилин Рис. 48 20 дра и конуса перпендикулярно этой оси (рис. 21 ). Ограниченный конус без вершины гомеоморфен «проколотой» плоскости. Гомеоморфизмом является центральное проектирова ние из точки М центра эллипса, основания конуса, на плос - кость, перпендикулярную оси конуса и проходящую через верши ну конуса. н' 7t Рис.21 Таким образом, мы получили следующие классы гомеоморф ных между собой вещественных алгебраических поверхностей второго порядка: 1) эллипсоид, сфера; 2) плоскость, эллиптический параболоид, гиперболический па раболоид, параболический цилиндр, открытый круг; 3) однополостный гиперболоид, эллиптический цилиндр, от крытое кольцо на плоскости, «проколотая» плоскость, плоскость без замкнутого круга; 4) пара пересекающихся плоскостей; 5) двуполостный гиперболоид, пара параллельных плоскостей, гиперболический цилиндр; х2 у2 z2 а Ь с 6) конус 2 + - 2 + -т =0. Осталось показать, что любые два пространства разных клас сов негомеоморфны. Эллипсоид компактен, все остальные поверхности некомпакт ны. Следовательно, 1) + 2), 3), 4), 5), 6). Двуполостный гиперболоид несвязен, все остальные поверхно сти связны, следовательно, 5) + 1), 2), 3), 4), 6). 49 Плоскость негомеоморфна «проколотой» плоскости, так как «проколотая» плоскость обладает ретракцией на окружность с центром в этой точке (посредством проектирования из этой точки), а плоскость не ретрагируется на окружность. Таким образом, 2) + 3). Покажем, что плоскость негомеоморфна паре пересекающихся плоскостей. Рис.22 Любая топологическая окружность (т. е. гомеоморфный образ окружности) разбивает плоскость, т. е. дополнение до нее несвязно (по теореме Жордана). На паре пересекающихся плоскостей, как видно из рисунка, это не всегда так (рис. + 4). Следовательно, 2) Аналогично: + 4). No 7. 1. Установим 3) 22). взаимно однозначное соответствие между мно жествами К и С. Из построения канторова множества С и множе ства К видим, что каждой точке как множества С, так и множества К соответствует некоторая последовательность 50 i1 , i2 , ••• , in, ... , где in = О или in = 1 (*). Будем считать соответствующими точки х Е К и х' Е С, которым отвечают одинаковые последовательно- сти(*). Отрезки Лi .. .iп и сr 11 ___ 1п , индексы которых совпадают, также 1 будем считать соответствующими. 2. Докажем, что отображения а) К • С и 6) С ➔ К непрерыв ны . Но так как всякое взаимно однозначное непрерывное отображе ние бикомпактного топологического пространства Х в хаусдорфово пространство У является топологическим (теорема 19), а простран ство К бикомпактно (в силу замкнутости и ограниченности на пря мой (теорема 28)) и пространство С хаусдорфово (как и любое дру гое метрическое пространство), то достаточно доказать только непрерывность отображения а). Докажем, что для любой точки х0 Е К и для любого Е >О су- ществует такая окрестность Ох0 точки х0 в пространстве К, что для любого х Е К, такого, что х Е Ох0 , имеем Пусть х0 Е К, в lx' - х~ 1< Е. > О . Возьмем такое п Е N, что 1/З п < Е, и рас смотрим отрезок Л 11 •• •in ранга п, содержащий точку х~ . Его длина равна 1/Зп. Тогда искомой окрестностью точки х0 будет открытое множество Ох0 = К п cri1 •• •i,, ' где cr 11 ••• in есть отрезок ранга п, со держащий точку х~ и соответствующий отрезку Лi ...1,,. Действи 1 тельно, для любой точки х Е Ох0 соответствующая ей точка х' лежит на отрезке Л 11 •..iп и, следовательно, lx' - x~I::; 1/Зп < Е. №8. Пусть О < в отрезка [О, 1] < 1. Построим канторово множество меры удалим интервал ro совпадают с концами отрезка [О, cr1 1- в. Из длиной в/3, концы которого не 1]. Из оставшихся отрезков первого ранга стандартным образом (см. cr 0 и обобщение классиче ского построения канторова множества) удалим соответственно 2 интервалы ro0 и Ф~, сумма длин которых равна 2в/3 , и т. д. Из каждого отрезка cri 1 ••• in ранга п стандартным образом выбросим 51 соответственно Пусть 2n El3n+l. К= n {Кп интервалы Кп О\ ...in , сумма длин объединение которых отрезков равна ранга п, : n Е N}. Согласно решению задачи № 7, пространства К и С (как под пространства числовой прямой) гомеоморфны. Сумма длин вы- брошенных интервалов множества К равна 1- Е 2Е 4Е - + - 2 + - 3 + ... = Е. 3 3 3 Следовательно, мера Е. №9. Рассмотрим на числовой прямой R некоторый отрезок с ир 1 рациональными концами, например, отрезок [✓ 2, ✓3]. Перенуме руем произвольным образом все рациональные точки, лежащие на этом отрезке (их счетное множество). Из отрезка [✓ 2, ✓3] стандартным образом выбросим интервал с иррациональными концами, содержащий рациональную точку с первым номером. Из оставшихся отрезков cr O и cr1 первого ранга стандартным образом выбросим интервалы с иррациональными концами, содержащие рациональные точки с наименьшими номе рами на этих отрезках, и т. д. В результате получим множество К, гомеоморфное канторову множеству С ( см. задачу № 7). Все точки множества К являются иррациональными, так как из его построе ния видно, что все рациональные точки принадлежат выброшен ным интервалам. № 10. Рассмотрим подобие с коэффициентом 113n+I, переводящее отрезок [О, 1] в отрезок Лi 1 ...in ранга п . Очевидно, что при этом кан торово множество С взаимно однозначно отображается на множе ство С п Лi .. •in • Следовательно, множество всех точек множества 1 1 С, лежащих на отрезке Лi ..•i,, , имеет мощность континуума. Пусть а - произвольная точка множества С, Е такое п EN, что 1/Зп 52 < Е, > О. Возьмем 1 и рассмотрим отрезок п-го ранга Лi ...in, 1 ...in на котором лежит точка а. Так как длина отрезка Лi равна 1 / Зп (а, < f:, то он, содержа точку а, целиком лежит в окрестности О f:), которая содержит множество С n Лi1 •••in , имеющее мощность континуума. № 11. Докажем, что любой интервал содержит меньший интервал, полностью свободный от точек множества С. Пусть (а , Р) тервал на прямой. Если имеется точка х0 Е С : х0 ин- - Е (а, Р ), то найдется отрезок Лi .. .in , содержащий точку х0 и включающийся в 1 (а, Р) (длина отрезка ранга п равна 1/Зп). Тогда интервал 8~ .. .in длиной 1/ 3n+I с центром в середине этого отрезка не содержит то чек множества С и вместе с тем содержится в (а, р № ). 12. Базой из открыто-замкнутых множеств в пространстве С явля- ется система множеств ранга п, п канторова Е N}, L = {Ci1.. ,i,, = с Г') лi1 .. ,i,,, где лi1".in - отрезок т. е. элементами базы являются подмножества множества, состоящие можных отрезках Л~ .. .in , п Е N. из точек, лежащих на всевоз Система является базой топологии пространства С, индуцированной естественной топологией число вой прямой R 1 • Пусть Ос = (а, р) n С, где ( а, р) - интервал на прямой R 1 • Тогда для любой точки х0 Е Ос найдется отрезок Л~ .. .in достаточно высокого ранга п, содержащий точку х0 и вклю чающийся в (а, Р). Следовательно, х0 Е Ci ...in с Ос. Любое мно1 жество c i1.. .in замкнуто В с (так как отрезок лi1 ...in замкнут В R 1 ) И открыто в С (так как является пересечением с множеством С от крытого в R интервала, концы которого лежат на смежных к от резку Л~ .. .in интервалах). Очевидно, что канторово множество С 1 является Т1 -пространством и непусто. Следовательно, С- индук тивно нульмерное пространство . 53 Следствием индуктивной нульмерности канторова множества являются его несвязность и полная несвязность: С = v;_ = Сп (-1/ 2, 1/ 2), Множества v;_ , ~ v;_ u V2 , где = Сп (1/ 2, 3/ 2 ). ~ открыты в С, непусты и v;_ п V2 = 0. Таким образом, пространство С несвязно. Каждая точка канторова множества является пересечением всех содержащих ее отрезков Лi, .. .in, следовательно, квазикомпонента каждой точки содержит только ее. Следовательно, простран ство С вполне несвязно . Множество дополнение № F V =С п = C\ V ( О, 1/ 3) открыто в С, но не замкнуто. Его замкнуто, но не открыто . 13. Пусть D = {О, 1} есть простое двоеточие, т. е. дискретное топо логическое пространство, состоящее из двух точек. Пространство 00 D~ = П Dn состоит из точек х = {xi, ... , хп , .. .}, где xi = О или n=1 xi = 1, i = 1, 2, ... . Кантор о во множество С также эквивалентно множеству всех последовательностей из нулей и единиц . Таким образом, установлено взаимно однозначное соответствие между множествами D~0 и С. Соответствующие точки будем обозначать одинаковыми буквами. Докажем, что отображения а) D ~0 • рывны. Но, в соответствии с теоремой С бикомпактно, а D~0 - С и 6) С ➔ D~0 непре 19 и тем, что пространство хаусдорфово (теорема 24), достаточно доказать только непрерывность отображения а) . Докажем, что для любой точки х Е D ~0 и для любого Е > О существует такая окрестность Ох точки х в пространстве D ~0 , что для всех х' Е Ох имеем : р(х,х') < Е (расстояние в множестве С как в подпространстве числовой прямой R 1 ). Пусть х Е D~0 , Е > О. Возьмем такое п Е N , что 1/З п < Е. Рассмотрим отрезок Лi, ...in ранга п, содержащий точку х Е С. Длина этого отрезка равна 1/Зп. Точки 54 канторова множества, лежащие на этом отрезке, на местах п имеют фиксированные числа 1, 2, ... , (нули или единицы). Тогда ~' ... , in искомой окрестностью Ох точки х Е D~0 будет подмножество множества D~0 , состоящее из точек, которые на местах 1, 2, ... , п имеют те же фиксированные числа i1 , ... , in, что и точки множе- ства Сп Л 11 •••iп. Множество Ох открыто в пространстве D~0 с его тихоновской топологией. № 14. Пусть f С• 1 есть некоторое вложение канторова множества С в пространство иррациональных чисел 1 с R с 1 сR 1 . , т. е. С = f( С) с Так как С замкнуто в R (в силу бикомпактности канто 1 рова множества), то его дополнение R но, R 1 1 С открыто. Следователь \ С является объединением счетной системы попарно не пересекающихся интервалов ai, i = О, 1, 2, ... , среди которых два 1 \ интервала, пусть это а, 0 и а, 1 , не ограничены ( смежные интервалы множества С, их конечными концами являются точки множества С). Из каждого ограниченного интервалааi, i = 2, 3, ..., выбросим по одной рациональной точке . В результате вместо каждого интервала a,i получим два интервала a,iо 1 и а , 1 z. = 2 , 3 , ... , у каждого из которых один из концов является точкой множества С. Пусть А есть множество выброшенных рациональных точек. Пространство R сел 1 =:) 1 \ А содержит пространство иррациональных чи С. Построим отображение g: ( R \А) ➔ С следующим об1 v разом: каждои точке интервала а о 1 0 , а 1 , a,i, a,i' z. = 2 , 3 , ... , поставим в соответствие тот его конец, который является точкой множества С. Для любой точки х Е С считаем gx ние h отображения g на пространство жем, что отображение Пусть х0 El, Е h > О. = х. Рассмотрим / , т. е. h = g/l: 1 • ограниче С. Дока непрерывно. Найдем такую окрестность Ох0 точки х0 , что для любого х Е Ох0 имеем: lh(x)- h(x0 ) 1 < Е. 55 Пусть х0 Е /\С. Тогда х0 лежит в каком-нибудь из интерва 1. лов а 1 или а{, j = О, 1, i = 2, 3, ... , который отображается в ту же точку множества С, что и точка х0 , и, следовательно, множество всех иррациональных чисел, лежащих на этом интервале, можно считать искомой окрестностью Ох0 • Пусть х0 Е С. Рассмотрим два случая: а) х0 является концом 2. 6) х0 не является им. а) Пусть, для определенности, х0 является правым концом интервала а~. Тогда Ох0 = (а~ u [х0 , х1 )) n 1, где х1 есть некоторая некоторого смежного интервала, точка множества С, находящаяся от точки х0 на расстоянии, меньшем Е. 6) Пусть х1 и х2 есть некоторые точки множества С, лежащие по разные стороны от точки нии, меньшем Е. Тогда Ох0 х 0 и находящиеся от нее на расстоя = (х1 , х2 ) n 1. Очевидно, что и в случае а), и в случае 1 6) "i/x Е Ох0 имеем: h(x) - h(x0 ) 1 < Е. Таким образом, отображение h непрерывно и, следовательно, канторово множество является ретрактом пространства иррацио нальных чисел. No 15. Докажем, что для любых двух точек х1 , х2 Е С существует гомеоморфизм g: С• С, такой, что кажем, что для любой точки g(x1) = х2 • хЕС Для этого сначала до существует гомеоморфизм С ➔ С, который переводит точку х в точку О, т. f = ( 1.о1 , •• •, N, О= (О, ... ,О, ...). пусть 6ОГО kе Х о Е С Построим Х , о 56 (1, i 2 ,i3 , где .о lk =О ИЛИ .о lk непрерывных =l О. ДЛЯ ЛЮ- функций fi = h1 : С ➔ С, где если если х Е Л 1 , то hi каждой следующим образом: х Е Л0 , то функция точке х = ) последовательность {fk: С ➔ С, k Е N} 0 .о ln, ••• , e.fx = hi тождественна, 0 •••) ставит в соответствие точку х' = (О, i 2 , i3 , ••• ) с теми же координатами, кроме первой. Геометрически это означа ет, что отрезки Л 0 и Л 1 первого ранга меняются местами. Очевидно, что функция ~ взаимно однозначна и непрерывна (так как является изометрическим отображением). Заметим, что fi (х ) = (О, 1i, i~, 0 .. .). Построим функцию / 2 = ~ о ~ : С • = h1( х о Е Л 00 , то функция ~ тождественна, если ) функция ~ каждой точке х точку х' = (О, О, fз, 14 , •••) = (О, 1, fз, 14 , •• •) что функция /2 fi (х 0 J; (хо ) Е Л 01 , )= то ставит в соответствие с теми же координатами, кроме второй, т. е. меняет местами отрезки Л 00 и Л 01 второго ранга. Заметим, тождественна на множестве точек канторова мно0 жества, лежащих на отрезке Л~, /2 (х ) как и С, где если = (О,О,1~,1~, ...). Так же, функция ~ взаимно однозначна и непрерывна. ~, Следовательно, и композиция /2 = ~ о h1 взаимно однозначна и непрерывна. Продолжим этот процесс бесконечно. Если постро ены функции J;, / 2 , ••• , fп_ 1 , то fп где если fп_/х ) = hn-l O hn_2 ° ... 0 0 = hп lzi (х о hп-i о .•. о~ о~: С ➔ С, 0 ) Е Л.....___.... 00___0 , то функция fп п тождественна, если fп_1 ( х ) Е Л.....___.... 00 _ ..о 1 , то функция fп каждой 0 п-1 точке х = (О, ... , О, 1, 1п+~, ...) ставит в соответствие точку '--v----' п-1 х = (О, 1, . .. , О, 1п+1' ...) с теми же координатами, кроме п-й, т. е. fп '-----v------' п меняет местами отрезки Л 00 ___0 и Л 00 ___ 01 п-го ранга. Функция fп .....___.... ........_,,._.. п п-1 взаимно однозначна и непрерывна как композиция взаимно одно 0 значных и непрерывных функций, fп (х ) = (О, О, ... , О, 1~+1' ...). '-у--' п Функция fп тождественна на множестве точек канторова мно жества, лежащих на отрезках Л 1 , Л 01 , Л 00 ~, ••• , Л 00.. _01 • ........_,,._.. п-2 57 Таким образом, мы имеем последовательность непрерывных функций J;_, / 2 , ••• , fп, . . . (*), взаимно однозначно отображающих канторово множество на себя. Покажем, что последовательность (*) равномерно непрерывно сходится к такой взаимно однозначной функции/ С ➔ С, которая точку х 0 переводитвточкуО,т. е. f(x 0 )=0 и VkЕNфункция/ совпадает с функцией /2 на всех точках канторова множества, кроме его точек, лежащих на отрезке Л 00...о • ._.,-, k-1 Действительно, VЕ > О :3 k0 Е N, такое, что длина отрезка Лоо ...о k0-ранга равна 1/3k0 < Е. Тогда Vk ~ k 0 и Vx Е С имеем ._.,-, ko p(fx, fkx) < Е. По теореме взаимно 27 функция/непрерывна. Очевидно, что функция/ однозначна. Так как канторово множество является хаусдорфовым пространством и бикомпактно (как замкнутое огра- ниченное подмножество прямой R 1), то по теореме 19 функция f 0 является гомеоморфизмом, при этом f(x ) = О. Пусть х1 , х2 Е С. По доказанному, существуют гомеоморфиз мы С➔ С и g 1: 1 ция g~ : С• g2: С ➔ С такие, что gi(x1 ) = О, g 2(x2) = О . Функ- С является гомеоморфизмом (как обратная гомео морфизму). Следовательно, композиция гомеоморфизм и g = g; 1 0 g 1: С ➔ С - g( х1 ) = х2 • Таким образом, канторово множество топологически одно родно. № 16. Каждой точке канторова множества С и каждой точке множе ства К однозначно соответствует последовательность индексов i1 , i2 , ••• in, .. . , где in = О или in = 1 (*). Будем считать соответству- ющими точки х Е К и х' Е С, которым отвечают одинаковые по следовательности (*). значное соответствие 58 Таким образом, установлено взаимно одно f между множествами К и С. В силу бикомпактности К и хаусдорфовости С для доказатель ства гомеоморфности пространств К и С достаточно показать, что взаимно однозначное отображение f К С непрерывно . • Докажем, что для любой точки х0 Е К и для любого Е >О су ществует такая окрестность Ох0 точки х0 в пространстве К, что для любой точки х Е Ох0 имеем: lx' - х~ 1< Е. Пусть х0 Е К, Е > О. Возьмем такое п Е N, что 1/Зп < Е, и рас смотрим отрезок Л 11 •• •in ранга п, содержащий точку х~. Его длина равна 1/Зп. Тогда искомой окрестностью Ох0 точки х0 будет от крыто-замкнутое множество К11 ••• in с теми же индексами, что и от- резок лi, ...in, и, следовательно, lx' - х~ 1:: :; 1/Зп < Е. No 17. 00 1 Обозначим через К произведение П С , где С 1 - классиче- i=l ское канторово множество (V i Е N), ft - житель С 1 . Для любого i Е N проекция проекция К на сомно- ft непрерывна [3, гл. I, § 8, п . 2]. Пространство К бикомпактно (как произведение бикомпакт ных пространств) . Докажем, что пространства К на 2п Vn Е можно сделать разбиение N множеств с условиями задачи № 16. Обозначим через С~ .. .in множество точек канторова множества ci' i = 1, 2, ... ' лежащих на отрезке л i1...in • 1 Пусть п = 1. Сделаем разбиение сомножителя С на 2 множе 1 ства С6 и С1 • Тогда К= К0 u К1 , где множества К0 К1 = J;- 1C11 замкнуты (в силу непрерывности ресекаются, т. е. имеется разбиение К на 2 = J;- 1C6, fi ), непусты и не пе множества. Пусть п = 2. Сделаем разбиение сомножителя С на 4 множе 1 ства С6о' с61' С1 0' с1\' а сомножителя С 1 2 - на два множества ci 59 С1 . и Тогда 2 к00 = Jj-r- 1c100 К11 К = К00 u n 12-1с2О ' =1i-1 c;1 пf/С1 2 к 01 К01 u К10 u К11 , -r-1c101 n 12-1с2О' = 11 где к 10 множества -r- 1c1 10 = J\ n 12-1с21 ' замкнуты, непусты и попарно не пересекают- ся, т. е. имеем разбиение К на 2 2 множеств. При этом К0 :::) К00 , Ко :::)Koi, К1 :::)К10, К1 :::)К11· Пусть п = 3. Сделаем разбиение сомножителя С 1 на восемь множеств С~00 , C~oi, С~ 10 , с;00 , C~ 1i , C{0 i , с;10 , C{1 i , а сомножителя с2 С3 2 3 - на четыре множества на два множества ci с2 , с2 , 00 01 с2 , с2 ; 10 11 сомножителя и С(. Тогда получим разбиение К на множеств: где причем К1• \ :::) кООО =J-r-1 lclООО n n 1- lсЗ 3 О; к001 =J1.r- lcl001 n f 2- lc200 n 1-lсЗ 3 О; к010 =J1-r- lcl010 n 1-1с2 2 01 n 1-lсЗ 3 О; к011 =J1-r- lcl011 n 1- 1с2 2 01 n 1- lсЗ 3 О; к100 =J-r-1 lcl100 n 1-1с2 2 10 n 1-lсЗ 3 1; к101 = J1-r- lcl101 n 1- 1с2 2 10 n 1-lсЗ 3 1; к110 =J1-r- 1c1110 n 12-1с211 n к111 =11-r-1c1111 n 12- 1с211 n J3-r-1сз1 , К.. 1112 :::) К..1 121з. . 1 1- 1с2 2 00 -r- 1сз J3 1; Продолжим этот процесс бесконечно. При п = k делаем разбиения сомножителя С 1 на 2 k множеств l C~--ik' сомножителя теля Ck - 60 с2 - на 2 k-l множеств с2 ~ -- .ik- i, • • • , сомножи- на 2 множества с; и C1k. Получим разбиение про- странства К на 1 множеств К.11··· 1.k , причем К.11 ::, К1.. ::, 112 и т. д. Из построения видно, что каждая последова- ::, ... ::, Ki1i2 .••ik тельность кl. 2k ::) кl. i- ::) .. , ::) 1·~ кl. z· 1· 12 ·-- п ::) , , , имеет единственную об- щую точку х Е К. Следовательно, пространства К и С гомеоморф ны (см. задачу № № 16). 18. Для доказательства потребуется следующая лемма. Лемма. Любое компактное метрическое пространство для лю- бого п EN можно представить в виде объединения 2m, где т 2::: п, замкнутых множеств с диаметрами ~ 1/ 2п. Доказательство. Пусть Х странство, п EN. тыми шарами - компактное метрическое про Рассмотрим покрытие О(х, 1; 2n+I), х Е Х. Q пространства Х откры- Пусть О)= {O1(xi, 1/2п+~), ... , Ok(xk, 1/2п+~)} есть конечное подпокрытие покрытия Q. Обозна чим через Di = DJxi, 1; 2n+I) замыкание множества OJxi, 1/2п+~), i = 1, ... , k. Получим покрытие ёо = {D1 , ••• , Dk} пространства Х, состоящее из конечного числа замкнутых множеств с диаметрами ~ 1/2п. Пусть т есть такое наименьшее натуральное число, что т 2::: п и 2m 2::: k. Рассмотрим множество А= {i/2 ••• im, где i1 =О или i1 = 1, j = 1, 2, ... , т}, состоящее из 2m элементов, и постро им отображение <р множества А на множество ro таким образом (для определенности), чтобы для i = 1, 2, ... , k -1 прообраз <р - l ( Di) состоял из одного элемента. Обозначим <р ( 4... im) через Di1•• .im. Таким образом, пространство Х представлено в виде объединения 2m, где т 2::: п, замкнутых множеств Di1 ...im (индексы принимают значения О и 1) с диаметрами ~ 1/ 2п . Лемма доказана. Представим Х в виде объединения множеств Di1 ••• im, с диаметрами ~ 2т1 ( т1 2::: 1) замкнутых 1/ 2 (индексы i1 ,J = 1, .. . ,mi, 61 принимают значения О или подпространство D 11 •••im 1). Каждое компактное метрическое представим в виде объединения 2т(~ ··.im1 ) 1 2 ( m(i1 •• • im) г 2) замкнутых множеств с диаметрами : : :; 1/ 2 • Пусть 1 т; есть максимальное из чисел странство D 11 •••imi ···1 , • ). 1 Теперь каждое про- представим в виде о бъединения множеств с диаметрами : : :; 1/2 D11•••im, ...i m(4 ... im 2 • 2 т'2 замкнутых Обозначим эти множества через Таким образом, пространство Х представлено в виде т2 объединения 2~ ( т2 = т1 + т;) замкнутых множеств с диаметра- ми : : :; 1/ 2 и т. д. 2 Пусть п = k. Имеем представление Хв виде объединения замкнутых множеств D11•• imi .. i , .. i , ff½ ( mk-1 2mk- 1 mk-l =mi. + т;, + тз + ... + т~_1 ) с диаметрами : : :; 1/2k-i_ Каждое пространство D 11 •••i , представим в mk-1 виде объединения 2 mei··\п;,_1 ), где m(i1 •• .i , ) г k, тk-1 жеств с диаметрами : : :; 1/2k. Пусть т~ т(4 .. .i , ). Теперь каждое пространство mk-1 замкнутых мно- максимальное из чисел представим в Di ...i 1 mk-1 виде объединения 2mi замкнутых множеств с диаметрами : : :; 1/2k. Обозначим эти множества через D 11 •• .imi .. .imz ...imk • Таким образом, пространство Х представлено в виде объедине ния 2т1 , где mk = т1 + т; + т; + ... + т~, замкнутых множеств с диаметрами : : :; 112k и т. д. Построим отображение f канторова множества С на простран ство Х следующим образом. Каждому отрезку Лi всего 2т1 ) поставим в соответствие множество 1 •• •im1 ранга D 1, •.. im m1 (их с теми же 1 индексами, каждому отрезку Л 11 ___1~ 62 ранга т2 (их всего 2т2 ) по- ставим в соответствие множество Di 1 •• 1m 1 ".i , m 2 = D4...imA ...L с теми же ин- дексами и т. д. Каждому отрезку Лi1 .. . imk раша mk (их всего 2mk) поставим в соответствие множество Di1" 1m ...im, ...im, 1 = Di 1 ...imk же индексами и рассмотрим сюръективное отображение f nлi1 с теми k 2 С ➔ Х, ОС) которое произвольной точке ХЕ С, Х = ставит В соответ .. ,imk k=l n ОС) ствие точку У Е Х, У = Di1,. ,imk. Докажем, что f непрерывно. k=l Пусть х0 Е Х, у0 у0 • Пусть Di 1 ...imk = fx 0 , Оу0 - произвольная окрестность точки есть некоторое замкнутое множество, содержащее точку у0 и содержащееся в Оу0 • Рассмотрим отрезок Лi .. .imk ранга 1 mk, имеющий те же индексы, что и множество жит на этом отрезке, множество Ох0 ность точки х0 , что /: f(Ox0 ) = Лi1 с Оу0 • • • •imk Di 1 ...imk. Точка х0 ле п С есть такая окрест Таким образом, отображение С ➔ Х непрерывно. No 19. Представление открыто-замкнутого множества И в виде объ единения п, где п Е N, непустых, попарно не пересекающихся от крыто-замкнутых множеств будем называть делением множества И на п частей. Для доказательства нам потребуется следующая лемма. Лемма. Любое компактное метрическое нульмерное простран ство без изолированных точек для любого п Е N можно разделить на 2 m (т > п) частей с диаметрами ~ 1/ 2п. Доказательство. Пусть п EN, а Х- компактное нульмерное метрическое пространство без изолированных точек. Рассмотрим покрытие Q х Е Х. В пространства Х открытыми шарами О(х, 1; 2n+1) , силу нульмерности пространства Х для любого О(х, 1; 2n+l) существует такое открыто-замкнутое множество И, 63 что хе И и И с О(х, l/2n+I). Таким образом, получим покрытие Q' пространства Х открыто-замкнутыми множествами с диаметра ми ::; 1/2п. ro = {И~, Выберем И2 , ••• , Uk} из него конечное (элементы покрытия каться). Построим покрытие ro' ro подпокрытие могут попарно пересе пространства Х попарно не пере секающимися открыто-замкнутыми множествами И{, И~, ... , И{, где и; И{ =И1 , = uk \ (И1 U И~ =И2 uk-1). И2 U ... U каждый элемент покрытия ro' и; =И3 \(И1 uU2 ), ••• , Покажем, что для любого р Е N можно разделить нар частей. Пусть И е Возьмем И\ открыто и является окрестностью точки х0 • Существует ro'. {х1 } такое множество две И1 , \ Ох 0 различные точки х0 ,х1 е И. Множество элемент базы из открыто-замкнутых - множеств, что х0 Е Ох0 и Ох0 с И \ {х1 }. Множество Ох1 = И\ Ох0 открыто-замкнуто образом, И= Ох0 u и содержит точку Ох1 , т. е. имеем деление И на х1 • 2 Таким части. Если р > 2, то аналогично можно делить множества Ох0 , Ох1 и их части до тех пор, пока не получим деление И нар частей. Итак, рассмотрим покрытие ro' = {И{, И~, ... , И{} пространства Х Пусть т есть такое наименьшее натуральное число, что т ~ п и 2m :2:: k . Путем конечного числа делений элементов покрытия их частей можно получить деление пространства Х на Очевидно, что каждая часть имеет диаметр Теперь при решении задачи № замкнутое множество Di1 •• •im 18 ::; 1/2п. ro' и частей. 2m Лемма доказана. мы можем выбрать непустое таким образом, чтобы любые два за- мкнутых множества одного и того же ранга имели пустое пересече ние . Тогда каждая точка у е Х будет однозначно определяться последовательностью = Di1...imk D.11 "1mi . :::> D. . . 11 "Jщ "JП½ = D "J"'2 . 11 :::> ••• :::> D. . 11 "J"'I . . "Jfl'IJ, .. Jmfc :::> • • • непустых замкнутых множеств различных рангов, содержащих эту точку. По этой причине построенное в задаче № отображение 64 = f: С• 18 Х будет взаимно однозначным и непрерыв- ным, а следовательно, и гомеоморфным, так как С бикомпактно, а пространство Х- хаусдорфово (теорема 19). №20. ОС) Пусть Х = П Хп , где пространство Хп (п = 1, 2 , ... ) есть кon=I печное дискретное неодноточечное пространство . Очевидно, что пространство = 1, 2 , ...) Хп (п является компактным, метриче ским, индуктивно нульмерным. Следовательно, такими же свой ствами обладает и пространство Х (теоремы 21 , 22, 23). Покажем, что пространство Х не содержит изолированных точек. Пусть х , =( , ...) Е ХО' Xi,' х,2 , .. ., xk, , х - произвольная окрестность точки х'. Покажем, что Ох' содержит некоторую точку у Е Х, у =1= х'. Существует такой элемент базы И, что х' Е И, И Е Ох', и множе ство И состоит из всех точек {х1 , х2 , • •• , хп нечное число координат х1 , х1 , ••• , xi 1 k 2 ты соответственно из множеств Х11 Пусть у = {х1 , х2 , координата хР, р =I= • ••• , хп , • li , 12 , ... } • ••• , zk , - - у которых ко фиксированные элемен- Х12 , •• • , Е И , ... }, , X 1k • такая точка, у которой отлична от координаты 1 хР точки х'. Следовательно, у =I= х'. Таким образом, согласно решению за дачи № 19, пространствоХгомеоморфно канторову множеству. №21. Аналогично решению задачи № № 20. 22. Докажем сначала, что гильбертов кирпич Q 00 , т. е. метрическое пространство , точками которого служат всевозможные последова тельности х ={х1 , х2 , ••• , хп ,···} , где О~хп ~1/2п ,п=1 , 2, ... , а расстояние определяется формулой ОС) р(х , у) = L (yk - xk)2' k =l 65 гомеоморфен пространству 1~0 , т. е. топологическому произведе нию счетного числа прямолинейных отрезков. Действительно, так как все отрезки числовой прямой гомео- морфны, можно взять за отрезок [О, 1/2п] числовой прямой. In 00 Тогда пространство 1~ 0 = П In и гильбертов кирпич Q 00 состоят из n=l одних и тех же точек х = (xi,x2 , .. •), где О~ хп ~ 1/2п, п = 1, 2, ... . Докажем теперь, что тождественное отображение 1~0 на Q является гомеоморфизмом, ]~О • Q 00 И 6) Q • 00 т. е. докажем, что отображения 00 а) ]~О НеПрерЫВНЫ. а) Докажем, что для любой точки х = {хп} Е 1~0 = Q и для лю 00 бого в > О существует такая окрестность Ох с 1~0 , что для всех точек х' Е Ох имеем: р(х, х') < в (расстояние в Возьмем 00 L такое чтобы N, Q 00 ) . выполнялось условие 2 (1/2п)2 < в /2. Окрестность Ох точки х в Х определим ycлo- n=N+l виями, налагаемыми на координаты lx -x{I< ~ , ... ,lxN -x~I< ~ . 2N 2N 1 х~ точки х' = {xk} Е 1~ 0 : Легко заметить, что окрест- ность Ох удовлетворяет высказанному требованию. 6) Докажем, что для любой точки х = {хп } Е Q 00 = 1~0 и для лю бой ее р(х, х') окрестности <в в Q Можно х 1 = ( 1 1 х1 , х2 , ••• , существует такое в > О, что из следует, что х' Е Ох. предположить, ~' n2' . . . ' ns - 00 Ох с Х 1 xk, .. .) , что Ох состоит удовлетворяющих из всех при точек некоторых и Е 1, Е 2 ' ... 'Е s условиям lхп; - x~i < Е i. Если теперь Е наименьшее из чисел в 1 ,в 2 , ••. ,Е 8 , а х' 1 - произвольная точка, для которой р(х, х') < в, то для нее тем более lхп; - х:; < в ~ вi при 1 i = 1, 2 , ... , s. 66 Итак, пространства 1 и Q гомеоморфны. Пусть теперь 't : С • 1 есть непрерывное отображение канторова множества С на отрезок 1 = [О, 1] (см. § 3, 't - это подотоб ражение канторовой лестницы). Обозначим через fп композицию <р п о 't, где <р п - гомеоморфизм отрезка ]п =[0,1/2п],п=1, 1 = [О, 1] на отрезок 2, ... . Рассмотрим систему непрерывных отображений fп: С • 1п, 00 п= 1, 2, .... Тогда отображение f = П fп - произведение отоб- n=I ражений (определение 50) - есть непрерывное отображение (тео- рема 26) счетной степени канторова множества С~ 0 на простран ство ]~0 =Q Но С~0 гомеоморфно С (см. задачу № 17). Таким 00 • образом, гильбертов кирпич является непрерывным образом кан торова множества. Заметим, что этот результат непосредственно следует из реше ния задачи № 18, так как гильбертов кирпич метрическое пространство (теоремы - это компактное 22, 23). No 23. Канторово множество гомеоморфно счетной степени простого двоеточия D (см. задачу № 13). 1. Пространство D~0 индуктивно нульмерно (как произведе ние индуктивно нульмерных пространств). множество всюду - Так как канторово сепарабельное метрическое пространство плотным множеством ронних точек), то (по теореме является множество 11) оно имеет счетную (счетным всех односто базу. Следовательно, всякое подпространство канторова множества метризуемо, индуктивно нульмерно и имеет счетную базу. Таким образом, если существует гомеоморфное вложение некоторого пространства Х в канторово множество, то Х- индуктивно нуль мерное метризуемое пространство со счетной базой. 2. Докажем, что каждое метризуемое индуктивно нульмерное пространство Х со счетной базой можно вложить в С (- D~0 ). Из теоремы 14 следует, что в базе пространства Х, состоящей из открыто-замкнутых множеств, содержится счетная база В = {Ui}: 1 . 67 При D= = каждом {О, 1} - i ЕN определим отображение J;: Х • Di = простое двоеточие, положив Очевидно, что Vi Е N J;: Х • Di = D отображение непрерыв- ~ но. Обозначим через f: Х • D~ = П Di диагональное произве i=I дение отображений J;. Согласно теореме 25, отображение f непрерывно. Так как для любых двух различных точек х Е Х, х' Е Х существует такое Иа, что ХЕИа, х'ЕХ\Иа и,следовательно, f fax*fax' и fx-:1:-fx', то взаимно однозначно отображает пространство Х на некоторое множество У= jX с D~0 • При этом fl]2 = У пп: 1 (1), т. е. образы элементов базы В открыты в У. Таким образом, f есть открытое (т. е. образ любого открытого множества открыт), непрерывное взаимно однозначное отображе ние Х на пространство У с С физмом ( отображение f является гомеомор [3, гл. I, § 1]. №24. Сначала докажем следующую лемму. Лемма. В любом полном метрическом пространстве (Х, р) без изолированных точек для любого п Е N можно выделить непустые замкнутые непересекающиеся подпространства рами :::;; 1/2п, F'i и F2 с диамет- в которых тоже нет изолированных точек. Доказательство. Пусть п EN, (Х, р) - полное метрическое пространство без изолированных точек. Возьмем в Х две произ вольные различные точки 1/2т < p(xi,x2 ). х1 , х2 . Рассмотрим Существует такое сферические т Е N, что окрестности 01 = =0(xi, 1/2k+1) , 0 2 =0(х2 , 1/2k+l) точек х1 и х2 , где k=n, если п ~ т, и k = т, если п < т. Диаметры множеств 0 1 и 0 2 равны 68 1/2k::;1;2п. Пусть F'i=[O1 ], F2 =[O2 ] . Очевидно,что F;_ и F2 яв ляются замкнутыми непересекающимися подпространствами про странства Х с диаметрами ::; 1/2п. Покажем, что и F;_ F2 не имеют изолированных точек. Действительно, предположим, что х являет ся изолированной точкой какого-либо из этих подпространств пусть, для определенности, х Е F;_. Если х Е 0 1, то по аксиоме Т3 имеется окрестность Их точки х, которая содержится в со своим замыканием. Окрестность Их - 01 вместе является окрестностью точки х и в пространстве Х Следовательно, Зх' Е Х: х' *х и х' Е И с 0 1 с F;_ , т. е. х не является изолированной точкой в F;_. Если же х Е F;_ \ 0 1 , то любая окрестность точки х содержит точки множества 0 1 и, следовательно, точки множества F;_. Таким обра зом, и в этом случае х не является изолированной точкой в F'i. Лемма доказана. Итак, пусть (Х, р) изолированных множества F0 точек. сХ и полное метрическое пространство без - F'i Выделим непересекающиеся с Х с диаметрами ::; 1/ 2, замкнутые которые в топо- логии, индуцированной из Х, не имеют изолированных точек и являются замыканиями открытых в Х множеств. Так как F0 и F;_ также являются полными метрическими пространствами без изо лированных точек (в силу их замкнутости в Х [10, гл. то лемму можно снова применить к пространствам дельности множества - получим F00 с F0 , непустые F01 с F0 , 4, F0 непересекающиеся F'io с F'i, F;_ 1 с F;_ п. и 4.3.11]), F;_ в от- замкнутые с диаметрами ::; 1/ 22 , каждое из которых как подпространство пространства Хне имеет изолированных точек и является замыканием открытого в Х множества. Продолжая этот процесс по индукции, мы строим для каждой конечной последовательности ~, ... , ik , k Е N, состоящей из 1 нулей и единиц, непустые замкнутые в Х множества Р;, .. . ik без изо лированных точек таким образом, что: а) каждое б) F';,1 ...ik - замыкание открытого вХмножества; F1.1· · · 1.k 1•k+l с F1•1··· 1.k для любых i1, ... ,ik и k EN; 69 в) F;1...ik nF;; ...ik =0, если {i1, ... ,ik};t:{i{, ... ,i;}, г) diam 1\ ...ik Тогда ::;; 1/ 2k, k Е N. для l; = {i1, ... , ik, ...} любой бесконечной нулей и единиц п { F; _..ik: 1 ит ровно из одной точки (это последовательности k Е N} непусто и состо- вытекает из принципа вложенных шаров: для того чтобы метрическое пространство было полным, необходимо и достаточно, чтобы в нем любая последовательность вложенных друг в друга замкнутых шаров, радиусы которых стре мятся к нулю, имела непустое пересечение [8, гл. II, § 3, п. 2]. Обо значим через У множество всевозможных последовательностей из нулей и единиц (У можно интерпретировать как множество точек произведения счетного числа простых двоеточий, т. е. как канто рово Р множество). = u { п {F;1_.. ik: Легко показать, что подпространство k Е N}: l; Е У} гомеоморфно канторову множе- ству. Действительно, пусть f есть построенное взаимно однознач ное отображение канторова множества У= D~0 на пространство Р с Х. Рассмотрим произвольную точку l; 0 Пусть O(fl; 0 ) 3 п Е N: fl; 0 точки ~0 , Е произвольная окрестность точки - F;1_• •in fl; 0 • Тогда с О (f ~ 0 ). Следовательно, окрестностью образ которой содержится в множество {{4, = {i;, ... , if, ...} Е У. ... , ik, ...} 4 = 4°, O(fl; 0 ), ... , in = i~}, Ol; 0 можно считать которое, очевидно, открыто в произведении D~0 ( с его тихоновской топологией). №25. а) Пусть О - произвольный открытый круг на плоскости. Этот круг либо полностью свободен от точек множества S, либо содер жит хотя бы одну его точку М Докажем, что и в этом последнем случае в круге О найдется меньший круг от точек множества V, полностью свободный S. Чтобы убедиться в этом, рассмотрим замкнутый квадрат Кп ранга п, содержащий точку Ми такой, что его диагональ меньше расстояния от точки М до границы круга О (это можно сделать, так как диагонали замкнутых квадратов стре мятся к нулю при п • 70 оо). Этот квадрат целиком лежит внутри круга О (рис. 23). Тогда открытый квадрат (п + 1)-го ранга, лежа щий в середине квадрата Кп, полностью свободен от точек мно жества круг V, S (и тоже лежит внутри круга О). Следовательно, открытый вписанный в этот открытый квадрат, будет лежать внутри круга О и не будет содержать точек множества S- S. Таким образом, нигде не плотное множество на плоскости. о CJ V / м / Рис.23 6) Так как S п есть замкнутое множество Vп Е N, множество S = n {Sn, п = 1, 2, ... } замкнуто . Докажем, что S не имеет изолиро ванных точек. Пусть М0 Е S; опишем около М0 произвольную сферическую окрестность О и рассмотрим замкнутый квадрат Кп: М0 Е Кп,Кп с О. Границы этого квадрата принадлежат содержатся в О. Следовательно, М0 S и не является изолированной точкой. в) непосредственно вытекает из теоремы 28. №26. Аналогично решению задачи № 25. №27. Пусть I - пространство иррациональных чисел (подпростран ство числовой прямой R). Так как [/] = R , то I всюду плотно в R. 71 Пространство Jне замкнуто, так как * [I], 1 жество рациональных чисел на прямой 1= R \ Q (где Q- мно R). Множество Q счетно и, следовательно, является объединением счетной совокупности одно является Т 1 -пространством, то любое одноточечное множество замкнуто. Таким образом, Q есть множе точечных множеств. Так как ство типа G8 и Fcr. R В силу взаимной дополнительности множеств типа множество 1 является подмножеством типа G8 Fcr на прямой. №28. Базой из открыто-замкнутых множеств в пространстве 1 явля ется совокупность подмножеств иррациональных чисел, лежащих на всевозможных интервалах с рациональными концами. Действи тельно, для любых р, q е Q множество (р, q) п 1 открыто- замкнуто (в индуцированной топологии). Если И- открытое множество в в R. Пусть хе И, тогда хе интервал V. (p,q)cR, p,qeQ, 1, то И= V п 1, где V открыто Следовательно, существует такой что xe(p,q)cV (так как на пря мой R интервалы с рациональными концами образуют базу) . Тогда xe(p,q) nl сИ. По теореме 10 множество {(p,q)nl, где р , q е Q} - база в J. Очевидно, что 1 является Т гпространством и непусто. Следовательно, 1 индуктивно нульмерное простран ство . Следствием индуктивной нульмерности пространства 1 явля ется его несвязность и полная несвязность . №29. Пусть {хп};= 1 - последовательность иррациональных чисел, сходящаяся к некоторому рациональному числу а. Тогда в про странстве 1 последовательность {хп} ;=1 является фундаменталь ной, но ее предел не принадлежит этому пространству. Таким об разом, стандартная пространство Известно метрика на J не полна. Докажем, что 1 можно метризовать полной метрикой. [2, гл . 4, § 6], что пространство 1 иррациональных чи сел (рассматриваемое как подпространство числовой прямой) го меоморфно классическому пространству Бэра В(~ 0 ) . 72 Точкой пространства ность х = { nk, k Е у= {п~ , р(х,у) nk = п~ две = 1/ i(x, у), точки где i(x,y) для всех k Е является любая последователь натуральных чисел nk. Пусть х = { nk, k Е N}, N} k EN} - В(~ 0 ) пространства = min{knk :;t: п~} В(~ 0 ). и Положим р(х,у) = О, если N. Среди аксиом метрического пространства аксиомы тождества и симметрии очевидны . Легко проверить и аксиому треугольника даже в следующем 1/ i(y, z), то i (х, у), i (у, z), усиленном виде : р (у, z) = р (х, чисел и, следовательно, расстояний р(х,у) и где z) = 1/ i, i если р(х,у) есть наименьшее из двух 1/i - наибольшее из двух p(y,z). Сферической окрестностью О(х, 1/ k) точки х диуса 1/k является множество 1 которых п1 =~ ' = 1/ i(x, у), n2 = n 2 .. . nk 1 1 On1.. .nk = (п1 ,п2 , ...) ра- всех точек у= (п{, п~, ...), для = nk. Множество всех сферических окрестностей всевозможных точек х Е В(~ 0 ), очевидно, равномощно множеству всевозможных ко- нечных комбинаций натуральных чисел, т. е. имеет мощность ~о и образует базу топологии метрического пространства В(~ 0 ). Покажем, что метрика р пространства В(~ 0 ) является полной. Зафиксируем произвольную фундаментальную последователь ность {хп } ;= 1 , состоящую из элементов пространства В(~ 0 ), т. е. элементами хп (п = 1, 2, ...) являются последовательности ральных чисел. Для любого Е >О любых p(xp,xq) < Е. p,q ~ т 1/i(xp,xq) < E, т. е. имеем существует такое т Е N, что для i(xp,xq)>II E. Это Если Е ➔ О, то значит, = 1/ i(хп , а)< Е. чисел, что VE > О :3 т Е N: Vp что i(xp,xq) • oo. Следовательно, существует такая последовательность а натуральных нату = {ап } ;=1 ~ т р(хп , а)= Таким образом, любая фундаментальная последо вательность из элементов пространства В(~ 0 ) сходится к элемен ту этого пространства. 73 Пусть теперь f: В(~ 0 ) 1• гомеоморфизм. Определим но - d(x,y) = p(/(x),F(y)), метрическое пространство (/, d) полное. вую метрику в/, полагая х,у е /. Ясно, что №30. 1. Пространство 1 гомеоморфно классическому пространству Бэра В(~ 0 ), а пространства В(~ 0 ) и N-к 0 (т. е. топологическое произведение счетного числа пространств натуральных чисел) со стоят из одних и тех же точек х = (п1 , п2 , •.•), nk е N. Докажем, что тождественное отображение В(~ 0 ) на N-к 0 является гомеомор физмом. Действительно, система множеств {О(х, 1/ k): хе В(~ 0 ), k =1, 2, ... } образует базу пространства В(~ 0 ). Каждое множество О(х, состоит из точек у, первые координатам п1 , k координат которых равны 1/k) первым k ~, ... , nk точки х. Но этим точкам у соответствуют точки элементарного открытого множества On1~ .. .nk, состоящие из ОС) всех точек (i1, i2, ... ,ik,···) с П Ni = ~, i=l ik у которых i1 = п1 , i2 = п2 , ... , = nk. Совокупность элементарных открытых множеств такого вида образует базу в пространстве N-к0 ( с его тихоновской топологией). Таким образом, тождественное отображение В(~ 0 ) на N-к 0 пере- водит базу пространства В(~ 0 ) на базу пространства N-к0 • Следо вательно (теорема 12), пространства В(~ 0 ) и N-к 0 гомеоморфны. 2. Так как дискретные пространства N и Z гомеоморфны, то и пространства В(~ 0 ) и z-Ко гомеоморфны. №31. 1. Очевидно, что любое дискретное пространство топологиче ски однородно. (для любых двух точек х1 , х2 е Х, где Х кретное 74 пространство, отображение /: Х • Х, такое, дисчто f (х1 ) = х2 , f (х2 ) = х1 , а в остальных точках х Е Х отображение f тождественно является гомеоморфизмом.) Покажем, что произведение любого числа топологически од нородных пространств топологически однородно . Рассмотрим Х = П Ха, где для любого а Е А пространство аЕА Ха топологически однородно. Пусть х х = {ха} Е Х и х' = {х~} ЕХ, -:1:- х'. Покажем, что существует такой гомеоморфизм /: Х • что f(x) = х'. Действительно, для любого а Е А существует такой гомеоморфизм fa: ха ➔ ха, что fa (ха)= х~ (если ха= х~, то /: Х • Х есть произведение отображений fa: Ха • Ха, а Е А ( определе ние 50). Очевидно, что f(x) = х', f - взаимно однозначно, непреfa: Ха ➔ Ха Х, тождественное отображение). Пусть - рывно (теорема 26) и обратное отображение / - 1 : Х • непрерывно, т. е. Х также f- гомеоморфизм. Так как пространство 1 иррациональных чисел гомеоморфно N~ 0 ( см. задачу № 30), а N - дискретное пространство ( следова тельно, топологически однородное), то N~ 0 топологически одно родно. 2. Напомним определение: пространство Х называют локально бикомпактным, если каждая точка х Е Х имеет окрестность И, замыкание которой [ И] бикомпактно в Х Предположим, что в некоторой точке х пространство 1 локаль но бикомпактно, т. е. имеется такая окрестность И точки х, замы кание которой [ И] бикомпактно в пространстве /. Существует та кой элемент базы Ох= (р, q) nl, что х Е Ох с И. Множество Ох замкнуто в /, следовательно, Ох замкнуто в бикомпактном про странстве [И] . Замкнутое подпространство бикомпактного про странства бикомпактно [3, гл. 1, § 7]. Отсюда получаем, что Ох бикомпактно в Ох бикомпактно в евклидовом 28) Ох замкнуто в R, но [Ox]R [ И] и, следовательно, пространстве R. Тогда (по теореме = [p,q]-:1:- Ох. Таким образом, наше 75 предположение неверно и, следовательно, пространство J не явля ется локально бикомпактным ни в одной точке. №32. Доказательство № непосредственно следует из решения задач 23 и 9. №33. 1. Канторово множество можно вложить в пространство ирра циональных чисел. Это доказано в задаче № чи № 24, так как пространство 9 или следует из зада J иррациональных чисел полномет ризуемо и не содержит изолированных точек. 2. Пространство иррациональных чисел можно вложить в кан торово множество. Это следует из задачи № 23, так как простран ство J метризуемо, индуктивно нульмерно и имеет счетную базу. №34. Нам потребуется следующая лемма. Лемма. Пусть Х - нульмерное сепарабельное метрическое пространство. Для любого Е >О существует счетное покрытие со этого пространства непустыми попарно не пересекающимися от крыто-замкнутыми множествами диаметра, меньшего Е . Доказательство. Любое сепарабельное метрическое простран ство финально-компактно [3, гл. I, § 7]. Пусть Е > О, рассмотрим по крытие Q пространства Х открытыми шарами О(х, с./2), хе Х. В силу индуктивной О(х, с./2) нульмерности пространства Х для любого найдется такое открыто-замкнутое множество И, что хе И с О(х, Е/2). Таким образом, имеем покрытие Q' простран ства Х открыто-замкнутыми множествами с диаметрами меньше Е. Выберем из него счетное подпокрытие со = {U1 , ... , Ui, .... } . Далее полагаем, что Vi = и.; V2 76 =И2 \Vi_, ... , Vп =Ип \u{v;:i=l, ... ,n-1}, .... Очевидно, система со* = {v; : i Е N} состоит из попарно непере секающихся открыто-замкнутых множеств. Так как любого п Е N, то о/ diam Vn < Е для всех п Е N. Vn с Ип для Легко заметить, что покрытие Х Лемма доказана. - = S. Рассмотрим f: 1 Согласно лемме, существует счетное по- крытие со1 пространства (У, р) непустыми попарно непересекаю щимися открыто-замкнутыми множествами диаметром, не боль шим f: 1 со 1 со 1 = S. Вследствие того что (У, р) не бикомпактно, покрытие можно предположить = {Ui ½: i2 Е N} непустыми попарно замкнутыми множествами, и ui п И., f: 2 = 1/2 2 1 11 Ui1 ui1½ если i1 непересекающимися в И-11 diam Ui1 * i{. ~ S, Ui1 *0 для любого Теперь для каждого (значит, и в ~/4 для любого i2 EN и = u {Ui ;_ : i2 1·, Е N}. Х) множеств, ui1½ п ui{½ ui Е = 0, для 1 u {Ui1½: 4 Е N, i2 Е * Ui1½ 0 N}. ение для каждого Ui1½: i1 Е N, i2 Е N и 1 4Е N (J) и l открытокоторых * i~ если i2 Так как И,. не бикомпактно, то можно выбрать таким образом, чтобы Заметим, что У= пусть открыто рассмотрим счетную систему {Ui1i2 : i2 Е N} замкнутых diam = 0, Итак, бесконечное счетное покрытие пространства 1 (У, р) бесконечным. {Ui1·,;_: i2 для любого Е и N} i2 Е N. Проделаем то же постро- f: 3 = 1/23 и т. д. В результа те для каждой конечной последовательности натуральных чисел ii, ... ,in будем иметь открыто-замкнутое в Х множество Ui1 •• .in. При этом будут выполнены следующие условия: 1) И1- iл 2) и. 3) у 1 1 1·, ···п-lп . IJ ...lп-1 Г) И1-,;;.. =u -, -, 1 1 l·, ···n-ln {И.,., = 0, ., ., : in 1112 ,--ln-J ln Е еСЛИ in -::j; in'; N}; = u {Ui1: i1 Е N}; 4) diam uiJ-··iп ~ 112n; 77 5) И4 ...i,i :;z: 0 для любых ~ Условие 5) eN, ... , in eN. мы записали вследствие того, что на каждом шаге получаются небикомпактные множества. Рассмотрим теперь бес конечное счетное семейство {Хп: пе бесконечных счетных N} дискретных пространств (т. е. каждое Х гомеоморфно простран ству Nнатуральных чисел). Тогда каждая точках топологического произведения { П Хп : п е N} натуральных чисел: х есть счетная последовательность = {i1 ,i2 , • • • , in, ... }. Положим .. 00 fx = и. 1) пиIJI.. п ... пи1).••• . п ... = nи.1] .• . ln lп n=l Вследствие условий 1}--5) и полноты пространства (У, р) для { каждой точки х е П Хп: п е N} множество fx непусто и состоит ровно из одной точки у е У. Таким образом, мы построили отобра жение /: В(~0 ) • У. Из условий ние на все У, а из 1) 3) и 2) следует, что/- отображе следует его взаимная однозначность. В про странстве В(~)= П{Хп : п eN} множества V 0 .0 1 ···1n = {х = {iп: пе N} е еП{Хп : п eN}: i = ii , .. . , in = i~} образуют открытую базу, а множества ui1 ...iп , ~ Е Легко заметить, что N, .. . , in f (V0 Е .0 ) 11 •. ·'ii N, образуют базу пространства Х = И.110 •• ·'ii.0 • Следовательно, по теореме 12, отображение/-гомеоморфизм. А так как пространства В(~0 ) и I ( см. задачу № 29) гомеоморфны, то пространства I и (У, р) также гомеоу морфны. №35. х Точке функцию Рис.24 78 4 J; поставим в соответствие (рис. 24). Каждой точке Ait, лежащей на радиусе OAi и находящейся от точки О на расстоянии t, где О ::;; t < 1, поставим в соответствие функцию f it, по- лученную умножением функции J; рис. принцип 25-28 функции проиллюстрирован на число t, i = 1, 2, 3, ... . построения На графиков J; , i = 1, 2, 3, ... . у о а Ь-а Ь-а ---- 8 4 Ь-а ь х 2 - 1 ----L---------------~-----L------Рис . 25 у о a l х 1 1 1 1 1 1 1 1 1 -1 __ __ L _______ L _______ - ----L-----Рис . 26 79 у о а Ь-а 1 8 1 ь х 1 1 1 1 1 1 - 1 ___ _ L _ _ _ _ _,1_ _ Рис.27 у 1 ---- г ---г ----------- 1 1 1 1 1 1 1 1 Ь-а 1 4 о 1 -----г------ 1 1 1 1 Ь-а 2 а 1 1 1 1 1 1 1 i 1 1 1 lb х 1 1 1 1 1 1 1 -1 ____ L_J _ _ _ _ _ _ 1 _____ _ _ ____L Рис .28 Таким образом, получено взаимно однозначное отображение метризуемого «ежа» счетной или любой конечной «колючести» на подпространство пространства С[ а, Ь] . отображение является изометрическим. 80 Легко заметить, что это у №36. Достаточно доказать, что никакое че тырехточечное метрическое пространство, состоящее из точек О, А, В, С, где О центр круга, а А, В, С радиусов («иголою>), ски вложить ни в - - концы разных х нельзя изометриче какое евклидово про странство Х (линейное пространство, мет рика которого порождена произведением) (рис. с скалярным Рис.29 29). Докажем это от противного. Предположим, что f есть указан ное вложение . Обозначим А1 = f(A), В1 = f(B), С1 = f(C), 0 1 = /(О). В силу изометричности вложения f имеем: р(А1 ,В1 ) = = p(I3i,(7i) = p(ЛiCi) = 2 (где р - метрика в Х, порожденная скаляр ным произведением), р(Л~,В1 ) + р(В1 ,С1 ) > р(Л~С1 ) . Следовательно, точки А 1 , В 1 , С1 не лежат на одной прямой пространства Х Тогда существует единственная двумерная плоскость Е2 пространства Х, содержащая эти точки. Так как в пространстве Х (в силу изометрич ности л р( л1 , 0 1 ) = р(в1 , 0 1 ) = р( с1 O1 ) = = р(А1В1 ). т. е. 01 Следовательно, точка 01 1, то р( А1 , 0 1 ) = р( 0 1 , в1 ) = лежит между точками А1 и В1 , лежит на прямой А1 В1 с Е2 • Аналогично, 01 лежит между точками В1 и С1 и между А1 и С1. Но этого быть не может, так как точки А 1 , В 1 , С1 различны. Следовательно, метризуемый «еж» «ко лючести» 3 и выше изометрически не вкладывается ни в какое ев- клидово пространство (например, в Rn \;/п EN, в /2 ). №37. Метризуемый «еж» «колючести» метричен отрезку [О, 1] с R 1 изо с естественной метрикой, который является полным метри ческим пространством (как замкнутое под о пространство странства). Рис. 30 полного метрического Следовательно, «еж» «колючести» 1 - пространство (рис . 30). про метризуемый полное метрическое 81 Пусть К есть метризуемый «еж» «колючести» ~ Зафиксиру 2. ем произвольную фундаментальную последовательность {хп} точек пространства К. Если начиная с некоторого номера п0 Е ;= 1 N все точки этой последовательности расположены на одной «игол ке», то подпоследовательность {хп , xno+l' . .. } 0 фундаментальной последовательности {хп};=Р состоящая из точек единичного от резка, сходится к точке этого отрезка. Следовательно, к той же точке сходится и вся последовательность {xn};=I· Если же точки фундаментальной последовательности {хп};= 1 расположены на разных «иголках», то для любого Е такой номер т Е N, >О найдется что для всех п ~ т точки последовательности расположены внутри открытого круга с центром в точке О радиуса Е/2. Отсюда получаем, что последовательность {хп};= 1 сходится кточке ОЕК. Таким образом, доказана полнота метризуемых «ежей» любой «колючести». №38. Пусть r - произвольный радиус круга К. Совокупность пересечений всевозможных эле ментов вида о 1) из базы В (см. с радиусом r является множеством всевозможных открытых интервалов на радиусе ность Рис. § 8) вида 31 пересечений 2) концы лежат на окружности Таким образом, (r, 't r) - (рис. r А совокуп 31 ). всевозможных (соответственно, вида радиусом полуинтервалов на радиусе r 3)), элементов из базы В с есть множество таких всевозможных r, что принадлежащие полуинтервалам ro (соответственно, в центре круга К). отрезок с обычной евклидовой топо логией. №39. Пусть (К, 82 't). Q - произвольное открытое покрытие пространства Рассмотрим некоторый элемент и покрытия Q, покрываю- щий точку О вида 3) из - центр круга К. Тогда найдется такой элемент базы В, что О Е G с И (только элементы вида В покрывают точку О). Обозначим через рые не покрывают элемент каждом отрезке 11 , • •• , l n 3) из G базы отрезки, кото- G (т. е. 11 u 12 u ... u ln =К \ G). На топология 't индуцирует обычную евкли li, .. . , ln дову топологию . Следовательно, каждый из отрезков Ii, .. . , ln в индуцированной топологии бикомпактен. Обозначим через шi со вокупность непустых пересечений элементов покрытия О с отрез ком li' i = I, ... , п (т. = Оп li ). Выберем из покрытия шi z. = 1, ..., п. каждыи~ элемент покрытия е. шi о печное подпокрытие ш i , является пересечением отрезка li коо шi с некоторым элементом покры- тия О. Обозначим через О~ множество всех этих элементов из по крытия О, i = I, ..., п. Число элементов в системе О~ то же, что и в покрытии ш~. Пусть 0° = О~ u О~ u .. . u О~. Тогда 0° u {И} есть конечное подпокрытие покрытия О. Следовательно, пространство (К, -r) бикомпактно. №40. Хаусдорфовость пространства ственно. Пусть х1 , х2 Е К, х1 * х2 • (К, -r) проверяется непосред- Рассмотрим сначала случай, ко гда х1 , х2 не совпадают с центром круга К (рис. Пусть х1 и х2 лежат на разных радиусах но. Тогда их непересекающимися например, следующие элементы вида r1 32). и r2 соответствен окрестностями являются, из базы В ( см. § 8): 2) Ох1 = r1 \ {О}, Ох2 = r2 \ {О}. Пусть х1 и х2 лежат на одном и том же радиусе r= ОМ (рис. Возьмем произвольную точку х, лежащую на радиусе r 33). между точками х1 и х2 • Тогда непересекающимися окрестностями точек х1 и х2 будут, например, интервал (О, х) и полуинтервал (х, М] . Пусть теперь х1 = О (где О- центр круга). Возьмем точку х, ле жащую между точками х1 и х2 • Обозначим через ON радиус, содер- 83 жащий точки х2 и х1 (рис. стями точек вида х1 и 3) из базы В) и Тогда непересекающимися окрестно 34). х2 будут множества Ох1 =К\ [x,N] Ох2 = [x,N] (элемент (элемент вида 2) из базы В). о Рис. 32 Рис.33 Рис.34 No 41. Нормальность пространства из его бикомпактности ( см. задачу № 40) [8, гл. II, § 6]. (К, следует непосредственно -r) задачу № 39) и хаусдорфовости (см. No 42. Пусть точках не является центром круга К. Если х ~ ro, то счетной определяющей системой окрестностей точки х будет множество всех интервалов с концами в точках с рациональными координатами, которые содержат эту точку и яв ляются элементами вида 1) из базы В (см § 8). Если х Е ro, то счетной определяющей системой окрестностей точки х будет множество всех полуинтервалов, являющихся эле ментами вида 2) из базы В, с общим принадлежащим им концом в данной точке х и не принадлежащими им концами в точках с ра циональными координатами . Предположим теперь, что точка О - центр круга К, имеет счетную определяющую систему окрестностей представляет собой множество типа G8 , 11· Тогда точка О так как является пересе- чением счетного числа открытых множеств элементов системы Для любой окрестности И точки О системы щийся в ней элемент вида 11 11 · имеется содержа 3) из базы В. Но каждый элемент вида 3) из базы В является дополнением до круга К лишь конечного числа 84 отрезков . Следовательно, пересечение счетного числа элементов вида 3) из базы В представляет собой дополнение до круга К лишь счетного числа отрезков, т. е . не является множеством, состоящим из единственной точки О. Полученное противоречие показывает, что в точке О не выполняется первая аксиома счетности. №43. Пространства (К, р') и (К, 't) состоят из одних и тех же точек. Покажем, что тождественное отображение f: (К, р') (К, • 't) яв ляется уплотнением. Взаимная однозначность отображения что отображение Пусть х ЕК, странстве (К, 't). f f очевидна. Покажем, непрерывно. Ох произвольная окрестность точки х в про- - Существует элемент И базы В, содержащий точ ку х и содержащийся в Ох. Если х не является центром круга К, то И есть элемент вида 1) или элемент вида другом случае найдется такое е Здесь Of, x={x' ЕК:р'(х, х') < е}, > из базы В. И в том и в О, что f(Of, x) = Of,x с И с Ох. если х ЕФ , то е =8, где длина полуинтервала И; если х ~ro, то Е где а 1 , а 2 - 2) = min{p(x, a 1) , 8 - р(х,а 2 )}, концы интервала И (или полуинтервала И) (рис. 35). Рассмотрим случай, когда х есть центр круга К (точка О) . Тогда И является =К\ {11 элементом u 12 u . .. u Jn}, где вида 3) 11 , ••• ,In - базы В, т. е . И= отрезки, удовлетворяющие свойствам а)-г) Обозначим для Е = 1- 8 (§ 8, п. 3) (рис. 36). через 8 наибольшую из имеем: f(Of,x) о из длин этих отрезков. Тогда = Of,x с И с Ох. о Рис. 35 Рис. 36 85 Таким образом, для любой точки х е К и любой ее окрестно сти Ох в пространстве ( К, -r) существует такая Е - точки х в пространстве (К, р), что /(Оех) ственное отображение f окрестность = Оех с Ох, т. е. тожде непрерывно. №44. Пусть Х- подмножество гильбертова кирпича № 22), Q 00 ( см. задачу состоящее из всех точек, у которых имеется не более одной отличной от нуля координаты (множество всех точек координат ных осей). У становим взаимно однозначное соответствие между множе ствами (К, -r)t-{ 0 • (К, и Х. Для этого перенумеруем «иголки» «ежа» -r)t-{0 Для любого п eN обозначим через fп линейную функ цию, отображающую (гомеоморфным образом) отрезок [О, 1] чис ловой прямой на отрезок [О, 1/2п] числовой прямой. Тогда, в силу того что любая «иголка» «ежа» гомеоморфна отрезку [О, 1] число вой прямой, можно в качестве п-й «иголки» взять отрезок [О, 1/2п] числовой прямой и считать, что каждая точка «ежа» (К, ет координаты (п, х/2п), где О::; х:::;; 1, п - -r)t-{0 име- номер «иголки» (при этом х/2п есть обычное евклидово расстояние от точки (п, х/2п) до точки О - центра круга К). Обозначим через f отображение множества (К, ство Х, которое точке (п, х/2п) Е (К, 't")t-{ 0 -r )t-{0 на множе- ставит в соответствие точку (О, О, О, х/2п, О, ... ) Е Х, п-я координата которой равна х/2п, а остальные координаты - нули. Очевидно, что отображение f взаимно однозначно. Докажем, что/- гомеоморфизм пространства (К, 00 странство Х с Q компактно задачу № (см. • -r)~ на про- Для этого (так как пространство (К, -r)~ би 39), а пространство Х хаусдорфово, как любое метрическое пространство) достаточно доказать, что отоб ражение 86 /: (К, -r)t-{0 • Х непрерывно (теорема 19). Докажем, что для любой точки М Е (К, 't)\'{ и любой окрест 0 ности Олм) точки/(М) найдется такая окрестность Ом точки М, что/( Ом )с of(M)· М(п0 , х0 /2п0 ) Е (К, 't)\'{ • Пусть 0 Рассмотрим произвольную окрестность Оf(M) точки }СМ) = (О, ... , О, х0 12no , О, ... ) Е Х. Так как Х - метрическое Oef(M) с Олм)· пространство, то существует такое Е Рассмотрим случай, когда х0 >О > О, что (т. е. точка М -=f:. О, где О - центр круга К). Возьмем Е столь малым, чтобы выполнялось условие О < Е < < x0 /2no. В этом случае Oef(M) состоит из всех таких точек (О, ... , О, х0 ;2no, О, ...) Е Х, что lx/ 2n° - х0 /2п0 1 < Е. Тогда искомой окрестностью Ом точки М(п0 , x 0 /2no) будет множество всех та ких точек (п0 , х0 /2п0 ), что lx- х0 1 < 2no Е. Действительно, множе ство Ом содержит точку М(п0 , x 0 /2no), является элементом вида 1) или вида /(Ом)= 2) из базы В (т. е. открытым в (К, 't)\'{ Oef(M) с Олм)· Пусть теперь х0 = множеством) и 0 =О (т. е. М = О-центр круга К) . Тогда}СМ) = (О, О, ... , О, вие О < Е ...). Возьмем Е столь малым, чтобы выполнялось усло < 1. В этом случае Oef(M) состоит из всех таких точек (О, ... , О, х0 /2п, О, ...) Е Х, Ом точки М = О (п, х/2 п ) Е (К, 't)\'{ 0 , что х/ 2п < с:. будет что х/ 2п множество < с:. содержит точку М = О, /(Ом)= Тогда искомой окрестностью всех таких точек Действительно, множество Ом Oef(M) с Олм) . Множество Ом является элементом вида следует из того, что Зт Е 3) из базы В (см. § 8). Это Vx:O:::;;x:::;;1 имеем х/2п <Е, т. е. множеству N: Vn"c:.m и Ом принадлежат все точки «иголок», начиная с номера т, а на 87 «иголках» с номерами п, п точки, кроме точек, < т, множеству Ом принадлежат все лежащих (п, х/ 2 п ) и (п, 1 / 2п ), где х/ 2п на соединяющих точки = Е. Таким образом, отображение f- отрезках, f непрерывно. гомеоморфизм и пространство (К, -r)~0 Следовательно, метризуемо. No 45. Доказательство такое же, как и доказательство задачи № 38. No 46. Если точка х е К не является центром круга, то существова ние счетной определяющей системы окрестностей в этой точке (в пространствах (К, -r), (К, и в задаче № -r)~0 ) доказывается точно так же, как 42. Предположим, что точка О - центр круга К, имеет счетную определяющую систему окрестностей точки О из системы 3) базы I (см . ri I. Для любой окрестности имеется содержащийся в ней элемент вида § 9). Следовательно, точка О имеет счетную опре деляющую систему окрестностей 3) базы ri. ~' состоящую из элементов вида Покажем, что существует такая окрестность точки О, в которой не содержится ни один элемент системы но , и системы Пусть ~ ~' а следователь ri . = {И1 , И2 , .. . , И~, ... } . Рассмотрим пространство Будем считать, что номера полуинтервалов окрестностей 2, ..., (К, Т)~. Ui, i = 1, соответствуют номерам «иголою>, на которых они лежат. Пусть 0 окрестность И точки О в пространстве (К, Т)~ , являющаяся элемен- том вида 3) базы L, такова: длина первого полуинтервала меньше длины первого полуинтервала окрестности И1 е полуинтервала меньше длины второго ~' длина второго полуинтервала окрестности И2 е ~ и т. д., длина п-го полуинтервала меньше длинь1 п-го полуин- тервала окрестности Ип е ~ и т. д. Очевидно, что в этой окрестности И точки О не содержится ни один из элементов системы 88 ~' следова- тельно, и системы 11. Таким образом, система не является опреде 11 ляющей системой окресmостей точки О. Теперь рассмотрим пространство (К, Т). Каждая окрестность Ui (i = 1, ... , п, ...) системы~ является объединением континуума полуинтервалов произвольной длины, идущих по всевозможным направлениям из точки О. Зафиксируем счетное подмножество «иголок» В каждой окрестности Ui возьмем подмножество {71, r2 , ... , ип, ... }. (i = 1, 2, ...), v; состоящее лишь из тех точек окрестности Ц, которые лежат на этих «иголках». Так же, как и в предыдущем случае, будем счи тать, что номера полуинтервалов подмножеств Vi (i = 1, 2, ...) со ответствуют номерам «иголок», на которых они лежат. Рассмот рим окрестность И точки О в пространстве (К, Т), являющуюся элементом вида L, базы 3) у которой на «иголках» лежат соответственно полуинтервалы рых длина полуинтервала а, а , а 1 2 , •.. , ап, r1 , r2 , ••• , rn, ... ... , для кото меньше длины первого полуинтер 1 вала подмножества Vз. с И1 и т. д., длина полуинтервала ап мень ше длины п-го полуинтервала подмножества Vn с Ип Е ~ и т. д. Остальные идущие из точки О полуинтервалы окрестности И точ ки О имеют произвольные длины. Очевидно, что в этой окрестно сти И точки О не содержится ни одно подмножество 2, ...), v; с Ui (i = 1, а следовательно, ни один из элементов системы ~ и ни один из элементов системы 11 · Таким образом, и в этом случае система 11 не является определяющей системой окрестностей точки О, т. е. в точке О не выполняется первая аксиома счетности. №47. Пространства (К, Т) и (К, р) (соответственно (К, Т)~ 0 и 0 (К, р)~ ) состоят из одних и тех же точек. Покажем, что тожде ственное (К, Т)~ 0 • отображение (К, р)~ 0 ) /: (К, Т) • (К, р) (соответственно /': является уплотнением. Взаимная однозначность отображений Покажем, что отображения f и f' f и f' очевидна. непрерывны. 89 Пусть х ЕК, (соответственно Ох х произвольная окрестность точки х - =f в пространстве (К, р)~ х) в пространстве 0 ). ское пространство, то ЗЕ (К, р) (соответственно Так как (К, р) (и (К, р)~ ) 0 > О: Of,x с Ох. = fx - метриче- Если х не является цен тром круга К, то возьмем Е столь малым, чтобы выполнялось усло вие О < Е < р(х,О). Тогда или элементом вида 2) из базы место предложение(*) : является или элементом вида Of,x L (см. § 9). Таким образом, имеет существует такая окрестность Of,x точки х в пространстве (К, Т) (соответственно в пространстве (К, р)~ что f(Of,x)=Of,xcOx 1), (соответственно 0 ), f'(Of,x)=Of,xcOx). Пусть теперь х есть центр круга К- точка О. Возьмем Е столь малым, чтобы выполнялось условие О< Е элементом вида 3) из базы L, < 1. Тогда является Of,x а именно объединением полуинтер валов длины Е, начинающихся в точке х и идущих по всевозможным направлениям из этой точки. Таким образом, и в этом случае имеет место предложение(*), т. е. отображения f и f' непрерывны. №48. Хаусдорфовость неметризуемого «ежа» (К, Т) (соответствен- 0 но (К, Т)~ ) вытекает из существования его уплотнения на метри- 0 зуемый «еж» (К, р') (соответственно (К, р')~ ) (см. задачу № Метризуемые пространства (К, р) и (К, р')~ 0 47). хаусдорфовы, прообразы любых двух непересекающихся открытых множеств при непрерывном взаимно однозначном отображении являются непересекающимися открытыми множествами. Заметим, что хаус дорфовость пространств (К, Т) и (К, Т)~ 0 легко проверить и непосредственно. Докажем, что пространство (К, Т) (соответственно (К, T)'t-{0 ) регулярно. Пусть точка х Е(К, Т) (соответственно (К, T)'t-{0 ), Ох - произ- вольная ее окрестность. Тогда существует такая базисная окрестность 0 1х 90 точки х, что х Е 0 1х с Ох. Если х = О (центр круга К), то 0 1х - элемент вида 3) из базы окрестность точки х - I (см. § 9). Обозначим через 02 х такую элемент вида 3) базы I, - длина каждого полуинтервала которой равна половине длины содержащего его по луинтервала окрестности O1 х. Тогда замыкание [O2 х] получается присоединением к окрестности 0 2х не принадлежащих концов всех ее полуинтервалов и очевидно, что [O2 х] с Ох (рис. Пусть х I. -=1:- О. Тогда O1 х - элемент вида 1) или 37). вида Очевидно, что найдется окрестность 02 х точки х вида 1) или вида 2) из базы I, - отрезок, содержащийся в O1 х (рис. Рис.37 2) из - замыкание которой базы элемент [ 02 х] есть 38). Рис. 38 Таким образом, выполняется аксиома Т3 и, в силу своей хаус дорфовости, пространства (К, Т) и (К, Т)Хо регулярны. No 49. Пусть Q - произвольное открытое покрытие пространства 0 (К, Т)~ • Так как пространство (К, Т)Хо на каждой «иголке» индуцирует евклидову топологию, то из любого покрытия Q i i = 1, 2, ... (где ri - произвольная «иголка», i = 1, 2, ...) = Q n ~, можно вы- брать конечное подпокрытие Q~, i = 1, 2, .... Каждый элемент покрытия Q~ является пересечением «иголки» ri, i = 1, 2, ... с некоторым элементом покрытия Q . Обозначим через ш ~ множество всех этих элементов из покрытия Q , i = 1, 2, 91 Число элементов в системе ш ~ то же, что и в системе Q~. Тогда ш = ш~ u ш; u . .. u ш ~. u ... есть счетное подпокрытие покрытия Q. Следовательно, пространство (К, Т)~ финально-компактно. №50. Пусть [а, Р) ЕВ, т. е. [а, Р) что множество открытое множество. Очевидно, S \ [ а, Р) является или элементом базы В, или сум мой двух элементов [а, р) = S \ ( S \ [а, р)) ства. - базы В, т. е. открыто. Тогда множество замкнуто как дополнение открытого множе Следовательно, стрелка - индуктивно нульмерное про странство (так какS есть непустое Т 1 -пространство) . №51. 1. Пусть (х, у) с S. Покажем, что интервал (х, у) можно пред- ставить в виде суммы элементов базы В. Действительно, пусть а - середина отрезка [х, у], а1 - середина отрезка [х, а] , а 2 - середина отрезка [х, а 1 ], ... , а п середина отрезка [х, а п_ 1 ], .... Тогда [а 2 , ап_ 1 ) u (х, у)= [а, у) u [а 1 , а 2 ) u ... u интервал (х, у) о .... Следовательно, открытое подмножество стрелки (рис. - 39). у х Рис.39 2. Пусть [x, y]cS, тогда S \ [x, y]=[0, x) u (y, 1) - множество как сумма открытых множеств (рис. зом , [О, х) с S. Множество о х (х, 1) = S \ [О, х] у Рис.40 о х Рис. 4 1 92 40). Таким обра открыто (рис. 1 открытое 41). Итак, отрезок есть замкнутое подмножество стрелки (как до полнение открытого множества). 3. Полуинтервал [х, у), где О::;; х <у< 1, является элементом базы В, следовательно, является открыто-замкнутым подмноже ством стрелки (рис. о 42). у х Рис.42 4. Полуинтервал замкнутое (х, у], где О< х подмножество S \ (х, у]= [О, х] u стрелки, (у, 1) (рис. < у < 1, так ни открытое, ни как 43) или S \ (х, у]= его дополнение {О} u (у, 1) (рис. 44) не является ни открытым, ни замкнутым подмножеством стрелки . о х у Рис. 43 о у Рис. 44 №52. Пусть О< а< 1. Тогда S = [О, а) u [а, 1), где множества [О, а) и [а, 1) непусты, не пересекаются и открыты. Следовательно, несвязно (рис. S 45). а о Рис. 45 Каждая точка х стрелки является пересечением всех содержащих ее полуинтервалов [х, а), следовательно, всех содержащих ее откры- то-замкнутых множеств. Таким образом, квазикомпонента каждой точки содержит только ее, т. е. пространство S вполне несвязно. 93 №53. Для любой точки х Е S существует счетная определяющая си стема окрестностей. Она состоит из всех элементов базы В, кото рые имеют вид [х, х+ 1/ п], где п = 1, 2, 3, .... №54. а) Открытое покрытие {[О, 1-1/п), п = 2, 3, ...} стрелка не со- держит конечного подпокрытия. Следовательно, стрелка не би компактна. Пусть 6) х, х' Е S, х :;t х', О~ х окрестностями точек х и [х, х') и [х' , 1) (рис. х' < х' < 1. Непересекающимися будут соответственно множества 46). х х 1 О 1 Рис. в) Пусть множества F;. и F;. и F2 жем, что у множеств 46 замкнуты в F2 S, F;. п F2 = 0. Пока имеются непересекающиеся окрест ности. Пусть хЕ OxnF2 =0. F;., окрестность Ох = S \ F2 точки х такова, что Возьмем элемент базы [х,ух)сОх, где Ух >х. Оче видно, что [х, ух) п F2 =0 . Аналогично, если х Е F2 , то существует элемент базы = 0. OF; = u [х, ух ), х Е F; [х, ух), где Ух> х, такой, что [х, ух) п F;. Рассмотрим окрестности где i = 1, 2. F2 EF2 , F;, Покажем, что эти окрестности не пересекаются. Дей ствительно, если их" множеств 3~ EOF;. n OF2 , то найдутся такие точки х' EF;. что~ Е [х' ,Ух,)п [х',Ух,). Но тогда получается, что или Е[х',Ух, )=0, или F;. n[x',Yx,):;t0, что противоречит постро ению полуинтервалов [х, Ух). Таким образом, OF;. п OF2 = 0. г) Следствием нормальности и хаусдорфовости стрелки явля ется ее полная регулярность и, следовательно, регулярность (тео ремы 94 16, 17). №55. а), тие cr Пусть Х с 6) Рассмотрим произвольное открытое покры S. пространства Х Каждое множество из системы ресечением Х с некоторым множеством, открытым в нием Х с суммой полуинтервалов из базы cr является пе S, т. В. е. пересече Поэтому для доказательства наследственной финальной компактности стрелки достаточно доказать, что покрытие пространства Х с К= Х \ [ха, уа) с теми же концами. U (ха, Уа) Е А} = {[ха, Уа) п Х, а Е А} содержит счетное подпокрытие. S Для каждого полуинтервала (ха, уа), а Е А, {Оа, а рассмотрим интервал Покажем, что множество не более чем счетно. аЕА Действительно, для каждого х Е К = [х,уа(х)). что Оа(х) найдется такое а(х) Е А, Из построения множества К следует, что если х, х' ЕК, x=f:.x', то [ха,Уа(х))п[х~,Уа(х'))=0. Таким образом, мы получили систему со попарно не пересекающихся полуинтер валов. Возьмем в каждом полуинтервале по рациональной точке, тогда получим, что мощность системы со не превосходит ~о, сле- довательно, IKI::;; ~о- Множество Х \ К с топологией, индуцированной обычной топо логией вещественной прямой, обладает счетной базой. Известно, что всякое пространство, имеющее счетную базу, финально компактно [3, § 7]. Значит, покрытие {(ха,Уа) пХ,а ЕА} множества Х\К содержит счетное подпокрытие множества. Тогда семейство {(ха. , Уа. ) {оа(х), х ся счетным подпокрытием покрытия l l п Х, i = 1, 2, ...} этого Е К} u {оа;, i = 1, 2, ...} {Оа, а Е А} множества Х Та являет ким образом, стрелка наследственно финально компактна и, следова тельно, финально-компактна. в) Докажем, что любое открытое подмножество стрелки является объединением счетной системы ее замкнутых подмножеств (т. е. имеет тип Fcr ). Пусть Х открыто в S, тогда Х = U [ха, уа). Про- а ЕА странство Х финально компактно, следовательно, у покрытия 95 {[ха·, ,Уа 1. ) , i = 1, 2, .. .}. имеется счетное Каждый полуинтервал подпокрытие [ха , Уа ), а Е А, за- 00 мкнут, и Х = U[xa· ,Уа. ). Следовательно, стрелка совершенно нор, l i=l мальна. г) Всякое регулярное финально компактное пространство нор мально [3, § 7]. Поэтому следствием регулярности и наследствен ной финальной компактности стрелки является ее наследственная нормальность. № 56. Счетным всюду плотным множеством является множество ра циональных точек полуинтервала [О, 1). Сепарабельность доказана. Докажем теперь, что любое подпространство Х с S сепара бельно . Обозначим через У множество всех изолированных точек про- странства Х. Покажем, что IYI ~ ~о . того, что подпространство УсS наследственной № 55) финальной Действительно, это следует из финально компактно компактности стрелки, см . (в силу задачу и каждая точка х еУ является открытым в У множеством (в силу того, что у любой точки х е У имеется окрестность Ох с Х, которая не содержит ни одной точки из Х, кроме ее самой; так как Ох = Х п И, где И открыто в S, то х = Ох п Х = И п У). Обозначим через разует счетное Z множество всех точек из Х \ У, которое об всюду плотное множество в Х \ У относительно топологии, индуцированной обычной топологией числовой пря мой (Х\ У сепарабельно, так как является подпространством мет рического пространстваR со счетной базой (теорема Докажем, что У u Z 11)). образует счетное всюду плотное множе ство в Х Пусть х е Х, докажем, что любая окрестность Ох этой точки содержит точку из У u Z. Если хе У, то х и является той точкой из держится в любой ее окрестности. 96 Yu Z , которая со Пусть х Е Х\ У, Ох произвольная окрестность точки х. Так как - х не является изолированной точкой в Х, в любой ее окрестности со держится отличная от нее точка из Х Рассмотрим базисную окрест ность [х,х+с:) пХсОх. Пусть х'ЕХ,х'*х, х' Е[х,х+с:)пХ Следовательно, х' Е (х, х+с:) пХ. Если х' Е У, то х' и является точкой из YuZ, содержащейсявОх.Если х' ЕХ\У, то (х,х+с:)п(Х\У) непустое открытое множество в Х \У относительно топологии, ин дуцированной обычной топологией прямой, а так как Z всюду плотно в Х \ У, то существует z Е Z: z Е (х, х +с:) п (Х \ У). Следователь- но, z Е (х, х + с:) п Х с Ох. Таким образом, доказано, что множество У u Z всюду плотно в Х Так как У u Z счетно, то Х сепарабельно, а стрелка наследственно сепарабельна. №57. Воспользуемся теоремой Александрова - Урысона (теорема 14). Покажем, что база В не содержит никакого счетного подсемейства В' с В, являющегося базой. Действительно, если [х, х') ЕВ и [у, у') ЕВ' удовлетворяет условию: х Е [у, у') с [х, х'), то х = = у.Следовательно, во всякой подбазе В' с В непременно имеют ся элементы вида [х, х') при любом х Е[О, Отсюда вытекает, 1). что любая подбаза базы В имеет мощность континуума. Следова тельно, вес пространства S равен с. №58. Топологический квадрат стрелки S х S содержит, во-первых, подмножество как его L = {(х, 1- х): О< х < 1}, которое замкнуто в S, так дополнение открыто (рис. 47) и гомеоморфно дискретному пространству, имеющему мощность континуума с, во-вторых, счетное всюду плотное подмножество К, состоящее из всех точек S х S, обе координаты которых - Для доказательства того, что рациональные числа. S х S не нормально, нам потре буется следующая лемма. Лемма. Если непрерывное отображение f всюду плотного подмножества А некоторого топологического пространства Х 97 1 - - - - - - - - - - - - - - -, в хаусдорфово пространство У непре рывно продолжается на Х, то продол жение однозначно определено отобра жением/ Доказательство. и F2 : Х • У отображения В={х о Рис. Для каждого х Е С имеем: ствуют открытые F2 (x) ЕИ2 и Докажем, что множество f для С= {х Е Х: этого, замкнуто. По И1 что F'i (х) :;t Fi х)} F;_ ( х) :;t F2 ( х), множества и У Fi:X • различные продолжения - EX:Fi(x)=F2 (x)} кажем 47 Пусть И2 И1 nИ2 =0. Множество множество открыто в Х следовательно, в У суще такие, что F'i-1 (U1 ) n F;_ (х) Е И~, есть F 2- 1 (U2 ) окрестность точки х, содержащаяся в С. Таким образом, С открыто, а В =Х \ С замкнуто в Х Так как А с В, то Х этому В = Х. = [А] с В (по свойству замыканий) и по- Лемма доказана. Из леммы следует, что любая непрерывная функция из в S х S определяется своим сужением на множество К. Таким обра- R зом, на S х S существует только 21'{0 ных функций. Если же пространство =с непрерывных веществен S х S было бы нормальным, то по теореме ций, 18 каждая из 2с непрерывных вещественных функ определенных на L , могла бы быть продолжена на S х S, что невозможно, так как 2с > с. Следовательно, топологический квад рат стрелки не нормален . №59. а) Тождественное отображение f множества точек полуинтер вала [О, 1) на себя является уплотнением стрелки на полуинтервал [О, 1), рассматриваемый как подпространство R. Действительно, базой на полуинтервале [О, 1) являются множе ства вида: 1) (х, у), Множества вида 98 1) и где 2) 0 < х < у < 1, открыты в S и 2) [О,х), где 0 < х < 1. относительно топологии, ин- дуцированной базой В. Следовательно, прообраз любого открыто го в [О, 1) множества открыт в Отображение О:::;; х < 1, g: S • (О, 1], S при отображении/ заданное формулой где является уплотнением стрелки на полуинтервал (О, 1], рассматриваемый как подпространство отображении g R. Действительно, при прообразами элементов базы полуинтервала (О, 1], а именно множеств вида (х,у), где О 1) и 2), < х < 1, g(x) = 1-х, являются множества вида тельно, при отображении множества открыт в S, g О < х <у< 1, и открытые в (х, 1], где S. Следова прообраз любого открытого в (О, 1] т. е. взаимно однозначное отображение g непрерывно. 6) Рассмотрим (рис. 48). множество точек, лежащих на отрезке [О, 1] cR о о 1 Рис. 48 Обозначим через а0 точку О, через а1 середину отрезка [О, 1], через а3 R - точку 1, через а2 середину отрезка [а0 ,а2 ], - ... , через an+I - середину отрезка [а0 , ап], .... Построим отображение f: S • [О, 1] следующим образом: f(O) = О; если х Е [ап+1' ап), то f = fп, ГДе fп - ТаКаЯ ЛИНеЙНаЯ функция, ЧТО fп (an+l) = ап, fп(ап) = an+I' п = 1, 2, 3, .. . . Геометрически функция fп переворачивает полуинтервал По построению отображение что f- f это [an+I' ап), означает, что п = 1, 2, 3, .... взаимно однозначно. Докажем, непрерывное отображение стрелки на отрезок [О, 1], рас- сматриваемый как подпространство Пусть х = а0 • R. Любой элемент базы отрезка [О, 1], содержащий точку а0 (в топологии, индуцированной топологией прямой R), является множеством вида [О,х), где О< х < 1 (или [О, 1] ). Для лю- 99 бого [О, х) , О< х найдется такое т < 1, EN , что Vn с:. т имеем: (ап+1 ,ап ]с[О,х), а (ат , ат_1 ] n [О, х)=(ат, х). Тогда [О,х)=(ат,х)u u(Q (а"н, а.])- Множество Г'[О, х) = (f: ,(x), a- )u(,,Q [а.+1 , а.)) 1 открыто в S (как сумма открытых множеств) . Таким образом, в точке а0 отображение/непрерывно . Пусть х лежит на некотором полуинтервале п EN Пусть [an+J' ап ) с S, .fx, т. е. от произвольная окрестность точки Ofx - крытое в [О, 1] множество, содержащее fx. Существует такое Е что (fx- Е, fx + Е) n [О, 1] с Ofx. Тогда множество Ох > О, = fп- 1 (fx- Е, fx + Е) n(an+J' ап ]) открыто в S и содержит точку х, т. е. является окрестностью точки х в пространстве S. Очевидно, что f (Ох) с Ofx. Таким образом, доказано, что отображение f непрерывно в любой точке пространства S, т. е. f является уплотнением «стрелки» на отрезок. в) Рассмотрим множество точек, лежащих на отрезке Обозначим через а0 середину отрезка через а2 - [0,1]. через а1 - точку О, середину отрезка [а1 , а0 ] , .. . , через an+I - середину [ап , а0 ], .... Построим отображение разом. Если х Е[а0 , 1), то f- [0,1], /: S • (О, 1) следующим об тождественное отображение множе ства точек полуинтервала [а0 , 1) на себя. Если х Е[ап, ап+~), то j = fп 1, 2, 3, .. . ( ( Такая ЛИНеЙНая функция, ЧТО fп ап ) = an+l' fп an+l) = ап, n = (рис . 49). 1 о о Рис .49 По построению отображение гично случаю 100 6) f взаимно однозначно . Анало можно доказать, что f- непрерывное отобра- жение стрелки на интервал (О, 1), рассматриваемый как подпро странство R. №60. Пусть х1 , х2 ES, х1 * х2 • Рассмотрим полуинтервалы жащиеся в S отображение [4 , у1 ) и [х2 , у2 ): у1 и имеющие одинаковую длину (рис. /: S • S, которое на полуинтервалах [О, х1 ), [у1 , х2 ), кая линейная функция, что f = /2 содер Построим 50). [у2 , 1) является тождественным: если х Е[х1 , у1 ), то то < х2 , fi = [xi, у1 ) = [х2 , у2 ), - такая линейная функция, что /2 = = fi - f та если х E[xi, у1 ), [х 2 , у 2 ) = [х1 , у1 ) . Геометрически это означает, что отображение меняет места f ми полуинтервалы [х1 , у1 ) и [х2 , у2 ). Построим график отображения f (рис. 51 ). у 1 У2 Х2 YI Х] о Х] Х2 У1 Рис. У2 1 о -т-г--г~ 1 1 1 1 1 1 1 1 ---1 1 1 1 1 1 1 - и ---,- - 1,--и-+--: 1 1 1 1 1 -1--1---~ --1 - - - , - - - ----t--, 1 1 1 1 1 XJ У1 Х2 У2 1 х Рис . 5 1 50 Легко заметить, что прообраз любого элемента базы В при отображении f является суммой элементов базы В, т. е. открытым множеством . Следовательно, при отображении f прообраз любого открытого множества открыт, т. е. 1 и отображение /- : S • f непрерывно . Аналогично, S непрерывно. Таким образом, взаимно однозначное отображение f является гомеоморфизмом, который точку х1 переводит в точку х2 • 101 №61. Докажем два утверждения: 1) если подпространство стрелки несчетно, то оно неметри зуемо; 2) если подпространство стрелки не более чем счетно, то оно метризуемо. IXI >~ 1) Пусть Х с S, рабельна ( см. задачу № 0• Так как стрелка наследственно сепа 56), то Х сепарабельно. Аналогично дока зательству того, что стрелка не имеет счетной базы № 57), ( см. задачу можно доказать, что любое несчетное подпространство стрелки не имеет счетной базы. Следовательно, Х неметризуемо, так как для метризуемых пространств сепарабельность и наличие счетной базы эквивалентные условия (теорема - 2) Пусть Х с S, емости Урысона [3, IXI :::;~ гл. 0• 11). Воспользуемся критерием метризу I, § 8]: любое регулярное пространство со счетной базой гомеоморфно множеству, лежащему в гиль бертовом кирпиче (и, следовательно, метризуемо, см. задачу №22) . Пространство Х регулярно (как подпространство регулярно го пространства, см . задачу № 54). Счетную базу в подпро- странстве Х с S образует совокупность Вх = U Вх п Х, где хЕХ Вх - счетная определяющая система окрестностей точки х Е Х в пространстве (см. задачу № S 53). Следовательно, простран ство Х метризуемо. №62. Пусть Х с S, Х бикомпактно . Покажем, что для любой точ ки х Е Х имеется интервал (х - Е, х), который не содержит ни одной точки из Х. Действительно, предположим, что существует такая точка хЕХ, что 'v'E>O: (x -E,x)nX:;i:0. Тогда можно построить строго монотонно возрастающую последовательность {хп}, (в состоящую обычном из смысле) точек к ro={[O,x1 )nX; [х0 , 1) пХ, 102 пространства Х и точке х. Тогда сходящуюся открытое покрытие [xi,xi+1 )uX, где i=l,2,3, .. .} про- странства Х не имеет конечного подпокрытия (элементы по крытия ro попарно не пересекаются, непусты, и их счетное множество). Для каждой точки х Е Х возьмем интервал (х- Е, х), который не имеет точек из Х Эти интервалы попарно не пересекаются и образуют не более чем счетное множество (достаточно взять в каждом интервале по рациональной точке). Следовательно, 1 х1~ ~0№63. SхS Топологический квадрат стрелки сепарабелен, так как в нем имеется счетное всюду плотное множество, состоящее из всех точек S х S, обе координаты которых S пространство х S не наследственно сепарабельно, так как его странство L Действительно, одноточечное крыто в подпространстве тое в не у+Еу и любое подмножетсво бой точки (х, у) 1 52). ILI= С EL SхS L рациональные числа. Но ---------------1 подпро = {(х, 1- х): О< х < 1} сепарабельно (рис. - L ---- - у------ -1 i 1 от (для лю имеется открымножество И=[х,х+ЕсJх[у,у+Еу) о такое, что Рис.52 (x,y)=U n L). №64. Множества открыты (рис . (рис. (с, 54); d) = [а, d) (с, Ь) = (а, открыты d] = [а, d] = 56), (рис. 53); (а, d] = (а, Ь) [а, Ь) открыто-замкнуты 55), [с,Ь] замкнуто (рис. [а,Ь]=(с, Ь] замкнуты (рис. 57), [с, d] = [с, Ь) замкнуты (рис. 58), (а, d) открыто (рис . 59), ( а, Ь] ни открыто, ни замкнуто (рис. 60), [с, d) ни замк нуто, ни открыто (рис. 61 ). 103 у у ь а d с 1 а х о х d с Рис. о ь а о Рис. Рис . х 1 о Ь -+-- Рис. ь о х Рис. 59 о Ь х о d с Рис. 57 1 х 58 у ь а d с 55 а у а х 11--------- ---------;• -- 1 d с 56 у 1 у а 11----+-- d с d с 54 у у Ь 1 1------.---..г--- 11---->-----------;• 53 Рис. ь а 1 >----------.....--- о у с х d Рис. 60 ь а о с d Рис. х 61 №65. Такое название является следствием того, что подпространства С0 и С1 (в индуцированной топологии) гомеоморфны стрелке . При этом гомеоморфизмом является тождественное отображение. №66. Покажем, что базой из открыто-замкнутых множеств про странства 104 Х = С0 u С1 является совокупность В всех множеств вида (а', где G=[a,f3)u(a 1 ,f3 1 ] , f3 проекция полуинтервала (а, 1 ] - С0 (рис. у [a,f3)cC1 , f3] на а 62). Пусть х Е И, где множество И открыто в Х Так как система L i= 1 :3Г i : х ЕГi с И, что для любых i = 1, 2, G: х Е G с Гi. х Е Г i, реме 1О, ляется образует базу в Х, то или х ЕХ найдется Очевидно, i = 2. таких, элемент о что вида , а р' Рис. х 62 Таким образом, согласно тео- совокупность В открыто-замкнутых множеств вида базой топологии пространства Х пространство (очевидно), то Х G яв как Х есть Т 1индуктивно нульмерное про - Так странство. Следствием индуктивной нульмерности неодноточечного про странства Х является его несвязность и полная несвязность. Действительно, Х несвязно, так как в нем имеется нетривиаль ное открыто-замкнутое множество; Х вполне несвязно, так как каждая его точка является пересечением всех содержащих ее мно G жеств вида и, следовательно, всех содержащих ее открыто замкнутых множеств. №67. Пусть Х = С0 u со - произвольное открытое покрытие пространства С1 • Покажем, что из со можно выделить конечное подпо- крытие . Изобразим под двумя полуинтервалами С0 и С1 отрезок 1 с обычной топологией (также длины пространства Хна отрезок 1). Пусть f есть проектирование 1. Рассмотрим произвольную точку х от резка 1, прообраз которой при отображении f состоит ровно из двух точек: х1 Е С1 и х0 Е С0 . Эти две точки х1 и х0 содержатся в одном или двух Xi EU1 ЕСО, Г 2 из базы элементах х0 L, EU2 покрытия ffi. Пусть, для определенности, ЕСО. Тогда существуют такие элементы Г 1 и что х1 ЕГ 1 с И1 , х0 Е Г 2 с И2 (рис. 63). 105 у Следовательно, имеется такой ин Х] 1 1--to-t-----..--..-----~ С тервал V с 1, что х Е V и f - 1(V) = 1 = гl U 1 1 1 тервала 1 1 1 _______ Хо 1 Со х гда абсцисса точки х равна О или 1 / 1V..... 11 1), то, аналогично, найдется полуинтервал Vo v;_ (открытый или х Рис. Если же состоит из одной точки (в случае, ко- f 1 1 VI ro. прообраз точки х Е J при отображении 1 ......._ V содержится в объединении двух элементов покрытия 1 1 о Г 2 С И1 U И2, т. е. прообраз ин в обычной тополо гии отрезка), прообраз которого содер- 63 жится только в одном элементе покры тия ro. Таким образом, для каждой точки отрезка 1 имеется интер вал или полуинтервал (для концевых точек), прообраз которого содержится или в одном, или в объединении двух элементов по крытия ro. Рассмотрим покрытие Q отрезка 1 такими интервалами и полуинтервалами. В силу бикомпактности отрезка выберем из покрытия Q конечное подпокрытие Q 0 • Прообразы всех элемен- тов покрытия Q 0 образуют конечное покрытие пространства Х, каждый элемент которого содержится в одном или в объединении двух элементов покрытия ro. Следовательно, у покрытия ro про странства Х имеется конечное подпокрытие, т. е. Хбикомпактно. №68. Докажем, что пространство, являющееся объединением двух наследственно финально компактных подпространств, само наследственно финально компактно. Действительно, пусть У финально компактные Z = Z1 u Z2 , Z2 где (пространств = ½u У2 , где подпространства. Z1 = Z u ½ и J; ½, Z2 = Z u У2 , ½, ½ Пусть 106 Z1 с У. Тогда Z1 и соответственно) финально компактны. = {И Ero: И п Z1 :;t: 0}, тия ro1 и ro2 пространств Z подпространства Рассмотрим произвольное открытое покрытие Пусть ro 1 наследственно и Z2 ro 2 ro пространства = {И Ero: И п Z 2 :;t: 0}. Z. Покры- соответственно содержат счетные ro 1о подпокрытия и ro2о соответственно. т огда ro о = ro 1о u ro 2о по- крывает все Z, ro O с ro и ro O ~о. J J ::; Так как стрелка наследственно финально компактна (см. задачу № 55), а Х = С0 u С1 , где подпространства С0 и С1 гомеоморфны стрелке, то Х наследственно финально компактно. №69. Пространство Х сепарабельно. Счетным всюду плотным мно жеством является множество (r, О) и где (r, 1), все множества (r, О) и (r, 1) D, r рационально. D0 с D, состоящее из всех точек вида (Всюду плотными являются даже D 1 с D, состоящие из всех точек вида соответственно.) Наследственная сепарабельность двух стрелок из наследственной сепарабельности стрелки (задача № тельно, пусть Х0 с Х, тогда Х0 = (Х0 с С0 ) u простраства С0, С1 гомеоморфны стрелке). Пусть всюду плотное множество в Х0 Тогда Z = Z0 u Z1 n 56). (Х0 n С1 ) Z 0 (Z1) - вытекает Действи (где подсчетное С0 (соответственно в Х0 n С1 ). счетное всюду плотное множество в Х - №70. Для любой точки (х, О) ЕС0 или (х, 1) пространства Х, т. е. для любой точки ЕС1 имеется счетная определяющая система окрестностей. Она состоит из всех элементов базы В, которые име ют вид (х, x+1/n]u[x, х+1/п), п = 1, 2, 3, ... , где (х, х+1/п] луинтервал на С0 , [ х, х + 1/ п) - полуинтервал на С1 . -по- №71. Предположим, что пространство базу S. Тогда S 1 = С1 n S системы открытых Х = С0 u С1 множеств имеет счетную S0 = С0 n S и будут являться счетными базами в подпространствах С0 и С1 соответственно. Но пространства С0 и С1 не имеют счет ной базы, так как С0 и С1 гомеоморфны стрелке ( см. задачу № 65). 107 № 72. а) Хаусдорфовость двух стрелок проверяется непосредственно. 6) Выберем произвольно точку х Е Х и ее окрестность И. Су- ществует элемент ство G G базы В такой, что х Е открыто-замкнуто, то аксиома Т3 G с И. Так как множе Следовательно, выполнена [G] = G. ~ Т3 . Отсюда и из хаусдорфовости двух стрелок следует, что про странство Х регулярно. в)- г) Любое регулярное финально компактное пространство нормально Следовательно, Хнормально (см. задачу № [3, § 7]. 68) и наследственно нормально. д) Докажем, что любое открытое подмножество двух стрелок является объединением счетной системы ее замкнутых подмно жеств (т. е . имеет тип Fcr). Пусть множество И открыто в Х, тогда И = U Ga, где Ga - аЕА открыто-замкнутые множества из базы В . Так как Х наследственно финально компактно, то И финально компактно и, следовательно, у покрытия {Ga:a ЕА} имеется счетное подпокрытие ~ {Gai : i = 1, 2, ... }. Таким образом, И= ство Gi UGai, где Vi Е N множе- замкнуто в Х, т. е. пространство Х совершенно нормально. у №73. С1 х а) Пустьf Х • 1 есть проектирова- ние пространства Х на отрезок жем, что f непрерывно (рис . Пусть х ЕХ, окрестность 1 1 V Рис. 108 х 1 1 I 64 Дока- 64). произвольная Покажем, что существует такая окрестность Ох точки Со о Ofx точки fx Е /. 1. f(Ox)cO.fx. Так как Ofx это открытое в I множество, содержащее точку fx, то имеется х в пространстве Х, что такой элемент V базы в обычной тополо- гии отрезка, что fx ЕV с Ofx ( V - это интервал на отрезке полуинтервал вида [а, с) или (с, Ь] , где а, Ь с - 1 либо концы отрезка, а< с < Ь). Тогда, если х ЕС1 (С0 ), то существует такой эле- El, мент Г1 (Г2) из базы L, что х ЕГ1 с 1- v (х ЕГ2 с 1- v). 1 1 В качестве окрестности Ох можно взять элемент Г 1 ( соответ ственно, Г2). Очевидно, что /(Ох) с V с Отображение f - Ofx, т. е. f непрерывно . двукратное (прообраз каждой точки состоит не более чем из двух элементов). 6) g: Х • Построим непрерывное и строго двукратное отображение У двух стрелокХна окружность У(единичного радиуса). Пусть h1 : 1 • 11 есть гомеоморфное отображение отрезка 1 (еди 11 = [О, 2n] ( см. ничной длины) на отрезок - отображение отрезка 11 = (cost, sint) Е У, Е [О, задачу № 6), f½: 11 • 1 на окружность У, заданное формулой h2 непрерывно (в силу непрерывности координатных функций) (рис. 65). hz(t) t 2n]. Отображение у о t 2n о Рис . Тогда отображение g 1 х 65 = f½ о hi о f: Х • У (где f- построен ное в а) отображение двух стрелок на единичный отрезок) явля ется непрерывным (как композиция непрерывных отображений) и строго двукратным отображением двух стрелок на окружность. 109 № у а, Пусть а2+В а2 1 74. с, ai,a 2 Х• Х, что /(а 1 ) что гомеоморфизм такой существует Покажем, Е Х. f = а 2 (рис. 66). Сначала рассмотрим случай, когда точки , , 1 а+в а а 1 , а 2 ЕС1 , а 1 х а,2 и где =[ai, a i +E)u(a;,a;+E), полуинтервал на для < а2• [1, а 1 ), + Е, а 2 ], Х, а2 [а 1 [а 2 + Е, а 2 ), [а 2 которое «переставляет» t' = а2 - :s; t :s; а 2 + Е а1 множества непрерывно . 1 / - : Х• Х• + Е, 1) на С1 и на отрезках + t; каждой точке (t, 1): ставит в соответствие точку открыт, Обратное Х, которое на т. е. ставит в (t,O): a,~:s;f:s;a,~+E Легко заметить, что при отображении крытого = на С0 тождественно; каждой точке + Е, 1] и каждой точке соответствие точку (t, О): оai вида: на С0 ), (t,1): a 1 :s;f:s;a1+E и Рассмотрим базис- интервал на С0 (проекция ин окрестности Оа 1 и Оа 2 , т. е. отображение f [О, а 1 ], [а 1 одном s:s;min{a2 -ai,l-a2 }, [ai,ai +Е) - i = 1, 2. отображение f Х • полуинтервалах на определенности, следующего (а;, а;+ Е) - Ci, (ai,ai + Е) Рассмотрим находятся ные окрестности Оа 1 и Оа 2 точек а 1 Рис.66 тервала а,2 Пусть, уровне . о и а,1 f а2 :s; t :s; а2 + Е t' = а 1 - а2 + t. прообраз любого от f отображение у Х имеет такой же вид, что иf, и, следовательно, непрерывно. Из этого и взаимной однозначности отображения f следует, что f: Х • физм. При этом /(а 1 ) Теперь точки а 1 ,а 2 ЕХ 110 67). - гомеомор- = а2 • рассмотрим ных уровнях. (рис . Х случай, когда расположены на раз- Пусть а 1 Е С1 , а 2 Е С0 о 1 Рис. 67 х Пусть M(S, S). g: Х • Х центральная симметрия относительно точки - Очевидно, что вида Г 1 базы L g- взаимно однозначно и каждый элемент отображается на элемент вида Г2 базы рот. Следовательно, при отображении g база себя, т. е. 12). g- гомеоморфизм (теорема при этом а 2 Е С1 . физм, что Обозначим через I и наобо- отображается на Обозначим /2: Х • L g(a 2 ) = а2 , Х такой гомеомор f=./2 o g:X ➔ Х гомео гомеоморфизмов) и /(а 2 ) = а 1 • Тополо fi(a2)=a1• Тогда отображение морфно (как композиция гическая однородность двух стрелок доказана. № 1. 75. Топологический квадрат Х х Х двух стрелок - бикомпакт ное хаусдорфово пространство пространство Х х Х (теоремы 23, 24), следовательно, нормально [8, гл. II, § 6]. Однако топологи ческий квадрат двух стрелок не наследственно нормален, так как в нем имеется подпространство С1 х С1 (или С0 х С0 ), гомеоморфное топологическому квадрату стрелки . Топологический квадрат стрелки не нормален (см. задачу № 58). 2. Так как для бикомпактных хаусдорфовых пространств свойства наследственной финальной компактности и совершенной нормально сти эквивалентны между собой [3, гл. I, § 7], то топологический квад рат Х х Х не совершенно нормален. (Это следует из того, что про странство ХхХ не наследственно финально компактно. Действительно, если бы пространство Х х Х было бы наследственно финально компактным, то каждое его подпространство бьшо бы ре гулярным и финально компактным, т. е. нормальным № [3, гл. II, § 7].) 76. Докажем два утверждения : 1) если подпространство двух стрелок несчетно, то оно немет ризуемо; 2) любое не более чем счетное подпространство двух стрелок метризуемо. 1) Пусть У с Х, JYJ> ~ 0 • Предположим, что У метризуемо. Так как У= (У п С0 ) u (У п С1 ), то хотя бы одно из подпространств 111 У n С0 (или У n С1 ), гомеоморфных подпространству стрелки, несчетно. Пусть, например, IY n С0 1 > ~ 0• Тогда У n С0 - подпространство метризуемого пространства У неметризуемое ( Уn С0 с С0 - неметризуемо ( см. задачу № 61, утверждение 1), что невозможно. 2) Доказывается точно так же, как утверждение 2) задачи № 61. №77. В задаче № 18 доказано, что любое бикомпактное метрическое пространство является непрерывным образом канторова множе- ства (D ~O странство стрелки Однако не всякое бикомпактное хаусдорфово про- ). является диадическим бикомпактом. Например, две недиадический бикомпакт. Это вытекает из того, что - всякий диадический бикомпакт с первой аксиомой счетности мет ризуем (см. [2, гл. задачу дачу № 6, § 10]. Две стрелки - неметризуемое пространство № 71, следствие) с первой аксиомой счетности (см. за 70). №78. Построим все возможные интервалы в 1 2 • а) Интервалы вида (а, Ь) (рис. 68) и т. д. б) Интервалы вида (-оо, Ь) (или полуинтервалы вида [а, Ь), где а= (О, О)) (рис. 69). в) Интервалы вида (а, +оо) (или полуинтервалы вида (а, Ь], где Ь = (1, 1)) (рис. 70). 1. Для любой точки х Е 1 2 найдется интервал семейства В, со держащий х и включающийся в 1 (очевидно). 2. Для любых двух интервалов (а1 , Ь1 ) и ( а2 , Ь2 ) вида ( а, Ь) имеем: если (а1 ,Ь1 ) n (а2 ,Ь2 ) -=1= 0, то (а1 ,Ь1 ) n (а2 ,Ь 2 ) = (а 2 ,Ь1 ), где 2 (а2 , Ь1 ) - интервал вида ( а, Ь ). Для любых двух интервалов (-оо, а1 ), где а1 < а2 , имеем: ( -оо, а1 ) n (-оо, а2 ) = (-оо, а1 ), интервал вида (-оо, а). 112 (-оо, а2 ) вида (-оо, а), где (-оо, а1 ) - а :;: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 >Ь ,,ь ,,ь т •>Ь ас а а а т т т 1 1 1 1 1 1 1 1 1 ь 1 1 1 1 1 1 1 1 1 1 1 1 1 1 оь 1 1 1 1 1 1 1 1 1 1 а ь т ас l а,> 1 l ~ь ь ] 'Ь а, а> а,> 1 1 l ь ь l а_ а у у ь ь т 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ь а :: а 'Т Рис. 68 ь а Для любых двух интервалов где а 1 < а2 , имеем: интервал вида ( а1 , + оо), ( а2 , + оо) вида ( а, + оо), (ai, + оо) п (а2 , + оо) = (а2 , + оо), где (а2 , + оо) - ( а, + оо). Для любых двух интервалов (-оо, а1 ), и имеем: если (-оо,а1 )п(а2 ,+00)=1:-0, то ( а2 , + оо) семейства В (-оо, а1 ) п (а2 , + оо) = 113 ь -r 1 1 1 )Ь а ь а а а ь ь )ь ь а а а Рис. ь а 69 ь ь а ь а-;, 1 1 1 а ~------- Ь ~-------ь ь а а~ а Рис. 70 Следовательно, если точка х Е 1 2 принадлежит пересечению каких-либо двух интервалов из семейства В, то найдется интервал из семейства В, содержащий точку х и включающийся в это пере сечение. Таким образом, условия 1) и 2) теоремы 8 выполняются и, сле2 довательно, семейство В всех интервалов в 1 образует базу неко торой топологии (топологии, индуцированной линейным (лекси кографическим) порядком). 114 № 79. См. задачу № 78. Там построены все интервалы и полуинтер валы, составляющие базу топологии. Все полуинтервалы ни от крыты, ни замкнуты (рис. 71 ), все отрезки замкнуты (рис. q 1 1 1 1 1 1 1 "Ь >Ь т т ~--~---пЬ у 1 1 1 1 1 1 1 1 1 1 1 1 1 72). ь а, а, 1 1 l а а т 1 1 1 ] у у 1 1 1 1 1 1 ,ь ь ь а> а а у у у 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 •Ь а,> ] ь Рис. ь а, 71 ~ - - ~q_ _ь а --~--~ у 1 1 1 1 1 1 • Ь •Ь а ь ь ~ь а ] а а Рис. 72 115 №80. Хаусдорфовость квадрата 1 проверяется непосредственно. 2 Пусть а, Ь не лежат на одном вертикальном отрезке, (рис. 73). Тогда ОЬ=(Ь1 , + оо); Оа=(-оо,с), ОапOь=0 ОЬ=(с, +оо), а -=f:. Ь Оа=(-оо,а1 ), (а1 (Ь1 )-проекция точки а (Ь) на верхний (нижний) горизонтальный отрезок) (рис. 74, 75). а--~--~ ,,а а с ,, ь ь .___ _.___... Рис. ь 73 Рис. Ь• ь,, со с ) 74 С) ао Рис. Пусть a-=f:.b • 3c а, Ь лежат на 75 одном вертикальном Е[а,Ь] . Тогда Оа=(-оо,с), ОЬ=(с, +оо) отрезке, Оа пОь =0 . Для любых двух различных точек а, Ь Е 1 имеются непересе 2 кающиеся окрестности . №81. 1. Если точка z(x, у) Е12 не лежит на верхнем и нижнем гори зонтальных отрезках, то в качестве счетной определяющей системы окрестностей можно взять совокупность всех интервалов из базы В, которые имеют вид ( (х, у -1/п); (х, у+ 1/п) ), где п 2. Для точки (О, О) (соответственно, (1, 1)) EN (рис. 76). счетной определяю щей системой окрестностей является совокупность всех интерва- 116 лов из базы В, которые имеют вид (-оо, (О, 1/ п)) (соответственно, ((1,1-1 /п),+ оо), где п ЕN(рис . 77). у у, 1---------,(1, 1) ---l >---z 1 - -1 - -- - - -- - - - Y +- п 1 У-п 1 --- п ! о х х 1 (~~ 1 76 Рис . Рис. х 77 3. Для точки (х, 1) Е/ 2 , где О::; х < 1 (соответственно, для 2 (х, О) Е/ , где О< х:::;; 1) счетной определяющей системой окрест ностей является совокупность всех интервалов из базы В, которые имеют вид ((х, 1-1/ п), + оо), ( (х-1/п, 1), (х, 1/п) ), где п Е (x+l/n, О)) N (рис. 78). у 1 у (х, 1) п о 1 т 1 1 1 1 1 1 т 1 ~ -- 1- (соответственно, 1 1 1 1 1 1 1 1 1 1 1 1 х т 1 1 1 1 1 1 1 1 -----i---~ п 1 1 1 ;i 1 п О х х _J_ (х, О) 1 х 11 Рис . 78 No 82. Обозначим через D множество всех интервалов базы В, кото рые имеют вид ((х, О), (х, 1)), О ::; х ::;; 1 (рис. 79). 117 Очевидно, что интервалы множества ются и множество D попарно не пересека имеет мощность континуума. 2 всюду плотное множество в 1 , то каждый D Если Ммножества D содержит хотя интервал бы по одной точке множества М Сле довательно, М имеет мощность континуума. у у (х, 1 1) 11----------. 1 _ _ _ _ __ 2 о (х, О) Рис. о х х Рис . 79 80 №83. Приведем пример нефинально компактного подпространства пространства 1 (рис. 80). 2 Рассмотрим множество М = {(х, S), где О ::; х::; 1} с 1 2 • Подпро- странство Мс 1 2 является дискретным в индуцированной топо логии. Его покрытие, состоящее из одноточечных подмножеств, не содержит счетного подпокрытия . №84. Пусть ro - произвольное открытое покрытие пространства Покажем, что из ro можно выделить конечное подпокрытие (рис. 81). Рассмотрим проектирование f лексикографически упорядочен2 1 • ного квадрата 1 2 на евклидов отрезок [О, 1] с Ох. Рассмотрим произвольную точку х Е [О, 1]. Ее прообразом при проектировании f является отрезок [(х, О), (х, 1)] с 1 2 • Концы этого отрезка - точки (х, О) и (х, 1) - содержатся в одном или двух элементах покрытия ш. Пусть, для определенности, (х, О) Е И1 Е ш, (х, 1) Е И2 Е ш. То118 гда имеются такие у окрестности = ( (x-1/ni, 1), (х, 1/п1 )) точки (х, О) и Г 2 = ( (х, 1-1/~), (х + 1/п2 , О)) точки 1 где п 1 , п 2 Е N, из счетных опреде- 1 1- n2 ,----~--t 1 ,----~--t 1 Г1 (х, 1), - (см. задачу № что 81 ), n1 (х,О)еГ 1 сИ1 , (х,1) еГ 2 сИ2 • Пусть ется x-::f:-0 и концом Тогда x-::f:-1, имеется 1 1 l 1 1 (х, О) [О, 1] с Ох. такой ~ 1 1 1 1 1 1 1 1 г1 1 1 1 1 Г2 1 1 1 о т. е. хне явля- отрезка 1) 1 1 1 ляющих систем окрестностей этих то- чек (х, Рис. интервал Vx =(x-1lf1i,X + 1/~) с [О, 1], что Г Vх= = Г1 u Ф 2 u [(х, 1/п1 ), (х, 1-1/п2 )], где 1 1 х 81 1 [(х, 1/~), (х, 1-1/п2 )] обычный евклидов отрезок в индуцированной топологии. Выберем из покрытия сох подпокрытие со~ существует = со n = {И~ , ... , иik }. такой [(х, 1/п1 ), (х, 1-1/п 2 )] конечное Для любого элемента иii Е со~ элемент что n [(х, 1/п1 ), (х, 1-1/п2 )], i = 1, ..., k. Таким образом, f - 1vx о о ~о ~о = Г1 u 1 uГ2 uUЧ u ... uuxk cUl uИ2 uUXI u ... uuxk, т. е. гv: содержится в (рис . объединении конечного числа элементов покрытия со 82). у у 11----------<.,__~ 1 : 1 1 1 1- - 1 1 ~------- --- т----~) n2 1 1 1 -----------t---- 1 1 1 1 n1 1 о х о х n1 Рис . 82 119 Аналогично, если х луинтервал О = [О, 1/п2 ) с [О, (1-1/ п1 , 1] с [О, 1] с Ох), ( соответственно, 1] с Ох х = 1), то имеется по (соответственно, полуинтервал прообраз которого при отображении держится в объединении конечного числа элементов покрытия f со ro. Рассмотрим покрытие Q отрезка [О, 1] с Ох интервалами и полуинтервалами, обладающими указанным выше свойством. В силу бикомпактности отрезка [О, 1] с Ох выберем из покрытия Q нечное подпокрытие 0 0• ко- Прообраз каждого элемента покрытия Q 0 содержится в объединении конечного числа элементов покры тия ro, и к тому же прообразы всех элементов покрытия ставляют конечное покрытие пространства 2 1 . 00 со- Следовательно, покрытие ro пространства 1 содержит конечное подпокрытие. 2 No 85. Несовершенная нормальность пространства 1 2 вытекает из его хаусдорфовости (см. задачу № 80), бикомпактности (см. задачу № 84) и ненаследственной финальной компактности ( см. задачу № 83) [3, гл. I, § 7]. Докажем непосредственно, что пространство 1 не совершен 2 но нормально. Для этого приведем пример замкнутого в 1 мно 2 жества, которое не является пересечением счетного числа откры тых множеств (рис. 83). Рассмотрим где у Fi={(x,0):0~x~l}, F; ={(x,1):0~x~ l}. Множество F замкнуто в 1 F, 1 F=F;_uF2 , множество дополнение 2 1 \F= 2 (так как его U ((х,О),(х,1)) от- Osxsl крыто). Пусть F2 ность множества о 1 Рис. 120 OF 83 х произвольная F. окрест- Для любого х: О~х~1 найдутся такие окрестности Г 1 ( соответственно, Г2) точки (х, О) (соответственно, (х, 1)) (х, О) (х, 1) из счетных определяющих (соответственно, еГ 2 (х, = = (В1 ,В2 ) с OF где = (А1 ,А2 ) с Ор, 81). х : О < х < 1 имеется содержится [(х, О), (х, 1)] , и Их с OF (рис. (х, 1 1 1 1 I Г1 1 1 1 1 1 IA 1 2 81 ) 1 1 1 Г2 1 1 А2 в вертикальном 84). т 1 1 1 1 1 1 Г1 1 1 1 1 1 1 1 1 1 Г2 1 1 1 1 (х, О) В2 Рис . Аналогично, для х = отрезке 1) Г1 А1 (х, О) 1 такая окрест что Их= =(/4,В2 ) \ [А2 ,В1 ] , '( 1 точки (см. задачу № Dx ={(х, О),(х,1)} , [А2 , В1 ] отрезок окрестностей (х, О) еГ 1 что 1)), Таким образом, для любого ность Их множества систем х = 1) имеется такая окрестность И0 (соответственно И1 ) множества D0 = {(О, О), (О, 1)} (соответственно И0 с О 84 ( соответственно D 1 ={(l,0),(1,1)}), OF (соответственно И1 что И0 =[А1 ;В2 ) \ [А2 ;В1 ] = (А1 ;В2 ]\[~ ; В1 ] и и И1 с Ор )- Обозначим через а, 1 проекцию точки А1 на ось Ох, через р 2 проекцию точки В2 на ось Ох. Тогда проекцией множества Их (О < х < 1) на ось Ох является интервал (а 2 , Р 2 )х , а проекцией множества И0 (соответственно, И1 ) на ось Ох является полуинтервал [а1 , Р2 ) 0 ( соответственно, (а1 , Р2 J1)Рассмотрим покрытие ми [а 1 , Р 2 ) 0 , Выберем (а 1 , из P2Ji Q отрезка [О, 1] с Ох полуинтервала и интервалами (а 2 , Р 2 ) х , где О покрытия Q конечное = {[а1, Р 2 )0, (а,1, Р 2 ]1 , (а1 , P2 )xi , ..., (а 1 , Р 2 )х) · что окрестность U F = Ио U И1 U их1 U . . . U ИХп Оо < х < 1. подпокрытие Тогда получим, множества F со- 121 держится в окрестности Ор, Кроме того, ем до 1 2 UF является дополнени- конечного числа множеств, содержащихся в вертикаль- ных отрезках [(х, О), (х, 1)]. 00 00 00 Если F = ПО~, то F = ПИ~. Но ПИ~ является дополнением i=1 i=l до 1 2 i= l лишь счетного числа множеств, содержащихся в вертикаль00 пых отрезках [(х, О), (х, 1)], т. е. ПИ~ -::f:.F=F'i uF2 • Таким oбpai=l зом, замкнутое множество F не является пересечением счетного числа открытых множеств и, следовательно, пространство 1 2 не совершенно нормально. №86. у Рассмотрим множество где С0 = {(х, О): О <х ~ 1}, (рис . Х ством множества 1 точек, что и две 1 Рис. х 85 = С0 u С1 , Ci = {(х, 1):0 ~х <1} 85). Множество о Х является подмноже- и состоит из тех же стрелки (см. § 11). Каж2 дый интервал из базы В пространства 1 (см. задачу № 78) высекает на Х множе2 ство, которое является открытым в топо логическом пространстве «две стрелки» (см. задачу № вательно, две стрелки Аналогично, и пространства 1 2 64). Следо- подпространство пространства 1 • стрелка ( см. § 1О) является подпространством 2 • №87. Требуемым отображением является проектирование f про- странства 1 на отрезок [О, 1] с Ох (рис. 86). 2 Для любой точки х Е [О, 1] имеем f - x 1 = [(х, О), (х, 1)] с 1 2 , где f - 1x в индуцированной топологии является обычным евклидовым отрезком. 122 Покажем, что отображение/непрерывно. Элементы базы на от резке [0,1] с Ох являются множествами вида [О, а), (а, 1], (а, Ь), где 1 2 О < а, Ь < 1. При этом f - x = (([О, а))= (-оо, (а, О)) с 1 - открыт в 1 (рис. 87); f -1((a, Ь)) = ((а, 1), (Ь, О)) с 1 2 f -1((a,l]) = ((а, 1); +оо) с 12 2 - открыт в 1 (рис. 88); 2 открыт в 1 (рис. 89). 2 - у у 1~-------, 1 >----е----~ 1 1 1 1 1 1 1 1 1 1 о х Рис. 1 х о 86 а Рис. у , 1 х 1 х 87 у 1 1 1 о 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ь а 1 1 - 1 Рис.88 х 1 1 о а Рис . 89 Следовательно, прообраз любого открытого в [О, 1] множества открыт в 1 2 , т. е. отображение/непрерывно. No 88. Докажем утверждения в обратном порядке. 3) Докажем, что для точек 0(0, О) Е1 2 и M(l, 1) Е 1 2 не существует такого непрерывного отображения f(a) = О, f(b) =М (рис. f : [а, Ь] • 1 2 , что 90). 123 Предположим, что такое отображение у f: [а,Ь] • 1t - - - - - -- M связности 2 существует. Тогда, в силу отрезка [3, гл. I, § 4] и линейной 1 упорядоченности пространства 1 2 , мно жество .fП а, Ь]) содержит все точки, лежа щие между точками О и М, т. е. все точки пространства 1 о х • Действительно, если имеется такая точка Рис.90 А(х0 ,у0 )Е1 , что A~f([a,b]), то множе2 И1 = f([a, b])nl/ ства 2 И2 = f([a, b])nIJ, и = {(х, у) Е / 2 : (х,у) > А(х0 ,у0 )}, I/ где IJ = = {(х, у) Е / 2 : (х, у)< А(х0 , у0 )}, непусты, не пересекаются и открыты в пространстве f([a, Ь]) с 1 Следовательно, множество 2 • f([a, Ь]) несвязно. Это противоречит тому, что непрерьmный образ связного пространства (рассматривае мый как подпространство образа) связен [1, гл. 6, п. 6.1.4]. Таким образом, /: [а, Ь] • 1 - сюръекция. Обозначим через G множество всех интервалов 1)), где О~ х ~ 1. Множество G имеет мощность 2 (х, его элементы непусты, попарно не вида ((х, О), континуума, пересекаются и являются от- крытыми в 1 множествами. В силу непрерывности отображения/ прообраз каждого интервала из множества G открыт в отрезке [а, Ь] ( см. определение 14). Следовательно, в отрезке [а, Ь] имеется 2 континуум непустых, открытых, попарно не пересекающихся множеств. Но это невозможно, так как, в силу сепарабельности отрезка [а, Ь ], непустых, открытых, попарно не пересекающихся множеств не более чем счетное множество (достаточно каждому такому множеству поставить в соответствие одну точку из счетно го всюду плотного в [а, Ь] множества). Таким образом, простран- ство 1 не линейно связно. 2) Докажем, что пространство 1 2 локально связно. 2 Нам понадобится следующая лемма. Лемма. Если/ есть проектирование лексикографически упоря- доченного квадрата / 2 на отрезок [О, 1] с Ох, то прообраз любого связного в [О, 1] множества связен в 1 124 2 • Доказательство. В отрезке [О, 1] с Ох связными являются только подмножества вида: Ь :s; 1 [О,а), (а, 1], [а,Ь], [а,Ь), (а,Ь], (а,Ь), {а}, [О, 1], 0, (см. задачу № где О :s; а, 3). Обозначим через Х произвольное связ у ное подмножество отрезка [О, 1]. Предпо- 1-1Х несвязно в пространстве 1-1 Х = А u В, где множества А ложим, что 1 2 • Тогда l f--~---~ У1 --- , У2 --- , и В непусты, не пересекаются, открыто- замкнуты в 1- 1 х (рис. 91). Отображение I непрерывно ( см. задачу о 87) и замкнуто (т. е. образ любого замкнутого в 1 2 множества замкнут в [О, 1] ). (Это следует из того факта, что всякое х № х Рис. 91 непрерывное отоб- ражение бикомпактного топологического пространства Х в хау сдорфово пространство У замкнуто жение I' = I [3, гл. I, § 7].) Тогда и отобра- lг 1 х: 1- Х • Х также замкнуто. Покажем это. 1 1 Рассмотрим замкнутое в 1- х множество Т. Тогда в 1 суще2 ствует замкнутое множество F, в пересечении с 1- 1 х дающее множество Т. По условию множество fF замкнуто в [О, 1]. Следо- вательно, в Х замкнуто множество Х п fF = т. е. отображение l'=l-1X Обозначим через А1 = пусты, замкнуты, и Х l(l-1X п F) = JТ, • Х замкнуто. I I (А), В1 = = А1 u (В). Множества А1 и В1 не В1 • Докажем, что А1 n В1 = 0. Пусть это не так. Тогда Зх: х Е А1 u В1 • Следовательно, 1- х содержит две 1 точки - (х,у1 ) и (х,у2 ) (где О надлежит множеству А, а другая :s; Yi, у2 :s; 1), одна из которых при множеству В. Но этого быть не - может, так как точки (х,у1 ) и (х,у2 ) принадлежат одному и тому же вертикальному отрезку [(х, О), (х, ~ тикальныи отрезок пространства 12 1)]. Действительно, любой вер- в индуцированнои топологии ~ 125 у является обычным евклидовым который, 1 связен. Следова тельно, все точки любого вертикального 1 1 !х ' как известно, отрезком, отрезка пространства 1 ному из множеств § 1 1 о - 1 Рис. Таким 4]. А1 п В1 х принадлежат од или А, или В образом, [3, гл. доказано, I, что Тогда получается, что множе- ство Х несвязно, что противоречит усло вию. 92 = 0. - 2 Следовательно, множество 1- 1 х связно. Лемма доказана. Пусть z Е 1 2 , произвольная окрестность точки z. Дока Oz - жем, что существует такая связная окрестность Uz точки z, что Uz с Oz (рис. 92). так ( см . как 1 задачу № 2 81 ), пространство то для точки z с V V первои аксиомои имеется такая окрестность счетной определяющей системы окрестностей, что Если = (О, О) z или z = (1, 1), то z=(x,y), где = (х, 1) Uz с Oz. 0<у<1,то Иz-интервалсобыч- O:s;;x::;;1, Uz связно (рис. 93). лежит на верхнем основании квадрата 1 Иz=((х,1-1/п),(х+1/п,О)), п из Uz связно. ной евклидовой топологией, следовательно, Если z Uz полуинтервал с обычной Uz - евклидовой топологией, следовательно, Если счетности Пусть EN. f - 2 , то проектирование пространства 1 2 на отрезок [О, 1] с Ох. То- у гда Uz = f - 1 (х, х+ 1/п) u((x, 1-1/п), (х, 1)], где множество Х1 но, так как = ((х, 1-1/п), (х, 1)] является z связ 1 1 1 полуинтервалом ) с обычной топологией. Множество Х2 1 1 =f - 1 связно (по лемме). Точка ((x, 1-1/п), (х, 1)) z = (х, 1) так 126 как при = Х2 u {Z} присоединении к 1 1 1 являет ся предельной для множества Х Следова тельно, множество Х~ 1 1 о х 1 1 1 х+- связно, п связному Рис.93 х множеству любого множества его пре дельных жество точек получается мно 1 [2, гл. 4, § 3]. Так как Х1 п Х~ ства связное Х1 Uz = х~ u п. 6.1.10]. и Х~ = {Z} -::1= 0 и множе- связны, то окрестность xl = Xz u xl Аналогично, если связна z [1 О, = (х, О) на нижнем основании квадрата окрестность связна (рис. у Uz гл. 6, лежит 2 1 , о у т 1 1 1 1 1 1 1 1 1 1 1 1 1 1 l 1 х-- х 1 х п то = ((х-1/п, 1), (х, 1/п)) Рис. 94 94). 2 Таким образом, доказано, что пространство 1 локально связно. 1) Из леммы, доказанной в п. 2), следует, что пространство 1 2 связно. ЛИТЕРАТУРА 1. Энгелькинг Р. Общая топология / пер. с англ. М.Я. Антонов ского и А .В. Архангельского. М.: Мир, 2. Архангельский 1986. А.В., Пономарев В.И. Основы общей тополо гии в задачах и упражнениях. М.: Наука, 3. Колмогоров А.Н., 1984. Фомин С.В. Элементы теории функций и функционального анализа. М.: Физматлит, 2004. 4. Пасынков Б.А., Федорчук В.В. Топология и теория размерно сти . М .: Знание, 1984. 5. Очан Ю.С. Сборник задач по математическому анализу. М.: Просвещение, 1981 . 6. Александров П. С. Введение в теорию множеств и общую то пологию. СПб.: Лань, 2010. 7. Александров П.С. , Пасынков Б.А . Введение в теорию размер ности. М.: Наука, 1973. 8. Борисович Ю.Г., Близняков НМ., Фоменко ТМ. Введение в топологию. М. : Наука, 1995. 9. Коснёвски Ч Начальный курс алгебраической топологии / пер. с англ. В .М. Быкова; под ред. Е.Г. Скляренко. М.: Мир, 1983. 1О. Элементарная топология / О .Я. Виро, О .А. Иванов, Н.Ю. Нецветаев, В.М. Харламов. М. : МЦНМО, 2010. ОГЛАВЛЕНИЕ Предисловие Глава ................................................................................................... 3 1. Некоторые основные понятия и теоремы общей топологии ............................................................................................ 6 Глава 11. Классические примеры топологических пространств .. .. .. . 19 § 1. Некоторые простейшие подмножества Н1 ................................ 19 § 2. Канторово множество ................................................................ 20 § 3. Канторова лестНШJ;а .................................................................... 24 § 4. Ковер Серпинского .................................................................... 26 § 5. Универсальная кривая Менгера ................................................ 27 § 6. Пространство иррациональных чисел ...................................... 29 § 7. Метризуемые «ежи» (конечной, счетной и континуальной «колючести») ............................................................................... 29 § 8. Бикомпактные «ежи» ( счетной и континуальной «колючести») ............................................................................... 3 О § 9. Неметризуемые «ежи» ( счетной и континуальной «колючести») ............................................................................... 32 § 10. Стрелка Зоргенфрея ................................................................. 33 § 11. Две стрелки Александрова ...................................................... 34 § 12. Лексикографически упорядоченный квадрат ........................ 35 Глава 111. Решения задач .......................................................................... 37 Литература .................................................................................................. 129 Учебное издание Блудова Ирина Валентиновна Белянова Эльвира Николаевна Начала топологии в примерах и задачах Редактор С.А. Серебрякова Художник ЯМ Ильина Корректор ЛВ. Забродина Компьютерная верстка С.А. Серебряковой В оформлении использованы шрифты Студии Артемия Лебедева. Оригинал-макет подготовлен в Издательстве МГТУ им. Н.Э. Баумана. Подписано в печать Усл. печ. л. 8,13. Тираж 15.07.2016. Формат 60х90/16. 300 экз. Изд. № 131-2014. Заказ Издательство МГТУ им. Н.Э. Баумана. 105005, Москва, 2-я Бауманская ул., д. 5, стр. 1. [email protected] www .baumanpress.ru Отпечатано в типографии МГТУ им. Н.Э. Баумана. 105005, Москва, 2-я Бауманская ул., д. 5, стр. 1. [email protected]

Блудова И.В., Белянова Э.Н. - Начала топологии в примерах и задачах - 2016

Похожие документы

Разделы

Поддержка

Блудова И.В., Белянова Э.Н. - Начала топологии в примерах и задачах - 2016

Похожие документы

Добавить этот документ в коллекции

Добавить этот документ в сохраненные

Предложите, как улучшить StudyLib