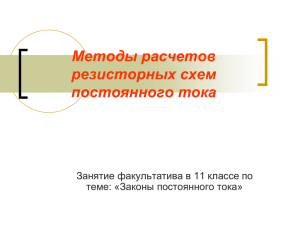
1.3. Пример расчёта электрической цепи постоянного тока с одним источником напряжения методом эквивалентных преобразований R4 Для заданной схемы простой электрической цепи, изображенной на рисунке, требуется: R3 1. Методом эквивалентных R1 R5 R6 U преобразований (путём последоваI3 тельных «свёртываний») найти обI6 I5 I1 I2 R2 щее эквивалентное сопротивление цепи и ток источника напряжения. 2. Определить токи во всех элементах цепи. 3. Проверить правильность расчётов составлением баланса мощностей развиваемой источником напряжения и потребляемой в цепи. Для схемы, приведённой выше, дано: U = 315 В, R1 = 31 Ом; R2 = 24 Ом; R3 = 53 Ом; R4 = 17 Ом; R5 = 46 Ом; R6 = 38 Ом. IO + I4 Решение Непосредственно определить токи в элементах схемы по закону Ома невозможно, так как неизвестно распределение напряжений на отдельных её участках. Обозначим токи в элементах по номерам резисторов; общий ток цепи (ток источника) обозначим I0. Сначала путём последовательного «свертывания» схемы найдём эквивалентное сопротивление цепи R0, что позволит определить общий ток I0 в неразветвленной её части. R1 U На схеме А резисторы R5 и R4 схема А a + R3 b U6 U5 R5 R2 - c I5 R6 I6 d 1 R6 подключены к одной паре узлов b и d, поэтому, согласно определению, соединены параллельно, значит их можно заменить одним эквивалентным сопротивлением RR 46 38 R56 5 6 20,81 Ом. R5 R6 46 38 R4 схема Б a I456 + I4 U56 R3 R1 U R56 R2 - I56 d c R456 схема В a I456 + R1 U R3 U3 На схеме В резисторы R456 и R3 включены параллельно (к паре узлов a и d). Заменим их эквивалентным сопротивлением RR 53 37,81 R3456 3 456 22,07 Ом. R3 R456 53 37,81 U456 I3 R2 - d c схема Г + R a I23456 3456 I3456 U3456 R1 U R2 I2 - На схеме Г резисторы R3456 и R2 образуют одну ветвь между узлами a и c, то есть соединены последовательно. Заменим их эквивалентным сопротивлением R23456 R3456 R2 22,07 24 46,07 Ом. c схема Д I23456 R 23456 a + U23456 R1 U U1 - На схеме Б резисторы R4 и R56 образуют одну ветвь, не имеющую разветвлений и включённую между узлами a и d, поэтому, согласно определению, они соединены последовательно. Заменим их одним эквивалентным сопротивлением R456 R4 R56 17 20,81 37,81 Ом. I1 На схеме Д резисторы R1 и R23456 образуют параллельное соединение между узлами a и c. Их эквивалентное сопротивление будет являться общим сопротивлением цепи RR 31 46,07 R0 1 23456 18,53 Ом. R1 R23456 31 46,07 c 2 схема Е I O + a RO U U - c Для схемы E определим общий ток цепи, являющийся током в неразветвленной части цепи и током источника, по закону Ома: U 315 I0 17,00 А. R0 18,53 Зная общий ток, будем поэтапно «развёртывать» схему в обратном порядке для определения токов в её элементах. Резистор R0 на схеме Е является эквивалентным со- противлением параллельно включенных резисторов R1 и R23456 на схеме Д, поэтому для перехода к схеме Д необходимо знать напряжение на нём. Так как он включен параллельно источнику напряжения, то напряжение на нём будет совпадать с напряжением источника U. На схеме Д резисторы R1 и R23456 соединены параллельно, поэтому U1 U 23456 U 315 В. U 315 Тогда I1 1 10,16 А. R1 31 Резистор R23456 на схеме Д является эквивалентным сопротивлением последовательно включенных резисторов R3456 и R2, поэтому для перехода к схеме Г необходимо знать ток в нём: U 315 I 23456 23456 6,84 А. R23456 46,07 Так как на схеме Г резисторы R3456 и R2 соединены последовательно, то I 3456 I 2 I 23456 6,84 А. Резистор R3456 схемы Г является эквивалентным сопротивлением параллельного включения резисторов R3 и R456 схемы В. Найдём по закону Ома напряжение на нём: U 3456 I 3456 R3456 6,84 22,07 150,96 В. По свойству параллельного соединения, на схеме В U 3 U 456 U 3456 150,96 В. U 150,96 Тогда I 3 3 2,85 А. R3 53 Для «развёртывания» резистора R456 схемы В, так как он является эквивалентным сопротивлением последовательно включенных резисторов R4 и R56 схемы Б, необходимо знать ток в нём: U 150,96 I 456 456 3,99 А. R456 37,81 3 На схеме Б со свойству последовательного соединения I 4 I 56 I 456 3,99 А. Резистор R56 схемы Б заменял эквивалентным сопротивлением параллельно включенные резисторы R5 и R6 схемы А. Найдём по закону Ома напряжение на нём: U 56 I 56 R56 3,99 20,81 83,03 В. На схеме А по свойству параллельного соединения U 5 U 6 U 56 83,03 В. Тогда, по закону Ома, найдём два последних неизвестных тока: U 83,03 U 83,03 I5 5 1,81 А; I6 6 2,19 А. R5 46 R6 38 Таким образом мы определили неизвестные токи во всех элементах цепи. Проверим правильность произведённых расчётов на основании закона сохранения энергии путём составления баланса мощностей развиваемой источником напряжения и потребляемой в цепи. Рассчитываемая цепь содержит один источник напряжения, поэтому развиваемая им мощность будет равна Pист UI 0 315 17,00 5355,00 Вт. Мощность i-го приёмника определяется как Pi пр I i2 Ri , где Ii – ток i-го приёмника, Ri – его сопротивление. Мощность, потреблённая всеми приёмниn ками в цепи, определится как Pпот I R , где n – количество приёмников 2 i i i 1 энергии в цепи. Для рассчитываемой цепи Pпот I12 R1 I 22 R2 I 32 R3 I 42 R4 I 52 R5 I 62 R6 10,162 31 6,842 24 2,852 53 3,99 2 17 1,812 46 2,19 2 38 5356,93 Вт. Относительное расхождение баланса мощностей будет равно: P Pпот 5355,00 5356,93 ист 100% 100% 0,04% . Pист 5356,93 Относительное расхождение баланса мощностей составило 0,04 % – расчёт цепи методом эквивалентных преобразований можно считать верным. 4