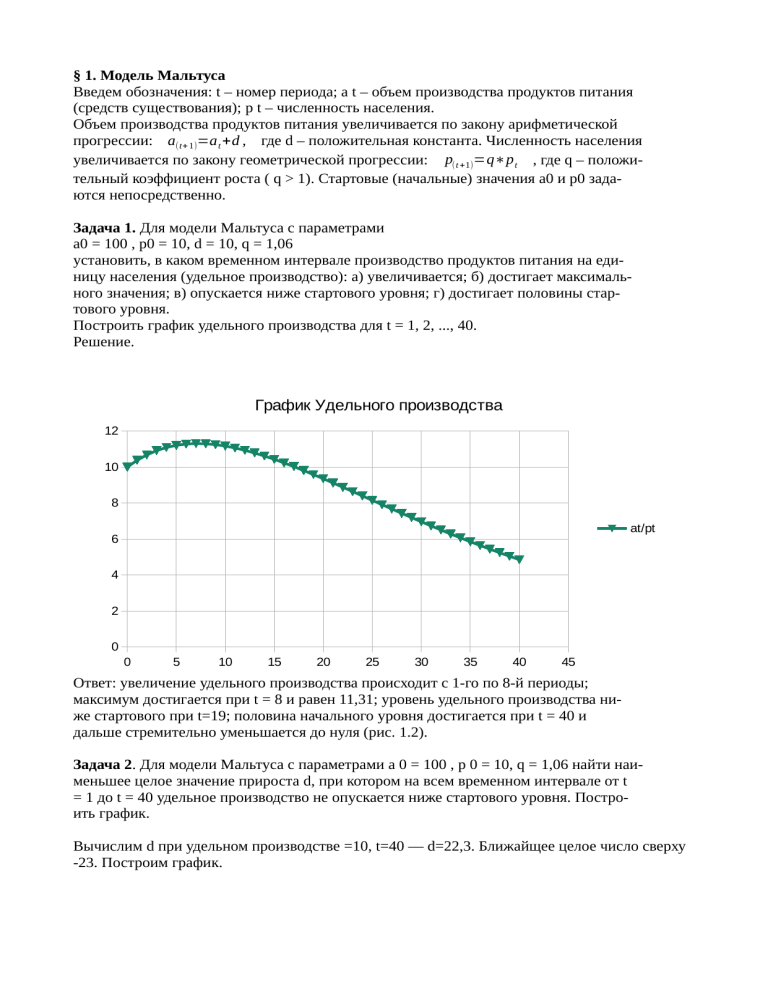
§ 1. Модель Мальтуса Введем обозначения: t – номер периода; a t – объем производства продуктов питания (средств существования); p t – численность населения. Объем производства продуктов питания увеличивается по закону арифметической прогрессии: a(t+ 1)=a t +d , где d – положительная константа. Численность населения увеличивается по закону геометрической прогрессии: p(t +1)=q∗p t , где q – положительный коэффициент роста ( q > 1). Стартовые (начальные) значения a0 и p0 задаются непосредственно. Задача 1. Для модели Мальтуса с параметрами a0 = 100 , p0 = 10, d = 10, q = 1,06 установить, в каком временном интервале производство продуктов питания на единицу населения (удельное производство): а) увеличивается; б) достигает максимального значения; в) опускается ниже стартового уровня; г) достигает половины стартового уровня. Построить график удельного производства для t = 1, 2, ..., 40. Решение. График Удельного производства 12 10 8 at/pt 6 4 2 0 0 5 10 15 20 25 30 35 40 45 Ответ: увеличение удельного производства происходит с 1-го по 8-й периоды; максимум достигается при t = 8 и равен 11,31; уровень удельного производства ниже стартового при t=19; половина начального уровня достигается при t = 40 и дальше стремительно уменьшается до нуля (рис. 1.2). Задача 2. Для модели Мальтуса с параметрами a 0 = 100 , p 0 = 10, q = 1,06 найти наименьшее целое значение прироста d, при котором на всем временном интервале от t = 1 до t = 40 удельное производство не опускается ниже стартового уровня. Построить график. Вычислим d при удельном производстве =10, t=40 — d=22,3. Ближайщее целое число сверху -23. Построим график. График Удельного производства Ответ: 25 20 15 at/pt 10 5 0 0 5 10 15 20 25 30 35 40 45 наименьшее целое значение прироста d, при котором на всем временном интервале от t= 1 до t = 40 удельное производство не опускается ниже стартового уровня -23. Задача 3. Для модели Мальтуса с параметрами a 0 = 100 , p 0 = 10, d = 10 найти наибольший целый процент увеличения населения, при котором на всем временном интервале от t = 1 до t = 40 удельное производство растет. Построить график. Замечание. Одному проценту соответствует q = 1,01, двум процентам соответствует q = 1,02 и т. д. Найдем производную от удельного прироста по времени. f (t)=q(−t +1) / p 0∗(d−(a0 + d( t−1))lnq ) Найдем значение q при t=40 и f`(t)=0 численно — q t 40=1,02333 Из характера функции производной определим, что q ¿ <q t 40 Наибольший целый процент -2 Построим график. График Удельного производства Ответ: 50 45 40 35 30 at/pt 25 20 15 10 5 0 0 5 10 15 20 25 30 35 40 45 наибольший целый процент увеличения населения, при котором на всем временном интервале от t = 1 до t = 40 удельное производство растет равен 2. § 2. Демографическая модель Пусть Xt – численность женского населения в первой возрастной группе (до 20 лет); Уt – численность женского населения во второй возрастной группе (от 20 до 40 лет); Zt – численность женского населения в возрасте после 40 лет; Nt – полная численность населения (женское плюс мужское); a – поправка на бездетность (доля женщин способных к рождению); b – среднее число рождений, приходящихся на одну женщину; c – доля девочек среди родившихся; d – коэффициент выживаемости в первой возрастной группе. Один временной шаг полагаем равным 20 годам (смена одного поколения). Динамика процессов определяется следующими соотношениями: в группу женского населения до 20 лет попадают все девочки, рожденные второй возрастной группой за 20 лет (с учетом вероятности рождения девочки и поправки на бездетность), а именно: X t =c b a Y (t 1) , где a Y_(t1) – количество способных к рождению женщин второй возрастной группы; b a Y (t 1) – количество рождений; c b a Y (t 1 ) – количество девочек среди новорожденных; 2) во вторую возрастную группу перейдет все женское население из первой возрастной группы с учетом выживаемости: Y t =d∗X(t 1) ; 3) численность третьей возрастной группы (после 40 лет) составляет 0,65 от суммарной численности первых двух возрастных групп: Zt=(Xt +Yt )∗0 , 65 ; 4) суммарная численность всего населения (мужское плюс женское) равно полному женскому населению с коэффициентом 1,9 (мужское население составляет 90% от женского) N t=( X t +Y t + Z t) 1 , 9 . Задача 1. Промоделировать динамику численности населения на временном интервале в 30 поколений для следующих значений параметров: a = 0,98 (поправка на бездетность; из 100 женщин второй возрастной группы 2 бездетны); b = 2,0 (среднее число детей, приходящихся на одну женщину в полной или неполной семье); c = 0,49 (вероятность рождения девочки); d =0,975 (коэффициент выживаемости в первой возрастной группе); X0 =20, Y0 =25 (стартовые значения численностей первой и второй возрастных групп). Ответ: график построенной модель изображен ниже: 160 Население,млн чел 140 120 100 80 60 40 20 0 0 5 10 15 20 Поколения 25 30 35 Задача 2. Для данных из задачи 1 найти наименьшее значение параметра b (среднее число детей в семье), при котором будет обеспечено простое воспроизводство, т.е. население не будет уменьшаться. Ответ дать с двумя десятичными знаками после запятой. Найдем точное значение,для которого население не уменьшается для любого t. Тогда прирост населения за шаг Nt−N (t−1) =0 (*) Выразим все переменные (*) через x(t−1) , y(t −1) Получим уравнение: (cba−1)Y (t −1) +( d−1) X (t−1) =0 Подставим X0 и Y0(t=1) и известные коэфиициенты c a d и найдем b≈2,147. Построим график численности населения от номера поколения. 155 С учетом Население,млн чел 150 145 140 135 130 0 5 10 15 20 25 30 35 Поколения характера графика, посчитаем прирост за два шага:(Nt+1-Nt-1)=0 Получим уравнение (abcd−1)(X 0+ Y 0)=0 . Найдем b≈2,13586 141,6 141,5 Население,млн чел 141,4 141,3 141,2 141,1 141 140,9 140,8 0 5 10 15 20 25 30 35 Поколения Ответ: среднее число детей в семье, при котором будет обеспечено простое воспроизводство - b≈2,14. Задача 3. Для данных из задачи 1 найти значение параметра b (среднее число детей в семье), при котором полная численность населения удвоится за 5 поколений. Построить график. Запишем уравнение для условия задачи: N t 5=2∗Nt 0(¿) (*) Воспользуемся результатами вычислений предыдущей задачи. Тогда N (t +2) =cbad∗( X t+Y t )∗k , k =0,65∗1,9 по мат индукции N (t +2 )=cbad i∗( X t +Y t )∗k , k=0,65∗1,9 Тогда N (t +2 +1 )=cbad 2∗(X (t+ 1)+ Y (t +1) )∗k =cbad 2∗(cbaY t +dX t )∗k , k=0,65∗1,9 Подставим в (*) при t=0 2 cbad ∗(cbaY 0 + dX 0)∗k=2k∗(X 0 +Y 0 ) , k=0,65∗1,9 Подставим значения коэффициентов и решим относительно b b≈2,785 Построим график численности населения для найденого значения b для первых 5ти поколений i 2 280 Население,млн чел 260 240 220 200 180 160 140 0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 5 Поколения Ответ: среднее число детей в семье, при котором полная численность населения удвоится за 5 поколений - b≈2,785 § 3. Модель распространения инноваций (нововведений) Эта модель описывает следующие процессы: распространение политических и научных идей, технологий, новых товаров, вовлечение людей в общественные движения, получение знаний в новой области и т. д. Пусть M – емкость рынка (максимально возможное число лиц, способных принять нововведение); X 0 – первоначальное число, принявших нововведение; X t – число охваченных нововведением в t - й момент. Формула для прироста числа сторонников нововведения имеет вид: X t −X (t−1)=aX (t −1)∗M − X(t −1 ) Комментарий. Распространение нововведения осуществляется за счет контактов X t лиц охваченных и M-Xt лиц неохваченных нововведением. Число контактов пропорционально произведению этих величин. Эффективность контактов (скорость вовлечения новичков, “сила”, привлекательность идеи) задается положительным коэффициентом a . Рекуррентное соотношение для нахождения процесса Xt имеет вид: X t =aX (t−1)∗( M − X(t −1 ))+ X (t−1) Стартовое значение задается непосредственно X0 . Задача 1. Построить график процесса Xt для t =1, 2, ..., 20 при следующих значениях параметров модели: M =40 , a =0,01. Построить графики первой и второй производной процесса. Решение. Первая производная - X (t)=X (t+1)− X (t)/(t +1−t ) -скорость Вторая производная - X (t)=X (t +1)−X (t)/(t +1−t ) ускорение График процесса: Распространение инноваций(логистический рост) Кол-во охваченных 50 40 30 20 10 0 0 5 10 15 20 25 Время(t) График производных: Характеристики логистического роста 5 4 3 Скорость Ускорение 2 1 0 0 -1 5 10 15 20 25 § 4. Модели “хищник-жертва” Обозначения: N 0 – численность популяции зайцев (жертв), M 0 – численность популяции волков (хищников) в стартовый момент времени; N t , M t – численности популяций в t -й момент времени. Предполагается, что зайцы располагают неограниченным пространством и неограниченным количеством пищи, а также, что волки питаются зайцами. 4.1. Модель М1. Отсутствие взаимодействия Предполагается, что популяции не взаимодействуют, например, волков и зайцев разделяет стена, и, следовательно, волкам нечем питаться. Прирост численности зайцев пропорционален текущей численности популяции (числу потенциальных семейных пар) и определяется по формуле N t−N (t −1) =aN (t 1 ), где a 0 – коэффициент прироста, который учитывает и коэффициент рождаемости, и коэффициент естественной смертности. Из-за отсутствия пищи численность волков может только убывать, поэтому прирост (точнее, уменьшение) численности волков определяется по формуле M t−M (t−1)=−bM (t 1 ), т.е. уменьшение пропорционально текущей численности волков с коэффициентом b. Таким образом, рекуррентная модель имеет вид N 0=N 0 , M 0=M 0 (стартовые значения), N t =aN (t−1) + N (t −1) , M t =−bM (t 1)+ M (t −1) ,(динамика) Задача 1. Промоделировать на промежутке t=1, 2, ..., 10 динамику численности популяций по модели М1 с параметрами N0 =31, M0= 9,5, a= 0,1, b= 0,3 и построить на одном точечном графике траектории Mt , Nt . Сделать выводы о характере процессов изменения численностей популяций. Динамика изменения численности популяций 250 Кол-во животных 200 150 Зайцы Волки 100 50 0 0 2 4 6 8 10 12 14 16 18 20 Время Вывод: Количество зайцев непрерывно увеличивается, более чем в геометрической прогрессии с параметром a, Прирост числа зайцев также увеличивается с каждым шагом. Популяция растет. Количсетво волков непрерывно уменьшается и хотя абсолютное значение прироста числа волков за шаг с каждым шагом становится меньше, прирост волков за шаг всегда остается отрицательным. Волки вымрут(приблизительно через 9 шагов по времени). 4.2. Модель М2. Взаимодействие популяций Предполагается, что популяции взаимодействуют (стену убрали), т.е. волки имеют доступ к пище (зайцам). В формуле для прироста численности зайцев появляется отрицательное слагаемое, учитывающее количество зайцев, ставших пищей для волков. Это количество пропорционально произведению численности волков и численности зайцев с коэффициентом пропорциональности с 0 . И тогда N t−N (t −1) =aN (t 1 )−сN (t−1)∗M (t−1) (1) В формуле для прироста численности волков появляется положительное слагаемое, отражающее факт естественной рождаемости волков при наличии пищи. Прирост пропорционален произведению числа потенциальных семейных пар и количества потенциальной пищи – численности зайцев, коэффициент пропорциональности d 0 . Имеем M t−M (t−1)=−bM (t 1 )+dN (t −1)∗M (t−1) (2) Таким образом, рекуррентная модель имеет вид: N t =( a−cM (t−1) +1)∗N (t−1) , M t =(−b+ dN (t −1 )+1)∗M (t−1) Задача 2. Промоделировать для t 1, 2, ..., 140 динамику численности популяций по модели М2 с параметрами N0 =31, M0= 9,5, a= 0,1, b= 0,3,c=0,01, d=0,01. 1. Построить на одном точечном графике траектории M t , N t . Установить циклический характер динамики и оценить длину цикла (длину временного интервала между соседними пиками). 2. Построить фазовую траекторию процесса (точечный график зависимости численности волков в зависимости от численности зайцев N N (M ) ). Выяснить характер спирали (закручивается или раскручивается с течением времени). 1. Построим график зависимости Кол-ва животных от времени Динамика обеих популяций имеет цикличный характер. Длина одного цикла для волков и зайцев совпадает и равна 37 шагам по времени. Временной сдвиг пиков обеих популяций относительно друг друга составляет примерно четверть периода. Динамика изменения численности популяций 40 35 Кол-во животных 30 25 Зайцы Волки 20 15 10 5 0 0 20 40 60 80 Время 100 120 140 160 2. Построим фазовые траектории процесса Фазовая траектория динамики популяции зайцев и волков 18 16 14 Кол-во волков 12 10 8 6 4 2 0 20 22 24 26 28 30 32 34 36 38 Кол-во зайцев Как видно из обоих графиков, спираль раскручивается с увеличением времени. Система выходит из равновесного состояния. Так как количество животных ограниченно 0, то со временем вымрет хотя бы одна из популяций. Волки умрут в любом случае( Задача 3. В задаче 2 изменить стартовые численности популяций N0=30, M0=10. Прокомментировать результат. Вывести формулы для стартовых значений, при которых численности популяций не меняются со временем (зависимость N0 и M0 от параметров a, b, c и d). Построим график динамики изменения численности популяций Динамика изменения численности популяций 35 Кол-во животных 30 25 20 Зайцы Волки 15 10 5 0 0 20 40 60 80 Время 100 120 140 160 40 Как видно, из графика число животных не меняется со временем, Фазовая траектория представляет собой точку. Система находится в состоянии равновесия.(неустойчивого) Расчитаем стартовые значения, при которых численность популяции не меняетс со временем => Приросты популяций (1) и (2) =0 . Выразим M (t−1) =a /c , N(t −1)=b /d , Для любого t. Возьмем t=1, тогда M0=a/c, N0=b/d - стартовые значения, при которых численности популяций не меняются: 4.3. Модель М3. Учет эффекта перенаселенности. Предполагается, что с увеличением численности зайцев начинает проявляться эффект перенаселенности, обусловленный ограниченностью пространства и нехваткой пищи. Чем выше плотность популяции, чем больше число встреч между особями, тем выше вероятность стрессов, конфликтов, заболеваний. Это приводит к уменьшению темпов прироста и увеличению смертности. Для учета этого обстоятельства в формулу динамики численности зайцев добавляется отрицательное слагаемое. Число встреч между зайцами пропорционально квадрату их численности; e– коэффициент пропорциональности. Задача 4. Промоделировать для t 1, 2, …, 140 динамику численности популяций по модели М3 с параметрами N0=45, M0=8, a=0,1, b=0,3, c=0,01, d=0,01, e=0,002. Построить на одном точечном графике траектории Mt, Nt . Прокомментировать характер динамики и оценить время установления равновесия. Оценить равновесные значения численностей популяций. Построить фазовую траекторию процесса (точечный график зависимости численности волков в зависимости от численности зайцев N=N(M ) ). Выяснить характер спирали (закручивается или раскручивается с течением времени). Построим график изменения динамики популяции Динамика изменения численности популяций 50 45 Кол-во животных 40 35 30 Зайцы Волки 25 20 15 10 5 0 0 20 40 60 80 100 120 140 160 Время Характер изменения числа особей в популяции носит периодичный характер с периодом в 50 шагов для обеих популяций. Высота пиков уменьшается со временем- система приходит в состояния равновесия. остроим фазовую траектория процесса Фазовая траектория динамики популяции зайцев и волков 8 7 Кол-во волков 6 5 4 3 2 1 0 20 25 30 35 40 45 50 Кол-во зайцев Спираль закручивается со временем, опять же, система приходит в состоние равновесия. Задача 5. Решить предыдущую задачу для различных пар стартовых значений численностей популяций: 1) N0=45, M0=2; 2) N0=3, M0=2; 3) N0=3, M0=13. Значения параметров: a=0,1, b=0,3, c=0,01, d=0,01, e=0,002. 1) Динамика изменения численности популяций Фазовая траектория динамики популяции зайцев и волков 50 14 45 12 Кол-во животных 40 Кол-во волков 10 8 6 35 30 Зайцы Волки 25 20 15 10 5 4 0 0 2 20 40 60 80 100 120 140 160 Время 0 15 20 25 30 35 Кол-во зайцев 40 45 50 2) Динамика изменения численности популяций 60 Кол-во животных 50 40 Зайцы Волки 30 20 10 0 0 20 40 60 80 100 120 140 160 Время Фазовая траектория динамики популяции зайцев и волков 9 8 7 Кол-во волков 6 5 4 3 2 1 0 0 10 20 30 Кол-во зайцев 40 50 60 3) Динамика изменения численности популяций 60 Кол-во животных 50 40 Зайцы Волки 30 20 10 0 0 20 40 60 80 100 120 140 160 Время Фазовая траектория динамики популяции зайцев и волков 14 12 Кол-во волков 10 8 6 4 2 0 0 10 20 30 40 50 60 Кол-во зайцев 4.4. Краткая постановка задачи. Задача 6. Найти траектории процессов Nt , Mt , t =1, 2 , … , 50, а также фазовую траекторию N=N(M) для следующих значений управляемых параметров: N0=45, M0=8, a=0,1, b=0,3, c=0,01, d=0,01, e=0,002. Динамика изменения численности популяций 50 45 Кол-во животных 40 35 30 Зайцы Волки 25 20 15 10 5 0 0 10 20 30 40 50 60 Время Фазовая траектория динамики популяции зайцев и волков 14 12 Кол-во волков 10 8 6 4 2 0 15 20 25 30 35 Кол-во зайцев 40 45 50









