Документ 630459

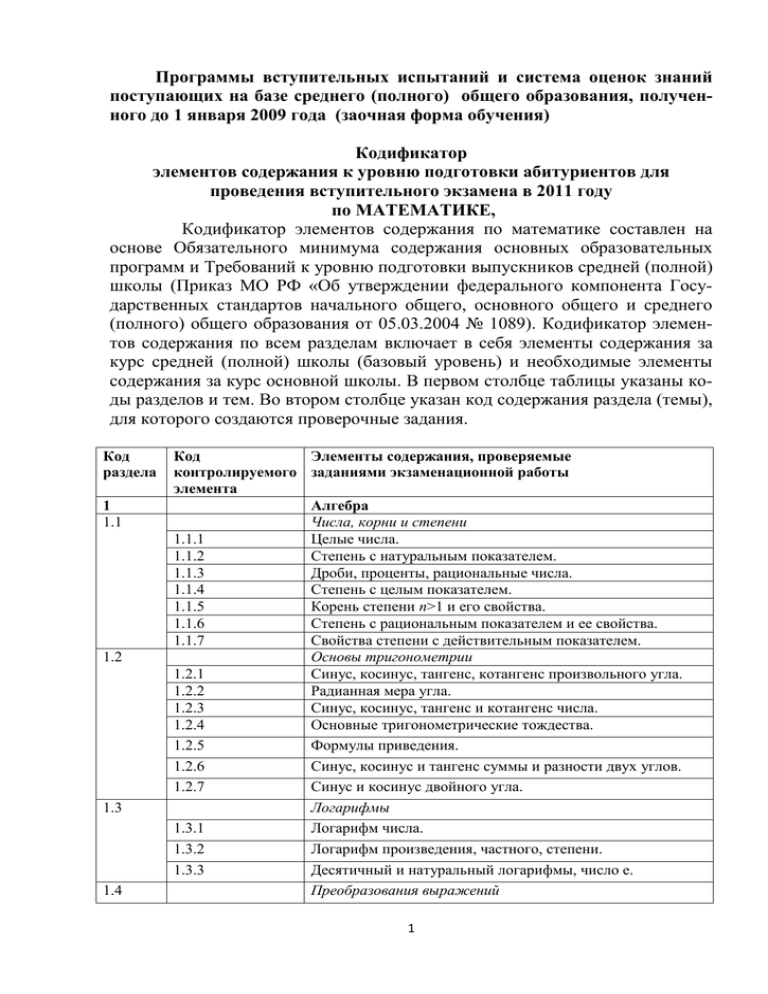
Программы вступительных испытаний и система оценок знаний
поступающих на базе среднего (полного) общего образования, полученного до 1 января 2009 года (заочная форма обучения)
Кодификатор
элементов содержания к уровню подготовки абитуриентов для
проведения вступительного экзамена в 2011 году
по МАТЕМАТИКЕ,
Кодификатор элементов содержания по математике составлен на
основе Обязательного минимума содержания основных образовательных
программ и Требований к уровню подготовки выпускников средней (полной)
школы (Приказ МО РФ «Об утверждении федерального компонента Государственных стандартов начального общего, основного общего и среднего
(полного) общего образования от 05.03.2004 № 1089). Кодификатор элементов содержания по всем разделам включает в себя элементы содержания за
курс средней (полной) школы (базовый уровень) и необходимые элементы
содержания за курс основной школы. В первом столбце таблицы указаны коды разделов и тем. Во втором столбце указан код содержания раздела (темы),
для которого создаются проверочные задания.
Код
раздела
1
1.1
1.2
1.3
1.4
Код
Элементы содержания, проверяемые
контролируемого заданиями экзаменационной работы
элемента
Алгебра
Числа, корни и степени
1.1.1
Целые числа.
1.1.2
Степень с натуральным показателем.
1.1.3
Дроби, проценты, рациональные числа.
1.1.4
Степень с целым показателем.
1.1.5
Корень степени n>1 и его свойства.
1.1.6
Степень с рациональным показателем и ее свойства.
1.1.7
Свойства степени с действительным показателем.
Основы тригонометрии
1.2.1
Синус, косинус, тангенс, котангенс произвольного угла.
1.2.2
Радианная мера угла.
1.2.3
Синус, косинус, тангенс и котангенс числа.
1.2.4
Основные тригонометрические тождества.
1.2.5
Формулы приведения.
1.2.6
Синус, косинус и тангенс суммы и разности двух углов.
1.2.7
Синус и косинус двойного угла.
Логарифмы
1.3.1
Логарифм числа.
1.3.2
Логарифм произведения, частного, степени.
1.3.3
Десятичный и натуральный логарифмы, число е.
Преобразования выражений
1
1.4.1
1.4.2
1.4.3
1.4.4
1.4.5
1.4.6
2
2.1
2.1.1
2.1.2
2.1.3
2.1.4
2.1.5
2.1.6
2.1.7
2.1.8
2.1.9
2.1.10
2.1.11
2.1.12
2.2
2.2.1
2.2.2
2.2.3
2.2.4
2.2.5
2.2.6
2.2.7
2.2.8
2.2.9
2.2.10
3.
3.1
Преобразования выражений, включающих арифметические
операции.
Преобразования выражений, включающих операцию возведения в степень.
Преобразования выражений, включающих корни натуральной степени.
Преобразования тригонометрических выражений.
Преобразование выражений, включающих операцию логарифмирования.
Модуль (абсолютная величина) числа.
Уравнения и неравенства
Уравнения
Квадратные уравнения.
Рациональные уравнения.
Иррациональные уравнения.
Тригонометрические уравнения.
Показательные уравнения.
Логарифмические уравнения.
Равносильность уравнений, систем уравнений.
Простейшие системы уравнений с двумя неизвестными.
Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных.
Использование свойств и графиков функций при решении
уравнений.
Изображение на координатной плоскости множества решений уравнений с двумя переменными и их систем.
Применение математических методов для решения содержательных задач из различных областей науки и практики.
Интерпретация результата, учет реальных ограничений.
Неравенства
Квадратные неравенства.
Рациональные неравенства.
Показательные неравенства.
Логарифмические неравенства.
Системы линейных неравенств.
Системы неравенств с одной переменной.
Равносильность неравенств, систем неравенств.
Использование свойств и графиков функций при решении
неравенств.
Метод интервалов.
Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем.
Функции
Определение и график функции
2
3.1.1
3.1.2
3.1.3
3.1.4
3.1.5
3.2
3.2.1
3.2.2
3.2.3
3.2.4
3.2.5
3.2.6
3.3
3.3.1
3.3.2
3.3.3
3.3.4
3.3.5
3.3.6
3.3.7
4
4.1
4.1.1
4.1.2
4.1.3
4.1.4
4.1.5
4.1.6
4.2
4.2.1
4.2.2
4.3
4.3.1
4.3.2
Функция, область определения функции.
Множество значений функции.
График функции. Примеры функциональных зависимостей
в реальных процессах и явлениях.
Обратная функция. График обратной функции.
Преобразования графиков: параллельный перенос, симметрия относительно осей координат.
Элементарное исследование функций
Монотонность функций. Промежутки возрастания и убывания.
Четность и нечетность функций.
Периодичность функций.
Ограниченность функций.
Точки экстремума (локального максимума и минимума)
функции.
Наибольшее и наименьшее значения функции.
Основные элементарные функции
Линейная функция, ее график.
Функция, описывающая обратную пропорциональную зависимость, ее график.
Квадратичная функция, ее график.
Степенная функция с натуральным показателем, ее график.
Тригонометрические функции, их графики.
Показательная функция, ее график.
Логарифмическая функция, ее график.
Начала математического анализа
Производная
Понятие о производной функции, геометрический смысл
производной.
Физический смысл производной, нахождение скорости для
процесса, заданного формулой или графиком.
Уравнение касательной к графику функции.
Производные суммы, разности, произведения, частного.
Производные основных элементарных функций.
Вторая производная и ее физический смысл.
Исследование функций
Применение производной к исследованию функций и построению графиков.
Примеры использования производной для нахождения
наилучшего решения в прикладных, в том числе социально-экономических, задачах.
Первообразная и интеграл
Первообразные элементарных функций.
Примеры применения интеграла в физике и геометрии.
3
Кодификатор
требований к уровню подготовки абитуриентов
для проведения вступительного экзамена по МАТЕМАТИКЕ в 2011 году
на базе средней (полной) школы ( 11 кл.)
Кодификатор требований к уровню подготовки по математике абитуриентов, поступающих на базе средней (полной) школы составлен на основе
Обязательного минимума содержания основных образовательных программ
и Требований к уровню подготовки выпускников средней (полной) школы
(Приказ МО РФ «Об утверждении федерального компонента Государственных стандартов начального общего, основного общего и среднего (полного)
общего образования от 05.03.2004 № 1089).
Кодификатор требований по всем разделам включает в себя требования
к уровню подготовки абитуриентов, поступающих на базе средней (полной)
школы (базовый уровень). В соответствии со стандартом средней (полной)
школы в требования к уровню подготовки включаются также знания, необходимые для освоения соответствующих умений. В первом столбце таблицы
указаны коды разделов, на которые разбиты требования к уровню подготовки
по математике. Во втором столбце указан код требования, для которого создаются экзаменационные задания. В третьем столбце указаны требования
(умения), проверяемые заданиями экзаменационной работы.
Код
раздела
Код
контролируемого
требования
(умения)
1
1.1
1.2
1.3
2
2.1
2.2
2.3
3
3.1
Требования (умения), проверяемые заданиями экзаменационной работы
Уметь выполнять вычисления и преобразования
Выполнять арифметические действия, сочетая устные и
письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма.
Вычислять значения числовых и буквенных выражений,
осуществляя необходимые подстановки и преобразования.
Проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции.
Уметь решать уравнения и неравенства
Решать рациональные, иррациональные, показательные,
тригонометрические и логарифмические уравнения, их системы.
Решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать
для приближенного решения уравнений и неравенств графический метод.
Решать рациональные, показательные и логарифмические
неравенства, их системы.
Уметь выполнять действия с функциями
Определять значение функции по значению аргумента при
различных способах задания функции; описывать по графику поведение и свойства функций, находить по графику
4
3.2
3.3
4.1
4
4.2
4.3
функции наибольшие и наименьшие значения; строить
графики изученных функций.
Вычислять производные и первообразные элементарных
функций.
Исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения
функций.
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей).
Решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей,
объемов); использовать при решении стереометрических
задач планиметрические факты и методы.
Определять координаты точки; проводить операции над
векторами, вычислять длину и координаты вектора, угол
между векторами.
Инструкция
по выполнению экзаменационной работы по математике
для абитуриентов, поступающих на заочное отделение
1. Работа состоит из трех частей. В первой части- части А- 5 заданий (тестовые задания по алгебре), во второй – части В— 5 задания по алгебре и началам анализа (записать
краткий ответ) в третьей части одно задание, необходимо дать подробное описание решения. На выполнение всей работы отводится 3 ч.
2. При выполнении заданий первой части нужно указывать только ответы.
К заданию приводятся варианты ответов (четыре ответа, из них верный только
один);
Решение заданий из части А оформляем в виде таблицы :
А1
А2
А3
А4
А5
а
б
а
в
Г
в
3.
Если вы ошиблись при выборе ответа, то зачеркните отмеченный результат
и ниже запишите новый результат, если зачеркнутый вариант является верным, то он не
засчитывается правильным. Корректирующим карандашом пользоваться запрещается.
Все необходимые вычисления, преобразования и т. д. выполняйте в черновике.
Черновики не проверяются.
5
4. При выполнении заданий из части В сначала укажите его номер, а затем приведите решение, а затем в таблицу занесите ответ.
В1
В2
В3
В4
В5
102
15,8
0
280
0,369
5.Каждый экзаменационный вариант в части С содержит 1 задания, где необходимо
дать полное решение этих заданий.
Система оценивания экзаменационной работы
по математике
Общий балл формируется путем суммирования баллов, полученных абитуриентами
за выполнение первой и второй частей работы. За каждое верно решенное задание части
А абитуриенту начисляется 3 балла. За каждое верно решенное задание части В абитуриенту начисляется по 10 баллов. Задание части С - 30 баллов Система формирования общего балла приводится в таблицы.
Таблица . Система формирования общего балла
Максимальное количество баллов за одно задание
Часть А
Часть В
За работу
в целом
Задания
А 1-5
В1
В2
В3
В4
В5
3
10
10
10
10
10
С1
35
100
Задания частей А и В считается выполненными верно, если в таблице указан вариант верного ответа задания из части А и правильный ответ задания из части В.
Задание части С считается выполненным верно, если абитуриент выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен
верный ответ.
Баллы
Критерии оценки выполнения задания С
35
Найден правильный ход решения, все его шаги выполнены верно с
необходимыми пояснениями и получен правильный ответ.
25
Ход решения правильный, даны необходимые пояснения, но допущена одна ошибка вычислительного характера.
15
Ход решения правильный, нет необходимых пояснения и допущена
одна ошибка вычислительного характера.
0
Другие случаи, не соответствующие указанным критериям.
6
Программа для подготовки к вступительным испытаниям по русскому языку
Программа содержит основные положения курса русского языка в средней общеобразовательной школе, необходимые для подготовки к вступительным испытаниям, по
основным разделам: фонетике и графике, морфемике и словообразованию, морфологии и
синтаксису, орфографии и пунктуации.
Содержание учебного материала
1. Фонетика и графика русского языка
Звуки и буквы. Система гласных звуков русского языка. Гласные ударные и безударные.
Система согласных звуков русского языка. Согласные глухие и звонкие, твердые и
мягкие.
2. Морфемика и словообразование
Виды морфем: корень, приставка, суффикс, окончание.
Основа слова и окончание. Разбор слова по составу.
3. Морфология
Самостоятельные части речи: имена существительные, прилагательные, числительные, местоимение, глагол, наречие.
Причастие и деепричастие.
Служебные части речи: предлоги, союзы, частицы.
4. Синтаксис.
Грамматическая основа предложения. Главные члены предложения: подлежащее и
сказуемое.
Типы подлежащего и сказуемого.
Второстепенные члены предложения: определение, дополнение, обстоятельство.
Простое предложение. Структурные типы простых предложений: односоставные и
двусоставные; распространенные и нераспространенные; полные и неполные.
Однородные члены предложение. Обобщающие слова при однородных членах.
Однородные и неоднородные определения. Обособленные члены предложения (определения, приложения, дополнения, обстоятельства). Вводные слова и вводные конструкции.
Обращение.
Сложное предложение.
Предложения сложносочиненные, сложноподчиненные и бессоюзные сложные.
Виды придаточных предложений.
5. Орфография
7
Употребление гласных букв О-Е после шипящих и Ц. Употребление Ь и Ъ. Правописание гласных в корнях. Правописание согласных в корнях.
Правописание приставок. Правописание суффиксов. Написание Н и НН в различных частях речи. Правописание падежных и родовых окончаний.
Слитное и раздельное написание НЕ с различными частями речи. Правописание
НЕ и НИ со словами. Правописание отрицательных местоимений и наречий.
Правописание словарных слов.
Слитное, дефисное, раздельное написание.
6. Пунктуация
Знаки препинания между подлежащим и сказуемым.
Знаки препинания при однородных членах без союзов. Знаки препинания при однородных членах с союзами.
Знаки препинания при обособленных определениях. Знаки препинания при
обособленных обстоятельствах.
Знаки препинания при вводных словах и конструкциях.
Знаки препинания в союзном сложном предложении.
Знаки препинания в бессоюзном сложном предложении.
Знаки препинания в сложном предложении с союзной и бессоюзной связью.
8