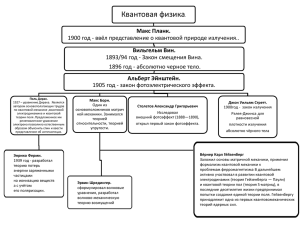
Вариационный принцип. В методах научного описания мира существует крайне ограниченный набор формальных способов вводить основные законы изменчивости исследуемых систем. Почти всегда такие законы постулируются или в форме “уравнений движения” или в форме экстремального принципа. Как правило, такие формулировки равносильны: если имеется уравнение движения, то из его вида выводится функционал, для которого исходное уравнение является уравнением Эйлера-Лагранжа соответствующей вариационной задачи, и наоборот. Однако, экстремальные принципы обладают большей эвристической и обобщающей силой. Почему камень, брошенный под углом к горизонту, движется по параболе? Можно указать на квадратичное уравнение равнопеременного движения тела. Само это уравнение представляет следствие второго закона Ньютона для тела, движущегося под действием постоянной силы. Впрочем, парабола может быть представлена и геодезической линией – решением уравнений Эйнштейна из общей теории относительности для движений в сильных полях и с высокими скоростями. Закон Ньютона и уравнения Эйнштейна могут быть выведены из принципа наименьшего действия с определенной формой экстремизируемого лагранжиана. Таким образом, существует несколько уровней объяснения явлений, каждый из которых может служить исходным постулатом. Однако, уравнения равнопеременного движения относятся лишь к узкому классу явлений, второй закон Ньютона описывает все движения в несильных полях и с невысокими скоростями, уравнения Эйнштейна лишены этих ограничений, а принцип наименьшего действия применим ко всем формам механического и электромагнитного движений. Обращаясь к таким теориям как, механика, геометрическая оптика, термодинамика, мы находим, что в центре каждой из них стоит принцип оптимальности (иначе его называют еще экстремальным или вариационным принципом) – утверждение о минимуме (или максимуме) некоторой величины (“функционала”, “целевой функции”). В оптике это – принцип скорейшего пути Ферма, в механике – принцип наименьшего действия, в термодинамике – принцип максимума энтропии. Из истории вариационных принципов Мысль о том, что “природа действует простейшим образом” (И. Бернулли), т.е. “наиболее экономно”, чрезвычайно стара и послужила источником многих научных идей и методических приемов. Еще И. Ньютона, в своих “Началах” говорил, что не должно принимать в природе иных причин сверх тех, которые истинны и достаточны для объяснения явлений, что природа ничего не дает напрасно, а было бы напрасным совершать многим то, что может быть сделано меньшим, что природа проста и не роскошествует излишними причинами вещей. Эта мысль была источником не только методологии Ньютона, но и чисто физической идеи о равенстве тяжелой и инертной масс – идеи, имевшей столь далекие последствия в общей теории относительности. Вскоре в математике и физике идея “экономии” в природе получила воплощение в развитии экстремальных принципов. Исторически первым таким принципом был “принцип Ферма” в геометрической оптике. П. Ферма предположил (1662 г.), что световой луч избирает не кратчайший путь, а путь наименьшего времени. Содержание всякого экстремального принципа является утверждение о минимуме (или максимуме) некоторой величины. Расчет траектории рассматривается как отыскание “истинного” пути среди всего множества возможных. Истинное движение отличается от всех возможных своей “оптимальностью”, т.е. тем, что для него некоторая величина достигает минимума (или максимума). Таким образом, основная проблема состоит в том, чтобы найти минимизируемую величину, выяснить ее конструкцию. Не всегда это так просто сделать, как в оптике: механике пришлось ждать около ста лет, прежде чем соответствующая конструкция была найдена для нее. 15-го апреля 1744 года П. Мопертюи представил Парижской Академии мемуар, в котором предлагался новый универсальный принцип механики – принцип наименьшего действия: истинное движение отличается от всех возможных тем, что для него величина действия минимальна. Само понятие действия – как произведения массы m, скорости V и пути S – было введено еще Г. Лейбницем, причем ему, видимо, даже было известно, что в “истинных” движениях действие имеет всегда минимальное значение. Однако Лейбниц воздержался от формулировки какого-либо общего принципа, связанного с этим свойством действия. Мопертюи же провозгласил его наиболее общим законом природы. Законы движения и покоя, по мнению Мопертюи, выведенные из этого принципа, являются точно теми, которые наблюдаются в природе, и мы можем восхищаться результатами его применения ко всем явлениям: движение животных, произрастание растений, вращение светил является только его следствиями. Мемуар вызвал среди ученых того времени ожесточенную полемику, далеко выходящую за рамки механики. Главным предметом спора было: являются ли события, происходящие в мире, причинно обусловленными или они телеологически направляются неким высшим разумом посредством “конечных причин”, т.е. целей? Окончательная формулировка принципа наименьшего действия, свободная от всякой “метафизики”, принадлежит Ж. Лагранжу. В 1760—1761 годах, когда Жозеф Луи Лагранж ввёл строгое понятие вариации функции, придал вариационному исчислению современный вид и распространил принцип наименьшего действия на произвольную механическую систему (то есть не только на свободные материальные точки). Тем самым было положено начало аналитической механике. Дальнейшее обобщение принципа осуществил Карл Густав Якоб Якоби в 1837 году — он рассмотрел проблему геометрически, как нахождение экстремалей вариационной задачи в конфигурационном пространстве с неевклидовой метрикой. В частности, Якоби указал, что при отсутствии внешних сил траектория системы представляет собой геодезическую линию в конфигурационном пространстве. В 1834—1835 годах Уильям Роуэн Гамильтон опубликовал ещё более общий вариационный принцип, из которого следовали все более ранние как частные случаи: Здесь L — лагранжиан динамической системы, — обобщённые координаты. Гамильтон положил этот принцип в основу своей «гамильтоновой механики» и дал решение вариационной задачи в виде «канонических уравнений». В ХХ веке революция, вызванная в физике теорией относительности и квантовой механикой, привела к пересмотру роли и места экстремальных принципов. Выяснилось, что понятия и законы, лежащие в основании ньютоновской физики, не являются абсолютными: они изменяются при переходе от одной системы отсчета к другой. Действительно, основными законами природы могут считаться лишь те, которые остаются неизменными в любой системе отсчета. Оказалось, что этому требованию отвечают лишь экстремальные принципы. Подход Гамильтона оказался универсальным и высокоэффективным в математических моделях физики, особенно для квантовой механики. Его эвристическая сила была подтверждена при создании Общей теории относительности, когда Давид Гильберт применил гамильтонов принцип для вывода окончательных уравнений гравитационного поля (1915 год). Можно считать, что в настоящее время этот спор решен окончательно: основные законы физики (а весьма вероятно, что и любой другой науки) должны иметь экстремальную форму. Все экстремальные принципы можно свести к общей форме: действительное движение или состояние системы отличается от всех возможных при данных граничных условиях тем, что некий функционал, характеризующий систему в целом, стационарен и принимает экстремальное значение. Другими словами, любая система ведёт себя так, чтобы одна из ее основных характеристик принимала минимальное или максимальное значение из всех возможных. Во многих экстремальных принципах выражается через разность двух энергетических характеристик системы. Например, минимум разности кинетический и потенциальной энергии в принципе Гамильтона Фейнман полушутя объяснял равновесием между желанием раздобыть как можно больше потенциальной энергии и желанием как можно сильней уменьшить количество кинетический энергии . Для электромагнитного поля минимизируется разность квадратов напряженностей электрического и магнитного полей. В универсальном экстремальном принципе термодинамики И. Дьярмати максимизируется разность производства энтропии и потенциалов рассеивания. Одна из возможных причин распространенности ПНД в том, что он описывает переход энергии из одного вида в другой, другая в том, что лагранжиан не зависит от преобразований пространства-времени. По мнению Фейнмана, фундаментальные физические законы могут быть выражены в виде ПНД. Л.С. Полак считал, что принцип Гамильтона выражает некоторое свойство неорганической природы, общее ряду форм движения. В.А. Ассеев указывает на то, что экстремальные принципы почти невозможно вывести из более общих принципов и законов, так как в общей формулировке они сами являются предельно общими. Л. С. Полак писал, что формула закона сохранения энергии может быть выведена из принципа Гамильтона, обратное же без дополнительных предположений невозможно. Глубже и полнее всего физический смысл принципа Гамильтона выражает теорема Э. Нетер, связывающая свойства симметрии и сохранения с действием. Фейнман считал, что связь между законами симметрии и законами сохранения объясняется законами квантовой механики, выраженными через ПНД. Существует аналогия принципа Гамильтона с законом, говорящим, что всякая система стремится к состоянию с минимумом потенциальной энергии. Например, принцип минимума полной энергии поля говорит, что «правильное поле и есть то единственное, которое из всех полей, получаемых как градиент потенциала, отличается наименьшей полной энергией». Это же поле отличается минимальной величиной действия. Вариационный принцип минимума потенциальной энергии лежит в основе исследования задач устойчивого равновесия, и применим, кроме прочего, ко второму началу термодинамики. В неравновесной термодинамике уже общепринято, что экстремумы термодинамических потенциалов (в том числе максимум энтропии) задают конечные «состоянияаттракторы, к которым самопроизвольно стремится система». ПНД одинаково эффективен для описания детерминистических процессов механики, статистических процессов термодинамики и вероятностных процессов квантовой механики? По словам Э. Маха, ПНД говорит лишь, что в соответствующих случаях происходит только то, что при данных условиях может происходить, что им определено и притом однозначно. Однако, критикуя гипотезу о всеобщности экстремальных принципов, И. Пригожин писал, что природа не может быть всемогущим калькулятором, и в ней нет упорядоченной истории. Одновременно Пригожин абсолютизировал экстремальный принцип синергетики, согласно которому в диссипативных системах поиск максимальной устойчивости играет роль естественного отбора. Фейнман предположил, что квантовая частица одновременно движется по всем возможным траекториям, чьи амплитуды вероятности складываются так, что максимальная вероятность падает на узкий пучок траекторий вокруг действительного пути, для которого вариация действия равна нулю. Этот подход Фейнман распространял и на обычные объекты. Таким образом, каждый раз, когда мы идем через комнату, наше тело заблаговременно «обнюхивает» все возможные пути, даже те, что ведут к далеким квазарам, а затем все их складывает. Вариацио́нное исчисле́ние Вариацио́нное исчисле́ние формулируется как — раздел анализа, в котором изучаются вариации функционалов. Ещё в античные времена появились первые вариационные проблемы, относящиеся к категории изопериметрических задач — например, задача Дидоны. Древнегреческим математикам уже было известно: 1. Из всех фигур с заданным периметром наибольшую площадь имеет круг. 2. Из всех многоугольников с заданным числом сторон и заданным периметром наибольшую площадь имеет правильный многоугольник. 3. Из всех тел с заданной площадью поверхности наибольший объём имеет шар. Аналогичную задачу для шаровых сегментов решил Архимед, а Зенодор во II веке до н. э. написал книгу «Об изопериметрических фигурах» (сохранились обширные цитаты из неё в трудах других авторов). Основными формулами вариационного исчисления являются уравне́ния Э́йлера — Лагра́нжа основаные на принципе наименьшего (стационарного) действия (принцип Гамильтона) — система движется по траектории, которая соответствует минимальному действию (хотя бы в некоторой малой окрестности множества возможных траекторий). Действием S называют интеграл по времени от лагранжиана при заданной траектории. Под стационарностью подразумевается, что действие не меняется в первом порядке малости при бесконечно малом изменении траектории, с закреплёнными начальной и конечной точками. Принцип Гамильтона запишется в виде Любая такая траектория называется прямым путём между двумя точками. Все остальные пути называются окольными. Уравнения полученные Леонардом Эйлером и Жозефом-Луи Лагранжем в 1750-х годах широко используются для вычисления траекторий в механике. В теоретической физике вообще - это (классические) уравнения движения в контексте получения их из написанного явно выражения для лагранжиана. Нахождения из этих уравнений экстремума функционала в некотором смысле аналогично использованию теоремы дифференциального исчисления, утверждающей, что лишь в точке, где первая производная функции обращается в ноль, гладкая функция может иметь экстремум. Механическая система характеризуется обобщёнными координатами и обобщёнными скоростями . Механической системе ставится в соответствие функция Лагранжа - лагранжиан, зависящая от обобщённых координат и скоростей, и, возможно, непосредственно от времени . Функция Лагранжа для классической механики вводится в виде разности между кинетической энергией и потенциальной энергией. Интеграл по времени от лагранжиана при заданной траектории называют действием S: Если функционал S достигает для лагранжиана экстремума то должно выполняться обыкновенное дифференциальное уравнение которое и называется уравнением Эйлера — Лагранжа. Рассмотрим простейший пример вариационного исчисления: найти кратчайший путь между двумя точками плоскости. Ответом, очевидно, является отрезок, соединяющий эти точки. Попробуем получить его с помощью уравнения Эйлера — Лагранжа в предположении, что кратчайший путь существует и является гладкой кривой. Пусть точки, которые надо соединить, имеют координаты (a,c) и (b,d). Тогда длина пути y(x), соединяющего эти точки, может быть записана следующим образом: Уравнение Эйлера — Лагранжа для этого функционала принимает вид: откуда получаем, что Таким образом, получаем прямую линию. Учитывая, что y(a)=c и y(b)=d, т. е. что она проходит через исходные точки, получаем верный ответ: отрезок, соединяющий точки. Примеры Лагранжианов Электромагнитный лагранжиан В общем случае лагранжиан в лагранжевой механике равен где T — кинетическая энергия и V — потенциальная энергия. Для заряженной частицы с массой m, зарядом q и скоростью v, находящейся в электромагнитном поле со скалярным потенциалом φ и векторным потенциалом A, кинетическая энергия задаётся выражением а потенциальная энергия: где c — скорость света. Тогда электромагнитный лагранжиан запишется в виде Лагранжиан квантовой электродинамики Плотность лагранжиана для КЭД где ψ — биспинор, — его дираковское сопряжение, — тензор электромагнитного поля, D — калибровочная ковариантная производная, и — обозначение Фейнмана для . Лагранжиан Дирака Плотность лагранжиана для дираковского поля . Лагранжиан квантовой хромодинамики Плотность лагранжиана для квантовой хромодинамики где — калибровочная ковариантная производная КХД, и тензор напряжённости глюонного поля. — Используемая литература: 1. Вариационные принципы в научном знании* Г.А. Голицын, А.П. Левич http://www.chronos.msu.ru/old/RREPORTS/golitsyn_variatsionnye/golitsyn _variatsionnye.htm 2. https://ru.wikipedia.org/wiki/Вариационный_метод 3. https://ru.wikipedia.org/wiki/Вариационные_принципы 4. https://science.wikia.org/ru/wiki/Лагранжиан 5. https://ru.wikipedia.org/wiki/Лагранжева механика 6. https://ru.wikipedia.org/wiki/Уравнение_Эйлера_—_Лагранжа 7. Философские и научные проблемы принципа наименьшего действия. Терехович В. Э. УДК 116:53.02:531.011