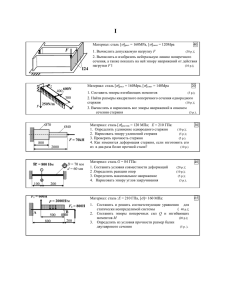
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования “Ивановский государственный архитектурно-строительный университет” Кафедра строительной механики ПЕРЕМЕЩЕНИЕ ПЛОСКИХ СТЕРЖНЕВЫХ СИСТЕМ Методические указания и контрольные задания по курсам «Строительная механика» и «Сопротивление материалов» для студентов заочного отделения Иваново 2007 Составитель Ю.А.Федоров, В.Д. Кондратенко УДК 624.04 Перемещение плоских стержневых систем: Методические указания и контрольные задания по курсам «Строительная механика» и «Сопротивление материалов»/ Иван. гос. архит-строит. ун-т.; сост. Ю.А.Федоров, В.Д. Кондратенко. - Иваново, 2000. – 37 с. В настоящих методических указаниях приведено содержание индивидуальной расчетно-проектировочной работы по определению перемещений в плоских стержневых системах при различных нагрузках, а также изложены основные теоретические положения и сведения, рассмотрен пример выполнения работы. Методические указания предназначены для студентов-заочников специальности 290300 - «Промышленное и гражданское строительство», но могут использоваться студентами дневной и заочной форм обучения и других строительных специальностей. Методические указания рассмотрены и утверждены на заседании кафедры механики. Ил. 24 Табл. 2 Библиогр.: 4 назв. 2 ВВЕДЕНИЕ Строительная механика – одна из базовых дисциплин в подготовке инженеров-строителей и служит основой для изучения курсов металлических, железобетонных, деревянных конструкций и их проектирования. Строительная механика – это наука о методах расчета сооружений на прочность, жесткость и устойчивость, и целью ее изучения является овладение этими методами. Выполнение индивидуальных домашних расчетно-проектировочных работ служит одним из основных способов усвоения студентом теоретических положений. Уметь решать задачи строительной механики – значит уметь проектировать сооружения, оценивать их прочность и надежность. Настоящие методические указания, предназначенные для студентовзаочников строительных специальностей, содержат основные теоретические положения по теме «Определение перемещений в плоских статически определимых стержневых системах», примеры решения задач, а также комплект вариантов задач по заданной теме с текстом задания и таблицей исходных данных. Методические указания имеют также своей целью показать объем задания, порядок решения задач, дать пример оформления задания. Прежде чем приступать к разбору примера, помещенного в указаниях, и выполнению домашнего задания, студент должен проработать и усвоить соответствующие теоретические положения, изучить общий порядок решения задач по учебникам и учебным пособиям. Без изучения теории приступать к самостоятельному решению задач невозможно, так как только знание теории дает возможность решать любые задачи во всем их многообразии. Определение перемещений является основным этапом при расчете на жесткость упругих стержневых систем, а также при расчете статически неопределимых систем. Поэтому изучение данной темы имеет большое значение для успешного освоения второй части курса. Приступая к изучению темы, следует внимательно разобрать теоремы о взаимности работ и взаимности перемещений и общую формулу Мора для определения перемещений от различных воздействий. Важное практическое значение при вычислении интеграла Мора имеет способ Верещагина. Для его успешного усвоения очень важно приобрести навыки построения эпюр изгибающих моментов в статически определимых системах и взаимного их «перемножения», обратив внимание на технику деления сложных эпюр на части. 3 1. ОБЩИЕ ТРЕБОВАНИЯ И УКАЗАНИЯ Домашнее задание должно выполняться в полном соответствии с требованиями и указаниями, изложенными ниже. Исходные данные для решения задач и номер схемы выбираются студентом из таблицы вариантов в соответствии, с его личным учебным шифром (номером зачетной книжки). Шифром считаются три последние цифры. Таблица вариантов разделена на три части. Для получения исходных данных надо выписать из таблицы три строчки: одну, отвечающую первой цифре шифра, вторую, отвечающую второй (средней) цифре, и третью, отвечающую последней - третьей цифре шифра. Работы, выполненные не по шифру и не в соответствии с таблицей исходных данных, не зачитываются и возвращаются без рассмотрения. Контрольная работа должна выполняться на одном листе стандартного формата, с размещением на нем всех чертежей и расчетов или оформляться в виде тетради. Перед решением каждой задачи необходимо вычертить заданную схему и указать на ней все размеры и нагрузки. Схемы и графики рекомендуется выполнять карандашом в строго выбранных масштабах с помощью чертежных инструментов. Характерные ординаты графиков рекомендуется отмечать цветным карандашом. На схемах следует проставить как буквенные обозначения, так и числовые значения размеров, нагрузок и опорных реакций с указанием размерностей. На графиках следует проставлять значения характерных ординат с указанием размерностей. Каждый пункт расчета должен иметь подзаголовок, указывающий содержание пункта. При вычислениях требуется исходное выражение записать сначала в буквенном виде и только после этого подставить численные значения. Если при выполнении вычислений производятся какие-либо сокращения, то зачеркивание сокращаемых величин не допускается. При расчете не следует оперировать с большим числом цифр. Рекомендуется соблюдать правила приближенных вычислений с точность до трех значащих цифр, с указанием размерностей. Все расчеты должны сопровождаться краткими и последовательными (без сокращения слов) пояснениями. Получив после рецензирования контрольную работу, студент обязан выполнить все указанные преподавателем исправления и дополнения, даже если работа зачтена. В случае незачета работы необходимо внести требуемые исправления на том же листе (если позволяет место) или на отдельном и представить всю работу целиком на повторную рецензию. Нельзя стирать или заклеивать отмеченные преподавателем ошибки, а также вырывать листы с замечаниями. 4 2. СОДЕРЖАНИЕ ЗАДАНИЯ И УКАЗАНИЯ К ВЫПОЛНЕНИЮ Указания. В задаче № 5 определение перемещения в балке следует выполнять по формуле Мора, вычисляя интегралы по правилу Верещагина. Строить эпюры изгибающих моментов (грузовые и единичные) следует со стороны растянутых волокон, сопровождая построение расчетами. Сложные эпюры для «умножения» их на единичные рекомендуется делить на части, чтобы обеспечить определение их площади и положение центров тяжести. Можно определить перемещения отдельно от силы Р и нагрузки q с последующим сложением результатов. В задаче № 6, поскольку жесткости стержней различны и заданы только их соотношения (для вcex стержней Е=const), искомые перемещения должны быть выражены через EJ1 или EJ2. При решении данной задачи полезно и весьма эффективно применять матричную форму расчета. ЗАДАЧА № 5 Определение перемещений в статически определимой балке Для заданной статически определимой балки (рис.1), с выбранными согласно шифру из табл.1 схемой балки, ее размерами и нагрузкой, требуется определить прогиб или угол поворота одного из сечений. Таблица 1 Первая цифра шифра ℓ, 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 0 10,0 8,0 9,6 12,0 12,4 13,0 14,0 15,0 16,0 18,0 1,0 1,2 1,6 2,0 2,4 2,8 3,0 3,6 5,0 4,0 1 2 3 4 5 6 7 8 9 0 4,0 4,5 5,0 3,6 2,0 3,2 8,0 6,0 3,0 2,0 1 2 3 1 2 3 1 2 3 1 1 2 3 4 5 6 7 6 9 0 Прогиб Прогиб Прогиб Прогиб Прогиб Угол поворота Угол поворота Угол поворота Угол поворота Угол поворота м q, Вторая Р, № Последняя кН/м цифра кН сечения цифра шифра шифра (№ схемы) 5 Вид перемещений 1 6 Р 2 1 ℓ/2 2 ℓ/4 Р q ℓ/2 3 ℓ/4 7 Р 1 8 ℓ/2 Р q 2 1 ℓ/2 4 ℓ/2 ℓ/2 ℓ/2 ℓ/4 3 2 3 ℓ/4 ℓ/2 ℓ/2 q ℓ/4 ℓ/4 2 3 2 ℓ/4 ℓ/4 q ℓ/4 q 1 3 Р 1 3 ℓ/4 2 1 ℓ/2 Р q ℓ/2 3 ℓ/2 ℓ/2 ℓ/2 ℓ/4 ℓ/4 9 Р ℓ/3 ℓ/3 ℓ/3 ℓ/3 q 1 3 2 1 Р q 2 ℓ/4 ℓ/3 ℓ/4 3 ℓ/4 ℓ/2 0 5 Р ℓ/2 ℓ/2 ℓ/3 ℓ/4 ℓ/2 Рис. 1 6 Р 2 1 3 2 1 ℓ/2 q q 3 ℓ/4 ℓ/4 ℓ/4 q h/2 1 J2 h/2 J1 ℓ/2 J2 1 J2 q J1 2 ℓ ℓ 3 J2 J2 h/3 h/4 h/4 q 2 ℓ Р 3 J2 J1 q J2 q ℓ/2 J2 ℓ/4 J2 2 q 3 ℓ Рис. 2 7 ℓ/2 ℓ 1 h/2 J1 0 Р h/2 h/3 3 Р 2 J2 1 h ℓ/4 J1 J1 ℓ Р ℓ 3 h/2 2 J1 8 h/2 7 ℓ/2 q 3 q 1 2 J2 1 J2 J2 h/2 J2 h/2 h/2 h/2 h/2 J1 1 9 1 J1 J2 6 Р Р 3 ℓ/2 J2 2 q ℓ ℓ 5 3 2 ℓ/2 3 h/2 h/2 q h/3 2 h/2 h/2 J1 h/3 h/2 1 3 ℓ 4 Р 1 Р J1 J2 h/2 ℓ/2 J1 h 2 Р Р 2 3 h/3 1 ЗАДАЧА № 6 Определение перемещений в статически определимой раме Для заданной статически определимой рамы (рис.2), с выбранными согласно шифру из табл.2 схемой рамы, ее размерами и нагрузкой требуется определить горизонтальное перемещение или угол поворота одного из сечений. Таблица 2 Первая ℓ, q, Вторая Р, h, № Последняя Вид перемещения, цифра м кН/ цифра кН м сече- цифра шифра J1:J2 шифра шифра ния (№ схемы) м 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 9,0 9,5 8,0 8,5 5,0 5,5 6,0 7,5 6,2 6,5 1,0 1,2 1,5 1,8 2,0 2,4 3,0 2,5 3,2 3,5 1 2 3 4 5 6 7 8 9 0 9 2 5 4 3 10 7 8 I 6 6,0 5,5 5,0 9,5 9,0 8,5 8,0 6,5 10,0 7,0 1 2 3 1 2 3 1 2 3 1 1 2 3 4 5 6 7 8 9 0 Угол поворота 1:2 Угол поворота 2:1 Угол поворота 1:3 Угол поворота 3:1 Угол поворота 2:3 Гориз. смещение 3:2 Гориз. смещение 3:5 Гориз. смещение 5:3 Гориз. смещение 3:4 Гориз. смещение 4:3 3. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ 3.1. Работа внешних и внутренних сил В процессе приложения внешних нагрузок к упругой системе, ее элементы выходят из состояния покоя и, перемещаясь, приобретают некоторые скорости и ускорения, величина которых зависит от скорости возрастания нагрузки. При медленном возрастании нагрузки силы инерции, пропорциональные ускорению перемещающихся элементов, будут невелики по сравнению с величиной нагрузки, и ими можно пренебречь. Такое плавное (постепенное) приложение нагрузки называется статическим. Внешние нагрузки, в процессе их приложения совершают работу на перемещениях системы ими вызванных. Полагаем, что материал упругой системы удовлетворяет закону Гука, деформации системы малы и справедлив принцип независимости действия сил. Следовательно, перемещения отдельных точек конструкции прямо пропорциональны величине, вызывающей их нагрузки, т.е. (1) u P, где u - перемещение по направлению действия нагрузки Р, - коэффициент, зависящий от материала, схемы и размеров сооружения. Увеличим нагрузку Р на бесконечно малую величину d Р. Это прира8 щение нагрузки вызовет дополнительное перемещение на величину du. Тогда работа, совершенная нагрузкой в процессе ее увеличения (Р + dР) на дополнительном перемещении, ею вызванном (du) dW (P dР) du . (2) Отбрасывая бесконечно малые второго порядка малости и учитывая (1), получим dW P du Р dР . Интегрируя это выражение в пределах полного изменения нагрузки от нуля до ее конечного значения F, получим F F 1 W Р dР Р dР F2 . 2 0 0 Учитывая, что - конечное значение перемещения, вызванное F конечным значением нагрузки, то 1 (3) W F . 2 Итак, работа, совершенная нагрузкой в процессе ее статического приложения, равна половине произведения конечного значения нагрузки (F) на конечное значение перемещения (∆), ею вызванного. При этом ∆ - перемещение точки приложения нагрузки в направлении нагрузки. Под термином «нагрузка» понимается любое внешнее воздействие (сосредоточенная сила F, сосредоточенный момент m и др.), а под термином «перемещение» понимается тот вид перемещения, на котором данный вид нагрузки совершает работу (линейное перемещение в направлении силы, угловое перемещение и др.), т.е. перемещение, соответствующее конкретному виду нагрузки. При статическом нагружении сооружения группой нагрузок работа, ими совершенная, равна полусумме произведений конечного значения каждого вида нагрузки на конечные перемещения, соответствующие данному виду нагрузки, вызванные конечными значениями группы нагрузок 1 W Fi i . (4) 2 i Работа, совершенная внешними нагрузками в процессе их приложения, может быть вычислена через внутренние усилия (М, Q, N), возникающие в поперечных сечениях стержней под действием внешней нагрузки. Выделим из стержня бесконечно малый элемент dz (рис. 3). При нагрузках, действующих в одной плоскости, совпадающей с одной из главных плоскостей инерции поперечного сечения, на элемент dz будут действовать продольная сила N, изгибающий момент М и поперечная сила Q (рис. 3,б). Усилия N, M, Q, являющиеся внутренними усилиями для стержня, представляют собой внешнюю нагрузку для выделенного элемента dz. Поэтому работа W может быть вычислена как интегральная сумма работ, совершенных статически приложенными усилиями М, Q и N на соответствую9 щих им перемещениях элемента dz. Рассмотрим влияние каждого из этих усилий на элемент dz, полагая левое его сечение неподвижным. б) а) у F m M Q M z z N Q dz N dz Рис. 3 Под действием только продольной силы N (рис. 4,а) правое сечение переместится в результате удлинения элемента d z на величину (dz) = Ndz , EA где EА – жесткость стержня при растяжении (сжатии). ∆φ б) а) N dz M ∆(dz) dz Рис. 4 При этом продольная сила N в процессе статического приложения совершает работу 1 Ndz . (5) dWN N (dz) N 2 2EA Под действием изгибающего момента М (рис. 4,б) правое сечение повернется в результате изгиба элемента dz на угол Md z , EJ где EJ - жесткость стержня при изгибе. На этом угловом перемещении статически прикладываемый момент М совершает работу 1 Mdz dWM M M . (6) 2 2EJ Под действием поперечной силы Q (рис. 5,а), являющейся равнодействующей касательных напряжений (рис. 5,б), правое сечение сдвинется относительно левого на величину y γ dz 10 G dz , где γ - угол сдвига, G - модуль сдвига. Касательные напряжения при поперечном изгибе стержней определяются по формуле Журавского QS , bJ где S - статический момент части поперечного сечения, расположенной выше (или ниже) уровня y, на котором определяются касательные напряжения τ; b - ширина поперечного сечения на уровне y; J - момент инерции сечения относительно центральной оси х. а) γ б) у ∆у dz γ γ 1 у • z τ dz b ∆у z ∆у ∆у у ω dу dу у Q в) γ τ 0 dA dу у x ∆у ∆у Рис. 5 Работа, совершенная, касательными напряжениями τ при сдвиге правого конца элементарного слоя толщиной dy на величину ∆у, будет равна 1 1 Q 2 (S ) 2 dА у dА dz dА d z . 2 2 G 2Gb 2 J 2 Проинтегрировав полученное выражение по всей площади поперечного сечения А, получим работу, совершенную поперечной силой при статическом ее приложении Q2 (S )2 1 Q2dz (S )2 Q2d z . (7) dWQ dА dz dА 2 2 2 GJ 2 А b2 2GА А 2Gb J А (S )2 Здесь dА - безразмерный коэффициент, зависящий только J 2 А b2 от формы поперечного сечения. Так, например, для прямоугольного сечения = 1,2; для круглого – =10/9; для двутаврового – ≈A/Аст, где Аст – площадь поперечного сечения стенки двутавра. Q dz Обозначив у , можно dWQ представить в виде GА 1 1 Qdz dWQ Q у Q . 2 2 GА 11 При одновременном действии на элемент dz продольной силы N, изгибающего момента М и поперечной силы Q полная работа равна сумме работ от каждой силы в отдельности, поскольку каждое из перечисленных усилий не совершает работу на перемещениях, вызванных другими усилиями, т.е. 1 Mdz 1 Ndz 1 Qdz dW dWM dWN dWQ M N Q . 2 EJ 2 EA 2 GА Интегрируя полученное выражение в пределах стержня (участка стержня) и суммируя полученные результаты по всем стержням (участкам стержней), получим следующее выражение для работы внешних сил, записанное через внутренние усилия W i i 0 Mdz M 2EJ i i 0 Ndz N 2EA i Qdz . 2GА Q i 0 (8) В данном соотношении М, N, Q – внутренние усилия в поперечном сечении с координатой z i – того стержня, а множители Mdz/EJ , Ndz/EA , Qdz/GА – соответствующие им деформации элемента dz. Из полученной формулы следует, что 1) работа внешних сил – величина всегда положительная (подынегральные функции положительны); 2) работа внешних сил не зависит от последовательности приложения нагрузок, а зависит только от конечного значения внутренних усилий. 3.2. Теорема о взаимности работ Рассмотрим два состояния упругой системы, находящейся в равновесии. Пусть в одном состоянии на систему в точке «к» действует сосредоточенная сила Fк (рис. 6,а), а в другом состоянии на систему в точке « j » действует сосредоточенная сила Fj (рис. 6,б). В результате деформации системы все ее точки получат перемещения. a) б) Fк Fj j к к ∆кк ∆кj ∆jк «к»–ое состояние ∆jj «j»–ое состояние Рис. 6 В к–ом состоянии перемещение точки «к» обозначим ∆кк, а перемещение точки «j» – ∆jk. При статическом приложении сила Fк совершает работу Wкк 1 Fк 2 i кк i 0 М dz Мк к 2EJ i i 0 12 N dz Nк к 2EA i i 0 Qк Q к dz . 2GА (9) В j–ом состоянии перемещение точки «к» обозначим ∆кj, а перемещение точки «j»–∆jj. При статическом приложении сила Fj совершает работу i i i М jdz N jdz Q jdz 1 Wjj Fj jj Мj Nj Qj . (10) 2 2EJ 2EA i 0 2GА i 0 i 0 Рассмотрим статическое нагружение системы силами Fк и Fj в следующей последовательности. Сначала прикладываем силу Fк, под действием которой стержень изогнется, и точки «к» и «j» получат перемещения ∆кк и ∆jк соответственно (рис. 7). Сила Fк при этом, возрастая от нуля до своего конечного значения, совершит работу Wкк Fк кк / 2 . к упругая линия от действия силы Fк Fк ∆кк j Fj ∆jк ∆кj ∆jj упругая линия от действия сил Fк и Fj Рис. 7 Затем приложим силу Fj, стержень получит дополнительные деформации, а точки « к » и « j » получат дополнительные перемещения - ∆кj и ∆jj соответственно. При этом сила Fj, возрастая от нуля до своего конечного значения, совершит работу на дополнительном перемещении ∆jj, равную Wjj Fjj jj / 2 , а сила Fк, оставаясь постоянной, совершит работу на дополнительном перемещении ∆кj , равную Wкj Fк кj . Полная работа, совершенная силами Fк и Fj в процессе их приложения 1 1 W Wкк Wjj Wкj Fк кк Fj jj Fк кj . (11) 2 2 С другой стороны работа, совершенная внешними силами в процессе их приложения, может быть вычислена согласно (4) 1 1 W Fк к Fj j , (12) 2 2 где ∆к = (∆кк +∆кj), ∆j = (∆jj +∆jк) - конечные полные значения перемещений точек «к» и «j», вызванных обеими силами Fк и Fj. Учитывая, что работа внешних сил не зависит от последовательности их приложения, и, приравнивая (11) и (12), получаем 1 1 1 1 Fк кк Fj jj Fк кj Fк ( кк Fj ( jj кj ) jк ) 2 2 2 2 или Fк кj Fj jк . (13) Здесь слева записана работа силы Fк на перемещении точки «к» – ∆кj, j 13 вызванном силой Fj, а справа записана работа силы Fj на перемещении точки « j » – ∆jк, вызванном силой Fк . Следовательно, Wкj Wjк . Таким образом, работа сил к – ого состояния на соответствующих им перемещениях j–ого состоянии (вызванных силами j–ого состояния) равна работе сил j–ого состояния на соответствующих им перемещениях к–ого состоянии (вызванных силами к–ого состояния). Полученный вывод носит название теоремы о взаимности работ или теоремы Бетти. j 3.3. Формула перемещений (интеграл Мора) Работа нагрузок к–ого состояния на соответствующих им перемещениях j–ого состояния, равная Wкj Fк кj может быть выражена через внутренние усилия (изгибающие моменты, продольные и поперечные силы), возникающие в к–ом и j–ом состояниях системы. Из (11) получаем Wкj W Wкк Wjj , где W - полная работа, совершаемая статическими нагрузками Fк и Fj в процессе их приложения, Wкк и Wjj - работа, совершаемая нагрузками Fк и Fj при их раздельном приложении, определяется согласно (9) и (10) соответственно. Полную работу, совершенную нагрузками Fк и Fj в процессе их приложения, согласно (8) можно записать в виде i (М к М j ) 2 dz N j ) 2 dz i (N к (Qк i Q j ) 2 dz , (14) 2EJ 2EA 2GА i 0 i 0 i 0 где Мк, Nк, Qк - внутренние усилия в стержнях системы в к–ом состоянии (от нагрузок - Fк), Мj, Nj, Qj внутренние усилия в стержнях в j–ом состоянии (от нагрузок - Fj), а суммы (Мк+Мj), (Qк+Qj), представляют собой внутренние усилия в стержнях системы, при одновременном действии нагрузок Fк и Fj . Вычитая из выражения (14) соотношения (9) и (10), после несложных алгебраических преобразований получаем W Wкj i Мк М jdz i Nк N jdz i Qк Q jdz , (15) EJ EA GА i 0 i 0 i 0 Пусть к–ое состояние системы есть единичное состояние, т.е. система находится под действием одной единичной силы Fк=1, приложенной в точку «к». Обозначим внутренние усилия, возникающие при этом в стержнях, M к , N к , Qк и назовем их единичными внутренними усилиями. Пусть j–ое состояние системы есть состояние под действием любой заданной группы нагрузок. Обозначим возникающие при этом внутренние усилия в поперечных сечениях стержней М, N, Q. 14 Согласно (13) работа сил к–ого (единичного) состояния на перемещениях j–ого (заданного) состояния имеет вид Wкj Fк кj 1 кj . Записав Wкj через внутренние усилия в к–ом (единичном) и j–ом (заданном) состоянии, получим i i Мdz Ndz Qdz Wкj 1 кj Мк Nк Qк . (16) EJ EA GА 0 0 0 i i i Поскольку здесь кj – есть перемещение в направлении силы Fк = 1 точки «к» системы в результате ее деформации под действием заданных внешних нагрузок Fj, то полученное выражение (16) позволяет определить перемещение любой интересующей нас точки системы от действия любой внешней нагрузки, т.е. i i i Мdz Ndz Qdz М N Qк . (17) к к к EJ EA GА i 0 i 0 i 0 Полученное выражение носит название формулы перемещений или интеграла Мора. Здесь и везде далее состояние системы под действием внешних нагрузок будем называть "грузовым" состоянием, опуская индекс «j». Определение перемещений с помощью интеграла Мора производится в следующем порядке: 1. находятся выражения внутренних усилий М, N и Q в стержнях системы от заданной нагрузки как функции координаты z произвольного сечения; 2. по направлению искомого перемещения прикладывается соответствующая ему обобщенная единичная сила Fк=1 (при линейном перемещении сосредоточенная сила, при угле поворота - сосредоточенный момент); 3. определяются выражения единичных внутренних усилий Mк , N к и Qк в стержнях системы от единичной силы как функции координаты z произвольного сечения; 4. найденные выражения M, N, Q, Mк , N к , Qк подставляются в формулу перемещений и, суммируя результаты интегрирования в пределах каждого стержня (участка стержня), получают искомое перемещение. Если полученный результат положителен, то найденное перемещение совпадает с направлением приложенной единичной силы Fк=1, если результат вычисления отрицателен, то перемещение противоположно направлению единичной силы. В случае необходимости определения линейного взаимного перемещения точек «К » и «С» следует приложить две единичные сосредоточенные силы Fк=1 и Fс=1, направив их по линии КС (рис.8,б). При определении взаимного угла поворота двух сечений «К» и «С» следует приложить два единичных сосредоточенных момента тк и тс (рис. 8,в). i 15 q а) К С б) в) FK=1 К С FC=1 mK=1 К С mC=1 Рис. 8 Следует отметить, что относительный вклад сумм в выражении (17) не равноценен и зависит от вида деформации, который испытывают стержни системы. Не приводя здесь подробного анализа (его можно найти, например, в [1]), сообщим, что для систем, работающих преимущественно на изгиб - рамы, балки - основной вклад в величину перемещений от действия внешней нагрузки дает первое слагаемое, учитывающее влияние изгибающего момента в стержнях, т.е. с достаточной для практических расчетов точностью Мdz . (18) EJ 0 i Для систем, стержни которых работают на растяжение (сжатие) фермы, вантовые системы - основной вклад в величину перемещений дает второе слагаемое, учитывающее влияние продольных сил в стержнях, т.е. i к i Мк Ndz . EA 0 i Учитывая, что в таких конструкциях жесткость поперечного сечения (ЕА), продольная сила в единичном (Nк) и грузовом (N) состояниях, как правило, постоянны в пределах i–ого стержня, т.е. EA i = const, N к = const, к Nк N =const, то последнее соотношение примет вид N кi Ni i . к EA i i (19) Здесь N кi - продольная сила в i–ом стержне от действия единичной силы Fк=1, N i - продольная сила в i–ом стержне от действия заданной нагрузки, EA i - жесткость поперечного сечения при растяжении i–ого стержня, i - длина i–ого стержня. При определении перемещений в системах, элементы которых испытывают изгиб с растяжением (сжатием), причем влияние продольных сил 16 N на величину перемещения сопоставимо с влиянием изгибающего момента (например, арки), в соотношении (17) следует учитывать два слагаемых, а в ряде случаев и все три внутренних усилия (M, N и Q). Способы вычисления интеграла Мора 3.4. При определении перемещений в упругих системах необходимо вы Мdz . Для этого существуют различные EJ 0 способы: аналитический, графоаналитический (правило А.Н.Верещагина), способ численного интегрирования, матричный способ. числять интегралы вида i Мк 3.4.1. Аналитический способ вычисления интеграла Максвелла-Мора Этот способ называют способом непосредственного интегрирования. Им можно воспользоваться, если подынтегральная функция М к М/EJ принадлежит к числу интегрируемых, и, кроме того, эта функция и результат ее интегрирования имеет не слишком сложное выражение. Пример 1. Определить вертикальное перемещение сечения «К» (∆vк) рамы, изображенной на рис.9. Решение. q=5кН/м Согласно порядку определения перемещения с помощью интеграла Мора К 2EJ m=30кН Мdz JJ 3EJ М , к к м EJ J h=3м i i изложенного в п. 3.3.: 1) Рассмотрим заданное состояние рамы (рис. 10,а) и запишем выражения изгибающего момента М(z) в стержнях от заданной нагрузки как функцию продольной координаты z. ℓ=6 м Рис. 9 а) I q=5кН/м б) B К m=30кН м z 120 z z1 II ℓ=6 м А 120 30 II h=3м М Рис. 10 17 МI=(z) z1 МII=(z1) 120 Стержень KВ: 0 ≤ Z ≤ ℓ; МI ( z) Стержень ВА: 0 ≤ Z1 ≤ h; М II ( z1 ) z 2 m q 2 m qz 30 2,5z 2 (кНм) ; 120 (кНм) . Эпюра изгибающих моментов М представлена на рис. 10,б. 2) Рассмотрим единичное состояние рамы (рис. 11,а) и запишем выражения изгибающего момента Мк (z) от вертикальной единичной cилы Fк=1, приложенной в точку «К». 6 Fк=1 а) б) I 6 B К z1 МI=(z) z1 z z I II II h=3м МII=(z1) Мк ℓ=6 м 6 Рис. 11 Рис. 9 Стержень KВ: 0 ≤ Z ≤ ℓ; М кI ( z ) Fк z z II Стержень ВА: 0 ≤ Z1 ≤ h; М к ( z1 ) Fк 6 Эпюра единичных изгибающих моментов Мк представлена на рис. 11,б. 3) Подставляя полученные выражения изгибающих моментов в формулу Мора (18), получаем Мdz 1 I 1 h II I М М (z) М ( z )dz М к (z1 )М II ( z1 )dz1 vк к к I II i i 1 6 ( z) 2EJ 0 EJ EJ EJ 0 30 2,5z 2 dz 0 1 3 ( 6)( 120) dz1 3EJ 0 1395 (м). EJ Положительный результат означает, что перемещение сечения происходит в направлении приложенной единичной силы Fк =1, т.е. вниз. 3.4.2. Графоаналитический способ (правило Верещагина) Этот прием вычисления интегралов типа i М к Мdz был предложен в 0 1925 году студентом Московского института инженеров железнодорожного транспорта (МИИЖТ) А.Н. Верещагиным, именуемый с тех пор правилом Верещагина. Правило позволяет вычислить интегралы указанного типа при условиях: 1. стержни, образующие конструкцию, прямолинейны, 2. жесткость стержней на участках постоянна ЕJ = const, 3. одна из эпюр, входящих в подынтегральное выражение, прямолинейна. 18 Суть правила Верещагина состоит в том, что вычисление интегралов заменяется «перемножением» эпюр М и Мк (см. рис. 12). у M(z) dΩ=M(z)dz •C Ω • эп. М z a ℓ ЕJ=const dz z zc α эп. Мк ... уС MК(z)=z·tgα z Рис. 12 Интеграл Мора по длине стержня может быть преобразован к следующему виду М(z)dz 1 a 1 a Мк (z) М к ( z ) М(z) dz z tg d 0 поскольку EJ a 1 tg zd EJ a a zd a zc EJ a 1 tg EJ EJ a zc 1 EJ уc , - представляет собой статический момент пло- щади Ω (площади эпюры М (z)) относительно оси у, равный произведению площади Ω на расстояние Zc от центра тяжести фигуры Ω до оси у. Учитывая, что tg z c уc , получаем, что интеграл от произведения моментов М к и М по длине стержня равен произведению площади Ω эпюры М (кри- волинейной эпюры), на ординату у c эпюры М к (прямолинейной эпюры), взятую под центром тяжести площади Ω (криволинейной эпюры). Просуммировав результаты «перемножения» эпюр М и М к по всем стержням конструкции, получаем 1 i 1 (20) М М к dz у ci , к i i EJ i 0 i EJ i где EJi - жесткость i–ого стержня при изгибе; i - площадь эпюры М (эпю- ры изгибающих моментов от заданной нагрузки) на i–м стержне; уci - ордината эпюры М к (эпюры изгибающих моментов от единичной обобщенной силы, приложенной в точку «к»), взятая под центром тяжести эпюры М 19 (грузовой эпюры) на i–ом стержне. у ci > 0, если Произведение i i и уci имеют одинаковые знаки, т.е. эпюры М и М к расположены с одной стороны оси стержня; произведение i у ci < О, если i и уci имеют разные знаки, т.е. эпюры М и М к расположены с разных сторон от оси стержня. Таким образом, для вычисления интеграла Мора по правилу Верещагина необходимо уметь определять площади фигур, представляющих собой эпюру М, и положение центров тяжести этих фигур. При вычислении площади сложной фигуры (эпюры) она может быть разбита на простые фигуры, площади и положения центров тяжести которых известны. В таблице 3 приведены значения площадей и положение центров тяжести наиболее часто встречающихся фигур, а также приемы разбиения сложных фигур на простые. Таблица 3 Прямоугольник •С Треугольник •С t ==t Ω = ℓ·t A t Zc=ℓ/2 Ω ==t С• _ Ω = 23 ℓ·t t ℓ a t b D ℓ D A D b ℓ C E C D a B C a B A ℓ·a + 12_ ℓ·b ΩАВСD =ΩАВD+ΩАCD= 1_ 2 A 2 qℓ ___ t= 8 D B a a С• t ℓ Zc=2ℓ/3 Ω _ ℓ·t ==t Ω = 1 2 Zc=ℓ/2 ℓ Ω Параболический сегмент A b b D B C b B B C 2 C qℓ ___ E t= 8 ΩАВCED =ΩАВCD+ΩDEC _ ΩАВСD =ΩАDВ-ΩАBC= 12_ a·ℓ - 12b·ℓ 20 Проиллюстрируем процедуру применения правила Верещагина на примере. Пример 2. Определить вертикальное перемещение сечения «К» vк рамы, изображенной на рис. 9. Решение. Для определения искомого перемещения воспользуемся формулой Мора Мdz 1 Мк уci , vк i EJ EJ i i i i h/2 h/2 а интегралы вычислим по правилу Верещагина. 1. Рассмотрим заданное состояние (рис. 10,а) и построим эпюру изгибающих моментов М от заданной нагрузки (рис. 10,б). 2. Рассмотрим единичное состояние (рис. 11,а) и построим эпюру единичных изгибающих моментов М к от действия вертикальной силы Fк = 1, приложенной в точку «К» (рис. 11,б). 3. Вычислим интеграл Мора, «перемножая» эпюры М и М к по правилу Верещагина по участкам. Для "перемножения" эпюр М В´ М а) и М к на участке КВ предста´ b=120 вим сложную фигуру эпюры К´ М (рис. 13,а) как сумму параa=30 болического сегмента К'В' К В ℓ=6м площадью 1 с положительZc1=ℓ/2 б) В´ ными ординатами и трапеции К´ • С1 КК'В'В с отрицательными t=qℓ2/8 В´ Ω1 ординатами, состоящей из К´ b=120 двух треугольников КК'В и • С2 К'ВВ' площадью 3 И 2 соa=30 С3 • К Ω2 В Ω3 ответственно (рис. 13,б). Zc2=ℓ/3 Zc3=ℓ/3 Результат перемножения эпюр М и М к на участке d =6 КВ можно записать в виде в) 1 1 В К М У М Мdz [- 1 у c1 К С У 3 С к УС 1 2 г) 120 6 2EJ 0 2EJ В´ В В В´ 2 у c2 3 у c3 ] , Ω4 2 q 2 МК • где 1 - площадь 3 8 С4 УС 4 ´ параболического сегмента; А А 1 А´´ А´ b - площадь треу2 2 Рис. 13 гольника К'ВВ'; 21 1 1 2 1 a - площадь треугольника КК'В'; у c1 d , у c2 d , у c3 d 2 2 3 3 ординаты эпюры М к , взятые под центром тяжести i - ой фигуры, составляющей эпюру М, вычисляются из геометрических соображений. Для «перемножения» эпюр М и М к на участке ВА достаточно вычислить площадь прямоугольника 4 , представляющего собой эпюру М, и 3 умножить на ординату уc4 единичной эпюры М к , взятую под центром тяжести С4 эпюры М, т.е. посередине стойки h М к Мdz 4 у c4 . 0 Окончательно перемещение сечения «К» равно vк i i Мк Мdz EJ 1 i EJi i у 1 ci 2EJ 1 2 5 62 1 1 2 [ 6 6 6 120 6 2EJ 3 8 2 2 3 1 уc1 2 уc2 3 уc3 1 1 1 6 30 6] 120 6 6 2 3 3EJ 1 у 3EJ i ci 1395 ( м) . EJ 3.4.3. Приближенное вычисление интеграла Мора Существуют различные способы приближенного вычисления интегралов, основанные на разбиении интервала интегрирования на отрезки и замене подынтегрального выражения простыми функциями на каждом отрезке (способ прямоугольников, способ трапеций, способ квадратной параболы - способ Симпсона и др.). Согласно способу Симпсона при разбиении интервала интегрирования на два равных отрезка интеграл Мopa может быть вычислен следующим образом н н М ксрМ ср М кк М к Мdz М к М . (21) Мк 4 н ср к EJ 6 EJ EJ EJ 0 Здесь М кн , М кср , М кк - значения единичного изгибающего момента М к в начале, середине и конце стержня соответственно; М н , М ср , М к - значения изгибающего момента от заданной нагрузки М в начале, середине и конце стержня; EJ н , EJ ср , EJ к - жесткость стержня при изгибе в начале, середине и конце стержня соответственно. В случае если М к (z) - линейная функция, М(z) - степенная функция не выше 3-го порядка, ЕJ=const, то формула Симпсона дает точное значение интеграла. 22 Суммируя результаты интегрирования в пределах каждого участка, получаем следующее выражение для перемещения Мdz i (Мн Мн 4Мср Мср М к М к ) . (22) М к к кi i кi i кi i EJ i i i 6EJi Здесь, как и ранее, i - номер стержня. Продемонстрируем применение данного способа на примере. Пример 3. Определить вертикальное перемещение сечения «К» рамы, изображенной на рис. 9. Решение: Для определения искомого перемещения воспользуемся соотношением (22). Согласно порядку определения перемещений: 1. Рассматриваем заданное состояние (рис. 10,а) и, построив эпюру изгибающих моментов в стержнях ремы от заданной нагрузки М (рис. 14,а), определяем величины изгибающих моментов в начале, середине и конце каждого стержня. Стержень КВ: М Мк н 1 2 q 2 m Стержень ВА: М н 30кНм; М m 30 2,5 62 М ср 1 m q 2 2 ср 2 30 2,5 32 120 кНм . Мк m 1 2 q 2 30 2,5 62 120 кНм . к Мк = 6 к М =120 К Мн=120 н К Мн=30 Мср=52,5 В н Мк= 0 h/2 М 52,5 кНм; Мк Мср=120 ср Мк = 3 В Мк = 6 ср Мк = 6 h/2 А ℓ/2 ℓ/2 А к М =120 ℓ/2 ℓ/2 к Мк = 6 Рис. 14 2. Рассматриваем единичное состояние (рис. 11,а) и, построив эпюру единичных изгибающих моментов М к в стержнях рамы от единичной вертикальной силы Fк=1, приложенной в точку «К» (рис. 14,б), определяем величины единичных изгибающих моментов начале, середине и конце каждого стержня. Fк 3 м ; М кк Fк 6 м. Стержень КВ: М кн 0 ; М кср 2 23 Стержень ВА: М кн М кср М кк Fк 6 м. 3. Подставляем найденные значения в выражение (22) и определяем h н ср [М кIн М нI 4М кIср М ср М ккI М кI ] [М кII М нII 4М кII М ср vк I II I II 6EJ 6EJ 6 М ккII М кII ] [0 ( 30) 4 ( 3)( 52,5) ( 6)( 120)] 6 2EJ 3 1395 [( 6)( 120) 4 ( 6)( 120) ( 6)( 120)] ( м) . 6 3EJ EJ 3.4.4. Матричный способ определения перемещений Выражение (21) можно записать в виде произведения трех матриц н н МксрМ ср Мкк М к Мdz Мк М (23) Мк 4 Мкт LМ , н ср к EJ 6 EJ EJ EJ 0 если значения изгибающих моментов от единичной силы и заданной нагрузки в начале, середине и конце каждого стержня представить в виде трехмерного вектора 1 Мк М кн М кср , М М кк EJ н Мн М ср , Мк а L 6 0 0 4 EJ 0 ср 0 0 0 - матрица податли- 1 EJ к вости стержня; М кт [ М кн , М кср , М кк ] - матрица-строка, транспониронный вектор единичных изгибающих моментов. Просуммировав выражение (23) по всем стержням конструкции, получим матричную форму записи для определения перемещений i Мdz т М М L М (24) к к кi i i . EJ i 0 i Продемонстрируем данный способ для определения перемещения сечения «К» рамы, изображенной на рис. 9 (пример 3). 1. Рассмотрим заданное состояние (рис. 10,а), определим величины изгибающих моментов в начале, середине и конце каждого стержня (рис. 14,а). 2. Рассмотрим единичное состояние (рис. 11,а), определим величины единичных изгибающих моментов в начале, середине и конце каждого стержня 24 (рис. 14,б) от действия вертикальной силы Fк=1, приложенной в точку «К». 3. Сформируем векторы единичных и грузовых моментов и матрицы податливости для каждого стержня ср т н к [ М кI , М кI , М кI ] [0, 3, 6] , Стержень КВ: М кI 1 МI М нI М ср I к МI 0 EJ нI 30 52,5 , LI 120 6 4 0 EJ ср I 0 т Стержень ВА: М кII М II М ср II М кII 0 100 6 0 40 ; 6 2EJ 0 01 1 0 EJ кI к [М нкII , М ср кII , М кII ] [ 6, 6, 6] , 1 М нII 0 120 120 , LII 120 0 EJ нII h 6 0 4 0 0 EJ ср II 0 0 100 3 0 40 . 6 3EJ 0 01 1 EJ кII 4. Определяем искомое перемещение, перемножая матрицы согласно выражению (24) Мdz 1 т т т М М L М М L М М L М vк к кi i i кI I I кII II II [0, 3, 6] EJ 2EJ i i i 10 0 040 0 01 30 52,5 120 ( 6)( 120 )] 10 0 1 [ 6, 6, 6] 040 6EJ 0 01 120 120 120 1 [0( 30) ( 3)( 4 52,5) 2EJ 1 1395 [( 6)( 120 ) ( 6)( 4 120 ) ( 6)( 120 )] ( м). 6EJ EJ 25 4. ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ Задача 1. Для заданной статически определимой балки (рис. I5) определить прогиб и угол поворота сечения 1. Принять ЕJ = const. q=0,8 кН/м F=10кН ℓ/2=3м ℓ/2=3м 1 d=3 в=1м м a=4м ℓ=6м Рис. 15 Решение. I. Определим прогиб сечения 1, используя формулу Мора (18), применяя для вычисления интегралов правило Верещагина (20) i Мdz EJ 1 у ci . 1 i EJ 0 i i i 1. В соответствии с порядком определения перемещении (см. п. 3.3.) рассмотрим заданное состояние (рис. 16,а) и построим эпюру изгибающих моментов М в балке от заданной нагрузки. а) Строим схему взаимодействия балок АС и CD (рис. 16,б). б) Строим эпюру М на балке СD - опорные реакции: RD q 0, RD q 0,8 3 2,4 кН ; mom C 0 , 2 2 mom D 0 , RС q 0, RС q 2,4 кН . 2 2 - изгибающие моменты в характерных точках: М С 0 , М D 0 ; М1 момент в середине М max RС q 2 8 q 2 24 в) Строим эпюру М на балке АС - опорные реакции: F R В qa( mom А 0 , 2 1 a a a 1 RB F q ( ) RC 10 2 2 2 a RА F qa mom В 0 , 2 2 1 aa a 1 4 RА F q RC 10 0,8 2 2 2 2 6 26 3,6 кНм . a ) R C ( a ) 0 , 2 4 6 4 0,8 (6 2) 2,4 13,27 кН ; 6 6 RC a 2,4 4 6 0, 2,33 кН . a) F=10кН А q=0,8 кН/м В ℓ/2=3м ℓ/2=3м q=0,8 кН/м б) F=10кН А 1 RA ℓ/2=3м ℓ/2=3м 2ℓ 32 в) б) АВ С RС ℓ=6м С5• • М С6 ℓ/2=3м 2,8 • 1 ℓ 1d 32 3 1d 3 d/2 __ F1=1 В К ℓ/2 d _ _ 3,6 Рис. 16 1 С __ RС уС4 F1=1 _ _ _ уС5 уС6 уС3 уС2 уС1 _ 3 1,5 RA RD • 7 1ℓ 32 ℓ/2 RB d=3м в=1м С4 •С2 •С 1 a) А D С RС 16 С3 2ℓ 32 ℓ=6м В К В D С 1 d=3м в=1м D RС М1 С RB RD Рис. 17 __ a) А m1=1 В К D С 1 _ б) А В 1 0,5 RA _ уС1 уС4 _ _ уС3 уС2 RС 1 RС М М´1 уС5 уС6 1 __ С m1=1 _ _ RB М1 Рис. 18 27 RD - изгибающие моменты в характерных точках: МА 0 , Мк R А 2,33 3 7 кНм ; М С 0 , 2 в М1 R С в qв 2,4 1 0,8 1 0,5 2,8 кНм , 2 а МВ R С а qа 2,4 4 0,8 4 2 16 кНм , 2 По полученным значениям строим эпюру М (рис. 16,б). 2. Рассмотрим единичное состояние (рис. 17,а) и построим эпюру единичных изгибающих моментов М1 от действия вертикальной силы F1 =1, приложенной в точку 1. а) Строим схему взаимодействия балок АС и CD (рис. 17,б). б) На балке СD эпюра М1 0 , т.к. балка СD не нагружена – в данном состоянии и R С R D 0 . в) Строим эпюру М1 на балке АС - опорные реакции: 1 1 mom А 0 , R В F1 ( d ) 0 , R B F1 ( d ) (6 3) 1,5 ; 6 1 1 mom В 0 , R А F1 d 0 , R А F1 d 13 0,5 . 6 - изгибающие моменты в характерных точках: МА 0 , МК RА 0,5 3 1,5 м , 2 МС 0 , F1 d 13 3 м. М1 0 , М В По полученным значениям строим эпюру М1 (рис. 17,б). 3. Определяем перемещение сечения 1, «перемножая» эпюры и по правилу Верещагина на участках АК, КВ и В1. Для «перемножения» эпюр, на участке КВ разобьем эпюру М на две фигуры (рис. 19): КВВ' площадью Ω2 с отрицательными ординатами (рис. 19,б) и КВК' площадью Ω3 с положительными ординатами (рис. 19,в). Чтобы «перемножить» эпюры на участке В1, разобьем эпюру М на три фигуры (рис. 20): - параболический сегмент В'G1' площадью Ω4 и положительными ординатами (рис. 20,б); - и два треугольника ВВ'1' площадью Ω5 и В11' площадью Ω6 с отрицательными ординатами (рис. 20,в). Определив с помощью таблицы 3 (стр. 21) положение центров тяжести фигур, составляющих эпюру М, вычисляем значения ординат усi единичной эпюры М1 , взятых под центрами тяжести этих фигур, из геомет28 рических соображений 2 2 КК 1,5 , (рис. 17,б) уС1 3 3 1 2 1 2 2 КК ВВ 1,5 3 , уС 3 КК (рис. 19,г) уС 2 3 3 3 3 3 1 1 2 2 ВВ 3 , уС 5 ВВ 3, (рис. 17,б; 20,г) уС 4 2 3 3 3 Окончательно i 1 0 i 4 М1 Мdz EJ у С4 5 1 i EJ i у С5 i у ci 1 у С1 2 уС 6 у С2 3 2 1 1,5 3, 3 3 1 1 ВВ 3. 3 3 у С3 1 1 2 1 1 2 [ 3 7 1,5 3 16 ( 1,5 3) EJ 2 3 2 3 3 у С6 ) 6 1 ( EJ 1 ВВ 3 1 2 1 2 32 1 1 2 1 1 78 3 7( 1,5 3) 0,8 3 3 3 16 3 3 2,8 3] ( м) . 2 3 3 3 8 2 2 3 2 3 EJ Положительный результат означает, что под действием заданной нагрузки сечение 1 перемещается в направлении приложенной единичной силы FК =1, т.е. вниз. а) В′ В′ а) 16 М К 7 К′ К в) К 7 К′ г) К′ 1,5 К 16 В Ω3 1ℓ 32 _ УС3 1′ G 1 б) В′ Ω2 • С2 С3• М • В ℓ/2 б) _ Ω4 •С4 G В′ 16 В В в) В′ 16 Ω5 С5 • В d/3 1ℓ 32 _ УС2 С6 d/2 • 1 2 qd ___ t= 8 1′ 2,8 1 Ω6 d/3 d=3м В′ 3 М1 В г) В′ 3 В Рис. 19 _ _ _ УС5 УС4 УС6 Рис. 20 29 _ 1 М1 II. Определим угол поворота сечения 1, используя правило Верещагина при вычислении интеграла Мора. Согласно порядку определения перемещения (см. п. 3.3.): 1. Рассматриваем заданное состояние (рис. 16,а) и строим эпюру изгибающих моментов М от заданной нагрузки (рис. 16,в). 2. Рассматриваем единичное состояние (рис. 18,а) и строим эпюру единичных изгибающих моментов М1 от действия единичного внешнего момента m1 =1, приложенного в точку 1. а) Строим схему взаимодействия балок АС и CD (рис. 16,б). б) На балке СD эпюра М1 0 , т.к. балка СD не нагружена – в данном состоянии и R С 0 . в) Строим эпюру М1 на балке АС - опорные реакции: m1 1 mom А 0 , R В m1 0 , ; RB 6 m1 1 . mom В 0 , R А m1 0 , RА 6 - изгибающие моменты в характерных точках: 1 1 МА 0 , МК RА 3 0,5 , М В RA 6 1 6 2 6 m1 1. М 1 лев 0 , М1АВ МС 0 , По полученным значениям строим эпюру М1 (рис. 18,б). 3. Определим угол поворота сечения 1, «перемножая» эпюры М и М1 по правилу Верещагина, предварительно разбив эпюру М на участках КВ и В1 на простые фигуры (см. рис. 19 и рис. 20) и определив ординаты усi единичной эпюры М1 , взятые под центрами тяжести фигур, составляющих эпюру М (рис. 18,б). 1 2 2 1 2 уС1 0,5 , уС 2 0,5 1 , уС 3 0,5 1 , уС 4 уС 5 уС 6 1 . 3 3 3 3 3 Окончательно i 1 i 4 0 у С4 М1 Мdz EJ 5 у С5 1 i EJ i 6 i у С6 ) у ci 1 ( EJ 1 у С1 2 у С2 3 у С3 1 1 2 1 1 2 [ 3 7 0,5 3 16 ( 0,5 1) EJ 2 3 2 3 3 1 2 1 2 32 1 1 36 3 7( 0,5 7) 0,8 31 3 16 1 3 2,8 1] ( рад) . 2 3 3 3 8 2 2 EJ Положительный результат означает, что под действием заданной нагрузки сечение 1 поворачивается в направлении единичного момента m1 =1, т.е. по часовой стрелке. 30 Задача 2. Для заданной статически определимой рамы (рис. 2I) определить горизонтальное перемещение и угол поворота сечения 1, ∆Х1, φ1. Решение. у F=6кН 1 Для определения искомых ___ q=4 кН h м величин воспользуемся интегра2 =3м 2EJ лом Мора в матричной форме (24). EJ h=3м I. Определим горизонтальное пе2 ремещение сечения 1. Согласно h порядку определения перемеще2 =3м ний: х 1. Рассмотрим заданное состояние ℓ/2=2м ℓ/2=2м (рис. 22,а) и построим эпюру изгибающих моментов М в стержРис. 21 нях рамы от заданной нагрузки. 242424 5 а) Определяем опорные реакции mom А 0 , R В h F qh 2 2 0, RВ 1 h2 F q 2 2 1 62 6 4 2 2 4 21 кН ; h h2 1 62 qh 0, RА q F 4 mom К 0 , R А F 2 2 2 4 2 2 Х 0, H A qh 4 6 24 кН . qh H A 0 , 1 6 15 кН ; 2 б) Определяем величину изгибающих моментов в характерных точках рамы: h h h q 24 3 1,5 54 кНм ; МА 0 , МD HA 2 2 4 21 2 42 кНм ; М В 0 , М1 0 , М G R B 2 По полученным значениям строим эпюру М (рис. 22,б). 2. Рассмотрим единичное состояние (рис. 23,а) и построим эпюру единичных изгибающих моментов М1 от действия единичной горизонтальной силы F1 =1, приложенной в точку 1. а) Определяем опорные реакции 3 3 mom А 0 , R В F1 h 0 , R В F1 2 2 3 3 mom К 0 , R А F1 h 0 , R А F1 2 2 Х 0, H A F1 H A F1 0 , 31 h 3 6 1 2 4 h 2,25 ; 1. 2,25 ; а) F=6кН кН q=4 ___ м G 2EJ C EJ D 1 б) h=3м 2 EJ А НА=24кН RВ=21кН RA=15кН _ б) 1 F1=1 h 2 =3м G C 6 4,5 3 НА=1 А RВ=2,25 _ 3 В • 1,5 6 h 2 =3м D М1 h 2 =3м К ℓ=4м RA=2,25кН Рис. 23 m1=1 а) 1 C D h 2 =3м В RВ=14 0,75 б) h 2 =3м G RА= 14 М 54 Рис. 22 а) НА=0 А 42 72 h 2 =3м • 57 К ℓ/2=2м ℓ/2=2м 72 h 2 =3м В 21 h 2 =3м • К ℓ=4м Рис. 24 32 0,5 0,25 _ М1 б) Определяем значения единичных изгибающих моментов в характерных точках рамы: МА 0 , МС НА h 1 6 6 , М В 0 , М1 0 , h МG RB F1 2,25 2 1 1,5 3. 2 4 По полученным значениям строим эпюру М1 (рис. 23,б). Анализ эпюр М и М1 показывает, что для определения искового перемещения необходимо вычислить интеграл Мора на четырех стержнях (участках стержней) АС, СG, G1, В1. 2. Для вычисления перемещения ∆Х1 , используя матричную форму записи интеграла Мора, необходимо сформировать: векторы единич ных моментов М 1 , используя эпюру М1 (рис. 23,б), векторы грузо вых моментов М , используя эпюру М (рис. 2,б) и матрицы податливостей L для каждого стержня (участка стержня). Элементы векторов М 1 и М представляют собой значения единичных и грузовых изгибающих моментов в начале, середине и конце каждого стержня (участка стержня). Элементы диагональной матрицы податливостей L представляют собой податливость при изгибе ℓ/EJ в начале, середине и конце каждого стержня. Стержень АС: h 0 0 н EJ М Мн 0 1 0 100 4h h М М ср 54 , М1 М1ср 3 , L 0 0 0 40 . EJ EJ 72 6 0 01 Мк М1к h 0 0 EJ h h h Здесь М ср Н А q 24 3 4 3 1,5 54 кНм - изгибающий 2 2 4 момент в середине стержня АС в грузовом состоянии (рис. 22,б), h М1ср НА 3 - изгибающий момент в середине стержня АС в еди2 ничном состоянии (рис. 23,б); Стержень СG: 1 0 0 н н М 2 ЕJ М 1 72 6 4 1 М М ср 57 , М1 М1ср 4,5 , L 0 0 . 2 ЕJ 42 3 Мк М1к 0 0 1 2ЕJ 33 3 F 21 3 6 1 57 кНм - изгибающий момент в 4 4 середине стержня G1 в грузовом состоянии (рис. 22,б), 9h М1ср R А HА 2,25 1 1 6,75 4,5 - изгибающий момент в се4 8 редине стержня СG в единичном состоянии (рис. 23,б); Здесь М ср 2 RB h 1 4 2 Стержень G1: М М н 2 42 М ср Мк 21 , 0 1,52 22 М1 М1н М1ср М1к 2,5 м - длина стержня СG. 3 1,5 , 0 L 2 0 0 2ЕJ 4 2 0 0 . 2ЕJ 0 0 2 2ЕJ 21 1 21 кНм - изгибающий момент в середине 4 стержня G1 в грузовом состоянии (рис. 22,б), h М1ср R В F1 2,25 1 1 0,75 1,5 м - изгибающий момент в 4 8 середине стержня G1 в единичном состоянии (рис. 23,б); Здесь М ср 2 RB 2 2 1,52 22 2,5 м - длина стержня G1. 2 Стержень 1В: М 0 , М1 0 , В соответствии с матричной формой записи формулы Мора 10 0 0 i Мdz h М1 М1тi Li М i [0, 3, 6] 0 4 0 54 Х1 EJ EJ i 0 i 0 0 1 72 h 4 1 0 0 72 1 0 0 42 1 2 [ 6, 4,5, 3] 0 4 0 57 [ 3, 1,5,0] 0 4 0 21 2EJ 2EJ 0 0 1 42 0 01 0 72 2,5 [ 6, 4,5, 3] 4 57 2EJ 42 42 2,5 [ 3, 1,5,0] 4 21 2EJ 0 2,5 ( 6 72 4,5 4 57 3 42 ) 2EJ 6 ( 3 4 54 6 72 ) EJ 2,5 ( 3 42 1,5 4 21) 2EJ 34 0 6 [0, 3, 6] 4 54 EJ 72 8775 ( м). EJ Отрицательный результат означает, что перемещение сечения 1 рамы под действием заданной нагрузки происходит в сторону противоположную направлению единичной силы F1 =1, т.е. вправо. II. Определим угол поворота сечения 1 рамы под действием заданной нагрузки. Согласно порядку определения перемещений: 1. Рассмотрим заданное состояние (рис. 22,а) и построим эпюру изгибающих моментов М в стержнях рамы от заданной нагрузки (рис. 22,б). 2. Рассмотрим единичное состояние (рис. 24,а) и построим эпюру единичных изгибающих моментов М1 в стержнях рамы от единичного внешнего момента m1 =1, приложенного в точку 1. а) Определяем опорные реакции (рис. 24,а): m1 1 mom А 0 , R В m1 0 , RB ; 4 m1 1 mom К 0 , R А m1 0 , RА . 4 Х 0, HA 0 . б) Определяем изгибающие моменты в характерных точках рамы: 1 МА 0 , МС 0 , МG RА 2 0,5 м , 2 4 1 М1AEB RА 4 1 , М1 прав 0 , М В 0 . 4 По полученным значениям строим эпюру М1 (рис. 24,б). 3. Для вычисления искомого угла поворота сформируем векторы единич ных моментов М 1 , используя эпюру М1 (рис. 24,б), для каждого стерж ня. Векторы грузовых моментов М и матрицы податливостей на каждом стержне были сформированы ранее при определении горизонтального перемещения сечения 1 рамы. Стержень АС: М1 0 ; Стержень 1В: М1 0 ; Стержень СG: 1 0 0 2 ЕJ М1н 0 72 4 1 М 57 , М1 М1ср 0,25 , L 0 0 . 2ЕJ 42 0,5 М1к 0 0 1 2ЕJ 1 RА 1 0,25 - изгибающий момент в середине Здесь М1ср 4 4 стержня СG в единичном состоянии – от действия единичного момен- 35 та m1 =1(рис. 24,б). Стержень G1: М1 М1н М1ср М1к 0,5 0,75 , 1 М 42 21 , 0 L 2 0 0 2ЕJ 4 2 0 0 . 2ЕJ 0 0 2 2ЕJ 3 1 3 0,75 - изгибающий момент в середине 4 4 стержня G1 в единичном состоянии – от действия единичного момента m1 =1 (рис. 24,а). Окончательно 1 0 0 72 i Мdz М1 М1iт Li М i [0, 0,25, 0,5] 1 0 4 0 57 1 EJ 2EJ i 0 i 0 0 1 42 Здесь М1ср RА 1 0 0 42 2 [ 0,5, 0,75, 1] 0 4 0 21 2EJ 0 01 0 42 2,5 [ 0,5, 0,75, 1] 4 21 2EJ 0 72 2,5 [0, 0,25, 0,5] 4 57 2EJ 42 2,5 ( 0,25 4 57 0,5 42) 2EJ 2,5 202 ,5 ( 0,5 42 0,75 4 21) ( рад). 2EJ EJ Отрицательный результат означает, что поворот сечения 1 под действием заданной нагрузки происходит в направлении противоположном единичному моменту m1, т.е. против часовой стрелки. БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Строительная механика / Под. ред. Даркова А.В. М.: Высшая школа, 1976. 600 с. 2. Киселев В.А. Строительная механика. Общий курс. М.:Стройиздат, 1986. 520 с. 3. Руководство к практическим занятиям по курсу строительной механики (статика стержневых систем) / Под ред. Г.К.Клейна М.: Высшая школа, 1980. 384 с. 4. Митропольский M.М. Строительная механика: Методические указания и контрольные задания. II-е изд. М.: Высшая школа, 1982. 63 с. 36