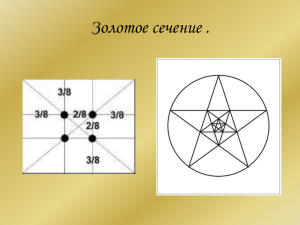
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный педагогический университет им. Л.Н. Толстого» Кафедра алгебры, математического анализа и геометрии КУРСОВАЯ РАБОТА по дисциплине Алгебра и геометрия: элементарная геометрия на тему: Золотое сечение и гармонизация пространства в архитектуре Выполнила: студентка 4 курса группы 120961 факультета МФиИ направления «Педагогическое образование» Илюшина Валерия Александровна Руководитель: доцент к.ф.-м.н., доцент Реброва Ирина Юрьевна Тула 2020 Цели и задачи Цель данной работы: провести обзор истории и математической сущности гармонии золотого сечения, и попытаться осмыслить ее роль в архитектуре, современной математике и современной жизни. Из цели вытекают следующие задачи: 1)Проанализировать литературу, выявить математическую сущность золотого сечения, выявить закономерности, принципы и свойства; 2)Выявить сущность архитектурной гармонии; 3)На основе архитектурного строения древности Парфенона проанализировать математическую сущность гармонии; 4) Привести примеры использования золотого сечения в архитектуре и интерьере; Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей a: b = b: c или с: b = b: а. Второе золотое сечение BC⊥AB, BC=AB/2 ω(C, BC)⋂AC=D ω2 (A, AD)⋂AB=E AE:EB=62:38 С∈ 𝐴𝐵, так что 𝐴𝐶: 𝐶𝐵 = 62: 38 CD⊥ 𝐴𝐵, CD=AB CE-биссектриса, такая что DE:AE=56:44 Правильный пятиугольник Точное деление окружности на 5 равных частей, описанное в 'Альмагесте' Птолемея. Ок 150 до н. э. (а). Приближенное построение пятиугольника по заданной стороне из 'Руководства к измерению' Дюрера 1525 (б). Цифрами обозначены последовательные положение ножки циркуля ΔBCD ∞ ΔАВС=>АВ: ВС=ВС:DB т.к. ВС = CD = AD то: Пусть AF = AD = 1, полагая DB = x и, следовательно АВ = 1 + х, тогда: Так как то мы окончательно находим: x = DB = AE = EF =...= φ, AD = DC = CB = AF = ... = 1, ED = EG = ...= = 1 - φ = φ2 Повторяя наши рассуждения для треугольника DGH, в котором DG = y, легко видеть, что стороны внутренней звезды будут равны φ3, а стороны ее внутреннего правильного пятиугольника - φ4 Последовательность правильных пятиугольников и вписанных в них звезд образует ряд золотого сечения: Ряд золотого сечения можно неограниченно продолжить и в сторону увеличения, и в общем виде ряд золотого сечения будет иметь вид или аддитивное свойство: Если продолжить стороны правильного пятиугольника до пересечения, то получим звезду, сторона которой х находится со стороной исходного пятиугольника AF = 1 в золотом отношении, т. е. 1/х = φ ⇒ 1/φ = (√5 + 1)/2 = Φ Именно благодаря аддитивному свойству ряд золотого сечения играет важную роль в архитектуре Ряд Фибоначчи и, пользуясь аддитивным свойством ряда, будем выражать степени Φn через Φ: коэффициенты при Φ, также, как и первые слагаемые, образуют последовательность натуральных чисел Некоторые представления коэффициента золотого сечения 1 2 3 Последовательности, в которых каждый член определяется как некоторая функция предыдущих, называются рекуррентными или возвратными. Архитектурные пропорции - это математика зодчего Пропорциональность является наиболее ярким, зримым, объективным и математически закономерным выражением архитектурной гармонии. Витрувий справедливо называет совершенными те сооружения, в которых достигнута "точная соразмерность" всех частей с основной мерой. И вот с тех пор "точную соразмерность", стали понимать в простейшем арифметическом смысле - как кратность всех частей сооружения основному модулю Модуль в архитектуре (от лат. modulus - мера) - это единица измерения, принимаемая для согласования размеров частей сооружения между собой и со всем сооружением. Иррациональные пропорции Парфенон был и остается совершеннейшим из архитектурных сооружений Парфенон Различные методы анализа пропорций Парфенона: Жолтовский (а), Хэмбидж (б), Мессель (в), Шевелев (г) Храм Василия Блаженного Пропорции храма Василия Блаженного в Москве определяются восемью членами ряда золотого сечения: 1, φ, φ2, φ3, φ4, φ5, φ6, φ7 Пирамида Хеопса Нотр-Дам де Пари Исаакиевский собор Кунсткамера Дом Советов В современной архитектуре формула расчёта золотого сечения позволяет проектировать уникальные формы, которые несут прочность, спокойствие и красоту. Золотое сечение в оформлении интерьера Даже если дом возведен по типовому проекту, можно внутри его создать интерьер, максимально приближенный к идеальной пропорции 1:1,62. Например, благодаря дополнительным перегородкам или расположению мебельных групп, а также можно изменить дверные или оконные проемы, чтобы соотношение ширины к высоте было в золотом сечении. Аналогичная ситуация и с цветовым оформлением интерьера, здесь действует упрощенное правило: • 60% — основная палитра; • 30% — дополнительный оттенок; • 10% — близкий тон, который усиливает восприятие основного и дополнительного. Правило 1/1,62 в интерьере должно сопровождаться во всем: в соотношении мебели к общей площади, в ее высоте по отношению к параметрам комнаты.