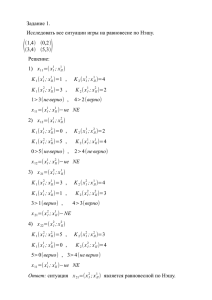Задание 1.
Множества допустимых стратегий игроков: S2={O; P}, S2={O;P}, где О- выбрать орла, Р –
выбрать решку.
Тогда платежи выглядят так:
u1(O,O)=1
u1(P,P)=1
u1(O,P)=-1
u1(P,O)=-1
u2(O,O)=-1
u2(P,P)=-1
u2(O,P)=0
u2(P,O)=0
Данные в виде матрицы:
О
Р
О
Р
1; −1 −1; 1
−1; 1 1; −1
1. Проверяем, имеет ли платежная матрица седловую точку
Игроки
В1 В2 𝑎 = min(𝐴𝑖)
А1
1 −1
−1
А2
−1 1
−1
𝑏 = max(𝐵𝑖) 1
1
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(a i) = 1, которая указывает на максимальную чистую стратегию A1.
Верхняя цена игры b = min(bj) = 1.
Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры
находится в пределах -1 ≤ y ≤ 1.
2. Находим решение игры в смешанных стратегиях.
Для игрока 1
𝑝1 − 𝑝2 = 𝑦
−𝑝1
+ 𝑝2 = 𝑦
{
𝑝1 + 𝑝2 = 1
Для игрока 2
𝑞1 − 𝑞2 = 𝑦
−𝑞1
+ 𝑞2 = 𝑦
{
𝑞1 + 𝑞2 = 1
y=0
p1=1/2
p2=1/2
Оптимальная смешанная стратегия игрока 1: P(1/2; ½)
q1=1/2
q2=1/2
Оптимальная смешанная стратегия игрока 2: Q(1/2; ½)
Ответ: y=0; P(1/2; ½); Q(1/2; ½)
Задание 2.
0 1
1 0
3. Проверяем, имеет ли платежная матрица седловую точку
Игроки
А1
А2
𝑏 = max(𝐵𝑖)
В1 В2
0
1
1
0
1
1
𝑎 = min(𝐴𝑖)
0
0
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(a i) =
0.
Верхняя цена игры b = min(bj) = 1.
Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры
находится в пределах 0 ≤ y ≤ 1. Находим решение игры в смешанных стратегиях.
Для игрока 1
𝑝2 = 𝑦
{ 𝑝1 = 𝑦
𝑝1 + 𝑝2 = 1
Для игрока 2
𝑞2 = 𝑦
{ 𝑞1 = 𝑦
𝑞1 + 𝑞2 = 1
Y=1/2
p1=1/2 (вероятность применения 1-ой стратегии).
p2=1/2(вероятность применения 2-ой стратегии).
Оптимальная смешанная стратегия игрока 1: P=(1/2; ½)
q1=1/2 (вероятность применения 1-ой стратегии).
q2=1/2(вероятность применения 2-ой стратегии).
Оптимальная смешанная стратегия игрока 1: Q=(1/2; ½)
Цена игры y=1/2
Ответ: P=(1/2; ½), Q=(1/2; ½), y=1/2
Задание 3.
4 6 3 5
3
7
2
2
1. Проверяем, имеет ли платежная матрица седловую точку.
Игроки
А1
А2
𝑏 = max(𝐵𝑖)
В1 В2 В3
4 −6 3
3
7
2
4
7
3
В4 𝑎 = min(𝐴𝑖)
5
−6
2
2
5
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(a i) = 2.
Верхняя цена игры b = min(bj) = 3.
Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры
находится в пределах 2 ≤ y ≤ 3.
2. Проверяем платежную матрицу на доминирующие строки и доминирующие
столбцы.
С позиции проигрышей игрока В стратегия B3 доминирует над стратегией B1 (все
элементы столбца 3 меньше элементов столбца 1), следовательно, исключаем 1-й столбец
матрицы. Вероятность q1 = 0.
С позиции проигрышей игрока В стратегия B3 доминирует над стратегией B4 (все
элементы столбца 3 меньше элементов столбца 4), следовательно, исключаем 4-й столбец
матрицы. Вероятность q4 = 0.
В платежной матрице отсутствуют доминирующие строки.
Мы свели игру 2 x 4 к игре 2 x 2.
−6
7
3
2
Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока
I будет случайной величиной. В этом случае игрок I должен выбрать свои смешанные
стратегии так, чтобы получить максимальный средний выигрыш.
Аналогично, игрок II должен выбрать свои смешанные стратегии так, чтобы
минимизировать математическое ожидание игрока
3. Находим решение игры в смешанных стратегиях.
Решим задачу геометрическим методом, который включает в себя следующие
этапы:
1. В декартовой системе координат по оси абсцисс откладывается отрезок, длина
которого равна 1. Левый конец отрезка (точка х = 0) соответствует стратегии A1,
правый - стратегии A2 (x = 1). Промежуточные точки х соответствуют
вероятностям некоторых смешанных стратегий S1 = (p1,p2).
2. На левой оси ординат откладываются выигрыши стратегии A1. На линии,
параллельной оси ординат, из точки 1 откладываются выигрыши стратегии A2.
Решение игры (2 x 2) проводим с позиции игрока A, придерживающегося
максиминной стратегии. Доминирующихся и дублирующих стратегий ни у одного
из игроков нет.
Выделяем нижнюю границу выигрыша B1NB2. Максиминной оптимальной
стратегии игрока A соответствует точка N, лежащая на пересечении прямых B 1B1 и
B2B2, для которых можно записать следующую систему уравнений:
𝑦 = −6 + (7 − (−6))𝑝2
{
𝑦 = 3 + (2 − 3)𝑝2
p1=5/14
p2=9/14
y=13/14 (цена игры)
Теперь можно найти минимаксную стратегию игрока B, записав соответствующую
систему уравнений
𝑦 = −6𝑞1 + 3𝑞2
{ 𝑦 = 7𝑞1 + 2𝑞2
𝑞1 + 𝑞2 = 1
q1=1/14
q2=13/14
Ответ: цена игры y=33/14; Q(1/14; 13/14); P(5/14; 9/14)
Задание 4.
0
1
A
0
2
1
1
2
0
1
2
0
0
1
1
2
1
1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то
выписываем решение игры в чистых стратегиях.
Игроки
𝐴1
𝐴2
𝐴3
𝐴4
𝑏 = max(𝐵𝑖)
𝐵1 𝐵2
0
1
1
1
0
2
2
0
2
2
𝐵3 𝐵4
1
1
2
1
0
2
0
1
2
2
𝑎 = min(𝐴𝑖)
0
1
0
0
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(a i) = 1,
которая указывает на максимальную чистую стратегию A2.
Верхняя цена игры b = min(bj) = 2.
Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры
находится в пределах 1 ≤ y ≤ 2.
2. Проверяем платежную матрицу на доминирующие строки и доминирующие
столбцы
Стратегия A2 доминирует над стратегией A1 (все элементы строки 2 больше или равны
значениям 1-ой строки), следовательно, исключаем 1-ую строку матрицы. Вероятность
p1 = 0.
1
0
2
1 2
2 0
0 0
1
2
1
С позиции проигрышей игрока В стратегия B2 доминирует над стратегией B4 (все
элементы столбца 2 меньше элементов столбца 4), следовательно, исключаем 4-й столбец
матрицы. Вероятность q4 = 0.
1
0
2
1 2
2 0
0 0
Мы свели игру 4 x 4 к игре 3 x 3.
Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока
I будет случайной величиной. В этом случае игрок I должен выбрать свои смешанные
стратегии так, чтобы получить максимальный средний выигрыш.
Аналогично, игрок II должен выбрать свои смешанные стратегии так, чтобы
минимизировать математическое ожидание игрока I.
3. Находим решение игры в смешанных стратегиях.
Математические модели пары двойственных задач линейного программирования можно
записать
𝑥1 + 2𝑥3 ≥ 1
𝑥1 + 2𝑥2 ≥ 1
{
2𝑥1 ≥ 1
𝐹 (𝑥 ) = 𝑥1 + 𝑥2 + 𝑥3 → 𝑚𝑖𝑛
𝑦1 + 𝑦2 + 2𝑦3 ≤ 1
2𝑦2 ≤ 1
{
2𝑦1 ≤ 1
𝑍(𝑦) = 𝑦1 + 𝑦2 + 𝑦3 → 𝑚𝑎𝑥
Решаем симплекс-методом.
Оптимальный план:
y1=1/2; y2=1/2; y3=0
Z(y)=1
Оптимальный план двойственной задачи:
x1=1, x2=0, x3=0
F(x)=1
Цена игры g=1/F(x)=1
Оптимальная смешанная стратегия игрока 1: qi=g*xi
p1=1
p2=0
p3=0
P(1;0;0)
Оптимальная смешанная стратегия игрока 2: qi=g*yi
p1=1/2
p2=1/2
p3=0
Q(1/2; ½; 0)
Ответ: цена игры g=1; P(1;0;0); Q(1/2; ½; 0)
Задание 5.
5 3 6 8 7 4
5 4 8 1
7 5
1 3 1 10 0 2
9 9 7
1 3 6
Критерий Вальда.
По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших
условиях гарантирует максимальный выигрыш
𝐴𝑖 П1 П2 П3 П4 П5
𝐴1 5 −3 6 −8 7
𝐴2 7
5
5 −4 8
𝐴3 1
3 −1 10 0
𝐴4 9 −9 7
1
3
П6
4
1
2
−6
min(𝑎𝑖𝑗)
−8
−4
−1
−9
Выбираем из (-8; -4; -1; -9) максимальный элемент max=-1
Вывод: выбираем стратегию N=3.
Критерий Севиджа.
Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной
стратегии ту, при которой величина максимального риска минимизируется в наихудших
условиях, т.е. обеспечивается:
a = min(max rij)
Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния
природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
Находим матрицу рисков.
Риск – мера несоответствия между разными возможными результатами принятия
определенных стратегий. Максимальный выигрыш в j-м столбце bj = max(aij)
характеризует благоприятность состояния природы.
1. Рассчитываем 1-й столбец матрицы рисков.
r11 = 9 - 5 = 4; r21 = 9 - 7 = 2; r31 = 9 - 1 = 8; r41 = 9 - 9 = 0;
2. Рассчитываем 2-й столбец матрицы рисков.
r12 = 5 - (-3) = 8; r22 = 5 - 5 = 0; r32 = 5 - 3 = 2; r42 = 5 - (-9) = 14;
3. Рассчитываем 3-й столбец матрицы рисков.
r13 = 7 - 6 = 1; r23 = 7 - 5 = 2; r33 = 7 - (-1) = 8; r43 = 7 - 7 = 0;
4. Рассчитываем 4-й столбец матрицы рисков.
r14 = 10 - (-8) = 18; r24 = 10 - (-4) = 14; r34 = 10 - 10 = 0; r44 = 10 - 1 = 9;
5. Рассчитываем 5-й столбец матрицы рисков.
r15 = 8 - 7 = 1; r25 = 8 - 8 = 0; r35 = 8 - 0 = 8; r45 = 8 - 3 = 5;
6. Рассчитываем 6-й столбец матрицы рисков.
r16 = 4 - 4 = 0; r26 = 4 - 1 = 3; r36 = 4 - 2 = 2; r46 = 4 - (-6) = 10;
𝐴𝑖 П1 П2
𝐴1 4
8
𝐴2 2
0
𝐴3 8
2
𝐴4 0 14
П3 П4
1 18
2 14
8
0
0
9
П5 П6
1
0
0
3
8
2
5 10
𝐴𝑖
𝐴1
𝐴2
𝐴3
𝐴4
П1 П2
4
8
2
0
8
2
0 14
П3 П4 П5
1 18 1
2 14 0
8
0
8
0
9
5
П6 max(𝑎𝑖𝑗)
0
18
3
14
2
8
10
14
Выбираем из (18; 14; 8; 14) минимальный элемент min=8
Вывод: выбираем стратегию N=3.
Критерий Гурвица.
Критерий Гурвица является критерием пессимизма - оптимизма. За оптимальную
принимается та стратегия, для которой выполняется соотношение:
max(si)
где si = y min(aij) + (1-y)max(aij)
При y = 1 получим критерий Вальде, при y = 0 получим – оптимистический критерий
(максимакс).
Критерий Гурвица учитывает возможность как наихудшего, так и наилучшего для
человека поведения природы. Как выбирается y? Чем хуже последствия ошибочных
решений, тем больше желание застраховаться от ошибок, тем y ближе к 1.
Рассчитываем si.
s1 = 0.2*(-8)+(1-0.2)*7 = 4
s2 = 0.2*(-4)+(1-0.2)*8 = 5.6
s3 = 0.2*(-1)+(1-0.2)*10 = 7.8
s4 = 0.2*(-9)+(1-0.2)*9 = 5.4
𝐴𝑖 П1 П2
𝐴1 5 −3
𝐴2 7
5
𝐴3 1
3
𝐴4 9 −9
П3
6
5
−1
7
П4
−8
−4
10
1
П5 П6
7
4
8
1
0
2
3 −6
max(𝑎𝑖𝑗)
7
8
10
9
min(𝑎𝑖𝑗)
−8
−4
−1
−9
y min(aij) + (1 − y)max(aij)
4
5.6
7.8
5.4
Выбираем из (4; 5.6; 7.8; 5.4) максимальный элемент max=7.8
Вывод: выбираем стратегию N=3