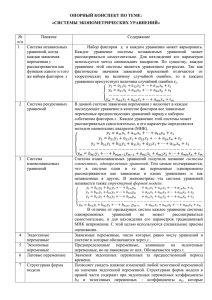
Системы эконометрических уравнений Система независимых уравнений Каждая зависимая переменная рассматривается как функция одного и того же набора факторов. y1 a11 x1 a12 x2 ... a1n xn 1 , y a x a x ... a x , 2 21 1 22 2 2n n 2 ................................................... ym am1 x1 am 2 x2 ... amn xn m . Система рекурсивных уравнений Зависимая переменная одного уравнения y выступает в виде фактора в другом уравнении. y1 a11 x1 a12 x2 ... a1n xn 1 , y2 b21 y1 a21 x1 a22 x2 ... a2 n xn 2 , y3 b31 y1 b32 y2 a21 x1 a22 x2 ... a2 n xn 2 , ......................................................................... ym bm1 y1 ... bm ,m1 ym1 am1 x1 am 2 x2 ... amn xn m . Система взаимозависимых (совместных, одновременных) уравнений Одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть системы. a11 x1 a12 x2 ... a1n xn 1 , y1 b12 y2 b13 y3 ... b1m ym a21 x1 a22 x2 ... a2 n xn 2 , y2 b21 y1 b23 y3 ... b2 m ym a21 x1 a22 x2 ... a2 n xn 2 , y3 b31 y1 b32 y2 ... b3m ym ............................................................................................ ym bm1 y1 bm 2 y2 ... bm ,m1 ym1 am1 x1 am 2 x2 ... amn xn n . Эта система уравнений называется также структурной формой модели. Структурная и приведенная формы модели • Эндогенные переменные – это зависимые переменные, число которых равно числу уравнений в системе. • Экзогенные переменные – это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них. В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные). Для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели. Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных. y1 11 x1 12 x2 ... 1n xn u1 , y x x ... x u , 2 21 1 22 2 2n n 2 ................................................... ym m1 x1 m 2 x2 ... mn xn um , ij – коэффициенты приведенной формы модели. Проблема идентификации Идентификация – это единственность соответствия между приведенной и структурной формами модели. Структурная модель в полном виде содержит m (m + n - 1) параметров, а приведенная форма модели в полном виде содержит mn параметров. Т.е. в полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Соответственно m (m + n - 1) параметров структурной модели не могут быть однозначно определены из mn параметров приведенной формы модели. С позиции идентифицируемости структурные модели можно подразделить на три вида: 1) идентифицируемые; 2) неидентифицируемые; 3) сверхидентифицируемые. Модель идентифицируема, если все её структурные коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема. Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение. Необходимое условие идентификации (счётное правило) H – число эндогенных переменных в i-м уравнении системы. D – число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение. D 1 H D 1 H D 1 H уравнение идентифицируемо уравнение неидентифицируемо уравнение сверхидентифицируемо Достаточное условие идентификации Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного. функция потребления функция инвестиций функция денежного рынка тождество дохода где Ct – расходы на потребление в период t, Yt – совокупный доход в период t, It – инвестиции в период t, rt – процентная ставка в период t, Mt – денежная масса в период t, Gt – государственные расходы в период t, Ct -1 – расходы на потребление в период t -1, It -1 – инвестиции в период t -1. Ct, Yt , It, rt – эндогенные переменные лаговые переменные Mt, Gt, Ct -1, It -1 – предопределённые переменные экзогенные переменные Первое уравнение: – переменные, отсутствующие в 1-м уравнении, – коэффициенты при этих переменных в остальных уравнениях. Второе уравнение: Третье уравнение: Приведенная форма модели в общем виде Методы оценки параметров структурной формы модели Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели: 1. Косвенный метод наименьших квадратов; 2. Двухшаговый метод наименьших квадратов; 3. Трехшаговый метод наименьших квадратов; 4. Метод максимального правдоподобия с полной информацией; 5. Метод максимального правдоподобия при ограниченной информации.