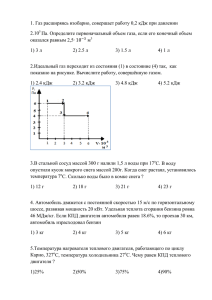
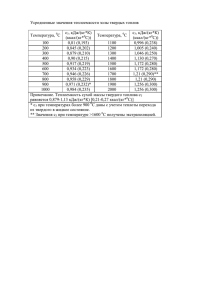
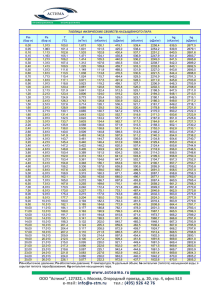
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЕ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ Кафедра металлургии КУРСОВАЯ РАБОТА по дисциплине: ___________________________________________________________ Методы исследования физико-химических систем (наименование учебной дисциплины согласно учебному плану) ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Термодинамический анализ системы Сr–S–O Тема работы: _____________________________________________________________ Автор: студент гр. ____________ МЦ-17 _____________ /________________/ Хисматуллин Р.Р. (подпись) (Ф.И.О.) ___________ ассистент _____________ /________________/ Куртенков Р. В. (должность) (подпись) (Ф.И.О.) (шифр группы) Оценка: ___________________ Дата: ___________________ Проверил: руководитель работы Санкт-Петербург 2019 Задание (непечатная страница) 2 ВВЕДЕНИЕ .................................................................................................................. 4 ЛИТЕРАТУРНЫЙ ОБЗОР ............................................................................................. 5 2.1.Получение. Распространенность. Устойчивое состояние .................................................... 5 2.2. Характеристика методик расчета равновесного состава многокомпонентных систем. Основы термодинамического моделирования системы. ...................................................................... 6 2.3. Описание расчетной методики по Ванюкову (упрощенный метод стехиометрических реакций). ................................................................................................................................................... 8 2.4. Обзор химических взаимодействий в системе Cr-S-O ........................................................ 8 2.5 Подбор координат для диаграммы потенциалов. Описание химических реакций в системе с позиции подобранных координат ........................................................................................ 10 ТЕРМОДИНАМИЧЕСКИЙ РАСЧЁТ ОСНОВНЫХ УРАВНЕНИЙ ХИМИЧЕСКИХ РЕАКЦИЙ ............................................................................................................................. 11 ПОСТРОЕНИЕ ДИАГРАММЫ ПОТЕНЦИАЛОВ ПО ВАНЮКОВУ................................ 15 ПОСТРОЕНИЕ ДИАГРАММЫ ПОТЕНЦИАЛОВ В HSC 5.1 ......................................... 19 5.1 «Lpp» и «Tpp» диаграммы .................................................................................................. 19 5.2. Интерпритация результатов. Преимущества каждого из методов. ................................. 21 ЗАКЛЮЧЕНИЕ........................................................................................................... 23 БИБЛЕОГРАФИЧЕСКИЙ СПИСОК ............................................................................. 25 3 ВВЕДЕНИЕ В основе многих металлургических процессов лежит ряд учений, основанных на изучении сродства металла к ряду неметаллов, принимающих участие в металлургических процессах добычи металла [1]. Ряд действий, необходимых для извлечения чернового и затем чистого металла, характеризуется диаграммами фазового равновесия, однако в то же для получения более полной картины термодинамики, а то есть и энергетики, вероятности процесса используются диаграммы парциальных давлений, поскольку большинство металлургических процессов протекают при высоких температурах, при которых парциальные давления принимают значительные значения [1]. На рис.1 представлена выдержка из источника [1], где демонстрируется зависимость давления диссоциации окисла от температуры, известно, что для восстановления металла требуется такая температура, чтобы упругость диссоциации окисла была выше парциального давления кислорода в атмосфере [1]. Таким образом, можно полагать, что равновесные давления паров в металлургических системах находятся при таких значениях, что измерить их не представляется чрезмерно затруднительным и они имеют весомые значения в численном эквиваленте, а также оказывают большое влияние на процесс. Рис.1 В работе [2] констатируется, что использование диаграмм парциальных давлений в системах имеет явный практический и физический смысл только для реакций второго типа, то есть для реакций с участием газовой фазой, поскольку такие реакции характеризуются активностью этой газовой фазы. Это утверждение не входит в противоречие с описанными выше, однако там же указывается, что это справедливо 4 для низких температур, когда газы ведут себя относительно идеально. При росте же температуры возрастают такие характеристики, как фугитивность, а активность газовой фазы не определяется сугубо парциальным давлением определенных веществ в этой фазе. Данным явлением и будет обусловлена погрешность теоретических данных при сравнении с тем, что происходит в металлургических комбинатах в действительности. [2]. Тем не менее, несмотря на тезисы работы [2], ряд других авторов в трудах [3,4,5,6,7,8,9] утверждают, что анализ систем посредством диаграмм парциальных давлений возможен и при высоких температурах. Смею судить, что это связано с тем, что в действительности расчет опирается на энергию Гиббса и константу равновесия, которая учитывает фугитивность и термодинамическую «искаженность» процесса. ЛИТЕРАТУРНЫЙ ОБЗОР 2.1.Получение. Распространенность. Устойчивое состояние Хром был получен в 1797 году французским химиком Л. Вокленом из минерала крокоита PbCrO4, что был прислан ему из Сибири русским геологом М. Палласом, прокипятив минерал с поташом химик получил хромат калия, который затем он перевел в состояние CrO3 и восстановил метал из связанного кислородом состояние в чистое путем спекания с углем [10]. Содержание хрома в земной коре сравнимо с содержанием в ней ванадия и хлора, численно это значение равно 0, 0122% по массе. Промышленное значение для получения хрома имеет только хромит FeCr2O4 [11]. Хром производят в виде двух продуктов: феррохром путем восстановления хромита углем, этот сплав используется как легирующая добавка при производстве твердых и нержавеющих сталей, чистый хром получают восстановлением Cr2O3 кремнием или алюминием, сам же оксид получают окислением хромита на воздухе в расплаве щелочи и последующим выщелачиванием осадка хромата натрия, который восстанавливают углеродом до оксида [11]. О устойчивости окисленных состояний можно судить по диаграмме Фроста на рис.2 [12]. Наиболее устойчиво состояние хрома в степени окисления 3+ 5 Рис.2 2.2. Характеристика методик расчета равновесного состава многокомпонентных систем. Основы термодинамического моделирования системы. Равновесие системы характеризуется нулём одной из функций состояния (энергия Гиббса 𝐺, Гельмгольца 𝐹) при заданных определенных термодинамических параметрах [13]. При переходе в область локального минимума система переходит в метастабильное состояние равновесия. Методы термодинамического анализа и моделирования систем в целом основываются на следующих уравнениях: 6 2.2.(а): G = min. 2.2.(б): d2G≥0; 2.3(в): dG = 0 В итоге существует два метода анализа системы: метод глобальных минимумов энергий Гиббса и метод стехиометрических реакций [5]. В работе [6] в введении явно обозначено, что для термодинамического анализа системы исходный состав системы является избыточной информацией, если речь идет о решении прикладной задачи. По самому условию равновесия при наступлении оного концентрации в относительных значениях моль/кг остаются постоянными и такие значения достаточны для описания системы [6]. Образующими веществами систем являются соединения с кратным отношения атомов, компоненты же с дробным отношением в составе следует игнорировать [6]. Важно, что вещества, имеющие один состав, но входящие в разные фазы, считаются разными компонентами системы [6]. Очевидно, что при процессе анализа следует исключить воздействие таких явлений, как электрическое, гравитационное, магнитное поля [6]. Метод стехиометрических реакций используется для анализа следующий равновесий: равновесие стального расплава с соединением стехиометрического состава [5], равновесие стального расплава с совершенным раствором переменного состава [5], равновесие стального расплава с неидеальным шлаковым раствором переменного состава [5], и так далее. Метод, основанный на поиске минимума энергии Гиббса, позволяет рассчитывать равновесие систем, содержащих большое количество фаз, как постоянного, так и переменного состава (растворов) [5]. В итоге, можно заключить, что весь общий объем методов термодинамического анализа системы необязателен в применении для расчета диаграмм парциальных давлений [8]. Даже для описания технологических процессов порой можно ограничиться упрощенным методом стехиометрических реакций [5,8]. Метод же минимума энергии Гиббса лучше подходит для расчета именно фазовых диаграмм и диаграмм поверхностной растворимости кислорода в металле [5]. Однако, всё же следует упомянуть про ряд различных моделей с дополнениями к основным методам термодинамического анализа систем гетерогенного состава, типа модели идеальных растворов, модели регулярных растворов, модели Редлиха7 Кистера [14]. Масса этих дополненных моделей учитывает коэффициент активности и применяется для особо точных расчетов, которые имеет смысл рассматривать при моделировании нового металлургического процесса. 2.3. Описание расчетной методики по Ванюкову (упрощенный метод стехиометрических реакций). В главе IX источника [8] подробно описывается расчет диаграммы парциальных давлений «вручную». Сначала следует расписать все химические процессы в системе и выразить десятичный логарифм константы равновесия каждого из процессов в форме К р . Расчет самой константы при заданной температуре не представляет трудностей. Затем следует обнаружить нонвариантые равновесные точки, где «встречаются» различные фазы. Логика данных вычислений хорошо отражается следующей формулой, которая вытекает из условия равновесия, данная формула может быть представлена не только для двух не стандартных энергий Гиббса процессов, но и более (до трёх включительно): 2.3. (а) RT ln( K1 ) RT ln( П1 ) RT ln( K2 ) RT ln( П2 ) ; K1,2 – константа равновесия П1,2 – суммарный дополнительный химический потенциал, влияющий на энергию Гиббса, где в знаминателе находятся реагенты процесса, влияющие на константу равновесия, а в числителе – продукты. Часто – их парциальные давления, и в нашем примере тоже. Таким образом можно составить ряд систем уравнения, позволяющих обнаружить опорные точки диаграммы. [8] 2.4. Обзор химических взаимодействий в системе Cr-S-O Хром образует ряд сульфидов серы CrS, Cr2S3, Сr3S4 [7]. Наиболее устойчивой окисью хрома является Cr2O3 [7,12]. Стандартное изменение превращения 4/3 CrO3= 2/3 Сr2O3 + O2 8 составляет 1310 Дж/г-моль, что пересчитывается в давление диссоциации порядка 0,6 бар, что в свою очередь говорит о слабой устойчивости хромового ангидрида [7]. Общий массив реакций в системе Cr-S-O для рассмотрения затруднителен. В целом, для анализа и подбора необходимых в расчетах по Ванюкову реакций следовало бы рассчитать энергию Гиббса каждой из возможных реакций, которых было бы очень много, а затем выбрать те из них, которые имели бы значение меньше нуля. Воспользовавшись программой HSC5 можно найти значения различных энергий Гиббса для ряда превращений в данной системе и обозначить самые активно протекающие реакции, которые нельзя не учитывать. Так, реакция образования сульфата хрома из чистых компонентов смеси имеет энергию Гиббса при 973 К порядка -1806 кДж/моль. В свою очередь сульфит хрома в данной системе по данным HSC 5 не образуется вовсе. По такой же системе можно выделить еще ряд образующихся соединений в данной системе при температурах 873-973 К Cr2O3, Cr, CrS, Cr2S3, Cr2(SO4)3. Пример подобного расчета программой можно видеть ниже на рис.3. Рис.3 9 2.5 Подбор координат для диаграммы потенциалов. Описание химических реакций в системе с позиции подобранных координат Ванюков утверждает, что для подбора координат ключевое значение имеет технология процесса, что в свою очередь влияет на равновесие системы и устойчивые соединения в данном конкретном случае. Так, например, для агломерации сульфидных концентратов используют диаграммы lg[PSO2] и lg[PO2]. Эти координаты так же пригодны для характеристики диссоциации и окисления сульфидов [8]. Для остальных же случаев в системах металл-кислород-сера выгодно использовать координаты, учитывающие парциальные давления S2 и О2 [8]. Это приводит к своеобразным последствиям, а именно уравнения реакций нужно представлять именно посредством участия этих соединений. Если для кислорода это может иметь технологическое значение, то для S2 это справедливо в меньшей мере. [16]. Итак, представим реакции в системе Cr – S – O с допущением того, что процесс происходит в газовой фазе S2 - O2. Справедливы и обратные реакции для обозначенных, более того, ряд реакций имеет положительную энергию Гиббса, что говорит о протекании обратных процессов. В любом случае, для построения диаграммы потенциалов будут использоваться равновесные состояния: 1)2Cr 1.5O2 Cr2 O3 2)Cr 0.5S 2 CrS 3)2Cr 1.5S 2 Cr2 S3 4)Cr2 O3 0.5S 2 0.75O2 CrS 5)2Cr 1.5S 2 6O2 Cr2 ( SO4 )3 6)Cr2 O3 1.5S 2 1.5O2 Cr2 S3 7)Cr2 O3 1.5S 2 4.5O2 Cr2 ( SO4 )3 8)2CrS 0.5S 2 Cr2 S3 9)Cr2 S3 6O2 Cr2 ( SO4 )3 10)2CrS O2 Cr2 O3 S 2 10 ТЕРМОДИНАМИЧЕСКИЙ РАСЧЁТ ОСНОВНЫХ УРАВНЕНИЙ ХИМИЧЕСКИХ РЕАКЦИЙ Исходные данные: Процесс изобарный и характеризуется изобарным потенциалом – энергией Гиббса. Элементы: Сr – S – O Температура: 873 К ; 973 К. Справочные данные: Cr O2 CrS Cr2(SO4)3 Cr2O3 Cr2S3 S2 f H 298 0 0 -135 -2910,810 -1154,701 -364,008 0 S298 0 0 65 258,87 81,154 147,628 0 441,196 101,391 34,671 -2756,373 39,627 3,286 a 26,906 22,06 31,597 358,065 b -3,784 20,887 51,207 79,498 c -2,785 1.621 0,287 -89,746 -20,019 -3,343 -2,816 d 8,860 -8,207 -4,356 -0,001 5888,443 -0,0290 -0,312 Основные расчётные формулы: 11 r H 298 f H 298 (прод.) f H 298 ( реаг.); r S 298 f S 298 (прод.) f S 298 ( реаг.); T r H r H 298 T С dT ; к p 298 T r S r S 298 T к С p dT 298 T ; CP a b 103 T c 105 T 2 d 106 T 2 ; G H T S ; GT lg K p ; ln10 RT Рассчитанные значения: 1. 2Cr 1.5O2 Cr2O3 H 873 1154,110 кДж; H 973 1122,809 кДж; S873 252,89 Дж/К; S973 251, 477 Дж/К; G873 903,337 кДж, G973 878,122 кДж, K 1 p 3 2 K ; lg K 54, 054 1 p 3 2 ; lg K 47,145 O2 O2 2. Cr 0.5S2 CrS H 873 193,819 кДж; H 973 193,118 кДж; S873 62, 287 Дж/К; S973 61,526 Дж/К; G873 139, 442 кДж, G973 133, 253 кДж, K 1 p 1 2 ; lg K 8,344 K S2 1 p S2 3. 2Cr 1.5S2 Cr2 S3 12 1 2 ; lg K 7,154 H 873 547, 482 кДж; H 973 545, 422 кДж; S873 224, 778 Дж/К; S973 222,544 Дж/К; G873 351, 251 кДж, G973 328,886 кДж, K 1 3 2 p ; lg K 21, 018 K S2 1 p 3 2 ; lg K 17, 657 S2 4. 0.5Cr2O3 0.5S2 0.75O2 CrS H 873 368, 236 кДж; H 973 368, 287 кДж; S873 64,158 Дж/К; S973 64, 213 Дж/К; G873 312, 226 кДж, G973 305,808 кДж, K p p 3 4 O2 1 2 ; lg K 18, 683 K S2 p p 3 4 O2 1 2 ; lg K 16, 418 S2 5. 2Cr 1.5S2 6O2 Cr2 (SO4 )3 H 973 3052,595 кДж; H 873 3062, 297 кДж; S973 1280, 711 Дж/К; S873 1291, 228 Дж/К; G973 1806, 463 кДж, G873 1935, 054 кДж, K K 1 3 2 p p S2 ; lg K 115, 791 1 3 2 p p S2 6 ; lg K 96,986 6 O2 O2 6. Cr2O3 1.5S2 1.5O2 Cr2 S3 H 873 576, 628 кДж; H 973 577,387 кДж; S873 28,113 Дж/К; S973 28,933 Дж/К; G873 552, 086 кДж, G973 549, 236 кДж, K p pO2 3 2 3 2 ; lg K 33, 036 K S2 p pO2 S2 13 3 2 3 2 ; lg K 29, 488 7. Cr2O3 1.5S2 4.5O2 Cr2 ( SO4 )3 H 873 1938,186 кДж; H 973 1929, 786 кДж; S873 1038,338 Дж/К; S973 1029, 234 Дж/К; G873 1031, 717 кДж, G973 928,341 кДж, K 1 3 2 p p S2 9 2 ; lg K 61, 736 K O2 1 3 2 p p S2 9 2 ; lg K 49,841 O2 8. 2CrS 1.5S2 Cr2 S3 H 873 547, 482 кДж; H 973 545, 422 кДж; S873 224, 778 Дж/К; S973 222,544 Дж/К; G873 351, 251 кДж, G973 328,886 кДж, K 1 p 3 2 ; lg K 4,330 K S2 1 p 3 2 ; lg K 3,349 S2 9. 2CrS O2 Cr2 O3 S2 H 873 736, 473 кДж; H 973 736,573 кДж; S873 128,317 Дж/К; S973 128, 425 Дж/К; G873 624, 452 кДж, G973 611, 615 кДж, K pS 2 p О2 ; lg K 37,366 3 2 K pS 2 p О2 3 2 ; lg K 32,837 10. Cr2 S3 6O2 Cr2 (SO4 )3 H 873 2514,815 кДж; H 973 2507,173 кДж; S873 1066, 451 Дж/К; S973 1058,167 Дж/К; G873 1583,803 кДж, G973 1477,577 кДж, K 1 p 6 ; lg K 94, 772 K О2 1 p О2 14 6 ; lg K 79,329 Пример вычислений: 2Cr 1.5O2 Cr2O3 1. Вычисление термодинамических функций при температуре 298 К: r H 298 f H 298 Cr2O3 2 f H 298 Cr 1.5 f H 298 O2 1154, 701кДж r S298 f S298 (Cr2O3 ) 2 f S298 Cr 1.5 f S298 O2 81,154 Дж/К 2. Вычисление термодинамических функций при температуре 973 К: r a a Cr2 O3 2 a Cr 1.5 a O2 441,196 26,906 2 -22,06 1,5=354,294Дж/моль К r b b Cr2 O3 2 b Cr 1.5 b O2 2756,373 (3, 784) 2 -20,887 1,5 2780,1355 Дж/моль К r c c Cr2 O3 2 c Cr 1.5 c O2 20, 019 (2, 785) 2 -1,621 1,5 16.8805 Дж/моль К r d d Cr2 O3 2 d (Cr ) 1.5 d (O2 ) 5888, 443 8,8860 2 -(-8,207) 1,5= 5882.9815 Дж/моль К r b 1 1 9733 2 (9732 2982 ) 103 r c ( ) 105 r d ( 2 973 298 3 (2780,1355) 1154, 701 (354, 294) (973 298) (973 298) 103 16,8805 105 2 1 1 9733 2983 ( ) 5882,9815( ) 106 1122,809 кДж 973 298 3 3 c 1173 1 1 9732 2982 r S973 r S 298 r a ln r b (1173 298) r ( ) d ( ) 106 r 298 2 9732 2982 2 2 973 16,8805 105 353, 008 354, 294 ln (2780,1355) (973 298) 103 298 2 1 1 9732 2982 5 ( ) 10 5882,9 815 ) 106 251, 477 Дж/К 2 2 9732 2982 G973 r H 973 T r S973 1122,809 973 (251, 477) 878,122 кДж r H 973 r H 298 r a (973 298) 3. Расчёт константы равновесия: G973 878,122 47,145 ln10 R T 2,303 8,314 973 1 2 ; lg pO2 lg K 31, 43 3 3 2 lg K K p O2 ПОСТРОЕНИЕ ДИАГРАММЫ ПОТЕНЦИАЛОВ ПО ВАНЮКОВУ Общий алгоритм построения диаграммы приведен в работе [8] в разделе «Влияние состава газовой фазы на равновесие оксисульфидных систем. Активность компонентов». 15 Выше, так же ссылаясь на работу [8], были выбраны координаты для построения диаграммы – это y lg[ PO2 ]; x lg[ PS2 ] . Построение диаграммы начнем с линий равновесия. Из реакций можно обнаружить ряд равновесий, типа Cr – CrS. Для данного равновесия возможно рассчитать парциальное давление серы (реакция 2 раздела 2.5) : 1 lg K p lg[ PS2 ]; 2 lg[ PS2 ] lg K p 2 7,154 2 14,308 Из расчета следует, что на координате x =-14,308 проведена вертикальная линия равновесия Cr – CrS. Далее похожие действие следует выполнить для равновесия Cr-Cr2O3 (реакция 1 раздела 2.5): 3 lg K p lg[ PО2 ]; 2 lg K p 47,145 lg[ PО2 ] 31, 43; 1,5 1,5 Следовательно, на координате y=-31,43 следует провести горизонтальную линию равновесия Cr-Cr2O3 до пересини с линией Cr – CrS, за которой образуется СrS. Полученная точка является нонвариантной точкой, здесь в равновесии находятся три фазы Cr – CrS - Cr2O3. О присутствии чистого металла под горизонтальной и левее вертикальной, обнаруженных выше, линий, судить можно по следующей логике: поскольку с ростом парциального давления кислорода или серы растет смещение реакции в сторону продуктов по принципу Ле-Шателье, то в обратном случае будет расти концентрация реагентов, среди которых и расположен чистый металл хром. Полученные линии обозначении на диаграмме в «Приложении 1» красным и желтым цветами. Теперь следует изучить ряд равновесий типа CrS – Cr2S3, CrS – Cr2O3, Cr2S3 – Cr2O3, которое приведет к обнаружению второй нонвариантной точки равновесия трех фаз. К данной мысли легко прийти, если посмотреть на список устойчивых в данных условиях соединений: Cr, CrS, Сr2S3, Cr2O3, Сr2(SO4)3. То есть, в принципе тут возможны следующие варианты нонвариантных точек: Сr - CrS - Cr2S3 , Сr – Cr2O3 – 16 Cr2(SO4)3, СrS - Cr2S3 - Cr2O3 , Сr2(SO4)3 - Cr2S3 - Cr2O3, и так далее. Для того, чтобы не заниматься бездумным перебором, стоит просто обозначить равновесные линии, так же, как сделано выше. Найдем линию CrS – Cr2S3 (реакция 8 раздела 2.5) : 1 lg K p lg[ PS2 ]; 2 lg K P 3,349 lg[ PS2 ] 6, 698 0.5 0.5 Следовательно, на координате x= - 6,698 следует изобразить вертикальную линию равновесия CrS – Cr2S3 . Теперь рассмотрим равновесие Cr2O3 - Cr2S3, чтобы точнее очертить область оксида, учитывая равновесия CrS – Cr2S3 (парциальное давление серы равно парциальному давлению серы в этом равновесии), в итоге получим вторую нонвариантную точку CrS – Cr2S3 – Cr2O3 (реакция 10 раздела 2.5) lg K p 1.5lg[ PS2 ] 1.5lg[ PO2 ]; lg[ PS2 ] 6, 698; lg K p 29, 488; lg[ PO2 ] (1.5lg[ PS2 ] lg K p ) ( 6, 698 1.5 29, 488) 1.5 26,3567; Таким образом, координаты нонвариантной второй точки x=-6,698; y=-26,3567. Очевидно, что с ростом концентрации кислорода и серы, вероятность появления такого соединения, как Cr2(SO4)3, то есть, оно скорее всего расположено в правой верхней части диаграммы. Чистый металл уже окружен двумя фазами, таким образом, переход в состояние сульфата возможен посредством через трисульфид или оксид (моносульфид окружен фазами трисульфида и оксида). равновесия Cr2S 3 Начать следует с - Cr2(SO4)3, а затем равновесие Cr2O3 - Cr2(SO4)3 (реакции 7 и 9 раздела 2.5) 17 Cr2 S3 Cr2 ( SO4 )3 : lg K p 6 lg[ PO2 ]; lg K p 79,329; lg[ PO2 ] lg K p 6 13, 2215; Cr2 O3 Cr2 ( SO4 )3 : lg K p 1.5lg[ PS2 ] 4.5lg[ PO2 ]; lg K p 49.841; lg[ PO2 ] 13.2215 lg[ PS2 ] ( lg K p 4.5lg[ PO2 ]) 1.5 (49.841 4.5 (13, 2215)) 1.5 6, 43783; Итак, координаты третьей нонвариантной точки x=6.43783, y=-13,219. Остается только изобразить до конца линию Cr2O3 - Cr2(SO4)3. Видно, что эта линия постепенно, с ростом содержания в системе серы, переходит в линию Cr2S 3 - Cr2(SO4)3. Для того, чтобы достроить Cr2O3 - Cr2(SO4)3 слева, представим, что в системе находится избыток кислорода, и lg[PO2]=0; lg K p 1.5lg[ PS2 ] 4.5lg[ PO2 ]; lg K p 49.841; lg[ PO2 ] 0 lg[ PS2 ] ( lg K p 4.5lg[ PO2 ]) 1.5 (49.841 0) 1.5 33, 227; Линия Cr2O3 - Cr2(SO4)3 уходит в левый верхний угол диаграммы. Диаграмма построена, стоит только произвести дополнительные расчеты для того, чтобы удостовериться, что в некоторых пределах диаграммы не происходит никаких превращений, однако в нашем случае надобности в этом нет, поскольку равновесные линии уже рассчитаны. Получившаяся диаграмма для системе при температуре 973 К изображена в «Приложение 1». 18 ПОСТРОЕНИЕ ДИАГРАММЫ ПОТЕНЦИАЛОВ В HSC 5.1 5.1 «Lpp» и «Tpp» диаграммы Программный пакет модулей «HSC Chemistry» имеет в списке своих инструментов в том числе два модуля для расчета потенциальных диаграмм. Два модуля – это «Tpp diagram» и «Lpp diagram». Первый модуль ведет расчет диаграммы через метод глобальных минимумов энергий Гиббса, второй же модуль ведет расчет методом стехиометрических реакций. «HSC Chemistry» имеет обширную базу термодинамических свойств вещест, поэтому этот программный пакет позволяет рассчитывать диаграммы даже точнее, чем вручную, при том учитывая соединения с дробными отношениями атомов. [17]. Ниже, на рис.4-7 представлены «Lpp» и «Tpp» диаграммы для системы Cr –S – O при температурах 873 - 973 К; Рис.4 Lpp-диаграмма при 873 К 19 Рис.5 Lpp-диаграмма для 973 К Рис.6 Tpp-диаграмма для 873 К 20 Рис.7 Tpp-диаграмма для 973 К 5.2. Интерпритация результатов. Преимущества каждого из методов. Результат демонстрирует, что метод глобальных минимумов энергий Гиббса не в своем точнейшем, т.е. при расчете ЭВМ, приближении, близок к упрощенному методу стехиометрических коэффициентов (по Ванюкову). Точнейшее посредством ЭВМ решение по методу демонстрирует стехиометрических присутствие в системе коэффициентов дополнительных превращений оксида хрома в другие его полиморфные структуры. Такого же результата можно было добиться и при «ручном» расчете, если бы данные соединения были учтены. Расчет посредством HSC 5.1 наглядно показывает, что соединения CrS в системе Cr - S – O по существу нет, в системе присутствует бертолид сотава CrS1.7 . Lpp диаграмма имеет подменю, изображенное на рис. 8-9, где изображены точные значения энергий Гиббса предложенных программным модулем реакций, а 21 также сами реакции, координаты нонвариантных точек (можно обратить внимание на погрешность «ручного» расчета). Рис.8 22 Рис.9 ЗАКЛЮЧЕНИЕ Диаграммы потенциалов, или же диаграммы парциальных давлений – достаточно наглядный и практически-пригодный способ термодинамического описания металлургических систем в случаях, когда давление постоянно и не очень велико, порядка 1 атм., а температура постоянна. Данный тип диаграмм – простое плоскостное изображение процессов в системе, чтение которой не так осложнено, как чтение диаграмм состояния. После построения диаграмм для системы Cr – S – O, приведенного в данной курсовой работе, можно судить о том, что в данной системе при 873 К и 973 К смещение диаграммы происходит слабо, в связи с тем, что энергии Гиббса для процессов в данной системе с изменением температуры меняются слабо. Это говорит о малом вкладе энтропии в термодинамику процесса [15]. 23 Построение диаграмм вручную является довольно точным методом, однако отличия от диаграмм, построенных посредством программных модулей, всё же наличествуют. К сожалению, диаграмма потенциалов для металлургии конкретно хрома имеет слабое значение, поскольку основные металлургические процессы для данного металла протекают не в оксисульфидных системах.[7]. 24 БИБЛЕОГРАФИЧЕСКИЙ СПИСОК 1. А.Н. Вольский, Е.М. Сергиевская Теория металлургических процессов, М: «Металлургия», 1968. 344 с. 2. Р.М. Гаррелс, Ч.Л. Крайст Минералы, равновесия, М: «Мир», 1968. 366с. 3. Трофимов Е. А.//Физическая химия 2014 Том 6 №2 , с. 45-53 4. Трофимов Е. А.. Михайлов Г.Г.H.// Вестник ЮУрГУ 2009 V №36с.16-19 5. Казаков А.А., Рябошук С.В. Основы металлургической экспертизы, СПБ: Издательство Политехнического университета, 2013. 111с. 6. Ватолин Н.А., Моисеев Г.К., Трусов Б.Г. Термодинамическое моделирование в высокотемпературных неорганических системах, М: «Металлургия», 1994. 330 с. 7. Плинер Ю.Л., Игнатенко Г.Ф., Лаппо С.И., Металлургия хрома, М: «Металлургия», 1965. 176с. 8. Ванюков А.В., Зайцев В.Я. Теория пирометаллургических процессов, М: «Металлургия», 1993. 383 с. 9. Есин О.А., Гельд П.В. Физическая химия пирометаллургических процессов, М: «Металлургия», 1966. 690 с. 10. Дроздов А.А., Зломанов В.П., Маз Г.Н.,Спиридонов Ф.М. Неорганическая химия Том 3 Химия переходных элементов, М: «Академия», 2007. 350 с. 11. Гринвуд Н., Эрншо А. Химия элементов Том 2, М: «Лаборатория знаний», 2008. 667 с. 12. Шрайвер П., Эткинс Д., Неорганическая химия Том 1, М: «Мир», 2004. 343 с. 13. Герасимов Я. И. Курс физической химии: учеб. пособие / Я. И. Герасимов, В. П. Древинг, Е. Н. Еремин и др. - М.: Государственное научно техническое издательство химической литературы, 1963. – 625 с. 14. Куценко С.А.,Цымай Д.В., Термодинамические расчеты химико- металлургических процессов, Орел: Издательство Орел ГТУ, 2003. 63с. 15. Колесников И.М., Винокуров В.А. Термодинамика физико-химических процессов, М: «Нефть и газ», 2005. – 480 с. 16. Копылов Н.И., Смирнов М.П.,Тогузов М.З. Диаграммы состояния систем в металлургии тяжелых цветных металлов, М: «Металлургия», 1993. – 303с. 17. Outotec, CHEMISTRY SOFTWARE LTD : http://www.outotec.ru/products/digitalsolutions/hsc-chemistry/ 25 26