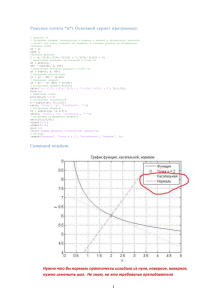
Импульсные системы
Отчет по лабораторной работе № 4
Линейные дискретные системы
Выполнили:
Студент гр. 4307 Гильман Д.В.
Проверил:
доцент кафедры АСОИУ Мокшин В.В.
Вариант
4
1. Исследование разомкнутой дискретной системы
Передаточная функция системы:
1,8𝑧 2 − 1,9𝑧 − 2,7
𝐹(𝑧) = 2
𝑧 + 0,1𝑧 + 0,3
Реакция системы на единичный ступенчатый входной сигнал при нулевых начальных
условиях:
𝑣[0] = 1,8
𝑣[1] = 4,16
𝑣[2] = 3.323
𝑣[3] = 3.059
𝑣[4] = 2.636
𝑣[5] = 2.832
Нули передаточной функции:
𝑧1 = −2.0960769
𝑧2 = 0.4490181
Полюса передаточной функции:
𝑝1 = −0.5
𝑝2 = 0.3
Устойчивость:
Система устойчива, т.к. существует коэффициент усиления звена в установившемся
режиме
Z-преобразование входного сигнала e1[k]:
𝐸1 (𝑧) = 𝑧 −1 + 2𝑧 −2 + 𝑧 −3
Z-преобразование входного сигнала e2[k]:
𝐸2 (𝑧) = 2𝑧 0 + 𝑧 −1 + 𝑧 −3 + 2𝑧 −4
Результаты моделирования системы при входах e1 (v1), e2 (v3), e1+e2 (v) и
0,5(e1+e2) (v3):
Выводы:
Свойство однородности выполняется, потому что умножение входного сигнала на
постоянную приводит к умножению выходного сигнала на ту же постоянную.
Свойство суперпозиции выполняется, т.к. реакция на сумму сигналов равна сумме
реакций этой системы на отдельные сигналы
Z-преобразование сигнала e[k] = e1[k] + e2[k]:
𝐸(𝑧) = 2𝑧 0 + 2𝑧 −1 + 2𝑧 −2 + 2𝑧 −3 + 2𝑧 −4
Z-преобразование сигнала e3[k] = 0,5·e[k]:
𝐸3 (𝑧) = 𝑧 0 + 𝑧 −1 + 𝑧 −2 + 𝑧 −3 + 𝑧 −4
Z-преобразование запаздывающего сигнала edelay[k] = e[k-2]:
𝐸𝑑𝑒𝑙𝑎𝑦 (𝑧) = 2𝑧 −2 + 2𝑧 −3 + 2𝑧 −4 + 2𝑧 −5 + 2𝑧 −6
Реакция на запаздывающий сигнал edelay[k]:
Выводы:
Условие стационарности выполняется, т.к. запаздывающий сигнал в точности
повторяет значения своевременного сигнала.
z-преобразование единичного ступенчатого сигнала u[k]:
𝑧
𝑈(𝑧) =
𝑧−1
z -преобразование сигнала выхода системы v[k] при входе u[k]:
1,8𝑧 2 − 1,9𝑧 − 2,7
𝑧
𝑉(𝑧) = 𝐹(𝑧) ∗ 𝑈(𝑧) = 2
∗
𝑧 + 0,1𝑧 − 0,12 𝑧 − 1
Начальное и конечное значения выходного сигнала (теоретически):
1,8𝑧 2 − 1,9𝑧 − 2,7
𝑧
𝑣[0] = lim 𝑉(𝑧) = lim 2
∗
= 1,7
𝑧→∞
𝑧→∞ 𝑧 + 0,1𝑧 − 0,12
𝑧−1
𝑧−1
1,8 − 1,9 − 2,7
𝑣[∞] = lim
𝑉(𝑧) =
= 2.762
𝑧→1 𝑧
1 + 0,1 − 0,12
Реакция системы на единичный ступенчатый сигнал:
Выводы:
Теоретические расчеты подтверждаются моделированием.
2. Исследование дискретной модели в пространстве состояний
Модель в пространстве состояний:
0.75 −0.45
𝐴=[
]
1
0
1
𝐵=[ ]
0
𝐶 = [0.24 0.29]
𝐷=0
Собственные числа матрицы A:
0.375 + 0.5562149i
0.375 - 0.5562149i
Устойчивость:
Система асимптотически устойчива, т.к. все собственные числа матрицы А по модулю
меньше 1.
Импульсная характеристика:
Переходная характеристика:
Передаточная функция:
0.29 + 0.24𝑧
0.45 − 0.75𝑧 + 𝑧 2
Полюса передаточной функции:
0.375 + 0.5562149i
0.375 - 0.5562149i
Выводы:
Система асимптотически устойчива, т.к. полюса по модулю меньше 1.
Обратный переход в пространство состояний:
0.5750176 −1.144813
𝐴=[
]
305187 0.1749824
−0.4641563
𝐵=[
]
0.5608555
𝐶 = [−0.5170672 0]
𝐷=0
Выводы:
Модели в пространстве состояний оказались разными, т.к. это связано с тем, что одной
и той же системе соответствует бесконечное множество моделей в пространстве
состояний
Статический коэффициент усиления системы:
𝑘 = 0.7571429
Выводы:
Установившееся значение переходной характеристики совпадает
Время переходного процесса:
𝑡п = 16
3. Исследование замкнутой системы
Передаточная функция регулятора:
0,97𝑧 − 0.71
𝑧 + 0.46
Структурная схема системы:
Переходные процессы в системе:
Передаточная функция разомкнутой системы:
0,97𝑧 − 0.71
0.29 + 0.24𝑧
𝑊𝑜𝑝𝑒𝑛 (𝑧) = 𝐶(𝑧) ∗ 𝐺(𝑧) =
∗
𝑧 + 0.46
0.45 − 0.75𝑧 + 𝑧 2
Передаточная функция замкнутой системы:
0,97𝑧 − 0.71
0.29 + 0.24𝑧
∗
𝐶(𝑧) ∗ 𝐺(𝑧)
𝑧
+
0.46
0.45
− 0.75𝑧 + 𝑧 2
𝑊𝑜𝑝𝑒𝑛 (𝑧) =
=
1 + 𝐶(𝑧) ∗ 𝐺(𝑧) 1 + 0,97𝑧 − 0.71 ∗ 0.29 + 0.24𝑧
𝑧 + 0.46
0.45 − 0.75𝑧 + 𝑧 2
Полюса передаточной функции замкнутой системы:
0.0311437 + 0.4639471i
0.0311437 - 0.4639471i
-0.0050875
Устойчивость:
Система асимптотически устойчива, т.к. полюса по модулю меньше 1.
Статический коэффициент усиления замкнутой системы:
𝑘𝑊 = 0.1188136
Время переходного процесса:
𝑡п = 132
Листинг программы:
clc
n2 = 1.8;
n1 = -1.9;
n0 = -2.7;
d1 = 0.1;
d0 = -0.12;
n = poly([n0 n1 n2],'s','coeff')
d = poly([d0 d1 1] ,'s','coeff')
f = syslin ('d', n, d )
z = roots(n)
p = roots(d)
absP = abs(p)
k = horner(f, 0)
e1 = [0 1 2 1 0]
v1 = flts(e1, f)
e2 = [2 1 0 1 2];
v2 = flts(e2, f)
scf()
t = [0:1:6]
plot(t, v1)
t = [0:1:5]
plot(t, v1)
t = [0:1:4]
plot(t, v1)
plot(t, v2, 'r-')
e = e1 + e2
v = flts(e, f)
plot(t, v, 'g-')
err1 = v - e
disp(norm(err1), 'err1 = ')
e3 = e/2
v3 = flts(e3, f)
err2 = v3 - e3
disp(norm(err2), 'err2 = ')
t = 0:4
plot(t, v1, '--', t, v2, '--', t, v, '-o', t, v3, '-o'))
scf();
plot(t, v1, '--', t, v2, '--', t, v, '-o', t, v3, '-o')
eDelay = [0 0 e]
vDelay = flts(eDelay, f)
scf();
t1 = 0:6;
plot2d2(t, v, style=color('blue'))
plot2d2(t1, vDelay, style=color('red'))
scf();
plot2d2(t, v, style=color('blue'))
plot2d2(t1, vDelay, style=color('red'))
t = 0:20
u = ones(t)
vu = flts(t,f)
hf = scf()
plot2d(t, vu, style=color('blue'))
hf.children(1).font_size=5
vu = flts(u,f)
hf = scf()
plot2d(t, vu, style=color('blue'))
hf.children(1).font_size=5
exec('C:\Users\fonFa\Documents\2018\Ильяс\lab4-2.sce',-1)
eigA = spec(G.A)
t = [0:15]
xImp = zeros(t)
xImp(1) = 1
yImp = dsimul(G, zImp)
yImp = dsimul(G, xImp)
scf()
title('Импульсная характеристика' , 'fontsize', 3)
xlabel('t, сек', 'fontsize', 3)
plot2d(t, yImp, style=color('blue'));
t=[0:15]
xStep = [0, 1, 2, 1.5, 1.333333333, 1.25, 1.2, 1.166666667, 1.142857143, 1.125,
1.111111111, 1.1, 1.090909091, 1.083333333, 1.076923077, 1.071428571, 1.066666667]
yStep = dsimul(G, xStep)
scf()
title('Передаточная характеристика' , 'fontsize', 3)
xlabel('t, сек', 'fontsize', 3)
plot2d(t, yStep, style=color('blue'));
Gtf = ss2tf(G)
nG = numer(Gtf)
dG = denom(Gtf)
p = roots(dG)
G1 = tf2ss(Gtf)
k = horner(Gtf, 1)
err = abs(yStep-iInf)
err = abs(yStep-k)
ind = find(err >= 0.05k)
ind = find(err >= 0.05*k)
set_time = t(max(ind)+1)
nC = 0.97*%z - 0.71
dC = %z +0.46
Ctf = syslin('d', nC, dC)
xcos
scf();
subplot(2,1,1);
plot2d2(u1.time, u1.values);
xlabel('Сигнал выхода');
subplot(2,1,2);
plot2d2(out.time, out.values);
xlabel('Время, сек');
title('Сигнал управления');
subplot(2,1,1);
xlabel('Время, сек');
title('Сигнал выхода');
Wtf = Ctf*Gtf /. 1
dWtf = denom(Wtf)
pWtf = roots(dWtf)
kWtf = horner(Wtf, 1)