Modelirovanie_sistem_2010_sohr - d-edit

МОДЕЛИРОВАНИЕ СИСТЕМ
Лекция 1
Ведение:
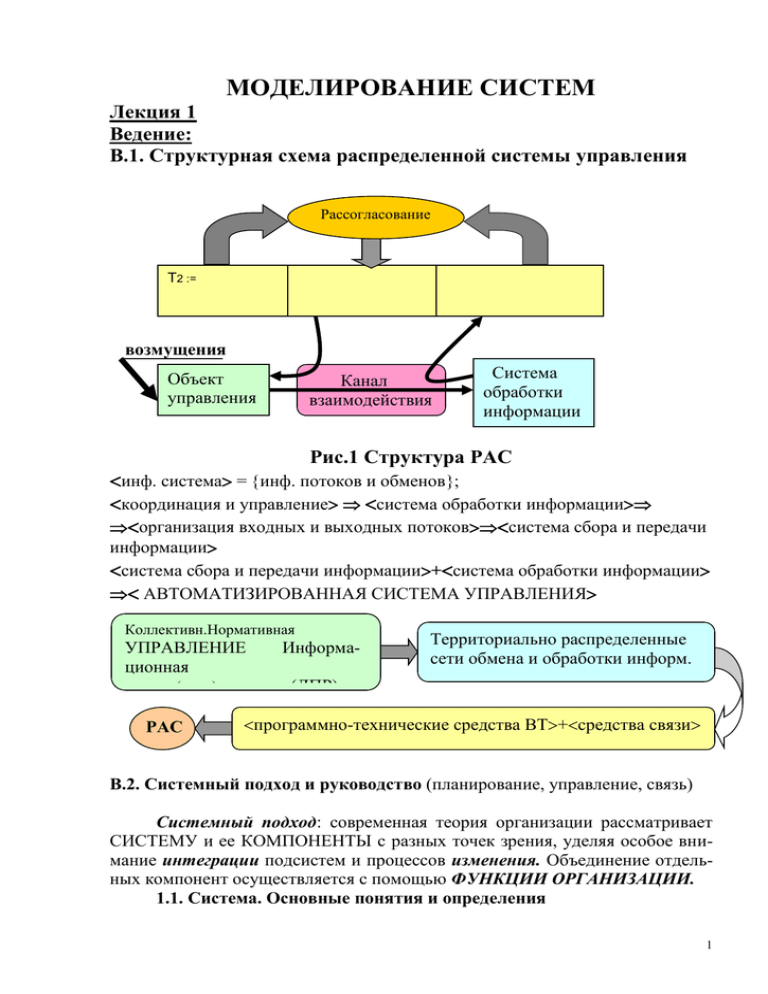
В.1. Структурная схема распределенной системы управления
Рассогласование
Т2 :=
возмущения
Объект
управления
Канал
взаимодействия
Система
обработки
информации
Рис.1 Структура РАС
инф. система = инф. потоков и обменов;
координация и управление  система обработки информации
организация входных и выходных потоковсистема сбора и передачи
информации
система сбора и передачи информации+система обработки информации
 АВТОМАТИЗИРОВАННАЯ СИСТЕМА УПРАВЛЕНИЯ
Коллективн.Нормативная
УПРАВЛЕНИЕ
ционная
модель (план)
Информа-
Территориально распределенные
сети обмена и обработки информ.
(ЛПР)
модель
программно-технические средства ВТ+средства связи
РАС
вычисл. ресурс
Коллективн. инф. обеспечение
Децентрализация управления
В.2. Системный подход и руководство (планирование, управление, связь)
Системный подход: современная теория организации рассматривает
СИСТЕМУ и ее КОМПОНЕНТЫ с разных точек зрения, уделяя особое внимание интеграции подсистем и процессов изменения. Объединение отдельных компонент осуществляется с помощью ФУНКЦИИ ОРГАНИЗАЦИИ.
1.1. Система. Основные понятия и определения
1
ЭЛЕМЕНТ
СТРУКТУРА
СИСТЕМА
ФУНКЦИЯ
ОРГАНИЗАЦИЯ
Структурная
организация
Функциональная
организация
Определения
Элемент – минимальный неделимый объект, рассматриваемый как
единое целое в рамках решаемой (поставленной) задачи.
Система – совокупность взаимосвязанных элементов, объединенных в
одно целое для достижения некоторой цели, определяющей назначение системы.
Основные свойства, присущие системе:
целостность; связность; организованность (способ достижения поставленной цели за счет выбора структуры и функции); интегративность
(эмержентность)
Вывод:
1) понятие система не сводится к простой совокупности (перечню)
элементов;
2) расчленяя систему, изучая ее отдельные части, нельзя познать все
свойства системы в целом.
Структура . Функция
Функциональная организация – определяется способом порождения
функций системы, достаточных для достижения цели. Функциональное описание системы должно включать описание параметров, процессов и иерархию.
Структурная организация – определяется набором элементов и связей
между ними, обеспечивающими возможность реализации функций, возлагаемых на систему.
Функции первичны, структура – вторична.
Таким образом, система – организованное сложное целое.
Отличительные признаки сложных систем
2
1.2. Модель. Моделирование
Моделирование - это замещение одного объекта (оригинала) другим
(моделью) и фиксация и изучение свойств модели.
Любая система S может быть описана количественно с помощью
определенной совокупности величин.
Эту совокупность можно разделить на два класса:
ВНУТРЕННИЕ
ХАРАКТЕРИСТИКИ
СИСТЕМА
ПАРАМЕТРЫ
ВНЕШНИЕ
ПАРАМЕТРЫ
ПАРАМЕТРЫ
ВНУТРЕННИЕ
задают структурную и
функциональную организацию системы
ВНЕШНИЕ
задают воздействия
внешней среды
Параметры – величины, описывающие первичные свойства системы,
ее элементов и независимые от других величин;
Характеристики – величины (зачастую, векторные), описывающие
качественные свойства системы и являющиеся вторичными по отношению к
параметрам, т.е. зависящие от параметров
Модель — это тоже система со своими множествами параметров и характеристик. Оригинал и модель сходны по одним параметрам и различны по
другим.
Моделирование целесообразно, когда у модели отсутствуют те признаки оригинала, которые препятствуют его исследованию.
Модель адекватна (соответствует) оригиналу в рамках поставленной задачи.
Теория моделирования — взаимосвязанная совокупность положений,
определений, методов и средств создания моделей и их исследования.
Подмечено, что динамика функционирования разных по физической
природе систем характеризуется однотипными зависимостями, что позволяет моделировать их на ЭВМ.
3
1.3. Классификация моделей
В основу классификации положена степень абстрагирования модели от
оригинала. Предварительно все модели можно подразделить на 2 группы —
материальные (физические) и абстрактные (мысленные) (см. плакат 1).
Материальные (физические) модели. Ф.М. обычно называют систему,
эквивалентную или подобную оригиналу, но возможно имеющую другую
физическую природу.
Мысленные (абстрактные) модели (языки химических формул, схем,
чертежей, карт, диаграмм и математические модели)
Математические модели (ММ). Математические модели представляют
собой формализованное представление системы с помощью математических
соотношений, отражающих процесс функционирования системы.
Математические модели можно классифицировать на детерминированные и вероятностные, аналитические и численные. Имитационные.
Аналитической моделью называется такое формализованное описание
системы, которое позволяет получить решение уравнения в явном виде, используя известный математический аппарат.
Численная модель характеризуется зависимостью такого вида, который
допускает только частные решения для конкретных начальных условий и количественных параметров моделей.
Имитационная модель (ИМ) — это совокупность описания системы и
внешних воздействий, алгоритмов функционирования системы или правил
изменения состояния системы под влиянием внешних и внутренних возмущений. Эти алгоритмы и правила позволяют имитировать процесс функционирования системы и производить вычисления интересующих характеристик. Имитационные модели могут быть созданы для гораздо более широкого класса объектов и процессов, чем аналитические и численные. Поскольку
для реализации имитационных моделей служат вычислительные системы
(ВС), средствами формализованного описания ИМ служат универсальные и
специальные алгоритмические языки. ИМ в наибольшей степени подходят
для исследования РСУ на системном уровне.
4
2. Математические схемы моделирования систем
2.1. Основные подходы к построению ММ систем
Математическую схему можно определить как звено при переходе от
содержательного к формализованному описанию процесса функционирования системы с учётом воздействия внешней среды.
«Выстраивается» как бы цепочка: содержательно описание
кон
аналитическая модель
цептуальная модель
математическая схема
имитационная модель
(концепция – лат.conceptio – восприятие) способ рассмотрения каких-либо
явлений, понимание чего-либо; общий замысел чего-либо).
ММ системы S, можно представить в виде совокупностей величин,
описывающих процесс функционирования реальной системы:
- входных воздействий хiХ, i=1…nx;
- воздействий внешней среды vlV, l=1…nv;
- внутренних (собственных) параметров hkH, k=1…nh;
- выходных характеристик системы yjY, j=1…ny.
X (t );V (t ); H (t ) – независимые (экзогенные) переменные (детерминированные,стохастические), Y (t ) - зависимые переменные (эндогенные).
Процесс функционирования S описывается оператором FS:

Y (t ) 
F
S
( X ,V , H , t )
(2.1)
(2.1) - динамическая модель системы S. Статическая ММ

  
Y  f ( X ,V , H )
(2.2)
Соотношения (2.1), (2.2) могут быть получены через свойства системы
в конкретные моменты времени, называемые состояниями.
Состояние системы S в интервале времени t0<tTl полностью определяется c помощью 2-х векторных уравнений:
5

0   
Z (t )  ( z , X ,V , h , t ) ;


Y (t )  F ( Z , t ) .
иначе:
0   
Y (t )  F (( z , X ,V , h , t )) .
(2.3)
(2.4)
(2.5)

Совокупность всех возможных значений состояний { Z } называется
пространством состояний объекта моделирования Z, причём zkZ.
Время в мод. S может рассматриваться на интервале моделирования (t0,
T) как непререрывное., так и дискретное, квантованное на отрезке длин. t.
Таким образом под ММ объекта понимаем конечное множество пере-
  
X
менных { , Z , h } вместе с математическими связями между ними и харак-

теристиками Y .
Моделирование называется детерминированным, если операторы F,
Ф детерминированные, т.е. для конкретного входа выход детерминированный.
Моделирование называется стохастическим, если операторы F, Ф
случайны, т.е. для конкретного входа выход характеризуется определенным
распределением вероятностей возможных своих значений.
Детерминированное моделирование - частный случай стохастического
моделирования.
В практике моделирование используют типовые математические
схемы: диф. уравнения, конечные и вероятностные автоматы, СМО и т.д.
Типовые математические схемы имеют преимущество простоты и
наглядности, но при существенном сужении возможности применения.
В качестве детерминированных моделей для представления систем,
функционирующих в непрерывном времени, используются дифференциальные, интегральные и др. уравнения, а для представления систем, функционирующих в дискретном времени — конечные автоматы и конечно разностные
схемы.
В качестве стохастических моделей для представления систем с дискретным временем используются вероятностные автоматы, а для представления систем с непрерывным временем — системы массового обслуживания
(СМО).
Большое практическое значение при исследовании сложных индивидуальных управленческих систем имеют так называемые агрегативные модели.
При агрегативном описании сложный объект расчленяется на конечное
число частей (подсистем), сохраняя при этом связи, обеспечивая взаимодействие частей.
6
Лекция 2.
2.1. Проектирование РИСУ и анализ их производительности
Проектирование информационной системы можно представить как решение последовательности проектных задач, которая включает задачи синтеза и задачи анализа системы и ее частей.
Любая задача синтеза состоит в том, чтобы из заданного множества
элементов построить некоторую систему, обладающую заранее определенными свойствами.
Задача анализа является обратной по отношению к задаче синтеза и состоит в выделении отдельных элементов заданной системы и установлении
их параметров. При проектировании РИСУ задача анализа рассматривается
как задача проверки того, обладает ли построенная система заранее указанными свойствами. Задачи анализа и синтеза РИСУ и её частей решаются с
помощью моделей проектируемой РИСУ, в качестве которых используются
описания, схемы, чертежи, математические модели и т. д.
Результаты решения задач анализа используются при решении задач
синтеза, а результаты синтеза вновь подвергаются анализу. Этот цикл представлен на рис. 1.1. Он повторяется многократно для разных частей или для
одной и той же части применяемых моделей РИСУ. Модели РИСУ развиваются, уточняются и на определённой стадии превращаются в проект РИСУ,
т. е. в совокупность документов, содержащих сведения, необходимые и достаточные для изготовления спроектированной РИСУ в заданных условиях.
Техническое задание
на проектирование РИСУ
Синтез моделей РИСУ
Проект РИСУ
Анализ работоспособности
и эффективности РИСУ
Рис. 1.1
Комплекс заранее указанных свойств, которыми должна обладать проектируемая РИСУ, подразделяется на два подытоживающих свойства, называемых работоспособностью и эффективностью.
Работоспособность РИСУ состоит в правильном выполнении заданных
функций, т. е. в правильной реализации заданного множества алгоритмов обработки информации.
7
Эффективность РИСУ заключается в ограниченности или минимальности разного рода затрат, связанных с изготовлением и применением РИСУ.
Таким образом, задачи анализа РИСУ сводятся при проектировании к
анализу работоспособности и анализу эффективности РИСУ.
Эффективность РИСУ оценивается показателями, характеризующими
затраты на изготовление и эксплуатацию РИСУ. К таким величинам относятся, например, габариты РИСУ и её устройств.
Затраты времени на получение системой каких-либо полезных результатов называются показателями производительности. К их числу относятся,
например, средние значения времён ответа РИСУ на разные типы запросов,
средние числа задач разного типа, решаемых системой в единицу времени,
коэффициенты загрузки устройств РИСУ и другие показатели.
Задача анализа производительности является одной из важнейших среди задач проектирования РИСУ и состоит в том, чтобы оценить показатели
производительности при заданных параметрах технического и программного
обеспечения РИСУ с учетом влияния, в общем случае, внешней среды. Решая
задачу анализа производительности, как правило, необходимо учитывать
случайную природу многих факторов, от которых зависит производительность РИСУ. Так, случайными часто являются моменты поступления в РИСУ
требований, объёмы подлежащей обработке информации, последовательность необходимых для ее обработки операций. При анализе производительности РИСУ все более широко применяется метод математического моделирования.
Моделирование – один из наиболее широко распространенных методов
исследования процессов функционирования сложных систем. Известно довольно большое количество методов построения математических моделей и
средств реализации моделирующих алгоритмов. Наиболее часто используемыми среди них являются системы и сети массового обслуживания.
В терминах систем массового обслуживания описываются многие реальные
системы: вычислительные системы, узлы сетей связи, системы посадки самолетов, магазины, производственные участки – любые системы, где возможны
очереди и/или отказы в обслуживании.
Целью использования СМО как модели является анализ качества
функционирования указанных систем-оригиналов. В свою очередь, СеМО
используют для определения важнейших системных характеристик информационных систем: производительности, времени доставки пакетов, вероятности потери сообщений и блокировки в узлах, области допустимых значе8
ний нагрузки, при которых обеспечивается требуемое качество обслуживания, и др.
Система массового обслуживания – одна из основных моделей, используемых инженерами-системотехниками. Как модель СМО рассматривается
в теории массового обслуживания (другое название – теория очередей). В
теории СеМО фундаментальным является понятие состояния сети. Важнейшая характеристика сетей МО – вероятности их состояний. Для определения
вероятностей состояний СеМО исследуют протекающий в сети случайный
процесс. В качестве моделей протекающих в СеМО процессов наиболее часто используют марковские и полумарковские.
Марковским процессом с непрерывным временем описывают функционирование экспоненциальных СеМО. Сеть называется экспоненциальной,
если входящие в каждую СМО потоки требований пуассоновские, а времена
каждого этапа обслуживания, реализуемого на любой СМО сети, имеют экспоненциальное распределение. Это позволяет считать, что этапы обслуживания независимы между собой и не зависят ни от параметров входящего потока, ни от состояния сети, ни от маршрутов следования требований.
Теория экспоненциальных СеМО разработана лучше других, и ее широко применяют для исследования как сетей ПД, так и мультипроцессорных
вычислительных систем (ВС). Разработаны практические формы расчета
ВВХ таких сетей и систем.
Целью использования СМО как модели является анализ качества
функционирования отдельных систем-оригиналов. В свою очередь, СеМО
используют для определения важнейших системных характеристик информационных систем: производительности, времени доставки пакетов, вероятности потери сообщений и блокировки в узлах, области допустимых значений нагрузки, при которых обеспечивается требуемое качество обслуживания, и др.
В теории СеМО фундаментальным является понятие состояния сети.
Важнейшая характеристика сетей МО – вероятности их состояний. Для определения вероятностей состояний СеМО исследуют протекающий в сети случайный процесс. В качестве моделей протекающих в СеМО процессов
наиболее часто используют марковские и полумарковские.
Марковским процессом с непрерывным временем описывают функционирование экспоненциальных СеМО. Сеть называется экспоненциальной,
если входящие в каждую СМО потоки требований пуассоновские, а времена
каждого этапа обслуживания, реализуемого на любой СМО сети, имеют экс9
поненциальное распределение. Это позволяет считать, что этапы обслуживания независимы между собой и не зависят ни от параметров входящего потока, ни от состояния сети, ни от маршрутов следования требований.
Теория экспоненциальных СеМО разработана лучше других, и ее широко применяют для исследования как сетей ПД, так и мультипроцессорных
вычислительных систем (ВС). Разработаны практические формы расчета
ВВХ таких сетей и систем.
CеМО – это прежде всего совокупность взаимосвязанных систем массового обслуживания. Поэтому необходимо вспомнить основные особенности этих систем.
2.2. Система массового обслуживания как модель
Системы массового обслуживания (англ. queuing system)называют Qсхемами. Под СМО понимают динамическую систему, предназначенную для
эффективного обслуживания случайного потока заявок при ограниченных
ресурсах системы. Обобщённая структура СМО приведена на рисунке 2.1.
Рис. 2.1. Схема СМО.
Q - схемы можно исследовать аналитически и имитационными моделями.
10
В любом элементарном акте обслуживания - две основные составляющие: ожидание заявкой обслуживания и собственно обслуживание заявки.
ui
Hi
w
i
Пi
Ki
yi
Рис. 2.2. Схема прибора СМО
На каждый элемент прибора обслуживания Пi поступают потоки событий: в накопитель Hi поток заявок wi , на канал ki - поток обслуживания ui.
Потоком событий (ПС) называется последовательность событий,
происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных событий.
Однородный ПС характеризуется только моментами поступления этих
событий и задаётся последовательностью моментов поступления либо в виде
последовательности промежутков времени между n-ым и (n-1)-ым событиями {n}.
Неоднородным ПС называется последовательность {tn, fn} , где tn- вызывающие моменты; fn- набор признаков события.
Однородный ПС с ограниченным последействием, ординарный, стационарный.
Среднее число событий, наступающих на участке t в единицу времени
составляет P1(t, t)/t. Если существует предел
lim P1(t, t)/t=(t)*(1/един.вр.),
то он называется интенсивностью (плотностью) ОПС. Для стандартного ПС
(t)==const.
Заявки, обслуженные каналом ki и заявки, покинувшие прибор Пi по
различным причинам не обслуженными, образуют выходной поток yiY.
11
Процесс функционирования прибора обслуживания Пi можно представить как процесс изменения состояний его элементов во времени Zi(t).
Многоканальное обслуживание (многоканальная Q-схема), и многофазное обслуживание (многофазная Q-схема).
Т.о. для задания Q-схемы необходимо оператор сопряжения R, отражающий взаимосвязь элементов структуры.
Различают разомкнутые и замкнутые Q-схемы. В разомкнутой выходной поток не может снова поступить на какой-либо элемент, т.е. обратная
связь отсутствует.
Собственными (внутренними) параметрами Q-схемы будут являться
кол-во фаз LФ, количество каналов в каждой фазе, Кj, j=1… КФ, количество накопителей каждой фазы Lj, j=1… LФ, ёмкость j-ого накопителя LiH.
В зависимости от ёмкости накопителя применяют следующую терминологию:
 системы с потерями (LH=0, накопитель отсутствует);
 системы с ожиданием (LH);
 системы с ограниченной ёмкостью накопителя Н (смешанные).
Для задания Q-схемы также необходимо описать алгоритмы её функционирования, которые определяют правила поведения заявок в различных
неоднозначных ситуациях.
В зависимости от места возникновения таких ситуаций различают алгоритмы (дисциплины) ожидания заявок в накопителе Нi и обслуживания заявок каналом ki. Неоднородность потока заявок учитывается с помощью введения класса приоритетов.
В зависимости от динамики приоритетов Q-схемы различают статические и динамические. Относительные и абсолютные.
Необходимо также знать набор правил, по которым заявки покидают Н i
и ki:
для Нi – либо правила переполнения, либо правила ухода, связанные с
истечением времени ожидания заявки в Нi;
для ki – правила выбора маршрутов или направлений ухода.
Кроме того, для заявок необходимо задать правила, по которым они
остаются в канале ki, т.е. правила блокировок канала. При этом различают
блокировки ki по выходу и по входу. Такие блокировки отражают наличие
12
управляющих связей в Q-схеме, регулирующих поток заявок в зависимости
от состояний Q-схемы. Набор возможных алгоритмов поведения заявок в
Q-схеме можно представить в виде некоторого оператора алгоритмов поведения заявок А.
Т.о., Q-схема, описывающая процесс функционирования СМО любой сложности однозначно задаётся в виде набора множеств: Q = <W, U, H, Z, R, A>,
где
W – поток заявок;
U – поток обслуживания;
H – правила ухода заявок из накопителя (дисциплины ожидания);
Z – состояния (процесс изменения состояний, если во времени);
R – связи, задающие структуру схемы;
A – алгоритмы (правила поведения заявок в неоднозначных ситуациях).
Символика характеристик СМО (5 разрядов)
1-й разряд
2-й разряд
3-й разряд
4-й разряд
5-й разряд
Характеристика Характеристика Особенности Особенности Приоритет
входящего
обслуживания
структуры
очереди
j
потока
системы
fi
однородных
(число
событий
приборов)
Распределения:
M – экспоненциальное;
D – регулярное;
E – эрланговское;
G – произвольное;
i = 0, 1, 2;
J = 0, 1;
i = 0 – обслуживание без приоритета;
i = 1 – относительный приоритет;
i = 2 – абсолютный приоритет;
j = 0 – требование, заставшее все места занятыми, теряется;
j =1 – вновь прибывшее требование вытеcняет требование с более низким приоритетом.
13
2.2. Аналитический анализ СМО
2.2.1. Экспоненциальная система массового обслуживания
2.2.1.1 Одноканальная однородная экспоненциальная СМО
Λ
Т обс
K
Рис. 2.3
Приходы заявок образуют пуассоновский поток событий. Это означает,
что время между приходами любых двух последовательных заявок есть независимая случайная величина с экспоненциальной функцией распределения
вероятностей

F(Х) = 1  e x
(2.6)
Одноканальная экспоненциальная СМО задается параметрами λ, Т обс .
Цель ее анализа заключается в расчете характеристик, важнейшие из которых следующие:
- коэффициент загрузки ρ;
- средняя длина L очереди;
- среднее число М заявок в СМО;
- среднее время Т ож ожидания обслуживания;
- среднее время Т пр пребывания заявки в СМО.
Коэффициент загрузки рассчитывается по формуле
ρ = λ · Т обс .
(2.7)
Если выполняется условие
ρ ≤ 1,
(2.8)
то существует стационарный режим функционирования СМО.
В стационарном режиме среднее число М заявок в СМО постоянно.
Следовательно, в стационарном режиме интенсивность потока уходящих заявок равна λ. Коэффициент загрузки ρ в стационарном режиме есть:
а) среднее значение той части единицы времени, в течение которой канал занят;
б) вероятность того, что канал занят;
в) среднее число заявок в канале.
14
Средняя длина очереди (среднее число заявок в очереди) в одноканальной экспоненциальной СМО рассчитывается по формуле
ρ2
L
.
1 ρ
(2.9)
Среднее число М заявок в СМО равно сумме среднего числа L заявок в
очереди и среднего числа ρ заявок в канале:
М=
ρ
.
1 ρ
(2.10)
Заявка перемещается в очереди в среднем с постоянной скоростью.
Среднее число переходов заявки в очереди на одно место вперед за единицу
времени равно λ.
При такой скорости перемещения L переходов произойдет за время,
равное в среднем
Т
ρ
обс
.
Т ож =
1 ρ
(2.11)
Формула (2.11) дает среднее время прохождения заявки через очередь.
Это есть среднее время ожидания.
Среднее время пребывания заявки в СМО есть
Т пр =
Т обс
.
1 ρ
(2.12)
Вероятность наличия в системе k требований определяется с помощью
геометрического закона распределения в виде
(1  ρ)  ρk , k  0,1,2,...
Многоканальная экспоненциальная СМО отличается от одноканальной
следующим. Число каналов в ней более одного. Приходящая заявка становится в очередь, если все каналы заняты. В противном случае заявка занимает свободный канал.
2.2.2. Многоканальная экспоненциальная СМО
Многоканальная экспоненциальная СМО задается тремя параметрами:
интенсивностью Λ прихода заявок, средним временем Т обс обслуживания и
числом К каналов (рис. 2.4).
Формулы для расчета характеристик многоканальной экспоненциальной СМО немногим сложнее (2.6)  (2.12).
15
Коэффициент загрузки определяется в виде
ρ
λ Т обс
K
.
Его значение должно отвечать условно стационарности (2.8).
Т обс
К
λ
К
Рис. 2.4
Средняя длина очереди в блоке ожидания
L  β0
(λ Т обс) K  1


2
K !K 1 -
λ Т обс 
K
,


где β0  стационарная вероятность того, что в СМО нет заявок. Эта вероятность определяется в виде
β0 =
1
К
K-1
(λ T обс )
(λ T обс )
 
λT
m!
K !(1 - обс ) m 0
K
m
.
Остальные характеристики вычисляются через параметры СМО следующим образом:
М = L + K·ρ ; Т ож =
L
; Т пр = Т ож + Т обс .
λ
Многоканальную СМО можно поставить в соответствие, например,
многопроцессорному блоку вычислительной системы, имеющему общую
память для всех процессоров и, следовательно, общую очередь задач.
2.3. Сети массового обслуживания
16
Сеть массового обслуживания представляет собой совокупность конечного числа N обслуживающих узлов, в которой циркулируют заявки, переходящие в соответствии с маршрутной матрицей из одного узла в другой.
Узел всегда является разомкнутой СМО (причем СМО может быть любого класса). Отдельные СМО отображают функционально самостоятельные
части реальной системы, связи между СМО  структуру системы, а требования, циркулирующие по СеМО,  составляющие материальных потоков.
СеМО классифицируют по нескольким признакам (рис. 2.5).
СеМО
Линейные
Замкнутые
Разомкнутые
Однородные
Экспоненциальные
Неэкспоненциальные
Нелинейные
Комбинированные
Неоднородные
Приоритетные
Бесприоритетные
Рис. 2.5. Классификация СеМО
Сеть называется линейной, если интенсивности потоков заявок в узлах
связаны между собой линейной зависимостью  j   ij  i , где ij  коэффициент пропорциональности, или относительно источника  j   j  0 .
Коэффициент  j (коэффициент передачи) характеризует долю заявок,
поступающих в j-й узел от источника заявок, либо среднее число прохождений заявки через данный узел за время ее нахождения в сети.
Если интенсивности потоков заявок в узлах сети связаны нелинейной
зависимостью (например,  j   j  0 ), то сеть называется нелинейной.
Сеть всегда линейна, если в ней заявки не теряются и не размножаются.
17
Разомкнутая сеть – это такая отрытая сеть, в которую заявки поступают из внешней среды и из которой уходят после обслуживания во внешнюю среду. Особенностью разомкнутой СеМО (РСеМО) является наличие
одного или нескольких независимых внешних источников, которые генерируют заявки, поступающие в сеть, независимо от того, сколько заявок уже
находится в сети. В любой момент времени в РСеМО может находиться произвольное число заявок (от 0 до  ).
В замкнутой СеМО (ЗСеМО) циркулирует фиксированное число заявок, а независимый внешний источник отсутствует. Исходя из физических
соображений, в ЗСеМО выбирается внешняя дуга, на которой отмечается
псевдонулевая точка, относительно которой могут измеряться временные характеристики. Число заявок в замкнутой сети постоянно.
Комбинированная сеть – это сеть, в которой постоянно циркулирует
определенное число заявок и есть заявки, поступающие от внешних независимых источников.
В однородной сети циркулируют заявки одного класса. В неоднородной
сети могут присутствовать заявки нескольких классов. Заявки относятся к
разным классам, если они различаются хотя бы одним из следующих атрибутов:
– законом распределения длительности обслуживания в узлах;
– приоритетами;
– маршрутами (путями движения заявок в сети).
В экспоненциальной сети длительности обслуживания во всех узлах
распределены по экспоненциальному закону и потоки, поступающие в разомкнутую сеть, простейшие (пуассоновские). Во всех остальных случаях сеть
является неэкспоненциальной.
Если хотя бы в одном узле осуществляется приоритетное обслуживание, то это – приоритетная сеть. Приоритет – это признак, определяющий
очередность обслуживания. Если заявки в узлах обслуживаются в порядке
поступления, то такая сеть называется бесприоритетной.
Таким образом, экспоненциальной будем называть СеМО, отвечающую следующим требованиям:
– входные потоки СеМО пуассоновские;
– во всех N СМО время обслуживания заявок имеет экспоненциальную
функцию распределения вероятностей, заявки обслуживаются в порядке
прихода;
18
– переход заявки с выхода i-й на вход j-й СМО является независимым
случайным событием, имеющим вероятность p ij , i, j  1, N ; pi 0 – вероятность ухода заявки из CeМО.
Для наглядного представления СеМО используется граф, вершины которого (узлы) соответствуют отдельным СМО, а дуги отображают связи
между узлами.
2.4. Анализ разомкнутых экспоненциальных СЕМО
2.4.1. Свойства разомкнутой экспоненциальной СеМО
Приведем еще раз определение сети массового обслуживания. СеМО
называют совокупность СМО, в которой заявки с выходов одних СМО могут
поступать на входы других. Входными потоками заявок СеМО будем называть потоки, поступающие на входы отдельных СМО из внешней среды
СеМО, т. е. не с выхода какой-либо СМО. В общем случае число входных
потоков СеМО равно числу СМО.
Разомкнутая экспоненциальная СеМО задается следующими параметрами:
1) числом СМО N;
2) числом K1, …, KN каналов в СМО (1, …, N);
3) матрицей P  p ij вероятностей передач, i = 1, …, N; j = 0, …, N;
4) интенсивностями входных потоков заявок I1, …, IN;
5) средними временами обслуживания заявок в СМО Tобс1,
, TобсN .
Например, СеМО, изображенная на рис. 2.6, будет задана численно в следующем виде:
1) N = 3;
2) K1 = 1; K2 = 1; K3 = 2;
0
1
2
3
1 0,1 0 0,5 0, 4
0 ;
3) P  2 0 1 0
3 0 1 0
0
4) I1 = 1; I2 = 0; I3 = 0;
5) Tобс1 = 0,07; Tобс2 = 0,06; Tобс3 = 0,35.
19
I1
Tобс1
P10
P13
Tобс2
P12
Tобс3
Рис. 2.6
С помощью СеМО можно промоделировать, например, вычислительную систему в РИСУ. Тогда входные потоки заявок СеМО будут изображать
запросы, поступающие на вход вычислительной системы, отдельные СМО
будут соответствовать этапам их обработки на устройствах (процессорах, периферийных устройствах и др.), выходные заявки СеМО – результатам обработки запросов.
В экспоненциальной СеМО поток заявок на входе СМО складывается
из входного потока СеМО (возможно, имеющего нулевую интенсивность) и
потоков, поступающих с выходов других СМО, и может отличаться от пуассоновского. Это значит, что СМО в сети не экспоненциальные. Тем не менее,
довольно часто считают, что СМО ведут себя в ней во многом как экспоненциальные. В частности, характеристики СМО отвечают выражениям (1.2)–
(1.8), поэтому для их расчета в заданной СеМО достаточно найти интенсивности 1 , ,  N входных потоков СМО.
Интенсивности 1 ,
,  N определяются на основе уравнений баланса
сети с учетом простых свойств слияния и разветвления потоков. При слиянии
n потоков заявок с интенсивностями 1, ,  N образуется поток, имеющий
интенсивность   1 
  N . При ветвлении потока с интенсивностью λ на
n направлений, вероятности перехода заявки в которые равны p1 ,
разуется n потоков c интенсивностями p1 ,
, pn , об-
, pn соответственно.
В любой фиксированной части стационарной СеМО среднее число заявок постоянно. Отсюда следует, что суммарная интенсивность входящих в
эту часть потоков равна суммарной интенсивности выходящих. Запись данного закона в математической форме называется уравнением баланса. Выделяя в СеМО различные части и составляя для них уравнения баланса, можно
20
получить систему уравнений, связывающую неизвестные интенсивности
1 , ,  N c известными I1, …, IN. Обычно при этом в качестве отдельных
частей СеМО выделяют все СМО. В этом случае для N неизвестных имеется
N уравнений. Можно добавить к ним уравнение баланса для входных и выходных потоков всей СеМО. Тогда получится N + 1 уравнение, и одно из них
можно использовать в качестве проверочного.
Например, баланс интенсивностей в сети, изображенной на рис. 2.1,
можно учесть, обозначая интенсивности на входах и выходах СМО и СеМО
так, как показано на рис. 2.7. Применяя свойства слияния и ветвления потоков, запишем:
1  I1   2  3; I1  p101;
(2.9)
 2  p121; 3  p131.
I1
1
1
p10
p13
2
2
3
p12
3
Рис. 2.7
При известных I1 = 1, р10 = 0,1, р12 = 0,5, р13 = 0,4 из последних трёх
уравнений находим λ1 = 10, λ2 = 5, λ3 = 4. Используя первое уравнение в
(2.9) для проверки, подставляем в него найденные значения интенсивностей
и получаем тождество 10 = 1 + 5 + 4, подтверждающее правильность вычислений.
Проверка стационарности СеМО. СеМО стационарна, если стационарны все СМО, т. е. если
 j  1, j  1, N .
(2.10)
Проверить эти условия после того, как определены  j , не составляет
труда. Например, для СеМО, изображенной на рис. 2.8, условие (2.10) выполняется, поскольку
1  1Tобс1  10  0,07  0,7 ;
3   3Tобс3  2   4  0,35  2  0,7 .
2   2Tобс2  5  0,06  0,3 ;
21
Для стационарной экспоненциальной СеМО с известными интенсивностями λj расчёт локальных характеристик сводится к применению формул
(1.2)–(1.8). Например, для СеМО, приведенной на рис. 2.7 находим:
ρ1 = 0,7;
ρ2 = 0,3;
L1 = 1,63;
L2 = 0,13;
M1 = 2,33;
M2 = 0,43;
Tож1 = 0,163;
Tож2 = 0,026;
Tпр1 = 0,233;
Tпр2 = 0,086;
3 = 0,7; 0 = 0,176; L3 = 0,402; M3 = 1,802; Tож3 = 0,1; Tпр3 = 0,45.
Контрольные вопросы
1. Какую функцию распределения вероятностей имеет время обслуживания в
одноканальной экспоненциальной СМО с параметрами λ и Tобс ?
2. Перечислите характеристики СМО.
3. Какой характер имеет зависимость характеристик М, λ, Tпр от ρ в одноканальной экспоненциальной СМО?
4. Подстановка K = 1 в (2.2)–(2.8) должна дать формулы для расчёта характеристик одноканальной СМО. Проверьте, так ли это.
5. Что такое экспоненциальная СеМО?
6. Что такое уравнения баланса, и для чего они применяются?
3. Пример: расчет системы телеобработки данных
В качестве примера практического применения аппарата РСеМО рассмотрим задачу, заключающуюся в обоснованном выборе аппаратуры передачи данных (модема) и системного блока центрального вычислительного
комплекса из соответствующих унифицированных рядов для комплексирования системы телеобработки заданий.
Задания поступают от отдельных терминалов на концентратор в виде
потоков запросов (требований). Будем полагать, что концентратор представляет собой статистический мультиплексор/демультиплексор и обеспечивает
суммирование поступающих от терминалов парциальных потоков заданий и
распределение ответов с решениями по источникам запросов. Полагаем, что
любой источник выдает новый запрос только после получения соответствующего ответа на ранее переданный запрос, т. е. источники имеют единичные
емкости. Это позволяет оценивать среднее время задержки на концентраторе
по суммарной интенсивности потока запросов, поскольку в силу единичной
емкости источников на концентратор поступает либо запрос, либо ответ на
него с решением.
22
Примем также, что запросы и ответы с решениями имеют фиксированный объем и передача запросов и ответов по каналу связи происходит без
ошибок. Точнее, их влиянием на конечный результат в рамках поставленной
задачи пренебрегаем.
В рамках приведенных ограничений решаем следующую задачу: из
унифицированных устройств аппаратуры передачи данных (АПД) (модемов)
и системных компьютерных блоков выбрать такие, которые обеспечили бы
получение ответа на запрос за время, среднее значение которого не превышало бы заданного значения. Будем также полагать, что естественным ограничением по умолчанию является обеспечение наименьшей стоимости реализации системы.
3.1. Задание
Дано:
 структура системы телеобработки данных (СТОД) (рис. 3.1), где Т –
терминалы; К – концентратор; АПД (модем) – аппаратура передачи данных;
КС – канал связи; ЦВК – центральный вычислительный комплекс;
 суммарный поток требований (запросов), поступающих от терминалов через концентратор на вход АПД, – пуассоновский с интенсивностью
I вх ;
 объем запроса – Bз , байт;
 объем результата решения – Bр , байт;
 скорость АПД – v j , j  1,
, J.
Т
Т
К
АПД
КС
АПД
ЦВК
Т
Рис. 3.1
Характеристики решаемых задач:
 трудоемкость алгоритма (число машинных операций) – Qk , k 
 1,
, K;
 число обращений за данными – Dk , k  1,
, K;
 вероятность прохождения k-го алгоритма – pk , k  1,
, K;
23
 структура ЦВК (рис. 3.2), где ПР–ОП – процессор–оперативная память (системный блок); ВЗУ – внешнее запоминающее устройство. ВЗУ1
хранит данные; ВЗУ2 хранит программы задач;
 интенсивность обслуживания: на ВЗУ1 – 1 , на ВЗУ2 –  2 , 1/c;
 быстродействие процессора – wi , i  1,
, I , операций/с;
 допустимое время получения ответа – Tдоп .
Поток запросов
Поток решений
Очередь
ПР–ОП
ВЗУ1
Очередь
ВЗУ2
Очередь
Рис. 3.2
Требуется: выбрать процессор из ряда wi , i  1,
v j , j  1,
, I , и АПД из ряда
, J , так, чтобы среднее время получения ответа с решением
отв i, j  удовлетворяло условию Tдоп  отв i, j  .
3.2. Решение
Время получения ответа отв i, j  складывается из времени задержки
задания/ответа с решением на концентраторе k  j  , времен передачи задания
зпрд j  и ответа рпрд j  и времени ЦВК i  , затрачиваемого на решение за-
дания на ЦВК:
отв i, j   зпрд j   рпрд j   ЦВКi   k  j  ,
где j – номинал скорости передачи АПД, двоичных знаков/с; i – номинал быстродействия ПР–ОП, операций/с.
Поскольку АПД обеспечивает дуплексный канал,
8Bр
8B
зпрд j   з ; рпрд j  
.
V
V
j
j
Для оценивания значений ЦВК i  и k  j  требуется формализовать
процесс решения.
Задержка на концентраторе может возникнуть из-за ожидания передачи
задания либо ответа с решением источнику по причине занятости канала передачи данных. Формализуем работу концентратора экспоненциальной одно-
24
канальной однородной СМО (см. рис. 1.2). Среднее время обслуживания для
такой СМО определяется средним временем занятости АПД, которое определим в виде
Tk 

8 Bз  Bр
2V j
,
и среднее время задержки на концентраторе определим как среднее
время ожидания в очереди, согласно (1.6):


2
16 Bз  Bр I вх
T I T
.
k  j   k вх k 
1  I вхTk V j V j  4 Bз  Bр I вх


 
(3.1)
Отметим, что при расчете нужно следить за тем, чтобы выполнялось


соотношение 4 Bз  Bр I вх  1 , поскольку мы рассматриваем стационарную
СМО.
Для формализации расчета ЦВК используем схему разомкнутой сети
массового обслуживания (рис. 3.3), где S1 отображает ПР–ОП; S2 отображает
ВЗУ1; S3 отображает ВЗУ2.
Iвх
1
2
3
S1
S2
S3
1
2
p10
p12
Iвых
p13
3
Рис. 3.3
СеМО, изображенная на рис. 3.3, задается следующими параметрами:
1) числом N СМО – N = 3;
2) числом каналов обслуживания в каждой СМО ai  1, i  1, 2, 3 ;
3) матрицей P  pij вероятностей передачи i, j  0, N , 0 – внешняя
среда;
4) интенсивностями I1
I n входных потоков – здесь I1  I вх ;
5) средними временами обслуживания Tобс1 ,
, TобсN заявок в СМО –
здесь Tобс1  Tпроц ( Tпроц – время обслуживания отдельного требования на
процессоре, зависит от значения производительности wi ),
Tобс2  TВЗУ1  1  ВЗУ1 ; Tобс3  TВЗУ2  1 ВЗУ2 .
25
Среднее время пребывания заявки в СеМО рассчитывается по формуле
ЦВК 
1
I
N
  jTпреб j  ,
j 1
где I  I1  I 2 
 I n ; здесь I  I вх , Tпреб j  – время пребывания заяв-
ки
в j-й СМО, j = 1, 2, 3.
Необходимо найти интенсивности 1 ,  2 ,  3 и Tпреб1, Tпреб2 , Tпреб3 .
Рассмотрим алгоритм расчета среднего времени пребывания заявки в
ЦВК:
1. Интенсивности 1 ,  2 ,  3 определяются на основе уравнений баланса сети с учетом свойств слияния и разветвления потоков. Слияние и разветвление задаются матрицей переходов Р. В нашем случае, согласно
рис. 3.3,
0 1 0
0
p
0 p12 p13
P  10
.
0 1 0
0
0 1 0
0
1.1. Система уравнений баланса. Для сети без потерь I вх  I вых ,
 jвх   jвых , j  1, 2, 3 :
1  I вх   2  3 ;
 2  1 p12 ;
(3.2)
3  1 p13 ;
I вх  I вых  1 p10 .
1.2. Решение системы (3.2):
p
1
1  I вх
 1I вх ;  2  1 p12  I вх 12   2 I вх ;
p10
p10
3  1 p13  I вх
p13
 3 I вх ,
p10
(3.3)
где  j – передаточные коэффициенты. Заявка входит в сеть. Ее маршрут в сети случаен, поэтому случайно и число проходов заявки через j-ю
СМО. Среднее число проходов  j называется передаточным коэффициентом.
26
1.3. Усредним число обращений за данными по всем задачам (запросам). Среднее число обращений к данным на ВЗУ1
k
D   Pi Di .
(3.4)
i 1
Как видно из рис. 3.4, в процессе решения задача как бы «проходит»
через ПР–ОП  D  2  раз: 1 раз идентифицируется и обращается к ВЗУ2 (за
программой), D раз прерывается для обращения за данными к ВЗУ1 и 1 раз
обработка задания завершается и готовое решение выходит из СМО S1 во
внешнюю среду.
ПР–ОП
Запрос
Решение
ВЗУ2
D раз
ВЗУ1
Рис. 3.4
1.4. Следовательно, переходные вероятности можно теперь определить
в виде
D
1
1
; p12 
; p13 
.
(3.5)
D2
D2
D2
1.5. Согласно (3.3) и (3.5), имеем выражения для передаточных коэф-
p10 
фициентов: a1  D  2 , a2  D , a3  1.
1.6. И соответственно,
1  1I вх   D  2  I вх ;  2  2 I вх  DI вх ; 3  3 I вх .
(3.6)
Теперь можно записать:
ЦВК 
1
I вх
3
3
 iTпрi    iTпрi  .
i 1
(3.7)
i 1
2. Определение Tпр (время пребывания заявки в СМО).
2.1. Для экспоненциальной СМО
Tпр 
1
,
 1   
(3.8)
27
где  – интенсивность обслуживания заявки.
2.2. Здесь     – коэффициент загрузки,
   Tобс .
(3.9)
2.3. Определим время обслуживания отдельного запроса на ПР–ОП
(S1):
2.3.1. Средняя трудоемкость решения задачи
Q
K
 pk Qk .
(3.10)
k 1
2.3.2. Трудоемкость обслуживания отдельного обращения
Q
.
(3.11)
D2
2.3.3. Время обслуживания отдельного обращения при быстродействии
процессора wi , i  1, , I ,
Q1 
Tобс i  
Q1
.
wi
(3.12)
2.4. Интенсивности обслуживания  2 и  3 заданы на ВЗУ1 и ВЗУ2 соответственно, тогда
1i   1Tобс1 i  ;
(3.13)
2   2  2 ;
(3.14)
3   3 3 .
(3.15)
2.5. Времена пребывания отдельного обращения (требования) в соответствующих СМО
Tобс1 i 
Q1
1
Tпр1 


;
(3.16)
1 1  1  1  1 i  wi  1Q1
Tпр 2  
1
1

 ВЗУ1 1  2   2   2
(3.17)
Tпр 3 
1
1

 ВЗУ2 1  3  3  3
(3.18)
Таким образом, определены передаточные коэффициенты ai , i  1, 2, 3 ,
и времена пребывания отдельных требований Tпр1 , Tпр 2  , Tпр 3 в соответствующих СМО. Подставим выражения для нахождения этих величин в (3.7)
и определим ЦВК .
28
3. Время решения задачи на ЦВК
ЦВК1 
3
  jTпрji    D  2  w
j 1
i
Q1
1
1
. (3.19)
D

 1Q1
 2   2 3   3
4. Итак, составляющие времени ответа с решением определены.
Напомним, что общее среднее время ответа складывается из времен передачи
запроса и решения, времени задержки на концентраторе (3.1) и времени получения решения на ЦВК (3.19):
8
(3.20)
отв j , i  
Bз  Bр  TЦВК i   kj .
Vj


Это общее время получения ответа на запрос должно удовлетворять
условию
(3.21)
отв j , i   Tдоп
и задавать допустимый вариант комплексирования АПД и ЦВК.
Приведем основные шаги последовательности расчета среднего времени пребывания заявки в ЦВК:
Преамбула: формализация системы ЦВК в виде РСеМО.
1. Нахождение интенсивностей входных потоков отдельных СМО: 1 ,
 2 , 3 :
1.1. Построение системы уравнений баланса (3.2).
1.2. Решение системы уравнений баланса (3.3).
1.3. Усреднение числа обращений за данными на ВЗУ1 (3.4).
1.4. Вычисление переходных вероятностей (3.5).
1.5. Определение значений передаточных коэффициентов.
1.6. Определение интенсивностей входных потоков отдельных СМО
(3.6).
2. Определение времени пребывания требований в СМО S1, S2, S3:
2.1. Нахождение времени пребывания заявки в системе отдельной СМО
(3.8).
2.2. Определение коэффициента загрузки (3.9).
2.3. Определение времени обслуживания отдельного запроса:
2.3.1. Определение средней трудоемкости решения задачи (3.10).
2.3.2. Определение средней трудоемкости обслуживания отдельного
обращения (3.11).
2.3.3. Определение времени обслуживания отдельного запроса (3.12).
2.3.4. Определение коэффициентов загрузки S1, S2, S3 (3.13)–(3.15).
29
2.3.5. Определение времени пребывания отдельного обращения (требования) в соответствующей СМО (3.16)–(3.18).
3. Вычисление среднего времени, затрачиваемого на получение решения в ЦВК по запросу (3.19).
4. Выражение для вычисления общего времени ответа на запрос (3.20).
5. Условие для комплексирования вариантов АПД и процессоров в систему (3.21).
Отметим довольно универсальный характер рассмотренной схемы расчета. Концептуально к схеме СТОД (см. рис. 3.1) можно свести топологию
локальной сети (ЛС) технологии «клиент – сервер»: терминалы – рабочие
станции ЛС, канал ПД (АПД + КС) – моноканал ЛС (общая среда передачи),
ЦВК – сервер. Величину
  1 отв j , i 
можно рассматривать как оценку производительности локальной сети.
4. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ СИСТЕМ МАССОВОГО
ОБСЛУЖИВАНИЯ
Имитационное моделирование (ИМ) — это метод исследования, который основан на том, что анализируемая динамическая система заменяется
имитатором, и с ним производятся эксперименты для получения сведений об
изучаемой системе. Роль имитатора зачастую выполняет программа ЭВМ.
4.1. Система массового обслуживания как модель и оригинал
Система массового обслуживания (СМО) – одна из основных моделей,
используемой инженерами – системотехниками, Заявки (требования) на обслуживание поступают через постоянные или случайные интервалы времени.
Приборы (каналы) служат для обслуживания этих заявок. Обслуживание
длится некоторое время, постоянное или случайное. Если в момент поступления заявки все приборы заняты, заявка помещается в ячейку буфера и ждет
там начала обслуживания. Заявки, находящиеся в буфере, составляют очередь на обслуживание. Если все ячейки буфера заняты, заявка получает отказ в обслуживании и теряется. Вероятность потери заявки (вероятность отказа) - одна из основных характеристик СМО. Другие характеристики: среднее время ожидания начала обслуживания, средняя длина очереди, коэффициент загрузки прибора (доля времени, в течение которого прибор занят обслуживанием) и т.д.
30
В терминах СМО описываются любые реальные системы, где возможны очереди и (или) отказы в обслуживании.
В вычислительной системе роль обслуживающего прибора играет
ЭВМ, роль заявок - решаемые задачи. Источником заявок служат терминалы
пользователей. Моментом выдачи заявки является момент нажатия клавиши
для подачи директивы о запуске подачи на решение. Операционная системы
ЭВМ исполняет роль диспетчера: определяет очередность решения задач. В
роли ячеек буфера выступают ячейки памяти ЭВМ, хранящие сведения о задачах, требующих решения.
СМО как модель рассматривается в теории массового обслуживания.
При этом оригиналом являются реальные системы: вычислительные, производственные, транспортные и т.д. Целью использования СМО как модели является анализ качества функционирования указанных систем-оригиналов. В
относительно простых случаях анализ можно провести аналитическими методами (т.е. по формулам) с помощью теории массового обслуживания. Но в
более сложных случаях приходится прибегать к моделированию на ЭВМ,
чтобы определить вероятность потери заявки, коэффициент загрузки прибора
и другие характеристики СМО.
Имитационная модель СМО - это программа для ЭВМ, воспроизводящая шаг за шагом процесс поступления заявок, взятия их на обслуживание и
завершения обслуживания, сопровождающегося освобождением прибора.
Эти события имитируются в ЭВМ в том же порядке, в каком они происходят
в реальности. Целью имитации процесса функционирования СМО является,
как и при теоретическом анализе, определение вероятности потери заявки,
коэффициента загрузки прибора и других характеристик. Но при имитационном моделировании СМО выступает в роли оригинала, а моделью является
программа имитации или алгоритм, по которому эта программа составлена.
Разработку такой программы и прогон ее на ЭВМ с целью нахождения характеристик СМО принято называть имитационным моделированием (в англоязычной литературе -simulation).
Недостатком имитационного моделирования по сравнению с аналитическими методами является численный характер результатов. Моделирование позволяет получить результат в виде числа при конкретных значениях
исходных данных, тогда как аналитическое исследование дает общий результат в виде формулы.
Моделирование СМО и других систем, где необходим учет случайных
факторов, производится методом статистического моделирования (методом
31
Монте-Карло). Суть этого метода в том, что искомый результат получается
путем осреднения большого числа частных результатов, полученных при
различных значениях случайных факторов, формируемых в соответствии с
их законами распределения. Из-за этого для моделирования требуются большие затраты машинного времени.
При сопоставлении моделирования с аналитическим исследованием
надо учитывать также, что аналитическое исследование доступно лишь высококвалифицированному специалисту, владеющему математическими методами, тогда как имитационное моделирование, особенно если оно производится на основе специальных языков и трансляторов, не требует столь высокой квалификации. Разумеется, квалификация предоставляет большие дополнительные возможности, так как и моделирование, и аналитическое исследование дают наибольший эффект при совместном применении, а для
совместного их применения требуются особые знания и опыт.
4.2. Иллюстративный пример: моделирование посадки самолетов.
Цель: определение необходимого количества посадочных полос.
Самолеты пребывают в зону и подают заявку на посадку в случайные
моменты времени (рис. 4.1).
 – интервал между соседними заявками задается
F ( x)  P(  x) .
Если в момент подачи заявки полоса свободна – начинается процесс
посадки, который длится фиксированное время
 обс
.
В течение этого вре-
мени полоса занята.
Если в момент поступления очередной заявки полоса занята – такая заявка получает отказ. Это нежелательное событие. Если часто отказ – необходима дополнительная полоса. Непосредственная цль моделирования –
нахождение (оценивание) вероятности отказа Р.
Процесс смены состояний – дискретный. Время – непрерывное. Особые моменты – моменты поступления заявок и моменты освобождения полосы.
Имитация процесса на ЭВМ: воспроизведение шаг за шагом численных
значений особых моментов и значений переменных в эти моменты.
В памяти ЭВМ достаточно отвести одну или несколько ячеек для каждой из характеристик имитируемого процесса и обновлять содержимое этих
ячеек, имитируя изменение характеристик во времени.
32
z
1
t
0
 обс

- момент поступления заявки;
- момент окончания обслуживания
- моменты поступления заявок, получающих отказ.

– интервал
 обс
между соседними заявками;
– интервал
обслуживания отдельной заявки.
Рис. 4.1. Имитация процесса посадки самолетов
Перечислим переменные, которые должны хранится и обновляться в
памяти ЭВМ для данного примера:
tт – текущий особый момент;
tз – предстоящий момент поступления очередной
из таких моменов после tт);
tосв – предстоящий момент освобождения полосы;
заявки (ближайший
Z – состояние полося в особый момент (непосредственно перед tт);
n – количество заявок, поступивших к текущему моменту;
к – количество отказов, наблюдавшихся за то же время.
Счетчики n и к накапливают статистики (выборочные данные), по
которым определяется оценка

Р=
к
.
n
Правило остановки процесса имитации: когда значение n достигнет
значения n зад (надо задать).
33
Исходные данные:
n зад ,  обс 
(F(x) – специальная подпро-
грамма). Помимо указанных переменных используются:
-–
n зад ,  обс
, параметры
–– Вспомогательные
F(x) – постоянные;

переменные:
, Е – (event – событие) содержит
тип события: 1 – поступление заявки, 0 – освобождение полосы; Z L (Last –
прошлое) – представляет предыдущее значение Z.
Как следует из приведенного примера, имитация, как процесс, заключается в организации продвижения системного времени и отображения в нем
траектории функционирования оригинала. В данном примере – отображении
процессов генерации заявок и их обслуживании. Функционирование отображается сменой состояний оригинала. Ибо смена состояний дает информацию,
по которой можно вычислить интересующие исследователя (проектировщика) оценки характеристик оригинала.
Если система (оригинал) стохастическая, то пребывание системы в том
или ином состоянии (вектор) и наступление состояний носят вероятностный
характер.
Таким образом, имитационное моделирование включает два важнейших аспекта: построение моделирующего алгоритма и разыгрывание состояний системы. Моделирующий алгоритм обеспечивает продвижение системного времени и отображение состояний системы, а реализация случайных
факторов и объектов, присущих системе, осуществляется методом статистических испытаний – методом Монте-Карло.
Вопросы для самопроверки и задания для упражнения
1. Предложите примеры систем, моделями которых являлись бы СМО с
отказами, с ожиданием и смешанного типа. Укажите, что является заявкой,
прибором, моментом выдачи заявки.
2. Чем отличается относительный приоритет от абсолютного?
3. Предложите примеры систем с приоритетами.
4. С какой целью осуществляется моделирование СМО?
5. При аналитическом исследовании СМО является моделью, а при
имитационном моделировании - оригиналом. Поясните это утверждение. Что
является моделью при имитационном моделировании СМО? Какие существенные черты оригинала сохранены в этой модели?
34
6. Почему прибегают к имитационному моделированию СМО, а не
ограничиваются аналитическим исследованием методами теории массового
обслуживания?
7. Каковы преимущества и недостатки имитационного моделирования
по сравнению с аналитическим исследованием?
4.3. Концепция статистического моделирования
В основе статистического моделирования лежит процедура, применяемая для моделирования случайных величин и функций и носящая название
метода статистических испытаний (метод Монте-Карло).
Общая схема метода Монте-Карло может быть записана в виде
1
   y( x ) p( x )dx   
M
~
M
 y(x ),
i 1
i
x i  p( x ),
(4.1)
Результат ищется как математическое ожидание некоторой случайной
величины Y, которая чаще всего является неслучайной функцией случайной
величины X, имеющей распределение р(х). Случайная величина Х имеет распределение р(х) и запись Х  р(х) означает, для непрерывной случайной величины, что для непрерывной случайной величины плотность вероятности
равна р(х); для дискретной случайной величины функцию р(х) надо понимать
как функцию вероятности. Для случайной дискретной величины интеграл
(4.1) заменяется суммой у(х) р(х), в которой суммирование осуществляется
по всем возможным значениям Х. Функция у(х) может иметь несколько аргументов, т.е. зависеть от нескольких случайных величин. В таком случае запись (4.1) остается в силе, только интеграл надо считать многомерным, Х
рассматривать как вектор, а р(х) – как многомерную плотность (или функцию) вероятности. Приближенная оценка неизвестного математического
ожидания, совпадающая с искомым результатом, находится как среднее
арифметическое результатов независимых опытов. Это отражено в правой
части (4.1). По закону больших чисел среднее арифметическое сходится к
математическому ожиданию.
В каждом опыте разыгрывается реализация х случайной величины Х (в
i- м опыте реализация x i ) в соответствии с распределением р(х) и вычисляется значение функции в виде у ( x i ). Индекс i подчеркивает, что для каждой
(i-й) реализации процесса аргументы, составляющие вектор Х, имеют свои
случайные значения. Вычисленное очередное значение у ( x i ) добавляется к
35
накапливаемой сумме  у ( x i ). На этом заканчивается очередной опыт. После того как проведено М опытов, вычисляется итоговая оценка в виде правой части выражения (4.1). Опыты повторяются до тех пор, пока дисперсия
~
оценки θ не снизится до требуемой величины, зависящей от допустимой погрешности и коэффициента доверия. Структурная схема эксперимента по
имитационному моделированию представлена на рис. 4.2.
Входные исследуемые процессы
Функции влияния
Базовые величины,
внешние факторы
Датчик случайных
объектов (величин,
процессов)
Выходные
результаты
X
Статистическая
обработка
результатов
Y
Модель системы
Принятые
решения
Организация и управление
экспериментом
Выбор вида исследуемого процесса и воздействия
Результат
текущей
обработки
Рис. 4.2.Структурная схема эксперимента по имитационному
моделированию
4.3. Пример: оценка надежности системы
Проиллюстрируем суть метода Монте-Карло относительно простым
примером. Пусть требуется оценить надежность системы (Рис. 4.3).
Система выполняет свою функцию, если работают цепочки блоков:
1,2,5,7; 1,3,5,7; 1,4,6,7. Каждый блок характеризуется временем безотказной
работы i,
i  1,7.
Пусть заданы плотности распределения рi (i),
i  1,7.
Ка-
кие-то блоки могут отказать. Какова надежность системы в целом?
36
Рассмотрим случайную величину
 = min1, max [min (4, 6), min [max (2, 3),]], 7,
(4.2)
где  - время безотказной работы системы.
2
5
1
3
7
4
6
Рис. 4.3. Блочная структура системы
В одном опыте разыгрывается значения всех i, i  1,7. в соответствии с
рi(i),
i  1,7.
Используя полученные реализации i,
i  1,7. , по формуле (4.2)
вычисляем реализацию . Один опыт дает одну реализацию (одно выборочное значение) . Проводим М опытов (испытаний), получаем «статистический» материал (выборку). Берем среднее арифметическое времени безотказной работы системы ср в качестве оценки надежности системы. При необходимости можно построить закон распределения вероятностей случайной
величины  в виде соответствующей гистограммы.
Таким образом, испытания реальной системы заменены испытаниями
математической модели. Каждое испытание сопровождается расчетом. Поэтому имитационное моделирование и называют численным экспериментом
на ЭВМ с математической моделью (модель выступает как объект исследования). При реализации испытания возможны и логические операции. И расчетные и логические операции реализуются на ЭВМ с помощью соответствующих алгоритмов, которые в совокупности и составляют моделирующий
алгоритм.
Моделирующий алгоритм обеспечивает построение траекторий смены
состояний системы во времени, а воспроизведение случайных факторов,
определяющих эти состояния, конструируется с использованием заданных
37
законов случайных событий и величин и реализуется с помощью датчиков
базовой случайной величины (БСВ).
Вопросы для самопроверки и задания для упражнения
1. Почему метод статистических испытаний применяют при имитационном моделировании?
2. для реализации какой значений какой переменной используется метод Монте-Карло в примере разд 4.2, 4.3?
3. В чем достоинства и недостатки применения метода Монте –Карло?
4. Как Вы думаете, эффективен ли метод статистических испытаний
для разыгрывания маловероятных событий?
5. Построение моделирующего алгоритма
5.1. Моделирование на ЭВМ процесса функционирования СМО
В памяти ЭВМ отводится несколько ячеек для переменных, характеризующих состояние СМО в целом и отдельных её элементов. Содержимое
этих ячеек изменяется в соответствии с алгоритмом моделирования так, как
это происходит в реальной СМО при её функционировании. Отдельная ячейка содержит текущее системное время, указывающее к какому моменту времени относится состояние СМО, записанных в памяти ЭВМ. Содержимое
указанных ячеек памяти меняется путем циклического повторения основной
части алгоритма моделирования, называемой шагом (циклом) имитации. За
один шаг осуществляется переход к следующему значению системного времени, т.е. продвижение по времени, или, как иногда говорят, продвижение
стрелок системных часов. Попутно изменяется значение переменных, характеризующих состояние СМО. Таким образом, шаг за шагом, имитируется
смена состояний СМО, т.е. моделируется процесс функционирования СМО.
Рассмотрим принципы продвижения по времени.
Принцип t – увеличивать системное время за один шаг на постоянную величину t. При использовании этого принципа возникает проблема
выбора длины интервала t. Как правило, алгоритм шага рассчитан на имитацию одного события: поступления заявки, завершения фазы обслуживания
и т.п. Событие - это любое изменение в системе. Все изменения, связанные
друг с другом причинно-следственными связями и происходящие в один и
тот же момент времени, обычно рассматриваются как одно событие. Допустим, поступила заявка. При этом увеличилось число заявок в системе. Если
эта заявка сразу поступила на обслуживание, то изменилось состояние при38
бора и количество занятых приборов. Все это - одно событие: поступление
заявки.
Может случится, что за время t в СМО произойдет несколько событий
(в разное время). В таком случае алгоритм, рассчитанный на имитацию одного события за один шаг, неправильно отразит изменения, произошедшие в
системе. Чтобы избежать этого есть два пути.
Первый путь - разработка алгоритма шага, рассчитанного на имитацию
нескольких событий. Этот путь приводит к значительному усложнению алгоритма.
Другой путь - использование столь малого интервала t , что за это
время практически не происходит более одного события. Этот путь приводит
к резкому увеличению затрат машинного времени, т.к. с уменьшением t соответственно возрастает число шагов, которое надо выполнить, чтобы имитировать процесс на заданном отрезке времени. При малом t большинство
шагов окажутся пустыми, так как события будут происходить лишь на некоторых интервалах t , а на прочих интервалах состояния СМО будет сохраняться таким же, как на соседних интервалах.
Принцип особых моментов. Последнее замечание наводит на мысль,
что целесообразно проскакивать за один шаг весь промежуток времени между соседними событиями и тем самым избегать пустых шагов. Это - принцип
особых моментов. Особым моментом принято называть такой момент времени, когда в системе происходит какое-либо изменение состояния, иначе
говоря - происходит событие. За один шаг осуществляется продвижение по
времени на случайный отрезок: от одного особого момента до другого.
Рис.5.1. демонстрирует способы представления и управления временем
в обоих случаях.
По оси x времени отложена одна и та же последовательность событий
ei . Как видно, два события e4 и e5 появляются одновременно. Стрелки указывают на точки, в которых происходит приращение времени на один такт, и
моменты наступления очередных событий в обеих моделях.
В модели, использующей принцип особых моментов (Рис.5.1,б), имитируемое время при изменении сдвигается вперед точно на момент наступления самого раннего из последующих событий.
Никаких жестких и достаточно эффективных правил определения какой из двух методов задания временных шагов лучше нет. В каждом кон-
39
кретном случае метод выбирается разработчиком в зависимости от характера
системы, которую необходимо моделировать.
е1
е2
t
0
е3
е4=е5
е6
S3
S4
S5
t
S1
S2
Рис. 5.1,а. Течение модельного времени в модели с фиксированным
Шагом (принцип t)
е1
е2
е3
е4=е5
е6
время
0
S1
S2
S3
S4
S5
Рис. 5.1,б. Течение модельного времени в модели с шагом до следующего
события (принцип особых моментов)
Тем не менее, принцип t работает лучше, если:
1) события появляются регулярно и распределены во времени относительно равномерно;
2) в течение шага (цикла) моделирования появляется много событий,
причем математическое ожидание продолжительности событий мало;
3) точная природа существенных событий не ясна;
С другой стороны, принцип особых моментов выгоден тем, что
1) позволяет экономить машинное время, когда существенные события
могут длительное время не наступать;
2) не требует определения величины приращения времени;
3) может эффективно использоваться при неравномерном распределении событий во времени.
Чтобы ЭВМ могла вычислить очередной особый момент, используется
так называемый календарь. Календарь, или расписание предстоящих событий, - это группа ячеек памяти, где для каждого типа события указан ближайший момент, когда такое событие произойдет. Имея календарь, нетрудно
40
определить очередной особый момент. Это наименьший из моментов, записанных в календаре.
Чтобы заполнить календарь и в дальнейшем корректировать его содержимое, осуществляется планирование событий. Допустим, в текущий момент
поступила заявка и сразу была взята на обслуживание первым прибором, так
как он оказался свободным. Закон распределения времени обслуживания задан наряду с другими данными. Обратившись к специальной подпрограмме датчику случайных чисел, ЭВМ генерирует случайное время обслуживания в
соответствии с указанным законом распределения. Прибавив это время к текущему моменту, ЭВМ вычисляет момент, когда освободится первый прибор, и заносит это число в ячейку календаря, отведенную для первого прибора. Аналогично заполняются другие ячейки календаря.
При моделировании СМО целью является определение характеристик
качества функционирования СМО, например вероятности потери заявки, или
других величин: коэффициента загрузки прибора, средней длины очереди и
т.п. Эти характеристики и вычисляются по окончании имитации на основе
статистик, накопленных в процессе имитации. Примеры статистик: Кз - количество поступивших заявок, Кп - количество потерянных заявок, Тсз - суммарное время занятости прибора. На основании этих статистик можно вы^
числить оценки искомых характеристик: вероятности потери заявки P пот=
^
Кп/Кз и коэффициента загрузки одного прибора P зп= Тсз/Т, где Т - длина реализации, т.е. длительность имитированного процесса. Операторы, осуществляющие пополнение статистик, входят в состав алгоритма шага.
Основная часть алгоритма имитации представляет собой циклическое
повторение шагов имитации до тех пор, пока не будет выполнено условие
остановки. Остановка производится после выполнения заданного числа шагов или достижения заданного значения системного времени (длины реализации). Чем длиннее реализация, тем точнее оценки искомых характеристик.
Рассмотрим организацию цикла на примере моделирования СМО с отказами (рис. 5.1)..
Предполагается получить оценку вероятности потери заявки (вероятности отказа) путем воспроизведения на ЭВМ достаточно длинного отрезка
реализации.
41
Два способа оценивания: по заявкам
Т
Ротк 
Т 1 , где
К от
ТМ
з
Ротк 
К от ;
Кс
– количество заявок, получивших отказ;
количество заявок, поступивших в систему;
прибор находится в занятом состоянии;
ТМ
Т1
по времени
Кс
– общее
– суммарное время, когда
– общее время моделирования.
z
tз
tз
1
toсв
t
0

 обс
Z - состояние системы; Z=0-свободен, Z=1- занят;
- интрвал между заявками;
 обс
- время обслуживания заявки
tз
t - момент поступления заявки
toсв - момент освобождения прибора (канала) обслуживания
tт - текущий момент
Рис. 5.2. Поток заявок, состояние СМО
Цикл, организованный по принципу ∆t (рис.5.3). Перед началом цикла в
памяти хранится:
t з , если Z=0;
toсв, если Z=1. Время измеряется числом
тактов
42
начало
В
да
нет
Z=o
То= То+1
А
Т1= Т1+1
нет
tT=tз
j
tT=tзj
да
да
Ко:= Ко+
Z:=1
 обс
Tобс:=tT+ обс
Кс:= Кс+1
да
Z:=0
tT=toсв

tT:= tT+1
Tз(j+1):= T+
В
Рис. 5.3. Цикл, организованный по принципу ∆ t
Цикл, организованный по принципу особых моментов (рис. 5.4)
Особый момент: поступает заявка, закончено обслуживание заявки
(освобождение прибора). К началу цикла в памяти хранится:
tп – последний особый момент;
tз – момент поступления очередной заявки;
tосв – момент освобождения прибора, следующий за tп, если в момент tп система занята.
Начинается цикл с того, что последний особый момент рассматривается как предыдущий, и определяется очередной особый момент.
43
начало
да
tT=tзj
То= То+(tT- tп)
Z:=1
 обс
нет
Z=o
да
tT < tзj
tT=tзj
Т1= Т1+(tT- tп)
нет
tT=tосв
Т1= Т1+(tT- tп)
Ко:= Ко+1
Z:=0
Tобс:=tT+ обс
Кс:= Кс+1

tз(j+1):= tT+ 
tп:= tT
Рис. 5.4. Цикл, организованный по принципу особых момен
Вопросы и задания
1. Почему принцип особых моментов предпочтительнее, чем принцип t?
2. Что такое календарь и зачем он нужен?
3.Как осуществляется первоначальное заполнение и последующая корректировка календаря?
4. В состав алгоритма шага (цикла) входят следующие части: определение
момента очередного события, изменение состояния системы в целом (имитация события), планирование событий (корректировка календаря) Что еще добавить в указанный перечень?
5.2. Примеры моделирования СМО с отказами
Напомним, что СМО с отказами - это разновидность СМО, отличающаяся отсутствием буферных ячеек (мест для очереди). В такой СМО за44
явка, поступившая в момент, когда все приборы заняты, получает отказ и
теряется. Наибольший интерес при анализе СМО с отказами представляет
вероятность потери заявки Рпот. Кроме нее полезно определить коэффициент загрузки прибора, распределение числа занятых приборов и некоторые
другие характеристики.
5.2.1. Подготовка исходных данных и назначение переменных
Выберем конкретные исходные данные. В системе два прибора. Интервал между заявками  распределен по экспоненциальному закону с математическим ожиданием m=1000 (все интервалы времени будут указываться в одних и тех же условных единицах, под которыми можно подразумевать, например секунды). Время обслуживания заявки постоянно и
равно 2000.
Состояние системы и отдельных приборов описывается следующими переменными:
X1 - состояние первого прибора (0 - свободен, 1 - занят);
X2 - состояние второго прибора (0 - свободен, 1 - занят);
Y - состояние системы по окончании текущего шага
(характеризуется количеством занятых приборов);
Yi - состояние системы по окончании предыдущего шага.
Процесс смены состояний показан на рис 5.5.
Для обозначения типа текущего события будем использовать переменную JT. Будем различать следующие типы событий: поступление заявки (JT= 0), освобождение прибора (JT = 1), освобождение второго прибора
(JT = 2).
Время описывается следующими величинами:
ТТ - момент текущего события;
TL - момент предыдущего события;
ТЗ - предстоящий момент поступления заявки;
Т1 - предстоящий момент освобождения первого прибора;
Т2 - предстоящий момент освобождения второго прибора;
Если первый прибор свободен, то Т1= , так как свободный прибор
никогда не освободится. Аналогично для второго прибора: Т2= , если он
свободен. Бесконечность записывается в ЭВМ достаточно большим числом, заведомо превышающим возможные значения ТТ. Календарь в этом
примере состоит из трех переменных: ТЗ ,Т1, Т2.
45
Z1
Z2
Y
2
1
0
Рис 5.5. Временные диаграммы смены состояний СМО:
 - моменты поступления обслуженных заявок;
х- моменты поступления потерянных заявок;
 - моменты освобождения приборов
В процессе имитации накапливаются следующие статистики:
Кз - количество поступивших заявок;
Кпот - количество потерянных заявок;
S0 - суммарное время, в течение которого оба прибора свободны;
S1 - суммарное время, в течение которого занят один прибор;
S2 - суммарное время, в течение которого заняты оба прибора.
На основе этих статистик можно вычислить оценки (приближенные
значения) следующих характеристик:
Рпот = Кпот/Кз – вероятности потери заявки;
Р0 = S0/Tт – вероятности того, что в произвольный момент оба прибора свободны,;
Р1 = S1/Tт – вероятности того, что занят один прибор;
Р2 = S2/Tт – вероятности полной занятости (заняты оба прибора).
46
Здесь Тт - то значение текущего системного времени, которое достигнуто на момент окончания имитации. Заметим, что Р2 также является оценкой вероятности потери заявки, поскольку при полной занятости системы заявка теряется. Эту оценку называют оценкой по времени, в отличие от Рпот,
которую называют оценкой по заявкам. Коэффициент загрузки прибора можно определить как среднюю долю числа занятых приборов в общем числе
приборов. При двух приборах эта величина определяется по формуле
Рзп = (0*Р0 +1*Р1+2*Р2)/2 = (Р1 + 2Р2)/2
В принципе это то же самое, что доля времени, в течение которой
прибор занят, а также вероятность занятости прибора в произвольный момент, но только при условии, что для обоих приборов эти вероятности
одинаковы. В описанном ниже алгоритме при обоих свободных приборах
занимается всегда первый прибор, поэтому он занят в среднем чаще, чем
второй. В таких случаях, когда коэффициент загрузки приборов неодинаков, указанная величина Рзп дает осредненный коэффициент загрузки.
Добавим еще несколько обозначений:
N - номер шага,
DT - интервал времени между текущим и предыдущим событиями.
Теперь можно перейти к описанию алгоритма. Рассмотрим два варианта
построения алгоритма: по схеме событий и по схеме процессов.
5.2.2. Моделирование СМО с отказами по схеме событий
5.2.2.1. Построение блок-схем алгоритма имитации
На рис. 5.6 — 5.10 приведены блок-схемы алгоритмов имитации.
47
Вход
Подготовка: ввод исходн. данных;
установка начальн. значений
1
Шаг имитации
2
3
Условие остановки
выполнено
Вычисление оценок
4
5
Выдача результатов
(печать)
6
1
7Повторение
моделирования
на основе
других
значений
случайных
чисел с тем
же законом
распределения
88
Изменение
числа
опытов
N
Меню
2
3
4
99
Изменение
параметров
и / или
законов
распределения
10
Конец
работы
выход
Рис.5.6 Блок –схема алгоритма имитации СМО М/М/2
48
Вход
N:=N+1; YL:=Y; TL:=tT
2.1
tT:=min (TЗ, T1, T2)
2.2
JT=0
JT=2
JT=1
2.5
Обработка поступившей
заявки
2.4
2.6
В памяти хранятся
спланированные зн
чения TЗ, T1, T2
Обработка окончания
обслуживания 2-го прибора
Обработка окончания
обслуживания 1-го прибора
Пополнение суммарного
5.3.2. времени
пребывания в соответствующем
состоянии
3
N<Nзад
нет
Выход
Рис. 5.7.Блок-схема алгоритма шага имитации
(схема событий, СМО, М / D / 2)
JT=0
=0
да
нет
нет
Y<2
Ко:= Ко+1
Z1=0j
да
Z2:=1
Z1:=1
Т1= tT +
 обс
Y:=Y+1
Т2= tT +
 обс
Кз:= Кз+1
ТЗ:= t T+

Рис.5.8. Блок-схема частного алгоритма «Обработка поступившей заявки»
49
JT = 2
JT = 1
Z2:=0
Z1:=0

Т1:=
Y := Y - 1
Выход
JT = 1VJT = 2
Рис. 5.9. Блок-схема частного алгоритма «Обработка окончания
обслуживания 1-го и 2-го приборов»
Вход (блок 2.6)
DT := tL - TL
SyL := SyL + DT
TL – предыдущий особый Момент;
DT- интервал времени, в течении которого система находилась в состоянии SyL
Суммируются интервалы времени
нахождения системы в состоянии Sy
Рис. 5.10 Блок- схема частного алгоритма «Пополнение суммарного времени
в соответствующем состоянии»
Алгоритм моделирования записан на псевдокоде. Использованы
общеизвестные конструкции структурного программирования и ступенчатая запись. Блоки одного уровня записываются с одной и той же позиции
строки. Описания внутренних блоков сдвинуты немного вправо. Кон50
струкция строится из кирпичей – модулей. Какие у нас (для шага имитации):
– определение момента и типа события;
– имитация события;
– пополнение статистик;
– планирование событий (корректировка календаря).
5.2.2.2. Моделирование СМО с отказами по схеме событий
(Описание алгоритма)
подготовка:
ввод данных (mt, tобсл,, правило остановки)
установка начальных значений переменных, соответствующих
нулевому шагу
основная часть:
do шаг имитации (подробно раскрыт ниже)
until выполнено условие остановки (напр., пройдено Nдоп
шагов)
end do
вычисление оценок искомых характеристик (Рпот, Р0, Р1, Р2, Рзп
указанным выше формулам)
завершение:
выдача результатов
запрос пользователю на выбор дальнейшего действия (выдача
меню) и переход в соответствующее место программы в
зависимости от ответа пользователя)
end моделирования.
Далее раскрыт алгоритм шага имитации
Шаг имитации
увеличение номера шага (N:=N + 1)
запоминание значений некоторых переменных (YL:=Y; TL:=TT)
определение момента и типа очередного события:
TT := min(Tз,Т1,Т2);
0, Т Т  Т З
JT:= 1, Т Т  Т!
2, Т  Т
Т
2

имитация события:
51
if поступила заявка (JT=
then if есть свободный прибор (Y<2)
then поиск номера свободного прибора (Jv), начиная
с первого прибора
занятие прибора Jv (Х Jv :=1)
увеличение числа занятых приборов (Y:=Y+1)
end if
else (освободился прибор Jт)
перевод прибора в свободное состояние (XJт:=0)
уменьшение числа занятых приборов (Y:=Y-1)
end if
пополнение статистик:
if поступила заявка (Jт = 0)
then пополнение счетчика заявок (Кз:=Кз + 1)
if заявка потерялась ( L0 =2)
then пополнение счетчика потерянных заявок
(Кпот:=Кпот+1)
end – if
end - if
пополнение суммарного времени пребывания в соответствующем состоянии (ДТ:=Тт-ТL; S := S  +ДТ)
L
L
планирование событий (корректировка календаря):
if поступила заявка (JT=0)
then планирование следующей заявки (Тз:= TТ+,  получается обращением к датчику случайных чисел)
if заявка поступила в прибор JV (YL<2)
then планирование его освобождения ( TJ :=ТТ+обсл)
V
end – if
else (освободился прибор JТ)
TJ T
:=
end – if
end - шаг
Отметим, что в алгоритме шага четко разделены этапы: имитация
события, пополнение статистик, планирование событий. Если отказаться
от такого разделения, можно избежать повторения некоторых пpoвeрок и
введения переменной ТL. Однако опыт программистов показал, что строй52
ность и четкость важнее экономии. Поэтому приведенный вариант представляется более предпочтительным.
Хотя рассмотренный пример очень прост, он показывает основные
принципы построения моделирующего алгоритма, пригодные и для более
сложных случаев. Перечислим эти принципы. За один шаг имитируется
одно событие. Каждому шагу соответствует определенное (текущее) значение системного времени ТТ - тот особый момент, когда происходит имитируемое на этом шаге событие. Продвижение по времени за один шаг
производятся от момента предыдущего события до момента текущего события (принцип особых моментов). Интервал между особыми моментами,
т.е. моментами наступления события, как правило, имеет случайную длину.
Очередной особый момент находится путем поиска минимума в календаре. Календарь содержит по одной ячейке для каждого типа события.
В нем указаны ближайшие после ТТ моменты наступления событий. Если
состояние системы в текущий момент таково, что данное событие принципиально произойти не может (например, свободный прибор не может
освободиться), то в соответствующей ячейке календаря записывается бесконечность. В машине бесконечность представляется очень большим числом, заведомо превышающим значения системного времени, достигаемые
в процессе имитации.
Тип события, которое подлежит имитации на текущем шаге, определяется одновременно с моментом события. Если, например, наименьшее
число в календаре оказалось в ячейке, где записывается момент поступления заявки, значит ближайшим событием является поступление заявки и
такое событие следует имитировать на текущем шаге. Имитация события
сводится к изменению значений переменных, описывающих состояние отдельных элементов и системы в целом.
После имитации события производится пополнение (корректировка)
статистик, нужных для последующего вычисления оценок искомых характеристик
Текущее событие может сделать возможным определение моментов
некоторых последующих событий или, как говорят, планирование событий. Допустим, на текущем шаге поступила заявка и сразу была поставлена на обслуживание в прибор. В таком случае можно определить момент
очередного поступления заявки и момент освобождения прибора. Для этого надо к текущему времени прибавить соответственно интервал между за53
явками или время обслуживания. Как правило, интервалы времени являются случайными, и для их определения используется датчик случайных
чисел.
Бывает так, что переменная получает новое значение при выполнении шага, а на более поздних этапах должно использоваться ее прежнее
значение. По этой причине приходится запоминать в отдельных ячейках
значения некоторых переменных в самом начале шага я сохранять их до
конца шага.
Итак, алгоритм шага содержит следующие части: запоминание
значений некоторых переменных, определение момента и типа очередного
события, имитация события, пополнение статистик, планирование событий.
Шаги выполняются до тех пор, пока не будет воспроизведена реализация заданной длины. Длина реализации измеряется либо числом шагов,
либо системным временам. Не исключены и другие правила остановки,
например по количеству обслуженных заявок.
До начала шагов производятся ввод исходных данных и установка
начальных значений переменных, а по окончании шагов - подсчет оценок
искомых характеристик по накопленным статистикам и выдача результатов.
Описанные принципы моделирования пригодны как для простых,
так и .для сложных случаев, но в сложных случаях потребуется трудная
работа по составлений перечня возможных событий и разработке алгоритмов имитации этих событий. Трудность состоит в том, что многие события
оказываются взаимообусловленными и должны рассматриваться как одно
сложное событие, включающее ряд элементарны событий. Рассмотрим,
например, моделирование СМО, в которой имеется буфер. Имитация поступления заявки включает несколько частей: выяснение, имеется ли свободный прибор; поиск свободного прибора и его занятие; в случае отсутствия свободного прибора - поиск и занятие свободной ячейки буфера. Если заявка имеет абсолютный приоритет, возможно вытеснение менее приоритетной заявки из прибора. Тогда надо будет еще учесть дальнейшую
судьбу вытесненной заявки. Таким образом, в рамках одного события
имитируются многие элементарные события, отражающие изменения состояний сразу нескольких объектов: поступившей заявки, прибора, ячейки
6yфеpa, вытесненной заявки.
54
Описанная схема построения моделирующего процесса носит название - схема событий, или принцип событий. Ее основная отличительная
черта - описание возможных изменений в системе с помощью взаимоисключающих (непересекающихся) событий и имитация на каждом шаге одного из возможных событий. Кроме этой схемы используется схема процессов.
Вопросы и задания
1. Составьте программу по описанному алгоритму. Постройте таблицу и временные диаграммы для первых десяти шагов, используя теперь
случайные числа, генерируемые датчиком вашей машины. Затем проведите расчет тех же десяти шагов на ЭВМ с помощью вашей программы. При
отсутствии ошибок результаты должны совпасть. Эта проверка называется
пошаговым тестированием.
2. Вычислите по этой же программе оценку вероятности потери заявки для случая, когда средний интервал между заявками равен длительности обслуживания заявки. Реализация должна быть достаточно длинной,
например 7000 шагов. Сравните полученную оценку с точным значением
вероятности потери заявки, которое в данном случае равно 0.2. Такая проверка называется статистическим тестированием. Подумал те, насколько может оценка отличаться от точного значения, чтобы это расхождение
не вызывало сомнений в правильности программы.
3. Карие еще статистики надо накапливать, чтобы определить среднее время непрерывной занятости системы и средний интервал, в течение
которого система полностью свободна? Как будут выглядеть формулы для
оценки этих величин?
4. Сформулируйте основной признак схемы событий.
5. Какие части в алгоритме шага можно поменять местами?
6. Проведите эксперименты, чтобы сравнить точность двух оценок
вероятности потери заявки: оценки по заявкам и оценки по времени.
5.3. Схемы построения моделирующего алгоритма
Наряду с рассмотренной выше схемой событий, большое распространение получила и схема процессов. Прежде чем рассматривать эту
схему процессов, сформулируем необходимые понятия: событие, работа,
процесс и др.
Событие - это изменение в системе, относящееся к какому-то моменту времени. Применительно к модели это - скачкообразное изменение
55
одной или нескольких дискретных величин либо достижение непрерывно
.изменяющихся величиной заданной границы. Примеры событий: поступление заявки, освобождение прибора, наступление срока хранения скоропортящегося продукта.
Работа - действие, происходящее в моделируемой системе в течение
определенного промежутка времени. Примеры: подготовка заявки, обслуживание заявки в приборе. Время, требующееся для работы, может быть
случайной величиной, но к моменту имитации работы случайная величина
должна получить конкретное значение (с помощью датчика случайных чисел). Работа начинается и заканчиваются событиями.
Отвлечемся слегка, чтобы на основе понятий работы и события подчеркнуть различие между системным временем и машинным временем. В
моделируемой системе событие происходит мгновенно, а работа требует
времени (системного). В имитационной модели картина обратная: на имитацию события затрачивается некоторое машинное время, а имитация работы практически не требует машинного времени, так как имитируется не
сама работа, а завершающее ее событие.
Как правило, для начала работы требуется наличие определенных
условий. Например, чтобы начать кирпичную кладку, требуются кирпичи,
раствор и рабочий-каменщик. При моделировании дискретных процессов в
качестве условий чаще всего рассматривается наличие ресурсов. Например,
чтобы начать обслуживание заявки, требуется наличие свободного прибора. Ресурс можно понимать как оборудование, необходимое для выполнения работы (станок, прибор), но это может быть и работник. Для ресурса
характерно, что он занимается в момент начала работы (или заранее) и
освобождается в момент ее окончания.
Процесс - последовательность событий и работ, описывающая поведение во времени какого-либо объекта в моделируемой системе. Приведем
три примера.
Процесс "генерирование заявок источником":
подготовка заявки (работа);
выдача заявки (событие).
Процесс "прохождение заявки":
занятие прибора (событие);
обслуживание заявки в приборе (работа),
освобождение прибора (событие).
Процесс "обработка детали на станке":
56
занятие рабочего (событие),
занятие станка (событие);
обработка детали (работа);
освобождение станка (событие),
контрольные измерения (работа)",
освобождение рабочего (событие).
Каждая работа или событие - это фаза процесса. Имитация процесса
на ЭВМ производится по фазам. Фаза имитируется без прерывания, но по
окончании имитации фазы возможно прерывание и переход к имитации
другого процесса.
Опираясь на введенные понятия, рассмотрим основные черты схемы
событий и схемы процессов, их положительные и отрицательные стороны.
При моделировании по схеме событий понятия работы и процесса не
используются. Выделяется несколько событий так, чтобы они исключали
друг друга и в совокупности охватывали все возможные изменения в системе. это напоминает разбиение множества элементарных событий на непересекающиеся подмножества (события) в теории вероятностей с той
разницей, что событие - это не только подмножество элементарных событий, но и причинно-следственные связи между элементарными событиями.
Например, при моделировании СМО событие "поступление заявки" охватывает несколько элементарных событий: выдача заявки источником, занятие прибора, начало обслуживания, потеря заявки (в случае отсутствия
свободного прибора). Видно, что элементарные события взаимосвязаны;
если не удастся занять прибор, то обслуживание не начнется, а произойдет
потеря заявки. В алгоритме имитации отражаются не все элементарные события, а только те, без которых невозможно построение реализации, обеспечивающее нахождение искомых характеристик.
Основная трудность при разработке модели по схеме событий выделение типов событий и составление алгоритмов для каждого типа так,
чтобы не упустить каких-то нужных элементарных событий и правильно
учесть взаимосвязи.
Каждому типу события соответствует блок в алгоритме имитации, а каждому событию - определенное место в календаре. Алгоритм
шага состоит в выяснении типа очередном события (с помощью календаря)
и выполнении тех блоков алгоритма, которые соответствуют этому типу
события
57
При моделировании по схеме процессов за основу берется понятие
процесса. Процесс отражает поведение одного объекта (источника, заявки,
детали, рыси, зайца и т.п.), а объектов в системе много. Поэтому параллельно развиваются несколько процессов. Их имитация производится поочередно (на одном процессоре). Если бы процессы были независимы,
можно было бы имитировать до конца один процесс, а потом переходить к
имитации другого процесса. Однако процессы пользуются общими ресурсами. Если очередная фаза процесса состоит в занятии ресурса, а свободного ресурса нет, процесс приостанавливается и ждет освобождения ресурса. При этом ЭВМ переходит к имитации другого процесса. Таким образом, ЭВМ поочередно продвигает процессы на одну или несколько фаз,
учитывая их взаимодействие во времени и в использовании общих ресурсов.
Продвижение процессов по системному времени можно осуществлять по принципу t или по принципу особых моментов. По тем же соображениям, что приводились выше, будем придерживаться принципа особых моментов. Какому процессу отводится место в календаре, где указывается, с какой фазы надо начать или продолжить имитацию процесса и к
какому моменту системного времени это событие относится.
Процессы могут быть постоянными (т.е. развиваться бесконечно
долго) и временными. Временный процесс создается в некоторый момент
времени, существует какое-то время, после чего ликвидируется. Одна из
фаз процесса может представлять собой создание нового процесса. В связи
с существованием временных процессов количество заполненных мест в
календаре оказывается переменным. Признаком свободного места в календаре может быть нуль в ячейке, отведенной для обозначения (метки) очередной фазы процесса. Если число одновременно существующих временных процессов не имеет ограничения сверху, число мест в календаре отводится с большим запасом, а в случае переполнения календаря должно выдаваться соответствующее сообщение. При создании процесса отыскивается свободное место в календаре, и номер этого места становится номером процесса. После ликвидации процесса его место в календаре освобождается.
За один шаг (основной цикл в алгоритме) производится поочередный
просмотр всех процессов и имитация тех из них, для которых созрели
условия, в частности наступило время исполнения очередной фазы. В ходе
имитации очередной фазы процесса мотет освободиться ресурс которого
58
не хватало для имитации ранее просмотренных процессов. Кроме того,
может быть создан процесс и помещен на свободное место в календаре под
меньшим номером, чем текущий процесс. В обоих случаях требуется повторный просмотр процессов в рамках того же шага. Для организации повторного просмотра удобно использовать флаг - двоичную переменную.
Этой переменной перед началом просмотра присваивается значение единицы ("подъем" флага). Освобождение ресурса или создание нового процесса влечет за собой "сброс" флага в нуль. Завершение шага и переход к
следующему шагу производится только если флаг остался поднятым.
Отметим теперь, что термин "процесс" имеет два разных смысла:
процесс как алгоритм и процесс как структура данных. Процесс как алгоритм относится ко всему множеству процессов одинакового типа, а процесс как структура данных описывает конкретного представителя этого
множества. Например, процесс "генерирование заявок J-м источником"
может отражаться следующими величинами (их часто называют атрибутами процесса):
- номер источника ( J );
- емкость источника (максимальное число заявок в нем);
- приоритет, присвоенный, заявками этого источника;
- среднее время подготовки заявки источником;
- среднее время обслуживания заявки этого источника в приборе;
- число заявок в источнике в данный момент
- предстоящий момент выдачи очередной заявки.
- метка очередной фазы процесса.
Первые пять величин постоянны (но у каждого источника имеют
свои значения), остальные три меняются в ходе имитации. Две последние компоненты календаря, эта совокупность данных занимает определенную
группу ячеек в памяти ЭВМ. Номер этой группы - это номер процесса. О
требуемом количестве групп можно сказать то же, что сказано выше о требуемом числе мест в календаре и о возможности переполнения.
Процесс "генерирование заявок источником", понимаемый как алгоритм, существует в виде части программы моделирования. Когда эта часть
программы выполняется, она использует значения атрибутов для конкретного источника. Создание процесса - это заполнение группы ячеек атрибутами этого процесса. Имитация процесса сопровождается изменением переменных атрибутов. Ликвидация процесса означает освобождение группы
ячеек, занятых атрибутами.
59
Чтобы различать указанные два смысла, можно поступить двояко.
Первый путь: термин процесс оставить за алгоритмом, а структуру данных
называть экземпляром процесса. Второй путь: термин процесс применять
к структуре данных, а алгоритм называть классом процессов. Будем далее придерживаться второго пути. В языках моделирования применяется и
другие термины, но они не использует слово процесс, которое желательно
сохранить.
Часть программы, управляющая динамикой модели, т.е. последовательностью выполнения отдельных блоков программы в процессе имитации, носит название монитор. Рассматриваемые схемы построения моделирующего алгоритма (схема событий и схема процессов) имеют существенные различия, но принцип построения монитора у них одинаковый повелительный. Повелительный (императивный) принцип состоит в том,
что для предстоящих событий заранее определяется время их наступления
(оно записываются в календарь), и события имитируются, когда приходит
их время. Календарь как бы предписывает, в какие моменты должны происходить события, в каком порядке их имитировать - отсюда и название
принципа. События, которые запланированы на один и тот же момент времени, могут имитироваться в любом порядке. То обстоятельство, что при
использовании принципа процессов некоторые события "забегают вперед",
не меняет сути монитора: в пределах одного процесса последовательность
событий не нарушается, а ее нарушение между событиями носит временный характер (сначала один процесс забегает вперед, потом другой). Главное - для всех событий указано время, когда они должны произойти.
С целью дополнительного пояснения заметим, что повелительный
принцип ассоциируется с синхронными процессами. Синхронные процессы управляются внешними часами: события в них происходят в заранее заданные моменты времени. Повелительный принцип построения монитора
применен в алгоритме моделирования СМО по схеме событий и достаточно ясен из этого примера.
После сказанного о принципах событий и процессов естественно посмотреть, как будут выглядеть алгоритмы моделирования, составленные
по схеме событий и по схеме процессов. Рассмотрим примеры этих алгоритмов.
60
5.4. Моделирование СМО с отказами по схеме процессов
Напомним, что рассматривается СМО с отказами (т.е. без буфера),
имеющая два обслуживающих прибора. Интервал  между заявками распределен по экспоненциальному закону с математическим ожиданием m. Время
обслуживания обсл постоянно. Оценивается вероятность потери заявки Рпот,
распределение числа занятых приборов (Р0, Р1, Р2) и коэффициент загрузки
прибора Рзп . Обозначения будут те же, что в алгоритме из раздела 2.3.1, и
немного добавлено: Ксп,- количество свободных приборов, К - максимальное
число одновременно существующих процессов (емкость календаря) и др. Календарь теперь указывает не моменты наступления событий, а моменты активизации процессов. Активизацией процесса называется выполнение алгоритма, соответствующего очередной фазе этого процесса. Календарь содержит и момент активизации процесса Т(J) и метку очередной его фазы M(J) ,
где J -номер процесса (J=f,...,K ).
В приведенном ниже алгоритме первая цифра метки соответствует номеру процесса, а вторая - номеру фазы в этом процессе.
Моделирование СМО с отказами по схеме процессов
ввод данных ( m, обсл, правило остановки)
установка начальных значений переменных,
заполнение календаря (N:=0, ТT:=0, КЗ:=0, КПОТ:=0,
S0:=0, S1:=0, S2:=0, T(J)=0,
J=1..K; M(1):=11; M(J):=0, J:=2..K, KСП:=2)
do шаг имитации (раскрыт ниже)
until выполнено условие остановки
end - do





в
том
числе

вычисление оценок  pпот , p0 , p1 , p2 , p3П 


выдача результатов
end-моделир.
Шаг имитации
увеличение номера шага (N:=N+1)
запоминание особого момента ( TL:=TT)
определение очередного особого момента (Тт:= minT(J)|M(J)0)
пополнение суммарного времени пребывания в определенном
состоянии (y:=2-KСП; ДТ:=ТТ-ТL; Sy:= Sy +ДT)
установка текущего номера процесса в нуль (JТ: = 0 )
do определение очередного номера процесса (JT:=JT+1)
подъем флага (IFL:= 1)
if процесс с номером JT существует (М(JT)0)
61
then if запланированный момент активизации совпадает с текущим моментом (T(JТ=TТ)
then имитация процесса о номером JТ, начиная с фазы
М(JТ) до тех пор, пока это возможно по алгоритму соответствующего класса
end if
end if
if флаг сбросился ( IFL = 0 )
then возврат к началу списка процессов (JТ := 0)
end if
until просмотрен и, если надо, имитирован последний процесс, а
флагостался
поднятым (JТ=K & IFL =1)
end do
end шаг
Класс процессов "генерирование заявок источником"
{предполагается единственный источник бесконечной емкости)
(11) подготовка заявки в течение времени :
генерирование интервала  (обращение к датчику случайных
чисел, реализующему экспоненциальное распределение с математическим ожиданием m)
планирование выдачи заявки источником (T(1):=T(1)+ ;
M(1):=12 процесс этого класса существует постоянно,
причем в единственном числе; поэтому ему постоянно
отведена группа под номером 1}
(12) создание процесса "прохождение заявки":
поиск свободной группы и присваивание ее номера перемен
ной Jv {группа с номером J свободна, если M(J)=0}
создание процесса под номером Jv (T(Jv):=T(1); M(Jv):=21)
пополнение счетчика заявок (Kз:=Kз+1 )
установка указателя активной фазы на начала процесса
(М(1):=11))
end класс "ГЗИ"
Класс процессов "прохождение заявки"
переход к запланированной фазе (goto М (.Jт))
(21) занятие прибора:
if есть свободный прибор ( Кcп>0)
then занятие прибора (Ксп :=Кcп-1), установка на обслуживание (М(Jт):=22)
else потеря заявки (Кпот:=Кпот+1),
установка на ликвидацию процесса (M(Jт):=24)
62
end if
переход к соответствующей фазе (gоto М Jт) )
(22) обслуживание заявки в течение времени обсл:
планирование освобождение прибора (Т(Jт):=Т(Jт)+обсл)
прерывание до наступления запланированного момента (goto
end класс"ПЗ")
[23) освобождение прибора:
увеличение числа свободных приборов (Ксп:= Ксп+1)
сброс флага ( lFL:= 0)
(24) ликвидация процесса (M(Jт):=0)
end класс"ПЗ"
Сопоставим схему событий и схему процессов, так как их можно
считать конкурирующими. Схема событий более стройна: события не пересекаются, за один шаг имитируется одно событие, события имитируется
в хронологическом порядке, алгоритм шага делится на этапы с четким
функциональным назначением (имитация события, пополнение статистик,
планирование новых событий). Однако в сложных ситуациях довольно
трудно сформировать перечень типов событий и правильно разработать
соответствующие им части алгоритма. С этой точки зрения схема процессов удобнее, так как не требует при разработке алгоритма учитывать сразу
все, что может происходить в системе, а допускает раздельную разработку
отдельных процессов. Особенно упрощается разработка имитационных
моделей при использовании универсальной системы моделирования, когда
пользователю требуется только описать последовательность событий и работ в процессах, а учет взаимодействия процессов, сбор статистики,
управление порядком имитации процессов берет на себя система моделирования. Схема процессов не позволяет выделить функционально различные части алгоритма: пополнение статистик и планирование событий исследуют с операциями смены состояний в рамках одной фазы процесса.
Это чревато упущениями при разработке алгоритма. Подводя итоги, можно оказать, что на этапе начального обучения моделирование и при моделировании простых систем целесообразно применять схему событий, а при
моделировании сложных систем с использованием универсальных средств
предпочтительнее схема процессов.
Для повышения эффективности моделирующих алгоритмов применяются семафоры и списковые структуры данных.
Вопросы и задания
1. Перечислим отличия схемы событий (СC) от схемы процессов
(СП).
СС: В календаре отведены места для событий.. СП: ... для процессов.
63
СС: В календаре для каждого события одна величина (момент события.). СП: В календаре для, каждого процесса две величины (момент активизации и метка фазы).
СС: за один шаг имитируется одно событие. СП: За один шаг имитируется одна или несколько фаз одного или нескольких процессов.
СС: Все объекты существуют постоянно. СП: Возможны временные
объекты.
Продолжите этот перечень.
2. В чем состоят преимущества и недостатки схемы процессов по
сравнению со схемой событий?
3. Составьте программу моделирования СМО по схеме процессов,
реализующую приведенный алгоритм. Убедитесь, что она дает те же средние значения искомых характеристик, что и программа, построенная по
схеме событий,
4. Измените алгоритм моделирования СМО так, чтобы он учитывал
возможность существования неограниченной очереди к приборам (потерянных заявок не будет). При этом используйте семафор.
5. Сравните по быстродействию три способа организации календаря:
простой список, связный список, двусвязный список.
5.5. Семафоры и связные списки
Семафоры являются удобным механизмом разделения общих ресурсов. Семафор - это целочисленная переменная, характеризующая текущее
состояние группового ресурса, например группы одинаковых приборов.
Если значение этой переменной неотрицательное, оно показывает количество свободных приборов, а если отрицательное, то без учета минуса это
будет количество процессов, стоящих в очереди к данному групповому ресурсу.
С семафорами производятся две операции, обычно обозначаемые как
Р и V. Операция Р производится, когда какой-то процесс пытается занять
ресурс. Состоит эта операция в вычитании. единицы из семафора, что как
раз отражает результат попытки. Действительно, если имелся свободный
прибор, то он был занят, и потому число оставшихся свободных приборов
должно быть уменьшено на единицу. Если же свободных приборов нет,
процесс становится в очередь и вычитание единицы из семафора как раз
отражает удлинение очереди. Операция V, напротив, состоит в прибавлении единицы к семафору, Она производится при освобождении прибора
(элемента группового ресурса) и отражает либо уменьшение очереди, либо
увеличение числа свободных приборов. Анализируя содержимое (семафо64
ров, можно определять по какой ветви алгоритма следует направить выполнение программы. Отсюда и термин семафор.
Для организации календаря и всякого рода очередей полезно применять связные списки (рис. 5.11).
Список
Ад
Информация
Ад
Информация
Ад
Информация
Элементы списка
Головной элемент
— ссылка на следующий элемент
Рис. 5. 11. Кольцевая очередь
Список состоит из элементов, содержащих какую-то информацию,
например данные о процессе. Элемент имеет номер, или адрес, по которому его можно разыскать в памяти ЭВМ. Связный список отличается от
простого списка тем, что каждый его элемент, помимо основной информации, составляющей содержание элемента, имеет ссылку на следующий элемент, т.е. адрес следующего элемента. Элементы как бы связаны в цепочку, причем соседние элементs этой цепочки могут быть расположены далеко друг от друга, т.е. иметь существенно различные адреса.
Связный список снабжается головным элементом, который состоит
только из ссылки на первый элемент описка. Последний элемент на месте
ссылки содержит признак конца описка, например ноль.
Удобство применения связных списков в том, что для удаления элемента из списка, включения нового элемента или перестановки элементов
достаточно изменить некоторые ссылки, основная же информация остается
на месте без изменения.
Рассмотрим, как организуется календарь процессов с помощью связного описка. В рассмотренном выше календаре каждый процесс имел номер, обозначенный J, и содержал две величины: T(J) и М). Следовательно,
65
календарь был представлен двумя массивами: Т и М - каждый длиной К.
Это был простой список.
Чтобы получить связный список, добавим для ссылок массив А той
же длины и ячейку А для головного элемента. Свяжем процессы по
принципу возрастания запланированного момента активизации. Тогда А
будет содержать номер процесса с наименьшим значением (ТJ). Допустим,
Т(5)Т(7)T(2). Тогда А=5, А(А)=А(5)=7, А(А(А))=А(7)=2 и т.д.
Выясним, что дает связный список по сравнению с ранее рассмотренной организацией календаря в виде простого списка. Во-первых, теперь
не надо просматривать подряд элементы календаря, чтобы найти те процессы, момент активизации которых совпадает с текущим моментом tт, так
как, если такие есть, то они занимают первые места в цепочке. Во-вторых,
чтобы найти tт , не надо искать минимальный элемент - это Т(А ).
Но за преимущества всегда надо чем-то платить. Это не только дополнительные затраты памяти на массив А, но и дополнительные операции. Если раньше для создания нового процесса достаточно было отыскать
номер свободной группы Jv и написать параметры нового процесса в T(Jv)
и M(Jv), то теперь надо еще вставить новый процесс на определенное место в цепочку. Для этого надо отыскать такой номер J, что
T(А(J))Т(Jv)Т(А(А(J))), после чего проделать следующие операции со
ссылками: А(Jv):-=A(A(J)); A(J):=Jv. При ликвидации процесса с номером
J, помимо обычной операции М(J):=0, потребуется операция со ссылкой
А(JL):-=A(A(J)), где JL - номер процесса, стоящего в цепочке перед процессом J. Для нахождения JL потребуется: просмотреть цепочку от начала до
элемента J. Чтобы избежать этого просмотра, можно применить двусвязный список. В нем имеется еще один массив, который содержит ссылки на
предыдущий элемент цепочки.
5.6. Алгоритмы обслуживания очередей
Чаще всего применяю следующие алгоритмы управления (обслуживания)
очередями:
• FIFO
• Приоритетное обслуживание, которое называют также «подавляющим»
• Взвешенное обслуживание
• 1) Традиционный алгоритм FIFO
66
Достоинство — простота реализации и отсутствие необходимости конфигурирования. Недостаток — невозможность дифференцированной обработки заявок
различных потоков.
• 2) Приоритетное обслуживание (Priority Queuing)
Сначала необходимо решить отдельную задачу - разбить общий входной поток устройства на классы (приоритеты). Признак, по которому производят
разбивку на классы, помещают в поле приоритета.
Затем требование помещается в очередь, соответствующую заданному приоритетному классу.
Рассмотрим пример с четырьмя приоритетными очередями: высокий, средний, нормальный и низкий приоритет.
Рис. 5.12. Приоритетное обслуживание
Здесь очереди имеют абсолютный приоритет — пока не обработаны пакеты
из очереди более высокого приоритета не производится переход к более низкоприоритетной очереди.
При моделировании можно:
■ Выделить одинаковое количество буферов для всех очередей
• На основе анализа трафика поступлений установить нужный размер для
каждой из очередей.
Недостаток:
Если высока интенсивность высокоприоритетного трафика, обслуживание
низкоприоритетного трафика может совсем не производиться.
Этот метод можно, например, использовать при моделировании сети, если в
качестве высокоприоритетного будет выбран голосовой трафик (IP-телефония). Это
связано с тем, что его интенсивность невелика (обычно 4-16 Кбит/с).
Если же в сети в качестве высокоприоритетного выбран видеотрафик,
остальным потокам может и не достаться пропускной способности.
3) Взвешенные настраиваемые очереди (Weighted Queuing)
Здесь делается попытка предоставить всем классам определенный минимум
пропускной способности, т.е. обслуживания, и гарантировать некоторые требования
к задержкам.
Под весом для каждого класса понимается процент предоставляемой
классу пропускной способности (от полной выходной пропускной способности).
67
Алгоритм, используемый администратором для назначения весов, называется
настраиваемой очередью.
Рис.5.13. Взвешенные настраиваемые очереди
Очереди обслуживаются циклически, и в каждом цикле обслуживания
из каждой очереди выбирается такой объем нагрузки, который соответствует весу
этой очереди.
Например: цикл = 1 сек., скорость выходного интерфейса = 100
Мбит/с. В каждом цикле из очередей выбираются следующие объемы данных:
■ 1 — 10 Мбит
■ 2—10 Мбит
■ 3 — 30 Мбит
■ 4 — 20 Мбит
■ 5 — 30 Мбит
Здесь, как и в приоритетном обслуживании, можно назначать различные длины очередям. Тем самым появляется возможность сглаживания нагрузки.
Вопросы и задания
1. Измените алгоритм моделирования СМО так, чтобы он учитывал
возможность существования неограниченной очереди к приборам (потерянных заявок не будет). При этом используйте семафор.
2. Сравните по быстродействию три способа организации календаря:
простой список, связный список, двусвязный список.
6. Оценки искомых характеристик и их дисперсии
6.1. Структура оценок
Следуя традициям математической статистики, обозначим искомую
характеристику символом , а ее приближенную оценку, найденную в ре-
68
зультате модулирования

θ . При моделировании СМО, как правило,
оценки имеют вид дроби - отношения двух статистик
θ
ξ
η
Это обусловлено тем, что нахождение оценки при имитационном
моделировании обычно связано с осреднением, В числителе стоит некоторая сумма, накопленная в процессе имитации, а в знаменателе величина,
характеризующая число слагаемых в этой сумме. Приведем несколько
примеров.
1.  - вероятность потери заявки
а. Оценка по заявкам. Здесь  - число поступивших заявок,  - число
потерянных.
б. Оценка по времени. Здесь  - пройденное системное время (длина
реализации),  - суммарное время, в течение которого система была полностью занята (пришедшую в это время заявку некуда принять и поэтому она
теряется).
В оценке 16 знаменатель не характеризует количество слагаемых в
явном виде. Однако аналогию нетрудно усмотреть. Предположим, что
время отсчитывается дискретно, и t - единица -времени. Тогда  - количество интервалов t, пройденных в процессе имитации, а  - количество интервалов, на которых наблюдалась полная занятость. В этом случае каждое
из слагаемых числителя равно либо единице (если система полностью занята), либо нулю (в иных случаях), а знаменатель представляет собой количество слагаемых. Предположение о дискретном счете времени является
даже не предположением, а фактом ввиду ограниченной разрядности
ЭВМ. Под t можно понимать цену младшего разряда в представлении величин, связанных с системным временем.
2.  - среднее время ожидания начала обслуживания
а. Оценка по заявкам с раздельным учетом времени ожидания.  число обслуженных заявок,  - суммарное время, проведенное этими заявками в очереди (в буфере). Для каждой заявки надо хранить момент ее
прихода t' и момент поступления на обслуживание t''.
69
Величина  складывается из разностей (t// -t/). Для тех заявок, которые
сразу попадают на обслуживание, эта разность равна нулю. Хранить t / и t//
надо только до тех пор, пока их разность не добавлена в статистику , после этого их можно стереть из памяти. Добавление производится на том
шаге, на котором имитируется поступление заявки на обслуживание.
б. Совместный учёт времени ожидания. Можно обойтись без запоминания моментов t/ и t// если вычислять  по шагам. На каждом шаге к
накопленному значению  добавляется произведение (TT-TL)L, в котором
(TT-TL)- системное время, пройденное от момента предыдущего события
до момента текущего события, L- количество заявок, стоявших в очереди
на этом интервале.
3. -средняя длина очереди
Необходимо уточнить смысл слова «средняя». Если интересоваться
длиной очереди в произвольный момент времени, надо усреднять по всему
пройденному времени. Если же интересоваться длиной очереди в момент
прихода заявки, то надо рассматривать только моменты прихода заявок.
Эти средние длины очереди, вообще говоря, неодинаковы. Приведём простой пример. Допустим, заявка некоторое время ждёт начала обслуживания, но успевает поступить на обслуживание к моменту появления следующей заявки, и так происходит для всех заявок. Тогда в момент прихода
заявки длина очереди всегда равна нулю, и средняя длина очереди, следовательно, тоже равна нулю. Но средняя длина очереди по отношению к
произвольному моменту времени не равна нулю, так как на некоторых отрезках времени длина очереди равна единице.
3. / Средняя длина очереди в момент поступления заявки.
- число поступивших заявок;    Li , где Li - длина очереди в моi
мент поступления i-й заявки.
3.// Средняя длина очереди в произвольный момент времени
-пройденное системное время (длина реализации); - то же, что в
примере 2б, только роли другие: там (ТТ-ТL) – усредняемая величина, а Lкоэффициент; здесь же L-осредняемая величина, а (ТТ-ТL)- коэффициент.
Поясним, почему в третьем примере варианты помечены штрихами,
а не буквами, как в первых двух примерах. Это сделано, чтобы подчерк-
70
нуть различие: в третьем примере рассматриваются разные характеристики
СМО, а в первых двух - разные виды оценок.
На этих трёх примерах мы убедились, что оценки имеют вид дроби.
Рассмотрим теперь, как формируются числитель и знаменатель. Это - статистики, накапливаемые по шагам в ходе имитации. В состав алгоритма
шага входят операторы, добавляющие к статистикам  и  приращения.
Выбор той или иной оценки в конечном итоге сводится к определению вида этих приращений. Рассмотрим вид приращений для приведённых выше
примеров оценки.
1а. Вероятность потери заявки, оценка по заявкам
1, если на данном шаге поступила и потеряна заявка,

0 в иных случаях
1, если на данном шаге поступила заявка,

0 в ином случае.
1б. Вероятность потери заявки, оценка по времени
TT-TL, если перед началом шага система полностью занята,

0 в ином случае
 = TT-TL (на всех шагах, независимо от их типа).
ТТ – момент текущего события (текущее системное время),
TL – момент предыдущего события.
2а. Среднее время ожидания, раздельный учёт ожидания
 t// - t/, если на данном шаге завершилось обслуживание заявки
(т.е. освободился прибор)

0 в иных случаях
71
t/, t// - соответственно момент прихода этой заявки и момент начала
обслуживания (они могут совпадать, тогда будет =0).
1, если на данном шаге освободился прибор

0 в ином случае.
2б. Среднее время ожидания, совместный учёт
 = (TT-TL)L (на всех шагах, независимо от их типа).
L - длина очереди перед началом шага (число занятых ячеек буфера;
может быть равно и нулю)
1, если на данном шаге освободился прибор

0 в ином случае.
3/. Средняя длина очереди в момент прихода заявки
L, если на данном шаге поступила и потеряна заявка,

0 в иных случаях
1, если на данном шаге поступила заявка,

0 в ином случае.
3//. Средняя длина очереди в произвольный момент времени
 = (TT-TL)L
 = TT-TL
По аналогии с приведёнными примерами можно выбрать вид оценки
и приращений для других случаев с учётом смысла оцениваемой характеристики. Оценки некоторых характеристик можно вычислить через оценки
других характеристик. Например, оценка средней длины очереди, наряду с
оценкой 3//, может быть вычислена по формуле

Lср 
Lmax

LP
L C
L
72
где

P
L
- оценка вероятности того, что в произвольный момент времени
длина очереди равна L (занято L ячеек буфера);
Lmax - число ячеек в буфере (емкость буфера).
Для получения этой формулы взята формула, определяющая математическое ожидание, и вместо входящих в неё величин подставлены оценки этих
величин. Аналогичным путём получают и другие соотношения между
оценками. В частности, оценку коэффициента загрузки буфера можно вычислить по формуле


K зб  L / Lmax
ср
Вопросы и задания:
1. Термин «статистика» употребляется во многих смыслах:
а) математическая наука, изучающая методы оценки параметров и проверки гипотез о законах распределения по результатам наблюдений (математическая статистика);
б) совокупность данных о явлениях, имеющих случайный характер (в этом
смысле говорят «сбор статистики»)
в) функция выборки, т.е. функция, аргументами которой являются наблюдавшиеся значения случайной величины.
В каком смысле мы говорим, что оценка характеристики СМО обычно
является отношением двух статистик?
2. Термин «оценка» тоже имеет несколько смыслов:
а) приближённое значение неизвестного параметра, вычисленное по выборке (точнее было сказать «значение оценки»);
б) правило (алгоритм или формула), по которому вычисляется значение
оценки по выборке (в этом смысле можно говорить о свойствах оценки:
несмещённости, состоятельности, эффективности, достаточности);
в) процесс выбора правила и вычисления по нему значения оценки (такой
смысл имеет заголовок главы «оценка параметров» в учебниках по математической статистике, хотя в некоторых книгах пишут более удачно:
«оценивание параметров»). В каком смысле употребляется термин «оцен
ка» в этом разделе? В каком смысле можно утверждать, что оценка    
является статистикой?
3. Постройте оценки для следующих характеристик:
а) средняя длина очереди в момент освобождения прибора;
б) вероятность того, что в произвольный момент времени все приборы
свободны;
73
в) среднее время пребывания обслуженной заявки в системе (время ожидания в очереди плюс время обслуживания).
Иными словами, укажите, что представляют собой    ?
4. Подумайте, всегда ли оценки 1а и 1б совпадают в среднем с вероятностью потери заявки. Если не всегда, то какая из двух оценок непригодна и
чем это объяснить? (Ответ есть в следующем разделе).
6.2. Дисперсия оценки
Хорошая оценка должна быть несмещённой, т.е. в среднем должна
совпадать с истинным значением оцениваемой характеристики. Это требование можно выразить формулой:

M    θ
 


где M   - математическое ожидание оценки 
 
 - истинное (но неизвестное) значение характеристики.
Несмещённость обеспечивается правильностью моделирующего алгоритма, в частности - правильным построением оценки и соответствующим выбором приращений  . Процедура вычисления этих приращений и добавление их к статистикам  и  является составной частью алгоритма шага. Особых рекомендаций для обеспечения правильности этой части алгоритма нет. Надо руководствоваться здравым смыслом и приведёнными примерами. Если же остаются сомнения в несмещенности выбранной оценки, можно осуществить статистическое тестирование, методика
которого описана в разделе 7.
К сожалению, «здравый смысл» иногда подводит, и даже тестирование может ввести в заблуждение. К построению оценки следует подходить
очень внимательно.
Хотя несмещенная оценка в среднем совпадает с истинным значением оцениваемой характеристики, но при каждом прогоне программы моделирования получается своё значение оценки, отличающиеся от истинного
значения на некоторую случайную величину. Это обусловлено тем, что в
разных прогонах используются разные отрезки последовательности случайных чисел. Желательно, чтобы отклонения были поменьше. Величина
случайных отклонений характеризуется дисперсией. Для несмещенной
оценки дисперсия определяется формулой:
74
 


D    М   θ 
 


2
Нас будет интересовать среднеквадратическое отклонение оценки


 D  
 
При моделировании СМО можно считать, что оценки имеют нормальное распределение. Это утверждение частично определяется ссылкой
на центральную предельную теорему теории вероятностей, хотя она здесь
непосредственно не применима и подтверждается практикой моделирования. Для нормального распределения известны вероятности тех или иных
отклонений случайной величины от своего математического ожидания, в
частности,


Р   θ  2σ   0,955




Р   θ  3σ   0,997


В общем случае


Р   θ  
γ
доп 


где доп  К γ  - допустимая абсолютная погрешность, выраженная
через ;
 - коэффициент доверия (вероятность того, что отклонение не
превысит доп)
Между  и К γ имеется однозначное соответствие, определяемое по
таблицам нормального закона распределения. В частности, как только что
отмечалось:
К γ =2=0,955;
К γ =3=0,997
Итак, мы видим, что в 95% случаев значение несмещенной оценки
отличается от точного значения искомой характеристики не более чем на
2. Следовательно, погрешность оценки удобно характеризовать величиной . Иногда удобнее иметь дело с дисперсией, равной 2 , но это не имеет принципиального значения.
Проблема заключается в том, что дисперсия оценки обычно не известна и может быть приближённо определена лишь в ходе моделирова75
ния. С этой целью выполняют не один прогон, а n прогонов, например 10


или 20. В результате получают n значений оценки:  ,..., n
В качестве окончательного значения оценки берётся среднее ариф



метическое
  ...  n
n
Дисперсия у этой оценки будет та же, что у оценки, полученной по
одному прогону, но в n раз более длительному. Однако, выполнив n коротких прогонов вместо одного длинного, мы получим информацию о дис



персии оценки. Действительно, имея выборку  ,..., n  можно тем или


иным способом (см. ниже) приближённо вычислить дисперсию частной
оценки

ки :
 
σ 2  D  I  , а по ней определить дисперсию осреднённой оцен1
 
σ12
2
σ 
n
Здесь предполагается, что



,..., некоррелированы, поскольку в
n
разных прогонах используются разные отрезки последовательности случайных чисел. При наличии корреляции дисперсия осреднённой оценки
будет несколько иной: положительная корреляция увеличивает дисперсию,
а отрицательная уменьшает. Иногда отрицательную корреляцию искусственно вводят для уменьшения дисперсии оценки [8]. Рассмотрим способы определения 1 по выборке.
1. оценка по двум статистикам:
n

S1   i ,
i 1
n
2
S2   i
i 1
Эти статистики формируются в двух ячейках. По окончании очередного прогона в первую добавляется вычисленная оценка, а во вторую - её
квадрат. Когда проведено n прогонов, вычисляется оценка дисперсии:

2
σ1
2

  S2 S1

n  n  1

2. оценка по размаху:

σ1  w k(n),
76
где W- коэффициент между максимальными и минимальными элементами
выборки. Коэффициент
k(n) , на который надо разделить размах W, зави-
сит от числа элементов выборки. Если элементы выборки распределены по

k(n) можно найти в таблицах математической статистики. В частности, k (10)=3.08, k (20)=3.73.
нормальному закону (а для

i
это верно), то
Известен способ нахождения дисперсии оценки по одной реализации, разделённой точками регенерации на независимые отрезки. Точкой
регенерации называется такой момент времени, после которого процесс
развивается независимо от того, как он развивался этого момента. В точке
регенерации процесс как бы начинается заново. При моделировании СМО
точкой регенерации является момент, когда в пустую систему поступает
заявка. Так как система пустая, её прошлые состояния не оказывают влияния на будущие состояния. Для приближённого вычисления дисперсии
надо иметь хотя бы несколько десятков точек регенерации, т.е. за один
прогон система должна несколько десятков раз опустеть. Если ввести исходные данные, соответствующим реальным СМО, то придётся очень долго ждать возвращения системы в полностью свободное состояние, так как
реальные СМО работают с достаточной нагрузкой и пустыми практически
не бывают. Однако за точку регенерации не обязательно брать пустую систему. Можно брать то состояние системы, к которому она чаще всего возвращается. При нагрузке 0.5 таким состоянием может быть состояние,
когда в системе находиться одна, две или даже более заявок.
Вопросы и задания:
1. Какая оценка называется несмещённой?
2. Почему вместо погрешности оценки можно интересоваться
дисперсией оценки либо среднеквадратическим отклонением?
3. Во сколько раз надо увеличить длину реализации, чтобы
уменьшить дисперсию оценки в десять раз?
4. Во сколько раз надо увеличить длину реализации, чтобы
уменьшить погрешность оценки в десять раз?
5. Сколько примерно шагов надо выполнить, чтобы оценить вероятность события, примерно равную 10-4 с точностью порядка 20%?
6. Сопоставьте два варианта, одинаковых по затратам машинного
времени: а)десять прогонов с длиной реализации Т; б) один прогон с
длиной реализации 10Т. В чём преимущество первого варианта?
77
7. Тестирование имитационной модели
Когда составлена программа моделирования, её проверяют с помощью тестов, т.е. решая задачи с заранее известными ответами.
Пошаговое тестирование состоит в проверке правильности выполнения алгоритма по шагам. В простых случаях можно рассчитать значения
переменных для нескольких первых шагов и убедиться, что ЭВМ выдаёт
те же значения. В более сложных случаях можно ограничиться выводом
значений переменных для первых шагов и анализом этих данных с позиций здравого смысла. Например, если оказалось, что приборы принимают
заявки на обслуживание, но ни на одном шаге не происходит освобождение прибора, значит, явно где-то ошибка. Для наглядности можно строить
временные диаграммы, демонстрирующие изменения состояний приборов
во времени, изменение числа заявок в системе и т.п.
Наряду с пошаговым тестированием необходимо проводить статистическое тестирование хотя бы потому, что никаким пошаговым тестированием не проверить программу генерирования случайных чисел. Если
датчик случайных чисел не обеспечивает нужного закона распределения,
то оценка оказывается смещённой даже при правильном её построении и
правильном алгоритме имитации. Статистическое тестирование проводится путём сравнения полученного значения оценки о точным значением
оцениваемой характеристики, найденным теоретическим путём. Так как
оценка имеет случайный характер, точного совпадения не будет. Насколько сильно должна отклониться оценка от точного значения, чтобы разница
была признана недопустимой и потребовалось выяснение причины такого
отклонения? Ответ зависит от назначенного коэффициента доверия.
Наиболее распространённым в практике значением коэффициента доверия
является 0.95. При этом пороговым значением при принятии решения является величина 2. При таком пороге в пяти процентах случаев (более
точно – 4.5%) отклонение, превысившее порог, будет вполне естественным, а отрицательный результат теста будет фактически «ложной тревогой». Но в подавляющем большинстве случаев (95.5%) отклонение, превышающие 2, всё же говорит о каком-то неблагополучии. Обнаружив такое отклонение, надо, прежде всего, получить ещё одну выборку и убедиться, что тревожный предыдущий результат не был ложной тревогой.
Если снова отклонение окажется недопустимо большим, значит либо тестовые данные (точное значение) ошибочны, либо программа моделирова78
ния выдаёт неправильные оценки. Надо выяснить причину. Подготовка тестовых данных при моделировании СМО требует значения теории массового обслуживания. Приведём без доказательства простой способ расчёта
тестовых данных, который пока отсутствует в учебниках и книгах по теории массового обслуживания. Изложить его проще всего на конкретном
примере.
Пример. Рассматривается СМО с тремя приборами и двумя ячейками буфера. Имеется пять источников заявок одного типа. Интервал между
заявками отельного источника распределён по экспоненциальному закону
со средним значением Т. Время обслуживания заявки распределено тоже
по экспоненциальному закону, но со средним значением Т0.
На рис. 7.1 изображён граф, отражающий возможные состояния
СМО и переходы из одного состояния в другое. Цифра в кружочке указывает текущее количество заявок в системе. Это и есть характеристика состояния СМО. Например, в состоянии 4 заняты все три прибора и одна
ячейка буфера. В состоянии 2 заняты два прибора; поскольку один прибор
свободен, буфер, естественно, пуст.
На дугах указаны интенсивности переходов, где =1/T- интенсивность потока заявок одного источника, =1/T0- интенсивность обслуживания. Предполагается, что источники заявок имеют конечную ёмкость, равную
Рис.7.1. Граф состояния СМО.
единице. Это означает, что источник, выдав заявку, оказывается пустым и
ждёт, пока его заявка вернётся в этот источник по окончании обслуживания. После возврата заявки в источник она вновь выдаётся через случайный интервал времени, распределение которого указано выше. При единичной ёмкости источника под интервалом между заявками следует понимать время от возврата заявки в источник до выдачи заявки. Это как бы
время, требующееся для подготовки очередной заявки. При бесконечной
ёмкости источника время подготовки заявки совпадает с интервалом между заявками.
79
В состоянии 0 в каждом из пяти источников находится по одной заявке, любой из них может выдать заявку, поэтому интенсивность перехода
0I равна 5. По мере увеличения числа заявок в системе обслуживания
уменьшается число источников, содержащих заявку, поэтому интенсивности переходов, связанных с выдачей заявки, уменьшается от 5 до . В
случае, когда источники обладают бесконечной ёмкостью, на всех дугах,
идущих слева направо, будут интенсивности 5.
Дуги нижнего ряда связаны с переходами, обусловленными окончанием обслуживания заявок. Например, в состоянии 4, когда заняты три
прибора (четвёртая заявка находится в буфере), любой из трёх приборов
может завершить обслуживание заявки, поэтому интенсивность перехода 4
3 равна 3. В состоянии 2 заняты только два прибора, поэтому интенсивность перехода 21 равна 2.
Вычисление вероятностей состояний применительно к установившемуся режиму работы легко осуществляется по графу состояний. Для
каждой вершины вычисляются величины, которые назовём индексами и
обозначим А. Чтобы вычислить Аi –индекс i-й вершины, надо выделить
подграф, состоящий из путей, ведущих к этой вершине. Подграф должен
содержать по одной дуге, выходящей из каждой вершины, кроме корневой,
т.е. i-й. Примеры подграфов приведены на рис.7.2. Для наглядности обозначены только корневые вершины.
Рис.7.2. Подграфы для вычисления индексов вершин.
Индекс вершины вычисляется как произведение интенсивностей,
указанных на дугах подграфа. Индексы вершин для данного примера следующие:
А0=*2*(3)3, А3=5*4*3*(3)2, А1=5*2*(3)3,
А4=5*4*3*2*3, А2=5*4*(3)3, А5=5*4*3*2*,
80
При небольшом навыке можно сразу написать формулы для индексов, глядя на исходный граф и мысленно выделяя пути, ведущие к корневой вершине. Следует предупредить, что для графов более сложной структуры (имеющих ответвления, перескоки дуг через соседние вершины и
т.д.) методика вычисления индексов вершин иная и требует отдельного
описания.
Вероятность того, что в произвольный момент времени в системе
находится i заявок, вычисляется по формуле:
A
Р  i
i A
i
i
По вероятностям Рi можно вычислить целый ряд характеристик
СМО. Приведём примеры. Вероятность того, что все приборы заняты, равна Р3+Р4+Р5. Вероятность того, что буфер пуст, равна Р0+Р1+Р2+Р3. Коэффициент загрузки прибора равен Кзп = (Р1+Р2*2+(Р3+Р4+Р5)*3)/3.
Коэффициент загрузки буфера Кзп = Р4+Р5*2)/2. Вероятность потери
заявки равна Р5, так как при экспоненциальных законах распределения она
совпадает с вероятностью полной занятости. При других законах распределения это не так. Следует помнить, что описанная методика расчета вероятностей состояний верна только при экспоненциальных законах распределения интервалов между заявками и длительностей обслуживания.
Рассмотрим пример статистического тестирования. Допустим, были
получены выборочные значения оценки вероятности потери заявки в результате моделирования двухканальной СМО с отказами при экспоненциальных законах распределения: 0.204, 0.197, 0.192, 0.226, 0.192, 0.177,
0.206, 0.191, 10199, 0.182. Воспользуемся описанной методикой, чтобы
подсчитать точное значение вероятности потери заявки Рпот для этого случая.
Рис. 7.3. Граф состояний двухканальной СМО.
81
По графу состояний (рис.7.3) нетрудно написать индексы вершин
А0=22,
А1=2, А2=2.
Отсюда находим вероятность полной занятости Р2, которая совпадает с вероятностью потери заявки Рпот, так как в этом примере законы экспоненциальные
Рпот=Р2=А2/A0+A1+A2=2/22+2+2.
Математические ожидания Т и Т0 задавались равными единице, поэтому обратные им значения интенсивностей  и  тоже равны единице.
Подставляя ==1 в формулу, находим Рп=0.2.
В качестве оценки

P
ных выше десяти оценок,
клонения
n
примем среднее арифметическое приведён-

P
n
=0.197. Оценка среднеквадратического от-

σ =0.014. учитывая, что среднее из десяти значений имеет сред1
неквадратическое отклонение в 10 раз меньше, чем каждое из значений,
получаем
значения
 = 1/ 10 0.004. Видим, что отличие оценки от точного

pn  pn
 0,003 , не превысило , а допускается 2. Следователь-
но, тест прошёл успешно.
Один успешно закончившийся тест ещё не свидетельствует о правильности программы моделирования. Как хорошо известно, исчерпывающее тестирование вообще невозможно, так что абсолютно уверенно
утверждать, что программа правильна, нельзя никогда. Однако степень
уверенности в правильности программы возрастает с каждым успешно
проведённым тестом. В то же время достаточно одного неудачно завершившегося теста, чтобы перестать доверять выдаваемым программой результатам и приступить к выяснению причины несоответствия. Нередко
отрицательный результат тестирования объясняется простой невнимательностью: в программу введены исходные данные, не соответствующие тем,
при которых вычислялось точное значение.
Одной из возможных причин неудачного тестирования может быть
отличие характеристик последовательности случайных чисел от требуемых. Экспоненциально распределённые случайные числа получаются из
базовых случайных чисел. Базовые случайные числа должны быть равномерно распределены в интервале [0,1] и некоррелированы.
Вопросы и задания:
82
1. Почему пошаговое тестирование необходимо дополнить статистическим тестированием?
2. Почему при статистическом тестировании необходимо осуществлять не один прогон программы, а несколько, хотя бы десяток?
3. Во сколько раз разница между оценкой и точным значением
может превышать среднеквадратическое отклонение оценки, чтобы эта
разница ещё считалась допустимой?
8. Случайные факторы и их модели
Под случайным фактором условимся понимать случайное событие,
случайную величину, многомерную случайную величину, случайную функцию одного или нескольких переменных и вообще любые объекты, выбор
которых определяется соответствующими вероятностными распределениями.
А под реализацией случайного фактора - сам акт выбора, то есть статистическую выборку одного элемента из множества, наделенного вероятностной
мерой.
В данной главе рассмотрение будет ограничено моделированием случайных событий и случайных величин.
При моделировании случайных факторов будем исходить из того, что
используемый датчик БСВ является идеальной моделью базовой случайной
величины z ~ R[0,1], то есть выдает равномерно распределенные и независимые случайные значения z i . Это позволит нам строить модели случайных
факторов и устанавливать их свойства теоретически - опираясь только на положения теории вероятностей и не прибегая к громоздким процедурам статистического тестирования.
В то же время в целях наглядности, модели случайных факторов будем
иллюстрировать примерами с простой статистической обработкой выходных
данных.
8.1. Моделирование случайных событий
Пусть задана некоторая система непересекающихся событий {A 1 , ... ,
A n } c их вероятностями p 1 , ... , p n соответственно; p1  ...  pn  1.
Чтобы построить программную модель такого события, разобьем интервал
(0,1) на n отрезков длиной p 1 ,p 2 , ... ,p n . Это всегда возможно, так как
p1  ...  pn  1. Тогда модель случайного события A может быть написана в
83
соответствии с простым алгоритмом, изображенным на рис. 8.1, где запись
(p i ) обозначает "отрезок длиной p i ".
В качестве примера построим модель операции, состоящей в вытаскивании шара из урны, содержащей пять белых шаров (Б), три красных (К) и
два черных (Ч). Так как исходы Б,К,Ч имеют вероятности p 1 = 0.5, p 2 = 0.3 и
p 3 = 0.2
соответственно, то интервал (0,1) разбиваем на отрезки (0;0.5),
(0.5;0.8) и (0.8;1).
Алгоритм моделирования имеет примерно следующий вид:
(1) Получить значение z из датчика БСВ.
(2) Если z  1/2 , вывести "Б", иначе, если z  8/10 , вывести "К", иначе
вывести "Ч".
Датчик БСВ
Проверка z
Исход A1
Исход A2
Исход An
Рис. 8.1. Модель случайного события
Вот пример 60-кратного выполнения этого алгоритма на компьютере;
мы видим, что частота появления каждого исхода примерно соответствует
его вероятности:
БКБКБКБКББКЧБББККББКЧЧББЧЧКББЧБЧББЧБКЧЧБББККББЧКБЧКББЧ
КБЧББ.
Так, исход "Б" здесь появился 31 раз (52% случаев), "К" - 15 раз (25%)
и "Ч" - 14 раз (23%).
84
8.2. Моделирование дискретных случайных величин
Моделирование дискретной с.в. в принципе ничем не отличается от
моделирования случайного события. Дискретная с.в. d задается множеством
возможных значений {d 1 , ... ,d n } и их вероятностями p 1 , ... , p n . Поэтому
дискретная с.в. реализуется по алгоритму рис.8.1, только вместо "Исход A i "
в нем нужно записать " d=d i " для всех i=1,... ,n.
Единственное, что здесь имеет смысл добавить сверх сказанного, это о возможности модифицировать алгоритм рис. 3.4. в двух частных случаях с целью упрощения программы.
Первый случай - это когда d  { 0, 1, ... , n-1 } и исходы равновероятны: p
1
= ... = p
n
= 1/n. В этом случае все промежуточные операции, вклю-
чая разбиение интервала (0,1) на n отрезков и поиск среди них того, в который попало значение z, сокращаются за счет применения функции  x  вычисления целой части от x. И весь алгоритм сворачивается в одну формулу:
d =  nz .
(8.1)
Действительно, в этом случае при z  (0,1/n) будет d = 0, при z  (1/n,2/n)
будет d = 1 и т.д. Случаи, когда z попадает точно на границы отрезков,
здесь не рассматриваются, так как их вероятность равна нулю.
Ясно, что формулу (8.1) легко приспособить к близким ситуациям.
Например, для моделирования игральной кости с числом очков от 1 до 6
можно ее "выбрасывание" реализовать по формуле
d =  6z  + 1,
(8.2)
где z получается от датчика БСВ, d - выпавшее число очков.
Применение формулы (8.2) для 60-ти "выбрасываний кости" компьютером дало последовательность:
321236246263321315464215224214664122142366236246611664533544.
Здесь цифры 1,2,3,4,5,6 выпали соответственно 9,14,9,11,4 и 13 раз, т.е. в
процентах это составило 15%, 23%, 15%, 18%, 7% и 22%.
Второй случай, когда алгоритм рис. 8.1 следует упрощать, касается
дискретной с.в. с бесконечным множеством возможных исходов. В такой ситуации часто можно получать компактную программу, применяя рекурсивный (циклический) вариант алгоритма.
В качестве примера построим генератор пуассоновской с.в. Пуассоновская
с.в. может принимать значения {0, 1, ... , K, ...}, вероятности которых определяются по формуле
85
a k ea
p 
k
k!
,
(8.3)
где a - параметр распределения, a > 0.
Убедимся, что сумма вероятностей исходов равна единице:

 a k ea a  a k a a
 e   e e 1
 pk  
k 0
k 0
k  0 k!
k!
Разобьем мысленно интервал (0,1) на бесконечное число отрезков длиной p0 , p1 , ... , p k , ... . Согласно рис. 8.1 мы должны обратиться к датчику
БСВ и для полученного значения z найти отрезок, в который оно попало.
Проверить для первого отрезка условие z  ( p 0 ) можно с помощью неравенства z  Г0, где Г0 - правая граница интервала (p 0 ), т.е. Г0=р0=е-а . Если
после отрезка (p k ) нужно проверять отрезок (p k 1 ), то для этого используем неравенство z  k 1 , где k 1 - правая граница отрезка (p k 1 ) - получается по формуле k 1  k  pk 1 . Вычисление p k 1 будем выполнять не непосредственно по (8.3), а по соответствующему рекуррентному выражению
p
a
p
k 1 k 1 k

чтобы не считать факториалов и степеней.
Алгоритм, соответствующий высказанным соображениям, представлен
на рис. 8.2
Переменные Г и P, изменяющиеся при повторении цикла, соответствуют величинам k 1 и k 1 Полученный алгоритм имеет достаточно компактный вид. Что касается быстродействия алгоритма, то его можно охарактеризовать числом N повторений цикла. Очевидно, что N = d + 1, где d вычисленное случайное значение пуассоновской с.в. Поскольку M(d) = a, то
среднее число повторений цикла составляет
M(N) = M(d + 1) = a + 1.
Нетрудно определить и дисперсию D(N):
D(N) = D(d + 1) = D(d) = a.
Датчик БСВ
86
К=0
Г=е-а
Рис.8.2. Схема генератора пуассоновской с.в.
На рис. 8.3. приведена частотная гистограмма для 100 000 реализаций
пуассоновской с.в., полученных с помощью описанного генератора.
25
Тысячи
20
15
10
5
0
0
1
2
3
4
5
6
7
8
9
10
11 12
Рис. 8.3. Пуассоновская с.в. при а=3..5
8.3. Моделирование непрерывных с.в. методом обращения
Пусть требуется реализовать непрерывную с.в. x, которая имела бы заданную функцию распределения вероятностей (ф.р.в.) F(t) = P { x  t}, т.е.
требуется, чтобы было x ~ F(t). Согласно методу обращения это можно сделать с помощью БСВ z по следующей формуле:
x = F-1 (z).
Примечание. Выражение x = F-1 (z) для расчета x через z можно получить
следующим известным способом:
87
(1). Записать формальное уравнение F(x) = z.
(2). Разрешить его относительно x.
8.3.1. Моделирование экспоненциальной с.в.
Экспоненциальная с.в. x имеет ф.р.в.
F(t) = 1 – e-t ,
где t0 и параметр  > 0 . Для экспоненциальной с.в. x
M(x) = 1 /  , D(x) = 1 / 2.
Для построения генератора такой с.в. используем метод обращения.
(1) . Записываем формальное уравнение F(x) = z:
1 – e-t = z.
(2) . Решаем его относительно x:
x = - (1/) ln(1-z).
(8.4)
Формулу (8.4) можно упростить, заменив 1 - z на z, т.к. обе эти величины совпадают по распределению. Тогда из (8.4) получаем:
x = - (1 / ) ln(z).
(8.5)
2.0
3.0
4.0
0
5.0
1000
2000
3000
4000
5000
Рис. 8. 4. Частотная гистограмма
экспоненциальной с.в. (м.о. = 1) при n = 10000
При независимых z генератор (8.5) дает независимые значения экспоненциальной с.в. x. На рис. 8.4 приводится частотная гистограмма, полученная при испытании этого генератора для  = 1 . Оценки моментов составили
M̂ = 0.990, D̂ = 0.978.
8.4. Линейные преобразования с.в.
Пусть x - с.в. и
y = Ax + B,
(8.6)
88
где A, B - константы; A - коэффициент, B - смещение. Преобразование
с.в. x вида (8.6) называется линейным.
Многие непрерывные с.в. в результате линейного преобразования не меняют
вид распределения (меняются только его параметры). К таким относятся экспоненциальной или эрланговской с.в. вид распределения сохраняется только
при масштабном преобразовании, т.е. когда смещение B = 0.
Очевидно, при линейном преобразовании (8.6) имеет место:
M(y) = AM(x) + B,
D(y) = A 2 D(x).
Линейное преобразование (8.6) часто применяется для того, чтобы при
наличии генератора непрерывной с.в. x получить другую с.в. y с тем же распределением, но с другими значениями м.о. и дисперсии.
8.5. Моделирование равномерной с.в.
Равномерно распределенную с.в. x можно реализовать путем линейного преобразования БСВ z:
x = Az + B.
(8.7)
При этом, поскольку z ~ R[0,1], а преобразование (8.7) увеличивает диапазон значений с.в в A раз и смещает вправо на величину B, то x будет
иметь диапазон значений (B,B+A), т.е.
x ~ R[B,B+A].
Кроме того, поскольку M(z) = 1/2, D(z) = 1/12, то
M(x) = A/2 + В,
D(x) = A 2 /12.
9. ПЛАНИРОВАНИЕ СТАТИСТИЧЕСКОГО ЭКСПЕРИМЕНТА
9.1. Задача планирования
Пусть X = (x1 , ... ,xk ) - вектор случайных величин, имеющий распределение P X . Во многих случаях цель статистического эксперимента может
быть сведена к определению математического ожидания с.в. y = g(X), где
g(x) - заданная функция с.в. X. Поэтому типовая схема статистического эксперимента имеет вид рис. 9.1.
i = 1..n
89
: Xi
yi
g(X)
Xi ~ P
X;
1 n
Mˆ y   y i
n i 1
X i = (x 1i , ... ,x ki )
y i - значение с.в. y в i-ом опыте
n - число опытов
Рис. 9.1. Типовая схема статистического эксперимента

Здесь оценка M y приближается к точному значению M(y) с ростом
числа опытов n. Задача планирования статистического эксперимента состоит в нахождении такого n, при котором достигается заданная точность

оценки M y .
9.2. Теоретическое решение задачи планирования

Оценка M y является случайной величиной, т.к. представляет собой
функцию от случайных величин:
1 n
€
M   y
y n
i
i 1
(9.1)
В типовой схеме статистического эксперимента (рис. 9.1) используются независимые реализации xi , поэтому с.в. yi в формуле (9.1) также независимы. Из центральной предельной теоремы вытекает, что с.в. M̂ y
в (9.1) при
больших n имеет нормальное распределение, т.е. M̂ y ~ N[m,]. Определим
параметры этого распределения:
1 n  1
M  yi  nM y My  ,
n

 i 1  n
 
€
σ2 D M
1 n  1


y  D n  y i   2 nD y  Dy  n ,
 i 1  n
  D y  n   y
n
90
Таким образом, при увеличении числа опытов на порядок  уменьшается в 10  3 раза. На рис. 9.2. схематически показан вид распределения
оценки M̂ в зависимости от n.
Рис. 9.2. Распределение с.в. M̂ y в зависимости от n
Диапазон вероятных отклонений оценки от точного значения M(y)
сужается пропорционально
n . Параметр  используют как показатель
точности оценки. Поскольку M̂ y имеет нормальное распределение, то практически достоверно, что M̂ y отклоняется от искомого M(y) не более, чем на
3. Можно сказать, что  является аналогом абсолютной погрешности, а 3
- самой абсолютной погрешностью.
В качестве аналога относительной погрешности для с.в. M̂ y можно
рассматривать ее коэффициент вариации:
v =

,
m
(9.5)
а в качестве самой относительной погрешности - величину 3v. Из (9.2)
и (9.4) находим, что
v =
y
vy

=
,

m n M  y
n
где
v y - коэффициент вариации с.в.
(9.6)
y.
91
Соотношения (9.4) и (9.6) показывают, что "абсолютная погрешность"
3б и "относительная погрешность" 3v оценки M̂ убывают пропорционально
n.
Из формулы (9.4) находим решение задачи планирования: для достижения заданной точности  требуется
 y
n
 





2
(9.7)
опытов. Если требование к точности задано в форме коэффициента вариации v, то требуемое число опытов определяется из формулы (9.6) в виде:
 vy
n  
 v





2
(9.8)
В решении (9.7) кроме заданного  для определения n необходимо
знать  y , в варианте (9.8) - коэффициент вариации v y . Ни то, ни другое до
эксперимента, как правило, не известно. Поэтому планирование числа опытов на практике осуществляется в ходе самого статистического эксперимента. Достаточно удобными методами такого планирования являются метод автоостанова и метод интерактивного контроля.
9.3. Метод автоостанова
Метод автоостанова покажем на примере достижения точности v =
0.01. Схема статистического эксперимента с автоостановом изображена на
рис. 9.3.
Генератор с.в. Х
S
Mˆ y  1
n
S2
2

 ( Mˆ )
ˆ
n
Dy
v' y =
Dˆ y
Mˆ y
92
Рис. 9.3. Схема эксперимента с автоостановом
Как видно из рисунка, в ходе эксперимента ведется непрерывный контроль за оценкой v' коэффициента вариации v. Когда оценка v' устойчиво
входит в зону v' < 0.01, эксперимент завершается.
Устойчивое достижение неравенства v' < 0.01 здесь обеспечивается
требованием, чтобы это неравенство было подтверждено A = 10 раз.
Заметим, что минимальное начальное значение счетчика подтверждений на рис. 9.3., задаваемое в начале алгоритма, должно составлять A = 2,
т.к. необходимо исключить одно ложное подтверждение, которое имеет место при n = =1. Действительно, при n = 1 оценка дисперсии равна нулю, поэтому получается v' = 0. При A = 10 получится несколько "лишних" повторений цикла. Однако, так как n обычно составляет десятки тысяч, то увеличение его на несколько лишних единиц не имеет существенного практического значения.
10. Замечание о языках моделирования
Когда говорят о языке моделирования, предполагают, что в распоряжении исследователя имеется соответствующий транслятор, переводящий
93
программу, записанную на языке моделирования, в программу на языке
вычислительной машины. Язык моделирования вместе с соответствующим
транслятором образует систему моделирования. Создано большое число
языков моделирования, и даже предпринята попытка их систематизации.
Исторически первым языком моделирования можно считать GPSS
(General Purpose Sistems Simulatoг), разработанный фирмой IBM. Первое
представление о языке GPSS дает простейший пример, приведенный ниже.
Моделируется СМО с одним прибором и неограниченным числом
мест для очереди. Заявки поступают через случайные промежутки времени, распределенные равномерно в интервале, который иначе можно записать в виде 18±6. Время обслуживания заявки в приборе распределено аналогично, но в интервале 164. Предполагается получить одну реализацию
длиной 1000, т.е. имитировать функционирование указанной СМО в течение 1000 единиц системного времени. В процессе моделирования должны
быть собраны статистические данные, по которым исследователь смог бы
судить о загрузке прибора, длине очереди, времени ожидания.
Приведем текст программы на языке GPSS.
SIMULATE
Моделирование СМО с одним npи6opом и очередью
GENERATE 18, 6 генерирование заявок через интервалы 18±6
QUEUE
QPR постановка в очередь, имя которой QPR
SEIZE
PR занятие прибора
DEPART QPR уход из очереди
ADVANCE 16,4 обслуживание (задержка на время 16±4)
RELEASE PR освобождение прибора
TERMINATE уход заявки из системы
Второй сегмент: условие остановки
GENERATE 1000 выдача таймером сигнала в момент 1000
TERMINATE 1
завершение реализаций (прогона)
Видно, что это действительно язык моделирования, так как используются характерные для моделирования термины: генерировать, очередь занять, задержать (на время выполнения работы), освободить.
Написать программу моделирования в этих терминах значительно легче, чем составить алгоритм на псевдокоде и потом перевести его на алгоритмический язык. В этом и состоит цель применения языков моделирования.
Здесь, в частности, не надо думать ни о календаре, ни о планировании событий, ни о пополнении статистик - обо всем позаботится интерпретатор.
94
Убедившись на этом примере в полезности применения языков моделирования, перейдем к краткому обзору характерных особенностей
наиболее известных языков.
Начнем с GPSS. GPSS является языком самого низкого уровня среди
языков моделирования. Он имеет ряд существенных недостатков: жесткая
разметка полей в строках программы; жесткие форматы и обозначения
операндов, требующие запоминания роли каждого поля и практически исключающие применение мнемоники; целочисленное измерение времени,
зачастую требующее масштабирования; громоздкое задание законов распределения путем перечисления квантилей, жесткий состав и форма выдачи основных результатов моделирования. Другие языки моделирования
обычно не имеют этих недостатков.
Разработки языков моделирования велась с использованием идей и
приемов, содержащихся в универсальных языках программирования: алголе. фортране, Паскале и др. Как правило, в основе языка моделирования
лежит какой-то универсальный язык программирования; либо имеется существенное сходство в структуре программы. Язык моделирования представляет собой расширение универсального языка путем добавления специальных средств моделирования, либо на основе универсального языка
создан пакет программ для моделирования. В последнем случае не нужен
специальный транслятор, можно воспользоваться транслятором универсального языка.
В основе каждого языка лежит одна из схем построения моделирующего алгоритма: схема событий, схема процессов, схема работ (схема в
пособии не рассматривалась). Соответственно говорят о языке событий,
языке процессов и языке работ. GPSS по этому признаку надо считать языком процессов. Но его называют также языком транзактов, так как в нем
понятие транзакта играет существенную роль.
Транзакт- это временный объект, который появляется в системе,
продвигается в ней и покидает систему. Само слово транзакт ассоциируется с пассивным объектом, которого кто-то ведет (transact - вести). Активность – это постоянно присутствующий в системе объект, который занимается передвижением транзактов Активность принимает транзакт на некоторое время, а потом передает его другой активности. Примеры транзактов: заявки, детали, покупатели. Примеры активностей: приборы, ячейки
буфера; станки, склады; кассиры, продавцы.
Применительно к программе моделирования транзакты и активности
95
– это некоторые структуры данных, содержимое которых меняется, моделируя передвижение транзактов. Информация, содержащаяся в атрибутах
транзактов и активностей, зачастую дублируется. Например, момент перехода заявки из буфера в прибор может быть записан и в транзакте, описывающем заявку, и в активности, описывающей буфер, и в активности, описывающей прибор. В некоторых языках моделирования используется
структуры данных только одного вида: либо транзакты, либо активности.
Чаще используются оба вида, но какой-то является ведущим. По этому
признаку подробная классификация языков моделирования приведена Е.
Киндлером.
Разработки языков моделирования велись в направлении устранения
неудобств и предоставления пользователю все более универсальных
средств для составления программ. Это привело фактически к слиянию
универсальных языков с языками моделирования. Уже язык SIMULA-67
(Норвегия,1968) в дополнении к средствам языка ALGOL-60 содержит
удобный аппарат описания новых понятий, средства обработки текстовой
информации, стандартные средства ввода-вывода, средства для организации квазипараллельного исполнения компонентов программы. SIMULA-67
позволяет создать специализированный язык моделирования и пакет прикладных программ для конкретной предметной области с использованием
терминов из этой области. Это значительно облегчает специалистам разных областей использование моделирования на ЭВМ для решения своих
проблем.
Многие из языков моделирования позволяют в рамках одной программы моделировать системы, в которых взаимодействуют дискретные и
непрерывные процессы. К таким языкам относятся НЕДИС, GASP IV,
СИМФОР, СЛАМ II и др.
В эпоху персональных компьютеров разработаны программные
средства, объединяющие идеологию моделирования (как правило, по схеме процессов) с богатыми возможностями персональных компьютеров по
обеспечению сервиса. Обычно это - мощные инструментальные программные системы, совместимые с такими распространёнными языками
как:MODUL-2, ТURBO-C, TURBO-C++.
Приобрело популярность объектно-ориентированное программирование. В понятии «объект» совмещены структуры данных к описанию
процедур, способных оперировать с этими данными. Вспомним , что понятие процесса рассматривалось нами в двух смыслах: как структура данных
96
и как алгоритм. Теперь эти два понятия объединены в одном понятии объекта. Объекты взаимодействуют между собой подобно процессам в системе.
SIMULA-67
послужил
идейным
источником
объектноориентированного программирования.
Для языков, используемых в задачах моделирования, можно составить классификацию следующего вида (см. рис. 10.1)
Вопросы и задания
1. Система моделирования и язык моделирования - каково соотношение этих понятий?
2. Чем программа на языке GPSS напоминает программу на языке
ассемблера?
3. Как может быть связан язык моделирования с универсальным
языком программирования?
4. Что в приведенной программе (с . ) свидетельствует о том, что
GPSS' язык процессов?
5. Что в приведенной программе подкрепляет утверждение, что
GPSS язык транзактов?
6, Рассмотрите приведенные алгоритмы моделирования СМО (по
схемам событий и процессов), чтобы определить их ориентации: на транзакты или да активности.
7. В чем состоят главные достоинства языка СИМУЛА - 67?
97
Рис. 10.1. Классификация языков моделирования.
98