gidravlika zadachi

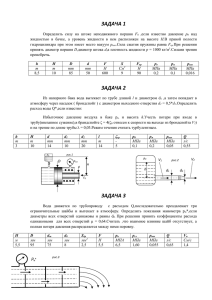
КОНТРОЛЬНАЯ
РАБОТА
ПО ДИСЦИПЛИНЕ
ГИДРАВЛИКА
ВАРИАНТ 3
СОДЕРЖАНИЕ
ЗАДАЧА 1 ............................................................................................................................... 3
ЗАДАЧА 2 ............................................................................................................................... 6
ЗАДАЧА 3 ............................................................................................................................... 8
ЗАДАЧА 4 ..............................................................................................................................11
ЗАДАЧА 5 ............................................................................................................................. 14
ЗАДАЧА 6 ............................................................................................................................ 17
ЗАДАЧА 7 ............................................................................................................................ 20
ЗАДАЧА 8 ............................................................................................................................ 27
ЗАДАЧА 9 ............................................................................................................................ 31
ЛИТЕРАТУРА ....................................................................................................................... 34
2
ЗАДАЧА 1
Условие.
На рис. 1 представлено начальное положение гидравлической системы дистанционного управления (рабочая жидкость между поршнями не сжата). При
перемещении ведущего поршня (его диаметр D) вправо жидкость постепенно
сжимается, и давление в ней повышается. Когда манометрическое давление pм
достигает определённой величины, сила давления на ведомый поршень (его
диаметр d) становится больше силы сопротивления F, приложенной к штоку
ведомого поршня. С этого момента приходит в движение вправо и ведомый
поршень. Диаметр соединительной части δ, длина l.
Требуется определить диаметр ведущего поршня D, необходимый для того,
чтобы при заданной величине силы F ход обоих поршней был один и тот же.
Коэффициент объёмного сжатия рабочей жидкости принять β W =
0,0005 1/МПа.
Рис. 1. Расчетная схема.
Дано:
d = 56 мм = 0,056 м;
L = 72 мм = 0,072 м;
δ = 28 мм = 0,028 м;
3
l = 2,4 м;
F = 67,9 кН = 67900 Н.
___________________
Найти: D = ?
Решение.
1. Ведомый поршень начнёт движение вправо, когда сила давления жидкости на него станет равной силе трения F, приложенной к штоку. Исходя из
этого, определяем манометрическое давление pм, при котором начнётся движение ведомого поршня, по формуле:
рм 
F 67900

 27567910Па = 27.57 МПа,
S 0,0025
где F – сила сопротивления, Н;
S
  d 2   0,0562

 0,0025 м2 - площадь поршня.
4
4
2. Для достижения этого давления при сжатии жидкости ведущий поршень
должен пройти некоторый путь ΔL, соответствующий уменьшению первоначального объёма жидкости на величину ΔW, после чего начинается движение
обоих поршней. При этом объём жидкости, вытесняемый из левой полости системы, равен объёму, поступающему в правую полость.
На основании заданного условия должно выполняться равенство:
  D2
  d2
  L  L  
 L.
4
4
С другой стороны – на основании формулы коэффициента объёмного сжатия:
  D2
 L  W  w  W  pм ,
4
где W – первоначальный (исходный) объём гидравлической системы дистанционного управления, который определяется по формуле:
4
  D2
  2
W
L 
 l.
4
4
3. Используя эти уравнения, выразим искомую величину необходимого
диаметра ведущего поршня D:
   D2
  D2
  2    d 2
 L  w  рм  
L
 l 
 L;
4
4
4
 4

d 2  L  w  рм  2  l
D2 
.
L  w  рм  L
4. Откуда искомый диаметр ведущего поршня:
d 2  L  w  рм  2  l
D

L  w  рм  L

0,0562  0,072  0,0005  27.57  0,0282  2,4

0,072  0,0005  27.57  0,072
= 0,06 м = 60 мм.
Ответ: D = 60 мм.
5
ЗАДАЧА 2
Условие.
В вертикальном цилиндрическом резервуаре (рис. 2), имеющем диаметр D,
хранится нефть, вес её G, плотность ρ = 850 кг/м3, коэффициент температурного
расширения βt = 0,00072 1/°С. Расширение стенок резервуара не учитывается.
Рис. 2. Расчетная схема.
Требуется определить:
1. Объём нефти в резервуаре при температуре 0 °С.
2. Изменение уровня нефти в резервуаре, если температура повысится на
ΔТ, °С
Дано: D = 5 м;
G = 3000 кН = 3000000 Н;
ΔT = 40 °С;
___________________
Найти: W0 = ? ΔW = ?
Решение.
1. Первоначальный объем нефти в резервуаре определяется по формуле:
W0 
G 3000000

 359.8м3,

8338
6
где G – общий вес нефти, Н;
γ = ρ·g = 850·9,81 = 8338 Н/м3 – вес единицы объёма нефти.
2. Из формулы для коэффициента температурного расширения жидкости:
t 
1 W

,
W0 T
где W0 – первоначальный объём нефти в резервуаре, м3;
ΔW – изменение первоначального объёма при изменении температуры на
ΔТ, °С;
получаем изменение объёма жидкости при изменении ее температуры:
ΔW = βt·W0·ΔT = 0,00072·359.8·40 = 10.36 м3.
Ответ: W0 = 359.8 м3; ΔW = 10.36 м3.
7
ЗАДАЧА 3
Условие.
Круглый горизонтальный резервуар (рис. 3), имеющий диаметр D и длину
L, заполнен жидкостью, плотность которой ρ. Манометр, установленный на
уровне верхней образующей, показывает избыточное давление p.
Рис. 3. Расчетная схема.
Требуется определить:
1. Горизонтальную силу гидростатического давления P x, действующую на
круглый торец резервуара.
2. Расстояние e, на которое отстоит линия действия горизонтальной силы
от оси резервуара.
3. Вертикальную силу Pz, действующую на верхнюю половину резервуара.
Дано:
D = 2,5 м;
p = 0,04 МПа = 40000 Па;
ρ = 850 кг/м3;
L = 6 м.
___________________
Найти: Px = ? Pz = ? е = ?
8
Решение.
1. Поскольку избыточное давление равно p = 40000 Па, то пьезометрическая поверхность будет находиться выше места присоединения манометра на
величину:
hp 
p
40000

 4,8 м.
  g 850  9,81
2. Определяем горизонтальную силу гидростатического давления P x, действующую на круглый торец резервуара (рис. 4):
Pх = pс·S = ρ·g·hс·S = 850·9,81·6,05·4,91 =
= 247700 Н = 247,7 кН,
где pc = ρ·g·hс – избыточное гидростатическое давление в центре тяжести торцевой стенки резервуара площадью S;
  D 2   2.52
S

 4,91 м2 – площадь круглого торца резервуара;
4
4
hc 
D
2,5
 hp 
 4,8  6,05 м – глубина погружения центра тяжести рассмат2
2
риваемой плоской фигуры под пьезометрической поверхностью (расстояние от
центра тяжести плоской фигуры до пьезометрической поверхности).
Рис. 4. Определение силы Рх.
9
3. Линия действия силы Px находится ниже центра тяжести плоской фигуры на величину e (эксцентриситет):
е
Ic
1,92

 0,065 м = 65 мм,
h c  S 6,05  4,91
  D4   2,54
где Ic 

 1.92 м4 – центральный момент инерции круга относи64
64
тельно горизонтальной оси.
4. Вертикальная сила, действующая на верхнюю половину резервуара, рассчитывается по формуле
Pz = ρ·g·Wтд,
где Wтд – объём тела давления.
Телом давления называется объём, ограниченный сверху пьезометрической поверхностью, снизу – криволинейной цилиндрической поверхностью, с
боков – вертикальными линиями, проведёнными из краёв криволинейной поверхности до пьезометрической поверхности. Чтобы получить объём тела давления Wтд, нужно площадь поперечного сечения тела давления Sтд (на рис. 4
заштрихована) умножить на длину резервуара L.
Площадь поперечного сечения тела давления определяется по формуле:
Sтд  SABB'A ' 
S
4,91
 15,13 
 12,67 м2,
2
2
где SABB’A’ = D·hc = 2,5·6,05 = 15,13 м2.
Отсюда объём тела давления:
Wтд = Sтд·L = 12,67·6= 76,0 м3.
Подставляем и получаем:
Pz = ρ·g·Wтд = 850·9,81·76,0 = 63389 Н = 633,9 кН.
Так как жидкость и тело давления расположены по разные стороны от
криволинейной поверхности, то вертикальная сила Pz направлена вверх.
Ответ: Px = 247,7 кН; Pz = 633,9 кН; е = 65 мм.
10
ЗАДАЧА 4
Условие.
Вертикальный цилиндрический резервуар высотой H и диаметром D закрывается полусферической крышкой, сообщающейся с атмосферой через трубу внутренним диаметром d (рис. 5). Резервуар заполнен мазутом, плотность
которого ρ = 900 кг/м3.
Рис. 5. Расчетная схема.
Требуется определить:
1. Высоту поднятия мазута h в трубе при повышении температуры на Δt.
2. Усилие, отрывающее крышку резервуара при подъёме мазута на высоту
h за счет его разогрева.
Коэффициент температурного расширения мазута принять равным
βt = 0,00072 1/°С.
Дано:
D = 1.5 м;
Н = 2.5 м;
d = 100 мм = 0,1 м;
Δt =10 °С.
___________________
11
Найти: h = ? Pz = ?
Решение.
1. Сначала определяем объём резервуара, состоящий из цилиндрической и
полусферической частей. Это будет первоначальный объём мазута:
  D2
1   D3   1,52
1   1,53
W0 
H 

 2,5  
 5,3 м3,
4
2
6
4
2
6
где D, м – диаметр резервуара;
Н, м – высота резервуара.
2. Затем, используя формулу для определения коэффициента температурного расширения βt, находим приращение этого объёма за счёт его расширения
при нагреве на Δt:
ΔW = βt·W0·Δt = 0,00072·5,3·10 = 0,038 м3,
где βt = 0,00072 1/°С - коэффициент температурного расширения;
Δt = 10 °C – приращение температуры.
3. Разделив найденное приращение объёма ΔW на площадь поперечного
сечения трубы S, получим искомую высоту поднятия мазута h:
h
W
0,038

 4,84 м,
S
0,00785
  d 2   0,12

 0,00785 м2 - площадь поперечного сечения трубы.
где S 
4
4
4. Усилие, отрывающее крышку резервуара от плоскости разъёма, определяем по формуле:
Pz = ρ·g·Wтд = 900·9,81·8,95 = 79020 Н = 790,2 кН,
где
Wтд 
  D2
4
3
  1.52
D
 1 D
  h  
 W 
6
4
2
 2
 1.5
 1   1.5

 4,84   
 0,038 
6
 2
 2
3
= 8,95 м3 – объём тела давления, ограниченный полусферической крышкой,
пьезометрической поверхностью и вертикальными линиями, проходящими через концы криволинейной поверхности. Этот объём будет состоять из объёма
12
цилиндра диаметром D и высотой (D/2 + h) минус объём полусферы диаметром
D и объём малого цилиндра диаметром d и высотой h.
Ответ: h = 4,84 м; Pz = 790,2 кН.

13
ЗАДАЧА 5
Условие.
К системе, состоящей из двух параллельно соединённых трубопроводов,
имеющих длины соответственно l1 и l2 и диаметры d1 и d2 (коэффициент шероховатости n = 0,012), подводится к точке A вода, расход которой Q (рис. 6).
Рис. 6. Расчётная схема.
Требуется определить потерю напора на участке AA1 и величины расходов
воды на каждом участке.
Дано:
Q = 116 л/с = 0,116м3/с;
l1 = 400 м;
d1 = 200 мм = 0,20 м;
l2 = 450 м;
d2 = 300 мм = 0,3 м.
___________________
Найти: Q1 = ? Q2 = ? hl1 = ?
Решение.
1. Потери напора на каждом из двух параллельно соединённых трубопроводов одинаковы:
hl1 = hl2 = hl,
14
где hl1 и hl2 – потери напора по длине соответственно на первом и втором трубопроводах.
2. Модули расхода для первого и второго трубопровода определяем по
формуле:
К   С  R ,
где ω – площадь живого сечения;
С – коэффициент Шези;
R

 гидравлический радиус;

χ = π·d – смоченный периметр.
Коэффициент Шези вычисляем по формуле Маннинга:
1
1
C  R6,
n
где n = 0,012 - коэффициент шероховатости.
Для первого трубопровода:
χ1 = π·d1 = π·0,2 = 0.628 м;
  d12   0,22
1 

 0,0314 м2;
4
4
1 0,0314

 0,05 м;
1 0,628
R1 
1
1
1
1
C1   R16 
 0,056  50,58;
n
0,012
К1  1  С1  R1  0,0314  50,58  0,05  0.355.
Для второго трубопровода:
χ2 = π·d2 = π·0,3 = 0,94 м;
  d 22   0,32
2 

 0,0707 м2;
4
4
R2 
2 0,0707

 0,075 м;
2
0,94
15
1
1
1
1
C2   R 26 
 0,0756  54,1;
n
0,012
К2  2  С2  R 2  0,0707  54,1  0,075  1,05.
3. Определяем потерю напора на участке AA1:
h1 
Q2
 K1 K 2 



 l

l
1
2


2

0,1162
 0,355 1,05 



450 
 400
2
 2,98 м.
4. Определяем расходы в каждом из трубопроводов:
Q1  K1 
h1
2,98
 0,35 
 0,030м3/с =30 л/с;
l1
400
Q2 = Q – Q1 = 0,116 – 0,03= 0,086 м3/с = 86 л/с.
5. Вычисляем потери напора на каждом из параллельных участков AA1:
Q12
0,032
h l1  2  l1 
 400  2,94 м;
K1
0,352
Q22
0,0862
h l2  2  l 2 
 450  3,02 м.
K2
1,052
При правильном подсчёте Q1 и Q2 потери напора должны быть равны
между собой, то есть h l1  h l2 . Это условие соблюдается.
Ответ: Q1 = 30 л/с; Q2 = 86 л/с; h l1  h l2  3 м.
16
ЗАДАЧА 6
Условие.
Поршень диаметром D имеет n отверстий диаметром d 0 каждое (рис. 7).
Отверстия рассматривать как внешние цилиндрические насадки с коэффициентом расхода μ = 0,82; плотность жидкости ρ = 900 кг/м3.
Рис. 7. Расчетная схема.
Требуется определить скорость v перемещения поршня вниз, если к его
штоку приложена сила F.
Дано:
D = 70 мм = 0,07 м;
d0 = 8 мм = 0,008 м;
n = 6шт.;
F = 12 кН = 12000 Н.
___________________
Найти: v = ?
17
Решение.
1. Определяем величину давления под поршнем p, которое определяется
отношением силы, приложенной к поршню, к площади поршня без учёта суммарной площади отверстий:
p
F
4F
4  12000


 338500 Па = 3,385 МПа,
2
2
Sбо    D  n  d 0     0,07 2  2  0,0082 
где D, м – диаметр поршня;
N, шт. – количество отверстий в поршне;
d0, м – диаметр отверстий в поршне
Sбо 
   D2  n  d 02 
4
 площадь поршня без учёта суммарной площади отвер-
стий.
2. Расход жидкости из каждого отверстия (насадка) составляет:
Q1    1 
2p
2  338500
 0,82  5,03  105 
 3,58·10-3 м3/с,

900
где μ – коэффициент расхода;
ρ, кг/м3 – плотность жидкости
p, Па – давление под поршнем
  d 02   0,0082
1 

 5,03·10-5 м2 – площадь одного отверстия.
4
4
3. Так как все отверстия имеют одинаковый диаметр, и соответственно
одинаковую площадь, то расход жидкости из всех отверстий определяем по
формуле:
Q = n·Q1 = 6·3,58·10-3 = 0,0215 м3/с.
4. Скорость перемещения поршня вниз определяем как отношение суммарного расхода из всех отверстий к площади поперечного сечения поршня:
v
где S 
Q 4  Q 4  0,0215


 4,28 м/с,
S   D2   0,082
  D2
 площадь поперечного сечения поршня.
4
18
Ответ: v = 4,28 м/с
19
ЗАДАЧА 7
Условие.
Центробежный насос (рис. 8) откачивает воду из сборного колодца в резервуар с постоянным уровнем H по трубопроводам размерами lвс, dвс и lн, dн.
Рис. 8. Расчетная схема.
Эквивалентная шероховатость поверхности труб Δ, плотность воды ρ =
1000 кг/м3, кинематический коэффициент вязкости ν = 0,01 см2/с, расстояние
a = 1 м.
Характеристики насоса представлены следующими параметрами:
Q, л/с
0
2
4
6
8
10
12
14
16
18
20
Hн, м
45,0
47,5
48,5
48,0
47,0
45,0
40,0
35,0
30,0
22,5
15,0
-
-
8,2
8,0
7,6
7,0
6,6
6,0
5,5
4,75
4,0
доп
,м
Н вак
20
При расчетах принять суммарные коэффициенты местных сопротивлений
на всасывающей линии ζвс = 10, на напорной линии ζн = 6.
Требуется определить:
1. На какой глубине h установится уровень воды в колодце, если приток в
него Q?
2. Вакуумметрическую высоту всасывания при входе в насос Hвак, выраженную в метрах водяного столба (м в.ст.).
3. Максимальную допустимую геометрическую высоту всасывания при заданном расходе.
Дано:
Н = 33 м;
dвс = 100мм = 0,1 м;
lвс = 15м;
dн = 125 мм = 0,125 м;
lн = 40м;
Δ = 0.5 мм = 0,0005 м;
Q = 12 л/с = 0,012 м3/с.
___________________
доп
Найти: h = ? Hвак =? Нгв
?
Решение.
1. Пользуясь заданными параметрами, построим на рис. 9 характеристики
насоса, выраженные кривыми:
доп
 f Q,
Hн = f(Q) и Н вак
где Hн – напор, развиваемый насосом при заданном расходе Q;
доп
Нвак
 допустимая вакуумметрическая высота всасывания насоса по условию
кавитации при заданном расходе.
21
Рис. 9. Характеристики насоса.
2. По построенным кривым определим при заданном значении расхода
доп
 6.6 м.
Q = 12л/с величины Hн = 40 м и Нвак
3. Напор, развиваемый насосом, расходуется на подъём воды на геометрическую высоту Hг = H + h и преодоление потерь напора во всасывающей и
нагнетательной линиях:
Hн = Hг + hвс + hн = H + h + hвс + hн,
откуда искомая величина:
h = Hн - H - hвс - hн,
22
где hвс – потери напора во всасывающей линии, м;
hн – потери напора в нагнетательной линии, м.
4. Потери напора во всасывающей линии определяются как сумма местных
потерь напора и потерь напора по длине трубопровода:
hвс = hlвс + hмвс = 0,54 + 1,19 = 1,73 м,
где h lвс
2
lвс vвс
15 1.532
 вс 

 0,03 

 0.54 м - потери напора по длине во
dвс 2  g
0,1 2  9,81
всасывающей линии;
lвс – длина всасывающей линии, м;
dвс – диаметр всасывающей линии, м;
vвс 
4  Q 4  0,012

 1,53 м/с – средняя скорость движения воды во всасыва2
  d вс
  0,12
ющей линии;
Q – расход воды во всасывающей линии, м3/с;
 
68 
 вс  0,11  


 d вс Reвс 
0,25
68 
 0.5
 0,11  


 100 153000 
0,25
 0,03 - гидравлический ко-
эффициент трения во всасывающей линии,
Reвс 
vвс  d вс 1,53  0,1

 153000– число Рейнольдса на участке всасывающей

1  106
линии;
Δ – эквивалентная шероховатость поверхности труб, м;
ν – кинематический коэффициент вязкости, ν = 0,01 см2/с = 1·10-6 м2/с;
h мвс
2
vвс
1,532
  вс 
 10 
 1,19 м – потери напора в местных сопротивлени2g
2  9,81
ях;
ζвс – суммарный коэффициент местных сопротивлений на всасывающей линии.
5. Потери напора в нагнетательной (напорной) линии определяются как
сумма местных потерь напора и потерь напора по длине трубопровода:
hн = hlн + hмн = 0,45+ 0,29 =0,74 м,
23
lн vн2
0,982
40
где h lн  н  
 0,029 

 0,45 м – потери напора по длине в
dн 2  g
0,125 2  9,81
нагнетательной линии;
lн – длина нагнетательной линии, м;
dн – диаметр нагнетательной линии, м;
vн 
4  Q 4  0,012

 0,98 м/с – средняя скорость движения воды в нагнета  d н2   0,1252
тельной линии;
Q – расход воды в нагнетательной линии, м3/с;

68 
 н  0,11   

 d н Reн 
0,25
68 
 0.5
 0,11  


 125 122500 
0,25
 0,029 - гидравлический ко-
эффициент трения в нагнетательной линии;
Reн 
vн  d н 0,98  0,125

 122500 – число Рейнольдса на участке нагнетатель
1  106
ной линии;
Δ – эквивалентная шероховатость поверхности труб, м;
ν – кинематический коэффициент вязкости, ν = 0,01 см2/с = 1·10-6 м2/с;
h мн
vн2
0,982
 н 
 6
 0,29 м – потери напора в местных сопротивлениях в
2g
2  9,81
нагнетательной линии.
6. Подставляем полученные результаты и получаем глубину воды в колодце:
h = Hн - H - hвс - hн = 40 – 33 – 1,73 – 0,74= 4,53 м.
7. Вакуумметрическую высоту всасывания при входе в насос определяем
из уравнения Бернулли, составленного для сечений 1 – 1 и 2 – 2, приняв за горизонтальную плоскость сравнения сечение 1 – 1:
z1 
p1 1  v12
p
  v2

 z2  2  2 2  h w ,

2g

2g
24
где z1 – геометрическая высота сечения 1-1 над плоскостью сравнения. Так как
плоскость сравнения проведена по сечению 1-1, то z1 = 0;
z2 – геометрическая высота сечения 2-2 над плоскостью сравнения. Так как
плоскость сравнения проведена по сечению 1-1, то z2 = h + a;
p1
 пьезометрическая высота в сечении 1-1. Так как на свободную поверхность

воды в резервуаре действует атмосферное давление, то p1 = pатм;
p2
 пьезометрическая высота в сечении 2-2. Так как давление перед насосом

составляет pн, то p2 = pн;
1  v12
 скоростная высота в сечении 1-1. Так как скорость на поверхности ре2g
1  v12
 0;
зервуара v1 = 0, то
2g
 2  v 22
 скоростная высота в сечении 2-2. Так как скорость перед насосом со2g
2
 2  v 22 v вс

;
ставляет vвс, а коэффициент Кориолиса α = 1, то
2g
2g
hw = hвс – потери напора во всасывающей линии.
Подставляя найденные члены уравнения Бернулли, получаем:
2
pатм
pн vвс
0
 0  h  a   
 h вс .

 2g
Как известно, вакуум – это недостаток абсолютного давления до атмосферного, то есть рвак = ратм – рабс. Тогда величина вакуума перед насосом в метрах водного столба будет равна:
Н вак
2
pвак pатм pн
vвс
1,532



 h  a  
 h вс   4,53  1 
 1,73 



2g
2  9,81
= 7,38 м.
Вакуум в Паскалях :
рвак = Нвак·ρ·g = 7,38·1000·9,81 = 72398Па = 72,4кПа.
25
8. Максимальная допустимая геометрическая высота всасывания при заданном расходе определяется по формуле:
Н
доп
гв
Н
доп
вак
2
 вс  vвс
1  1,532

 h вс  6,6 
 1,73  4,75 м,
2g
2  9,81
где hвс – потеря напора во всасывающей линии, м;
2
 вс  vвс
 скоростной напор во всасывающей линии при заданном расходе, м;
2g
αвс = 1 – коэффициент кинетической энергии потока;
доп
Нвак
 допустимая вакуумметрическая высота всасывания, определяемая по
графику, м.
доп
Ответ: h = 4,53м; Hвак = 7,38м в.ст.; Нгв
 4,75 м.
26
ЗАДАЧА 8
Условие.
Жидкость плотностью ρ = 900 кг/м3 поступает в левую полость цилиндра
через дроссель с коэффициентом расхода μ = 0,62 и диаметром d под избыточным давлением pн; давление на сливе pс (рис. 10). Поршень гидроцилиндра
диаметром D под действием разности давлений в левой и правой полостях цилиндра движется слева направо с некоторой скоростью v.
Рис. 10. Расчетная схема.
Требуется определить значение силы F, преодолеваемой штоком гидроцилиндра диаметром dш при движении его против нагрузки со скоростью v.
Дано:
D = 80 мм = 0,08 м;
dш = 40 мм = 0,04 м;
d = 2.2 мм = 0,022 м;
pн = 15 МПа = 15·106 Па;
pс = 1 МПа = 1000000 Па;
v = 3.5 см/с = 0,035 м/с.
___________________
Найти: F = ?
27
Решение.
1. Поскольку поршень движется равномерно со средней скоростью v, то
сумма всех сил, действующих на поршень, равна 0:
ΣF = 0
или
Fлев = Fпр + F.
Силы, действующие слева:
Fлев = pраб·S.
Силы, действующие справа:
Fпр = pc·S’.
Тогда равновесие сил будет выражаться уравнением:
F + pc·S’= pраб·S;
или
  D2

р раб 
 F  pc    D 2  d ш2  ,
4
4
где pраб – давление в левой полости цилиндра ;
  D2
S
 площадь поршня в левой полости;
4
D – диаметр поршня гидроцилиндра;
pc – давление в правой полости;
S' 
   D2  d ш2 
4
 площадь поршня в правой полости, которая равна разности
площадей цилиндра и штока;
dш – диаметр штока гидроцилиндра;
2. Сила, действующая на поршень, определяется по формуле:
F  р раб 
  D2

 pc    D 2  d ш2  .
4
4
3. Рабочее давление гидроцилиндра:
рраб = рн – Δр.
28
4. Перепад давлений на входе в дроссель и на выходе из него составляет:
Δр = ρ·g·H,
где Н – напор перед дросселем, который определяется из формулы для определения расхода жидкости Q.
5. Расход гидроцилиндра определяется из условия равенства расходу, проходящему через дроссель:
Q  др  vдр    др  2  g  H,
откуда:
Q2
 v   .
H 2 2
 2 2
  др  2  g   др  2  g
2
Тогда:
   v  
Q2
p    g  H    g  2 2


  др  2  g 2   2  2др
2

900   0,035  5,03·103 
2  0,622   3,8  106 
2
2

= 2,5127∙106 Па = 2,51 МПа,
  D 2   0,082

 5,03·10-3 м2 - площадь поршня в левой полости;
где  
4
4
v – скорость движения поршня, м/с;
  d 2   0,00222
др 

 3.8·10-6 м2 – площадь дросселя;
4
4
vдр – скорость прохода жидкости через дроссель, м/с;
μ = 0,62 - коэффициент расхода.
6. Находим давление в левой полости цилиндра и силу, действующую на
поршень:
pраб = pн – Δp = 15 –2,5 = 12,5 МПа;
29
  D2

F  р раб 
 pc    D 2  d ш2  
4
4
  0,082

12,5  106 
 1  106    0,082  0,04 2  
4
4
= 59032 Н = 59,0 кН.
Ответ: F = 59 кН.
30
ЗАДАЧА 9
Условие.
Гидравлическое реле времени, служащее для включения и выключения
различных устройств через фиксированные интервалы времени, состоит из цилиндра, в котором помещен поршень диаметром D1 со штоком-толкателем диаметром D2. Цилиндр присоединён к ёмкости с постоянным уровнем жидкости
H0. Под действием давления, передающегося из ёмкости в правую полость цилиндра, поршень перемещается, вытесняя жидкость из левой полости в ту же
ёмкость через трубку диаметром d (рис. 11).
Рис. 11. Расчетная схема.
Требуется вычислить время T срабатывания реле, определяемое перемещением поршня на расстояние S из начального положения до упора в торец цилиндра.
Движение поршня считать равномерным на всём пути, пренебрегая незначительным временем его разгона. В трубке учитывать только местные потери
напора. Коэффициент сопротивления колена ζк = 1,5 и дросселя на трубке ζд.
31
Утечками и трением в цилиндре, а также скоростными напорами жидкости в
его полостях пренебречь.
Дано:
D1 = 100 мм = 0,10 м;
D2 = 50мм = 0,50 м;
H0 = 2.0 м;
d = 10 мм = 0,010 м;
S = 250 мм = 0,25 м;
ζд = 25.
___________________
Найти: Т = ?
Решение.
1. Сила давления жидкости на поршень справа:
Pп = ρ·g·H0·Sп,
где Sп – площадь поршня.
Сила давления слева:
Pл = ρ·g·H0·(Sп – Sш),
где Sш – площадь штока.
2. Равнодействующая сила, действующая на площадь (сила, перемещающая поршень):
P = Pп - Pл = ρ·g·H0·Sш.
3. При равномерном движении поршня эта сила должна уравновешиваться
силой сопротивления движению поршня со стороны жидкости, которая будет
равна:
F = Δp·(Sп - Sш),
где
р
v2
v2
v2
 к 
 д 

   к   д   потеря давления при прохождении

2g
2g 2g
жидкости по трубке из левой полости цилиндра в правую;
32
V – скорость движения жидкости по трубке, м/с;
γ – вес единицы объёма жидкости, Н/м3.
4. Приравняв правые части полученных формул, и подставив Δp, определяем скорость движения жидкости по трубке и расход Q.
Скорость:
v
2  g  Н 0  Sш

 к   д   Sп  Sш 
2  9,81  2.0  0,00196
 0,7 м/с,
1,5  25   0,0079  0,00196 
  D12   0,12

 0,0079 м2 - площадь поршня;
где Sп 
4
4
  D 22   0,052
Sш 

 0,00196 м2 – площадь штока.
4
4
Расход:
Q = v·ω = 0,7·7.85·10-5 = 5,5·10-5 м3/с,
  d 2   0,012

 7.85·10-5 м2 – площадь поперечного сечения трубки.
где  
4
4
5. Из уравнения неразрывности потока:
v    vп  Sп  Sш 
определяем скорость движения поршня vп:
v
Q
5,5·105
vп 


 9,26∙10-3 м/с.
Sп  Sш Sп  Sш 0,0079  0,00196
6. Зная расстояние S, на которое должен переместиться поршень, вычисляем время T срабатывания реле:
Т
S
0,25

 27 с.
vп 9,26 * 103
Ответ: Т = 27 с.
33
ЛИТЕРАТУРА
1. Башта Т.М. и др. Гидравлика, гидравлические машины и гидравлические
приподы. М.: Машиностроение, 1970.
2. Доманский И.В. Основы гидромеханики. Механика жидкости и газа. СПб.:
СПбГТИ (ТУ), 2014.
3. Земцов В.М. Гидравлика. М.: Издательство ассоциации строительных вузов,
2007.
4. Калекин А.А. Основы гидравлики и технической гидромеханики. М.: Мир,
2008.
5. Осипов П.Е. Гидравлика, гидравлические машины и гидропривод. М.: Лесная
промышленность, 1981.
34