Лекция №20 СМА 2015x

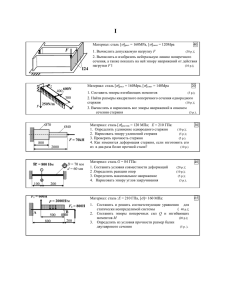
Лекция №20
Сложное сопротивление стержня прямоугольного сечения.
Размеры стержня и приложенная к нему расчетная нагрузка показаны
на рис.1. Коэффициент надежности по нагрузке  f  1,25 .Упругие
характеристики материала стержня: Е  200 ГПа = 2  108 кН2 ,   0,3 , G 
м
= 77  10 6 кН2 . Расчетное
м
E
2  (1   )
сопротивление R  200МПа = 2 10
5 кН
м2
Геометрические характеристики поперечного сечения стержня:
b  6 см, h  10 см, A  b  h  60см2 , J z  bh  500 см4,
12
2
3
bh
b2  h
b

h
4
3
J y  12  180см , Wz 
 100 см , W y 
 60 см3 .
6
6
3
Жесткость на растяжение (сжатие) EA  12 105 кН . Изгибные
жесткости: EJ z  103 kHм 2 , EJ y  360kHм 2 .
Отношение большей стороны прямоугольника к меньшей:  
h
 1,667.
b
Коэффициенты для определения напряжений и деформаций при кручении
определяются по табл. 1 с использованием линейной интерполяции:
k 1 0,236 , k 2 0,833 , k3  0,208 .
Таблица 1.
h/b
1
1.5
1.75
2
2.5
3
4

k1
0.208
0.231
0.239
0.246
0.258
0.267
0.282
0.333
1.0
0.859
0.820
0.795
0.766
0.753
0.745
0.742
k2
0.141
0.196
0.214
0.229
0.249
0.263
0.281
0.333
k3
Моменты сопротивления кручению и полярный момент инерции при
кручении равны ( h  b ):
W
W1  k1  h  b 2  85,1см3, W2  1  102,1см3, J x  k 3 h  b3  449,3 см4.
k2
Крутильная жесткость GJ x  345,6kHм2 .
Если h  b : W1  k1h b , J x  k 3 h b .
2
3
В формулах для W1 в квадрате меньшая сторона. В формулах для
J x в кубе меньшая сторона.
Абсцисса заданного сечения для проверки прочности x=0,1 м
(рис.1).
Рис.1 Размеры и расчетная нагрузка на стержень
Приведем силы к центру тяжести соответствующего поперечного
сечения (рис.2).
Рис.2 Приведение сил к центру тяжести сечений
К стержню, нагруженному сложной системой сил (рис.2) применим
принцип независимости действия сил.
Действующие силы разделим на четыре группы: 1) силы вызывающие
деформации растяжения – сжатия; 2) силы вызывающие деформации
кручения; 3) силы вызывающие деформации изгиба в плоскости xoy ; 4)
силы вызывающие деформации изгиба в плоскости xoz .
Для каждого из четырех видов деформации стержня раннее было
введено правило знаков для внутренних усилий и дана методика их
определения,
получены расчетные формулы для напряжений
и
перемещений.
Задачи проверки прочности, подбора сечения и определения
грузоподъемности в случае сложного сопротивления стержня решаются по
общей методике, но имеют свои особенности связанные с формой
поперечного сечения.
1.Центральное растяжение (сжатие).
Рассмотрим стержень, нагруженный силами, вызывающими только
деформации растяжения-сжатия (рис.1.1,а). Определим опорную реакцию
в точке О. Составим уравнение равновесия
получим Ro  40 кН
результате
F
x
 0,
Ro  40  0 , в
(рис
1.1,б).
Рис. 1.1 Центральное растяжение (сжатие)
Построим эпюру продольных сил. Начало координат примем в т. O .
Проведем сечение в произвольном месте первого участка. Сечение
зафиксируем координатой x (рис.1.2) . Продольная сила положительна,
если она направлена по внешней нормали к сечению. Для 1-го участка имеем:
0  x  0,9 м
F
x
 0 , N1 ( x )  40  0 , N1 ( x )  40 кН.
Рис. 1.2
Проведем сечение в произвольном месте второго участка. Сечение
зафиксируем координатой x (рис.1.3)
0,9 м  x  1,2 м
F
 0,
N 2 ( x )  40  40  0 ,
N 2 ( x)  0 .
x
Рис.1.3
На рис.1.1,в показана эпюра продольных сил N от заданной нагрузки.
Значение продольной силы в заданном сечении для проверки
прочности N (0,1)  40 кН.
Определим перемещение поперечного сечения стержня в точке c . Для
этого в точке с приложим единичную безразмерную силу (рис.1.1, г).
Соответствующая эпюра продольных сил n( x) показана на рис. 1.1,д.
Искомое перемещение найдем по формуле Мора, интеграл вычислим
по правилу Верещагина. Учтем, что перемещение необходимо вычислять от
нормативной нагрузки (  f  1, 25 ; EA  12 105 кН ).
u (1, 2) 
1
f
0,9
(
0
1,2
N1  n
N2  n
1
36 103
dx  
dx) 
(40)  0,9  ( 1) 
 0, 024 мм
EA
EA
 f  EA
1, 25 12 105
0,9
Величина перемещения положительна, следовательно, перемещение сечения
происходит по направлению действия единичной силы (против оси x ).
1. Кручение.
Рассмотрим стержень, нагруженный силами, вызывающими только
деформации кручения (рис.2.1,а).
Рис.2.1 Кручение
Определим опорную реакцию M o в точке О. Составим уравнение равновесия
m
x
 0 , M o  0, 4  0,12  0 , в результате получим M o  0,52кНм (рис
2.1,б).
Построим эпюру крутящих моментов. Начало координат примем в т.
O . Проведем сечение в произвольном месте первого участка. Сечение
зафиксируем координатой x (рис.2.2) . Крутящий момент M x в сечении
положителен, если при взгляде с конца оси x он направлен по ходу часовой
стрелки. Для 1-го участка имеем:
0  x  0,5 м
m
 0 , M x1 ( x )  0,52  0 ,
M x1 ( x )  0,52кНм
x
Рис. 2.2
Проведем сечение в произвольном месте второго участка. Сечение
зафиксируем координатой x (рис.2.3)
0,5 м  x  1,2 м
m
 0,
M x 2  0, 4  0,52  0 ,
M x 2  0,12кНм .
x
Рис. 2.3
На рис. 2.1,в показана эпюра крутящего момента M x ( x ) .
Значение крутящего момента в заданном сечении для проверки
прочности M x (0,1)  0,52 кНм.
Определим угол закручивания поперечного сечения в точке c . Для
этого в точке с приложим единичную пару сил (рис.2.1, г). Соответствующая
эпюра крутящих моментов m x показана на рис. 2.1,д.
Искомое перемещение найдем по формуле Мора, интеграл вычислим
по правилу Верещагина. Учтем, что перемещение необходимо вычислять от
нормативной нагрузки (  f  1, 25 ; GJ x  345,6kHм2 )
 x (1, 2) 
1
f
0,5
(
0
1,2
M x1 ( x)  mx ( x)
M ( x )  mx ( x )
dx   x 2
dx) 
GJ x
GJ
x
0,5
1
0,344
((0,52)  0,5  (1)  (0,12)  0, 7  ( 1)) 
 7,96 10 4 рад
 f  GJ x
1, 25  345, 6
.
Величина перемещения положительна, следовательно, перемещение
сечения происходит по направлению действия единичной пары сил.
3. Изгиб в плоскости xoy
Рассмотрим стержень, нагруженный силами, вызывающими изгиб в
плоскости xoy (рис.3.1,а).

Рис.3.1 Изгиб в плоскости x0y
Определим реакции опор в точке О. Составим уравнения равновесия:
4  1, 2  2  M o  0 ,
Fу  0 , R0  4  0 . В результате
mo  0 ,

получим: M o  2,8кНм , R0  4 кН (рис 3.1,б).
Построим эпюры поперечных сил Q y и изгибающих моментов M z .
Раннее было принято следующее правило знаков для внутренних усилий,
действующих в сечениях стержня.
Изгибающий момент M z ( x )  0 , если он растягивает нижнее волокно
стержня. Поперечная сила Qy ( x)  0 , если она вращает рассматриваемый
элемент стержня по ходу часовой стрелки.
Проведем сечение в произвольном месте первого участка. Сечение
зафиксируем координатой x (рис.3.2)
0  x  0,9 м
 F  0 , Q ( x )  4  0 , Q ( x)  4кН
 m  0 , M ( x )  2,8  4  x  0 ,
y
y1
y1
z1
k
M z1 ( x )  4 x  2,8 ,
M z1 (0)  2,8 кНм,
M z1 (0,9)  0,8 кНм.
Рис.3.2
Найдем координату точки, в которой M z1 ( x )  0 . Получим:
4 x  2,8  0 , x  0,7 м (рис.3.1, г).
Проведем сечение в произвольном месте второго участка. Сечение
зафиксируем координатой x (рис.3.3)
F
0,9 м  x  1,2 м
y
 0 , Qy 2 ( x )  4  0 ,
Qy 2 ( x )  4кН .
m
 0,
M z 2 ( x )  2,8  2  4  x  0 ,
M z 2 ( x )  4 x  4,8
M z 2 (0,9)  1, 2кНм ;
Рис.3.3
M z 2 (1, 2)  0
На рис.3.1,г показана эпюра изгибающего момента M z ( x ) .
k
Значения поперечной силы и изгибающего момента в сечении
для проверки прочности равны: Qy (0,1)  4 кН; M z (0,1)  2, 4кНм .
Определим прогиб на конце консоли. Для этого в точке с приложим
единичную силу (рис.3.1,д). Соответствующая эпюра изгибающих моментов
mz показана на рис. 3.1,е. Интегралы Мора вычислим по правилу
Верещагина. На рис. 3.4 показаны эпюры и M z и mz . Эпюра M z разбита на
три треугольника. Площади треугольников с учетом знака равны:
1  0,98 ,  2  0,08 , 3  0,18 . Ординаты эпюры mz , взятые под
центром
тяжести
треугольников,
равны:
Y1  0,967 ,Y2  0,367 ,
Y3  0, 2 . Таким образом, прогиб
на конце консоли от нормативной
нагрузки
образом (  f  1,25 ; EJ z  103 kHм 2 ):
V (1,2) 

определится
следующим
1
(1Y1  2Y2  3Y3 ) 
E  J z  f
1
(0,98  0,967  0,08  0,367  0,18  0,2) 103  0,7634 мм
3
10 1,25
Рис.3.4
Вычислим угол поворота концевого сечения балки. Для этого в сечении
с приложим единичную пару сил (рис.3.5,б). На рис. 3.5 показаны эпюры и
M z и mz .
Рис.3.5
Угол поворота сечения равен:
 z (1,2) 

1
(1Y1  2Y2  3Y3 ) 
E  J z  f
1
(0,98 1  0,08 1  0,18 1)  0,864 10 3 рад
3
10 1,25
4.Изгиб в плоскости xoz
Рассмотрим стержень, нагруженный силами, вызывающими изгиб в
плоскости xoz (рис.4.1,а).
Определим реакции опор в точке О. Составим уравнения равновесия:
mo  0 , 1, 2  0,5  8  M o  0 ,
Fz  0 , R0  8  0 . В результате


получим: M o  5, 2 кНм, R0  8кН (рис 4.1,б).
Рис.4.1 Изгиб в плоскости xoz
Построим эпюры поперечных сил Qz и изгибающих моментов M y .
Раннее было принято следующее правило знаков для внутренних
усилий, действующих в сечениях стержня.
Изгибающий момент M y ( x)  0 , если он растягивает наружное
волокно стержня. Поперечная сила Qz ( x )  0 , если она вращает
рассматриваемый элемент стержня против хода часовой стрелки.
Проведем сечение в произвольном месте первого участка. Сечение
зафиксируем координатой x (рис.4.2)
0  x  0,5 м
Fz  0 , Qz1 ( x)  8  0 ,

Qz1 ( x)  8кН .
 mk  0 M y1 ( x)  5,2  8  x  0 ,
M y1 ( x)  5,2  8 x , M y1 (0)  5,2
кНм, M y1 (0,5)  1,2 кНм.
Рис.4.2
Проведем сечение в произвольном месте второго участка. Сечение
зафиксируем координатой x (рис.4.3)
0,5 м  x  0,9 м
F
 0 , Qz 2 ( x)  8  8  0 ,
Qz 2 ( x)  0 .
 mk  0 ,
M y 2 ( x)  5,2  8  x  8(x  0,5)  0
, M y 2 ( x)  1,2 кНм.
z
Рис.4.3
Проведем сечение в
0,9 м  x  1,2 м (рис.4.4).
произвольном
месте
третьего
участка
Рис.4.4
Составляем уравнения равновесия:
Qz 3 ( x)  0 ;
m
k
F
z
 0 , Qz 3 ( x)  8  8  0 ,
 0 , M y 3 ( x)  5,2  8 x  8( x  0,5)  1,2  0 , M y 3 ( x)  0
Эпюры Qz и M y представлены на рис.4.1, в, г.
Значения поперечной силы и изгибающего момента в сечении для
проверки прочности равны: Qz (0,1)  8 кН; M y (0,1)  4,4 кНм.
Определим прогиб на конце консоли и угол поворота сечения c . Для
этого в точке с приложим единичную силу (рис.4.5,а) и единичную пару сил
(рис.4.5, а, в). Соответствующие эпюры изгибающих моментов m y1 и m y 2
показаны на рис. 4.5,б, г.
Рис.4.5
Интегралы Мора вычислим по правилу Верещагина. На рис. 4.6
показаны эпюры и M y и m y1 , m y 2 . Эпюра M z разбита на два треугольника и
один прямоугольник. Площади треугольников равны: 1  1,3 ,  2  0,3 ;
прямоугольника 3  0, 48 . Ординаты эпюры m y1 ,
взятые под центром
тяжести треугольников и прямоугольника равны: y1  1,033 , y2  0,867 ,
y3  0,5 .
Рис.4.6
Таким образом, прогиб на конце консоли от нормативной нагрузки
равен ( EJ y  360kHм 2 ):
w(1,2) 
1
(1Y1   2Y2  3Y3 ) 
E  J y  f
.
1
(1,3 1,033  0,3  0,867  0,48  0,5) 103  4,096 мм
360 1,25
Перемещение w(1,2) по направлению единичной силы (против оси z ).

Угол поворота сечения равен:
 y (1,2) 

1
(1 1   2 1  3  1) 
E  Jy  f
1
(1,3  0,3  0,48)  4,62 103 рад
360 1,25
Итак, составляющие перемещения конца консоли равны:
u(1,2)  0,024 мм , V (1,2)  0,7634 мм , w(1,2)  4,096 мм ,
 x (1, 2)  7,96 104 рад,  y (1,2)  4,62 10
3
рад ,  z (1,2)  0,864 103 рад
Полное перемещение равно
  u 2  V 2  w2  0,0242  0,76342  4,0962  4,17 мм .
Вид стержня в деформированном состоянии изображен на рис.4.7
Рис.4.7
5.Проверка прочности в заданном сечении стержня.
Усилия в заданном сечении стержня x  0,1м равны: N  40 кН,
M y  4,4 кНм, M z  2, 4 кНм, Qy  4 кН, Qz  8 кН, M x  0,52 кНм.
В расчетном сечении отметим характерные точки 1-9 (рис.5.1).
Рис. 5.1 Характерные точки сечения
Выпишем координаты точек 1-9 (табл.2)
Табл.2
№ т.
1
2
3
4
5
6
7
8
9
z
b/2
0
-b/2
-b/2
-b/2
0
b/2
b/2
0
y
h/2
h/2
h/2
0
-h/2
-h/2
-h/2
0
0
В табл.2 координата z у всех точек умножается на b / 2 , а координата
y умножается на h / 2 . Поэтому удобно перейти к безразмерным
координатам z  z / (b / 2) и y  y / (h/ 2) . Тогда табл.2 примет вид
Табл.3
№ т.
1
2
3
4
5
6
7
8
9
z  z / (b / 2)
1
0
-1
-1
-1
0
1
1
0
y  y / (h/ 2) 1
1
1
0
-1
-1
-1
0
0
Нормальные напряжения в отмеченных точках вычислим по формуле
x 
My
N Mz
z.
y+

A
Jy
Jz
Формулу (5.1) удобно записать в безразмерных координатах
(5.1)
M
My
Mz
N Mz
N
y
z

y y z 


J z (h / 2)
J y (b / 2)
A Jz
Jy
A
(h / 2)
(b / 2)
.
M
N M
  z y y z
A Wz
Wy
x 
Таким образом, имеем
x 
M
N My

z  z y.
A Wy
Wz
(5.2)
Вычислим составляющие напряжения:
A  60см2 ,Wz  100 см3, Wy  60 см3; N  40 кН, M z  2, 4 кНм,
N
 40

 10  3  6,667 MПа,

4
A 60  10
My
Mz
 2,4
4,4
3
3
MПа,


10
 73,33 MПа.


10


24
W y 60  10  6
W z 100  10 6
M y  4,4 кНм;
Тогда формулу (5.2) принимает простой вид
 x  6,667  73,33  z  24  y .
(5.3)
Подставляем значения безразмерных координат (табл.3) в (5.3) получим
Табл.4
/№ т.
z  z / (b / 2)
y  y / (h/ 2)
 x (МПа)
1
2
3
4
5
6
7
8
9
1
0
-1
-1
-1
0
1
1
0
1
1
1
0
-1
-1
-1
0
0
42,66
-30,67
-104
-80
-56
17,33
90,66
66,66
-6,67
Наибольшие сжимающие напряжения в т.3
наибольшие растягивающие напряжения в т.7
 3  104,0 MПа, а
 7  90,667 MПа (рис.5.2,а).
Рис.5.2 Нормальные и касательные напряжения
Вычислим касательные напряжения от кручения в середине сторон
прямоугольника.
Крутящий
момент
в
сечении
отрицательный
напряжений
M x  0,52МПа , следовательно, векторы касательных
направлены против хода часовой стрелки (рис.5.2,б). Численное значение
напряжения в серединах больших сторон (точки 4;8) равны:
0,52 103
Mx
 4,8 ( M x ) 

 6,1МПа.
W1
85,1 106
Напряжения в середине меньших сторон (точки 2;6):
0,52 103
Mx
 2,6 ( M x ) 

 5,1 МПа.
W2
102,1 106
Вычислим касательные напряжения от поперечной силы Q y в точках
4,8,9. Направление вектора касательных напряжений совпадает с
направлением оси y , так как в Qy  0 ( Q y  4 кН)
3Q y
3  4 103
 4,8,9 (Qy ) 

 1,0 МПА.
4
2  A 2  60 10
Касательные напряжения от поперечной силы Qz в точках 2,6,9.
Направление вектора касательных напряжений противоположно с
направлению оси z , так как в Qz  0 ( Qz  8 кН)
3  Q z 3  (8) 103
 2,6,9 (Qz ) 

 2 МПА
4
2 A
2  60 10
Результирующие касательные напряжения в точках 2,4,6,8 от изгиба и
кручения получаем как алгебраическую сумму в соответствующих точках:
 2   2 ( M x )   2 (Qz )  5,1  2,0  3,1 МПА.
 4   4 ( M x )   4 (Qy )  6,1  1,0  7,1 МПА,
 6   6 ( M x )   6 (Qz )  5,1  2,0  7,1 МПА,
 8   8 (M x )   8 (Qy )  6,1  1,0  5,1 МПА,
Результирующее касательное напряжение в т.9 ( 9 ) получается как
геометрическая сумма напряжений:  9 (Qy ) , 9 (Qz ) (рис.5.2,б). Модуль
вектора касательного напряжения равен
 9  [ 9 (Qy )]2  [ 9 (Qz )]2  (1) 2  (2) 2  2.24 МПа.
В угловых точках сечения:1,3, 5,7 простое одноосное напряженное
состояние: растяжение или сжатие. В окрестности точек 2, 4, 6, 8 , 9 имеет
место плоское напряженное состояние. Для точек 4,6,9 на рис.5.3 показана
картина напряженного состояния.
Рис. 5.3 Напряженное состояние в окрестности точек
В точках 1-9 поперечного сечения определим главные напряжения и
приведенные (эквивалентные) напряжения по третьей гипотезе (теории)
прочности:
 max  0,5    0,25   2   2 , 1   max ,  2  0 ,  3   min ,  i   1   3 .
min
Результаты вычислений представлены в табл.5.
 \№т
x

 max
 min
i
Таблица 5
1
2
3
4
5
6
7
8
9
42,66
-30,67
-104
-80
-56
17,33
90,66
66,66
-6,67
0
3,1
0
7,1
0
-7,1
0
-5,1
2,24
42.67
0,309
0
0,627
0
19,87
90,67
67,06
7,35
0
-30,98
-104,0
-80,63
56,0
-2,532
0
-0,39
-0,68
42,67
31,28
104,0
81,26
56,0
22,40
90,67
67,45
8,03
Поверхность приведенных (эквивалентных) напряжений показана на
рис.5.4,а.
Проверяем
выполнение
условия
прочности:
 imax  104МПа  R  200МПа
6. Подбор сечения стержня по наибольшим нормальным
напряжениям.
На рис.6.1,а представлена поверхность распределения приведенных
(эквивалентных) напряжений, построенная по 9-ти точкам поперечного
сечения. Из рисунка видно, что
в угловых точках 1,3,5,7 (рис.6.1,б)
напряжения  i   1   3 существенно превышают напряжения в центре и в
серединах сторон прямоугольника (точки 9,2,4,6,8).
Рис. 6.1 Поверхность распределения приведенных напряжений в точках
поперечного сечения
Исходя из этого, можно построить алгоритм подбора размеров
поперечного сечения стержня по наибольшим нормальным напряжениям в
угловых точках:
1) Зафиксируем ширину сечения b0 , найдем высоту h0    b0 .
2) Приведем силы, действующие на стержень, к центру тяжести
сечений.
3) Построим эпюры продольных сил N и изгибающих моментов
M z My.
4) Построим четыре эпюры нормальных напряжений в угловых
My
N Mz
z и определим
y+

A
Jy
Jz
глобальный по абсолютной величине максимум  max .
точках 1,3,5,7 по формулам  x 
5) Введем функцию f (b)  R   max и зафиксируем знак функции в
точке f (b0 )  R   max 0
6) Если f (b0 )  0 , то определяем величину b1 ,где f (b1 )  0
(выполняем пункты 1-5)
7) В дальнейшем находим искомую величину b (корень функции
f (b)  R   max ), используя метод деления отрезка пополам.
На рис. 6.2 показаны графики изменения нормальных напряжений в
угловых точках сечения, когда напряжение  7  R  200МПа .
На рис.6.1 показаны начальные значения b , h и подобранные, а
также отношение первоначально заданной площади поперечного сечения к
площади подобранного сечения.
Рис.6.2 Подбор размеров поперечного сечения