МНОЖЕСТВА ТОЧЕК НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
реклама
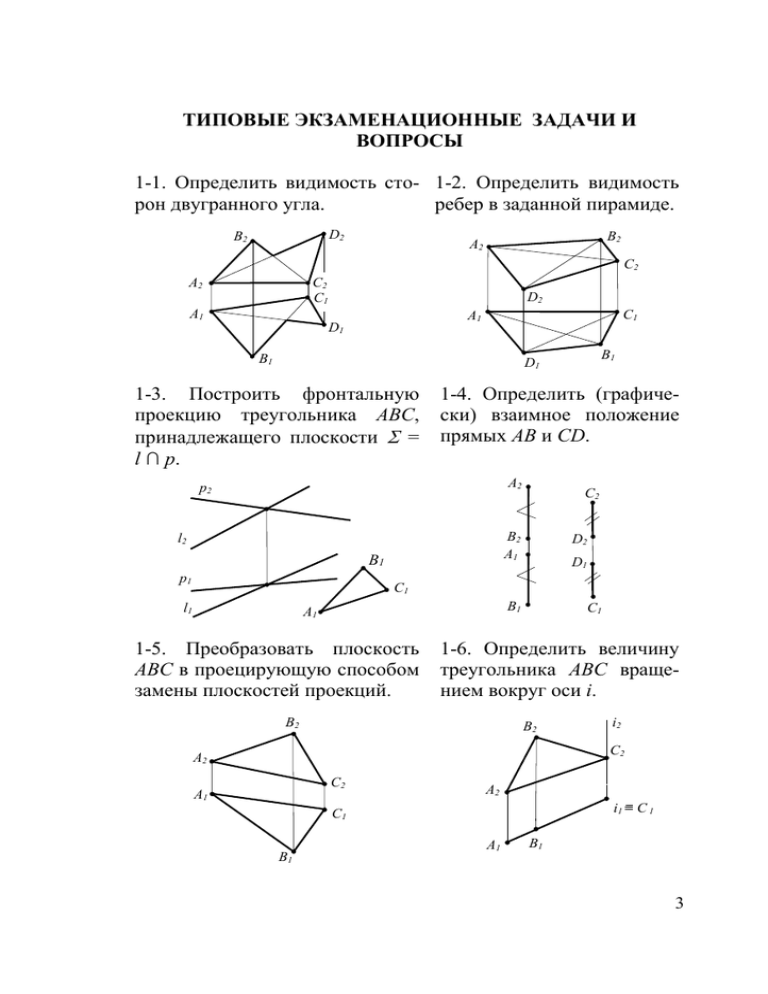
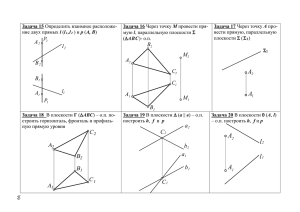
ТИПОВЫЕ ЭКЗАМЕНАЦИОННЫЕ ЗАДАЧИ И ВОПРОСЫ 1-1. Определить видимость сто- 1-2. Определить видимость рон двугранного угла. ребер в заданной пирамиде. D2 B2 B2 A2 C2 A2 C2 С1 D2 A1 C1 A1 D1 B1 B1 D1 1-3. Построить фронтальную проекцию треугольника ABC, принадлежащего плоскости = l ∩ p. 1-4. Определить (графически) взаимное положение прямых AB и CD. A2 p2 B2 A1 l2 B1 p1 С2 D2 D1 C1 l1 B1 A1 1-5. Преобразовать плоскость ABC в проецирующую способом замены плоскостей проекций. C1 1-6. Определить величину треугольника ABC вращением вокруг оси i. B2 B2 i2 C2 A2 С2 A1 A2 i1 С1 B1 A1 C1 B1 3 1-7. Определить величину отрезка и углы его наклона к плоскостям проекций: а) по правилу прямоугольного треугольника, б) вращением вокруг проецирующей оси, в) заменой плоскостей проекций, г) плоско-параллельным перемещением. а) B2 б) D2 г) в) M1 E1 F1 C2 N1 A2 F2 M2 C1 B1 A1 D1 E2 N2 1-8. Построить недостающие проекции точек, принадлежащих заданным поверхностям. l2 E2 С2 A2 p2 p1 D1 B1 А1 l1 1-9. Опустить перпен- 1-10. Достроить фронтальную продикуляр иp точки A на екцию треугольника ABC, если АВ – прямую h. прямая ската. В2 h2 B1 A2 A2 A1 С1 h1 4 A1 1-11. На прямой l отложить 1-12. Построить третьи проотрезок AB длиной 40 мм. екции заданных точек. B1 l2 z23 A2 A2 y13 x12 l1 A1 C3 С2 B2 A1 y13 1-13. Преобразовать заданные геометрические фигуры в проецирующие: способом замены плоскостей проекций, вращением вокруг проецирующей прямой и плоскопараллельным перемещением. N2 B2 A2 М2 С2 N1 A1 С1 М1 B1 1-14. Разделить отрезок 1-15. Через заданную точку провеAB точкой М в отноше- сти: а) профильно-проецирующую нии АМ:МВ = 2:5 прямую MN длиной 40 мм, б) фронталь под углом 60о к П3. В2 а) б) M2 A2 M1 A1 А2 В1 А1 5 1-16. Построить в заданной плоскости горизонталь, проходящую через точку А. а) p2 А2 1-17. Определить величину заданного линейного угла: а) способом замены, б) вращением вокруг фронтально-проецирующей оси. б) С2 В2 p1 l2 l1 С1 А1 В1 1-18. Какая фигура задана на чертеже – плоская или пространственная (показать графически)? 1-19. Построить горизонтальную проекцию точки М, принадлежащей прямой АВ. A2 D2 М2 С2 A2 B2 D1 B2 A1 A1 С1 B1 B1 1-20. Построить фронтальную проекцию точки А, принадлежащей заданной плоскости, и провести через нее прямую q параллельную прямой l. l2 p2 1-21. Через точку A провести прямую частного положения, перпендикулярную прямой l. Сколько возможно решений? l2 A2 l1 p1 l1 A1 A1 6 1-22. Построить точки пересечения прямой l с заданными плоскостями и определить видимость в задачах а, г, д и е. а) б) В2 p2 l2 p1 А2 C1 А1 В1 в) q2 С2 l2 q1 l1 l1 г) f2 B2 l2 l2 h2 С2 A2 l1 B1 f1 C1 l1 h1 д) C2 A1 е) A2 D2 l2 A2 C2 l2 B2 B1 B2 l1 B1 C1 A1 C1 l1 A1 D1 1-23. Через точку М прове- 1-24. Через точку К провести сти прямую, параллельную плоскость, параллельную зазаданной плоскости. данной плоскости. C2 C2 М2 К2 A2 A2 B2 B2 B1 B1 C1 A1 М1 C1 К1 A1 7 1-25. Построить линию пересечения заданных плоскостей. а) б) l2 p2 h2 Σ2 || p2 p1 f2 в) h1 f1 l1 Σ1|| f1 l2 Σ2 || h2 h2 г) n2 m2 p2 l2 h1 n1 l1 m1 l1 p1 1-26. Через точку А провести перпендикуляр к заданной плоскости. а) б) А2 A2 p2 l2 p1 Σ1 А1 l1 A1 в) г) M2 C2 K2 B2 M1 A1 A1 C1 B1 8 L2 A2 A2 K1 L1 1-27. Через точку А провести плоскость, перпендикулярную заданной прямой l. 1-28. Построить точки пересечения прямой l со сферой. l2 A2 l2 l1 A1 l1 1-29. Через прямую l провести плоскость, перпендикулярную заданной плоскости. а) б) C2 N2 l2 l2 A2 B2 K2 M2 N1 B1 l1 M1 C1 l1 K1 A1 г) в) A2 q2 l2 h2 l l2 p2 2 p1 q1 l1 l1 A1 h1 1-30. Построить в заданных плоскостях прямые наибольшего наклона: а) к фронтальной, б) горизонтальной и в) профильной плоскостям проекций. б) а) в) F2 K2 K3 B2 L3 L2 A2 С2 A1 G2 E2 G1 С1 B1 E1 F1 M2 M3 9 1-31. Определить (графически) параллельна ли прямая l заданной плоскости. 1-32. Как расположена прямая l относительно плоскости АВС? Определить видимость. p2 B2 l2 || А2С2 l2 h2 A2 C2 A1 С1 l1 || А1С1 l1 h1 p1 B1 3-1. Построить прямую, пересекающую прямые l, p и параллельную прямой m. m2 p2 3-2. Построить фронтальную проекцию точки А, удаленной от заданной плоскости (m ∩ n) на расстояние 25 мм. n2 l2 m2 m1 p1 l1 m1 A1 3-3. Определить расстояние между заданными параллельными плоскостями. l2 m2 n2 p1 3-4. Провести через заданные скрещивающиеся прямые параллельные плоскости и определить расстояние между ними. l2 p2 n1 p2 n1 l1 l1 10 m1 p1 3-5. Провести через точку К прямую, параллельную плоскости АВС и пересекающую прямую l. 3-6. Определить расстояние между заданными параллельными прямыми. p2 C2 К2 A2 l2 B2 l2 B1 l1 A1 l1 p1 К1 C1 3-7. Через точку А провести 3-8. На прямой l найти точки, прямую, пересекающую пря- удаленные от точки O на расмые l и р. стояние 35 мм. A2 O2 l2 p2 l2 l1 l1 A1 p1 O1 3-9. Построить равнобедренный прямоугольный треугольник с катетом ВС на прямой l. А2 l2 3-10. Определить расстояние от точки А до заданной плоскости. А2 l2 p2 l1 А1 l1 А1 p1 11 3-11. Построить в плоскостях АВС и KLM, соответственно, центры вписанной и описанной окружностей. С2 В2 В2 А2 А2 С2 А1 А1 В1 С1 С1 В1 3-12. Построить через точку В линейный угол, определяющий заданный двугранный угол, и найти его величину. 3-13. На прямой l найти точку, равноудаленную от граней заданного двугранного угла. В2 C2 l2 D2 D2 А2 А1 С2 A2 С1 A1 B2 C1 l1 D1 B1 В1 D1 3-14. Определить величину угла между: а) прямой l и заданной плоскостью, б) заданными плоскостями. a) p2 q2 l2 n2 б) m2 p1 q1 12 m1 l1 1 n1 3-15. Через точку А провести прямую, параллельную заданным плоскостям. А2 m2 h2 3-16. В плоскости АВС построить равносторонний треугольник на стороне ВС . С2 n2 f2 f1 А1 А2 B2 А1 B1 n1 m1 h1 3-17. Повернуть точку А вокруг прямой l так, чтобы она оказалась в плоскости Σ. С1 3-18. Построить прямоугольный треугольник АВС при условии, что АС – гипотенуза, а вершина прямого угла В лежит на прямой l. А2 C2 l2 l2 Σ2 А2 C1 l1 l1 А1 А1 3-19. Определить расстояние от точки М до плоскости АВС. В2 M2 A2 3-20. Построить квадрат АВСD, если задана сторона АВ и горизонтальная проекция прямой l, на которой расположена стороны АD. B2 А2 С2 С1 А1 В1 А1 M1 В1 l1 13 3-21. На прямой АВ найти точку, равноудаленную от точек С и D. 3-22. Построить плоскость, проходящую через прямую l и расположенную на расстоянии 20 мм от точки А. А2 D2 B2 С2 С1 B1 3-23. Построить высоту ВК в треугольнике АВС. 3-24. Построить горизонтальную проекцию отрезка АВ, параллельного плоскости, заданной прямой ската l. B2 B2 l2 С2 А2 l1 А1 А1 D1 l2 А2 А2 B1 l1 А1 С1 А1 3-25. В заданной плоскости (m || n) построить множество точек, равноудаленных от концов отрезка АВ. 3-26. Через точку А провести плоскость, перпендикулярную к заданным плоскостям Σ (l || p) и Г (m ∩ n). n2 B2 m2 А2 m2 n2 14 А2 l2 n2 m2 p2 p1 А1 m1 l1 B1 А1 n1 3-27. В треугольнике АВС построить биссектрису угла при вершине В. 3-28. Вращением вокруг оси i совместить точку А со сферой. B2 A2 i2 A2 C2 A1 B1 A1 i1 C1 4-1. Построить линию пересечения поверхностей: а) призмы и цилиндра, б) призмы и тора, в) цилиндра и шара, г) цилиндра и конуса, касательных к сфере д) цилиндра, конуса и шара, е) цилиндра и шара, ж) цилиндра и конуса, и) двух цилиндров. а) б) в) г) Р2 R е) ж) и) 1 д) Р1 R 15 4-2. Построить точки пересечения прямой l с заданными поверхностями. S2 S2 l2 l l2 l2 1 S1 l2 l1 l1 l1 l1 l S1 2 4-3. Построить сечения заданных фигур плоскостью и определить их натуральные величины. Γ2 Σ2 p2 h2 A2 h1 D2 B2 С2 В1 A1 C1 p1 D1 4-4. Достроить горизонтальные проекции заданных фигур. А2 А1 16 4-5. Провести через точку А прямые, составляющие с о плоскостью Σ угол 60 и пересекающие заданную прямую l. 4-6. Вращением вокруг фронтально проецирующей оси i совместить точку А с поверхностью конуса. i2 А2 A2 l2 2 А1 l1 i1 А1 Вопросы в экзаменационных билетах 1. Деление отрезка прямой в заданном отношении. 2. Определение видимости на чертежах с помощью конкурирующих точек. 3. Определение величины отрезка прямой и углов его наклона к плоскостям проекций (с помощью прямоугольного треугольника и способов преобразования чертежа ). 4. Прямые частного положения и свойства их проекций. 5. Взаимная принадлежность точек, линий и поверхностей. 6. Прямые уровня в плоскости. 7. Прямые наибольшего наклона в плоскости. 8. Способ замены плоскостей проекций. 9. Вращение вокруг проецирующей оси. Основные определения и свойства проекций. 10. Пересечение прямой с плоскостью. Алгоритм построения точки пересечения. 11. Перпендикулярность прямой и плоскости (прямой и обратный признаки). 12. Пересечение плоскостей. 13. Перпендикулярность плоскостей (прямой и обратный признаки). 14. Параллельность плоскостей. 17