Таблица записи чисел в четырех системах счисления
реклама
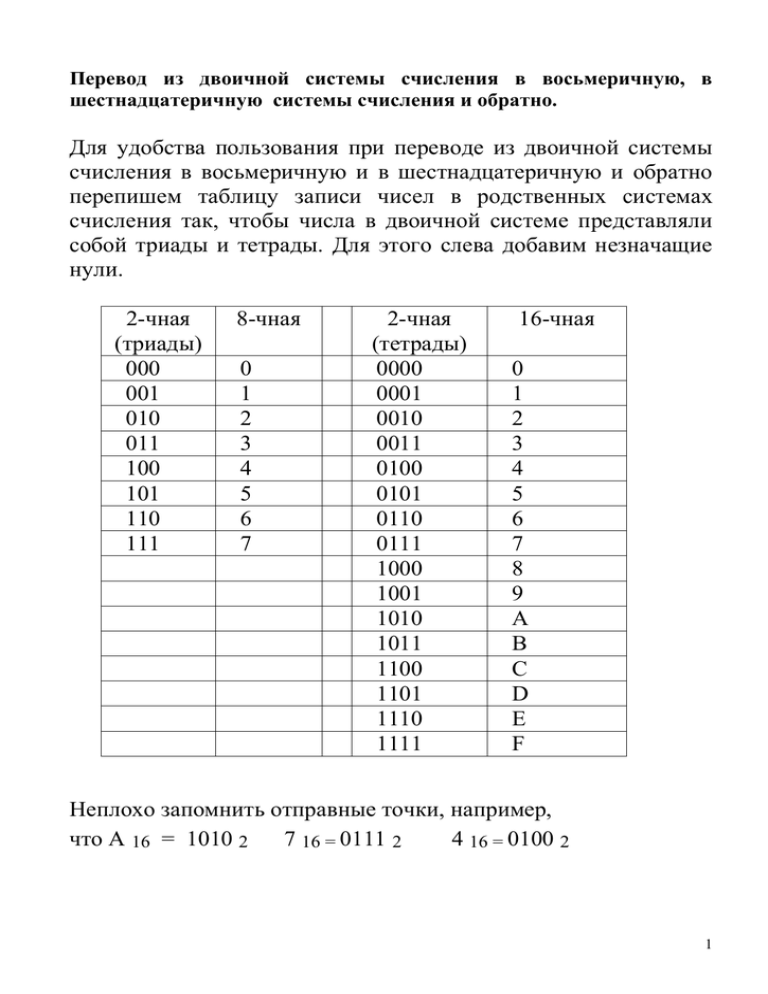
Перевод из двоичной системы счисления в восьмеричную, в шестнадцатеричную системы счисления и обратно. Для удобства пользования при переводе из двоичной системы счисления в восьмеричную и в шестнадцатеричную и обратно перепишем таблицу записи чисел в родственных системах счисления так, чтобы числа в двоичной системе представляли собой триады и тетрады. Для этого слева добавим незначащие нули. 2-чная (триады) 000 001 010 011 100 101 110 111 8-чная 0 1 2 3 4 5 6 7 2-чная (тетрады) 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 16-чная 0 1 2 3 4 5 6 7 8 9 A B C D E F Неплохо запомнить отправные точки, например, что А 16 = 1010 2 7 16 = 0111 2 4 16 = 0100 2 1 Алгоритм перевода восьмеричного числа в двоичное: Каждую цифру восьмеричного числа заменяем двочным кодом из трех бит (триадой). Задача. Перевести число 5718 в двоичную СС. 5 101 7 111 1 001 Ответ: 5718 = 1011110012 Потренируемся. Задача. Перевести число 734,46 8 в двоичную СС. 734,46 8 = 111 011 100, 100 110 2 Алгоритм перевода шестнадцатеричного числа в двоичное: Каждую цифру шестнадцатеричного числа заменяем двочным кодом из четырех бит (тетрадой). Задача. Перевести число AB1216 в двоичную СС. Мы запомнили, что А 16 = 1010 2 А 1010 В 1011 1 0001 2 0010 Ответ: AB1216 = 10101011000100102 2 Алгоритм перевода двоичного числа в восьмеричное: - Разбиваем двоичное число справа налево на группы из трёх бит (триады). - Если в самой левой группе меньше трёх бит, то дописываем слева незначащие нули. - Каждой триаде сопоставляем восьмеричную цифру. Задача. Перевести число 110111112 в восьмеричную СС. - Разбиваем двоичное число справа налево на группы из трёх бит (триады) 11 011 111. - В самой левой группе меньше трёх бит, дописываем слева один незначащий ноль 011 011 111 - Каждую триаду заменяем восьмеричной цифрой: 3 3 7 Ответ: 110111112 = 3378 Алгоритм перевода двоичного числа в шестнадцатеричное: - Разбиваем двоичное число справа налево на группы из четырёх бит (тетрады). - Если в самой левой группе меньше четырёх бит, то дописываем слева незначащие нули. - Каждой тетраде сопоставляем шестнадцатеричную цифру. Задача. Перевести число 100010001002 в шестнадцатеричную СС. - Разбиваем двоичное число справа налево на группы из четырёх бит (тетрады) 100 0100 0100. - В самой левой группе меньше четырёх бит, дописываем слева один незначащий ноль 0100 0100 0100 - Каждую тетраду заменяем шестнадцатеричной цифрой: 4 4 4 Ответ: 100010001002 = 44416 Это очень простые задачи. Обычно постановка задачи звучит чуть-чуть сложнее. 3 Задача. Дано А = С716, В =3778, а число С надо выбрать из четырех предложенных вариантов: 1) С = 10111111 2 2) С = 10011110 2 3) С = 10111010 2 4) С = 11011110 2 , так, чтобы A < C < B В ответе указать номер варианта значения С. Решение: существует несколько способов решения, но в любом случае все числа должны быть представлены в одной системе счисления. I способ: перевести А и В в двоичную систему и сравнивать с С. II способ: перевести А и В, а также все варианты С в десятичную систему и сравнить. Выбираем тот способ, который менее трудоемкий или какой лучше знаем. I способ: Заменяем восьмеричные цифры двоичными триадами, а шестнадцатеричные цифры двоичными тетрадами. А = A716 = 1010 0111 2 = 10100111 2 B = 2778 = 010 111 111 2 = 10111111 2 Находим из предложенных вариантов, то значение С, где А < C . Удобнее сравнивать, если записать друг под другом. 1) С = 10111111 2 2) С = 10011110 2 3) С = 10111010 2 4) С = 11011110 2 , А = 10100111 2 4 Сразу видно, что вариант 2 не подходит, т.к. C < A. Исключаем его. Оставшиеся варианты С сравниваем с В. Ищем, где С < В. 1) С = 10111111 2 3) С = 10111010 2 4) С = 11011110 2 , В = 10111111 2 Сразу видно, что вариант 1 не подходит, т.к. C = В. Исключаем его. Вариант 4 не подходит, т.к. С > В. Исключаем его. Остается 3 вариант. Действительно С < В. Ответ: 3. 5


