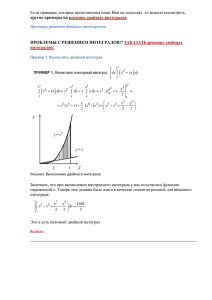
Интегральное исчисление функций многих переменных

А.Р. Морозова
N - КРАТНЫЕ ИНТЕГРАЛЫ
N - КРАТНЫЕ ИНТЕГРАЛЫ
Составитель: к.т.н., доцент А.Р. Морозова
2003 год
Рецензент: к.п.н., доцент Козлова С.Ж
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ
ПЕРЕМЕННЫХ
Раздел 1
ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
1.
Интегралы, зависящие от параметров
Рассмотрим функцию нескольких переменных
u  f ( x, y, z ,...w),
определенную и непрерывную в области
s  w  t.
a  x  b, c  y  d , l  z  m,...
Закрепив любые значения y, z ,..., w, мы получим функцию одной переменной x:
u   ( x)  f ( x, y, z,..., w),
Непрерывную, а значит, интегрируемую, на отрезке a  x  b . Интеграл от этой
функции


  ( x)dx   f ( x, y, z,..., w)dx,
где a    b, a    b,

зависит от выбранных нами значений y, z ,..., w т.е. является функцией от y, z ,..., w,
определенной в области
c  y  d , l  z  m,..., s  w  t.
Обозначим ее через F ( y, z ,..., w).
Таким образом,

F ( y, z,..., w)   f ( x, y, z,..., w)dx
(1)

Переменные y, z ,..., w, от которых зависит подынтегральная функция и которые при
интегрировании рассматриваются как постоянные, называются параметрами. Сам интеграл
(1) есть функция этих параметров.
1


2
есть функция одного
(1  y) 3 / 2  y 3 / 2
3
0
параметра y, определенная на любом отрезке c  y  d , где c  0 или, что то же, для всех
y  0.

Так, например, интеграл
1
Интеграл

2
dx
x2  y2  z2
 ln
x  y dx 
1 1 y2  z2
 2  4  y2  z2
z, определенная в любом прямоугольнике
( y  0, z  0); интеграл
есть функция двух параметров y и
c  y  d , l  z  m,
не содержащем начала
 /2
sin x( y 2  z 2  v 2 )
dx

x
 /4
есть функция трех параметров y, z, v, определенная для всех значений y, z, v. Этот
интеграл в элементарных функциях не берется, если y 2  z 2  v 2  0.
Поставим своей задачей изучение некоторых свойств функций F ( y, z ,..., w) по
известным свойствам функции f ( x, y, z,...w). Для простоты мы будем рассматривать
интегралы, зависящие от одного параметра. Полученные результаты могут быть перенесены
на случай любого числа параметров.
Пример. Вычислим интеграл.
 /2
 ln( a
2
 sin 2  )
(а > 1).
Здесь  - переменная интегрирования, а – параметр,
0
 /2
 ln( a
2
 sin 2  )  F (a).
0
Так как условия теоремы 3 выполнены, для любого a > 1 имеем:
 /2
2ad

F ' (a)   2

,
2
a2 1
0 a  sin 
откуда, интегрируя по а, найдем:
da
F (a)  
  ln( a  a 2  1  C ),
2
a 1
Для определения постоянной С представим интеграл F(a) в виде:
 /2
 /2

 sin 2  
 sin 2  
2


F (a)   ln a  ln 1 
2
d   ln a   ln 1  a 2 d ,
a




0 
0
Тогда
 /2

 sin 2  
1 
d ,
C   ln 1  1  2    ln 1 
a  0 
a 2 

и переход к пределу при a  , получим C   ln 2. Таким образом,
 /2
a  a2 1
.
0
2
Рассматривая интегралы, зависящие от параметров, мы предполагали пределы  и 
постоянными. Однако в приложениях часто случается, что при различных значениях
параметров интегрировать приходится в разных пределах, т.е.  и  сами являются
F (a) 
ln( a 2  sin 2  )   ln
функциями параметров.
 ( y)
Так, например, интеграл
f ( x, y )dx,


где a   ( y )  b , a   ( y )  b, есть функция
( y)
параметра y:
 ( y)
 f ( x, y)dx  F ( y).
 ( y)
Эта функция при определенных условиях, наложенных на функции f(x, y),  ( y ) и  ( y )
будет непрерывна и дифференцируема на отрезке [с, d].
Раздел 2
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ПЕРВОГО И ВТОРОГО РОДА
2.
Криволинейные интегралы первого рода (по длине дуги)
Рассмотрим задачу о нахождении массы материальной кривой. Эта задача
естественным образом приведет нас к одному из обобщений понятия определенного
интеграла – криволинейному интегралу по длине дуги.
Пусть вдоль некоторой кривой непрерывным образом распределена масса. Средней
плотностью какого-либо участка такой кривой называют отношение его массы к длине, а
плотностью распределения массы кривой в данной точке называют предел средней
плотности участка кривой, содержащего эту точку, при стягивании последнего к данной
точке.
Поставим своей целью определить массу материальной точки привой АВ, если
известна плотность распределения массы  в каждой ее точке М:    (M ) .
Эту задачу можно решить следующим образом. Разобьем дугу АВ точками М 1,
М2,…,Мn-1, на n дуг. Обозначим, кроме того, для удобства дальнейших записей, точку А
через М0, а точку В через Мn.
 i   ( N i ).
На каждой дуге Мi-1Мi выберем произвольную точку Ni и вычислим в этой точке
плотность распределения массы кривой.
Предполагая, что плотность во всех точках дуги Мi-1Мi постоянна и равна ее значению
в точке Ni найдем приближенное значение массы m дуги Мi-1Мi .
mi   ( N i )  si ,
где si - длина дуги Мi-1Мi
n
m   mi ,
i 1
Так как масса m всей дуги АВ равна сумме масс ее частей, то:
n
m    ( N i )si .
i 1
Полученная формула будет приближенной, так как плотность распределения массы на
каждой дуге Мi-1Мi
в действительности, вообще говоря, не постоянна. Естественно
ожидать, что чем меньше будут длины дуг деления, тем точнее будет это приближенное
равенство. За массу кривой АВ принимают предел полученного приближенного значения
при стремлении к нулю всех длин дуг деления:
m  lim
n
  ( N )s .
i
i 1
i
К изучению пределов сумм указанного вида сводится большое количество задач
механики и математики, в связи с чем представляется целесообразным исследовать эти
суммы, отвлекаясь от их конкретного содержания.
Рассмотрим в пространстве XYZ непрерывную спрямляемую кривую АВ, в точках
которой определена произвольная функция f(x y z).
Разобьем кривую АВ точками М1,…, Мn-1, занумерованными для определенности в
направлении от А к В на n частей (рис.2.1.1.). Точку А обозначим через М0, точку В через
Мn. На каждой дуге Мi-1Мi , выберем произвольную точку Ni ( i , i , i ) и умножим значение
функции f(x, y, z) в этой точке Ni на длину si дуги Мi-1Мi .
f ( i ,i ,  i )si .
Сложив все такие произведения, мы получим сумму:
n
 f ( , ,  )s .
i 1
i
i
i
i
Ее называют интегральной суммой для функции f ( x, y, z ), заданной на дуге АВ.
Интегральная сумма зависит от способа разбиения дуги АВ на части и от выбора точек Ni на
этих частях.
Рис. 2.1.1
Назовем шагом разбиения кривой АВ на части наибольшую из длин дуг деления и
обозначим ее через . Рассмотрим процесс, при котором число n дуг деления кривой АВ
будет неограниченно возрастать, а длины этих дуг будут стремиться к нулю. Этот процесс
можно характеризовать словами: «шаг разбиения  кривой АВ стремится к нулю».
Если при стремлении к нулю шага разбиения  существует предел интегральных сумм,
то этот предел называют криволинейным интегралом от функции f ( x, y, z ) по длине дуги
АВ и обозначают символом:
 f ( x, y, z)ds
AB
Криволинейный интеграл по длине дуги часто называют криволинейным интегралом
первого рода в отличие от криволинейных интегралов второго рода (по координатам).
Ниже будет показано, что если функция f ( x, y, z ) непрерывна на спрямляемой
непрерывной кривой АВ, то указанный предел существует, т.е. существует интеграл
 f ( x, y, z)ds .
AB
Сформулируем некоторые свойства криволинейного интеграла по длине дуги,
непосредственно вытекающие из определения этого интеграла. При этом каждый из
упомянутых ниже интегралов будем предполагать существующим.
1. Значение криволинейного интеграла по длине дуги не зависит от направления кривой
АВ.
2. Постоянный множитель модно выносить за знак криволинейного интеграла.
3. Криволинейный интеграл от суммы двух функций равен сумме двух интегралов от
этих функций.
4. Если кривая АВ точкой С разбита на две части АС и СВ, то
 f ( x, y, z)ds   f ( x, y, z)ds   f ( x, y, z)ds.
AB
AC
CB
5. Если в точках кривой АВ
f1 ( x, y, z)  f 2 ( x, y, z),
то
 f ( x, y, z)ds   f
1
AB
2
( x, y, z ).
AB
6.
 f ( x, y, z)ds  
AB
f ( x, y, z ) ds.
AB
7. Если f ( x, y, z )  1, то
n
 ds  lim  si  S ,
AB
 0
i 1
где S – длина кривой АВ.
8. Теорема о среднем. Если функция f ( x, y, z ) непрерывна на кривой АВ, то на этой
кривой существует точка ( , ,  ), такая, что:
 f ( x, y, z)ds  f ( ,, )  S ,
AB
где S – дина кривой АВ.
Возвращаясь к рассмотренной выше механической задаче, заключаем, что масса m
материальной кривой АВ вычисляется по формуле
m    ( x, y, z )ds,
AB
где  ( x, y, z ) - плотность распределения массы.
Выясним теперь, как связан криволинейный интеграл по длине дуги с обыкновенным
определенным интегралом.
Пусть АВ – непрерывная спрямляемая кривая, а f ( x, y, z ) - функция непрерывная на
этой кривой.
Установим на кривой АВ определенное направление, например от А к В. Тогда
положение любой точки M ( x, y, z ) кривой АВ можно характеризовать длиной s дуги АМ:
x  x(s ), y  y (s ), z  z (s ).
В частности, точке А соответствует s = 0, а точке В соответствует s = S, где S – длина
кривой АВ. При этом на уравнения x  x(s ), y  y (s ), z  z (s ), где s меняется в пределах
от s = 0 до s = S, можно смотреть как на параметрические уравнения кривой АВ.
Функция f ( x, y, z )  f ( x( s), y ( s ), z ( s )) становится сложной непрерывной функцией
параметра s, 0  s  S. Обозначая через si и  i значения параметра s, соответствующие
точкам Mi и Ni si 1    si , получим:
n

i 1
n
f ( i , i ,  i )si   f ( x( i ), y ( i ), z ( i )) si ,
i 1
где si  si  si 1 - длина дуги M i 1 M i .
В правой части равенства стоит интегральная сумма для обыкновенного определенного
интеграла от непрерывной функции f ( x( s ), y ( s ), z ( s )) на отрезке 0  s  S. Переходя к
пределу при стремлении к нулю шага разбиения  кривой АВ, получаем:
S
 f ( x, y, z)ds   f ( x(s), y(s), z(s))ds.
AB
(1)
0
Заметим, что эти рассуждения не только дают выражение (1) криволинейного
интеграла по длине через обыкновенный интеграл, но и доказывают существование
криволинейного интеграла о функции f ( x, y, z ) , непрерывной на рассматриваемой кривой
АВ.
Пусть теперь кривая АВ задана параметрическими уравнениями x = x(t), y = y(t), z =
z(t),   t   , где x(t), y(t), z(t) – непрерывно дифференцируемые функции любого
параметра t (не обязательно длины дуги s), причем точке А соответствует t   , а точке В
t   . Установим на кривой АВ направление от А к В. Тогда длина дуги АМ [ M ( x, y, z ) текущая точка кривой АВ] будет функцией параметра t:
t
s  s(t )   x' 2 (t )  y' 2 (t )  z ' 2 (t )dt.
(2)

Производя замену переменной в правой части формулы (1), будем иметь:

 f ( x, y, z)ds   f ( x(t ), y(t ), z(t ))
x' 2 (t )  y' 2 (t )  z ' 2 (t )dt.
AB
Если точке А соответствует большее значение параметра (t   ), чем точке В (t   ),
то, устанавливая на кривой АВ направление от В к А и производя аналогичные выкладки,
снова приходим к формуле (2), так как интеграл по длине дуги от направления кривой не
зависит.
Таким образом, для вычисления криволинейного интеграла по длине дуги надо,
используя параметрические уравнения кривой, выразить подинтегральную функцию через
параметр t, заменить ds дифференциалом дуги как функции параметра t и проинтегрировать
полученное выражение по t в пределах от меньшего до большего значения параметра t для
данной кривой.
Если АВ – плоская кривая, заданная уравнением y   (x), a  x  b, где  (x ) непрерывно дифференцируемая функция, то, принимая x за параметр, как частный случай
формулы (2) будем иметь формулу

AB
b
f ( x, y)ds   f ( x,  ( x)) 1   ' 2 ( x)dx.
a
Криволинейный интеграл по длине дуги имеет разнообразные приложения в механике
и математике. С помощью этого интеграла можно вычислить массу материальной кривой, ее
статические моменты относительно координатных осей и плоскостей, моменты инерции
относительно координатных осей, найти координаты центра тяжести такой кривой, решить
задачу относительно притяжении материальной точки материальной кривой и т.д.
Криволинейные интегралы второго рода
3.
Прежде чем дать определение криволинейного интеграла второго рода, рассмотрим
приводящую к нему задачу о вычислении работы переменной силы при перемещении
материальной точки вдоль некоторой кривой.
Будем говорить, что в области V пространства XYZ задано силовое поле с
напряженностью F, если в каждой точке М области определена сила F, действующая на
единицу массы, помещенную в эту точку. При этом величина и направление силы F
предполагаются зависящими только от положения точки М: F = F(M). Тогда проекции P Q R
силы F на оси координат будут функциями координат x, y, z точки М:
P  P ( x, y, z ), Q  Q( x, y, z ), R  R ( x, y, z ).
Вычислим работу, совершаемую силой F по перемещению единицы массы вдоль
непрерывной спрямляемой кривой АВ в направлении от А к В (короче, вычислим работу
поля вдоль кривой АВ).
Из механики известно, что если перемещение прямолинейно, а действующая сила F
постоянна по величине и направлению, то затраченная ею работа А равна скалярному
произведению силы F на вектор смещения l:
A  ( F , l ).
В случае непрямолинейного пути перемещения и переменной силы F определение
выполненной работы можно произвести следующим образом.
Разобьем кривую АВ в направлении от А к В точками М 0, М1,…,Мn, где точка М0
совпадает с А, Мn – с В, на n дуг.
Пусть xi, yi, zi – координаты точки Мi. На каждой дуге Мi-1Mi возьмем произвольную
точку N i ( i ,i ,  i ). Предположим, что в точках дуги Мi-1Mi действующая сила F постоянна
и равна ее значению в точке N1, и предположим также, что под действием этой силы
материальная точка перемещалась не по дуге Мi-1Mi, а по отрезку Мi-1Mi (рис.2.2.1).
Работу постоянной силы F(Ni) вдоль отрезка Мi-1Mi можно принять за приближенное
значение работы Аi поля вдоль дуги Мi-1Mi.
Таким образом, Ai  ( F ( N i ), M i 1 M i ) или, так как вектор M i 1 M i имеет координаты:
xi  xi  xi 1 , yi  yi  yi 1 , z i  z i  z i 1 ,
то
Ai  P( i ,i ,  i )xi  Q( i ,i ,  i )yi  R( i ,i ,  i )z i .
n
Считая, что работа А поля вдоль дуги АВ равна сумме работ вдоль ее частей: A   Ai
i 1
получаем:
n
A   P( i , i ,  i )xi  Q( i , i ,  i )y i  R( i , i ,  i )z i .
i 1
За точное значение работы по перемещению единичной массы вдоль кривой АВ из
точки А в точку В принимается предел, к которому стремится найденное приближенное
значение при стремлении к нулю наибольшей из длин дуг деления  :
A  lim P( i , i ,  i )xi  Q( i , i ,  i )y i  R( i , i ,  i )z i .
 0
Рис. 2.2.1
Будем изучать пределы указанного вида, отвлекаясь от конкретного содержания
рассмотренной задачи.
Итак, пусть АВ – непрерывная кривая в пространстве XYZ (в частности, на плоскости
XOY), а P(x, y, z) – произвольная функция, определенная на этой кривой.
Разобьем дуги АВ точками М0, М1,…,Мn в направлении от А к В на n дуг. Через xi, yi, zi
обозначим координаты точек Mi i= 1, 2, …, n. На каждой дуге Мi-1Mi выберем
произвольную точку N i ( i ,i ,  i ) и умножим значение функции P(x, y, z) в точке Ni на
величину xi  xi  xi 1 проекции дуги Мi-1Mi на ось OX. Сумма всех таких произведений:
 P( , ,  )x
i
i
i
(1)
i
называется интегральной суммой для функции P(x, y, z) на дуге АВ по переменной x.
Если при стремлении к нулю шага разбиения  кривой АВ такие интегральные суммы
имеют предел, то этот предел называют криволинейным интегралом по переменной x от
функции P(x, y, z) по кривой АВ в направлении от А к В и обозначают символом
 P( x, y, z)dx.
AB
Итак,
n
 P( , , )x
 P( x, y, z)dx  lim

AB
0
i 1
i
i
i
i
если этот предел существует.
Криволинейный интеграл по переменной x отличается от криволинейного интеграла по
длине дуги тем, что при составлении интегральной суммы значение функции в точке Ni дуги
Мi-1Mi умножается не на длину дуги Мi-1Mi, а на величину xi ее проекции на ось OX. Так
как, в отличие от длины дуги, величина проекции дуги М i-1Mi на ось OX существенно
зависит от направления дуги и меняет знак при перемене направления, заключаем, что
криволинейный интеграл по переменной x зависит от направления кривой АВ и при
перемене направления кривой меняет знак на обратный:
 P( x, y, z)dx    P( x, y, z)dx
AB
BA
(здесь АВ и ВА обозначают одну и ту же кривую, на которой в первом случае
установлено направление от А к В, а во втором случае – противоположное направление, от В
к А).
Аналогичным образом для любых функций Q(x, y, z) и R(x, y, z), заданных на кривой
АВ, можно определить криволинейные интегралы по этой кривой в направлении от А к В по
переменным y и z:
n
 Q( x, y, z)dy  lim  Q( i ,i ,  i )yi ,
 0
AB
(2)
i 1
n
 R( x, y, z)dz  lim  R( i ,i , i )zi ,
 0
AB
(3)
i 1
если эти пределы существуют. Криволинейные интегралы по переменным x, y и z
называют криволинейными интегралами второго рода. Сумму криволинейных интегралов
 P( x, y, z)dx,  Q( x, y, z)dy,  P( x, y, z)dz
AB
AB
AB
также называют криволинейным интегралом второго рода и обозначают:
 P( x, y, z)dx  Q( x, y, z)dy  R( x, y, z)dz.
AB
Каждый из этих криволинейных интегралов существенно зависит от направления
кривой, по которой производится интегрирование, и меняет знак при перемене направления
пути интегрирования, т.е.
  
AB
BA
Рассмотрим свойства криволинейных интегралов второго рода, непосредственно
вытекающие из их определения. При этом каждый из встречающихся ниже интегралов
будем предполагать существующим.
1. Постоянный множитель выносится за знак криволинейного интеграла:
 kPdx  k  Pdx,  kQdy  k  Qdy,  kRdz  k  Rdz ,
AB
AB
AB
AB
AB
AB
где k – число.
2. Криволинейный интеграл от суммы двух функций равен сумме соответствующих
интегралов от слагаемых:
 ( P1  P2 )dx   P1dx   P2 dx,
AB
AB
 (Q
1
Ab
 Q2 )dy   Q1dy   Q2 dy,
Ab
AB
 (R
1
 R dz   R dz.
 R2 )dz 
AB
AB
1
2
AB
AB
3. Если кривая АВ точкой С разбита на две части, то криволинейный интеграл по всей
кривой АВ равен сумме интегралов по ее частям:
   
AB
AC
CB
4. Криволинейный интеграл по замкнутой кривой L не зависит от выбора начальной
точки, а зависит от направления обхода кривой.
Действительно, выбирая точку А за начальную (точка А совпадает с конечной точкой
В), получаем:      где
AmA1nA
AmA1
A1nA
А1 – любая точка кривой L, отличная А.

A1nAmA2


A1nA


.
AmA1
Выбирая теперь точку А1 за начальную (точка А1 совпадает с конечной точкой В1),
получаем:


A1nAmA1

.
AmA1nA
Криволинейный интеграл по замкнутой области L (по контуру L) обычно обозначают
символом  . Кружок на знаке интеграла служит для обозначения контура. Направление
L
обхода контура L задается дополнительно.
В случае, если L – замкнутая кривая без точек самопересечения, лежащая в плоскости
XOY, условимся называть положительным направлением обхода контура L такое
направление обхода, при котором движение происходит против часовой стрелки, т.е. так, что
ограниченная контуром L часть плоскости остается слева. Противоположное направление
обхода контура будем называть отрицательным. Соответствующие криволинейные
интегралы принято обозначать символами:
 è .
L
L
При отсутствии дополнительных указаний о направлении обхода контура L, лежащего
в плоскости XOY, условимся подразумевать положительное направление обхода.
5. Если АВ – кривая, лежащая в плоскости, перпендикулярной оси OX, то
 P( x, y, z)dx  0.
AB
Действительно, в этом случае в соответствующей интегральной сумме все xi , i = 1,
2,.., n, равны нулю, а значит,
n
 P( x, y, z)dx  lim  P( i ,i ,  i )xi  0.
 0
AB
i 1
Аналогично для кривой АВ, лежащей в плоскости, перпендикулярной оси OY (OZ),
получаем:


ABQ( x, y, z)dy  0  AB R( x, y, z)dz  0 .
Сформулируем теперь достаточные условия существования криволинейных интегралов
второго рода.
Будем называть кривую АВ гладкой кривой, если существуют параметрические
уравнения этой кривой: x = x(t), y = y(t), z = z(t), t1  t  t1 где x(t), y(t), z(t) – непрерывно
дифференцируемые функции на отрезке [t1, t2]. Непрерывная кривая АВ называется кусочногладкой, если ее можно разбить на конечное число гладких дуг.
Теорема. Если гладкая кривая АВ – кусочно-гладкая, а функции P(x, y, z), Q(x, y, z),
R(x, y, z) непрерывны на кривой АВ, то криволинейные интегралы
 P( x, y, z)dx,  Q( x, y, z)dy,  R( x, y, z)dz,
AB
AB
AB
а следовательно, и криволинейный интеграл
 P( x, y, z)dx  Q( x, y, z)dy  R( x, y, z)dz,
AB
существуют.
Доказательство этой теоремы в данном курсе не рассматривается.
Возвращаясь к рассмотренной выше задаче о работе поля F = Pi + Qi + Ri вдоль кривой
АВ, заключаем, что при определенных условиях, наложенных на кривую и на функции P(x,
y, z), Q(x, y, z) и R(x, y, z), эта работа вычисляется по формуле
A   P( x, y, z )dx  Q( x, y, z )dy  R( x, y, z )dz.
AB
Вычисление криволинейных интегралов второго рода производится путем их
преобразования в определенные интегралы.
Пусть кривая АВ задана параметрическими уравнениями x = x(t), y = y(t), z = z(t), где
x(t), y(t), z(t) – непрерывно дифференцируемые; функции t, изменяющегося в пределах от
t   до t   (    или    ). Предположим, что точке А соответствует значение
параметра t   , точке В соответствует t   , причем изменению t от  к  соответствует
движение точки М(x(t), y(t), z(t)) по кривой АВ в направлении от А к В.
Тогда, если функции P(x, y, z), Q(x, y, z) и R(x, y, z) непрерывны на кривой АВ, то
криволинейные интегралы
 P( x, y, z)dx,  Q( x, y, z)dy и  R( x, y, z)dz,
AB
AB
AB
определяемые как пределы соответствующих интегральных сумм, существуют и,
следовательно, не зависят от способа построения этих сумм. Воспользовавшись этим,
построим интегральные суммы специальным образом.
Разобьем отрезок с концами t   и t   , оси Ot точками t 0   , t1, t2,…, t n   в
направлении от  к  на n частей. Обозначим через M i ( xi , yi , z i ) точку кривой АВ,
соответствующую значению параметра ti.
xi  x(t i ), yi  y (t i ), z i  z (t i ).
Точки М0, М1,…, Мn разобьют кривую АВ в направлении от А к В на n дуг. По теореме
Лагранжа
xi  xi  xi 1  x(t i )  x(t i 1 )  x' ( i )t i ,
где t i  t i  t i 1 , а  i - значение параметра t, лежащее между ti-1 и ti.
Пусть N i  ( i , i ,  i ) - точка кривой АВ, соответствующая значению параметра t   i
 i  x( i ),i  y( i ),  i  z ( i ). Эта точка лежит на дуге Мi-1Mi.
Составим интегральную сумму для интеграла
 P( x, y, z)dx,
используя полученное
AB
разбиение кривой АВ на части Мi-1Mi (i = 1, 2,…,n) и выбранные точки Ni на этих частях. По
построению имеем:
n
 P( , , 
i
i 1
i
n
i
)xi   P( x( i ), y ( i ), z ( i )) x' ( i )t i .
(5)
i 1
Правая часть равенства представляет собой интегральную сумму для определенного
интеграла от непрерывной функции P(x(t), y(t), z(t))x'(t) по переменному t, изменяющемуся
от t   до t   . При стремлении к нулю шага разбиения рассматриваемого промежутка
оси Ot, в силу непрерывности функций x'(t), y'(t), z'(t), будет стремиться к нулю шаг
разбиения кривой АВ. Переходя к пределу в равенстве (5), получим формулу, выражающую
криволинейный интеграл, по переменной x через определенный интеграл:

 P( x, y, z)dx   P( x(t ), y(t ), z(t )) x' (t )dt.
(6)
AB
Аналогичным образом выводят формулы:

 Q( x, y, z)dy   Q( x(t ), y(t ), z(t )) y' (t )dt,
(7)
AB

 R( x, y, z)dz   R( x(t ), y(t ), z(t )) z' (t )dt.
AB
(8)

В общем случае получаем:

 Pdx  Qdy  Rdz   Px' (t )  Qy ' (t )  Rz ' (t )dt.
AB
(9)

Таким образом, для вычисления криволинейного интеграла по нерешенным x, y и z по
кривой АВ надо составить параметрические уравнения пути интегрирования, выразить
формально пол знаком интеграла переменные x, y и z, а также их дифференциалы dx, dy и dz
через параметр, и затем вычислить от полученного выражения определенный интеграл в
пределах изменения параметра от значения, соответствующего началу пути интегрирования,
до значения, соответствующего концу.
Рассмотрим коротко вопрос о связи криволинейных интегралов первого и второго рода.
Пусть АВ – гладкая, а функция P(x, y, z), Q(x, y, z) и R(x, y, z) непрерывны на ней.
Установим на кривой АВ направление от А к В и выберем в качестве параметра длину s дуги
АМ, где М(x, y, z) – текущая точка кривой. При этом SA = 0, SB = S (S – длина дуги АВ) и
параметрические уравнения кривой запишутся в виде:
x  x( s), y  y ( s ), z  z ( s), 0  s  S.
Если обозначить через  ,  ,  углы, составляемые с осями координат касательной к
кривой АВ, направленной в сторону роста параметра s, то, как можно показать,
cos   x' ( s ), cos   y ' ( s ), cos   z ' ( s ).
Учитывая эти соотношения и формулы, выражающие криволинейные интегралы
первого и второго рода через определенные интегралы, получим:
S
 P( x, y, z)dx   P( x(s), y(s), z(s)) x' (s)ds 
 P( x, y, z) cosds,
AB
AB
0
S
 Q( x, y, z)dx   Q( x(s), y(s), z(s)) x' (s)ds   Q( x, y, z) cos ds,
AB
0
AB
S
 R( x, y, z)dx   R( x(s), y(s), z(s)) x' (s)ds   R( x, y, z) cos ds.
AB
0
AB
Таким образом, криволинейные интегралы второго рода выражаются
криволинейные интегралы по длине дуги, т.е. первого рода.
Для общего криволинейного интеграла второго рода имеем формулу:
 Pdx  Qdy  Rdz   (P cos  Q cos   R cos  )ds.
AB
через
AB
Условия независимости криволинейного интеграла (второго рода) от
формы пути интегрирования
Пусть функции P(x, y, z), Q(x, y, z) и R(x, y, z) непрерывны в некоторой области D
пространства XYZ. Будем рассматривать в этой области только кусочно-гладкие кривые.
Возьмем в области D две произвольные точки А и В. Их можно соединять различными
кривыми, лежащими в области D. По каждой из этих кривых интеграл  Pdx  Qdy  Rdz
4.
AB
имеет, вообще говоря, свое значение.
Вычислим, например, интеграл
 xdx  ydy  zdz
по
отрезку
прямой
AB
соединяющему точки А(1, 0, 0) и В(1, 1, 1)
x 1 y  0 z  0


, т.е. x = 1, y = z.
Уравнения прямой АВ:
0
1
1
Выбирая за параметр y, имеем:
1
 xdx  xydy  ydz   2 ydy  1.
AB
0
Вычислим теперь тот же интеграл по дуге параболы АВ, заданной уравнениями
x = 1, z = y2. Выбирая за параметр y (x = 1, y = y, z = y2, yA = 0, yB = 1), получим:
АВ,
1
7
2
ABxdx  xydy  ydz  0 ( y  2 y )dy  6.
Этот пример показывает, что значения интеграла
 xdx  xydy  ydz
зависят от формы
AB
кривой, по которой производится интегрирование.
Можно, однако, привести примеры криволинейных интегралов, значения которых по
любым кривых, соединяющим данные точки А и В, будут одни и те же. Такими, как можно
показать, являются интегралы:
 ( yz  1)dx  ( xz  2)dy  xydz,  xdx  ydy  zdz и др.
AB
AB
Будем говорить, что интеграл
 Pdx  Qdy  Rdz
в области D не зависит от формы пути
AB
интегрирования, если его значения по всевозможным кусочно-гладким кривым, лежащим в
данной области и имеющим общее начало и общий конец, одинаковы. В этом случае при
записи интеграла достаточно указывать лишь начальную и конечную точки пути
интегрирования, в связи с чем приняты обозначения:
( xB , y B , z B )
B
 Pdx  Qdy  Rdz
 Pdx  Qdy  Rdz.
или
A
( xA , yA ,z A )
Независимость криволинейного интеграла
 Pdx  Qdy  Rdz
в области D от формы
AB
пути интегрирования равносильна равенству нулю этого интеграла, вдоль всякой замкнутой
кривой L, лежащей в области D.
Теорема. Для того, чтобы криволинейный интеграл  Pdx  Qdy  Rdz , где P(x, y, z),
AB
Q(x, y, z) и R(x, y, z) – функции, непрерывные в области D, в этой области не зависел от
формы пути, необходимо и достаточно, чтобы выражение Pdx  Qdy  Rdz было полным
дифференциалом некоторой функции (в области D).
Теорема. Если функции P(x, y, z), Q(x, y, z) и R(x, y, z) в области D
a  x  b, c  y  d , l  z  k имеют непрерывные частные производные первого порядка, то,
для того чтобы выражение Pdx  Qdy  Rdz в этой области было полным дифференциалом
некоторой функции, необходимым и достаточным является выполнение условий:
P R
Q R
P Q

,


,
z x
z y
y x
в каждой точке области D.
Раздел 3
ДВОЙНЫЕ ИНТЕГРАЛЫ
5.
Определение двойного интеграла
Пусть в замкнутой квадрируемой области  плоскости XOY задана функция f ( x, y ) .
Разобьем область  произвольно на n частей  1 ,  2 ,...,  n , так чтобы области
 1 ,  2 ,...,  n , не имели общих внутренних точек. В каждой замкнутой области  i
(внутри или на границе) выберем произвольную точку Pi ( i ,i ) и умножим значение
функции f ( x, y ) в этой точке на площадь  i . Сложив все такие произведения, получим
сумму:
n
 f ( , )
i 1
i
i
i
(1)
,
которая называется интегральной суммой для функции f ( x, y ) в области  .
Интегральная сумма зависит от способа разбиения области  на части  1 ,  2 ,...,  n и от
выбора точек Pi на этих частях, т.е. для функции f ( x, y ) в области  можно составить
бесчисленное множество интегральных сумм.
Прежде чем переходить к операции предельного перехода, введем понятия диаметра
области и шага разбиения области. Диаметром замкнутой области (двухмерного или
трехмерного пространства) называется наибольшее из расстояний между двумя точками
границы этой области. Шагом разбиения области на конечное число частей называется
наибольший из диаметров областей деления.
Обозначим через  шаг разбиения области  на части  1 ,  2 ,...,  n . Процесс,
состоящий в неограниченном измельчении областей деления и соответственно в
неограниченном увеличении числа n областей деления, удобно характеризовать словами:
«шаг разбиения области  стремится к нулю».
Если при стремлении к нулю шага разбиения  области  интегральные суммы (1)
имеют предел, то этот предел называют двойным интегралом от функции f ( x, y ) по области
 и обозначают символами:
 f ( x, y)d или  f ( x, y)dxdy .


Здесь f ( x, y ) - подынтегральная функция,  - область интегрирования, x и y –
переменные интегрирования, d (dxdy) элемент площади. Таким образом, по
определению

n
f ( x, y )d  lim  f ( i ,i ) i ,
 0
i 1
если этот предел существует.
Функция f ( x, y ) , для которой существует двойной интеграл
 f ( x, y)d ,
называется интегрируемой в области  .
6.
Условия существования двойного интеграла и его свойства
Естественно возникает вопрос, для всяких ли функций, и если нет, то для каких,
существует по области  двойной интеграл.
Очевидно, что интегрируемая в области  функция должна быть ограничена в
замкнутой области  , так как в противном случае за счет выбора точек Pi интегральную
сумму можно было бы сделать сколько угодно большой по абсолютной величине, а значит,
не существовало бы предела интегральных сумм при стремлении  к нулю.
Сформулируем теперь достаточные условия существования двойного интеграла.
Теорема 1. Если функция f ( x, y ) непрерывна в замкнутой области  , то двойной
интеграл
 f ( x, y)d
существует.
Доказательство этой теоремы модно провести аналогично доказательству
соответствующей теоремы для определенного интеграла.
Теорема 2. Если функция f ( x, y ) ограничена в замкнутой области  и непрерывна в
ней всюду, кроме конечного числа кусочно-гладких линий, то двойной интеграл
 f ( x, y)d
существует. Доказательство этой теоремы в данном курсе не приводится.
Предполагая, что все встречающиеся ниже функции удовлетворяют условиям теорем (1
или 2) существования двойного интеграла в рассматриваемых областях, перечислим
простейшие свойства двойного интеграла. Доказательства этих свойств непосредственно
следует из определения двойного интеграла. Читатель легко докажет свойства 1-7 по
аналогии с соответствующими доказательствами для определенного интеграла.
1. Двойной интеграл  f ( x, y )dxdy не зависит от обозначения переменных

интегрирования.
2. Постоянный множитель k можно выносить за знак двойного интеграла:
 kf ( x, y)d  k  f ( x, y)d .


3. Двойной интеграл от суммы двух функций равен сумме двойных интегралов от
слагаемых:
  f1 ( x, y)  f 2 ( x, y)d   f1 ( x, y)d   f 2 ( x, y)d .



4. Если область  разбита на две области  1 и  2 , то
f ( x, y )d .
 f ( x, y)d   f ( x, y)d  

1
5. Если всюду в области 
2
f ( x, y )  0,
то
 f ( x, y)d  0
6. Если всюду в области 
f1 ( x, y)  f 2 ( x, y),
то
 f ( x, y)d   f
1
2
( x, y )d
7. Если функция f ( x, y ) задана в области  , то
 f ( x, y)d  
f ( x, y ) d
8.
 d  
Действительно, так как в данном случае f ( x, y, z )  1 в области  , то для любого
разбиения области  на части  1 ,  2 ,...,  n получим:
n
 d  lim   i  lim    .

 0
i 1
 0
Свойство 8 позволяет использовать двойные интегралы для нахождения плоских фигур.
7.
Геометрический смысл двойного интеграла
Вернемся к задаче об объеме цилиндрического тела. Так как рассматриваемая там
функция f ( x, y ) непрерывна в замкнутой области  , то
n
lim  f ( i , i ) i   f ( x, y )d ,
 0
i 1

каковы бы ни были точки Pi ( i ,i ) в замкнутых областях  i . Выбирая за Pi ( i ,i )
точки, в которых функция f ( x, y ) в областях  i достигает своих наименьших (mi) или
соответственно наибольших (Mi) значений, будем, в частности, иметь:

n
n
f ( x, y )d  lim  mi  i  lim  M i  i .
 0
 0
i 1
i 1
Слагаемые mi  i и M i  i равны объемам цилиндров с основанием  i вписанных и
описанных вокруг ограниченного сверху куском поверхности S цилиндрического столбика с
n
 m i  i и
тем же основанием  i . Суммы
i 1
n
 M 
i 1
i
i
равны соответственно объемам
«вписанных» и «описанных» вокруг данного цилиндрического тела V тел, состоящих из n
прямых цилиндров. Так как при   0 эти объемы имеют общий предел, данное тело
кубируемо и его объем V равен двойному интегралу:
V   f ( x, y )d .


Отсюда следует геометрический смысл двойного интеграла: двойной интеграл
f ( x, y )d от неотрицательной, непрерывной в замкнутой области  функции f ( x, y )
равен объему цилиндрического тела с основанием  в плоскости XOY, ограниченного
сверху поверхностью z  f ( x, y ).
В частности, если f ( x, z )  1 в области  , то цилиндрическое тело представляет собой
цилиндр с основанием  высоты h  1. Его объем численно равен площади основания  .
Таким образом, мы получаем уже известную формулу для вычисления площади области  с
помощью двойного интеграла    d или, что то же,    dxdy .

Если неположительная функция

f ( x, y ) непрерывна в области  , то, воспроизводя
рассуждения, приведенные в начале главы, получим, что двойной интеграл
 f ( x, y)d
равен взятому со знаком минус объему цилиндрического тела, ограниченного сверху
областью  плоскости XOY, снизу – поверхностью z  f ( x, y ) , сбоку – цилиндрической
поверхностью с образующими, параллельными оси OZ.
Предположим теперь, что функция f ( x, y ) непрерывна в области  , причем область 
можно разбить на конечное число, частей  1 ,  2 ,...,  n в каждой из которых функция
f ( x, y ) либо неотрицательна, либо неположительна. Тогда, заменяя двойной интеграл от
функции f ( x, y ) суммой интегралов по областям  1 ,  2 ,...,  n заключаем, что двойной
интеграл
 f ( x, y)d
равен алгебраической сумме объемов цилиндрических тел с
образующими, параллельными оси OZ, ограниченных с одной стороны частями поверхности
z  f ( x, y ) , с другой стороны – соответствующими областями  1 ,  2 ,...,  n плоскости
XOY. В эту сумму объемы тел, лежащих над плоскостью XOY, входят со знаком плюс, а
объемы тел, лежащих под плоскостью XOY, входят со знаком минус.
Указанные соображения используются при вычислении объемов тел с помощью
двойных интегралов.
8.
Теорема о среднем
Так же, как и для определенного интеграла, для двойного интеграла имеет место так
называемая теорема о среднем .
Теорема. Если функция f ( x, y ) непрерывна в замкнутой области  , то в этой области
существует точка P( i ,i ) такая, что
 f ( x, y)d  f ( ,)   .
9.
Вычисление двойных интегралов
Вычисление двойных интегралов сводится к вычислению определенных интегралов.
Теорема 1. Если функция f ( x, y ) непрерывна в замкнутой области  , ограниченной
линиями x = a, y = b (a < b), y   (x), y   (x) ( ( x) и  (x) - непрерывные функции на
отрезке [a, b], причем  ( x)   ( x) на этом отрезке), то имеет место равенство
b   ( x)

(1)
f
(
x
,
y
)
dxdy


a   ( x)f ( x, y)dy dx,


позволяющее вычисление двойного интеграла свести к последовательному
вычислению определенного интеграла от определенного интеграла (или, короче, к
вычислению повторного интеграла).
Повторный интеграл, стоящий в правой части равенства (1), обычно записывают в
виде:
b
 ( x)
a
( x)
 dx  f ( x, y)dy.
Теорема 2. Если функция f ( x, y ) непрерывна в замкнутой области  , ограниченной
линиями y = c, y = d (c<d), x   ( y ), x   ( y ) ( ( y ) и  ( y ) - непрерывные функции на
отрезке [c, d], причем всюду на этом отрезке  ( y )   ( y )), (рис.3.8.1.) то имеет место
равенство

d
 ( y)
f ( x, y )dxdy   dy
c
f ( x, y )dx,


(2)
( y)
позволяющее сводить вычисление двойного интеграла к вычислению повторного
интеграла.
Рис. 3.8.1
При вычислении двойного интеграла с помощью повторного по формуле (2) сначала
 ( y)
 f ( x, y)dx
вычисляется внутренний интеграл
при постоянном значении переменной y, в
 ( y)
пределах изменения x (для области  ) при постоянном значении y, c  y  d , затем
полученная функция от y интегрируется по y в максимальных пределах изменение y для
области  .
Пример. Вычислить интеграл  xdxdy по области  , ограниченной линиями

y   x, y  1, y  x . Так как выполнены условия теоремы 2, применяя формулу (2),
получаем:
2
1
1
1  y2 y3 
1
2

xdxdy

dy
xdx

(
y

y
)
dy

   .

0 y

20
2 2
3 
12
1
y
Рис. 3.8.2
 , удовлетворяющей
одновременно условиям теорем 1 и 2, то при вычислении двойного интеграла  f ( x, y )d
Если функция
f ( x, y ) непрерывна в замкнутой области

можно выбирать любой порядок интегрирования (внешний интеграл брать по x,
внутренний – по y или наоборот). Так, например, если граница области каждой прямой,
параллельной оси OX, и каждой прямой, параллельной оси OY, пересекается не более чем в
двух точках (см. рис. 3.8.2.), то применимы обе формулы (1) и (2), т.е.

b
f ( x, y )dxdy   dx
 ( x)


a
d
 ( y)
c
( y)
f ( x, y )dy   dy
( x)
f ( x, y )dx.


Если область  - прямоугольник со сторонами x = a, x = b, y = c и y = d, а f(x, y) –
функция, непрерывная в прямоугольнике a  x  b, c  y  d , то, применяя формулы (1) и
(2), получаем:

b
d
a
c
d
b
c
a
f ( x, y)dxdy   dx  f ( x, y)dy   dy  f ( x, y)dx.
b
 d


    f 2 ( y )dy .
f
(
x
,
y
)
dxdy

dx
f
(
x
)

f
(
x
)
dy

f
(
x
)
dx
f
(
y
)
dy

f
(
x
)
dx
2

a c 1
a 1
c 2
 1
 

a
 c

Например, если  - прямоугольник со сторонами x  1, y  2,
b
d
b
d
1
2
1
2
2 1 y
2
1 y
 x e dxdy   x dx  e dy 

2 3
(e  e 1 ).
3
В частности, если f ( x, y)  f i ( x)  f i ( y), то двойной интеграл по этому
прямоугольнику оказывается равным произведению двух определенных интегралов.
При вычислении двойного интеграла по области  более сложного вида обычно
применяется предварительное разбиение этой области на конечное число частей,
удовлетворяющих условиям теорем 1 или 2, интеграл по области  заменяется равной ему
суммой интегралов по ее частям, а каждый из полученных интегралов вычисляется по
формуле (1) или (2).
10.
Некоторые геометрические и механические приложения двойных
интегралов
Как уже говорилось выше, двойных интегралы можно применять к вычислению
площадей плоских фигур и объемов тел. Рассмотрим несколько примеров.
Пример 1. Найти площадь области  , ограниченной линиями y 2  x  1, x  y  1 .
Область  представляет собой параболический сегмент, ограниченный слева дугой
параболы x  y 2  1 , справа – отрезком прямой x  1  y. Решая совместно уравнения
параболы и прямой, находим ординаты точек их пересечения: y = -2, y = +1.
Следовательно,
1 y
1
1
9
   dxdy   dy  dx   (2  y  y 2 )dy  .
2

2
2
y 2 1
Примечание. Если бы мы выбирали обратный порядок интегрирования, область 
предварительно пришлось бы разбить на две части, так как эта область сверху ограничена
линией, заданной двумя различными уравнениями (дуга параболы и отрезок прямой).
Пример 2. Найти объем тела V, ограниченного поверхностями y = x2, y = 1, z = 0,
z = x2 + y2.
Так как данное тело представляет собой цилиндрическое тело с основанием  ,
ограниченное сверху параболоидом z = x2 + y2, то имеем:
y
5
1
1
 1 32

88
2
2
2
2
V   ( x  y )dxdy  2 dy  ( x  y )dx  2  y  y 2 dy 
.
3
105

0
0
0

Пример 3. Найти объем тела V, вырезаемого из бесконечной призмы с гранями
x  1, y  1 параболоидами x 2  y 2  4  z, x 2  y 2  4( z  2).
Объем тела V находим как сумму объемов V1 и V2 его частей, лежащих
соответственно над и под плоскостью XOY. При этом
1
1
1
1
40

2
2
2
2
V1   (4  x  y )dxdy  4 dx  (4  x  y )dy  4  4  x 2  dx  ,
3
3

0
0
0
1
1
 x2  y2

 x2  y2

22
V2   
 2 dxdy  4 dx  
 2 dy  .
4
4
3


 
0
0
62
V  V1  V2  .
3
Понятие двойного интеграла можно использовать для определения площадей не
только фигур, но и кривых поверхностей.
Будем называть поверхность S, в каждой точке которой определена касательная
плоскость и, следовательно, нормаль, гладкой, если положение касательной плоскости
непрерывно меняется с непрерывным перемещением по поверхности точки касания.
Последнее означает, что для любой точки М0 поверхности и для любого числа   0
существует такая  - окрестность точки М0, что для всех точек М поверхности, лежащих в
этой окрестности, углы между нормалями в точках М и М0 меньше, чем  .
Пусть, например, поверхность S задана уравнением z  f ( x, y ), где f ( x, y ) - функция,
имеющая непрерывные частные производные f ' x ( x, y ) и f ' y ( x, y ) в замкнутой
квадратируемой области  - проекции поверхности S на плоскость XOY. При таких
предположениях поверхность S имеет непрерывно меняющуюся касательную плоскость и
нормаль, т.е. является гладкой. Для определения площади поверхности поступим
следующим образом. Разобьем область  на n областей  1 ,  2 ,...,  n и обозначим через
S i часть поверхности S, проектирующуюся на плоскость XOY в область  i . При этом
поверхность S разобьется на n частей: S1 , S 2 ,..., S n . В каждой области  i возьмем
произвольно точку Pi ( i ,i ) восстановив в этой точке перпендикуляр к плоскости XOY до
пересечения с поверхностью S, получим на поверхности S i точку M i ( i , i ,  i ) . Проведем
в точке Mi касательную плоскость к поверхности и рассмотрим ту ее часть Ti , которая на
плоскость XOY проектируется в область  i . В силу гладкости поверхности вблизи точки
Mi касательная плоскость мало отклоняется от поверхности S i , поэтому естественно
считать площадь части S i поверхности приближенно равной площади части Ti
касательной плоскости.
Проводя указанные рассуждения для всех областей деления и суммируя результаты,
получим приближенное значение площади поверхности S в виде:
n
S   Ti
i 1
(Здесь Ti обозначает площадь плоской площадки Ti ).
За точное значение площади поверхности S по определению принимается число, равное
пределу, к которому стремится полученное приближенное значение при стремлении к нулю
шага разбиения  области  :
S  lim
 0
n
 T
i 1
i
Покажем, что в наших предположениях этот предел существует. Обозначим через  i
острый угол, составляемый с осью OZ нормалью к поверхности S, или, что тоже, нормально
к плоскости Ti , в точке Мi. Так как область  i есть проекция Ti , на плоскость XOY, их
площади связаны соотношением
Ti cos  i   i
Косинус угла находим, используя уравнение нормали к поверхности z  f ( x, y ) в точке
M i ( i ,i , f ( i ,i )) :
1
cos  i 
2
2
1  f ' x ( i , i )  f ' y ( i , i )
Следовательно,
Ti 
 i
2
2
 1  f ' x ( i , i )  f ' y ( i , i ) i
cos 
а значит,
n
S lim
 0

i 1
1  f ' x ( i , i )  f ' y ( i , i ) i
2
2
Под знаком предела стоит интегральная сумма по области 
для функции
 ( x, y )  1  f ' x 2 ( x, y )  f ' y 2 ( x, y ) i . Так как по условию эта функция непрерывна в
замкнутой области  , то указанный предел существует и равен двойному интегралу

1  f ' x ( x, y )  f ' y ( x, y ) dxdy
2
2
Таким образом, мы получили формулу для вычисления площади поверхности S:
S   1  f ' x ( x, y )  f ' y ( x, y )dxdy
2
2
Примечание. Если поверхность S задана уравнением вида y  f ( x, y ) или y  f ( y, z ),
то за плоскость проекции берется плоскость ZOX или соответственно YOZ.
Соответствующим образом видоизменяются определение площади поверхности и формула
(1).
В более сложных случаях при определении площади поверхности предварительно
разбивают ее на части рассмотренного выше вида и площадь поверхности S полагают равной
сумме площадей ее частей. Поверхность S, имеющую определенную указанным выше
образом площадь, называют квадрируемой.
11.
Формула Грина – Остроградского
Формула Грина – Остроградского устанавливает связь
криволинейными интегралами (второго рода).
P( x, y)
 y dxdy, причем
между двойными
и
 ( x)
P( x, y )
P( x, y )
 y dxdy  a dx ( x) y dy.
b
12.
Замена переменных в двойном интеграле
Якобиан и его геометрический смысл. Пусть даны две плоскости с выбранными на
них прямоугольными декартовыми системами координат UOV и XOY. Рассмотрим две
(ограниченные или неограниченные) области  и  , лежащие соответственно в плоскостях
UOV и XOY, и предположим, что функции
x   (u , v),
(1)
y   (u , v)
устанавливают взаимно однозначное соответствие между точками этих областей. Это
значит, что каждой точке (u0, v0) области  соответствует одна определенная точка (x0,y0),
где x0   (u0 , v0 ), y0   (u0 , v0 ) области  , называемая образом точки (u0, v0), и, наоборот,
каждой точке (x0,y0) области  соответствует одна определенная точка (u0, v0) области 
[именно та точка, образом которой является точка (x0,y0)]. Будем говорить, что формулы (1)
задают взаимно однозначное отображение области  на область  (и наоборот).
Пусть функции  (u , v) и  (u , v ) непрерывны в области  вместе со своими частными
производными первого порядка. Тогда определитель
x x
 u ' (u, v)  ' v (u, v) u v

 'u (u, v)  ' v (u, v) y y
u v
будет непрерывной функцией переменных u и v, определенной в области  . Этот
функциональный определитель, называемый определителем
Якоби, или якобианом
отображения (1), принято обозначать J (u , v) или символом
 ( x, y )
похожим на символ,
 (u , v)
обозначающий производную.
Вывод формулы замены переменных в двойном интеграле. Рассмотрим двойной
интеграл
(2)
 f ( x, y)dxdy

от функции f ( x, y ) , непрерывной в замкнутой области  , ограниченной кусочногладким контуром. Предположим, что формулы
x   (u , v),
(3)
y   (u , v)
задают взаимно однозначное отображение замкнутой области  плоскости UOV на
замкнутую область  плоскости XOY, причем это отображение удовлетворяет всем
условиям, указанным в начале параграфа.
 i  J (i , i ) i ,
Поставим своей целью заменить двойной интеграл (2) по переменным x и y (по области
 ) равным ему двойным интегралом по переменным u и v (по области  ). Для этого
разобьем область  с помощью кусочно-гладких кривых на n областей 1 ,  2 ,...,  n .
Образы этих кривых на плоскости XOY, в свою очередь, будут кусочно-гладкими кривыми.
Они разобьют область  на n областей  1 ,  2 ,...,  n . Площади соответствующих
областей  i и  i связаны соотношением
где M i (  i , i ) - некоторая точка в области  i , а J i (  i , i ) - якобиан отображения (3)
в этой точке (рис. 3.11.1.). Обозначим через Pi ( i ,i ) лежащий в области  i образ точки
M i (  i , i ) при отображении (3):
 i   ( i , i ), i ( ( i , i ), i  1, 2,..., n.
Для полученного разбиения области  на части  1 ,  2 ,...,  n и специального
выбора точек P1 , P2 ,...Pn , на этих частях составляем интегральную сумму для двойного
интеграла (3):
n
 f ( , ) .
i 1
i
i
i
По построению имеем:
n

i 1
n
f ( i , i ) i   f [ (  i , i ), (  i ,. i )] J(  i , i )  i
i 1
Рис. 3.11.1
(4)
В правой части этого равенства стоит интегральная сумма для двойного интеграла по
области  от непрерывной функции f ( (u, v),  (u, v)) J (u, v) . При стремлении к нулю шага
разбиения  области  стремится к нулю шаг разбиения  области  Переходя к
пределу в равенстве (3) получаем:
 f ( x, y)dxdy   f ( (u, v), (u, v)) J (u, v) dudv.


Эта формула и называется формулой замены переменных в двойном интеграле.
Раздел 4
ТРОЙНЫЕ ИНТЕГРАЛЫ
13.
Определение тройного интеграла и его свойства
Пусть в замкнутой кубируемой области V пространства XYZ задана произвольная
функция f ( x, y, z ) . Разобьем область V на n областей V1 , V2 ,..., Vn не имеющих общих
внутренних точек. В каждой точке области Vi возьмем произвольно точку M i ( i ,i ,  i ) .
Значение функции f ( x, y, z ) в точке M i умножим на объем Vi i-й области и сложим такие
произведения по всем областям деления. Полученная сумма
n
 f ( , , 
i 1
i
i
i
)Vi называется
интегральной суммой для функции f ( x, y, z ) по области V. Для функции f ( x, y, z ) можно
составить бесчисленное множество интегральных сумм по области V.
Если при стремлении к нулю шага разбиения  области V существует предел
интегральных сумм, то этот предел называется тройным интегралом от функции f ( x, y, z )
по области V и обозначается символами:
 f ( x, y, z )dV или  f ( x, y, z)dxdydz.
V
V
При этом f ( x, y, z ) - подынтегральная функция, V – область интегрирования, x, y и z –
переменные интегрирования, V (xyz ) - элемент объема.

n
f ( x, y, z )dV  lim  f ( i ,i ,  i )Vi
 0
V
i 1
Таким образом, если этот предел существует.
Из определения следует, что тройной интеграл, так же как и двойной, не зависит от
совершаемых при построении интегральных сумм разбиения области V на части и выбора
точек на этих частях.
Тройные интегралы являются непосредственным обобщением двойных интегралов на
случай трехмерного пространства.
Имеют место следующие достаточные условия существования тройного интеграла.
Теорема 1. Если функция f ( x, y, z ) непрерывна в замкнутой области V, то тройной
интеграл
 f ( x, y, z)dV
существует.
V
Решение задачи о массе области V с помощью тройного интеграла запишется в виде:
m    ( x, y, z )dV ,
V
где  ( x, y, z ) - плотность распределения массы.
В этом и заключается механический смысл тройного интеграла от неотрицательной
функции. Установить геометрический смысл тройного интеграла  f ( x, y, z )dV для
V
произвольной функции f ( x, y, z ) , не выходя за пределы трехмерного пространства, не
представляется возможным. В случае, если в области V
f ( x, y, z )  1,
то
n
 V
 dV  lim

0
V
i 1
i
 V.
Таким образом, объем тела V можно вычислять с помощью тройного интеграла по
формуле
V   dV   dxdydz.
V
V
Перечислим простейшие свойства тройных интегралов от функций, непрерывных в
рассматриваемых областях.
1. Тройной интеграл  f ( x, y, z )dxdydz от обозначения переменных интегрирования не
V
зависит, т.е.
 f ( x, y, z)dxdydz   f (s, t, u)dsdtdu.
V
V
и т.д.
2. Постоянный множитель можно выносить за знак тройного интеграла:
 kf ( x, y, z)dV  k  f ( x, y, z)dV ,
V
V
где k – число.
3. Тройной интеграл от суммы двух функций равен сумме соответствующих интегралов
от слагаемых:
 [f1 ( x, y, z)  f 2 ( x, y, z)]dV   f1 ( x, y, z)dV   f 2 ( x, y, z)dV .
V
V
V
4. Если область V разбита на две области V1 и V2, то
 f ( x, y, z )dV   f ( x, y, z )dV   f ( x, y, z )dV .
V
V1
V2
Примечание. Свойства 3 и 4 верны для любого фиксированного числа слагаемых.
5. Если в области V
f ( x, y, z )  0,
 f ( x, y, z )  0.
V
6. Если в области V
f1 ( x, y, z)  f 2 ( x, y, z),
то
 f ( x, y, z)dV   f
1
V
2
( x, y, z )dV .
V
7.
 f ( x, y, z )dV  
V
f ( x, y, z ) dV .
V
8. Теорема о среднем. Если функция f ( x, y, z ) непрерывна в замкнутой области V, то в
этой области существует точка M ( , ,  ) , такая, что
 f ( x, y, z)dV  f ( ,, )V ,
V
где V – объем данной области.
14.
Вычисление тройных интегралов
Вычисление тройных интегралов производится путем последовательного вычисления
интегралов меньшей кратности.
Теорема 1. Пусть область V ограничена снизу и сверху поверхностями z  h( x, y ) и
z  H ( x, y ) , где h( x, y ) и H ( x, y ) - непрерывные функции в замкнутой области  плоскости
XOY, и цилиндрической поверхностью, у которой образующие параллельны оси Oz, а
направляющей является граница области  . Тогда для любой функции f ( x, y, z ) ,
непрерывной в замкнутой области V, имеет место формула
H ( x, y )




(1)
f
(
x
,
y
,
z
)
dxdydz

f
(
x
,
y
,
z
)
dz

dxdy,




V
 
 h( x, y )

позволяющая свести вычисление тройного интеграл к вычислению двойного интеграла
от определенного интеграла (короче, к вычислению повторного интеграла).
Интеграл, стоящий в правой части равенства, обычно записывают в виде:
H ( x, y )
 dxdy  f ( x, y, z)dz.
h( x, y )
При вычислении тройного интеграла по формуле (1) с помощью повторного интеграла
сначала вычисляют внутренний интеграл по переменной z при постоянных x и y (x и y –
параметры) в пределах изменения z (для области V) при постоянных x и y, а затем
полученная функция x и y интегрируется по переменным x и y по области  .
Рис. 4.13.1
Если при этом область  плоскости XOY ограничена линиями x = a, y = b (a < b),
y   ( x), y   ( x) [  (x ) и  (x) непрерывные на отрезке [а, b] функции, причем
 ( x)   ( x) (рис. 4.13.1.)], то, перейдя от двойного интеграла по области  к повторному,
получаем формулу
b
 ( x)
H ( x, y )
a
( x)
h( x, y )
 f ( x, y, z)dxdydz   dx  dy  f ( x, y, z)dz,
V
(2)
позволяющую вычисление тройного интеграла заменить последовательным
вычислением трех определенных интегралов.
В частности, если область V – параллелепипед с гранями x = a, x = b (a < b), y = c, y =
d (c < d) , z = l, z = k (l < k), то по формуле (2) имеем:

V
b
d
k
a
c
l
f ( x, y, z )dxdydz   dx  dy  f ( x, y, z )dz.
Для функции f ( x, y, z ) , равной произведению функций, каждая из которых зависит от
одного лишь переменного:
f ( x, y, z )  f1 ( x)  f 2 ( y)  f 3 ( z ),
тройной интеграл по этому параллелепипеду V равен произведению трех определенных
интегралов:
Рис. 4.13.2

Рис. 4.13.3
b
d
k
a
c
l
f ( x, y, z )dxdydz   f1 ( x)dx  f 2 ( y)dy  f 3 ( z )dz.
V
Это равенство непосредственно следует из свойств тройных и двойных интегралов.
Пример 1. Вычислить интеграл  ( x  y  z )dxdydz по параллелепипеду,
V
ограниченному плоскостями x = -1, x = +1, y = 0, y = 1, z = 0, z = 2.
По формуле (2) имеем:
1
1
2
1
1
1
1
0
0
1
0
1
 ( x  y  z)dxdydz   dx dy  ( x  y  z)dz   dx (2 x  2 y  2)dy   (2 x  1)dx  2
V
Рис. 4.13.4
Пример 2. Вычислить интеграл  xdxdydz по области V, ограниченной плоскостями
V
x  y  z  2, z  1, x  0, y  0 (рис.4.13.3.).
Область V проектируется на плоскость XOY в треугольник  , ограниченный прямыми
x  0, y  0, x  y  1. Применяя формулы 1 и 2, получаем:
2 x  y
 xdxdydz   xdxdy

V

1
1 x
2 x  y
0
0
1
dz   xdx  dy
1

1
1 x
0
0
dz   xdx  (1  x  y)dy 
1 
1
1
   x 3  x 2  x dx  .
2
2 
24
0
1
Рис. 4.13.5
Наряду с указанными выше формулами при соответствующих условиях имеют место
формулы, получающиеся из них перестановкой переменных x, y и z.
В случае, если область V может быть разбита на части, удовлетворяющие условиям
теоремы 1 или теорем, получающихся из нее перестановкой переменных x, y и z, вычисление
тройного интеграла сводится к вычислению соответствующих интегралов по каждой из этих
частей.
Пример 3. Составить формулу для вычисления тройного интеграла
 f ( x, y, z)dxdydz
V
по области V, лежащей в первом октанте и ограниченной поверхностями x = 0, y = 0, z
= 0, x 2  y 2  z 2  1, x 2  y 2  z 2  4 (рис.4.13.4.). Так как поверхность, ограничивающая
область V снизу, задана двумя уравнениями (уравнение плоскости z = 0, уравнение сферы
x 2  y 2  z 2  1), разбиваем область V на две части цилиндрической поверхностью
x2  y 2  1.
Обозначим через  i часть круга x 2  y 2  1 , а через  i - часть кольца 1  x 2  y 2  4,
лежащие в первой четверти плоскости XOY, а через V1 и V2 – части области V,
проектирующиеся соответственно в  1 и  2 . Тогда
 f ( x, y, z )dxdydz   f ( x, y, z )dxdydz   f ( x, y, z )dxdydz.
V
V1
V2
Интегралы по областям V1 и V2 вычисляем, применяя формулы (1) и (2):
4 x 2  y 2
 f ( x, y, z )dxdydz   dxdy 
V1
1 x  y
2
1
4 x 2  y 2
dxdy 
 f ( x, y, z)dxdydz  

V2
2
2
4 x 2
1
0
  dx

1 x 2
0
0
1 x 2  y 2
1
4 x 2
4 x 2  y 2
0
1 x
f ( x, y, z )dz   dx
2
f ( x, y, z )dz   dx
0
4 x  y
2
dy
4 x 2  y 2
1

dy

dy
2
 f ( x, y, z )dz,
 f ( x, y, z)dz 
0
2
 f ( x, y, z)dz.
0
Примечание. Для перехода от двойного интеграла по области  2 к повторному надо
предварительно область  2 разбить на части  2 ' и  2 ' ' (см.рис. 4.13.5.).
15.
Некоторые механические приложения тройных интегралов
К вычислению тройных интегралов приводят задачи, связанные с непрерывным
распределением массы в пространственной области.
Если известна плотность распределения массы    ( x, y, z ) области V пространства
XYZ, то, рассуждая так же, как в двумерном случае, получим определения и формулы для
вычисления статических моментов области V относительно координатных плоскостей:
S xy   z ( x, y, z )dV ,
V
S yz   x ( x, y, z ) dV ,
V
S zx   y ( x, y, z )dV ,
моментов инерции относительно координатных осей:
J x   ( y 2  z 2 )  ( x, y, z )dV ,
V
J y   ( x 2  z 2 )  ( x, y, z )dV ,
V
J z   ( x 2  y 2 )  ( x, y, z )dV ,
координат центра тяжести:
xc 
 x ( x, y, z )dV
V
  ( x, y, z )dV

S yz

S zx
,
m

S xy
m
,
V
yc 
 y ( x, y, z )dV
V
  ( x, y, z )dV
V
zc 
 z ( x, y, z )dV
V
  ( x, y, z )dV
V
m
.
16.
Замена переменных в тройном интеграле
Для тройного интеграла имеет место следующее правило замены переменных.
Если функция f ( x, y, z ) непрерывна в замкнутой области V, а функции
x   (u, v, w),
y   (u, v, w),
z   (u, v, w)
(1)
имеют непрерывные частные производные в замкнутой области Т пространства UVW и
взаимно однозначно отображают эту область на область V пространства XYZ, то имеет
место следующая формула:
 f ( x, y, z)dxdydz 
V
  f ( (u, v, w), (u, v, w),  (u, v, w)) J (u, v, w) dudvdw,
(2)
T
x x x
u v w
 ( x, y, z ) y y x

где J (u, v, w) 
- якобиан отображения (1).
 (u, v, w) u v w
z z z
u v w
Подобно тому как в случае двух переменных модуль якобиана отображения равнялся
коэффициенту изменения бесконечно малой площади, модуль якобиана отображения (1)
равен коэффициенту изменения бесконечно малого объема при отображении (1).
Рис. 4.16.1
Примечание. Формула (2) остается справедливой также и в том случае, если
отображение области T на область V взаимно однозначно лишь для внутренних точек этих
областей.
Остановимся подробнее на двух наиболее употребительных случаях замены
переменных в тройных интегралах.
1. Переход в тройном интеграле к цилиндрическим координатам. Положение точки
M ( x, y, z ) пространства XYZ однозначно определяется заданием трех чисел  ,  , z, где  длина радиуса-вектора проекции точки М на плоскость XOY,  - угол, составляемый этим
радиусом-вектором с осью OX, z – аппликата точки М. Они связаны с декартовыми
координатами точки М соотношениями:
y   sin  ,
x   cos  ,
z  z.
По определению 0    ,    z  . Значение угла  будем брать в пределах
0    2 .
На формулы (3), где переменные  ,  , z изменяются в указанных пределах, можно
смотреть как на задание отображения полосы 0    , 0    2 ,   z  
пространства с прямоугольной системой координат z (рис 4.16.2.) на все пространство
XYZ. Отображение (3) взаимно однозначно всюду, кроме границы этой полосы.
При этом отображение (3) плоскости    0 пространства z соответствует в
пространстве XYZ цилиндрическая поверхность x 2  y 2   0 плоскости    0 и z  z 0
пространства z отображаются в пространстве XYZ соответственно в полуплоскость,
проходящую через ось OZ под углом  0 к оси OX и плоскость z  z 0 (рис.2.15.3.). Якобиан
отображения:
cos    sin  0
 ( x, y , z )
J ( , , z) 
 sin   cos  0  
(  ,  , z )
0
0
1
неотрицателен в данной полосе (   0 только на границе полосы).
2
Рис. 4.16.2
Применяя формулу замены переменных в тройном интеграле к отображению (3),
получим так называемую формулу перехода в тройном интеграле от декартовых координат к
цилиндрическим координатам:
 f ( x, y, z)dxdydz   f (  cos  ,  sin  , z) dddz.
V
T
Здесь Т – область пространства z , образом которой при отображении (3) является
область V.
Пример. Вычислить объем тела V, ограниченного поверхностями x 2  y 2  z, z  1,
в цилиндрических координатах.
Обозначим через Т область пространства z , ограниченную поверхностями
2
  z, z  1,   0,   2 (рис.4.16.4.). При отображении (3) ее образом в пространстве
XYZ будет данная область V. Поэтому
Рис. 4.16.3
2
1
1
0
0
2
V   dxdydz   dddz   d  d  dz 
V
T

2
.
Примечание. Расстановку пределов при вычислении тройного интеграла в
цилиндрических координатах можно производить, используя чертеж области V в
пространстве XYZ и геометрический смысл цилиндрических координат.
Рис. 4.16.4
Так, например, при расстановке пределов в полученном выше интеграле можно было
рассуждать следующим образом. Так как область V на плоскость XOY проектируется в круг
x 2  y 2  1, то цилиндрическая координата  точек тела изменяется в пределах от 0 до 2 .
В сечении тела полуплоскостью   const , 0    2 , получаем криволинейный
треугольник (см. заштрихованную область на рис.2.15.5.). Для его точек цилиндрическая
координата  изменяется в пределах от   0 до   1. Постоянному значению  ,
0    1 в пространстве XYZ соответствует цилиндр x 2  y 2   2 . В пересечении этого
цилиндра с заштрихованной в полуплоскости   const , областью получаем отрезок прямой,
вдоль которой переменная z изменяется от значения z для точки, лежащей на параболоиде,
до значения z = 1 (для точки, лежащей на плоскости z=1).
Выражая эти значения в цилиндрических координатах ( z   2 , z  1) , окончательно
получаем:
2
1
1

V   d  d  dz  .
2
0
0
2
2. Переход в тройном интеграле от декартовых к сферическим координатам.
Сферическими координатами точки M ( x, y, z ) пространства XYZ называются числа  ,
где  - длина радиуса-вектора OM точки М,  - угол, составляемый с осью OX проекцией
этого радиуса-вектора на плоскость XOY, а  - угол отклонения радиуса-вектора точки М от
плоскости XOY (рис. 4.16.6.). Задание этих трех чисел однозначно определяет положение
точки М в пространстве XYZ.
Рис. 4.16.5
Рис.4.15.6
Сферические координаты  , точки М связаны с ее декартовыми координатами x, y,
z формулами:
x   cos  cos  ,
y   cos sin  ,
z   sin  .
(4)
По определению 0     . Значения углов  и  будем брать в пределах:


0    2 ,    . Формулы (4), где переменные  изменяются в указанных
2
2
пределах, можно рассматривать как задание отображения полосы
Рис. 4.16.7



0    , 0    2 ,     
2
2

пространства с прямоугольными координатами  (рис. 4.16.7.) пространство XYZ.
При этом отображении плоскости    0 пространства  соответствует сфера
x 2  y 2  z 2   2 0 в пространстве XYZ, плоскости    0 - полуплоскость, проходящая
через ось OZ под углом  0 к оси OX, а плоскости    0 - круговой конус с вершиной О,
образующие которого наклонены к плоскости XOY под углом  0 (рис. 4.16.8.). Это
отображение взаимно однозначно всюду, кроме границы указанной выше полосы. Якобиан
отображения:
cos cos    cos sin    sin  cos 
( x, y, z )
J (  ,  , ) 
 cos sin   cos cos    sin  sin  
 (  ,  , )
sin 
0
 cos
 sin 
  cos sin 
 cos cos 
  sin  cos 
cos cos 
  cos
  sin  sin 
cos sin 
  cos sin 

 cos cos 
  2 cos sin 2    2 cos 3    2 cos .
В данной полосе якобиан отображения (4) неотрицателен и обращается в нуль лишь
на границе полосы.
Рис. 4.16.8
Применяя формулу замены переменных в тройном интеграле к отображению (4),
получим:
2
(5)
 f ( x, y, z)dxdydz   f (  cos cos  ,  cos sin  ,  sin  )  cosddd ,
V
T
где Т – область пространства  , образом которой является область V. Эта формула
называется формулой перехода в тройном интеграле от декартовых к сферическим
координатам.
При вычислении тройного интеграла в сферических координатах можно пользоваться
чертежом области V в пространстве XYZ и геометрическим смыслом сферических
координат.
Рис. 4.16.9
Раздел 5
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ПЕРВОГО РОДА (ПО ПЛОЩАДИ
ПОВЕРХНОСТИ)
17.
Определение поверхностного интеграла первого рода
Пусть S — квадрируемая поверхность в пространстве XYZ, а F(х, у, z) — функция,
определенная в точках этой поверхности. Разобьем поверхность S произвольно на n частей
∆S1, ∆S2, …, ∆Sn не имеющих общих внутренних точек. На каждой поверхности ∆Si выберем
точку M i ( i , i ,  i ) (рис. 5.17.1). Значение функции F(х, у, z) в точке Mi умножим на
площадь ∆Si поверхности ∆Si:
F ( i , i ,  i )S i
и сложим все полученные произведения. Сумма
n
 F ( , , 
i 1
i
i
i
)S i
называется интегральной суммой для функции F(х, у, z) по поверхности S. Для данной
функции F(х, у, z) можно составить бесчисленное множество интегральных сумм по
поверхности S.
Рис. 5.17.1
Если при стремлении к нулю шага λ поверхности существует предел интегральных
сумм, то этот предел называется поверхностным интегралом первого рода от функции F(х,
у, z) по поверхности S и обозначается символом
 F ( x, y, z)dS .
S
Таким образом,
n
 F ( x, y, z)dS  lim  F ( i , i ,  i )S i
 0
S
i 1
если этот предел существует.
Из определения предела следует, что интеграл
 F ( x, y, z)dS
не зависит от способа
S
разбиения поверхности S на части и от выбора точек Mi на этих частях.
Свойства поверхностных интегралов первого рода:
1.  dS  S .
S
2.
 kF( x, y, z)dS  k  F ( x, y, z)dS , где k — число.
S
3.
S
 [ F ( x, y, z)  F ( x, y, z)]dS   F ( x, y, z)dS   F ( x, y, z)dS .
1
2
1
S
2
S
S
4. Если поверхность S разбита на части S1 и S2, то
 F ( x, y, z )dS   F ( x, y, z )dS   F ( x, y, z )dS .
S
S1
S2
5. Если F1(х, у, z)  F2(х, у, z), то
 F1 ( x, y, z)dS   F2 ( x, y, z)dS
S
S
6.
 F ( x, y, z )dS   F ( x, y, z ) dS
S
S1
7. Теорема
поверхности
S,
такая, что
о среднем. Если функция
то
на
этой
поверхности
F(х, у, z) непрерывна на
( , ,  ) ,
существует
точка
 F ( x, y, z)dS  F ( , ,  )  S
S
где S — площадь поверхности.
18.
Условия существования и вычисление поверхностных интегралов
первого рода
Теорема 1. Если поверхность S может быть задана уравнением z  f ( x, y ) , где
функция f(x,у) и ее частные производные f'x(x, у) и f'y(x, у) непрерывны в замкнутой
ограниченной области  — проекции S на плоскость XOY, а функция F(х, у, z)
непрерывна на поверхности S, то интеграл
 F ( x, y, z)dS
S
существует.
К использованию этих условий, равно как и условий, получающихся из них
перестановкой переменных х, у и z, сводится большинство практически встречающихся
случаев.
Вычисление поверхностных интегралов первого рода обычно производится путем их
сведения к двойным интегралам.
Рис. 5.18.1
Пусть функция F(х, у, z) непрерывна на поверхности S, удовлетворяющей условиям
теоремы 1. Тогда для любого способа разбиения поверхности S на части и любого
выбора точек Мi на этих частях
n
lim
 0
 F ( , ,  )S   F ( x, y, z)dS
i 1
i
i
i
i
S
1
Построим интегральные суммы специальным образом. А именно, разобьем область в
плоскости XOY на части  1 ,  2 , …,  n не имеющие общих внутренних точек.
Обозначим через ∆Si часть поверхности S, проектирующуюся на плоскость XOY в область
 n (рис. 5.18.1). При этом поверхность S окажется разбитой на n частей: ∆S1, ∆S2, …,
∆Sn.
Площадь каждой части ∆Si может быть найдена по формуле

S i 

1  f x'2 ( x, y )  f y'2 ( x, y )dxdy .
i
Применяя к двойному интегралу теорему о среднем, получим:
1  f x' 2 ( i , i )  f y' 2 ( i , i ) i
S i 
где Pi ( i , i ) — некоторая точка области  i .
Обозначим через Мi точку поверхности
∆Si
с
координатами
( i , i ,  i ) ,
 i  f ( i , i ) , и составим интегральную сумму для интеграла от функции
F(х, у, z) по поверхности S, соответствующую произведенному разбиению поверхности S
на части и выбранным точкам Мi, i=1, 2, …, n, на этих частях.
По доказанному
n
n
i 1
i 1
 F ( i , i ,  i )S i   F ( i , i , f ( i , i )) 1  f x'2 ( i , i )  f y'2 ( i , i ) i .
В правой части равенства имеем интегральную сумму для двойного интеграла
от функции
F ( x, y, f ( x, y)) 1  f x'2 ( x, y)  f y'2 ( x, y) , непрерывной в области  .
При стремлении к нулю шага разбиения области  шаг разбиения поверхности S (в
силу непрерывности функций f'x(x, у) и f'y(x, у)) также стремится к нулю. В пределе
получаем формулу
 F ( x, y, z)dS   F ( x, y, f ( x, y))
1  f x'2 ( x, y)  f y'2 ( x, y)dxdy , (1)
S
выражающую интеграл по поверхности S через двойной интеграл по проекции
поверхности S на плоскость ХОY.
Аналогично получаются формулы, выражающие при соответствующих условиях
интеграл по поверхности S через двойные интегралы по ее проекции на плоскости ZOX и
YOZ.
При вычислении интегралов по поверхностям более сложного вида применяется
предварительное разбиение этих поверхностей на части указанного вида.
Пример. Вычислим интеграл
 zdS
по части поверхности конуса z  x 2  y 2 ,
S
1  z  2 (рис. 5.18.2).
Поверхность S проектируется на плоскость XOY в область  , представляющую
f ( x, y )  x 2  y 2 ,
кольцо 1  x 2  y 2  4 . В этом кольце функции
x
y
f x' ( x, y ) 
, f y' ( x, y ) 
- непрерывны. Следовательно,
2
2
2
x y
x  y2
собой
2
2
0
1
2
2
2
 zdS   x  y 2dxdy  2  d   d  2 2 
S

7
3
2
Рис. 5.18.2
19.
Некоторые приложения поверхностных интегралов первого род
С помощью поверхностных интегралов первого рода можно определять массы,
статические моменты, моменты инерции, координаты центров тяжести и тому подобные
величины для материальных поверхностей с известной плотностью распределения массы.
Решение этих задач ана логично решению соответствующих задач для случая
материальной кривой, материальной плоской и пространственной области.
Раздел 6
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО РОДА (ПО КООРДИНАТАМ)
20.
Двухсторонние поверхности. Ориентация поверхности.
Возьмем на гладкой поверхности S произвольную точку М, проведем в этой точке
нормаль к поверхности и выберем одно определенное направление нормали. Начнем
теперь непрерывно перемещать точку М по замкнутому контуру, лежащему на
поверхности S и не пересекающему ее границы, приписывая каждому из ее положений то
из двух возможных направлений нормали, в которое непрерывно переходит исходное
положение нормали. В прежнее положение точка М вернется либо с тем же направлением
нормали, что и исходное, либо с прямо противоположным направлением нормали (рис.
6.20.1).
Если на поверхности S есть хотя бы одна точка и хотя бы один не пересекающий
границу поверхности контур, при обходе по которому направление нормали в точке
меняется на противоположное, то поверхность S называется односторонней. Примером
такой поверхности может служить лист Мебиуса, модель которого изображена на рис.
6.20.2.
3
Рис. 6.20.1
Если для любой точки поверхности S и любого замкнутого, не пересекающего
границы поверхности S контура после обхода направление нормали не меняется, то
поверхность называется двухсторонней, а совокупность всех точек поверхности с
выбранными в них по непрерывности направлениями нормали называется стороной такой
поверхности.
Рис. 6.20.2
Для двухсторонней поверхности выбор направления нормали в одной ее точке
определяет направления нормалей во всех точках поверхности, т. е. определяет сторону
поверхности.
Примерами двухсторонних поверхностей могут служить любая плоскость, сфера,
эллипсоид, параболоид, любая поверхность, задаваемая уравнением z=f(x, у), где f(x, у),
f'x(x, у) и f'y(x, у) — функции, непрерывные в некоторой области о плоскости XOY и т. д.
Пусть S — незамкнутая двухсторонняя поверхность, ограниченная контуром L, не
имеющим точек самопересечения. Выберем определенную сторону поверхности. Будем
называть положительным направлением, обхода контура L то, при движении по которому
по выбранной стороне поверхности сама поверхность остается слева (рис. 6.20.2).
Аналогично устанавливается положительное направление обхода для любого
4
замкнутого контура (без точек самопересечения), лежащего на поверхности S.
Направление обхода контура, противоположное положительному, называется
отрицательным.
Двухсторонняя поверхность с установленным на ней таким образом положительным
направлением обхода контуров называется ориентированной поверхностью. Если
изменить сторону поверхности, то положительные и отрицательные направления обхода
контуров поменяются ролями. Таким образом, выбор стороны поверхности определяет ее
ориентацию и, наоборот, выбор положительного направления обхода контура L,
ограничивающего поверхность, однозначно определяет ее сторону. Рассмотрим теперь
кусочно-гладкую поверхность S, т. е. поверхность S, состоящую из любого числа m двухсторонних кусков S1, S2, …, Sm рассмотренного выше вида, соединенных между собой по
некоторым «ребрам» (рис. 6.20.3).
Рис. 6.20.3
В точках этих ребер касательная плоскость и нормаль к поверхности S может не
существовать, т. е. данное выше определение двухсторонней поверхности к поверхности
S, вообще говоря, неприменимо. Дополним это определение. А именно, будем называть
данную, поверхность S двухсторонней, если на контурах каждого из кусков S1, S2, …, Sm
можно так задать направления обхода, что общие части этих контуров («ребра») будут
описываться во взаимно противоположных направлениях. Выбирая направления обхода
контуров S1, S2, …, Sm указанным образом, мы тем самым на каждом из кусков S1, S2, …,
Sm определим сторону поверхности. Сторона поверхности S определится как совокупность
сторон ее частей.
21.
Определение поверхностных интегралов второго рода (по координатам)
и их простейшие свойства
Рассмотрим в пространстве XYZ двухстороннюю поверхность S, состоящую из
конечного числа кусков, каждый из которых либо задан уравнением вида z=f(x, у), либо
является цилиндрической поверхностью с образующими, параллельными оси OZ. Пусть К
R(х, у, z) — функция, определенная в точках поверхности S. Выберем определенную
сторону поверхности S. Затем разобьем поверхность S на n частей S1, S2, …, Sn, не
имеющих общих внутренних точек и таких, что каждая часть ∆Si целиком умещается на
одном из указанных выше кусков поверхности S.
Обозначим через (∆Si)xy площадь проекции на плоскость XOY поверхности деления
∆Si, взятую со знаком плюс, если на ∆Si выбранная сторона поверхности направлена в
сторону возрастания z (иначе, если в точках ∆Si выбранные направления нормалей
5
составляют острые углы с осью OZ), и со знаком минус, если на ∆Si выбранная сторона
поверхности направлена в сторону убывания z (выбранные направления нормалей в
точках ∆Si составляют тупые углы с осью OZ) (рис. 6.21.1). Если поверхность деления
лежит на, цилиндрическом куске поверхности S с образующими, параллельными оси OZ,
то проекция ∆Si на плоскость XOY
Рис. 6.21.1
представляет собой дугу кривой, так что вопрос о знаке (∆Si)xy в этом случае отпадает,
(∆Si)xy= 0.
Возьмем на каждой части ∆Si поверхности S произвольно точку M i ( i , i ,  i ) и
умножим значение функции R(x, у, z) в точке Мi на (∆Si)xy:
R( i , i ,  i ) (∆Si)xy
Сумма всех таких произведений
n
 R( , , 
i
i 1
i
i
) (∆Si)xy
называется интегральной суммой для функции R(x, у, z) по поверхности S по
переменным х и у. Естественно, что таких сумм для заданной на поверхности S функции
R(x, у, z) можно составить бесчисленное множество.
Если при стремлении к нулю шага разбиения  поверхности S интегральные суммы
имеют предел, то этот предел называют поверхностным интегралом (второго рода) по
выбранной стороне поверхности S от функции R(x, у, z) по переменным х и у и обозначают
символом
(1)
 R( x, y, z)dxdy .
S
Так как cимвол (1) не содержит указания на сторону поверхности S, ее приходится
задавать дополнительно. Таким образом,
n
 R( x, y, z)dxdy  lim  R( i , i ,  i )(S i ) xy ,
S
 0
i 1
если этот предел существует.
Аналогичным образом определяются поверхностные интегралы второго рода по
выбранной стороне поверхности S по переменным у и z (z и х) от функции P(x, у, z) (Q(x,
6
у, z)), определенной на поверхности S:
n
 P( x, y, z)dydz  lim  P( i , i ,  i )(S i ) yz ,
 0
S
(2)
i 1
n
 Q( x, y, z)dzdx  lim  Q( i , i ,  i )(S i ) zx .
 0
S
(3)
i 1
Если поверхность S такова, что для функций Р(х, у, z), Q(x, у, z) и R(x, у, z),
определенных в ее точках, существуют интегралы (1), (2) и (3), то можно ввести
поверхностный интеграл «общего» вида по выбранной стороне поверхности:
 P( x, y, z)dydz  Q( x, y, z)dzdx  R( x, y, z)dxdy 
S
  P( x, y, z )dydz   Q( x, y, z )dzdx   R( x, y, z )dxdy
S
S
(4)
S
К вычислению поверхностных интегралов второго рода приводит, например,
решение так называемой задачи о потоке векторного поля.
Если в каждой точке М(х, у, z) пространства XYZ (или некоторой его области) задан
вектор скорости a  P( x, y, z )i  Q( x, y, z ) j  R( x, y, z )k проходящих через эту точку
частиц движущейся жидкости, то количество жидкости, протекающее за единицу времени
через поверхность S (в выбранную сторону), равна интегралу
 P( x, y, z)dydz  Q( x, y, z)dzdx  R( x, y, z)dxdy
S
по выбранной стороне поверхности S.
Свойства поверхностных интегралов второго рода:
1. Любой поверхностный интеграл (второго рода) изменяет знак при перемене
стороны поверхности.
2. Постоянный множитель можно выносить за знак поверхностного интеграла:
 kPdydz  k  Pdydz ,
S
S
 kQdzdx  k  Qdzdx ,
S
S
 kRdxdy  k  Rdxdy ,
S
S
где k — любое число.
3. Поверхностный интеграл от суммы двух функций равен сумме соответствующих
интегралов от слагаемых:
 ( P1  P2 )dydz   P1dydz   P2 dydz ,
S
S
 (Q
1
S
 Q2 )dzdx   Q1 dzdx   Q2 dzdx ,
S
S
 ( R
1
S
 R2 )dxdy   R1 dxdy   R2 dxdy .
S
S
S
4. Если поверхность S разбита на части S1 и S2, то интеграл по всей поверхности S
равен сумме интегралов по ее частям:
     .
S
S1
S2
5. Если S — цилиндрическая поверхность с образующими, параллельными оси OZ,
то
 R( x, y, z)dxdy  0
S
7
6. Если S — цилиндрическая поверхность с образующими, параллельными оси ОХ,
то
 P( x, y, z)dydz  0
S
7. Если S — цилиндрическая поверхность с образующими, параллельными оси OY,
то
 Q( x, y, z)dzdx  0
S
22.
Существование и вычисление поверхностных интегралов второго рода
Пусть S — двухсторонняя поверхность, заданная уравнением z=f(x, у), где f(x, у) —
непрерывная функция в замкнутой области σ — проекции поверхности S на плоскость
XOY, a R(x, у, z) — непрерывная функция на поверхности S. Выберем верхнюю сторону
поверхности S.
Разобьем поверхность S сетью кусочно-гладких линий на n частей ∆S1, ∆S2, …, ∆Sn.
Проекциями этих линий на плоскость XOY область σ разобьется на n областей, обозначим
их соответственно  1 ,  2 , …,  n (рис. 6.22.1).
Рис. 6.22.1
Возьмем на каждой части ∆Si произвольную точку M i ( i , i ,  i ) и составим
интегральную сумму
n
 R( , , 
i 1
i
i
i
)( S i ) xy .
Так как сторона поверхности выбрана верхняя, то (∆Si)xy=  i , а значит
n
n
i 1
i 1
 R( i , i ,  i )(S i ) xy   R( i , i , f ( i , i )) i
В правой части равенства имеем интегральную сумму для двойного интеграла от
непрерывной функции R(х, у, f (x, у)) по области σ.
При стремлении к нулю шага разбиения поверхности S шаг разбиения области σ
8
также стремится к нулю. В пределе получаем формулу
 R( x, y, z)dxdy   R( x, y, f ( x, y))dxdy ,
(1)

S
выражающую интеграл по верхней стороне поверхности S по переменным х и у через
двойной интеграл по ее проекции на плоскость XOY.
Примечание. Интегрирование по нижней стороне поверхности S сводится к
интегрированию по верхней стороне после перемены знака перед интегралом.
Аналогичным образом устанавливается справедливость формул:
(2)
 P( x, y, z)dydz   P( f ( y, z), y, z)dydz

S
для функции P(x, у, z), непрерывной на двухсторонней поверхности S, заданной
уравнением x=f(y, z) (σ — проекция поверхности S на плоскость YOZ, сторона
поверхности S направлена в сторону роста х), и
(3)
 Q( x, y, z)dzdx   Q( x, f ( x, z), z)dzdx

S
для функции Q(x, у, z), непрерывной на двухсторонней поверхности S, заданной
уравнением y=f(x, z) (σ — проекция поверхности S на плоскость ZOX, сторона
поверхности S направлена в сторону роста переменной у). Формулы (1), (2), (3)
применяются при вычислении соответствующих поверхностных интегралов, а
предложенный вывод этих формул дает одновременно доказательство существования
рассматриваемых интегралов.
Если двухстороннюю поверхность S можно разбить на конечное число кусков,
каждый из которых либо задается уравнением вида z=f(x, у), где f(x, у) — функция,
непрерывная в замкнутой квадрируемой области — проекции соответствующего куска поверхности S на плоскость XOY, либо является цилиндрической поверхностью с
образующими, параллельными оси OZ, то интеграл по выбранной (любой) стороне
поверхности S от непрерывной на поверхности функции R(x, у, z):
 R( x, y, z )dxdy
S
существует и равен алгебраической сумме двойных интегралов по проекциям указанных
кусков поверхности S вида z = f(x,y) нa плоскость XOY.
Справедливость этого утверждения вытекает из проведенного при выводе формулы
(1) Доказательства и свойств поверхностных интегралов. Аналогичные утверждения
имеют место для интегралов вида
и
 P( x, y, z)dydz
 Q( x, y, z)dzdx
S
S
В случае, если поверхность S может быть задана уравнением z=f(x, у), где
функция f(x, у) к ее частные производные f'x(x, у) и f'y(x, у) непрерывны в замкнутой
квадрируемой области σ — проекции поверхности S на плоскость XOY, а функции P(x, у,
z), Q(x, у, z) и R(x, у, z) непрерывны на поверхности S, имеет место следующая формула:
(4)
 Pdydz  Qdzdx  Rdxdy   ( pP  qQ  R)dxdy
S

z
z
, q
выражающая поверхностный интеграл общего вида по верхней
x
y
стороне поверхности S через двойной интеграл по проекции поверхности S на плоскость
XOY.
где p 
23.
Связь между поверхностными интегралами первого и второго рода
Формула поверхностного интеграла общего вида:
9
 Pdydz  Qdzdx  Rdxdy   ( P cos   Q cos   R cos  )dS ,
S
S
где cos  , cos  , cos  - направляющие косинусы нормали к поверхности S в выбранную
(для интеграла слева) сторону поверхности.
24.
Формула Гаусса — Остроградского
Формула Гаусса — Остроградского устанавливает связь между поверхностным
интегралом (второго рода) по замкнутой поверхности и тройным интегралом по
пространственной области, ограниченной этой поверхностью.
 P Q R 

dxdydz   Pdydz  Qdzdx  Rdxdy



x y z 
V 
S
Формулу Гаусса — Остроградского можно использовать для вычисления
поверхностных интегралов по замкнутым поверхностям.
25.
Формула Стокса
Формула Стокса устанавливает связь между криволинейным и поверхностным
интегралами (второго рода).
Устанавливается следующее соотношение между криволинейным и поверхностным
интегралами:
 R Q 
 Q P 
 P R 
(1)
L Pdx  Qdy  Rdz  S  y  z dydz   z  x dzdx   x  y dxdy
Формула (1) имеет место для любой незамкнутой, ограниченной контуром L поверхности S, состоящей из конечного числа поверхностей рассмотренного вида, а также для
поверхностей, обладающих указанными свойствами, относительно других координатных
плоскостей. Эта формула называется формулой Стокса. Она выражает криволинейный
интеграл по контуру L через интеграл по поверхности S, «натянутой» на этот контур.
Сторона поверхности и направление обхода контура L взаимно определяют друг друга.
Частным случаем формулы Стокса (L - кривая в плоскости XOY, S — область
плоскости XOY, ограниченная этой кривой) является формула Грина — Остроградского:
 Q P 
L Pdx  Qdy  S  x  y dxdy .
Формулу Стокса можно использовать для вычисления криволинейных интегралов по
замкнутым кусочно-гладким контурам.
10
ЗАДАЧИ
1. Вычислить интегралы и вычертить области, на которые они распределены:


1 cos x
а)  dx
2
 y sin xdy;
0
2
в)
0
 dy

3 cos y
x

2
sin 2 ydx.
0
2

1
2
б)  dx
0
y
4
dy,
cos x
рекомендуется делать чертеж.
2. Перейти к полярным координатам r,  и расставить пределы интегрирования по
новым переменным в следующих интегралах:
а)  f ( x, y )dxdy,
(S )
где S – треугольник ограниченный прямыми y = x, y = -x, y = 1.
1
1
 y
б)  dx  f  dy .
x
1
x2 
Переходя к полярным координатам, вычислить
a
a2  x2
 dx 
0
x 2  y 2 dy.
0
3. Вычислить двойной интеграл
 xydxdy,
если область D ограничена прямой
D
y  x  4 и параболой y 2  2 x.
4. Изменить порядок интегрирования в интеграле:
1
I

 3
0
dx
 vdy.
 4 x 2
5. Найти площадь, ограниченную параболами
y 2  10 x  25 и y 2  6 x  9.
6. Найти площадь ограниченную, линией
2
 x2 y2 
x2 y2
 
 

.
9 
4
9
 4
7. Найти объем тел, ограниченных следующими поверхностями:
b
x2 z2
 2  1, y  x, y  0, z  0.
2
a
a
c
8.
Найти
объем
x 2  y 2  z 2  a 2 , z  0.
тел,
ограниченных
поверхностями
2az  x 2  y 2 ,
11
9. Найти площадь части поверхности цилиндра x 2  y 2  R 2 ( z  0), содержащуюся
между плоскостями z = mx и z = nx (m > n > 0).
10. Вычислить следующие интегралы:
a2  x2  y2
a2  x2
a
 dx 
0

dy
0
dz
a2  x2  y2  z2
0
.
11. Вычислить
2
2 x x2
0
0
 dx

a
dy  z x 2  y 2 dz
0
преобразовав его предварительно к цилиндрическим координатам.
12. Вычислить
R2  x2
R
 dx 
R
 R2  x2
dy
R2  x2  y2
2
 (x
 y 2 )dz,
0
преобразовав его предварительно к сферическим координатам.
13. Вычислить тройной интеграл
dxdydz
 1  x  y ,
если область D ограничена
D
плоскостями: x = 0, x = 1, y = 2, y = 5, z = 2, z = 4.
14. Вычислить тройной интеграл
I   ( x 2  y 2  z 2 )dxdydz, где область W
W
ограничена поверхностями 3( x  y )  z  3a .
2
2
2
2
15. Вычислить следующие криволинейные интегралы:
ds
,
а) 
x2  y2  4
C
где C – отрезок прямой, соединяющий точки О (0:0) и А(1;2).
б)  y 2 ds,
C
где С – первая арка циклоиды x = a(t - sint), y = a(1 – cost).
ds
в)  2
,
2
2
C x  y  z
где С – первый виток винтовой линии x  a cos t , y  a sin t , z  bt.
16. Определить координаты центра тяжести полуарки циклоиды
x  a(t  sin t ), y  a(1  cos t ), [0  t   ].
17. Найти первообразную функции U, если:
du  (3x 2  2 xy  y 2 )dx  ( x 2  2 xy  3 y 2 )dy.
12
18. С помощью формулы Грина преобразовать криволинейный интеграл


l   x 2  y 2 dx  y xy  ln( x  x 2  y 2 ) dy,
C
где контур С ограничивает область S.
19. Найти площадь, ограниченной замкнутой кривой: петлей декартова листа
x  y 3  3axy  0.
3
20. Вычислить следующие повторные интегралы:
2

1

1.  dy  x 2  2 y dx
0
0
4
2
3
dy
( x  y)2
1
1
1
2
x
1
1
x
2.  dx 
x 2 dy
3.  dx 
2
0
0 1 y
x 2 dy
y2
4.  dx 
3
5.  dy
3
5
 x  2 y dx
y 2 4 y
2
a
 d  rdr
6.
0
a sin

2
7.  d
3 cos 
r


2
sin 2 dr
0
2
1 x 2
1
8.  dx

0
1  x 2  y 2 dy
0
21. Написать уравнения линий, ограничивающих области, на
распространены нижеследующие двойные интегралы, и вычертить эти области:
1.
2
2 y
6
y2
1
4
 dy  f x, y dx
3
x 9
1
x2
10 y
2.  dx
4
3.  dy
 f x, y dy
 f x, y dx
0
y
3
2x
1
x
3
4.  dx  f  x, y dy.
3
25 x 2
0
0
5.  dx
 f x, y dy
которые
13
2
x2
1
x2
6.  dx
 f x, y dy
22. Расставить пределы интегрирования в том и в другом порядке в двойном
интеграле
 f x, y dxdy
S 
для указанных областей S:
1. S – прямоугольник с вершинами O(0;0), A(2;0), B(2;1),C(0;1).
2. S – треугольник с вершинами O(0;0), A(1;0), B(1;1).
3. S – трапеция с вершинами O(0;0), A(2;0), B(1;1),C(0;1).
4. S – параллелограмм с вершинами A(1;1), B(2;4),C(2;7), D(1;5).
23. Переменить порядок интегрирования в следующих двойных интегралах:
1.
2.
4
12 x
0
1
3x2
3x
0
2x
 dx  f x, y dy
 dx  f x, y dy
a2  x2
a
3.
 dx  f x, y dy
a2  x2
2a
0
4.
5.
a
2 ax x 2
a
2
0
2a
4 ax
0
2 ax x 2
1 y
 dx  f x, y dy
 dx  f x, y dy
1
6.
7.
 dy  f x, y dx
0
 1 y 2
1
3 y 2
0
y2
2
 dy  f x, y dx
R 2
2

8.
x
dx  f  x, y dy 
0
0

sin x
0
x2
9.  dx
R2  x2
R

R 2
2
dx
 f x, y dy
0
 f x, y dy
24. Вычислить следующие двойные интегралы:
1.  xdxdy , где S – треугольник с вершинами O(0;0), A(1;1), B(0;1).
S 
2.

 
dxdy
a2  x2  y 2
S
в первой четверти.
, где S – часть круга радиуса a с центром в точке O(0;0), лежащая
14
3.

 
x 2  y 2 dxdy , где S – треугольник с вершинами O(0;0), A(1;-1), B(1;1).

 
xy  y 2 dxdy , где S – треугольник с вершинами O(0;0), A(10;1), B(1;1).
S
4.
S
e

 
5.
x
y
dxdy , где S – криволинейный треугольник OAB, ограниченный параболой
S
y2=x и прямыми x=0, y=1 (рис. 2).
xdxdy
x2
6.  2
,
где
S
–
параболический
сегмент,
ограниченный
параболой
и
y

2
2
S  x  y
прямой y=x.
7. Вычислить интегралы и вычертить области, на которые они распространены:

а)  dx
0


1cos x
2
2
 y sin xdy ; б)  dx
0
0
1
4
 y dy ; в)
cos x
cos y
2


dy
x
2
sin 2 ydx .
0
2
При решении задач 8 – 15 рекомендуется предварительно делать чертёж.
8.  x y 2 dxdy ,
S 
если S есть область, ограниченная параболой y2=2px и прямой x=p.
9.  xydxdy ,
S 
распространённый на область S, ограниченную осью OX и верхней
полуокружностью (x-2)2+y2=1.
dxdy
10. 
,
2
a

x
S 
где S – круг радиуса a, касающийся осей координат и лежащий в первом квадранте.
Перейти к полярным координатам r,  и расставить пределы интегрирования по
новым переменным в следующих интегралах:
11.
12.
1
1
0
0
2
x
 dx  f x, y dy .
 dx f 
0
13.

x 2  y 2 dy .
0
f  x, y dxdy , где S – треугольник, ограниченный прямыми y=x, y=-x, y=1.

 
S
14.
15.
1
1
1
x2
 y
 dx  f  x dy .
f  x, y dxdy , где область S ограничена лемнискатой (x2+y2)2=a2(x2-y2).

 
S
В задачах 16 – 19 нарисовать тела, объёмы которых выражаются данными
двойными интегралами:
16.
1
1 x
0
0
 dx  1  x  y dy .
15
2
2 x
0
0
1
1 x 2
17.  dx
18.
 4  x  y dy .
 dx  1  x dy .
0
0
2
2
0
2 x
19.  dx  4  x  y dy .
Вычислить тройным интегрированием объемы тел, ограниченных данными
поверхностями:
20. z = 4 - y2 , z = 2+ y2 ,x = - 1, x = 2
21. z = x2 + y2 , z = 2x2 + 2y2 ,y = x2 , y= x
22. z= x2 + y2 , z = x + y
23. x2 + y2 + z2 =1, x2 + y2 + z2 = 16, z2 = x2 +y2 , x = 0,y = 0, z = 0 ( x0, y0, z0)
24. y2 = 4a2 - 3ax, y2 = ax, z =  h.
25. Вычислить криволинейные интегралы:
1.  x  y dl , L : x 2  y 2  ax
L
2.
xydl, L : ( ABCD ), A(0,0), B(4,0), C (4,2), D(0,2)
L
3. 2 y dl , L  1àðêà : x  at  sin t , y  a1  cos t 
L


4. x 2  y 2 dx, L : y  x 2 : O0,0, C 2,4
L
1,1
5.  xydx   y  x dy, L : 1) y  x,2) y  x 2 ,3) y  x 3 ,4) y 2  x
0 , 0 
6. ydx  xdy, L : x  a cos t , y  b sin t
L
7.
L
y 2 dx  x 2 dy
, L : x  a cos t , y  a sin t , t1  0, t 2  
x2  y2




8. 1  x 2 ydx  x 1  y 2 dy, L : x 2  y 2  R 2
L
26. Найти массу всей линии r = a ( 1 + cos ), если Р= k r
27. Найти работу силового поля F = xi + yj + zk при перемещении материальной
точки вдоль первого витка конической винтовой линии x = a et cost,y = a et sint, z = a et
из т.О(0,0,0) в т.М(а,0,а)
28. Вычислить линейный интеграл
 a, dr , a  y
 
2
i  x 2 j : OB  : O(0,0), D(1,1)
OB
1) отрезок прямой ОВ, 2) дуга линии y = x2 , 3) дуга линии y2 = x, 4) ломаная ОАВ,
А(1,0), 5 ломаная ОСВ, С(0,1)
16
29. Используя формулу Грина, вычислить интегралы:




1. x 2  y 2 dx  x 2  y 2 dy, L : y  r 2  x 2 , Ox.
L
2. x  y  dx  x  y  dy, L : y  sin x,0  x  
2
2
L
30. Найти поток вектора r = xi +yj + zr через часть поверхности x2 /a2 + y2 /b2 +z2 /c2
=1, лежащую в первом квадранте, в направлении внешней нормали.
40. Найти поток вектора a=x2 i-y2 j + z2 k через всю поверхность тела x2 +y2 +z2 R2 ,
0  z   x2 + y2 -R2 в направлении внешней нормали.
41. Используя формулу Остроградского - Гаусса, найти поток вектора a = x3 i+y3 j+R2
zk через всю поверхность тела H/R2 (x2 +y2 )  z H в направлении внешней нормали.
42. Вычислить циркуляцию вектора a = zi + xj + yk по линии x2 +y2 +z2 =R2 , x +y +z
=R в положительном направлении относительно орта k: 1) непосредственно 2) по формуле
Стокса.
43. Найти grad div a, a = x3i +y3j +z3k
44. Найти rot rot a, a = xy2i+yz2j+zx2k
45. Найти 2a , a = (y2+z2) xi + (x2+z2)yj+(x2+y2) zk
46. Найти потенциал поля a = 2xyi + (x2-2yz)j -y2k
47. Проверить соленоидальность поля:
 x 2  y 2 
xi  yj

a

2
2 32
2
2
x y
x y


48. Найти статический момент относительно плоскости Охуи положение центра масс
однородной полусферы
x2 +y2 +z2 =R2(z0)
17
ЛИТЕРАТУРА
1. Н.С. Пискунов Дифференциальное и интегральное исчисления. Ч.1,2.М.: " Наука",
1976
2. Г.Н. Берман Сборник задач по курсу математического анализа. М.: " Наука", 1975
3. В.А. Ильин, Э.Г. Позняк Основы математического анализа. Ч.1,2. М.: " Наука",
1982