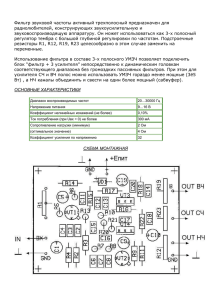
Зависимость коэффициентов передачи по току от частоты

УСИЛИТЕЛИ
3.1. Структурная и эквивалентные схемы усилителя
Под усилителем понимают электронное устройство, служащее для
увеличения энергии или мощности электрического сигнала без внесения в него заметных искажений. Простейший электронный усилитель
представляет собой линейный активный четырехполюсник, содержащий усилительный элемент, работающий в линейном режиме, и источник питания. Ко входу такого четырехполюсника подключается
источник сигнала, а к его выходу – требуемая нагрузка. В блок-схеме
такого усилителя, представленной на рис 3.1, P0 – мощность, потребляемая усилителем от источника питания; P1 – входная мощность, получаемая усилителем от источника сигнала; P2 – мощность, отдаваемая усилителем в нагрузку. Как следует из данного выше определения, основным свойством электронного усилителя является его способность увеличивать энергию или мощность входного сигнала, поэтому должно выполняться очевидное неравенство P1<P2. Из-за потерь энергии в пассивных и активных элементах усилителя имеет место и другое соотношение P2<P0, и тогда мощность потерь запишется
Pп=P0–P2.
Источник
сигнала
P1
Линейный активный
четырехполюсник
(3.1)
P2
Нагрузка
P0
Источник
питания
Рис. 3.1. Структурная схема усилителя
Коэффициент полезного действия (кпд) усилителя  по определению равен
63

P2
,
P0
(3.2)
а с учетом равенства (3.1) он выразится как

P2
.
P2  Pп
(3.3)
>
>>
Чаще всего значение  находится в пределах от 0,2 до 0,7 в зависимости от конкретного назначения усилителя.
Электронные усилители применяются в различных устройствах радиоэлектроники. При этом могут использоваться самые разнообразные источники усиливаемых сигналов и нагрузки. Рассмотрим соответствующие этим случаям эквивалентные схемы усилителей, определив предварительно такие понятия, как генератор (источник)
напряжения (эдс) и генератор тока (рис. 3.2).
Для идеальных генераторов напряжения и тока справедливы следующие определения: генератором напряжения называется такой источник постоянного или переменного напряжения, внутреннее (выходное) сопротивление которого Rг0, а генератором тока – такой источник постоянного или переменного тока, внутреннее сопротивление
которого Rг. Очевидно, что эквивалентные схемы реальных генераторов напряжения и тока будут иметь вид, показанный на рис. 3.2 а
и рис. 3.2 б соответственно.
Если входное сопротивление Rвх усилителя значительно превышает
выходное сопротивление источника сигнала Rг, то считается, что усилитель управляется напряжением (рис. 3.3 а, в). Если входное сопротивление усилителя Rвх значительно
меньше, чем выходное сопротивление источника сигнала, то усилитель
Rг
управляется током (рис. 3.3 б, г). ЕсRг
Iг
ли выходное сопротивление усилитеEг
ля намного меньше сопротивления
нагрузки, то он является источником
напряжения (рис. 3.3 а, г), а если
а
б
Рис. 3.2. Эквивалентные схемы:
намного больше – то усилитель можа – генератора напряжения; б –
но рассматривать как источник тока
генератора тока
(рис. 3.3 б, в).
64
I2
Rн Iг
U2
Eг
>>
Rвх
U1
Rвх
а
U2
Rн
Iг
>>
>>
Rвх
Rг
Rвых
U1
Rвх
Ег
U2
Rн
>
Rвых
Iг
I2
>
Eг
I1
I2
U1
Rн
U2
б
I1
Rг
Rвых
Iг
>
>
U1
Eг
Rг
Rвых
Rг
I2
I1
>>
I1
в
г
Рис. 3.3. Эквивалентные схемы усилителя: а – источник напряжения, управляемый
напряжением; б – источник тока, управляемый током; в – источник тока, управляемый напряжением; г – источник напряжения, управляемый током
3.2. Основные показатели
и характеристики усилителей
Коэффициент усиления. Для объективной оценки работы усилителей вводят ряд показателей и характеристик.
Одним из важнейших показателей является коэффициент усиления
K. При этом различают коэффициенты усиления по напряжению KU,
по току KI и по мощности KP, определяемые соответственно как
KU 
U вых
I
P
, K I  вых , K P  вых .
I вх
Pвх
U вх
(3.4)
Очевидно, что произведение KIKU =KP. Очень часто, говоря о коэффициенте усиления усилителя K, полагают, что K  KU. Если применя-
65
ется многокаскадная схема усиления с n-каскадами, то общий коэффициент усиления всей схемы равен
n
K общ   Ki ,
(3.5)
i 1
где Ki – коэффициент усиления i-го каскада. Выражение (3.5) справедливо для любого из коэффициентов усиления (3.4). Учитывая физиологические особенности восприятия человеком звука, коэффициент
усиления удобно выражать в логарифмических единицах, а именно, в
децибелах (дБ). При этом имеют место следующие соотношения:
KU[дБ]=20 lg KU, KI[дБ]=20 lg KI, KP[дБ]=10 lg KP.
(3.6)
В табл. 3.1 даны некоторые численные сравнительные значения коэффициентов усиления, выраженные в дБ и относительных единицах.
Т а б л и ц а 3.1
K, дБ
KI,U
KP
1
1,12
1,25
3
1,41
2
6
2
4
20
10
102
40
102
104
Несложно показать, что общий коэффициент усиления многокаскадного усилителя, выраженный в дБ, будет представлять собой сумму коэффициентов усиления отдельных каскадов, также выраженных
в дБ. Действительно,
 n

K общ дБ  20 lg   K i   20 lg K1  20 lg K 2  ...  20 lg K n 
 i 1 
 K1 дБ  K 2 дБ  ...  K n дБ.
(3.7)
Входное и выходное сопротивление. Важным параметром любого
усилителя, рассматриваемого как четырехполюсник (рис. 3.4), является
 вх  U1 I1 . При анализе раего комплексное входное сопротивление Z
боты усилителя напряжения низкой частоты в диапазоне малых входных
сигналов его входное сопротивление обычно полагают чисто активным
и обозначают последнее, как уже указывалось выше при рассмотрении
эквивалентных схем усилителя, Rвх. Сопротивление Rвх определяет ту
часть напряжения источника сигнала, которая выделяется непосредственно на входе усилителя. На рис. 3.5 представлена эквивалентная
схема входа усилителя, на основании которой можно записать следующее соотношение U1=EгRвх/(Rг+Rвх)=Eг/(1+Rг/Rвх). Это соотношение показывает, что только при выполнении неравенства Rвх>>Rг напряжение
66
.
I1
. Вход
.
U1 Zвх
.
.
I2
I1
Rг
Выход
.
.
Zвых U2
Ег
Рис. 3.4. Схематическое представление усилителя в виде четырехполюсника
U1
I2
Rвх
Rвых U2
Rн
Рис. 3.5. Усилитель в виде четырехполюсника с входной и выходной
цепями
на входе усилителя U1 практически равно эдс источника сигнала. Комплексное выходное сопротивление усилителя Z вых определяется отно вых  U 2 I2 (рис. 3.4) и также, как и для входного сопротившением Z
ления, часто полагается активным и равным Rвых (рис. 3.5).
Для высокочастотных усилителей важным становятся реактивные
составляющие, и поэтому для анализа их работы необходимо использовать комплексные величины Z вх и Z вых , которые в этом случае
называются соответственно входным и выходным импедансами.
Линейные искажения. Поскольку в любом реальном усилителе
имеются реактивные элементы (индуктивности L и емкости C), а параметры усилительных элементов зависят от частоты, то коэффициент
передачи K  j соответствующего четырехполюсника будет представлять собой комплексную величину
(3.8)
K  j  K  e j ,
где K()=K – модуль коэффициента передачи усилителя, который чаще всего называют коэффициентом усиления, а () – фазовый сдвиг
между входным и выходным гармоническими сигналами на определенной частоте.
Зависимость модуля коэффициента передачи K() от частоты называется амплитудно-частотной характеристикой (АЧХ) усилителя. Эта
зависимость обуславливает в нем частотные искажения сигнала. Коэффициент частотных искажений M определяется величиной, обратной относительному усилению Y
K
1
M 0 ,
(3.9)
K Y
где K0 – модуль коэффициента усиления на средних частотах усиливаемого диапазона.
67
K()
1
K0 = M
=
1
1
K()
K0
2
K0
Kн
н

2
Kв
в

1
М
Kв
K0
Kн
K0
н

в

а
б
Рис. 3.6. Амплитудно-частотные характеристики усилителя: а – ненормированная; б – нормированная
Зависимость фазового сдвига () от частоты называется фазочастотной характеристикой (ФЧХ) усилителя. Эта зависимость обуславливает в нем фазовые искажения сигнала.
Частотные и фазовые искажения являются линейными искажениями. Они, как выше отмечено, обусловлены одними и теми же причинами, а именно, наличием в схемах реактивных элементов L и C, и
проявляются в неодинаковом усилении гармоник сигнала, а также в
различном фазовом сдвиге между ними.
АЧХ усилителя представлено графически на рис. 3.6. По таким
графикам несложно оценить величину искажений на различных частотах. На рис. 3.6 а представлена ненормированная АЧХ усилителя, а
на рис. 3.6 б – нормированная характеристика, все значения коэффициента усиления которой разделены на его максимальную величину
K0. На графике рис. 3.6 а коэффициенты усиления на нижних частотах, средних частотах и верхних частотах обозначены соответственно
как Kн, K0, Kв. Рабочий диапазон частот или полоса пропускания усилителя определяется разностью
(3.10)
=в–н.
Как следует из представленных графиков, этот параметр является
интервалом, лежащим между значениями частот н и в, в пределах
которого коэффициент усиления усилителя уменьшается в 2  1,41
раза.
На рис. 3.7 представлены ФЧХ реального и идеального усилителей.
ФЧХ идеального усилителя описывается формулой общ= –tз, где tз –
время задержки сигнала, проходящего через усилитель, а знак «–» озна68
чает запаздывание выходного
напряжения
относительно
входного. Сдвиг фаз для многокаскадного усилителя определяется по формуле
()

n
общ   i ,
2
1
(3.11)
i 1
где i – фазовый сдвиг, вноРис. 3.7. Фазо-частотная характеристика
симый i-каскадом.
усилителя: 1 – идеального; 2 – реального
Нелинейные искажения.
Нелинейные искажения в усилителях возникают вследствие того, что вольтамперные характеристики (ВАХ) реальных усилительных элементов нелинейны. Этот вид
искажений проявляется в возникновении на выходе усилителя дополнительных гармоник, что поясняется с помощью спектрограмм входного и выходного сигналов, показанных на рис. 3.8. Величину нелинейных искажений можно охарактеризовать коэффициентом нелинейных искажений или коэффициентом гармоник . Различают коэффициент нелинейных искажений по отдельным гармоникам и общий
коэффициент нелинейных искажений общ. Так, коэффициенты по второй, третьей и т. д. гармоникам определяются следующими формулами:
2 
I
I
I2
,  3  3 , ... ,  n  n ,
I1
I1
I1
(3.12)
где I1, I2, I3,…, In – амплитуды тока первой (или основной), второй,
iвх
iвых


 2 3
n

а
б
Рис. 3.8. Спектрограммы сигналов: а – на входе усилителя; б – на выходе
усилителя
69
третьей и т. д. гармоник, а общий коэффициент гармоник вычисляется как
 общ   22   32     2n .
(3.13)
Формулу (3.13) с учетом равенств (3.12) можно представить в виде
 общ 
I 22  I 32    I n2
.
I1
(3.14)
Методы определения нелинейных искажений подробно рассматриваются в специальной литературе, посвященной электронным усилителям (см., например, [20], а также п. 3.11 настоящего курса).
Амплитудная характеристика. Амплитудной характеристикой
усилителя называется зависимость амплитуды первой гармоники
напряжения или тока на выходе усилителя от амплитуды гармонического напряжения или тока на его входе (рис. 3.9). В идеальном случае при отсутствии нелинейных искажений под амплитудной характеристикой понимают просто зависимость величины выходного
напряжения от величины входного.
Динамический диапазон усилителя. Различают динамический
диапазон усилителя Dу и динамический диапазон сигнала Dс, которые
соответственно равны
U вх max
Dу 
,
(3.15)
U вх min
Dс 
U с max
U с min
.
(3.16)
Здесь Uвх max и Uвх min определяются согласно рис. 3.9 на линейном
участке амплитудной характеристики, а Uс max и Uс min представляют
собой максимальное и минимальное значения напряжений входного
сигнала. Для нормальной работы усилителя должно выполняться неравенство
Uвых
Uш
Uвх min Uвх max Uвх
Рис. 3.9. Амплитудная характеристика усилителя
DcDу.
(3.17)
Величина напряжения Uш при Uвх=0 соответствует пороговому напряжению усилителя или напряжению его собственных
помех. Возникновение этих помех обусловлено, с одной стороны, внешними источниками (сигналы от различных про70
мышленных установок, генераторов, искровые разряды и т. д.), а с другой – такими внутренними источниками, как тепловые, дробовые и
фликкер-шумы усилительных элементов.
Классификация усилителей. Усилители можно подразделять на
различные группы и виды по определенным признакам и параметрам.
Например, по виду усиливаемых сигналов их можно разделить на
усилители гармонических сигналов и усилители импульсных сигналов; по ширине полосы пропускания  и значению нижней и верхней граничных частот усиления н и в – на усилители постоянного
тока (УПТ), усилители напряжения низкой частоты (УННЧ), широкополосные усилители (ШУ), полосовые усилители (ПУ) и избирательные усилители (ИУ). На рис. 3.10 для иллюстрации приведенной выше классификации показан характерный вид АЧХ каждого из перечисленных типов усилителей.
Помимо рассмотренных показателей и характеристик усилителей в
некоторых случаях может потребоваться и знание некоторых других,
например, амплитудно-фазовой характеристики (АФХ), представляющей собой зависимость модуля коэффициента передачи от фазового
K()
K()

а
K()
б

K()


в
г
K()

д
Рис. 3.10. Качественный вид АЧХ усилителей различного типа:
а – УПТ; б – УННЧ; в – ШУ; г – ПУ; д – ИУ
71
сдвига, построенную в полярной системе координат; переходной характеристики, являющейся зависимостью от времени напряжения на
выходе усилителя при подаче на его вход мгновенного скачка напряжения; коэффициента шума, характеризующего уровень шумов усилителя и т. д.
Рассмотренные основные показатели и характеристики усилителей
зависят как от типов активных элементов и способа их включения в
усилительном каскаде, так и от схемотехники конкретных каскадов и
их числа.
3.3. Биполярный транзистор как
усилительный элемент
В качестве усилительных элементов (УЭ) в электронных усилителях чаще всего используются биполярные и полевые транзисторы, а в
ряде специальных случаев – электронные лампы. Рассмотрение простейших усилителей стоит начать с усилительного каскада на биполярном транзисторе. При этом под усилительным каскадом понимается минимальная часть усилителя, которая способна выполнять усилительные функции.
Биполярный транзистор представляет собой полупроводниковую
структуру, разделенную на три области с поочередно меняющимися
типами проводимости. Схематически это показано на рис. 3.11. Контактные слои, расположенные в структуре слева и справа, называются
соответственно эмиттером (Э) и коллектором (К) прибора, а слой
Э
p
n
p
К
Б
а
Э
n
p
n
К
Б
б
p
p
К
Э
Еб
n Б
Ек
+
+
n
Э
R
Еб
n
К
p Б
Ек
+
R
+
г
в
Рис. 3.11. Схематическое изображение структур биполярного транзистора и его схемное включение в ативном режиме: а – структура
типа р-n-р; б – структура типа n-p-n; в – включение в схему транзистора типа р-n-р; г – включение в схему транзистора типа р-n-р
72
между ними – его базой (Б). Если область с электронной проводимостью находится между областями с дырочной проводимостью, то такой транзистор называется транзистором типа р-n-р (рис. 3.11 а). Если
область с дырочной проводимостью находится между областями с
электронной проводимостью, то такой транзистор является транзистором типа n-p-n (рис. 3.11 б).
В биполярных транзисторах перенос заряда осуществляют два типа
носителей – электроны и дырки, поэтому такие транзисторы и называются биполярными. Работа p-n-р транзистора аналогична работе
n-р-n транзистора, и при этом изменяется лишь полярность питающих
напряжений (рис. 3.11 в, г).
Возможны четыре режима работы транзистора.
1. Активный или усилительный режим, когда эмиттерный переход
смещен в прямом направлении, а коллекторный – в обратном.
2. Режим запирания или отсечки, когда оба перехода смещены в обратном направлении.
3. Режим насыщения, когда оба перехода смещены в прямом
направлении.
4. Инверсный режим, когда эмиттерный переход смещен в обратном направлении, а коллекторный – в прямом.
Ниже рассмотрим активный режим работы транзистора. Отметим
также, что в режимах запирания и насыщения транзисторы работают,
как правило, в импульсных и цифровых схемах, а в инверсном включении – в схемах двунаправленных переключателей, в которых используются симметричные транзисторы.
Так как транзистор имеет три электрода – эмиттер, базу и коллектор, то возможны различные схемы его включения. Но при этом в
усилительном режиме для любой схемы включения необходимо, чтобы базовый электрод был входным, а коллекторный – выходным. Поэтому возможны только три схемы включения транзистора как усилительного элемента: с общей базой (ОБ), с общим эмиттером (ОЭ) и с
общим коллектором (ОК). Для транзистора типа p-n-p эти схемы показаны на рис. 3.12 .
В соответствии с законом Кирхгофа для токов в цепи транзистора
можно записать
(3.18)
Iэ=Iк+Iб.
Направления протекающих при этом через электроды эмиттера, базы
и коллектора токов Iэ, Iб и Iк представлены на рис. 3.12.
73
Э Iэ
Iк
К
Б
Iб
Iк
Iб
Б
б
Iэ
Э
К
Э
Iэ
Б
Iб
Iк
К
б
а
в
Рис. 3.12. Схемы включения транзистора: а – с общей базой; б – с общим
эмиттером; в – с общим коллектором
Важнейшим параметром биполярного транзистора, включенного по
схеме с ОБ, является статический коэффициент передачи эмиттерного тока , который характеризует усилительные свойства транзистора
и вводится следующим образом. Для активной области работы прибора в схеме с ОБ справедливо равенство
(3.19)
Iк=Iэ +Iкб0,
где Iкб0 – обратный ток коллекторного перехода, обусловленный неосновными носителями заряда и который измеряется при обрыве эмиттера, т. е. когда Iэ=0. Из равенства (3.19) следует, что коэффициент
I  I кб 0
.
 к
(3.20)
Iэ
Но поскольку Iкб0<<Iк, то

Iк
.
Iэ
(3.21)
Обычно  находится в пределах 0,95  0,99.
Аналогично для схемы включения с ОЭ для тока коллектора справедливо равенство
(3.22)
Iк=Iб+Iкэ0,
где  – статический коэффициент передачи тока базы, а Iкэ0=(1+)Iкб0 –
обратный ток коллекторного перехода в схеме с ОЭ при обрыве базы,
т. е. когда Iб=0. Тогда из (3.22) следует, что
I  I кб 0
.
 к
(3.23)
I б  I кб 0
Но так как Iк>>Iкб0 и Iб>> Iкб0, то
74

Iк
.
Iб
(3.24)
Характерные значения  лежат в пределах 30  100.
При анализе работы биполярного транзистора в диапазоне малых
сигналов на переменном токе в соответствии с выражениями (3.21) и
(3.24) для статических коэффициентов  и  вводят также соответствующие дифференциальные параметры – дифференциальный коэффициент передачи тока эмиттера
д 
dIк
dI э
(3.25)
U кб  const
и дифференциальный коэффициент передачи тока базы
д 
dIк
dIб
.
(3.26)
U кэ  const
В большинстве практически важных случаев можно считать, что д
и д.
Параметр  может быть выражен через параметр  с помощью
формулы

.

(3.27)
1 
Зависимость коэффициентов передачи по току от частоты. Частотные свойства транзистора. Коэффициенты передачи транзистора, включенного как по схеме с ОБ, так и по схеме с ОЭ, строго говоря, можно считать постоянными только в определенной полосе частот, и при увеличении последней эти коэффициенты начинают
уменьшаться. Кроме того, с повышением частоты они становятся
комплексными величинами, в связи с чем вводят ряд количественных
параметров.
Важнейшими из них являются предельная частота передачи тока
эмиттера fh21б или f для схемы с ОБ и предельная частота передачи
тока базы fh21э или f для схемы с ОЭ. По определению под предельной
частотой транзистора понимают такое ее значение, при котором модули коэффициентов  и  уменьшаются в 2 раз, другими словами
на 3 дБ по отношению к их значениям на средней частоте. При этом
имеет место приближенное соотношение
(3.28)
fh21бh21эfh21э,
75

0

0/2
f
f
Рис. 3.13. Частотная зависимость коэффициента  в схеме с ОБ
и графическое определение предельной частоты передачи тока
эмиттера f
указывающее на лучшие частотные свойства транзистора, включенного по схеме с ОБ. В формуле (3.28) h21   .
Граничной частотой коэффициента передачи тока базы транзистора, включенного по схеме с ОЭ fгрfТ, принято считать такое ее значение, при котором коэффициент  становится равным единице. Между
параметрами fh21б и fгр существует связь
(3.29)
fh21б1,2fгр.
На рис. 3.13 приведена характерная зависимость коэффициента передачи транзистора по току  для схемы с ОБ от частоты усиливаемого сигнала.
3.4. Биполярный транзистор как четырехполюсник
Параметры транзистора в представлении его как линейного четырехполюсника (рис. 3.14) являются коэффициентами, связывающими
токи и напряжения на входе и выходе. В п. 2.10 отмечалось, что при
рассмотрении и анализе работы транзисторов и радиоэлектронных
схем на их основе, удобнее всего пользоваться H -параметрами. А с
Rг
I2
I1
3
1
Ег
U2
U1
Zн
4
2
Рис. 3.14. Усилительный элемент в представлении его в
виде четырехполюсника
76
учетом того, что в полосе рабочего диапазона частот УННЧ транзистор практически не вносит фазового сдвига между током и напряжением, комплексные H -параметры можно заменить их вещественными
аналогами, т. е. h-параметрами. Ниже рассмотрим примеры использования h-параметров для расчета коэффициентов усиления по напряжению Ku, току Ki и мощности Kp, а также входного и выходного сопротивлений Rвх и Rвых усилительного каскада, представленного в виде четырехполюсника.
Для решения данной задачи используем систему уравнений четырехполюсника в h-параметрах, которую запишем в виде
U1  h11 I1  h12U 2 ,
(3.30)
I 2  h21 I1  h22U 2 ,
где U1 и I1, U2 и I2 – малые переменные: напряжение и ток на входе и
выходе усилительного каскада соответственно.
Согласно схеме рис. 3.15 можно записать
U1  Eг  I1Rг ,
(3.31)
(3.32)
U 2   I 2 Rн .
По определению:
U
1. K u  2 . Исключим из уравнений системы (3.30) ток I2, для чего
U1
умножим первое уравнение системы на коэффициент, равный –h21, а
второе – на h11 и сложим их почленно. В результате этого получим
h11 I 2  h21U1  h11 h22U 2  h12 h21U 2  hU 2 . Но из уравнения (3.32) слеU
U
дует, что I 2   2 , тогда  h11 2  h21U1  hU 2 или  h11U 2 
Rн
Rн
 h21 RнU1  hRнU 2 . Откуда получим, что
I2
I1
>
>
Eг
U1
h12U2
<<
h11
Rг
1
h22
U2
Rн
Iг=h21I1
Рис. 3.15. Эквивалентная схема усилительного каскада, представленного в виде четырехполюсника
77
Ku 
U2
h 21 Rн
.

U1
h11  Rн h
(3.33)
I2
. Подставим напряжение U2 из уравнения (3.32) во второе
I1
уравнение системы (3.30). В результате получим I 2  h21 I1  h22 Rн I 2 ,
откуда
I
h21
.
Ki  2 
(3.34)
I1 1  h22 Rн
2. K i 
3. K p  K i K u и тогда K p 
h21 
h 21 Rн 
 
.
1  h22 Rн  h11  Rн h 
U1
. Подставим в первое уравнение системы (3.30) значение
I1
напряжения U2 из уравнения (3.32). При этом получим
h21
U1  h11 I1  h12 Rн I 2 . Из выражения (3.34) для I2 имеем I 2 
I1 .
1  h22 Rн
Тогда для напряжения U1 можно записать U1  h11 I1 
h21
 h12 Rн
I1 , откуда
1  h22 Rн
4. Rвх 
Rвх 
U1
h h R
h  hRн
.
 h11  12 21 н  11
I1
1  h22 Rн
1  h22 Rн
(3.35)
U2
. Сопротивление Rвых находится при коротком замыкаI2
нии по входу для переменного напряжения с генератора, т. е. при
условии, что U1=0 и Eг=0. В этом случае система (3.30) перепишется в
виде
0  Rг  h11 I1  h12U 2 ,
5. Rвых 
I 2  h21 I1  h22U 2 .
Умножим ее первое уравнение на коэффициент, равный (– h21 ), а второе – на Rг  h11  и затем сложим полученные уравнения почленно.
В результате будем иметь I 2 Rг  h11   h22 Rг  h11 U 2  h21 h12U 2 и
тогда
78
Rвых 
U2
Rг  h11
Rг  h11
.


I 2 h22 Rг  h11   h12 h21 h22 Rг  h
(3.36)
Помимо формализованных моделей или эквивалентных схем транзисторов на практике при расчете различных электронных устройств
широко применяются физические модели, построенные с использованием конкретных электрофизических параметров и электрических характеристик усилительных элементов.
Рассмотрим Т-образные физические эквивалентные схемы биполярного транзистора, включенного по схеме с ОБ и ОЭ (рис. 3.16).
Эти эквивалентные схемы справедливы для малых приращений токов
и напряжений усилительного элемента, т. е. тогда, когда можно пользоваться линейными участками его входных и выходных ВАХ, и поэтому они получили также название малосигнальных эквивалентных
схем или моделей.
На схеме (рис. 3.16 а) сопротивление rэ представляет собой дифференциальное сопротивление эмиттерного перехода. Этот переход
включен в прямом направлении, и его сопротивление по определению
равно
rэ 
dU эб
dI э U
.
(3.37)
кб  const
Величина сопротивления rэ мала и может быть оценена по следующей приближенной формуле:

rэ  T ,
(3.38)
Iэ
Iэ
rк
rэ
Iк
Э
>>
Iэ
К Б
rб
Сэ
Iб
Iб
r*к
rб
>>
Iб
Iк
rэ
Ск
Iэ
Б
Э
С*к
б
а
Рис. 3.16. Эквивалентные физические схемы биполярного транзистора:
а – включенного по схеме с ОБ; б – включенного по схеме с ОЭ
79
К
kT
– температурный потенциал (k – постоянная Больцмана,
e
e – заряд электрона, Т – термодинамическая температура), Iэ – постоянная составляющая тока эмиттера. Таким образом, значение сопротивления rэ в диапазоне рабочих температур прибора находится в пределах от нескольких единиц до нескольких десятков Ом. По этой причине емкость смещенного в прямом направлении эмиттерного перехода Сэ при включении усилительного элемента по схеме с ОБ можно
не учитывать, поскольку она шунтируется на низких частотах малым
сопротивлением rэ.
Сопротивление, обозначенное на рис. 3.16 а как rк, является дифференциальным сопротивлением коллекторного перехода, который
смещен в обратном направлении. Это сопротивление учитывает изменение коллекторного тока при изменении напряжения Uкб и по определению равно
где Т 
rк 
dU кб
dIк
.
(3.39)
I э  const
Характерные значения сопротивления rк лежат в пределах от 0,5 до
1 МОм, что значительно больше, нежели сопротивление rэ.
Емкость Ск – это емкость обратно смещенного коллекторного перехода. Отметим, что она, как и емкость Сэ, складывается из барьерной и диффузионной емкостей соответствующих переходов, а именно
коллекторного и эмиттерного. Но в отличие от Сэ, Ск шунтирует достаточно большое сопротивление rк, и поэтому ее влияние необходимо учитывать для частот, начиная с нескольких кГц и выше. В принципе же, во многих случаях при работе усилительного элемента по
схеме с ОБ на НЧ и СЧ до нескольких кГц емкости Сэ и Ск можно не
учитывать (поэтому на эквивалентной схеме рис. 3.16 а они обозначены пунктиром).
Сопротивление rб представляет собой объемное омическое сопротивление базы с характерным значением rб=100500 Ом и достаточно
часто можно считать, что rб>>rэ.
Наконец, генератор тока Iэ в коллекторной цепи учитывает прямую передачу тока эмиттера Iэ на выход четырехполюсника с коэффициентом .
На рис. 3.16 б показана физическая схема замещения биполярного
транзистора, включенного по схеме с ОЭ. Здесь сопротивления rэ и rб
80
по смыслу те же, что и для схемы с ОБ. Сопротивление rк* связано с
сопротивлением rк следующей формулой:
r
rк*  к ,
(3.40)
1 
и таким образом с его помощью учитывается изменение тока коллектора Iк при изменении напряжения Uкб. Очевидно также, что сопротивление rк* намного (не менее, чем на порядок) меньше сопротивления rк. Емкость С к* в этой схеме выражается через емкость Ск, а также
через коэффициент (1+) и равна
Ск*  Ск 1    .
(3.41)
Смысл формул (3.40) и (3.41), описывающих уменьшение активного
и реактивного сопротивления коллекторного перехода, становится понятным, если учесть, что при переходе от схемы с ОБ к схеме с ОЭ
входной ток, который является теперь базовым, уменьшается в (1+)
раз. При этом во входную цепь эквивалентной схемы рис. 3.16 б включается генератор тока Iб. Еще одной особенностью данной физической
модели является отсутствие в ней емкости Сэ, шунтирующим действием которой на нижних и средних частотах можно пренебречь по сравнению с шунтирующим действием гораздо большей емкости С к* .
В заключение отметим также, что эквивалентные схемы рис. 3.16
не содержат генераторов напряжения положительной обратной связи,
возникающей из-за эффекта модуляции ширины базы, поскольку значения коэффициентов обратных связей чрезвычайно малы.
Между введенными здесь физическими параметрами и h-параметрами транзистора существуют вполне определенные связывающие их
соотношения, которые достаточно подробно рассмотрены в соответствующей литературе. Приведем пример такой связи параметров для
схемы с ОБ: rэ=h11б(1–h21б)h12б/h22; rб=h12б/h22б; rк=1/h22б; =h22б.
3.5. Статические характеристики транзистора
и определение по ним h-параметров
При анализе работы усилительных каскадов широко используются
так называемые входные и выходные статические характеристики,
снятые при отсутствии активного сопротивления в цепях усилительных элементов. Для схемы включения усилительного элемента с ОЭ
81
вид этих характеристик приведен на рис. 3.17 (входные) и рис. 3.18
(выходные).
Для режима малых сигналов h-параметры транзистора можно определить по его статическим характеристикам, задаваясь соответствующими приращениями токов и напряжений в окрестности фиксированной (рабочей) точки. На характеристиках эта точка обычно обозначается как 0 или П. Формулы для определения h-параметров транзистора, включенного по схеме с ОЭ, в данном случае имеют вид:
Iб
Iб
Uкэ
Iб
Uкэ
Uкэ
П
Uкэ=Uкэ–Uкэ
П
Iбп
Uбэ
Uбэ
Uкэ
Uбэ
Uбэ
а
б
Рис. 3.17. Входные статические характеристики транзистора, включенного по схеме с ОЭ для определения h-параметров: а – для h11э; б – для h12э
Iк
Iк
Iб8
Iб7
Iб8
Iб7
Iб6
Iб6
Iб5
Iб5
Iб4
Iб4
Iб3
Iк
П
Uкэп
Iб3
Iб=Iб3-Iб1 Iб2
Iб2=Iбп
Iк
Iб1
Uкэ
П
Uкэ
Iб1
Uкэ
а
б
Рис. 3.18. Выходные статические характеристики транзистора для определения h-параметров: а – для h21э; б – для h22э
82