Цель работы: изучение собственных колебаний струны
реклама

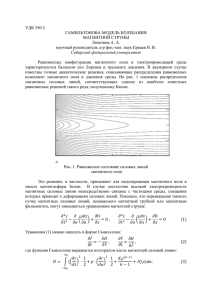
Цель работы: изучение собственных колебаний струны. Задача: определение характеристик собственных колебаний. Техника безопасности: перед началом работы с установкой необходимо убедиться, что она заземлена. Установка питается напряжением 220 В, поэтому токоведущие части должны быть закрыты. Приборы и принадлежности: панель со струной и постоянным магнитом, электронный блок. Общие сведения Хорошо известно, что если в среде, все частицы которой связаны между собой, возбудить в какой-либо точке колебания, то эти колебания будут распространяться по среде в виде волны. Возьмем, например, струну и одному из ее участков придадим колебательное движение, в этом случае колебание начнет распространяться в обе стороны от этого участка вдоль струны: по струне побегут волны. Если колебания частиц перпендикулярны к направлению распространения колебаний (т.е. частицы колеблются, например, вдоль оси y , а колебания распространяются вдоль оси x ), то бегущие волны, распространяющиеся вдоль и против оси x , называются поперечными и, соответственно, описываются уравнениями y1 A cos( 2t kx) и y 2 A cos( 2t kx ) . Здесь ось x считается направленной вдоль струны, y1 и y 2 обозначают смещения частиц струны в процессе колебаний, A - амплитуда колебаний, 2 2 – волновое число, – частота колебаний, – соответствуюk щая длина волны. Скорость распространения поперечной бегущей волны дается выражением F , S 3 (1) где F определяет силу натяжения, – плотность материала, а S – площадь поперечного сечения струны. Если оба конца струны с длиной l закреплены (как в настоящей лабораторной работе), то, отражаясь от них, бегущие волны распространяются навстречу друг другу и интерферируют. Колебания частиц струны при этом оказываются геометрической суммой колебаний (т.е. y y1 y 2 ), которые совершали бы частицы при распространении каждой из волн в отдельности. Это приводит к тому, что в одних точках струны колебания усиливают, а в других – ослабляют друг друга. В результате, если частота колебания совпадает с одной из собственных частот струны (см. далее выражение (2)), то в последней устанавливается стоячая волна y 2 A coskx cos2t с амплитудой | 2 Acoskx | , зависящей от x . Точки с наибольшей амплитудой колебаний называются пучностями стоячей волны. Точки с нулевой амплитудой колебаний называются узлами стоячей волны. Точки струны, находящиеся в узлах стоячей волны, колебаний не совершают. На рис.1 изображены несколько различных типов колебаний в струне. y n=1 n=2 n=3 0 x y 0 x y 0 x Рис.1 При n 1 наблюдаются одна пучность и два узла. При n 2 наблюдаются две пучности и три узла. И т.д. Расстояния между соседними пучностями и расстояния между соседними узлами равны половине длины волны , т.е. 2 “полуволне”. Поэтому длина струны l при n 1 равна 1 , при n 2 равна 2 4 2 и т.д. В общем случае можно сказать, что при выполнении условия 2 l n n / 2 (рис.1) в струне возникают стоячие волны с частотами 2 n n , n 2l (2) где n – произвольное целое число (n = 1, 2, 3, …). Как видно из (2), частоты n определяются только геометрией (длина l) и свойствами материала. Поэтому их часто называют собственными частотами такой струны, а соответствующие стоячие волны – собственными (или нормальными) колебаниями. Из соотношения (2) также следует, что такая струна может колебаться не с одной частотой, а с целым спектром частот. В общем случае в колебаниях струны одновременно присутствуют все n собственных колебаний. Иными словами, любое сложное колебание струны может быть представлено как наложение (суперпозиция) многих собственных колебаний, отличающихся не только величинами своих частот, но и величинами своих амплитуд для отдельных точек струны. Распределение величины смещения отдельных точек струны относительно их положения равновесия при собственных колебаниях для различных значений n как раз и изображено на рис.1. Методика эксперимента и экспериментальная установка Установка выполнена в настольном исполнении и состоит из объекта исследования и измерительного устройства. Объект исследования состоит из основания, на котором закреплены постоянные магниты, между полюсами которых натянута струна, и механизма натяжения струны. Сила натяжения струны измеряется при помощи указателя, перемещающегося по шкале при изменении натяжения струны. Измерение длины стоячих волн, образующихся на струне, производится по миллиметровой шкале, нанесенной на прозрачный кожух, закрывающий переднюю стенку объекта исследования. Для улучшения видимости струны, за ней размещена лампа подсветки. В состав измерительного устройства входят генератор синусоидальных колебаний с усилителем мощности для возбуждения колебаний струны и частотомер для измерения частоты генератора. На передней панели размещены следующие органы управления: - ручки ЧАСТОТА "ГРУБО" и ЧАСТОТА "ТОЧНО" – для установки частоты генератора; 5 - ручка УРОВЕНЬ – для установки необходимой амплитуды выходного напряжения генератора (амплитуда колебаний струны); - цифровое табло частотомера. Примечание: Запрещается задавать натяжение струны более 0,6 Н. Перед включением установки в сеть сетевой выключатель измерительного устройства должен находиться в положение "Выкл", ручки регулировки должны быть выведены в крайнее левое положение. Струна с текущим по ней переменным током I находится в поле постоянного магнита. Струна медная. Плотность меди = 8,9 103 кг/м3. Диаметр струны d = 0,15 мм. Магнитное поле ( В ) действует на проводник с током с силой (по закону Ампера) d F м I [ d l , В] , пропорциональной току. (Здесь dl – дифференциально малый элемент дли ны струны). Под действием силы F м струна начинает колебаться на участке действия магнитного поля. Распространяясь по струне в обе стороны от этого участка, колебания порождают в ней две бегущих волны, которые, отражаясь от закрепленных концов струны, формируют в результате интерференции стоячую волну. Порядок выполнения работы 1. Подключите установку к сети 220 В. Нажмите кнопку СЕТЬ устройства питания лампы. После этого должна загореться лампа подсветки струны. Нажмите кнопку СЕТЬ измерительного устройства. После этого должно загореться цифровое табло устройства. 2. Дайте установке прогреться в течение 3-5 мин. 3. Установите натяжение струны 0,2 Н. Ручку УРОВЕНЬ установите в среднее положение. 4. Изменяя при помощи ручек ГРУБО и ПЛАВНО частоту в диапазоне 2050 Гц, получите одну ( n 1) хорошо различимую полуволну на всей длине струны (см. рис.1). 5. Увеличивая частоту кратно полученной, получить различимые полуволны по струне, соответствующие n = 1, 2, 3 4. Зарисовать полученные картинки. Результаты занести в таблицу. 6. Повторить действия, указанные в п.п. 3 –5, для значений силы натяжения струны 0,3 Н; 0,4 Н. 6 7. Вычислить скорость распространения волн в струне по формуле (2) для значения силы 0,2 Н при n = 1, 2, 3 4 и по этим данным определить среднее значение скорости (назовем это значение экспериментальным) для данного значения силы. Проделать это для каждого значения силы. 8. Вычислить скорость распространения волн в струне по формуле (1) для каждого значения силы (назовем это значение скорости теоретическим). Найти (в процентах) отклонение экспериментального значения скорости распространения волн в среде от теоретического для каждого значения силы по формуле: э т 100 % . т Таблица Результаты измерений Количество полуволн n 1 2 3 4 F1 = 0,2 H , м/с ν, Гц F2 = 0,3 H , м/с ν, Гц F3 = 0,4 H , м/с ν, Гц Контрольные вопросы 1. Пояснить физический механизм распространения колебаний в струне. 2. Получить выражение (2). 3. Пояснить механизм возникновения стоячих волн в струне. Получить уравнение этих волн. 4. Возникнут ли в струне стоячие волны, если частота переменного тока не равна ни одной из собственных частот? 5. Возникнут ли в струне стоячие волны, если ток в ней будет отсутствовать, а вместо постоянного магнита будет использован электромагнит? Библиографический список 1. Савельев И.В. Курс общей физики: В 3т., т.1 / И.В.Савельев. – С.-Пб., 2008. - 432с. 2. Трофимова Т.И. Курс физики / Т.И.Трофимова.- С.-Пб., 2008. - 560с. 7