18 2 3 9

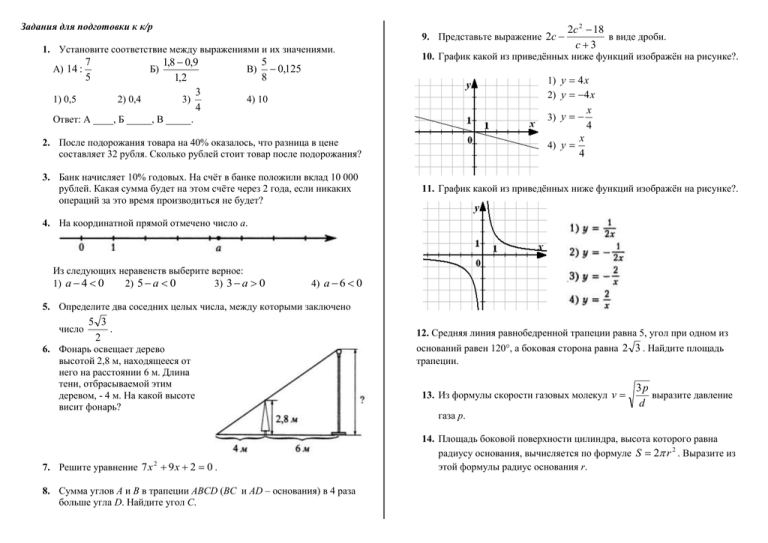
Задания для подготовки к к/р
9. Представьте выражение 2c 
1. Установите соответствие между выражениями и их значениями.
А) 14 :
7
5
1) 0,5
Б)
2) 0,4
1,8  0,9
1,2
3
3)
4
В)
5
 0,125
8
2c 2  18
в виде дроби.
c3
10. График какой из приведённых ниже функций изображён на рисунке?.
1) y  4 x
2) y  4 x
4) 10
3) y  
Ответ: А ____, Б _____, В _____.
2. После подорожания товара на 40% оказалось, что разница в цене
составляет 32 рубля. Сколько рублей стоит товар после подорожания?
3. Банк начисляет 10% годовых. На счёт в банке положили вклад 10 000
рублей. Какая сумма будет на этом счёте через 2 года, если никаких
операций за это время производиться не будет?
4) y 
x
4
x
4
11. График какой из приведённых ниже функций изображён на рисунке?.
4. На координатной прямой отмечено число а.
Из следующих неравенств выберите верное:
1) a  4  0
2) 5  a  0
3) 3  a  0
4) a  6  0
5. Определите два соседних целых числа, между которыми заключено
число
5 3
.
2
6. Фонарь освещает дерево
высотой 2,8 м, находящееся от
него на расстоянии 6 м. Длина
тени, отбрасываемой этим
деревом, - 4 м. На какой высоте
висит фонарь?
7. Решите уравнение 7 х 2  9 х  2  0 .
8. Сумма углов А и В в трапеции ABCD (ВС и AD – основания) в 4 раза
больше угла D. Найдите угол С.
12. Средняя линия равнобедренной трапеции равна 5, угол при одном из
оснований равен 120°, а боковая сторона равна 2 3 . Найдите площадь
трапеции.
13. Из формулы скорости газовых молекул v 
3p
выразите давление
d
газа р.
14. Площадь боковой поверхности цилиндра, высота которого равна
радиусу основания, вычисляется по формуле S  2 r 2 . Выразите из
этой формулы радиус основания r.
15. Вычислите координаты
точки А.
16. Решите неравенство 49 x 2  4 .
17. Решите уравнение x 6  16 x 4  2 x 2  32  0 .
18. Точки M, N, L, P – середины сторон AB, BC, CD, AD трапеции
соответственно. Докажите, что MNLP – параллелограмм.
19. Решите неравенство
1 x
 1 .
x3
20. При каких а число 3 заключено между корнями уравнения
x 2  2ax  a 2  1  0 ?
21. Моторная лодка, проехав по течению реки 6 км, вернулась обратно,
затратив на весь путь 35 минут. Найдите собственную скорость лодки,
если известно, что 18 км по течению реки она проплывает на 15 минут
быстрее, чем против течения.
6
4
2
22. x  14 x  56 x  64  0 .
Для каждого утверждения определите, верное он или нет.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
Через любую точку плоскости можно провести прямую.
Через любые две различные точки плоскости можно провести прямую.
Через любые три различные точки плоскости можно провести прямую.
Любые две различные прямые проходят через одну общую точку.
Через точку, не лежащую на данной прямой можно провести не более
одной прямой, параллельной данной.
Сумма вертикальных углов равна 180°.
Сумма двух смежных углов равна 180°.
Если угол равен 54°, то вертикальный с ним угол равен 34°.
Если угол равен 72°, то смежный с ним угол равен 18°.
Если две параллельные прямые пересечены третьей прямой, то
соответственные углы равны.
Если две параллельные прямые пересечены третьей прямой, то сумма
внутренних односторонних углов равна 90°.
Если две перпендикулярные прямые пересечены третьей прямой, то
сумма внутренних односторонних углов равна 180°.
Если при пересечении двух прямых третьей внутренние накрест
лежащие углы равны, то прямые параллельны.
Если при пересечении двух прямых третьей соответственные углы
равны, то прямые перпендикулярны.
Если при пересечении двух прямых третьей внутренние односторонние
углы равны 90°, то прямые параллельны.
Если две прямые перпендикулярны третьей прямой, то эти две прямые
перпендикулярны.
Внешний угол треугольника равен сумме двух его внутренних углов.
Сумма углов прямоугольного треугольника равна 90°.
Сумма углов равнобедренного треугольника равна 180°.
Если два угла треугольника равны 36° и 64°, то третий равен 100°.
Если один из углов равнобедренного треугольника равен 30°, то другой
его угол равен 120°.
Если в треугольнике АВС углы А и В равны соответственно 40° и 70°,
то внешний угол этого треугольника при вершине С равен 70°.
Если две стороны и угол одного треугольника равны двум сторонам и
углу другого треугольника, то такие треугольники равны.
Если три угла одного треугольника соответственно равны трём углам
другого треугольника, то такие треугольники равны.
Если три стороны одного треугольника равны трём сторонам другого
треугольника, то такие треугольники подобны.
Если катет и острый угол одного прямоугольного треугольника
соответственно равны катету и углу другого прямоугольного
треугольника, то такие треугольники равны.
27. Если острый угол одного прямоугольного треугольника равен углу
другого прямоугольного треугольника, тотакие треугольники равны.
28. Любые два равносторонних треугольника подобны.
29. Любые два равнобедренных треугольника подобны.
30. Любые два прямоугольных треугольника подобны.
31. Любые два равнобедренных прямоугольных треугольника подобны.
32. Каждая сторона треугольника равна сумме двух других сторон.
33. Каждая сторона треугольника меньше разности двух других сторон.
34. Треугольник со сторонами 3, 4, 5существует.
35. В треугольнике против меньшей стороны лежит меньший угол.
36. В треугольнике против большего угла лежит меньшая сторона.
37. В треугольнике АВС, для которого А  45, В  55, С  80
сторона АВ – наибольшая.
38. В треугольнике АВС, для которого АВ = 6, ВС = 7, АС = 8, угол С –
наибольший.
39. Сумма углов выпуклого четырёхугольникаравна 180°.
40. Сумма углов вписанного в окружность четырёхугольника равна 360°.
41. Через любые две различные точки плоскости можно провести не более
одной окружности.
42. Через любые различные три точки плоскости можно провести не менее
одной окружности.
43. Если расстояние от центра окружности до прямой меньше радиуса
окружности, то эта прямая и окружность пересекаются.
44. Если расстояние от центра окружности до прямой больше диаметра
окружности, то эти прямая и окружность не имеют общих точек.
45. Если расстояние между центрами двух окружностей меньше суммы их
радиусов, то эти окружности пересекаются.
46. Если радиус окружности равен 7, а расстояние от центра окружности до
прямой равно 5, то эти прямая и окружность не имеют общих точек.
47. Если расстояние между центрами двух окружностей больше суммы их
радиусов, то эти окружности не пересекаются.
48. Если радиусы двух окружностей равны 3 и 5, а расстояние между их
центрами равно 4, то эти окружности пересекаются.
49. Если радиусы двух окружностей равны 3 и 5, а расстояние между их
центрами равно 1, то эти окружности не имеют общих точек.
50. Длина окружности радиуса R равна  R .
51. Площадь круга радиуса R равна 2R .
52. Вписанные углы, опирающиеся на одну и ту же хорду, равны.
53. Если вписанный угол равен 24°, то дуга окружности, на которую он
опирается, равна 48°.
54. Если дуга окружности составляет 73°, то вписанный угол ,
опирающийся на эту дугу, равен 73°.
55. Центром окружности, описанной около треугольника является точка
пересечения его биссектрис.
56. Центром окружности, вписанной в треугольник, является точка
пересечения серединных перпендикуляров к его сторонам.
57. Центр окружности, описанной около прямоугольного треугольника,
находится на стороне этого треугольника.
58. Центром окружности, вписанной в правильный треугольник, является
точка пересечения его медиан.
59. Если сумма двух противоположных углов прямоугольника равна 180°,
около этого прямоугольника можно описать окружность.
60. Около любой трапеции можно описать окружность.
61. Если один из углов вписанного в окружность четырёхугольника равен
63°, то противоположный ему угол равен 117°.
62. В любой параллелограмм можно вписать окружность.
63. Если в четырёхугольник можно вписать окружность, сумма длин его
противоположных сторон равна 24, длина третьей стороны равна 14, то
длина оставшейся стороны равна 10.
64. Противоположные углы параллелограмма равны.
65. Если один из углов, прилежащих к стороне параллелограмма, равен 50°,
то другой угол, прилежащий к той же стороне, равен 40°.
66. Если в четырёхугольнике две стороны параллельны, то этот
яетырёхугольник параллелограмм.
67. Если в четырёхугольнике два угла прямые, то этот четырёхугольник –
параллелограмм.
68. Диагонали прямоугольника перпендикулярны.
69. Если в параллелограмме диагонали равны, то этот параллелограмм –
прямоугольник.
70. Если в четырёхугольнике диагонали равны и перпендикулярны, то этот
четырёхугольник – квадрат.
71. Треугольник АВС, у которого АВ = 20, ВС = 21, АС = 29, является
прямоугольным.
72. Площадь прямоугольника равна произведению двух его сторон.
73. Площадь треугольника равна произведению его стороны на высоту,
проведённую к этой стороне.
74. Площадь прямоугольного треугольника равна произведению его катета
на гипотенузу.
75. Площадь трапеции равна произведению суммы оснований на вцысоту.
76. Площадь параллелограмма равна произведению его стороны на высоту,
проведённую к этой стороне.
77. Отношение площадей подобных фигур равно квадрату коэффициента
подобия.