Занятие 19. Решение геометрических задач.

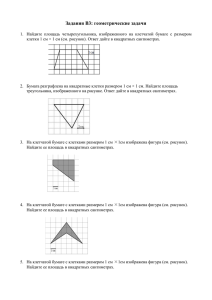
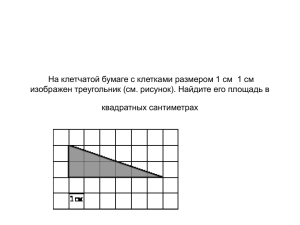
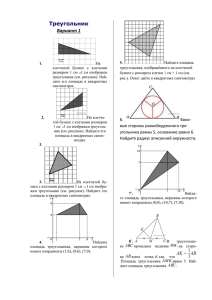
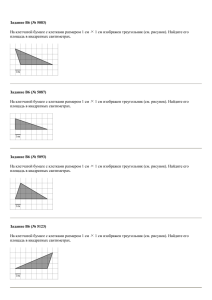
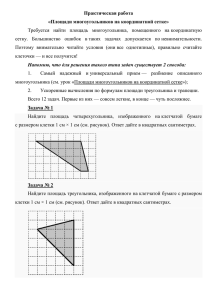
Занятие 19. Решение геометрических задач.
Задача 1.Найдите площадь четырехугольника, вершины которого имеют координаты
(8;0),(10;4),(2;8),(0;4).
Решение.
Диагональ четырехугольника разбивает его на два
h a
равных треугольника, высоту и основание которых
можно определить: h=4, a=10, следовательно можно
вычислить площадь треугольника, а затем и
h
1
четырехугольника: S   ah,
2
1
S=  10  4  20 , S=2.20=40
2
Ответ: 40
Задача 2. На клетчатой бумаге с клетками 1см  1 см
изображен треугольник. Найдите его площадь в квадратных см.
1
Решение. S   ah,
2
1
а=9, h=3. S=  9  3  13,5
2
h
Ответ: 13,5
a
Задача 3. . На клетчатой бумаге с клетками
1см  1 см изображена фигура. Найдите ее
площадь в квадратных сантиметрах. В ответе
s
запишите .

1 1
3
3
Решение. Sф=(  ) S êðóãà = R 2 =   2 2  1,5
4 8
8
8
S:   1,5
Ответ:1,5
Задача 4. . На клетчатой бумаге с клетками 1см  1 см изображен параллелограмм.
Найдите его площадь в квадратных
сантиметрах.
a
Решение. S=a.h, a=3, h=4, S=3.4=12
Ответ: 12
h
a
b
Задача 5. . На клетчатой бумаге с клетками
1см  1 см изображена трапеция.
Найдите ее площадь в квадратных сантиметрах.
Решение.
àâ
49
 h, S=
 5  32,5
S=
2
2
Ответ:32,5
h
a
Задача 6. .Найдите площадь ромба, если его высота
равна 2, а острый угол равен 30о.
Решение.
Высота ромба является в полученном прямоугольном треугольнике катетом, лежащим
против угла в 30о, следовательно, сторона ромба, являющаяся в треугольнике
гипотенузой, равна 4, а, значит, площадь ромба S=4.2=8
Ответ: 8