Задание по вариантам

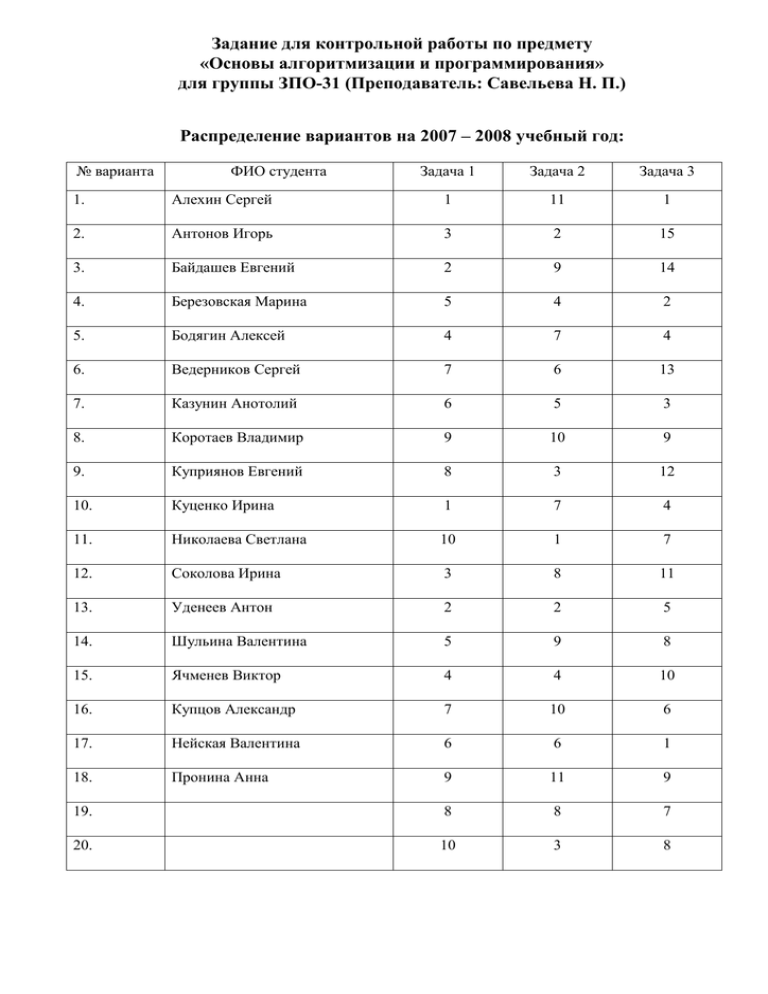
Задание для контрольной работы по предмету
«Основы алгоритмизации и программирования»
для группы ЗПО-31 (Преподаватель: Савельева Н. П.)
Распределение вариантов на 2007 – 2008 учебный год:
№ варианта
ФИО студента
Задача 1
Задача 2
Задача 3
1.
Алехин Сергей
1
11
1
2.
Антонов Игорь
3
2
15
3.
Байдашев Евгений
2
9
14
4.
Березовская Марина
5
4
2
5.
Бодягин Алексей
4
7
4
6.
Ведерников Сергей
7
6
13
7.
Казунин Анотолий
6
5
3
8.
Коротаев Владимир
9
10
9
9.
Куприянов Евгений
8
3
12
10.
Куценко Ирина
1
7
4
11.
Николаева Светлана
10
1
7
12.
Соколова Ирина
3
8
11
13.
Уденеев Антон
2
2
5
14.
Шульина Валентина
5
9
8
15.
Ячменев Виктор
4
4
10
16.
Купцов Александр
7
10
6
17.
Нейская Валентина
6
6
1
18.
Пронина Анна
9
11
9
19.
8
8
7
20.
10
3
8
Список Задач № 1:
1. вычислить длины медиан треугольника, у которого длины сторон a, b, c.
Формулы
ma 
2c 2  2b 2  a 2
1
, mb 
2c 2  2a 2  b 2 ,
2
2
1
2a 2  2b 2  c 2
2
Вычислить длины радиусов вписанной в треугольник и описанной возле треугольника
окружностей, если длины сторон треугольника равны a, b, c.
abc
S
abc
R
,r  ,P 
,
4S
P
2
Формулы
S  p ( p  b) * ( p  a ) * ( p  c )
вычислить площадь полной поверхности пирамиды, в основании которой лежит
правильный треугольник со стороной a, апофемой L
1
Формулы Sn=Sб+Sосн , Sб= Pосн* L, Росн – периметр основания
2
3a
Росн=3a, Sîñí  p ( p  a )( p  a)( p  a) , p 
2
mc 
2.
3.
4.
вычислить длины высот треугольника, у которого длины сторон a,b , угол между
сторонами х.
 

ab sin  x *

 
 
180 



Формулы
ha=bsin  x *
hb=asin  x *
hc=


c
 180 
 180 
c= a 2  b 2  2ab cos( x *
5.
6.
7.
8.

)
180
вычислить длины высот треугольника, у которого длины сторон a, b, c
2S
2S
2S
abc
Формулы ha=
, hb =
, hc=
,
p=
,
S= p( p  a)( p  b)( p  c)
a
b
c
2
вычислить площадь равнобедренной трапеции, длина малого основания а, длина боковой
стороны L, а угол при меньшем основании равен с
ab
 
 


*h
Формулы b=a+2Lcos 180  c *
h=Lsin 180  c *
S=
,

2
180 
180 


Где b –длина большего основания,
вычислить длину диагонали равнобедренной трапеции, длина меньшего основания равна
b, длина боковой стороны L, а угол при большом основании равен c.
 
 


Формулы b=a+2*lcos  c *
d= l 2  b 2  2lb cos  c *
,

 180 
 180 
вычислить площадь равнобедренной трапеции, длина большего основания a, длина
меньшего основания b, и диагональ d.
ab
a b
* h, h= d 2  

2
 2 
9. вычислить объем и полную поверхность конуса с радиусом основания R и высотой h
1
Формулы V= R 2 h , Sпол= R( R  l ), l  h 2  R 2
l –образующая
3
10. вычислить длины радиусов вписанной и описанной окружностей около правильного
восьмиугольника со стороной a.
a
a
, R1 
Формулы R2=
, n=8
2 sin(  / n)
2tg ( / n)
2
Формулы
S=
Список Задач № 2:
1. Даны длины сторон треугольника. Определить, является ли он прямоугольным и тогда
вычислить радиус описанной около треугольника окружности
2. Зная величину трех углов треугольника в градусах выяснить может ли существовать такой
треугольник. Если да, то является ли он равнобедренным, если да, то каково значение угла
при вершине
3. Даны длины сторон треугольника. Если он равнобедренный, но не равносторонний,
вычислить длину высоты треугольника.
4. По заданной координате точки определить в какой четверти она находится.
5. На дереве определенное количество веток, на каждой из которых одинаковое количество
листьев в форме квадрата. Выяснить, хватит ли этих листьев, чтобы покрыть крышу,
имеющую форму прямоугольника с заданными сторонами.
6. Продавец к основному окладу получает премию в размере 5 % от суммы проданных им
товаров. Зная величину оклада и сумму, на которую он продал товар, вычислить заработок
за месяц и выяснить за указанное количество месяцев хватит ли у него денег для покупки
компьютера желаемой стоимости. Сколько денег ему придется взять в долг, сколько денег
останется на покупку дополнительных устройств.
7. В квартире у юного ботаника определенная высота потолков. В детстве ему подарили
маленькую пальму, которая была высотой всего несколько см. Но, она очень быстро росла
на одинаковое количество сантиметров в день. Выяснить, поместится ли она в квартире
через несколько лет, а может быть ее придется обрезать - на сколько.
8. Составить программу, которая запрашивает оценки на вступительных экзаменах (всего 4
экзамена). По результатам анализа среднего балла выдаются следующие сообщения: если
ср.балл>=4, то поздравляют с поступлением, сообщая о дате занятий; если ср.балл<4,
выражают сочувствие.
9. В доме прорвало две трубы : горячую и холодную. Из холодной вытекает R литров в
минуту, а из горячей S литров в минуту. Утонут ли жильцы в ледяной воде или сварятся в
кипятке.
10. Составить программу, которая запрашивает данные о трех экзаменах, сданных студентом.
Получивший все оценки “пять” - получает повышенную стипендию (доплата 50 %);
получивший одну тройку - обычную стипендию; получивший две или более троек не
получает стипендию. Величину стипендии рассчитать, а обычную - спросить.
11. Найти корни квадратного уравнения AX2+BX+C. Предусмотреть возможность получения 2
решений.
Список Задач № 3:
1. Статистика криминальной обстановки в К городах Самарской области за прошедший
месяц показала количество краж личного имущества, убийств и тяжелых телесных
повреждений. Рассчитать общее количество преступлений в каждом городе и всех области.
Найти количество городов, где число преступлений не превысило заданную отметку
2. Замеряя температуру каждый день и ночь в течение двух недель, выяснить количество
дней с перепадом температуры ниже указанной отметки. Какова средняя дневная
температура за весь период.
3. Игроки НБА имеют из 100 штрафных бросков несколько попаданий. Имеется список N
игроков и число попаданий каждого. Вычислить процент попаданий в кольцо каждого
игрока и среднюю результативность команды. Сколько игроков имеют больше К %
попаданий
4. При начислении стипендии в группе N студентов решили каждому третьему повысить ее
на 50%, а остальным оставить обычную. Сколько человек получат повышенную
стипендию? Какой убыток это повышение стипендии принесет колледжу? Размер обычной
стипендии известен
5. Библиотечный каталог имеет 15 наименований книг в заданном количестве каждого вида.
Сколько наименований книг может предложить библиотека для группы N студентов,
чтобы книга была хотя бы у каждого второго студента. Каков общий книжный фонд
библиотеки.
6. В прошедшую сессию по химии имеются оценки 20 студентов. Высчитать средний балл по
всей группе и сколько студентов не сдал химию.
7. Каталог программ для компьютера имеет название и объем занимаемой памяти для каждой
программы. Какая программа занимает максимальное или минимальное количество байт.
Какого размера должен быть винчестер компьютера, чтобы разместить там все имеющиеся
программы.
8. Из списка городов России, зная год их основания, выяснить в каком году был основан
нужный вам город, а так же какие города моложе, чем указанный год.
9. Для бригады плиточников из 10-х человек рассчитать размер зарплаты, зная количество
положенной каждым плитки и цену укладки одной плитки. А так же, зная сколько дней
они работали, рассчитать их дневную производительность.
10. В ресторане был заказан комплексный обед, состоящий из N блюд. Зная цену каждого
блюда, выяснить в какую сумму обойдется обед фирму, если известно число ее
сотрудников.
11. Вступительные экзамены по математике сдавали К абитуриентов. Зная результаты каждого
(зачет или не зачет) высчитать количество мест, которое надо подготовить для следующего
экзамена и сколько писем с соболезнованиями придется отправить родителям
12. Имеется n-угольник и длины его сторон. Вычислить периметр. Какая длина у самой
длинная стороны
13. Имеется n-угольник и длины его сторон. Вычислить периметр. Какая длина у самой
короткой стороны
14. По статистике ДТП в городах России за прошедший год известно количество аварий,
пострадавших и умерших человек. Необходимо произвести анализ по этим показателям в
целом по стране и подсчитать количество городов, где была превышена отметка в 1000
аварий.
15. Учитывая прогнозы аналитиков, что $ за неделю теряет 1%, рассчитать сколько потеряю
К $ при хранении за год