Документ 580300

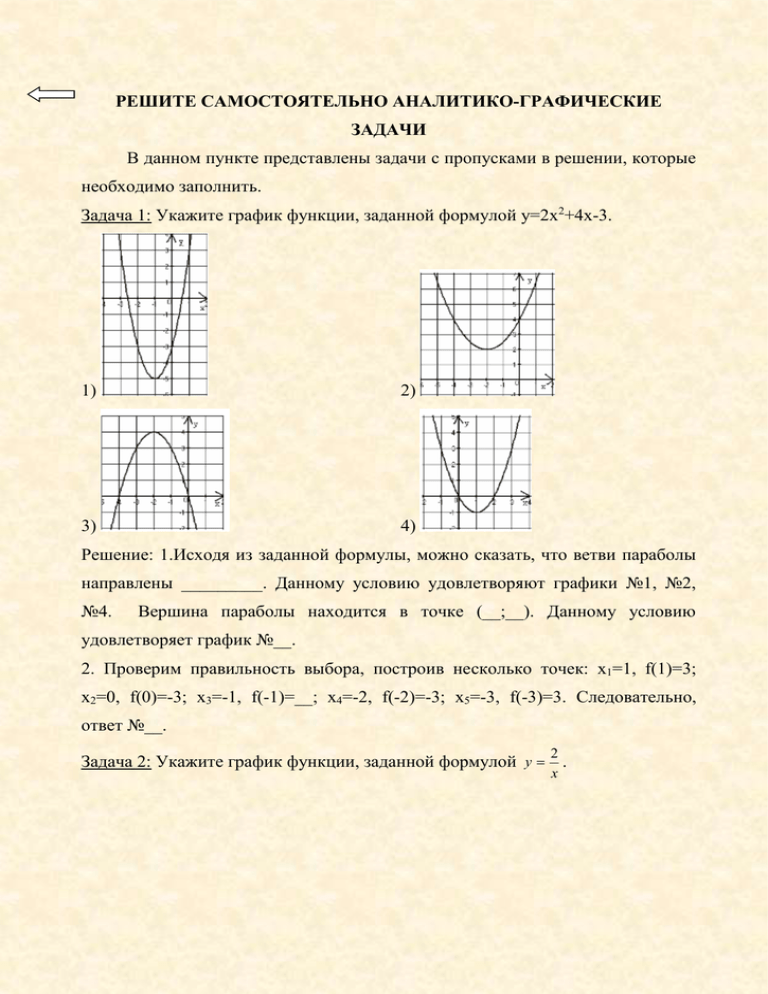
РЕШИТЕ САМОСТОЯТЕЛЬНО АНАЛИТИКО-ГРАФИЧЕСКИЕ
ЗАДАЧИ
В данном пункте представлены задачи с пропусками в решении, которые
необходимо заполнить.
Задача 1: Укажите график функции, заданной формулой у=2х2+4х-3.
1)
2)
3)
4)
Решение: 1.Исходя из заданной формулы, можно сказать, что ветви параболы
направлены _________. Данному условию удовлетворяют графики №1, №2,
№4.
Вершина параболы находится в точке (__;__). Данному условию
удовлетворяет график №__.
2. Проверим правильность выбора, построив несколько точек: x1=1, f(1)=3;
x2=0, f(0)=-3; x3=-1, f(-1)=__; x4=-2, f(-2)=-3; x5=-3, f(-3)=3. Следовательно,
ответ №__.
2
х
Задача 2: Укажите график функции, заданной формулой у  .
1)
2)
3)
4)
Решение: 1) Исходя из заданной формулы, можно сделать вывод, что график
данной функции находится в I и III четвертях и убывает на промежутках
(__;__) и (__;__). Данному условию удовлетворяют графики №2, №3.
2) Найдем контрольные точки: x1=1, f(1)=2, x2=2, f(2)=1, x3=4, f(4)=0,5, x4=0,5,
f(0,5)=4. Полученные точки удовлетворяют графику № ___.
Задача 3: Укажите график функции у=|x-1| из числа заданных вариантов
ответов.
1)
2)
3)
4)
Решение: 1) Зная формулу, можно сделать вывод, что график зависимости,
содержащий неизвестную под знаком модуля сдвинут вдоль оси Оx на 1
единицу ________ . Данному условию удовлетворяет график № ___.
Задача 4: Укажите график функции, заданной формулой у  х  1 .
1)
2)
3)
4)
Решение: 1) Исходя из формулы, можно сказать, что график данной функции
должен быть определен на промежутке (0; ∞) – _________.Данному условию
удовлетворяют графики №1, № 4.
2) Найдем контрольные точки для заданной функции: при х=1,
f(1)=0, при х=0, f(0)=-1, при x=4, f(4)=1. следовательно, ответ № ___.
 1
 х  3, х  2
Задача 5: Постройте график функции, заданной формулами f(x)=  2
.
 х  4, х  2
Решение: 1) График, заданной формулами функции – графики, состоящие из
1
2
двух графиков линейных функций, причем функция у   х  3 задана на
промежутке х  2, другая у=х – 4 на промежутке х>2.
1
2
2) При х  2 график функции у   х  3 убывает, ему принадлежат точки (0;2)
и (0;3). При х>2 график функции у=х–4 возрастает, причем графику
принадлежат точки (0;4) и (__;__). Тогда график функции выглядит
следующим образом:
________________________.
2 x 2  2, | х | 1;
Задача 6: Укажите график функции, заданной формулами у= 
1  х 2 , | х | 1.
1)
2)
3)
4)
Решение: Из заданных формул, можно сделать вывод, что это график,
состоящий из двух парабол, одна из которых задана на промежутке |х|  1,
другая – на промежутке |х|>1. Так как вершина параболы, рассматриваемой на
промежутке |x|  1, лежит в точке (0;-2), а второй параболы в точке (0;1), не
удовлетворяющей условию |х|>1, данным требованиям удовлетворяет график
№___.
Задача 7: Дана функция y=ax2+bx+c. На каком рисунке изображен график этой
функции, если известно, что a>0 и квадратный трехчлен ax2+bx+c имеет два
положительных корня?
a)
b)
c)
d)
Решение: 1) Проанализировав условие задачи, можно сделать вывод, ветви
параболы направлены _______. Данному условию удовлетворяют графики а и
__. Из того, что квадратный трехчлен имеет два положительных корня, можно
сделать вывод, что корни расположены справа от оси ____. Данному условию
удовлетворяет график ___.
2) Запишем ответ: ___.
Задача 8: На рисунке изображены графики функций вида y=kx+b. Установите
соответствие между графиками и знаками коэффициентов k и b.
a) k>0, b>0;
b) k<0, b>0;
c) k<0, b<0.
1)
2)
3)
Решение: 1) Проанализировав содержание задачи можно сделать вывод о том,
что эта задача на соотнесение, т.е. для каждой формулы должен быть найден
соответствующий график;
2) Исходя из заданных свойств и, пользуясь таблицей основных
элементарных функций, можно сделать вывод, что условию a соответствует
график №___, условию b соответствует график №3, условию с – график №___.
3) Запишем ответ: a№___, b№3, c№___.
Задача 9: На рисунке изображены графики функций вида у=ах2+с. Установите
соответствие между графиками и знаками коэффициентов а и с.
a) а>0, с>0;
b) а<0, с>0;
c) а>0, с<0.
1)
2)
3)
Решение: 1) Проанализировав содержание задачи можно сделать вывод о том,
что эта задача на соотнесение, т.е. для каждой формулы должен быть найден
соответствующий график;
2) Исходя из того, что в условиях а и с коэффициент а>0, можно
сделать вывод, что ветви параболы направлены ________. Данному условию
удовлетворяют графики №__ и №__. Следовательно, условию b соответствует
график № __. Из того, что при с>0 вершина параболы расположена выше оси
Ох, можно сделать вывод, что условию а соответствует график №__, а
условию с соответствует график №1.
3) Запишем ответ: a№__, b№__, c№__.
назад