Тест 47

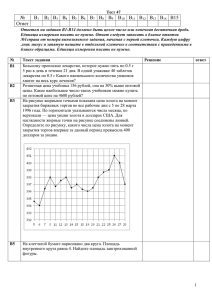
Тест 47
№
Ответ
1
1-2
2
3
4
5
6
7
8
9
10
11
12
13
14
Ответом на задания В1-В14 должно быть целое число или конечная десятичная дробь.
Единицы измерения писать не нужно. Ответ следует записать в бланке ответов
№1справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру
,знак минус и запятую пишите в отдельной клеточке в соответствии с приведенными в
бланке образцами. Единицы измерения писать не нужно.
№
1
1-2
2
Текст задания
Больному прописано лекарство, которое нужно пить по 0.5 г
5 раз в день в течение 21 дня. В одной упаковке 40 таблеток
лекарства по 0.5 г Какого наименьшего количества упаковок
хватит на весь курс лечения?
Розничная цена учебника 156 рублей, она на 30% выше оптовой
цены. Какое наибольшее число таких учебников можно купить
по оптовой цене на 4600 рублей?
На рисунке жирными точками показана цена золота на момент
закрытия биржевых торгов во все рабочие дни с 5 по 28 марта
1996 года. По горизонтали указываются числа месяца, по
вертикали — цена унции золота в долларах США. Для
наглядности жирные точки на рисунке соединены линией.
Определите по рисунку, какого числа цена золота на момент
закрытия торгов впервые за данный период превысила 400
долларов за унцию.
Решение
ответ
Мебельный салон заключает договоры с производителями
мебели. В договорах указывается, какой процент от суммы,
вырученной за продажу мебели, поступает в доход мебельного
салона.
Фирмапроизводите
Процент от выручки,
поступающий в доход
Примечания
1
ль
салона
«Альфа»
6%
Изделия ценой
до
руб.
«Альфа»
3,5 %
Изделия ценой
свыше
руб.
«Бета»
4%
Все изделия
«Омикрон»
5,5 %
Все изделия
В прейскуранте приведены цены на четыре софы. Определите,
продажа какой софы наиболее выгодна для салона. В ответ
запишите, сколько рублей поступит в доход салона от продажи
этой софы.
Фирма-производитель Изделие
Цена
«Альфа»
Софа «Неспешность» 13000 руб.
4
«Альфа»
Софа «Философ»
20000 руб.
«Бета»
Софа «Мысль»
17000 руб.
«Омикрон»
Софа «Шанс»
14500 руб.
На клетчатой бумаге нарисовано два круга. Площадь
внутреннего круга равна 4. Найдите площадь заштрихованной
фигуры.
5
На рисунке изображён лабиринт. Паук заползает в лабиринт в
точке «Вход». Развернуться и ползти назад паук не может. На
каждом разветвлении паук выбирает путь, по которому ещё не
полз. Считая выбор дальнейшего пути случайным, определите,
с какой вероятностью паук придёт к выходу .
6
Найдите корень уравнения
.
2
7
Окружность, вписанная в равнобедренный треугольник, делит в
точке касания одну из боковых сторон на два отрезка, длины
которых равны 5 и 3, считая от вершины, противолежащей
основанию. Найдите периметр треугольника.
8
На рисунке изображен график функции
,
определенной на интервале
. Найдите сумму точек
экстремума функции
.
9
В правильной четырёхугольной призме
известно, что
диагоналями
и
. Найдите угол между
. Ответ дайте в градусах.
10
11
12
13
14
Найдите значение выражения
.
Скейтбордист прыгает на стоящую на рельсах платформу, со
скоростью
м/с под острым углом к рельсам. От толчка
платформа начинает ехать со скоростью
(м/с), где
кг — масса скейтбордиста со скейтом, а
кг — масса платформы. Под каким максимальным
углом (в градусах) нужно прыгать, чтобы разогнать
платформу не менее чем до 0,4 м/с?
Конус и цилиндр имеют общее основание и общую высоту
(конус вписан в цилиндр). Вычислите объём цилиндра, если
объём конуса равен 18.
На изготовление 896 деталей первый рабочий тратит на 4 часа
меньше, чем второй рабочий на изготовление 960 таких же
деталей. Известно, что первый рабочий за час делает на 2
детали больше, чем второй. Сколько деталей за час
делает первый рабочий?
Найдите наибольшее значение функции
на
отрезке
.
15. а) Решите уравнение: cos(
3
 2 x)  2 sin x
2
9
б) Найдите все корни этого уравнения, принадлежащие промежутку [3 ;  ]
2
16. Основание пирамиды DABC – равнобедренный треугольник АВС, в котором,
3
АВ=ВС =13, АС=24. Ребро DB перпендикулярно плоскости основания и равно 20.
Найдите тангенс двугранного угла при ребре АС.
17. Решите неравенство: log 5 ( x  2)  log 5 (1  x)  log 5 ((1  x)( x 2  8 x  8)
18. Периметр равнобедренной трапеции равен136. Известно, что в эту трапецию можно
вписать окружность, причем боковая сторона делится точкой касания в отношении 9:25.
Прямая проходящая через центр окружности и вершину трапеции, отсекает от трапеции
треугольник. Найдите отношение площади этого треугольника к площади трапеции
19. Фермер взял в банке кредит 3 640 000 рублей под 20 % годовых.
Схема погашения кредита: раз в год клиент должен выплачивать банку одну и ту же
сумму, которая состоит из двух частей. Первая часть составляет 20% оставшейся
суммы долга, а вторая направлена на погашение оставшейся суммы.
Каждый следующий год проценты начисляются только на оставшуюся сумму долга.
Какой должна быть ежегодная сумма выплаты (в рублях), чтобы фермер полностью
погасил кредит тремя равными платежами?
20. Найдите все значения а, при каждом из которых общее решение неравенств у+2х  а и
у-х  2а являются решениями неравенств 2у-х>а+3
21. Натуральные числа m и n таковы, что m 3  n и m  m 3 делится на m 2  n 2
Найдите m и n
4