ТИПОВОЙ РАСЧЕТ ПО ЭЛЕКТРОСТАТИКЕ (С – 13) ВАРИАНТ 01-10

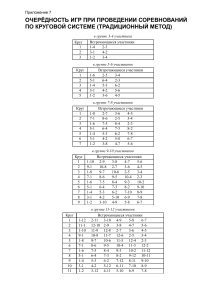
ТИПОВОЙ РАСЧЕТ ПО ЭЛЕКТРОСТАТИКЕ (С – 13)
ВАРИАНТ 01-10
Три квадратные металлические пластины
толщиной 1 мм и площадью 0,25м2 каждая имеют
заряды q1, q2, q3. Пространство между первой и
второй
пластиной
частично
заполнено
диэлектриком толщиной l и относительной
диэлектрической
проницаемостью
ε 1.
Пространство между второй и третьей пластиной
залито
жидкостью
с
диэлектрической
проницаемостью ε2 .
Необходимо:
1. Определить
значения
напряженности,
электрического смещения в точках A,B,C,D,F,G.
Принять значение потенциала в точке B за нуль.
2. Построить график зависимостей E(x),D(x) и φ(x).
3. Рассчитать
поверхностные
плотности
свободных зарядов на сторонах металлических пластин.
4. Найти поверхностную плотность связанных зарядов на границах
5. Найти плотность энергии электрического поля в точках A, B, C, D, F, G.
6. Определить силы, действующие на металлические пластины.
Записать данные своего варианта.
№ варианта
q1,Кл
q2,Кл
q3,Кл
l,мм
d1,мм
d1,мм
ε1
ε2
01
2∙10-6
-4∙10-6
1∙10-6
1
3
5
2,5
2
02
-2∙10-6
4∙10-6
-1∙10-6
2
3
4
2
1,5
03
3∙10-7
2∙10-7
-5∙10-7
1
2
4
4
2
04
-3∙10-7
5∙10-7
-2∙10-7
2
4
4
3
1,5
05
4∙10-8
4∙10-8
-5∙10-8
1,5
3
3
2,5
2
06
-4∙10-8
4∙10-8
5∙10-8
1
2
4
3
1,5
07
-3∙10-8
4∙10-8
-1∙10-8
2
3
3
4
2
08
2∙10-8
-5∙10-8
2∙10-8
1,5
2,5
5
5
2
09
-5∙10-9
5∙10-9
2∙10-9
2
3
4
4
2,5
10
5∙10-9
-5∙10-9
-2∙10-9
2
4
5
2
2
ТИПОВОЙ РАСЧЕТ ПО ЭЛЕКТРОСТАТИКЕ (С – 13)
ВАРИАНТ 11-20
Длинная
коаксиальная
цилиндрическая
система
образована
цилиндрическим
диэлектрическим стержнем. Радиус стержня R1,
относительная диэлектрическая проницаемость
ε1, объемная плотность заряда ρ. Металлическая
труба имеет внутренний радиус R2 и наружный
радиус R3. На единице длины трубы находится
заряд τ. Металлическая труба окружена
цилиндрическим слоем диэлектрика, радиуса R3
и
R4
относительная
диэлектрическая
проницаемость которого равна ε2.
Необходимо:
1. Рассчитать напряженность электрического поля, электрическое смещение и
электрический потенциал в точках A,B,C,D. Принять начало отсчета потенциала на
оси симметрии системы.
2. Построить графики E(r), D(r) и φ(r).
3. Найти поверхностную плотность связанных зарядов на границах диэлектриков.
4. Рассчитать энергию электрического поля заданной системы приходящуюся на
единицу длины в цилиндре радиуса rD.
5. Определить поверхностную плотность свободных зарядов на внутренней и
внешней поверхности металлической трубы.
6. Рассчитать потенциальную энергию электрического диполя pe = 10-28 Кл∙м,
находящегося в точке D и ориентированного под углом α к радиальному
направлению. Определить момент сил, вращающих электрический диполь.
Записать данные своего варианта.
№
ρ, 10-3
ε
варианта Кл/м3 1
11
12
13
14
15
16
17
18
19
20
1
2
-1
1,5
0,2
2
-0,2 2,5
0,01 3
-0,01 3
0,03 4
0,004 2,5
-0,002 3
0,002 2
ε2
R1,
см
R2,
см
R3,
см
R4,
см
rA,
см
rB,
см
rC,
см
2
1,5
2,5
2
3
3
4
2
3
4
1
1
1
1
1
1
1
1
1
1
2
2
3
3
2
2
2
3
2
2
3
3
5
5
3
3
2
5
3
5
4
4
6
6
4
4
4
6
6
6
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
3,5
3,5
5,5
5,5
3,5
3,5
2,5
5,5
3,5
5,5
rD, τ, 10-6 α,
см Кл/м рад
5
5
7
7
5
5
5
7
5
7
-2
-2
-0,2
0,3
0,02
0,003
0,003
-0,008
0,009
0,01
π/6
π
π/2
-π
π/4
-π
π/6
π/3
π/4
π
ТИПОВОЙ РАСЧЕТ ПО ЭЛЕКТРОСТАТИКЕ (С – 13)
ВАРИАНТ 21-40
Металлический шар радиуса R1 имеет заряд q1 и
окружен сферическим слоем диэлектрика с
относительной диэлектрической проницаемостью
ε1. Радиусы диэлектрического слоя равны R1 и R2.
Тонкая металлическая сфера радиуса R3 имеет
заряд q2, а тонкая металлическая сфера радиуса R4
имеет заряд q3. Пространство между сферами
заполнено диэлектриком с относительной
диэлектрической
проницаемостью
ε2.
Металлические сферы имеют общий центр с
металлическим шаром.
Необходимо:
1. Рассчитать напряженность, электрическое смещение и электрический потенциал в
точках O, A, B, C, D.
2. Построить графики зависимости E(r), D(r) и φ(r).
3. Рассчитать поверхностные плотности связанных зарядов на границе диэлектриков.
4. Определить энергию электрического поля данной системы зарядов.
5. Рассчитать потенциальную энергию, вращающий момент действующий на
электрический дипольный момент pe= 10-28Кл∙м, находящийся в точке D и
ориентированный под углом α к направлению радиуса.
Записать данные своего варианта.
№
21
22
23
24
25
26
27
28
28
30
q1,
q2,
-6
10 ∙Кл 10-6∙Кл
3
-1
2
3
2
-2
0,4
-0,5
-0,2
0,03
0,03
-0,05
0,06
0,05
0,005
-0,007
-0,005 -0,007
-0,06
0,007
q3,
ε
10-6∙Кл 1
2
2
-6
2
3
3
0,1
1
-0,2
2
0,04 3
0,003 2
0,005 4
0,005 3
0,001 2
ε2
1
3
2
3
2
4
4
2
3
3
R1,
см
2
1
2
2
3
3
1
1
2
1
R2,
см
3
2
3
4
4
5
5
4
3
3
R3, R4,
см см
5 7
3 4
4 5
6 8
5 6
7 8
7 10
6 8
5 7
5 7
rA,
см
2,5
1,5
2,5
3
3,5
4
2
3
2,5
2
rB,
см
4
2,5
3,5
5
4,5
6
6
5
4
4
rC, rD,
см см
6
8
3,5 5
4,5 6
7
10
5,5 8
7,5 10
8
12
7
10
6
8
6
9
α,
рад
π/6
π
π/3
π/3
π/4
-π
0
-π
0
π
φ(r)=0
r=0
r=∞
r=0
r=R2
r=R3
r=0
r=R4
r=0
r=∞
r=∞
№
31
32
33
34
35
36
37
38
38
40
q1,
10-6∙Кл
-3
-2
-2
-0,4
0,2
-0,03
-0,06
-0,005
0,005
0,06
q2,
10-6∙Кл
-1
3
-2
-0,5
0,03
-0,05
0,05
-0,007
-0,007
0,007
q3,
ε
10-6∙Кл 1
-2
2
-6
2
-3
3
-0,1
1
0,2
2
-0,04 3
-0,003 2
-0,005 4
-0,005 3
-0,001 2
ε2
1
3
2
3
2
4
4
2
3
3
R1,
см
2
1
2
2
3
3
1
1
2
1
R2,
см
3
2
3
4
4
5
5
4
3
3
R3, R4,
см см
5 7
3 4
4 5
6 8
5 6
7 8
7 10
6 8
5 7
5 7
rA,
см
2,5
1,5
2,5
3
3,5
4
2
3
2,5
2
rB,
см
4
2,5
3,5
5
4,5
6
6
5
4
4
rC, rD,
см см
6
8
3,5 5
4,5 6
7
10
5,5 8
7,5 10
8
12
7
10
6
8
6
9
α,
рад
π/6
π
π/3
π/3
π/4
-π
0
-π
0
π
φ(r)=0
r=0
r=∞
r=0
r=R2
r=R3
r=0
r=R4
r=0
r=∞
r=∞
Типовой расчет по электростатике выдается студентам лектором на 6 неделе. Устная защита
типового расчета не предусмотрена (просто ставиться оценка). При успешном выполнении
типового расчета до 14 недели (включительно), типовой расчет может быть оценен на "5". При
успешном выполнении типового расчета до 15 недели (включительно), типовой расчет может
быть оценен не выше, чем на "4". При успешном выполнении типового расчета до 16 недели
(включительно), типовой расчет может быть оценен не выше, чем на "3".