Разложение квадратного трехчлена на множители

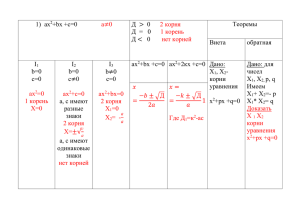
Разложение квадратного трехчлена на множители
 Вынесем за скобки в многочлене
ax2+bx +c
Получим ax2+ bx + c=a  х 2  b х  с 

a
множитель a.
а
Так как корни квадратного трехчлена ax2+ bx + c являются корнями квадратного
уравнения ax2+ bx + c = 0, то по теореме Виета
X 1 + X2 = –
,
X 1 ∙ X2 =
Отсюда
= – (X1 + X2 ),
= X 1 ∙ X2 .
.
Поэтому
x2 +
+ = x2- (x1+x2)x + x1x2 = x2 – x1x –
-x2x + x1x2 = x(x - x1) – x2(x – x1) = (x – x1)(x – x2).
Итак,
ax2+ bx + c=a(x – x1)(x – x2).
Покажем, что
Пусть квадратный трехчлен ax2 + bx + c не имеет корней.
Предположим, что его можно представить в виде произведения
многочленов первой степени:
ax2+bx +c = (kx + m) (px + g),
где k, m, p и g – некоторые числа, причем k ≠ 0 и p ≠ 0.
Произведение (kx + m) (px + g) обращается в нуль при x = - и x = Следовательно, при этих значениях x обращается в нуль и трехчлен
ax2 + bx + c,
т. е. числа – и – являются его корнями.
Мы пришли к противоречию, так по условию этот трехчлен
корней не имеет.
 Разложим на множители квадратный трехчлен
3x2 - 24x+21.
Решим уравнение 3x2 - 24x+21=0
a = 3, b = -24, c = 21
Д = b2 – 4aс
Д = (-24)2 - 4∙3∙21=576 - 252=324
X1; 2=
X1 =
=
X2 =
=7
=
=1
Решив уравнение 3 x2 - 24x+21=0, найдем корни трехчлена:
X1=7, X2= 1.
По теореме о разложении квадратного трехчлена на множители
имеем
3 x2 -24x+21=3(x-7)(x-1)
• Разложим на множители квадратный трехчлен
-4x2+24x - 36
Решим уравнение - 4x2 + 24x - 36=0
a = - 4, b = 24, c = -36
Д = b2 – 4ac
Д = 576-576=0
Д=0 уравнение имеет 1 корень
X=
=3
Решив уравнение
Значит,
-4x2 + 24x - 36=0, найдем корни трехчлена:
-4x2+24x-36=-4(x
- 3)(x - 3)
или иначе
-4x2+24x- 36=-4 (x - 3)2
X1 = X2 = 3
х 2  11х  24
х 2  64
 Сократим дробь
Разложим на множители квадратный трехчлен X2 _ 11x + 24.
X2 - 11x+24 =0
а = 1, b = -11, c = 24
D=b2 -4ac
D=121-96=25
D>0 уравнение имеет 2 корня
X1;2=
X1=
=
=
=8
X 2=
=
=
= 3.
Его корни равны 8 и 3.
Поэтому
X2 - 1 1x + 24 =(x - 8)(x – 3).
Значит,
( х  8)( х  3) ( х  8)( х  3) х  3
х 2  11х  24


=
2
2
х  64
( х  8)( х  8) х  8
х  64