Метод Галеркина с разрывными базисными функциями (РМГ)

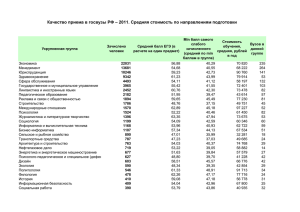
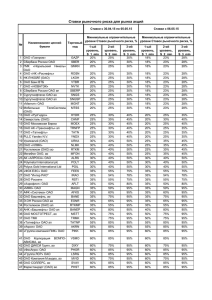
И Н С Т И Т У Т П Р И К Л А Д Н О Й М АТ Е М АТ И К И И М . М . В . К Е Л Д Ы Ш А
Р О С С И Й С К О Й А К А Д Е М И И Н АУ К
Исследование влияния лимитера на порядок
точности решения разрывным методом
Галеркина
Ладонкина М.Е., Неклюдова О.А., Тишкин В.Ф.
Международная молодёжная конференция – школа
«СОВРЕМЕННЫЕ ПРОБЛЕМЫ ПРИКЛАДНОЙ МАТЕМАТИКИ И ИНФОРМАТИКИ»
22-27 августа 2012 года, Дубна
План доклада
 Разрывный метод Галеркина для уравнений Эйлера.
 Лимитеры.
 Тестовая задача.
Метод Галеркина с разрывными базисными функциями
(РМГ) для уравнений Эйлера
Рассматрим уравнения одномерной идеальной газовой динамики
U F (U )

0
t
x
 u

 
 2

 
U   u  F   u  p 
 - плотность
u - скорость
- удельная внутренняя
 энергия
p - давление
E 
 
(1)
 ( E  p )u 


2 

u
- полная энергия
E    

2

на единицы объема
p  (  1) 
(2)
 - показатель адиабаты
Эти уравнения должны быть дополнены начальными и граничными условиями,
вид которых зависит от конкретной задачи, и будут конкретизированы далее.
0  x1/ 2  x 3/ 2  ...  x N 1/ 2  L
xi  ( x i 1/ 2  x i 1/ 2 )
приближенное решение системы уравнений (1) будем искать в виде
проекции вектора консервативных переменных U  (  , u, E )
на пространство полиномов P(х) степени р
в базисе
k ( x) с зависящими от времени коэффициентами.
p
 h ( x, t )    k (t )k ( x),
k 0
p
 uh ( x, t )    uk (t )k ( x),
Eh ( x, t ) 
k 0
p
 Ek (t )k ( x),
k 0
(3)
Приближенное решение системы (1) в разрывном методе
Галеркина ищется как решение следующей системы
 tU h ( x, t )  k ( x)dx   F (U h ( x, t )) xk ( x)dx 
Ii
Ii
 Fi 1/2  k ( xil1/2 )  Fi 1/2  k ( xir1/2 )  0
где i = 0,…,N, k = 0,1,2.
U h ( x, t )   h ( x, t ), uh ( x, t ), Eh ( x, t ) 
T
- вектор решения
k ( xil1/2 ),k ( xir1/2 ) - базисная функция с номером k на интервале I ,
i
вычисленная в точках xi 1/2 , xi 1/2
Fi 1/2 , Fi 1/2 - дискретные потоки, являющиеся монотонными функциями двух
переменных F
  (U ( xl , t ),U ( x r , t ))
i 1/2
i 1/2
h i 1/2
Fi 1/2   (U h ( xil1/2 , t ),U h ( xir1/2 , t ))
h
для которых выполнено условие согласования:
(U h ( xi , t ),U h ( xi , t ))  F (U h ( xi , t ))
Численные потоки
Поток Русанова-Лакса-Фридрихса
(U h ( xil1/2 , t ),U h ( xir1/2 , t )) 


1
F (U h ( xil1/2 , t )  F (U h ( xir1/2 , t ))  A  (U h ( xir1/2 , t )  U h ( xil1/2 , t ))) ,
2


A  max uil1/2  cil1/2 , uir1/2  cir1/2 ,
i
ui 1/2 - скорость
ci 1/2 - скорость звука
РусановВ.В. Расчет взаимодействия нестационарных ударных волн с препятствиями. 1961, Журнал
вычислительной математики и математической физики, т.I, №2, 267- 279.
Лимитеры
Ограничитель (лимитер) представляет собой некоторый оператор,
действующий на функцию приближенного решения на каждом
интервале xi 1 / 2 , xi 1 / 2
Обозначим действие этого оператора на функцию u через  hu
 x  xi 
Ограничитель Кокбурна для линейной функции u  u0  u1 


x
i 

 x  xi 
можно записать как  hu  u0  u1 
,


x
i 

где


 
u1  2  min mod u ( xi 1/2 )  u0i ,  ui 1/2  u0i ,   u0i  ui 1/2

u0 - среднее интегральное значение приближенного решения на интервале I i
u
u
u
u
ui 1/2  0i 1 0i , ui 1/2  0i 1 0i
2
2
 
 
u1i  min mod u1, u0i 1  u0i , u0i  u0i 1


s  min  a1 ,..., aN  , если s  sign(a1)  ...  sign(aN ),
min mod (a1,..., aN )  
иначе.

0,
Ограничитель Колгана
вместо функции min mod (a1,..., a N )
используется функция min mod K (a1 ,..., a N )
min modK (a1,..., aN )  sign(a1)  min(| a1 |,...,| aN |)
Обозначим его
 hK


 
u1  2  min modK u ( xi 1/2 )  u0i ,   ui 1/2  u0i ,   u0i  ui 1/2

.
Колган В.П. Применение принципа минимальных значений производной к построению конечноразностных схем для расчета разрывных решений газовой динамики. 1972, Ученые записки ЦАГИ. т. 3,
№6.,С. 68 – 77.
«Моментный» ограничитель
«Моментный» лимитер характеризуется тем, что сохраняет максимально
возможный порядок схемы.
Для применения данного лимитера перейдем к ортогональной системе базисных функций.
  x  x 2 1 
u2 
u1
u2

 x  xi 
i
u

u

,
u

,
u

.


u ( x)  u0  u1  2

u
6

,
0  0

1
2
 2 

12 
2
6

  xi  2 
 xi 


Решение лимитируется путем лимитирования его коэффициентов.
i
Коэффициент uk соответствует k- ой производной решения, и он сравнивается с
альтернативной аппроксимацией k-ой производной через правую и левую разности
(k-1)-ой производной.
i
Начиная со старших коэффициентов k=p, заменим uk на


 

uki  min mod uki , k uki 11  uki 1 , k uki 1  uki 11 .
.
i
i
Лимитер срабатывает, если uk  uk
i
i
i
В случае uk  uk лимитирование прекращается, иначе лимитируется коэффициент uk 1,
продолжая до тех пор, пока либо k=1,либо выполнится условие
uki  uki
Lilia Krivodonova, Limiters for high-order discontinuous Galerkin methods, 2007, Journal of Computational
Physics, vol. 226,pp. 879-896.
.
В случае нелинейных систем следует применять лимитеры к характеристическим
переменным.
Лимитер Кокбурна

 ~ 

Lu

2

min
mod
 1
 L u ( xi 1/2 )  u0i


j

j

,  L ui 1/2  u0i

j

,  L u0i  ui 1/2


,

j
Моментный лимитер
 ~i 

 Luk   min mod  Luki




j
 j  
, k L uki 11  uki 1
 j  
, k L uki 1  uki 11


,

j
j  1,2,3
где L - матрица левых собственных векторов Якобиана системы (1), вычисленная
в центральной точке хi интервала Ii , j-номер уравнения в системе.
После лимитирования возвращаемся к исходным консервативным переменным,
умножая результаты лимитирования на матрицу, ~составленную из правых

1 
u

L
Lu
собственных векторов Якобиана системы (1) 1
 1


Схема Рунге-Кутта третьего порядка .
U*


  h U n  tL(U n )
1
1
3

U **   h  U n  U *  tL(U * ) 
4
4
4

2
2
1

U n 1   h  U n  U **  tL(U ** ) 
3
3
3

.
Исследование влияние различных лимитирующих функций на
порядок точности решения разрывным методом Галеркина
Распределение плотности в начальный момент выберем в виде бесконечно гладкой
l

22 2 2

  1  e l  x , x  l
x [1,1], l  0.2,   5 / 3
1,
, иначе

Остальные гидродинамические параметры определяются из условий постоянства энтропии

2  (  1)
и инварианта R
u2
( 1)
 
, u
, E    
 1
2
На границах области были заданы  (1, t )  1, u(1, t )   10, E (1, t )  6,
функции:
2
постоянные граничные условия:
 (1, t )  1, u (1, t )   10, E (1, t )  6.
Начальные профили плотности, импульса и полной энергии:
Семейство характеристик, на которых инварианты постоянны в простой волне
является прямыми линиями,
и это дает возможность записать решение в неявном виде.
u ( x, t )  u ( x  t  (u ( x, t )  c( x, t )),0)  u0 ( x  t  (u0 ( x0 )  c0 ( x0 ))),
c( x, t )  c( x  t  (u ( x, t )  c( x, t )),0)  c0 ( x  t  (u0 ( x0 )  c0 ( x0 ))),
x0  x  t (u ( x0 )  c( x0 )),
1
c( x, t ) 2   1

 ( x, t )  


(


1)


Ландау Л.Д., Лифшиц Е.М .Гидродинамика, Теоретическая физика: Т.VI. –М.: Физматлит, 2001.
Решение данной задачи сохраняет гладкость до того момента времени, пока
характеристики, выпущенные из разных точек, не начнут пересекаться.
x  x0  t  u ( x0 ,0)  c( x0 ,0) 
x  x0  dx  t  u ( x0  dx,0)  c( x0  dx,0) 
Вычислим момент возникновения ударной волны
t
(l 2   2 )2
, для   5 3
 3
2l 2 (  1) 1/2 (  1)1/2 
2
( )(  ( )  1)
t
9  2/3 ( )(l 2   2 )2
16 10 l 2 (  ( )  1)
Из графика видно, что момент образования ударной волны
приблизительно равен T = 0.09
Вычисление порядка точности метода.
1
U* UT
L1


U *  U T dx
1
1
U U
*
T
2
L

 U
U U
p
T
4
L
U

   U* UT

 1

log 2 U h*  U T
log 2 U h*/2
U
Li
T
Li
,

T 2
1
1
*
*

dx
1/4
4



i  1,2,4.
Таблицы