Оценка влияния базы хаотических радиоимпульсов на

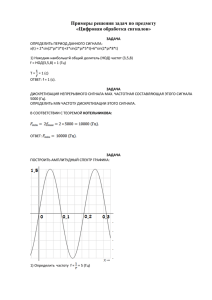
ОЦЕНКА ВЛИЯНИЯ БАЗЫ ХАОТИЧЕСКИХ
РАДИОИМПУЛЬСОВ НА ДАЛЬНОСТЬ
СВЯЗИ В СВЕРХШИРОКОПОЛОСНОЙ
ПРИЕМОПЕРЕДАЮЩЕЙ СИСТЕМЕ
Выполнил :
Студент 817 гр. Попов М.Г.
Научный руководитель: д.ф.-м.н., профессор Дмитриев А.С.
Московский физико-технический институт
(государственный университет),
ИРЭ им. В.А. Котельникова РАН,
2014
СШП системы связи
F = 3 – 10 ГГц
∆𝐹
𝐹𝐶
≥ 0.2 … 0.25 или ∆𝐹 ≥ 500 МГц
Дальность СШП систем
связи
d = 1…10 (30) м
Маска спектральной плотности
мощности излучения
Цель работы
Исследовать зависимости увеличения дальности в
прямохаотических системах связи при увеличении
базы сигнала.
Преимущества метода:
• Не затрагивает мощность передатчика
• Не влияет на диаграмму направленности антенн
• Минимальное аппаратного изменения
приемопередатчиков
Прямохаотическая
система связи
1. источник хаоса генерирует колебания
непосредственно в заданной полосе
2. ввод информационного сигнала
формированием соответствующего потока
хаотических радиоимпульсов
3. извлечение информации производится без
промежуточного преобразования частоты
Модель системы
передачи
Канал связи с аддитивным белым гауссовским шумом
Система является прямохаотической системой связи.
Прием – некогерентный энергетический.
База сигнала
Базой сигнала называется величина:
B  2F
Хаотические радиоимульсы – сигналы с сложной
базой:
B = 2F  1
Варьирование базы осуществляется путем
изменения времени импульса .
Полоса частот рассматривалась ΔF = 1000 МГц
Структура сигнала
 S0 (t )   (t ), если передается"0"
y (t )  
.
 S1 (t )   (t ), если передается "1"
Используется on-off модуляция, т.е S0(t)=0, S1(t) хаотический радиоимпульс.
Дискретная модель
сигнала
Сигналы:
S0 (i )  S0 (i / B) = 0
S1 (i )  S1 (i / B)
Шум:
 (i )   (i / B)
Получаемые энергии импульсов:
- если передается символ «0».
in1
d1   ( S1 (i)   (i)) 2 - если передается символ «1».
n
d0   2 (i)
i 1
Определения порога
При приеме величина энергии сравнивается с
порогом:
d < C – принят символ ‘0’
d > C – принят символ ‘1’
Порог выбирается исходя из оценки
распределений энергий для символов
Моделирование
Вероятности ошибки в системах связи зависит от
отношения:
K = E b / N0
В свою очередь в свободном пространстве
величина K связана с дальностью передачи и базой:
Pt
Aer  B  D
K

2
4R 2 N 0  F
Результаты
моделирования
1. При малых значениях базы слишком велик
разброс энергии между импульсами
2. С ростом базы уменьшается эффективность
Результаты
моделирования
Увеличение базы на 3 дБ приводит к увеличению дальности:
• На 2.5 дБ при начальной базе 10 дБ
• На 1.1 дБ при начальной базе 25 дБ
• На 1.0 дБ при начальной базе 35 дБ
При этом прирост независим от вероятности ошибки при передачи.
Кодирование информационного
бита серией импульсов
Вероятности ошибки в
этом случае:
Perr 
n
 (1  p)
k  n /2
n
k
n
* p *( )
k
где p – вероятность ошибки
без кодирования
n – количество логических бит
Детектирование
раздельных импульсов
1. Данный метод также обеспечивает увеличение дальности
передачи
2. Эффективность метода ниже
3. Не требует аппаратной модификации
Выводы
• Показано, что при увеличении базы сигнала от 15 дБ
до 40 дБ (в ~ 316 раз) возможно увеличение дальности
передачи до 8 раз (9 дБ) при практически
неизменной аппаратной части приемопередатчиков.
• Кодирование информационных бит посредством
серии импульсов является менее эффективным,
однако реализуемо программным путем
Спасибо за внимание