Задача 4.
реклама
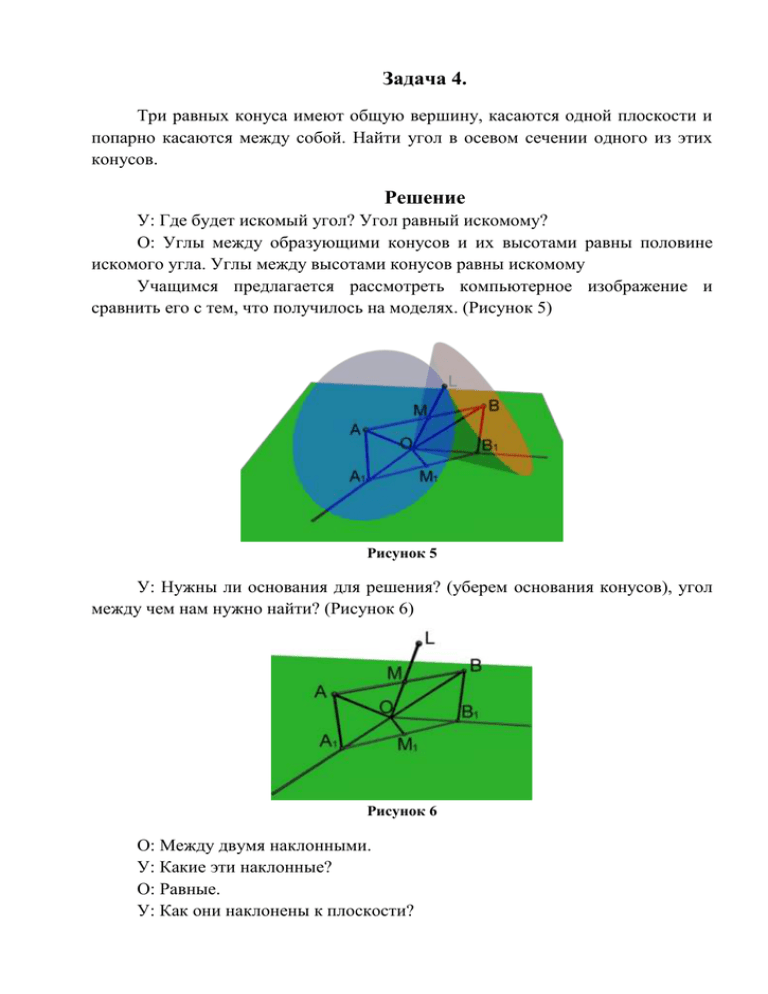
Задача 4. Три равных конуса имеют общую вершину, касаются одной плоскости и попарно касаются между собой. Найти угол в осевом сечении одного из этих конусов. Решение У: Где будет искомый угол? Угол равный искомому? О: Углы между образующими конусов и их высотами равны половине искомого угла. Углы между высотами конусов равны искомому Учащимся предлагается рассмотреть компьютерное изображение и сравнить его с тем, что получилось на моделях. (Рисунок 5) Рисунок 5 У: Нужны ли основания для решения? (уберем основания конусов), угол между чем нам нужно найти? (Рисунок 6) Рисунок 6 О: Между двумя наклонными. У: Какие эти наклонные? О: Равные. У: Как они наклонены к плоскости? О: Под одним и тем же углом. У: Чему равен угол наклона этих прямых к плоскости? О: Половине искомого угла. У: Можно ли определить угол между проекциями этих наклонных? О: Да. Проекции наклонных делят угол в 360° градусов на три равные части, значит, угол между ними равен 120°. У: Пусть высота конуса ℎ, искомый угол 𝛾. Какой отрезок входит и в треугольник, содержащий данный угол, и в треугольник, содержащий искомый угол? О: 𝑂𝐴1 . У: Выразим его длину через элементы треугольника 𝑂𝐴1 𝐴. 𝛾 О: 𝑂𝐴1 = ℎ ∙ cos . 2 У: Чем отрезок 𝑂𝐴1 является в треугольнике 𝑂𝐴1 𝑀1 ? О: Гипотенузой. У: Какая функция известного угла связывает 𝑂𝐴1 и 𝐴1 𝑀1 ? О: 𝑂𝐴1 = 𝐴1 𝑀1 sin ∠𝐴1 𝑂𝑀1 У: Можно ли выразить длину 𝐴1 𝑀1 или отрезка ему равного через обозначенные элементы? Есть ли отрезки равные 𝐴1 𝑀1 ? О: Да, отрезок 𝐴𝑀. У: Чему равна его длина? 𝛾 О: Из прямоугольного треугольника 𝑂𝑀𝐴: 𝐴𝑀 = ℎ ∙ sin . 2 У: Чему равен ∠𝐴1 𝑂𝑀1 ? 1 О: ∠𝐴1 𝑂𝑀1 = ∠𝐴1 𝑂𝐵1 = 60°. 2 У: Так чему равна длина отрезка 𝑂𝐴1 ? О: 𝑂𝐴1 = ℎ∙sin 𝛾 2 sin 60° 𝛾 = 2√3∙ℎ∙sin 2 3 . У: Приравняем выражения для 𝑂𝐴1 . 𝛾 2√3∙ℎ∙sin 2 3 О: ℎ ∙ cos = 𝛾 2 . Отсюда 𝑡𝑔 𝛾 2 = √3 . 2 У: Найдем величину искомого угла через 𝑎𝑟𝑐𝑐𝑜𝑠. О: cos 𝛾 = 𝛾 2 2 𝛾 2 ) 2 1−(𝑡𝑔 ) 1+(𝑡𝑔 = 3 4 3 1+ 4 1− 1 1 7 7 = . Значит, 𝛾 = arccos .


