Временная стоимость денег (ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ)

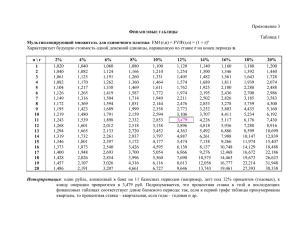
Основной областью
применения простых
процентной и учетной
ставок являются
краткосрочные
финансовые операции,
длительность которых
менее 1 года.
Простые проценты
Наращение – это процесс увеличения
первоначальной сумму (PV) до будущего значения
(FV), под действием ставки (r) за n периодов.
(Депозитная операция)
Виды ставок
1. Декурсивная ставка
2. Учетная (антисипативная)
ставка
(ставка дисконтирования)
𝐹𝑉−𝑃𝑉
𝑟𝑡 =
𝑃𝑉
𝐹𝑉−𝑃𝑉
𝑑𝑡 =
𝐹𝑉
Расчет будущей стоимости денег по
простым процентам:
1. Декурсивная ставка:
𝐹𝑉=PV(1+nr).
Задача 1
Ссуда в размере 120 000 руб. выдана на полгода по простой ставке
процентов 18 % годовых. Определите наращенную сумму.
Ответ : наращенная сумма (FV) 130800 рублей.
2. Антисипативная ставка:
𝑃𝑉
𝐹𝑉=
.
(1−𝑛𝑑)
Задача 2
Вексель учтен банком за 0,5 года до даты погашения по простой учетной
ставке 14 % годовых. Банк выплатил сумму 15000. Определить
номинальную стоимость векселя.
Ответ : номинальная стоимость векселя(FV) 16129,03 рублей.
Начисление процентов за полное
число дней:
1. Декурсивная ставка:
𝑡
𝐹𝑉=PV(1+ r).
𝑘
где К – временная база,
продолжительность года в
днях,
t – количество дней
проведения операции.
2. Антисипативная ставка:
𝐹𝑉=
𝑃𝑉
.
𝑡
(1− 𝑑)
𝑘
Точное число дней - по календарю или по специальной таблице номеров дней в
году. (Примеры определения: если деньги вложены 1 марта и вернут их 15
апреля – расчет по таблице 1 марта – 60-ый день в году, а 15 апреля 105-ый
день, то точное количество дней рассчитывается как (105-60) +1= 46 дней.
Точное число дней - по календарю или по специальной таблице номеров дней в году. (Примеры
определения: если деньги вложены 1 мая и вернут их через 5 месяцев – расчет по таблице 1 мая
– 121-ый день в году, а 5 месяцев пройдут и закончатся 30-ым сентября это 273-ий день, то
точное количество дней рассчитывается как (273-121) +1= 153 дня.
Определяя приближенную продолжительность ссуды, сначала
подсчитывают число полных месяцев и умножают его на 30. Затем
добавляют число дней в неполных месяцах.
ДЛЯ ВЕКСЕЛЕЙ ИСПОЛЬЗУЕТСЯ 2 СООТНОШЕНИЕ! 365/360
В некоторых задачах дается срок: например владелец предъявил вексель банку-эмитенту
для учета за 45 дней до даты погашения. В этом случае t=45 дней. (45/360)
Задача 3
Компании предложено купить товар с оплатой немедленно 100 000
рублей 1 марта 2011 года, либо оплатить товар через полтора месяца (15
апреля) обеспечивая поставщику 15% доходность. Рассчитать сумму через
полтора месяца тремя способами.
Ответ : 1) t = 46 , наращенная сумма (FV) 101890,41 рублей.
2) t = 46 , наращенная сумма (FV) 101916,70 рублей.
3) t = 45 , наращенная сумма (FV) 101875 рублей.
Задача 4
Ссуда в размере 10 млн. рублей выдана 1 мая с возвратом 31 декабря этого
года под 45% годовых (простая процентная ставка). Определить
наращенную сумму этого кредита по каждому из трех способов.
Ответ : 1) t = 244 , наращенная сумма (FV) 13,008 млн. рублей.
2) t = 244 , наращенная сумма (FV) 13,05 млн. рублей.
3) t = 241, наращенная сумма (FV) 13,013 млн. рублей. 241 день, потому что
8 месяцев умножить на 30 дней +1 день это 31 декабря.
Задача 5
Определить период начисления, если первоначальная сумма 10 000,00
рублей вырастет до 40 000,00 при 28 % .
Ответ : за 10,71 лет сумма 10 000,00 рублей вырастет до 40 000,00 при 28 % .
Задача 6
Определить простую ставку процента, при которой первоначальный
капитал 44 млн. достигнет 80 млн. через год.
Ответ : простая ставка 81,82%.
Дисконтирование – это процесс приведения
известного или предполагаемого FV к его
современному значению PV , под действием ставки
(r) за n периодов.
Виды ставок
1. Декурсивная ставка
(математическое
дисконтирование)
𝐹𝑉
PV=
,
1+𝑛𝑟
𝐹𝑉
PV=
𝑡
𝑘
1+ 𝑟
.
2. Учетная (антисипативная)
ставка (Банковский учет)
PV=FV(1 - nd),
𝑡
PV=FV(1 - d).
𝑘
Используется 2 соотношение k и t
Задача 7
Покупатель обязуется оплатить поставщику стоимость закупленных
товаров через 90 дней после поставки в сумме 1 млн. рублей. Уровень
простой процентной ставки составляет 30% годовых (обыкновенные
проценты). Определить текущую стоимость товаров?
Ответ : PV = 1 / (1 + 90 / 360 · 0,3) = 0,93 млн. рублей.
Задача 8
Владелец векселя номиналом 25 тыс. рублей обратился в банк с
предложением учесть его за 60 дней до наступления срока погашения.
Банк согласен выполнить эту операцию по простой учетной ставке 35%
годовых. Чему равна выкупная цена векселя и сумма дисконта?
Ответ : PV = 25000 · (1 – 60/360 · 0,35) = 23541,7 руб.,
d = FV – PV = 25000 – 23541,7 = 1458,3 руб.
Сложные проценты
Наращение
Дисконтирование
𝐹𝑉 = 𝑃𝑉(1 + 𝑟)𝑛 =PV*FM1(r,n),
где FM1(r,n)
мультипликатирующий множитель.
Формула наращения по сложным
процентам при начислении их m-раз в
году
𝑛∗𝑚
𝐹𝑉 = 𝑃𝑉(1 + 𝑟/𝑚)
где m ≠ 1
,
𝐹𝑉
PV=
(1+𝑟)𝑛
= 𝐹𝑉 ∗ 𝐹𝑀2 𝑟, 𝑛
где 𝐹𝑀2 𝑟, 𝑛 дисконтирующий множитель.
Формула дисконтирования по
сложным процентам при
начислении их m-раз в году:
𝐹𝑉
PV=
(1+𝑟/𝑚)𝑛𝑚
Задача 8
Ссуда размером 5 млн. рублей выдана на 2 года по номинальной сложной
процентной ставке 35% годовых с начислением процентов 2 раза в год.
Найти будущую сумму к концу срока ссуды.
Ответ : FV = 5 · (1 + 0,35 / 2)(2 · 2) = 9,531 млн. рублей.
Задача 9
Требуется определить современную стоимость платежа в размере 3 млн.
рублей, который должен поступить через 1,5 года; процентная ставка
составляет 40%. Рассчитать с учетом: а) m=1 раз в год; б) m=2 раза в год;
в) m=12 раз в год;
Ответ : при m = 1 - PV = 3 / (1 + 0,4)1,5 = 1,811 млн. рублей;
при m = 2 (начисление 1 раз в полугодие) PV = (3 / (1 + 0,4 / 2)(2 · 1,5) = 1,736
млн. рублей;
при m = 12 (ежемесячное начисление) PV = (3 / (1 + 0,4 / 12)(12 · 1,5) = 1,663 млн.
рублей.
Непрерывная
процентная ставка
Эффективная годовая
процентная ставка
𝑟 𝑚
𝑟 = (1 + ) − 1,
𝑚
F𝑉 = 𝑃𝑉 ∗ 𝑒 ϱ𝑛 ,
где e=2,71828, ϱ –
непрерывная ставка(сила роста)
Формула наращения по сложным
процентам при начислении их m-раз в
году
𝑛∗𝑚
𝐹𝑉 = 𝑃𝑉(1 + 𝑟/𝑚)
где m ≠ 1
,
Чем выше ставка, тем больше уровень
дохода.
Задача 10
Чему будет равна через 3 года сумма 250 тыс. рублей, если сегодня
положить ее на банковский депозит под 15% годовых, начисляемых
непрерывно?
Ответ : FV = 250 · e(0,15 · 3) = 392,1 тыс. рублей.
Задача 11
Предприниматель может получить ссуду: а) на условиях ежемесячного
начисления процентов из расчета 26% годовых; б) на условиях
полугодового начисления процентов из расчета 27% годовых. Какой
вариант наиболее предпочтительнее?
Ответ : а) r =(1+0,26/12)(12) -1=0,2933 или 29,3%
б) r =(1+0,27/2)(2) -1=0,2882 или 28,8%