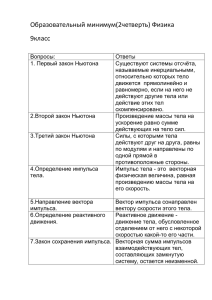
Закон сохранения момента импульса

Внутренние
силы
–
это силы
взаимодействия между материальными
точками механической системы.
Внешние силы – это силы, с которыми
на материальные точки механической
системы действуют внешние тела.
Замкнутая
система
–
это
механическая система тел, на которую не
действуют внешние силы.
Однородность пространства заключается в
том, что при параллельном переносе в
пространстве замкнутой системы тел как целого ее
физические свойства и законы движения не
изменяются, иными словами, не зависят от выбора
положения начала координат инерциальной
системы отсчета.
Пространство называется изотропным, если
поворот системы отсчета на произвольный угол не
приведет к изменению результатов измерений.
Центром масс (или центром инерции) системы
материальных точек называется воображаемая точка С,
положение которой характеризует распределение массы
этой системы. Ее радиус-вектор:
n

rc 
Скорость центра масс:
m r
i
i 1
i
m
n
dr i
m
i
 drc 
dt
i 1
Vc 


dt
m
n
Учитывая , что p   m  , а
i i
i 1
n
m V
i 1
i
i
m
 , то
 pi  p
n

p  mV c
i 1
т.е.импульс системы равен произведению массы системы
на скорость ее центра масс.
Подставим формулу для импульса системы во
второй закон Ньютона, получим:
dVc
m
 F1  F2  ...Fn
dt
- закон движения центра масс: центр масс
системы движется как материальная точка, в
которой сосредоточена масса всей системы и на
которую действует сила, равная геометрической
сумме всех внешних сил, приложенных к системе.
Закон сохранения импульса.
Рассмотрим механическую систему из n тел, масса
 и скорость


которых соответственно равны m1 ,m 2 ,, mn и 1 ,  2 , …,  n .
Второй закон Ньютона для каждого из n тел механической
системы:
 

d
m11   F1  F
dt
 

d
m2 2   F2  F
dt ……………….
 

d
mn n   Fn  Fn
dt
 

равнодействующие
внутренних
сил,
F1, F2,..., Fn действующих на каждое тело механической системы;
 

F1 , F2 ,..., Fn - равнодействующие внешних сил, действующих на
каждое тело механической системы.
 n 
p   mii - импульс системы .
i 1
Геометрическая сумма внутренних сил механической
системы по третьему закону Ньютона равна нулю.
Сложим почленно уравнения,
получим:


dp  
 F1  F2  ...  Fn
dt
Производная по времени от импульса механической
системы равна геометрической сумме внешних сил,
действующих на систему.
В случае замкнутой системы


dp n d
  mi i   0
dt i 1 dt
Внешние силы отсутствуют (или геометрическая сумма
всех внешних сил равна нулю).
http://www.youtube.com/watch?v=j2Bcjt2fWSk
Закон сохранения импульса: импульс замкнутой
системы сохраняется, т. е. не изменяется с течением
времени.
 n 
p   mii  const
i 1
Закон сохранения импульса - фундаментальный закон
природы (он универсален).
Закон сохранения импульса - следствие однородности
пространства.
Импульс сохраняется и для незамкнутой системы, если
геометрическая сумма внешних сил равна нулю.
Момент импульса.
Момент
импульса
материальной
точки
относительно неподвижной точки О - физическая
величина, определяемая векторным  произведением
радиуса-вектора материальной точки ri , проведенного


p

m

из точки О, на импульс
этой материальной
i
i i
  


точки:
L  r , p   r , m  
i
i
i
i
i
i
Модуль вектора момента импульса
Li  ri pi sin   mi  i ri sin   pi l ,


где α – угол между векторами ri и pi ;
l  r sin 
- плечо импульса. Перпендикуляр опущен из
точки на прямую, вдоль которой направлен импульс
частицы.

Li -
осевой вектор (псевдовектор), его
направление совпадает с направлением
поступательного движения
правого винта при


его вращении от ri к pi .
Момент импульса материальной точки
относительно неподвижной оси z - скалярная
величина Liz, равная проекции на эту ось вектора
момента импульса, определенного относительно
произвольной точки данной оси z.
Значение момента импульса Liz не зависит от
положения точки О на оси z.
Момент
импульса
отдельной
точки
вращающегося абсолютно твердого тела
Li Z  mi  i r
Момент импульса абсолютно твердого тела
относительно неподвижной оси z - сумма
моментов
импульса
отдельных
его
частиц
относительно той же оси равен произведению момента
инерции тела относительно той же оси на угловую
n
скорость:
LiZ   mi vi ri
i 1
LZ  J Z 
n
n
n
LZ   mi i ri   mi ri     mi ri 2  J Z 
2
i 1
i 1
i 1
Момент силы.
Момент силы относительно неподвижной точки
О - физическая величина, определяемая векторным

произведением радиуса-вектора r , проведенного
из

точки О в точку А приложения силы, на силу F
 
М  r, F

M - осевой вектор (псевдовектор), его направление
совпадает с направлением поступательного
движения


правого винта при его вращении от r к F .
Модуль вектора момента силы
M  F r sin  F l


 - угол между r и F ,
r sin  l - кратчайшее расстояние
действия силы и точкой - плечо силы.
между линией
Момент силы относительно неподвижной оси z скалярная величина Mz, равная проекции на эту ось
вектора M момента силы, определенного относительно
произвольной точки О данной оси z .
Значение момента Mz не зависит от выбора положения
точки О на оси z. Если ось z совпадает с направлением
вектора M , то момент силы представляется в виде
вектора, совпадающего с осью:
 


Mz  r F
  z
Закон сохранения момента импульса.
Еще одна форма записи уравнения динамики
вращательного
движения
твердого
тела
производная момента импульса твердого тела
относительно оси равна моменту силы относительно
той же оси.
dLZ
dt
 MZ
Продифференцировав LZ  J Z 
по времени, получим:
dLZ
d
 JZ
 J Z  M Z
dt
dt
Производная вектора момента импульса твердого тела
равна моменту (сумме моментов) внешних сил.


dL
M
dt
В замкнутой системе
момент внешних сил


dL
M 0
и
 0 , откуда
dt

L  const
Закон сохранения момента импульса: момент
импульса замкнутой системы сохраняется, т. е. не
изменяется с течением времени.
http://www.youtube.com/watch?v=UVrHMsfnNhQ
http://www.youtube.com/watch?v=0k276y9kuQQ&feature=r
elated
Закон сохранения момента импульса —
фундаментальный закон природы.
Закон сохранения момента импульса –
следствие изотропности пространства.
Изотропность
пространства
инвариантность физических законов
относительно выбора направления осей
координат
системы
отсчета
(относительно
поворота
замкнутой
системы в пространстве на любой угол).
Работа.
Работа силы – количественная характеристика процесса
обмена энергией между взаимодействующими телами.
Работа – величина скалярная.
Работа постоянной силы F , составляющей угол α с
направлением прямолинейного движения тела – равна
произведению проекции силы F на направление
перемещения ( FS  F cos  ), умноженной на перемещение
точки приложения силы:
S
A  FS s  F s cos 


Элементарная работа силы F на перемещении dr
 

dA  F dr  F cos ds  FS ds
Работа силы на участке траектории 1 – 2
2
2
1
1
A   F ds cos   FS ds
Для вычисления интеграла надо знать зависимость от
вдоль траектории 1 – 2.
Единица работы – 1Дж=1Н·м.
1джоуль – работа, совершаемая силой равной 1Н на пути
1м.
Геометрический смысл выражения для А искомая работа определяется на графике
площадью закрашенной фигуры.
Мощность.
Мощность – физическая величина, характеризующая
скорость совершения работы:
N
dA
dt
Мощность – величина
 
 скалярная.
За время dt сила F совершает работу F dr , и мощность,
развиваемая этой силой, в данный момент времени равна:
 
F dr  
N
 F
dt
Мощность, развиваемая силой
- равна скалярному
произведению вектора силы на вектор скорости, с
которой движется точка приложения этой силы:

N  F
Единица мощности –1Вт=1Дж/с.
1ватт – мощность, при которой за время 1с совершается
работа 1Дж.
Кинетическая энергия.
Кинетическая энергия механической системы – энергия
механического движения этой системы.

Сила F , действуя на покоящееся тело и вызывая его
движение, совершает работу, а энергия движущегося тела
возрастает на величину затраченной работы. Работа dA

силы
на пути, который тело прошло за время
F
возрастания скорости от 0 до  , идет на увеличение
кинетической энергии тела dЕк :

 
 
d 
 m 2 
F dr  m dr  m d  m d  d 
  dЕк
dt
 2 
Связь работы и кинетической энергии - приращение
кинетической энергии материальной точки (тела) на
элементарном перемещении равно элементарной работе
на том же перемещении: dЕк  dA
Кинетическая энергия тела массой , движущегося со
скоростью - определяется работой, которую надо
совершить, чтобы сообщить телу данную скорость:
m 2
Ек 
2
Характерные свойства кинетической энергии:
— всегда положительна;
— неодинакова в разных инерциальных системах
отсчета;
— является функцией состояния системы.
Работа сил при перемещении из точки 1 в точку 2:

  
m22 m12
A12   F dr   m d  m   d 

 Ек 2  Ек 1
2
2
1


2
2
2
1
1
Теорема о кинетической энергии – приращение
кинетической энергии материальной точки на некотором
перемещении равно алгебраической сумме работ всех сил,
действующих на материальную точку на том же
перемещении:
Ек 2  Ек1  A12
Континуальная концепция и
модель континуума.
Для описания силового взаимодействия тел в
классической механике использовались две концепции:
близкодействия (непосредственного взаимодействия
при соприкосновении) и дальнодействия (действия на
расстоянии).
Хотя при описании классического механического
движения в принципе неважно, какая из концепций
принята, с философской точки зрения явно была
предпочтительнее
концепция
близкодействия.
Поэтому, чтобы и гравитационные силы можно было
рассматривать как близкодействующие, было введено
понятие силового поля.
Одно тело видоизменяет свойства окружающего
пространства, т.е. создает вокруг себя силовое
поле, а другое тело подвергается воздействию силы
со стороны поля в том месте, где оно находится. Т.о.
силовое поле выполняет роль переносчика
взаимодействия. Второе тело оказывает на первое
тело воздействие аналогичным образом.
Сначала такой подход был чисто умозрительным,
но ситуация в корне изменилась, когда ученые
занялись исследованием явлений, связанных с
электромагнитными волнами. Был обнаружен
материальный
носитель
дальнодействующих
электромагнитных сил – электромагнитное поле.
Выяснилось,
что
все
фундаментальные
взаимодействия имеют полевую природу.
Силовые поля являются векторными. Векторное
силовое поле считается заданным, если в каждой
точке пространства, где есть поле, задан вектор
поля, через который однозначно может быть
определена сила, воздействующая на частицу,
помещённую в эту точку.
Потенциальное и непотенциальное
силовые поля.
Потенциальное поле – поле, которое может быть
выражено через некоторую скалярную функцию
 ( x, y, z, t ) , называемую потенциальной, по следующему
правилу:

       
F  
i
j
k 
y
z 
 x

F   grad

F   grad
Градиент скалярной функции – вектор,
направленный
в
сторону
максимально
быстрого возрастания этой функции и
численно равный скорости её возрастания в
указанном направлении.
Следовательно, сила направлена в сторону
максимально
быстрого
убывания
потенциальной функции, т.е. против вектора
градиента.
Частным случаем потенциальных
полей являются
консервативные поля – такие потенциальные поля,
которые явно не зависят от времени. В этом случае поле
является стационарным, а потенциальная функция П в
этом случае называется потенциальной энергией
частицы во внешнем консервативном поле.
Консервативные силы – силы, работа которых при
перемещении тела из одного положения в другое, не
зависит от того, по какой траектории это перемещение
произошло, а зависит только от начального и конечного
положений тела. Пример консервативной силы – сила
тяжести.
Диссипативная сила – сила, работа которой зависит от
траектории перемещения тела из одной точки в другую.
Пример – силы трения и сопротивления.
Работа консервативных сил по замкнутому пути равна
нулю.
A  A1b 2  A2 a1  0
Работы A1b 2 и A2 a1 не зависят от траектории перемещения;
они равны и отличаются только знаками.
Потенциальная энергия.
Потенциальная энергия – механическая энергия
системы тел, определяемая их взаимным расположением
и характером сил взаимодействия между ними.
Связь работы консервативных сил и
потенциальной энергии.
Работа
консервативных
сил
при
элементарном
(бесконечно малом) изменении конфигурации системы
равна приращению потенциальной энергии, взятому со
знаком «минус», так как работа совершается за счет
убыли потенциальной энергии.
dA  dЕп
Потенциальная энергия определяется с точностью до
некоторой произвольной постоянной:
 
П   F dr  C
С - постоянная интегрирования
Потенциальную энергию тела в каком-то определенном
положении считают равной нулю (выбирают нулевой
уровень отсчета), а энергию тела в других положениях
отсчитывают относительно нулевого уровня.
Связь между консервативной силой и потенциальной
энергией:

F   gradЕп
Для консервативных сил:
Fx  
Еп
x
В векторном виде:
Еп  Еп  Еп 
grad Еп 
i
j
k
x
y
z

i,
 
j, k
Fy  
Еп
y
Fz  
Еп
z

F   gradЕп
- градиент скаляра Е п
- единичные векторы координатных осей.
Закон сохранения полной
механической энергии.
Рассмотрим систему материальных точек массами
 

m , m ,, m , движущихся со скоростями  , , , .
Второй закон Ньютона для каждой из
материальных точек будет иметь вид:
1
2
n
1

d 1   
m1
 F1  F1  f 1 ,
dt



d 2 
m2
 F2  F2  f 2 ,
dt
 




d n
mn
 Fn  Fn  f n
dt
2
n
Точки движутся под действием сил, поэтому за время dt
 

совершают перемещения dr1 , dr2 ,, drn .
Каждое уравнение второго закона Ньютона умножим
скалярно на соответствующее перемещение, и учтем,
 
что dri   i dt , получим
    
 
m1 1 d1   F1  F1  dr1  f1 dr1 ,
    
m 2  2 d 2   F2  F2 dr2  f 2 dr2 ,




.....................................................
    
 
m n  n d n   Fn  Fn drn  f n drn


После сложения уравнений
   n  
Fi  Fi dri   f i dri
 m  d    
n
i 1
i


i
i
n
i 1

i 1
Первое слагаемое равно элементарному приращению
кинетической энергии системы dЕк :
 mi i2 
mi i di   d 
 dЕк

i 1
i 1
 2 
n


n
Второе
слагаемое
равно
элементарной
работе
внутренних и внешних консервативных сил, взятой со
знаком «минус», т.е. равно элементарному приращению
потенциальной энергии системы dЕп :

n
i 1

  
Fi Fi dri  dЕп
Правая часть равенства определяет работу внешних
неконсервативных сил, действующих на систему.
Изменение полной механической энергии системы –
равно работе внешних неконсервативных сил,
действующих на систему.
d Ек  Еп   dA
В случае отсутствия внешних неконсервативных сил:
d Ек  Еп   0
откуда
Ек  Еп  E  const
Закон сохранения механической энергии:
в системе тел, между которыми действуют только
консервативные силы, полная механическая
энергия сохраняется, т.е. не изменяется со
временем.
Ек  Еп  E  const
Еще одна формулировка закона сохранения энергии:
в консервативных системах полная механическая
энергия сохраняется, т.е. не изменяется с течением
времени.
Закон
сохранения
энергии
–
следствие
однородности времени.
Превращение энергии на примере свободного
падения тела.
Законы сохранения и свойства симметрии
пространства-времени. Теорема Нётер.
Рассмотренные законы сохранения импульса, момента импульса и
энергии применимы и за пределами механики. Это означает, что в
основе законов сохранения лежат более общие свойства природы,
чем те, которые изучаются в механике.
Согласно современным представлениям, законы сохранения
связаны со свойствами симметрии физических систем.
Согласно теореме Нётер каждой непрерывной симметрии
физической системы соответствует некоторый закон
сохранения.
И наоборот, если установлен экспериментально какой-либо закон
сохранения. То это позволяет сделать определенное заключение о
фундаментальных
свойствах
симметрии
рассматриваемой
системы. Симметрия и законы сохранения не следствия одно
другого, а равноправные проявления общих фундаментальных
свойств материи.
Амалия Эмми Нётер
(1882-1935)
выдающийся немецкий математик.
В 1915 году Нётер внесла вклад в разработку
Общей теории относительности.
В основном труды Нётер относятся к алгебре, где
они
способствовали
созданию
нового
направления,
известного
под
названием
абстрактной алгебры. В эту область Нётер внесла
решающую роль.
Большой вклад внесла Нётер в математическую
физику,
где
её
именем
называется
фундаментальная теорема теоретической физики,
связывающая законы сохранения с симметриями
системы. На этом плодотворном подходе основана
знаменитая серия книг «Теоретической физики»
Ландау-Лифшица. Особенно важное значение
имеет теорема Нётер в квантовой теории поля, где
законы
сохранения,
вытекающие
из
существования определенной группы симметрии,
обычно
являются
главным
источником
информации о свойствах исследуемых объектов.
Объединяющая роль закона сохранения
энергии в естествознании.
В основе явлений природы лежит движение материи.
Существует много форм движения материи. Для описания
механической формы движения вводится понятие
механического импульса. Для описания тепловой формы
движения материи вводятся иные характеристики
состояния, например, температура. Все такие величины
отражают качественные особенности различных форм
движения материи. Однако опыт обнаруживает взаимную
превращаемость различных форм движения материи.
Следовательно, различные формы движения материи имеют
нечто общее и могут, кроме специфических величин,
характеризоваться также величиной, которая с равным
правом относится ко всем формам движения и отражает их
взаимную превращаемость. Такой физической величиной
является энергия. Энергия есть общая мера различных
форм движения материи.
Закон сохранения и превращения энергии
утверждает: суммарная энергия изолированной
системы не изменяется; при эволюции системы
могут изменяться доли энергий различного
вида, что объясняется переходом энергии из
одного вида в другой.
Обмен энергией между природными системами
обусловливает объединяющую роль энергии в
природе и в естествознании. Преобразование
энергии происходит в любых природных процессах
и выполняющийся при этих преобразованиях
закон сохранения и превращения энергии
связывает все явления природы воедино.
Законы сохранения говорят о том, какие процессы
невозможны в природе. Любой процесс, в котором
нарушился хоть бы один из законов сохранения,
невозможен. Т.е. законы сохранения работают как
принципы запрета. В этом качестве законы
сохранения играют важную методологическую
роль. Они являются мощным инструментом
теоретического
исследования
всевозможных
процессов, происходящих в природе от микромира
до космических явлений.
 Курс физики. Учебник для вузов/под. ред. проф.
В.Н. Лозовского. СПб: Лань, 2009. Т.1
 Т.И. Трофимова. Краткий курс физики. Учебное
пособие для вузов. М: КноРус, 2010.
 Лозовский В.Н., Лозовский С.В. Концепции
современного естествознания. Учебное пособие
для вузов. - СПб: Лань, 2006.
 Википедия http://ru.wikipedia.org/