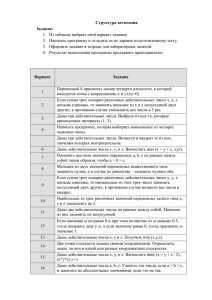
Приложение 6. Таблица вариантов заданий

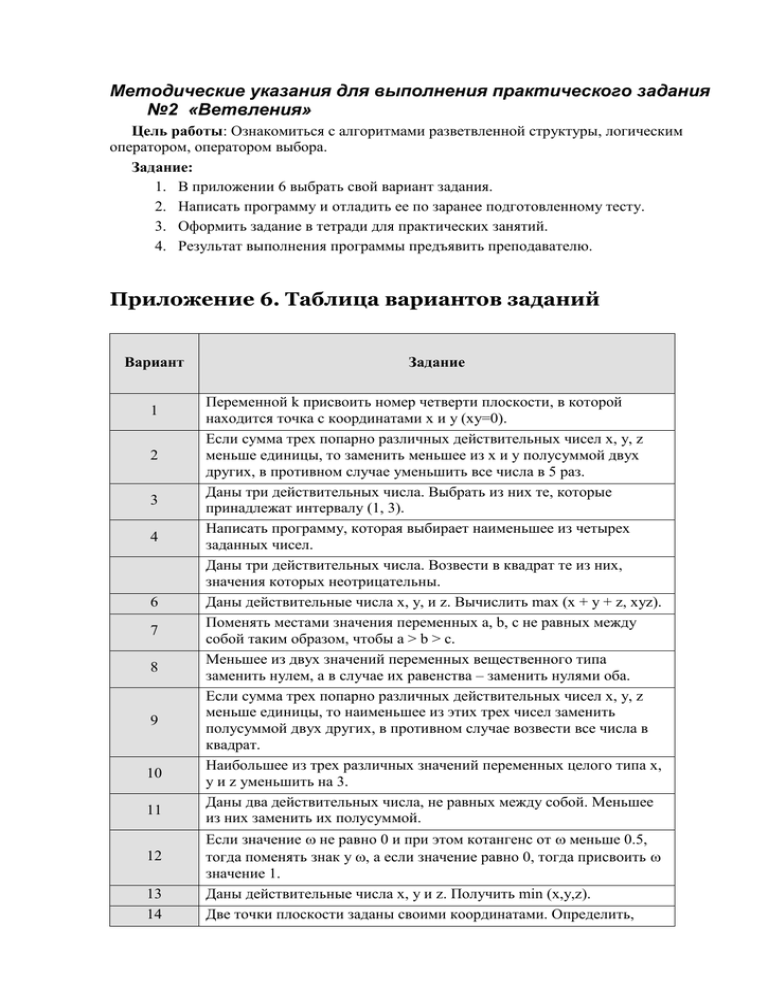
Методические указания для выполнения практического задания
№2 «Ветвления»
Цель работы: Ознакомиться с алгоритмами разветвленной структуры, логическим
оператором, оператором выбора.
Задание:
1. В приложении 6 выбрать свой вариант задания.
2. Написать программу и отладить ее по заранее подготовленному тесту.
3. Оформить задание в тетради для практических занятий.
4. Результат выполнения программы предъявить преподавателю.
Приложение 6. Таблица вариантов заданий
Вариант
1
2
3
4
6
7
8
9
10
11
12
13
14
Задание
Переменной k присвоить номер четверти плоскости, в которой
находится точка с координатами x и y (xy=0).
Если сумма трех попарно различных действительных чисел x, y, z
меньше единицы, то заменить меньшее из x и y полусуммой двух
других, в противном случае уменьшить все числа в 5 раз.
Даны три действительных числа. Выбрать из них те, которые
принадлежат интервалу (1, 3).
Написать программу, которая выбирает наименьшее из четырех
заданных чисел.
Даны три действительных числа. Возвести в квадрат те из них,
значения которых неотрицательны.
Даны действительные числа х, у, и z. Вычислить max (x + y + z, xyz).
Поменять местами значения переменных a, b, c не равных между
собой таким образом, чтобы а > b > c.
Меньшее из двух значений переменных вещественного типа
заменить нулем, а в случае их равенства – заменить нулями оба.
Если сумма трех попарно различных действительных чисел x, y, z
меньше единицы, то наименьшее из этих трех чисел заменить
полусуммой двух других, в противном случае возвести все числа в
квадрат.
Наибольшее из трех различных значений переменных целого типа х,
у и z уменьшить на 3.
Даны два действительных числа, не равных между собой. Меньшее
из них заменить их полусуммой.
Если значение  не равно 0 и при этом котангенс от  меньше 0.5,
тогда поменять знак у , а если значение равно 0, тогда присвоить 
значение 1.
Даны действительные числа х, у и z. Получить min (x,y,z).
Две точки плоскости заданы своими координатами. Определить,
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
лежат ли они в одной или разных координатных плоскостях.
Даны действительные числа х, у, и z. Вычислить min( (x + y + z / 2),
(x*y*z) ) +1.
Даны действительные числа a, b, c. Удвоить эти числа, если a > b > c,
и заменить их абсолютными значениями, если это не так.
Известно, что из четырех чисел одно отлично от трех других, равных
между собой. Присвоить номер этого числа переменной n.
Написать программу, которая выбирает наибольшее из четырех
заданных чисел.
Даны действительные числа x и y. если x и y отрицательны, то
каждое значение заменить его модулем; если отрицательно только
одно из них, то оба значения увеличить на 0.5, в противном случае
извлечь из каждого квадратный корень.
Две точки плоскости заданы своими координатами. Определить,
лежат ли они в одной (распечатать ее номер) или разных
координатных четвертях.
Даны два действительных числа. Заменить первое число нулем, если
оно меньше или равно второму, и удвоить оба числа в противном
случае.
Даны действительные числа a, b, c, d. Если a < b < c < d, то каждое
число заменить небольшим из них; если a > b > c > d, то числа
оставить без изменения; в противном случае все числа заменить их
квадратами.
Даны действительные числа х, у и z. Получить max (x,y,z).
Даны три действительных числа. Выбрать из них те, которые
принадлежат интервалу (1, 3).
Меньшее из двух значений переменных вещественного типа
заменить нулем, а в случае их равенства – заменить нулями оба.
Даны действительные числа х, у и z. Обнулить отрицательные числа.
Известно, что из трех целых чисел одно отлично от трех других,
равных между собой. Присвоить номер этого числа переменной n.
Наименьшее из трех различных значений переменных целого типа х,
у и z увеличить на 3.
Если сумма трех попарно различных действительных чисел x, y, z
больше единицы, то наибольшее из этих трех чисел заменить
полусуммой двух других, в противном случае возвести все числа в
квадрат.
Даны два действительных числа, не равных между собой.
Наибольшее из них заменить их полусуммой.