Нейронные сети
реклама
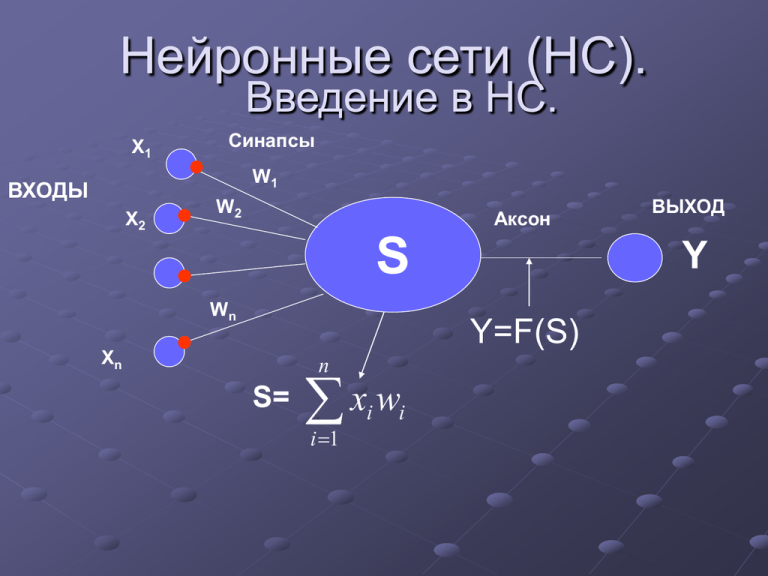
Нейронные сети (НС). Введение в НС. Х1 Синапсы W1 ВХОДЫ Х2 W2 Аксон S Wn Y Y=F(S) Хn n S= xw i 1 i i ВЫХОД Виды активационных функций F Название функция Область значений линейная f(s)= ks (-) полулинейная f(s)= ks , s > 0 f(s)= 0 , s <= 0 (0,) логистическая (сигмоидальная) f(s)= 1/(1+e-as) (0,1) гиперболический тангенс (сигмоидальная) f(s)= (eas-e-as) / (eas+e-as) (-1,1) Экспоненциальная f(s) = e-as (0,) Синусоидальная f(s) = sin(s) (-1,1) Сигмоидальная (рациональная) f(s) = s / (a+|s|) (-1,1) Шаговая (линейная с насыщением) f(s) = -1, s <= -1 f(s) = 0, -1 < s < 1 f(s) = 1, s >= 1 (-1,1) Пороговая f(s) = 0, s < 0 f(s) = 1, s >= 0 (0,1) Виды активационных функций Название функция Область значений Модульная f(s) = |s| (0, Знаковая (сигнатурная) f(s) = sgn(s), s!=0 f(s) = -1, s = 0 (-1,1) Квадратичная f(s) = s2 (-1,1) Радиально-базисная 1 f ( s) e 2 (X X ) 2 2 (-∞,∞) Классификация нейронных сетей №1 Классификация по топологии 1.1 Полносвязные сети: Каждый нейрон передает свой выходной сигнал всем остальным нейронам в сети, включая самого себя. 1.2 Многослойные или слоистые: Сеть разбивается на слои, где каждый слой содержит совокупность нейронов с едиными входными сигналами. Слои нумеруются слева на право, начиная с Многослойные сети делятся на: 1.2.1 Монотонные . 1.2.2 Сети без обратных связей: Обычная многослойная сеть, с 1-им ограничением, что нейроны q-ого слоя могут передавать сигнал нейронам (q+1)-ого слоя и никакому другому слою. 1.2.3 Сети с обратными связями: 1.2.3.1 Слоисто циклические: Многослойная сеть у которой выход передает свои сигналы 1-му слою 1.2.3.2 Слоисто-полносвязные: Состоит из слоев, каждый из которых представляет собой полносвязную сеть. 1.2.3.3 Полносвязные-слоистые: По своей структуре такие же как и 1.2.3.2, а функционально, в них не разделяют фазы обмена внутри слоя и передачи следующему, на каждом такте нейроны всех слоев применяют сигналы от нейронов как своего слоя, так и последующих. 1.3 Слабосвязанные сети: В слабосвязанных сетях нейроны располагаются в узлах прямоугольной форму или гексагональной решетки. Каждый нейрон связан с 4-мя (окрестность фон Неймана), 6-ью (окрестность Голея) или 8-мью (окрестность Мура) своими ближайшими соседями. №2 Классификация по типам структур: 2.1 Гомогенные: Нейроны одного типа с единой функцией активации. 2.2 Гетерогенные Нейроны с различными функциями активации. №3 Классификация по типу сигнала: Бинарные - двоичный сигнал Аналоговые. №4 Классификация по типу работы 4.1 Синхронные В момент времени t, лишь один нейрон меняет свое состояние. 4.2 Асинхронные Группа нейронов меняет свое состояние. как правило группа, значит весь слой. Типы задач, решаемые нейронными сетями. - Распознавание зрительных, слуховых образов - Ассоциативный поиск информации и создание ассоциативных моделей: синтез речи и формирование естественного языка; - Формирование моделей и различных нелинейных и трудно описываемых математических систем; - Системы управления и регулирования с предсказанием: управление роботами; - Разнообразные конечные автоматы: системы массового обслуживания, телекоммуникационные системы; - Принятие решений и диагностика, исключающие логический вывод, особенно в областях, где отсутствуют четкие математические модели: в медицине, криминалистике. Алгоритмы обучения НС делятся на обучение “с учителем" "без учителя" Схема обучения НС с учителем Входная обучающая выборка Нейронная сеть Выходной вектор нейронной сети Изменение веса Ошибка сети Известные значения Схема обучения НС без учителя Входная обучающая выборка Нейронная сеть Изменение веса Выходной вектор нейронной сети АЛГОРИТМЫ ОБУЧЕНИЯ НС Парадиг ма Правило обучения С Коррекция учителем ошибки Архитектура Алгоритм обучения Решаемая задача Однослойный и многослойный перцептрон Алгоритмы обучения перцептрона Обратное распространение Adaline и Madaline Классификация Распознавание образов Аппроксимация функций Прогнозирование Управление Больцмана Рекуррентная Алгоритм обучения Больцмана Классификация Распознавание образов Хебба Многослойная прямого распространения Линейный дискриминантный анализ Анализ данных Классификация Распознавание образов Векторное квантование Категоризация в середине класса Сжатие данных Соревновани Соревнование е Сеть ART ARTMap Классификация Распознавание Парадиг ма Правило обучения Без учителя Коррекци я ошибки Многослойная прямого распространения Проекция Саммона Категоризация в середине класса Анализ данных Хебба прямого распространения или соревнование Анализ главных компонентов Анализ данных Сжатие данных Сеть Хопфилда Обучение ассоциативной памяти Ассоциативная память Соревнование Векторное квантование Категоризация Сжатие данных SOM Кохонена SOM Кохонена Категоризация Анализ данных Сеть ART ART1, ART2 Категоризация Сеть RBF Алгоритм обучения RBF Классификация Распознавание образов Аппроксимация функций Прогнозирование Соревнов ание Смешан ная Коррекци я ошибки и соревнова ние Архитектура Алгоритм обучения Решаемая задача Задача классификации. С1-класс С2-класс Решение представим в виде р1 ……. р1 СМ-класс рN рN вектора c =c1,...,cM р2 0<cm<1 и р2 Ищем отображение PC или , Ищем отображение m(p). M cm 1 m1 Распознавание образов. Пусть темному полю соответствует Iij=1, светлому – Iij=0. Найти – по изображению распознать букву 1 вариант Решение – строится НС Ni* Nj входами, где каждому входу соответствует xk=Iij, k=1,…,Ni*Nj. Выходы сети – вероятность принятия данной буквы c1 I ij ... c M 2 вариант Решение – строится НС Ni* Nj входами, где каждому входу соответствует xk=Iij, k=1,…,Ni*Nj. Выход сети – номер m предъявленной буквы I ij m Прогнозирование одномерной функции. Функция задана на [0; t0], где t0 – текущее значение времени. Необходимо прогнозировать значение функции при t>t0. Считаем известными x0 f (t o ) x1 f (t 0 1 ) x2 f (t 0 1 2 ) x, i 0. xn f (t 0 1 n ) Будем прогнозировать значение функции в момент времени (t0+0) для 0>0. Как спрогнозировать несколько значений функции в разных точках? Возьмем i = = const, i=0,…,n+1. Х Нейронная сеть f(t0+0)=y Произведем сдвиг входных и выходного векторов xn : xn 1 x1 : x0 x0 : y Х Нейронная сеть f(t0+20)=y . Аппроксимация многомерной функции Рассматривается функция Y = f(x) Х Нейронная сеть y Литература 1. Навчальний посібник “Інтелектуальний аналіз даних/ Лєсна Н.С., Рєпка В.Б., Шатовська Т.Б. Харків: ХНУРЕ, 2003. 112 с. 2. А. Горбань, Д. Россиев Нейронные сети на персональном компьютере. – Новосибирск: Наука, 1996 – 276 c. 3. А.Н.Горбань Обучение нейронных сетей, М.: СП ПараГраф, 1991. 4. А.Н.Горбань, В.Л.Дунин-Барковский, А.Н.Кардин и др. Нейроинформатика, Отв. Ред. Новиков Е.А., РАН, Сиб. Отд., Институт выч. Моделирования – Новосибирск: Наука, 1998. 5. Keun-Rong Hsieh, Wen-Tsuen Chen A Neural Network Model which Combines Unsupervised and Supervised Learning// IEEE Trans. on Neural Networks. – 1993. – Vol.4, №2. 6. Горбань А.Н. Обучение нейронной сети. – М.: Изд-во СССР – США СП "Paragraph", 1990. – 160 с. 7. Ф. Уоссерман Нейрокомпьютерная техника. – М. Мир, 1992. 8. Нейронные сети. STATISTICA Neural Networks: Пер. с англ. – М.: Горячая линия – Телеком, 2000. – 182 с. 9. М.Б. Беркенблит. Нейронные сети. –М.: Мирос и ВЗМШ РАО, 1993. 10. Руденко О.Г., Бодянский Е.В. Основы теории искусственных нейронных сетей. – Харьков: ТЕЛЕТЕХ, 2002. – 317 с. 11. Kohonen, Т. Self-Organizing Maps, Second Edition, Berlin: SpringerVerlag, 1997.







