Лекция 1. Движение с постоянной скоростью

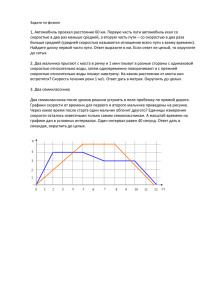
Курс дистанционного обучения
Физика
Лекция 1. Движение с постоянной скоростью
С.Е. Муравьев, к.ф.-м.н.,
доцент кафедры теоретической физики
НИЯУ МИФИ
Лекция 1. Движение с постоянной скоростью
1. Определение скорости
Рассмотрим три тела
1м
Какое
1с
из
11 м
них
10 с
перемещалось
19 м
быстрее?
20 с
Лекция 1. Движение с постоянной скоростью
Для сравнения быстроты перемещения тел нужно
брать перемещение каждого тела за один и тот же
интервал времени (например единичный)
S
v
t
Это отношение представляет собой расстояние,
пройденное за единицу времени
А если тело всегда двигалось.
Что такое
S ? И что такое t ?
Лекция 1. Движение с постоянной скоростью
Любые! Но соответствующие друг другу. Например:
500 км
А
В
10 ч
500 250 50
v


10
5
1
км
ч
Формулу, связывающую расстояние, время и
скорость, можно «прочитать» так, как нам нужно
S
v
t
S  vt
S
t
v
Лекция 1. Движение с постоянной скоростью
Пример 1. Маленький жук ползет с постоянной скоростью вдоль
сделанного из проволоки квадрата. Чтобы совершить полный оборот
жуку потребовалось время t . Какое время потребуется жуку, чтобы
проползти вдоль диагонали квадрата, если он будет двигаться с
вдвое большей скоростью?
a
a
4a
v
t
t1 
t1 
2t
8
2a
2at
2t


2v
2  4a
8
Лекция 1. Движение с постоянной скоростью
Пример 2. Два тела находятся на расстоянии l друг от
друга. Тела одновременно начинают двигаться навстречу
друг другу с постоянными скоростями v 1 и v 2 . Через какое
время и на каком расстоянии от начального положения
первого тела произойдет встреча? То же, если первое тело
движется за вторым ( v 1  v 2 ).
Лекция 1. Движение с постоянной скоростью
Основная идея решения этой задачи заключается в
совместном использовании этих соотношений для
обоих тел в момент их встречи.
l1  v1t
v1
l2  v 2 t
l1
l1  l2  l

l
t
v1  v2
l
v1t  v2t  l
v2
l2
Лекция 1. Движение с постоянной скоростью
Пример
движется
3.
Вагон
длиной
равномерно
l
со
v2
v1
скоростью v1 . Провожающий бежит
со скоростью v2 ( v1  v2 ). В начальный момент провожающий находится около начала вагона. Какой путь пробежит провожающий к
тому моменту, когда он окажется около конца вагона (начальное
положение вагона и провожающего показано на рисунке)?
Лекция 1. Движение с постоянной скоростью
l1  v1t
l2  v 2 t
v1t  v2t  l

v2l
l2 
v1  v2
v2
v1
l
t
v1  v2
1. Движение с постоянной скоростью
5. По озеру со скоростью vЛекция
движется
корабль длиной l . В некоторый
1
момент времени от кормы корабля к его носу начинает двигаться маленький катер. Скорость катера v2 ( v2  v1 ). Доплыв до носа корабля катер
разворачивается и движется в направлении кормы. Через какое время
после начала движения катер достигнет кормы?
Пример 4. Из пунктов A и B одновременно навстречу друг другу начинают двигаться два тела. Через некоторое время они встречаются и продолжают двигаться в тех же направлениях. Первое достигает конечного
пункта через время t1 после встречи, второе - через время t2 . Через какое время после начала движения тела встретились?
Лекция 1. Движение с постоянной скоростью
В.И.Арнольд (1937-2010). Еще студентом Арнольд
решил одну из проблем Гильберта – задач, поставленных
знаменитым
математиком
Д.Гильбертом
перед
математикой 20 века на Всемирном математическом
конгрессе в 1900 году. Наибольшую известность получили
работы Арнольда, посвященные доказательству теоремы,
которую позже назвали теоремой Колмогорова-АрнольдаМозера о стабильности интегрируемых гамильтоновых
систем. Несмотря на то, что Арнольд был одним из
глубочайших современных математиков, он считал, что
математика не может существовать ради математики, а
должна быть языком естествознания, т.е. … частью
физики.
Отметим, что по числу цитирований в научной литературе
Арнольд занимает первое место среди всех советских и
российских ученых.
Лекция 1. Движение с постоянной скоростью
Кажется, что мало данных! С другой стороны
s1  v 1t
s2  v 2 t
Но, то расстояние, что первое тело прошло до встречи, равно расстоянию, пройденному вторым после. И
наоборот. Поэтому
s1 v1t
t2  
v2 v2
t  t1t2
s2 v 2t
t1  
v1 v1
Лекция 1. Движение с постоянной скоростью

v
Пример 5. В системе, изображенной на рисунке,
2
левый блок движется вниз со скоростью v 1 , правый
- вверх со скоростью v 2 . Найти скорость груза.

v
1
Лекция 1. Движение с постоянной скоростью
За малый интервал времени t левый блок опустится
на расстояние v1t , правый - поднимется на расстояние
v2
A
D
E
v 2 t . Длина участка веревки от точки A до точки B
увеличится на величину v1t , длина участка веревки между
точками C и D увеличится на v1t  v2t  v1  v2  t , и
следовательно,
длина
участка
веревки
AD
B
C
F
v1
увеличится
на
v1t  v1  v2  t   2v1  v2  t . А так как сама точка E переместилась вверх
на величину
v 2 t , то груз за рассматриваемый интервал времени
переместится вверх на расстояние
скорость груза равна 2 v1  v2  .
2 v1  v2  t . Поэтому мгновенная
Лекция 1. Движение с постоянной скоростью
Пример.
Около
стенки
стоит
палочка
длиной l , на нижнем конце палочки сидит
жук. В некоторый момент времени палочка

v1

v
начинает двигаться так, что ее нижний
конец
движется
по
горизонтальной
поверхности
с
постоянной скоростью v , направленной от стенки. В этот же
момент времени жук начинает двигаться вдоль палочки с
постоянной (относительно палочки) скоростью v 1 . Найти
максимальную высоту, на которую жук поднимется над
горизонтальной поверхностью.
Лекция 1. Движение с постоянной скоростью
Пусть прошло время t . Тогда для высоты
подъема жука над поверхностью h(t ) в этот
v1t
момент имеем
h(t )  v 1t sin
где

(1)
- угол между палочкой и горизонтальной
поверхностью.
Из
прямоугольного
h

vt
треугольника,
который
составляют палочка, горизонтальная и вертикальная поверхности,
имеем
cos 
vt
l
(2)
Отсюда
h(t )  v1t 1 (vt / l )2
(3)
Лекция 1. Движение с постоянной скоростью
Дифференцируя функцию (3) по времени, получаем
v1v 2t 2
2
h '(t )  v 1 1  (vt / l ) 
l
2
1  (vt / l )
tmax 
2

v 1(l 2  2v 2t 2 )
l
2
1  (vt / l )
2
l
2v
(4)
(5)
Отсюда
cosmax 
hmax 
1
2
v1l
2v
(6)
(7)
Из формулы (6) следует, что жук оказывается на максимальной
высоте над поверхностью, когда палочка наклонена под углом
45 к поверхности независимо от скоростей палочки и жука.
Лекция 1. Движение с постоянной скоростью
Вектор перемещения тела
точки в конечную
r направлен из начальной
Вектор скорости
r
v
t
Смысл вектора скорости: вектор направлен так, как
и вектор перемещения тела, а его величина (модуль)
равна величине скорости
Лекция 1. Движение с постоянной скоростью
Зависимость координат тела от времени
О
x0
v
x
x  x0  vt

x0
v
О
x0  x  vt
x  x0  vt

x  t   x0  vx t
x
x  x0  vt
Лекция 1. Движение с постоянной скоростью
Зависимость координаты от
времени – линейная, график –
прямая, величина скорости
определяет наклон прямой
x  t   x0  vx t
Пример 6. На рисунках изображены графики зависимости координат четырех тел времени. Какой из графиков соответствует
равномерному движению?
x
x
1.
x
2.
t
x
3.
t
4.
t
t
Лекция 1. Движение с постоянной скоростью
Пример 7. Тело движется вдоль некоторой оси.
x
На рисунке представлен график зависимости
координаты
тела
от
времени.
В
каком
из
t (c )
1
2
3
4
нижеперечисленных интервалов времени величина скорости тела максимальна?
1. От 0 до 1 с
2. От 1 до 2 с
3. От 2 до 3 с
4. От 3 до 4 с
Лекция 1. Движение с постоянной скоростью
Закон сложения скоростей
Перемещение любого тела зависит не только от того, как
движется это тело, но и от наблюдателя.
Например, с одной стороны, мы сейчас покоимся, а с
другой, наблюдатель, сидящий на солнце, увидит, что мы
перемещаемся на 30 км за каждую секунду (скорость
Земли – 30 км/с).
Поэтому и скорость любого тела зависит не только от
тела, но и от наблюдателя (или от системы отсчета).
Лекция 1. Движение с постоянной скоростью
Галилео Галилей (1564-1642). Заложил основы механики,
выдвинул идею об относительности движения, установил
законы инерции, свободного падения, сложения движений.
Сконструировал телескоп с 32-кратным увеличением и
открыл горы на Луне, спутники Юпитера, фазы у Венеры,
пятна на Солнце. Активно защищал гелиоцентрическую
систему мира, за что был подвергнут суду инквизиции (1633).
Этот суд был в значительной степени спровоцирован самим
Галилеем. В попытке убедить церковь, что гелиоцентризм
совместим с католичеством, Галилей написал книгу «Диалог
о двух важнейших системах мира» - нейтральное обсуждение
разных точек зрения на эту проблему. Галилей переоценил
возможности логики, особенно в этом «ведомстве»! С самого
начала судебного преследования речь о казни Галилея не
шла - Галилей был приговорен к отречению от
«еретического» учения и домашнему аресту. Однако по
некоторым сведениям к Галилею во время процесса
применялись пытки (документально это не доказано).
Лекция 1. Движение с постоянной скоростью

v2

v1

rч.о. з.

rп.о. з.

rч.о.п.
rч.о. з.  rп.о. з.  rч.о. з.  rч.о. з.  rп.о. з.
vч.о. з.  vч.о. з.  vп.о. з.

Лекция 1. Движение с постоянной скоростью
Закон сложения скоростей означает, что векторы скорости
тела относительно первой системы отсчета vт.о.1. , относительно второй системы отсчета vт.о.2. и вектор скорости
первой системы относительно второй v1.о.2. образуют треугольник.
vт.о.2.
v1.о.2.
vт.о.1.
Углы этого треугольника – углы между направлениями
скоростей, стороны – значения скоростей.
Лекция 1. Движение с постоянной скоростью
Пример 8. Как закон сложения скоростей связывает друг с другом
скорости: Марса относительно Юпитера - vМ .отн.Ю. , Земли относительно Солнца vЗ.отн.С. , Венеры относительно Нептуна - vВ.отн.Н . ?
1. vМ .отн.Ю.  vЗ.отн.С.  vВ.отн.Н .
2. vМ .отн.Ю.  vЗ.отн.С.  vВ.отн.Н .
3. vМ .отн.Ю.  vЗ.отн.С.  vВ.отн.Н .
4. никак не связывает
Лекция 1. Движение с постоянной скоростью
Пример 9. Два автомобиля движутся по прямому шоссе, направленному с севера на юг. Первый автомобиль движется на юг со
скоростью v , второй – на север со скоростью 2v . Чему равна скорость второго автомобиля относительно первого?
1. v , направлена на юг
2. v , направлена на север
3. 3v , направлена на юг
4. 3v , направлена на север
v2 v2.o.1.
v2
v2  v2.o.1.  v1  v1  v2.o.1.
v1
v1
Лекция 1. Движение с постоянной скоростью
Пример 10. Поезд едет со скоростью v1 . В поезде перпендикулярно направлению его движения идет человек со скоростью v2 . Чему
равна скорость человека относительно земли?
1. v1  v2
2. v1  v2
3. v12  v22
4. v12  v22
vч.о. з.  v2  v1
v1
v2
vч.о. з.
Лекция 1. Движение с постоянной скоростью
Пример 11. Как закон сложения скоростей связывает друг с другом скорости: Марса относительно Юпитера - vМ .отн.Ю. , Юпитера
относительно Солнца v Ю .отн .С . , Солнца относительно Марса vС .отн.М . ?
1. vМ .отн.Ю.  vС .отн.М .  v Ю.отн.С .
2. vМ .отн.Ю.  vС .отн.М .  v Ю.отн.С .
3. vМ .отн.Ю.  vС .отн.М .  v Ю.отн.С .
4. никак не связывает
Если бы были даны скорости:
Марса относительно Юпитера,
Марса относительно Солнца
vМ .отн.Ю.  vМ .отн.С.  vС.отн.Ю.
и Солнца относительно Марса, то
Но
vМ .отн.С.  vС.отн.М .
и
vЮ.отн.С.  vС.отн.Ю.
Лекция 1. Движение с постоянной скоростью
Пример 12. Поезд движется на север со скоростью v . Пассажиру вертолета, пролетающего над поездом, кажется, что поезд движется на северо-запад под углом  к меридиану со
скоростью u . Найти величину скорости вертолета относительно земли.
Лекция 1. Движение с постоянной скоростью
v - это скорость поезда относительно земли
u - это скорость поезда относительно вертолета
v1
v  u  v1
где v 1 - искомая скорость вертолета относительно земли. Из
треугольника сложения скоростей по теореме косинусов находим
скорость вертолета относительно земли
v1  v 2  u 2  2uv cos 
u

v
Лекция 1. Движение с постоянной скоростью
Пример 13. Два катера, идущие вниз по реке с разными скоростями, одновременно обогнали плывущий по течению плот. Затем через одно и то же время катера повернули назад и поплыли с прежними относительно воды скоростями. Какой из катеров – быстрый
или медленный – раньше встретит плот?
1. Быстрый
2. Медленный
3. Одновременно
4. Мало информации для ответа
Лекция 1. Движение с постоянной скоростью
Если бы движение катеров и плота происходило в озере,
то тогда катера вернулись бы назад одновременно!
l1  v1t
l2  v2t
l1 v1t
t1  
t
v1 v1
l2 v 2 t
t2 

t
v2 v2
t1  t2
Но картина движения катеров и плота такая же, как в
озере, в системе отчета, связанной с водой. Поэтому
и в реке вернутся одновременно
Лекция 1. Движение с постоянной скоростью
Пример 14. Лодка переправляется через реку. Как лодка должна
плыть, чтобы переправиться на другой берег за минимальное
время?
Лекция 1. Движение с постоянной скоростью
Время переправы минимально, если вектор скорости лодки относительно воды направлен перu
пендикулярно берегу. Треугольник скоростей для
такого движения лодки приведен на рисунке. Из
v

v1
этого треугольника видно, что в системе отсчета,
связанной с землей, траектория наибыстрейшей переправы лежит
под углом
v 
 
  arctg   .
u